Evolution in Stage-Structured Populations

Abstract

For many organisms, stage is a better predictor of demographic rates than age. Yet no general theoretical framework exists for understanding or predicting evolution in stage-structured populations. Here, we provide a general modeling approach that can be used to predict evolution and demography of stage-structured populations. This advances our ability to understand evolution in stage-structured populations to a level previously available only for populations structured by age. We use this framework to provide the first rigorous proof that Lande’s theorem, which relates adaptive evolution to population growth, applies to stage-classified populations, assuming only normality and that evolution is slow relative to population dynamics. We extend this theorem to allow for different means or variances among stages. Our next major result is the formulation of Price’s theorem, a fundamental law of evolution, for stage-structured populations. In addition, we use data from Trillium grandiflorum to demonstrate how our models can be applied to a real-world population and thereby show their practical potential to generate accurate projections of evolutionary and population dynamics. Finally, we use our framework to compare rates of evolution in age- versus stage-structured populations, which shows how our methods can yield biological insights about evolution in stage-structured populations.

Evolution occurs when organisms exhibit differences in the vital rates of birth, death, and dispersal that are at least partly heritable. The best-developed body of evolutionary theory that accounts for interindividual variability in vital rates is for age-structured populations (e.g., Lande 1982a, 1982b; Charlesworth 1994). Yet in many species, age (time since birth) is not the best index for characterizing individual variation in demography. Many factors other than age, such as sex, body size, location, developmental stage, the magnitude of nutritional reserves, and measures of physiological condition, can be better predictors of birth and death than is age alone. As a concrete example—and indeed a motivation for this study—Trillium grandiflorum (Melanthiaceae) is a perennial, nonclonal herb that occupies mature forest in the deciduous biome of eastern North America. After reproduction, seeds germinate in their first year, then pass through a number of stages, each defined by the number and sizes of leaves, before reaching the reproductive stage (Knight 2004). It is not uncommon for an individual to live in, say, a three-leaf stage for some years, before becoming reproductive. Reproductive individuals can also regress to previous stages, particularly after being damaged by deer herbivory. Because this damage is correlated with flowering time, declining as the growing season progresses, within each season there is a component of selection in favor of later-flowering plants.

Evolutionary biologists who seek to predict adaptive evolution in species like Trillium, where vital rates depend primarily on stage, lack an established general framework for doing so comparable to the one available for age-structured populations (e.g., Charlesworth 1994). It is not known whether approaches developed for age structure will be valid for more general kinds of population structure. Indeed, describing evolutionary dynamics in stage-structured populations poses a major challenge not present for populations structured solely by age, since in stage-structured populations any given stage might at any time contain a mixture of cohorts of different ages, each of which could have a different history of selection.

Even if a general framework were available for studying evolution in stage-classified populations, its complexity might present a major obstacle to its utility for evolutionary biologists, due to “the difficulty of providing concise descriptions of evolutionary dynamics with these models” (Charlesworth 1994, p. 11). Moreover, some of the most basic tenets of evolutionary biology that are known to be valid with age structure have yet to be firmly established for stage structure. This lack of progress not only inhibits evolutionary biologists from applying stage-structured methods but also undermines the conceptual grounding of stage-structured population evolution within presumably general theories of evolution.

These considerations suggest that there is a serious need in evolutionary biology for a general, practical, and sound understanding of how evolutionary processes operate in stage-structured populations. It is equally important to understand how such processes relate to well-known evolutionary principles. To these ends, we focus here on three main objectives. First, we seek a general set of tools that can be used to model evolution by natural selection in any stage-structured population. Second, we assess whether Lande’s theorem (Lande 1976, 1979, 1982a, 1982b) holds for generally structured populations. Third, we derive a version of Price’s theorem (Price 1970) that applies to stage-classified populations. We also demonstrate the use of the general model and simplifications of it to a real population of Trillium and a hypothetical population with only two stages and then use our results to develop biological insights about rates and directions of evolution in age- versus stage-structured populations.

A General Model

We first describe how to construct a completely general discrete-time model of stage-structured population dynamics and evolution, assuming the population includes a number of discrete stages. The model tracks changes over time in both the population sizes and the joint probability density functions (PDFs) of genotypes and phenotypes for all stages. Selection could act on any set of stages through the stage-dependent vital rates, which can in turn be functions of a multivariate phenotype denoted by the vector z. The model we consider is completely general in that it permits transitions between any pair of stages, reproduction by any stage, and newborns in any stage.

The modeling framework we present focuses on evolution over single time steps (which we will generically call years) and so pertains directly to short-term analyses of populations living in variable environments or with density dependence. Making predictions about long-term evolution using this short-term framework, of course, requires one to make assumptions about variation in transitions through time owing to both environmental change and changes in population size and structure (e.g., if there is density dependence) and about sources of genetic variation such as mutation.

We also assume that numbers are large enough to ignore demographic stochasticity. Density dependence and stochasticity are important and realistic complications, but the framework we present here provides a necessary step for future extensions that directly explore the impact of such factors on evolution in stage-structured populations.

Let z p (z₁, z₂, …, z_m)^T represent a multivariate quantitative trait whose components are expressed in specific stages. Our framework extends beyond quantitative traits and can be used to describe allele and genotype frequency dynamics in stage-structured populations by letting z indicate allele or genotype content (e.g., Rice 2004). Let z = g + e, where g is the additive genetic (i.e., breeding) value and e is the nonadditive genetic value plus an environmental deviation (e.g., developmental noise).We also assume that, at birth (before selection), g and e are uncorrelated and the expected value of e is 0. Our model follows, at each time step and for each stage i, the number of individuals N_i and the joint PDF of g and z, denoted p_i(g, z).

An individual in stage j can contribute to stage i in the next year in two distinct ways: via reproduction or by making a direct transition. Direct transitions can include retention of individuals in a given stage, growth to a higher stage or regression to a lower stage. Let t_ij(z) be the probability of a direct transition (survival and retention, growth, or regression) to stage i in the next year from stage j in the current year, and let f_ij(z) be the number of surviving offspring in stage i the next year produced by an individual in stage j in the current year. Denote the total transition rate as a_ij (z) = t_ij (z) + f_ij (z). Our notation emphasizes that stage-specific transition probabilities and fertilities may depend on an individual’s phenotype z. Consideration of our general framework stresses that empirical information about how stage-dependent vital rates (direct transitions and reproduction) are determined by traits of interest is required for accurate projections of adaptive evolution in real populations. A real-world application is discussed below.

We begin by describing how abundances in each stage change through transition and reproduction over a time step. The average transition probability to stage i and fertility to stage i of a stage j individual are, respectively,

$${\overline{t}}_{ij}=\int \int t_{ij}(\mathbf{z})p_j(\mathbf{g},\mathbf{z})d\mathbf{z}d\mathbf{g},$$ (1)

$${\overline{f}}_{ij}=\int \int f_{ij}(\mathbf{z})p_j(\mathbf{g},\mathbf{z})d\mathbf{z}d\mathbf{g},$$ (2)

where the integrals are evaluated over all values of the vectors g and z. The number of current individuals that transition directly to i in the next year is $T_i^{\prime }={\sum }_j{\overline{t}}_{ij}{N}_j$, whereas the number of the next year’s newborns that begin in stage i is $F_i^{\prime }={\sum }_j{\overline{f}}_{ij}{N}_j$. Summing these contributions gives the total abundance of individuals in stage i next year:

$$N_i^{\prime }=T_i^{\prime }+F_i^{\prime }=\sum _j({\overline{t}}_{ij}+{\overline{f}}_{ij})N_j=\sum _j{ā}_{ij}{N}_j.$$ (3)

This shows that the population dynamics can be projected using a Lefkovitch matrix with ijth element equal to ā_ij = t̄_ij + f̄_ij (see Caswell 2001, chap. 5). The total population size in the next year is the sum of equation (3) over all stages: $N\prime ={\sum }_i{N}_i^{\prime }={\sum }_i{\sum }_j{\overline{a}}_{ij}{N}_j$.

Derivation of the change in the joint probability density function p_i (g, z) is considerably more involved than for N_i, and we relegate most of the details to appendix A. The reasoning there shows that the joint PDF of genotype and phenotype in stage i at the next time step is

$$p_i^{\prime }(\mathbf{g},\mathbf{z})={\theta }_i(\mathbf{g},\mathbf{z})\frac{T_i^{\prime }}{N_i^{\prime }}+{\varphi }_i(\mathbf{g},\mathbf{z})\frac{F_i^{\prime }}{N_i^{\prime }},$$ (4)

where $F_i^{\prime },T_i^{\prime }$, and $N_i^{\prime }$ are as defined above. The function θ_i (g, z) is the joint PDF of g and z of all individuals that transition directly to stage i (see eq. [A1]). This is weighted by $T_i^{\prime }/N_i^{\prime }$, the fraction of stage i individuals in the next year that reach that stage through direct transition. The second part of the sum in equation (4) describes contributions to the class i PDF via reproduction. The factor ϕ_i(g, z) is the joint PDF of genotypes and phenotypes among newborns in class i (eq. [A5]). The weighting factor $F_i^{\prime }/N_i^{\prime }$ is the proportion of stage i individuals next year that are newly born. The specific form of ϕ_i(g, z) depends on the genetic basis of inheritance, mating scheme, distribution of the environmental component of phenotype among offspring, and so forth. In appendix A, we derive ϕ_i(g, z) for a particular case with random mating, namely, the infinitesimal model of inheritance (Fisher 1918; Bulmer 1971) with a normally distributed environmental component. However, the above machinery applies much more broadly.

Taken together, recursions (3) and (4) provide a general model for projecting adaptive evolution in a stage-structured population. The framework does not require the population to have reached any particular state, such as a stable stage distribution (SSD), and with additional assumptions, it could be extended (along the lines, say, described in Caswell 2001) to accommodate more complex population dynamics, such as density dependence or variable environments. Moreover, as indicated in appendix A, the framework can be adapted to any genetic basis or mating system. We do not pursue such extensions here; rather, we illustrate the practical application of our approach below by using data from a real-world system (the Trillium study mentioned in the introduction). In the process, we also assess the accuracy of our approach by comparing its predictions to results generated by individual-based simulations.

The modeling framework developed in this section is completely general and provides a well-defined approach to developing accurate predictions of both short- and long-term evolutionary change in stage-classified populations. The approach is, however, sufficiently complex that it is not immediately apparent how—or even if—evolution in stage-structured populations can be related to important evolutionary concepts familiar from consideration of far simpler populations. In the next section, we demonstrate how one such result, Lande’s theorem, emerges from our general stage-classified modeling framework.

Lande’s Theorem

Lande’s theorem relates the rate of adaptive evolution of quantitative traits to the rate of population growth. It reveals a clear, simple link between evolutionary dynamics and demography. Although Lande (1982a, 1982b) showed that this striking result holds for populations classified by age, it has never been clear whether it applies to populations with other sorts of structure, such as those classified by developmental stage, body size, or spatial location. The goal of this section is to apply to stage-structured populations the assumptions required of Lande’s theorem and rigorously answer this question.

Lande’s theorem, in both its original and generalized forms (Lande 1976, 1979, 1982a, 1982b), assumes that breeding values and phenotypes have a joint normal distribution (Falconer and MacKay 1996; Lynch and Walsh 1998). This assumption is, strictly speaking, dubious (though perfectly reasonable as a starting point). It is more doubtful for stage-structured populations since even if distributions in stages and among newborns were normal in one year, the stage-specific distributions the next year, being mixtures of different normal distributions, would generally deviate from normality. Despite the added scope for violating assumptions of normality, we assume it applies in our modeling framework in an effort to derive a version of Lande’s theorem for stage-structured populations. Using the Trillium case study mentioned above (Knight et al. 2008), we show later that the normal-based simplification of our general model is capable of providing surprisingly accurate approximations of evolutionary and population dynamics in a situation where one might expect that the normality assumption would break down.

Assume that the joint genotype-phenotype distribution in stage j is Gaussian (normal), with means ḡ_j and z̄_j and correlation matrices G_j and P_j, and that the additive-genetic and nonadditive (environmental) components of the phenotype are uncorrelated. The genotype of an offspring is the average of the genotypes of its parents. Using these assumptions and definitions in equations (3) and (4), the stage i genotypic mean in the next year is

$${\mathbf{ḡ}}_i^{\prime }=\int \int \mathbf{g}{p}_i^{\prime }(\mathbf{g},\mathbf{z})d\mathbf{g}d\mathbf{z}=\frac{{\sum }_j{N}_j\int a_{ij}(\mathbf{z})\int \mathbf{g}{p}_j(\mathbf{g},\mathbf{z})d\mathbf{g}d\mathbf{z}}{N_i^{\prime }}=\sum _j{c}_{ij}{\mathbf{ḡ}}_j+\sum _j{c}_{ij}{\mathbf{G}}_j{\nabla }_{{\overline{\mathbf{z}}}_j}\text{ln }{ā}_{ij},$$ (5)

where $c_{ij}=N_j{\overline{a}}_{ij}/N_i^{\prime }$ is the fraction of individuals in stage i in the next year contributed by stage j. The last equation in (5) is obtained using integration by parts for the integration with respect to phenotype z. Overbars indicate expected values over the distribution of stage j, and ∇_z̄j = (∂/∂z̄₁, ∂/∂z̄₂, …, ∂/∂z̄_m)^T is the gradient operator with respect to trait means evaluated at z̄_j, the multivariate mean phenotype of stage j. The first sum in the last line of equation (5) is a weighted average of stage-specific mean genotypes contributing to stage i. The second sum describes the combined effects of selection.

The mean phenotype in the next year is determined by separate terms for direct transitions and for births, since with reproduction, the environmental component of the phenotype is assumed to be reset. The phenotypic recursion is

$${\overline{\mathbf{z}}}_i^{\prime }=\int \int \mathbf{z}{p}_i^{\prime }(\mathbf{g},\mathbf{z})d\mathbf{g}d\mathbf{z}=\frac{T_i^{\prime }\int \int \mathbf{z}{\theta }_i(\mathbf{g},\mathbf{z})d\mathbf{g}d\mathbf{z}+F_i^{\prime }\int \int \mathbf{z}\varphi (\mathbf{g},\mathbf{z})d\mathbf{g}d\mathbf{z}}{N_i^{\prime }}=\sum _j[c_{ij}^t{\overline{\mathbf{z}}}_j+c_{ij}^f{\mathbf{ḡ}}_j+c_{ij}({\mathbf{P}}_j{\nabla }_{{\overline{\mathbf{z}}}_j}{\overline{t}}_{ij}+{\mathbf{G}}_j{\nabla }_{{\overline{\mathbf{z}}}_j}{\overline{f}}_{ij})],$$ (6)

where $c_{ij}^t=N_j{\overline{t}}_{ij}/N_i^{\prime }$ and $c_{ij}^t=N_j{\overline{t}}_{ij}/N_i^{\prime }$ are the relative contributions to stage i by stage j through direct transition and reproduction, respectively. Note that $c_{ij}=c_{ij}^t+c_{ij}^f$.

Lande’s theorem for age-structured populations (Lande 1982a, 1982b) states that the mean phenotype eventually evolves at the same rate Δz̄ = z̄′ − z̄ at each age and that this shared asymptotic rate is

$$\mathrm{\Delta }\overline{\mathbf{z}}=\mathbf{G}{\nabla }_{\overline{\mathbf{z}}}\text{ln }\overline{\lambda },$$ (7)

where G is the additive-genetic covariance matrix for the characters z and is the geometric growth rate of the λ̄ population at the stable age distribution based on a Leslie projection matrix with vital rates averaged over the phenotypic distribution. Equation (7) shows that the change in the trait mean depends on the amount of heritable variation (G) and on the effect of a change in the trait on fitness (the gradient term). Besides multivariate normality, this result assumes selection is weak and evolution is slow relative to population dynamics.

In appendix B, we consider the same assumptions for a stage-classified population whose population dynamics are described by the Lefkovitch matrix Ā with elements ā_ij—the average values a_ij = t_ij + f_ij—and with the evolutionary dynamics of equations (5) and (6). We prove there that the asymptotic rate of evolution Δz̄ is the same for all stages, even if phenotypic means z̄_i and additive-covariance matrices G_j differ among stages. This shared rate of evolution is

$$\mathrm{\Delta }\overline{\mathbf{z}}=\frac{1}{\overline{\lambda }}\sum _{i,j}{v}_i{w}_j{\mathbf{G}}_j{\nabla }_{{\overline{\mathbf{z}}}_j}{ā}_{ij},$$ (8)

where is the population growth rate at the stable stage λ̄ distribution for Ā. The vector w = {w_i} describes the stable population structure, and v = {v_i} is the set of stage-specific reproductive values normalized so that v^Tw = 1. Moreover, if every class has the same mean z̄ and additive-genetic variance G, then the arguments in appendix B show that equation (8) collapses to Lande’s equation (7). To our knowledge, this is the first rigorous demonstration that Lande’s theorem is valid for stage-classified populations. Indeed, our proof shows it applies to any such population—including those that have multiple newborn and parental classes.

Application to a Real-World Case

We now illustrate the practical application of our general model (eqq. [3], [4]), normal approximations (eqq. [5], [6]), and the stage-structured version of Lande’s equation (7) to an empirical setting. Knight (2003, 2004) studied populations of Trillium grandiflorum declining due to increased deer herbivory on flowering plants. Consumed plants lose aboveground tissues but can survive and resprout from underground tissue. However, they do not reproduce in the year of consumption and have an increased probability of regressing to a nonreproductive stage the next year. The probability of browsing on a plant was higher for earlier-flowering plants and 0 for late-flowering plants. Knight et al. (2008) examined the evolution of flowering time in response to deer herbivory to discern whether selection could act rapidly and effectively enough to rescue populations from extinction. Here we show how the general and approximate modeling frameworks developed here can be used to address this issue.

The demographic model for Trillium includes six stages, the first being germinants and the last reproductive plants. Higher values of the phenotype z (flowering time in days) increase fecundity and reduce the probability of reproductive-stage regression (because of lower browsing). The matrix of phenotype-dependent vital rates, a_ij (z), is

$$\left[\begin{array}{cccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill \text{min }(2.291+0.587z,9.468)\hfill \\ \hfill 0.11\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0.33\hfill & \hfill 0.65\hfill & \hfill 0.04\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0.15\hfill & \hfill 0.84\hfill & \hfill 0.20\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.10\hfill & \hfill 0.64\hfill & \hfill \text{max }(0.5763-0.0291z,0.22)\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0.16\hfill & \hfill \text{min }(0.4237+0.0291z,0.78)\hfill \end{array}\right].$$ (9)

Element a₁₆ represents reproduction, and all other elements are direct transitions. Browsing as a function of flowering time was fitted using linear regression, giving 0.758 − 0.062z. This was used until it reached 0 at a flowering time of about z = 12.23 days, beyond which browsing was assumed to cease (causing the three elements in the right column of eq. [9], which depend on flowering time, to become constant). For the population represented by this matrix of vital rates, the measured distribution of flowering time z (of reproductive plants) had a mean of z̄ = 7.6 days and variance P = 10.543 days². We do not know the additive-genetic variance G for flowering time, so we projected dynamics using four assumed heritabilities h² = G/P.

We predicted evolution of mean flowering time z̄ (averaged over all stages) and dynamics of total density $N={\sum }_{i=1}^6{N}_i$ using four approaches: the general joint probability density function method (JPDF; eqq. [3], [4]), the Gaussian approximation (eqq. [5], [6]) with fixed variances but without the assumption that evolution is slow relative to population dynamics, Lande’s theorem (eq. [7]), and an individual-based model (IBM; see Knight et al. 2008 for details of this model). In the IBM, each individual is simulated, along with its genetics, with probabilities of each transition and fecundity given by the vital rate matrix (9). One hundred populations were simulated for each heritability with the IBM and the results averaged for all realizations that did not become extinct. The IBM approach incorporates many kinds of stochasticity in development, reproduction, inheritance, and death, unlike the other three approaches, which are all deterministic. The distributions of genotypes and phenotypes in the IBM and JPDF are not constrained to be Gaussian.

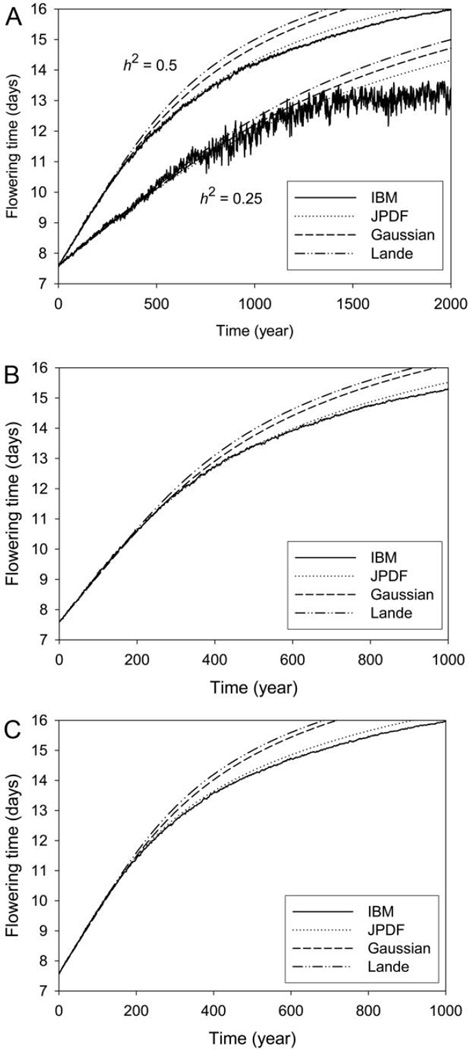
We compared the evolution of flowering time for this system using these four methods and four different heritabilities (fig. 1). All methods agreed quite well for the first several hundred years. Overall, the JPDF approach agrees very well with the IBM, except for rather late in the evolution at the lowest heritability (h² = 0.25; fig. 1A). Only for this heritability did extinctions occur in the IBM. Populations in the deterministic methods can approach arbitrarily close to zero abundance but do not become extinct; this limitation may account for the slightly more rapid evolution with the IBM seen up until about year 600 because only populations that persisted are depicted, and these would tend to have evolved faster than those that did not. The evolutionary plateau in the IBM for the lowest heritability (h² = 0.25; fig. 1A) may reflect depleted genetic variation due to selection and drift (these populations plummeted to low numbers; see fig. 2A). Where results differ among models, the deterministic methods all tend to evolve faster than the IBM, especially those based on Gaussian assumptions with fixed variances. Phenotypic variances from the IBM showed an initial increase followed by a significant decrease as selection removed genetic variation (see fig. 3). Thus, methods based on fixed variances would naturally be expected to evolve faster than the IBM. The JPDF method does not assume fixed variances and so can model variance depletion by selection; its evolution slows in a pattern similar to that of the IBM, although not quite as much. (Note that the JPDF accounts for non-normal distributions but not processes such as drift.)

Figure 1.

Evolution of mean flowering time (averaged over all stages), as predicted by four models of evolution for the Trillium system. A, Heritabilities (h²) of 0.25 and 0.5. B, h² = 0.75. C, h² = 1. Note the different scales on the abscissa. The other parameters used are described in the main text and are assumed to be the same for all models. JPDF (joint probability density function) corresponds to equations (1)–(4), Gaussian denotes equations (5) and (6), Lande denotes equation (7), and IBM (individual-based model) denotes the individual-based model (100 realizations were run, and the averages calculated over all populations that persisted).

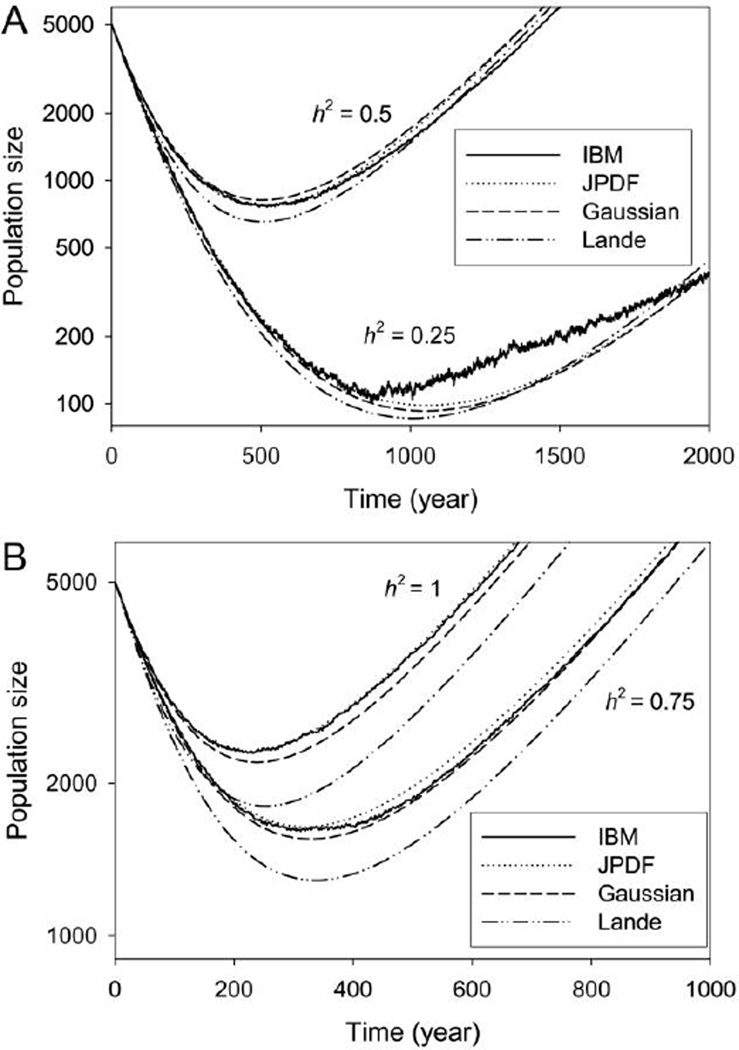
Figure 2.

Population dynamics for the four models of Trillium evolution, assuming an initial population of 5,000. Same notation and parameters as in figure 1. Geometric mean population size was used for the IBM (individual-based model). Note the logarithmic ordinate scale. A, h² = 0.25 and 0.5. B, h² = 0.75 and 1. JPDF = joint probability density function.

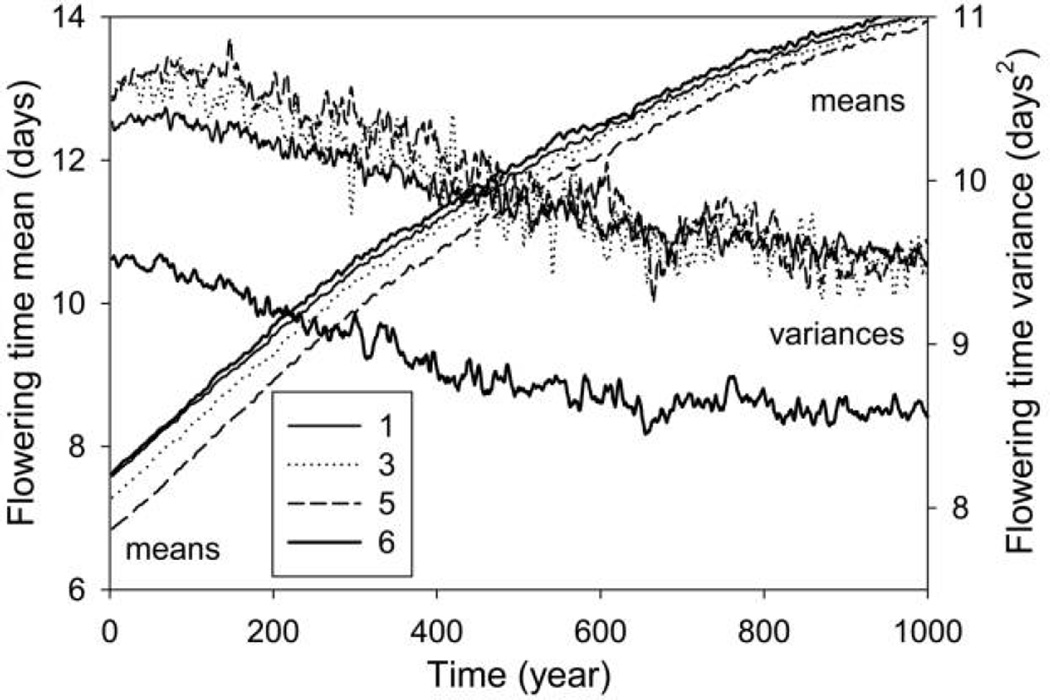
Figure 3.

Stage-specific phenotypic means and variances for flowering time in stages 1, 3, 5, and 6 (indicated by the key) from the IBM (individual-based model) for h² = 0.5 (averages over 100 runs). For clarity, values have been smoothed using a 5-year moving average, and stages 2 (similar to stage 1) and 4 (similar to 5) have been omitted. The bold lines are for stage 6.

Figure 2 shows corresponding trajectories for total abundance. It is intriguing that while Lande’s equation gives faster evolution than the other methods, it also predicts deeper declines in population. As far as population size projection is concerned, the Gaussian approximation is expected to be very similar to Lande’s equation: both use a transition matrix with each element averaged over an assumed normal phenotypic distribution. The difference is that Lande’s equation (as we have applied it) projects population size using the dominant eigenvalue of the average transition matrix, whereas the Gaussian method tracks abundance of each stage separately. That is, our implementation of Lande’s equation assumes a stable stage distribution each generation, whereas the Gaussian method does not. For this example, deviations from the SSD or from the normal approximations that emerge as selection takes place do not seem to have a strong quantitative effect on the rate of evolution or changes in population size. Taken together, these results support the validity and accuracy of our general JPDF modeling framework (indeed, the dynamics it predicted are almost identical to those in the IBM) and show that for this system, simpler approximations that assume normality work reasonably well.

Only the overall average flowering time is shown in figure 1, but the JPDF, Gaussian, and IBM methods also describe evolution of mean flowering time for each stage. These stage-specific evolutionary trajectories share the same general shape as the overall average (cf. figs. 1, 3), with some stages consistently higher (stages 1, 2, and 6), some lower (stages 4 and 5), and one about the same (stage 3) as the average. That pattern remains throughout, with the curves slowly converging with time (fig. 3). This convergence is probably due in part to the fact that over time, more individuals flower late enough to completely avoid browsing and, thus, avoid further selection. For the IBM, there is also a reduction of genetic variance, which is greatest for the reproductive stage (stage 6; bold lines in fig. 3) targeted by selection. Therefore, this stage evolves somewhat slower than do the others, and since its phenotype is higher than average, this contributes to the slow convergence.

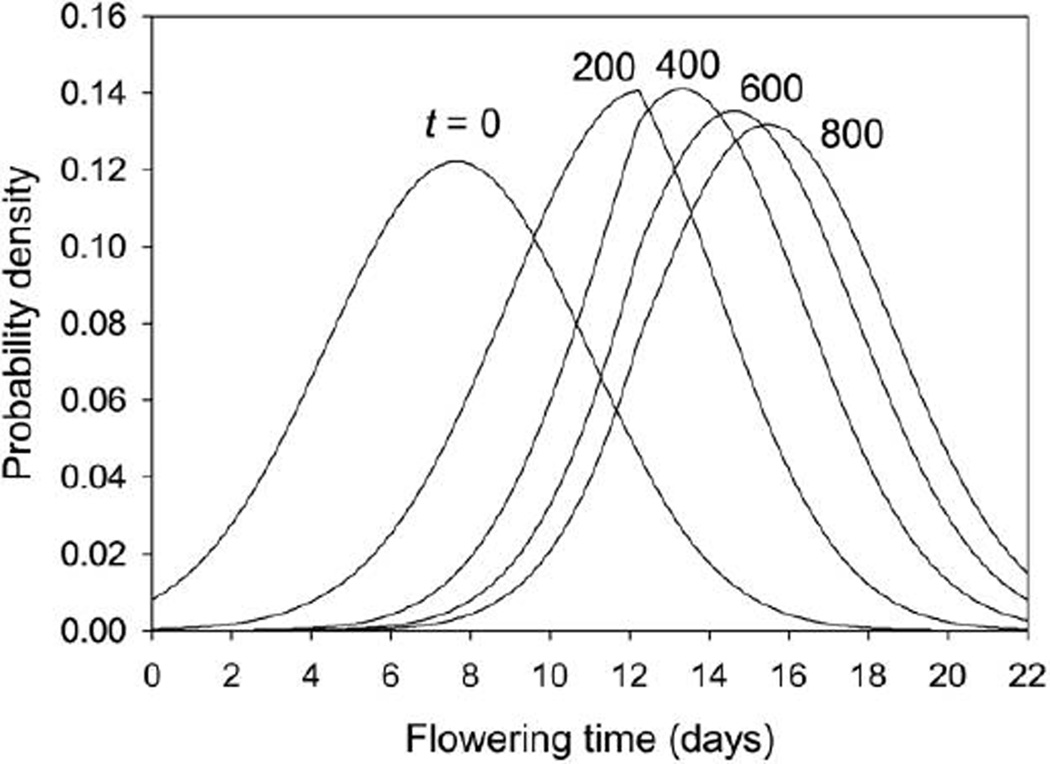
The JPDF method allows one to project evolution of the entire probability density function for the flowering-time phenotype, including evolved departures from normality. In this example, the initial distribution was Gaussian and, as the population evolved, the flowering-time distribution became right skewed (fig. 4). Notice too the kink that evolves in the distribution function at 12.23 days (the zero-browsing threshold). It is impossible to predict the evolution of such detailed features using the Gaussian approximation or Lande’s theorem for stage-classified populations.

Figure 4.

Probability density functions of the phenotype for the joint probability density function model for h² = 1 at 0, 200, 400, 600, and 800 years (from left to right).

Application to a Conceptual Question

The Trillium example demonstrates the practicality and versatility of both our general and approximate modeling frameworks for predicting the joint evolution and population dynamics of real-world stage-structured populations. Our methods can also be used to develop conceptual insights related to stage structure per se, as we illustrate now.

The basic question we consider is how does repeating a stage affect adaptation rates? For simplicity and clarity, we examine this issue by applying our extension of Lande’s theorem (eq. [8]) to a simple system, consisting of a pair of populations with different two-stage life histories. One might, for instance, imagine desert plants with two classes: seed and adult. One population is age structured, with juveniles that mature into adults in a year (or die), and adults that produce offspring and then die. The other population is identical, except that individuals can stay in the juvenile stage for multiple years (e.g., a desert plant might have a seed bank with long-lived seeds and delayed germination; a similar analysis could allow individuals to remain as adults for multiple years). For both populations, f₁₁ = f₂₁ = f₂₂ = t₁₂ = t₂₂ = 0, and the Lefkovitch matrix Ā contains elements ā₁₁ = t̄₁₁, ā₁₂ = f̄₁₂, ā₂₁ = t̄₂₁, and ā₂₂ = 0.We focus on the evolution of a simple quantitative trait z with mean z̄ that may affect one or more of these vital rates. (All derivations are provided in app. C in the online edition of the American Naturalist.)

Consider first the age-structured population (t̄₁₁ = 0 making Ā a Leslie matrix). In this case, the asymptotic growth rate of the population is λ̄_age = (f̄₁₂t̄₂₁)^1/2. The rate of adaptive evolution in this population, as derived in appendix C (eq. [C6]), is

$$\mathrm{\Delta }{\overline{z}}_{\text{age}}=\frac{1}{2}(G_1\frac{d\mathrm{ ln }{\overline{t}}_{21}}{d{\overline{z}}_1}+G_2\frac{d\mathrm{ ln }{\overline{f}}_{12}}{d{\overline{z}}_2}).$$ (10)

The notation d/dz̄_i indicates the derivative with respect to z̄ is evaluated at z̄_i

Compare these rates for an age-structured population to those of a stage-structured population for which the first stage can be repeated (t̄₁₁ > 0). The stage-structured population grows asymptotically at rate ${\overline{\lambda }}_{\text{stage}}=[{\overline{t}}_{11}+{({\overline{t}}_{11}^2+4{\overline{f}}_{12}{\overline{t}}_{21})}^{1/2}]/2$ and, as derived in appendix C (eq. [C8]), evolves at rate

$$\mathrm{\Delta }{\overline{z}}_{\text{stage}}=\frac{2{\overline{\lambda }}_{\text{age}}^2}{{\overline{\lambda }}_{\text{age}}^2+{\overline{\lambda }}_{\text{stage}}^2}(\frac{{\overline{t}}_{11}{\overline{\lambda }}_{\text{stage}}}{2{\overline{\lambda }}_{\text{age}}^2}{G}_1\frac{d\text{ ln }{\overline{t}}_{11}}{d{\overline{z}}_1}+\mathrm{\Delta }{\overline{z}}_{\text{age}}).$$ (11)

Observe that λ̄_stage > λ̄_age, which means the stage-structured population will grow faster than a comparable age-structured one (because of increased juvenile survival). It also implies that the factor in front of the parentheses is less than 1.

If the focal trait z has no effect on the probability of repeating the first stage, then dt̄₁₁/dz̄₁ = 0 and the first term inside the parentheses of equation (11) is 0. Since the leading factor is positive and less than 1, allowing retention in the first stage slows the rate of evolution without changing its direction compared with the rate in an age-structured population, all else being equal. (If we include t̄₁₁ but reduce the maturation rate t̄₂₁ by an equal amount [so stage 1 survival stays the same], then the same framework shows that evolution is still slowed [as is population growth] when dt̄₁₁/dz̄₁ = 0.)

If the focal trait does influence the probability a stage 1 individual survives and remains in that stage from one time step to the next (i.e., d ln t̄₁₁/dz̄₁ ≠ 0), then equation (11) shows that repetition of the first stage could accelerate, slow, or even reverse the direction of evolution relative to the comparable age-structured population. Stage- and age-structured populations would have opposite evolutionary directions if the magnitude of d ln t̄₁₁/dz̄₁ were large enough and its sign opposite to that of Δz̄_age, the direction of evolution in the age-structured population. Biologically, such a reversal might occur for a trait z, such as seed coat thickness, which might tend to be reduced if there is no seed bank but would be increased in a species with a seed bank if thicker coats give much higher seed survival. A similar analysis could be used to analyze the impacts of repeating the second stage. This could be relevant, for instance, to a plant with a perennial adult class but seeds that either germinate and become adults or die at each time step.

Price’s Theorem

In this section we show how evolution in stage-structured populations can be related to a simple, universal law of evolution, Price’s theorem (Price 1970), which provides a general statement about any evolutionary system—including a stage-structured one. Originally, Price’s equation was applied mainly to the levels-of-selection issue (e.g., Frank 1998; see Leigh 2010 for an overview), but it has recently begun to be applied to a wide range of evolutionary and ecological issues, including evolutionary epidemiology (Day and Gandon 2006) and even community and ecosystem ecology (e.g., Fox and Harpole 2008). Coulson and Tuljapurkar (2008) developed an age-structured Price equation, which has been used to draw interesting insights about stasis and change in body size of the red deer of Rhum (Coulson and Tuljapurkar 2008), the Soay sheep of St. Kilda (Ozgul et al. 2009), and yellow-bellied marmots in Colorado (Ozgul et al. 2010).

Here, we briefly remind the reader of Price’s theorem for a univariate trait in an unstructured population and then show how one can write a Price equation for a stage-structured population. To complement this derivation, we show in appendix D in the online edition of the American Naturalist how a Price equation can be derived directly from the recursions of the general joint PDF method (eqq. [3], [4]). This alternative derivation could be useful for instance in examining complicated mating systems and selection regimes.

Price’s equation for the change in a univariate trait over a single time step is (e.g., Rice 2004)

$$\mathrm{\Delta }\overline{z}=\frac{\text{Cov }(z,w)}{\overline{w}}+\frac{\text{Cov }(d,w)}{\overline{w}}+\overline{d},$$ (12)

where z is the phenotype of a “parent,” w is the number of its “offspring,” d is the average deviation of its offspring’s phenotypes from its own, and z̄, w̄, and d̄ are the respective averages of z, w, and d over all parents. Note that “parent” and “offspring” can be broadly defined such that an individual is treated as an offspring of itself. The deviation d can have a genetic basis or result from phenotypic plasticity or other factors such as maternal effects.

We obtain a stage-structured version of Price’s equation by applying the law of total covariance (a straightforward extension of the law of total variance or the conditional variance formula; e.g., Weiss 2005) to equation (12): Cov (X, Y) = Cov [E(X|V), E(Y|V)] + E[Cov (X, Y|V)], where X and Y are random variables and V is a given condition. Applying this law to the covariance terms in equation (12) and conditioning on stage directly yields the general (univariate) stage-structured form of Price’s equation:

$$\mathrm{\Delta }\overline{z}=\frac{\text{Cov }({\overline{z}}_j,{\overline{w}}_j)}{\overline{w}}+\frac{\text{Cov }({\overline{d}}_j,{\overline{w}}_j)}{\overline{w}}+\frac{\mathrm{E}[{\text{Cov}}_j(z,w)]}{\overline{w}}+\frac{\mathrm{E}[{\text{Cov}}_j(d,w)]}{\overline{w}}+\mathrm{E}({\overline{d}}_j),$$ (13)

where Cov_j (z, w) is the covariance between parental phenotype z and fitness w in stage j, Cov_j (d, w) is the covariance between d and w for parents in stage j, and z̄_j, w̄_j, and d̄_j are the respective averages of z, w, and d over all parents in stage j. Unsubscripted operators Cov and E are computed over stages. Here, we define parent and offspring to include the results of direct transitions as well as actual births (so if an individual changes from stage j to stage i, it is treated as a stage j individual giving rise to an offspring in stage i). It can be shown that Coulson and Tuljapurkar’s (2008) age-structured version of Price’s equation is a special case of equation (13), as is Taylor’s (1990) stage-structured formulation for allele frequency evolution. Unlike the latter, equation (13) holds regardless of whether a population has reached a stable stage distribution. Like Price’s original equation (12), equation (13) is easily extended to multivariate traits (see Rice 2004).

The first two components of equation (13) reflect changes in z̄ due to differences among stages. Indeed, the mean phenotype can change from one year to the next even if all individuals within a stage are identical (so that the third and fourth terms of eq. [13] are 0) and there is no average tendency for offspring phenotypes to differ from their parents (E(d̄_i) = 0). By comparison, the third and fourth components of equation (13) describe changes in z̄ due to variability within stages. Note that Cov_j (z, w) /w̄ is the selection differential (Robertson 1966) for z in stage j, which is nonzero if trait and fitness are correlated within that stage. The third term of equation (13) is thus the average selection differential over all stages. The fourth term is similar but reflects the relationship between fitness and parent-offspring phenotype difference. For example, this component would be positive if a parent who produces more offspring also tends to have offspring that have phenotypic values larger than its own.

Equation (13) makes no assumptions about the cause—genetic, environmental, or epigenetic—of any parent-off-spring phenotype difference d. Such differences could arise in Trillium if (for instance) there is a directional change in the environment (e.g., warming temperature) and flowering time is a plastic trait responsive to temperature. The second, fourth, and fifth components of equation (13) then account for the among-stage, within-stage, and overall impacts of this plastic response on change in the mean phenotype. Some stages could experience greater plasticity than others (second term), there could be more variance in the magnitude of such plastic responses among individuals within stages (fourth term), or the plastic response could manifest at the level of the entire population (fifth term).

Discussion

Our results provide three important advances for evolutionary biology. The first is a general set of modeling tools for prediction of joint evolution and demography of stage-structured populations. Such a framework has not been available, and its establishment completes the tool set available for understanding evolution in stage-structured populations, which previously contained only methods specialized for populations structured by age (e.g., Charlesworth 1994). Our next advance is the first rigorous verification that Lande’s theorem applies to stage-classified populations. Our derivation shows that this simple equation applies to any structured population, assuming only multivariate normality and evolution that is slow relative to population dynamics. Our third major result is extending a fundamental law of evolution—Price’s theorem—to stage-structured populations.

Our general framework extends Taylor’s earlier treatment of models of allele frequency change in stage-structured populations (Taylor 1990) by allowing standing variation and populations that have not reached a stable stage distribution. Our model can be used to predict the evolution of quantitative traits and, through use of indicator variables, allele or genotype frequencies. It can also be used to project the evolution of trait moments and distributions for an entire population or individual stages, providing null expectations for hypothesis testing in empirical systems.

There was good reason to doubt that Lande’s theorem would hold in general for stage-structured populations, and Caswell (1989; see also Caswell 2001, p. 284) hypothesized that it might apply only to stage-structured models with the same general flow of individuals as an age-structured model. Our analysis shows that given normality and slow evolution, Lande’s theorem applies to any stage-structured population, even if offspring are born into more than one class or individuals can repeat a stage or regress to a previous one, or there are differences among stages in trait means or variances. Assuming normality may seem problematic, because even if a population is at an SSD and phenotypes and breeding values initially have a joint normal distribution, the mixing of survivors from different stages tends to destroy normality. Our Trillium example shows that Lande’s equation approximates projections assuming Gaussian distributions but does deviate somewhat from the general model (which closely agrees with our individual-based simulations). Nevertheless, Lande’s formulation provides a quite reasonable description of this population’s evolution. Our result extends the domain of life histories over which this illuminating description of evolution should be applicable.

Our formulation of Price’s theorem shows how stage-classified evolution can be placed within this broad evolutionary principle and provides a relatively compact equation (13) that can be used as an alternative to our general modeling framework to project evolution of phenotypic means, variances, and other moments (e.g., Rice 2004). This may be useful in systematic comparisons among stage-structured taxa differing in life histories and patterns of inheritance. Some might find it easier to incorporate complications like nonrandom mating, phenotypic plasticity, temporal variability, and even density dependence using Price’s equation (13) than with our general formulation (eqq. [3] and [4]).

While the vital rates of almost all organisms are stage dependent, evolutionary biologists have until now lacked a general theoretical framework within which to organize stage-classified demographic data and analyze the implications of stage structure for evolution. Our results complete such a framework and provide relatively accessible formulas that can be used to understand evolutionary pasts and predict evolutionary futures of stage-structured populations.

Having escaped the devastating destruction of white-tailed deer, Trillium plants flower peacefully in a forest understory. Photograph by Tiffany Knight.

APPENDIX A

General Framework for Modeling Evolution of a Stage-Structured Population

This appendix provides details behind the general equation (4) for projecting the evolutionary dynamics of a stage-structured population. We use the definitions and assumptions described in the main text and find an equation for $p_i^{\prime }(\mathbf{g},\mathbf{z})$, the joint probability density function (PDF) of genotypic and phenotypic values in stage i in the next year, as a function of the PDF in the current year, p_i (g, z). The distribution in the next year is due to a mixture of current individuals who directly transition from all stages to stage i (including those that remain in stage i) and any new offspring recruiting into that stage. The joint PDF of individuals that transition to stage i from j is given by t_ij(z)p_j(g, z)/t̄_ij. The PDF of all individuals that transition to stage i is the weighted average of these distributions, with each weight equal to the fraction of all individuals transitioning to stage i that come from stage j:

$${\theta }_i(\mathbf{g},\mathbf{z})=\sum _j\frac{t_{ij}(\mathbf{z})p_j(\mathbf{g},\mathbf{z})}{{\overline{t}}_{ij}}·\frac{{\overline{t}}_{ij}{N}_j}{T_i^{\prime }}=\frac{1}{T_i^{\prime }}\sum _j{N}_j{t}_{ij}(\mathbf{z})p_j(\mathbf{g},\mathbf{z}).$$ (A1)

The next step is to find the joint PDF among newborns in stage i. Consider the distribution of g among parents of offspring born into stage i:

$${\mathrm{\Phi }}_i(\mathbf{g})=\sum _j\frac{\int f_{ij}(\mathbf{z})p_j(\mathbf{g},\mathbf{z})d\mathbf{z}}{{\overline{f}}_{ij}}·\frac{{\overline{f}}_{ij}{N}_j}{F_i^{\prime }}=\frac{1}{F_i^{\prime }}\sum _j{N}_j\int f_{ij}(\mathbf{z})p_j(\mathbf{g},\mathbf{z})d\mathbf{z}.$$ (A2)

Let R (g|g′, g″) be the probability that parents with genotypes g′ and g″ produce an offspring with genotype g. Assuming the population is either monoecious or without sex differences, and that parents mate at random, then the genotypic distribution among offspring in stage i is

$${\omega }_i(\mathbf{g})=\int \int R(\mathbf{g}|\mathbf{g}\prime ,\mathbf{g}″){\mathrm{\Phi }}_i(\mathbf{g}\prime ){\mathrm{\Phi }}_i(\mathbf{g}″)d\mathbf{g}\prime d\mathbf{g}″.$$ (A3)

(Though we do not do so here, one could employ the formalism of Barton and Turelli [1991; see also Kirkpatrick et al. 2002] in place of equation [A3] to allow practically any genetic basis or even nonrandom mating.)

A special case of interest is the infinitesimal model of inheritance (Fisher 1918; Bulmer 1971). With this model, the (multivariate) breeding value of an offspring is the average of the breeding values of its two parents plus a zero-mean normal random variable with covariance matrix V_LE—the additive-genetic covariance matrix among the m characters at linkage equilibrium. In this case, the offspring genotype PDF is given by

$${\omega }_i(\mathbf{g})={\mathrm{\Phi }}_i\left(\frac{\mathbf{g}}{2}\right)*{\mathrm{\Phi }}_i\left(\frac{\mathbf{g}}{2}\right)*\frac{1}{\sqrt{{(2\pi )}^m\text{ det }({\mathbf{V}}_{\mathrm{L}\mathrm{E}})}}\text{exp }(-\frac{1}{2}{\mathbf{g}}^{\mathrm{T}}{\mathbf{V}}_{\mathrm{L}\mathrm{E}}\mathbf{g}),$$ (A4)

where the asterisks indicates convolution. The arguments of the parents’ PDFs are halved because parental genotypes are averaged.

The phenotype of the offspring is the sum of the genotype and a zero-mean random variable representing the nonadditive genetic and environmental components of phenotype. The joint PDF of the offspring, ϕ_i(g, z), can be found from the genetic distribution, ω_i(g), using the fact that the joint probability of two outcomes is the product of the probability of the first outcome (genotype) and the probability of the second outcome (phenotype) given the first:

$${\varphi }_i(\mathbf{g},\mathbf{z})={\omega }_i(\mathbf{g}){\gamma }_i(\mathbf{z}|\mathbf{g}),$$ (A5)

where γ_i(z|g) is the PDF of the phenotype given the genotype for newborns, which is the PDF of the nonadditive genetic plus the environmental component of the phenotype evaluated at z − g. If this component has a multivariate normal distribution, then

$${\gamma }_i(\mathbf{z}|\mathbf{g})=\frac{1}{\sqrt{{(2\pi )}^m\text{ det }({\mathbf{V}}_{\mathrm{E}})}}\text{exp }[-\frac{1}{2}{(\mathbf{z}-\mathbf{g})}^{\mathrm{T}}{\mathbf{V}}_{\mathrm{E}}^{-1}(\mathbf{z}-\mathbf{g})],$$ (A6)

where V_E is the covariance matrix for the environmental component of the phenotype.

Returning to the general derivation, the last step in deriving the new joint distribution of genotypes and phenotypes in stage i is to average the contributions of existing individuals that transition into the stage with those of individuals that are newborn into that stage. Weighting by the relative contributions of those two sources shows, finally, that the joint PDF for the genotypes and phenotypes found in stage i in the next year is

$$p_i^{\prime }(\mathbf{g},\mathbf{z})={\theta }_i(\mathbf{g},\mathbf{z})\frac{T_i^{\prime }}{N_i^{\prime }}+{\varphi }_i(\mathbf{g},\mathbf{z})\frac{F_i^{\prime }}{N_i^{\prime }},$$ (A7)

which is equation (4) in the main text.

APPENDIX B

Lande’s Theorem for Stage-Structured Populations

We prove here that Lande’s equation, Δz̄ = G∇ ln λ̄, applies to random mating stage-structured populations under assumptions comparable to those used in the derivation for age-structured populations (Lande 1982b). To that end, it will be convenient to put equations (5) and (6) in the form of a matrix equation. Let the vector of phenotypes and genotypes be x_τ = (ζ̄, γ̄)^T, where ζ̄ = {z̄_i} and γ̄ = {ḡ_i}, and let the vector of selection terms be β = (β_z, β_g)^T, where β_z = {b_zi}, β_g = {b_gi}, b_gi = Σ_j c_ijG_j∇_z̄j ln ā_ij, and b_zi = Σ_j c_ij (P_j∇_z̄jt̄_ij + G_j∇_z̄jf̄_ij) (superscript T denotes the transpose). Also, define matrices of contributions of each stage to every other stage: $\mathbf{C}=\{c_{ij}\},{\mathbf{C}}^t=\{c_{ij}^t\}$ and ${\mathbf{C}}^f=\{c_{ij}^f\}$, and combine these into a single matrix:

$$\mathbf{K}=\left(\begin{array}{cc}\hfill {\mathbf{C}}^t\hfill & \hfill {\mathbf{C}}^f\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{C}\hfill \end{array}\right).$$ (B1)

The matrices C, C^t, C^f, and K contain only nonnegative numbers, and C = C^t + C^f. Under our assumptions, C is primitive (i.e., all the elements of the matrix power C^k are positive for some integer k > 0) and row stochastic (i.e., each row of C sums to 1). The matrix K is likewise row stochastic but is “reducible” because of the lower-left sub-matrix 0 that it contains. (Interested readers may consult Caswell [2001] and Meyer [2000] for more information about the matrix terminology, definitions, and results used in this appendix.) Using this notation, the recursions for evolution assuming normality, equations (5) and (6), can be written as the linear recursion

$${\mathbf{x}}_{\tau +1}=\mathbf{K}{\mathbf{x}}_{\tau }+\mathit{\beta }.$$ (B2)

To solve this equation, we need to assume that evolutionary dynamics are much slower than population dynamics. Also assume the population dynamics are density independent and described by the Lefkovitch matrix Ā with elements ā_ij, the average values of the a_ij over the phenotypic distribution. Since evolution is slow, Ā (and β) are nearly constant and the population maintains a stable-stage distribution (SSD; Caswell 2001). At SSD, all stages grow geometrically at the same rate, so $N_i^{\prime }=\overline{\lambda }{N}_i$ where λ̄ is the eigenvalue of largest magnitude of Ā. Let w = {w_i} and v = {v_i} be the respective right and left eigenvectors of Ā corresponding to λ̄. The elements of w sum to 1 and give the proportions in each stage at the SSD, and v (which contains reproductive values) is scaled so that v^Tw = 1. At SSD, the coefficients $c_{ij},c_{ij}^t$ and $c_{ij}^f$ take on constant values: $c_{ij}=N_j{\overline{a}}_{ij}/N_i^{\prime }={\overline{\lambda }}^{-1}{\overline{a}}_{ij}{N}_j/N_i={\overline{\lambda }}^{-1}{\overline{a}}_{ij}{w}_j/w_i$ and similarly for $c_{ij}^t$ and $c_{ij}^f$.

With these assumptions, direct iteration of equation (B2) gives

$${\mathbf{x}}_{\tau }={\mathbf{K}}^{\tau }{\mathbf{x}}_0+\sum _{i=0}^{\tau -1}{\mathbf{K}}^i\mathit{\beta },$$ (B3)

so the rate of evolution at time τ is

$$\mathrm{\Delta }{\mathbf{x}}_{\tau }={\mathbf{x}}_{\tau +1}-{\mathbf{x}}_{\tau }={\mathbf{K}}^{\tau }[(\mathbf{K}-\mathbf{I}){\mathbf{x}}_0+\mathit{\beta }].$$ (B4)

We need the following result for the reducible, stochastic matrix K (Meyer 2000, p. 698):

$${\text{lim}}_{\tau \to \infty }{\mathbf{K}}^{\tau }=\left(\begin{array}{cc}\hfill 0\hfill & \hfill {(\mathbf{I}-{\mathbf{C}}^t)}^{-1}{\mathbf{C}}^f\mathbf{1}{\mathbf{r}}^{\mathrm{T}}\hfill \\ \hfill 0\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}\hfill \end{array}\right),$$ (B5)

with I being the identity matrix, 1 a vector of all 1s, and r = {r_i} the left eigenvector of C, corresponding to its leading eigenvalue normalized so that r^T1 = 1. (Since C is row stochastic, its leading eigenvalue is 1, with a corresponding right eigenvector of 1.) Now observe that, since K is row stochastic, C^t1 + C^f1 = 1. Thus C^f1 = (I − C^t)1, which implies (I − C^t)⁻¹C^f1 = 1. (D. Watkins pointed out this latter result to us.) So, in fact,

$${\text{lim}}_{\tau \to \infty }{\mathbf{K}}^{\tau }=\left(\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}\hfill \end{array}\right)\stackrel{\scriptscriptstyle\mathrm{def}}{=}\hat{\mathbf{K}}.$$ (B6)

Combining equations (B4) and (B6),

$${\text{lim}}_{\tau \to \infty }\mathrm{\Delta }{\mathbf{x}}_{\tau }=\hat{\mathrm{K}}[(\mathbf{K}-\mathbf{I}){\mathbf{x}}_0+\mathit{\beta }]=\hat{\mathbf{K}}\mathit{\beta }={\mathbf{r}}^{\mathrm{T}}{\mathit{\beta }}_g(\begin{array}{c}\hfill \mathbf{1}\hfill \\ \hfill \mathbf{1}\hfill \end{array}).$$ (B7)

The second equality follows from the fact that K̂(K − I) is a matrix of zeros because r^TC = r^T by definition of r:

$$\hat{\mathbf{K}}(\mathbf{K}-\mathbf{I})=\left(\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}\hfill \end{array}\right)\left(\begin{array}{cc}\hfill {\mathbf{C}}^t-\mathbf{I}\hfill & \hfill {\mathbf{C}}^f\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{C}-\mathbf{I}\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}(\mathbf{C}-\mathbf{I})\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{1}{\mathbf{r}}^{\mathrm{T}}(\mathbf{C}-\mathbf{I})\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{1}({\mathbf{r}}^{\mathrm{T}}\mathbf{C}-{\mathbf{r}}^{\mathrm{T}})\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{1}({\mathbf{r}}^{\mathrm{T}}\mathbf{C}-{\mathbf{r}}^{\mathrm{T}})\hfill \end{array}\right)=\left(\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \end{array}\right).$$ (B8)

Result (B7) shows that, asymptotically,

$$\mathrm{\Delta }{\overline{\mathbf{z}}}_i=\mathrm{\Delta }{\mathbf{ḡ}}_i={\mathbf{r}}^{\mathrm{T}}{\mathit{\beta }}_g=\sum _i{r}_i\sum _j{c}_{ij}{\mathbf{G}}_j{\nabla }_{{\overline{\mathbf{z}}}_j}\text{ln }{ā}_{ij}\stackrel{\scriptscriptstyle\mathrm{def}}{=}\mathrm{\Delta }\overline{\mathbf{z}}$$ (B9)

for all stages i. It can be shown that r_i = v_iw_i. Recalling too that c_ij = λ̄⁻¹ā_ijw_j/w_i at the SSD and simplifying shows equation (B9) is equivalent to

$$\mathrm{\Delta }\overline{\mathbf{z}}=\frac{1}{\overline{\lambda }}\sum _{i,j}{v}_i{w}_j{\mathbf{G}}_j{\nabla }_{{\overline{\mathbf{z}}}_j}{ā}_{ij}.$$ (B10)

(Taylor [1990] used the same weighting vector r when analyzing models for allele frequency change in stage-structured populations at SSD.)

In his derivation for age-structured populations, Lande (1982a) assumed the mean phenotype and additive genetic covariance matrix were approximately the same for every age class. (He argued this is conceivable given weak selection.) If we make comparable assumptions for our stage-structured model (i.e., assume z̄_j = z̄ and G_j = G for all stages j), then the shared rate of evolution (B10) becomes

$$\mathrm{\Delta }\overline{\mathbf{z}}=\mathbf{G}\frac{1}{\overline{\lambda }}\sum _{i,j}{v}_i{w}_j{\nabla }_{\overline{\mathbf{z}}}{ā}_{ij}.$$ (B11)

Now consider

$${\nabla }_{\overline{\mathbf{z}}}\text{ln }\overline{\lambda }=\frac{1}{\overline{\lambda }}\sum _{i,j}\frac{\partial \overline{\lambda }}{\partial {ā}_{ij}}{\nabla }_{\overline{\mathbf{z}}}{ā}_{ij}=\frac{1}{\overline{\lambda }}\sum _{i,j}{v}_i{w}_j{\nabla }_{\overline{\mathbf{z}}}{ā}_{ij},$$ (B12)

where we combined the standard result ∂λ̄/∂ā_ij = v_iw_j/v^Tw (e.g., Caswell 2001, p. 209) with our regularization v^Tw = 1. Substituting equation (B12) in equation (B11) shows that Lande’s equation, Δz̄ = G∇_z̄ ln λ̄, holds for stage-structured populations.