Summary
In ~20 million people with drug-resistant epilepsy, focal seizures originating in dysfunctional brain networks will often evolve and spread to surrounding tissue, disrupting function in otherwise normal brain regions. To identify network control mechanisms that regulate seizure spread, we developed a novel tool for pinpointing brain regions that facilitate synchronization in the epileptic network. Our method measures the impact of virtually resecting putative control regions on synchronization in a validated model of the human epileptic network. By applying our technique to time-varying, functional networks, we identified brain regions whose topological role is synchronize or desynchronize the epileptic network. Our results suggest that greater antagonistic, push-pull interaction between synchronizing and desynchronizing brain regions better constrains seizure spread. These methods, while applied here to epilepsy, are generalizable to other brain networks, and have wide applicability in isolating and mapping functional drivers of brain dynamics in health and disease.
Keywords: network neuroscience, epileptic network, synchronizability, push-pull control, seizure spread
Introduction
Functional architecture of the epileptic neocortex has been studied extensively to better identify optimal targets for surgical resection and, more recently, the optimal location for focal ablation or implantable devices (Medvid et al., 2015; Morrell, 2011; Tovar-Spinoza et al., 2013). The prospect of patient-centric algorithms that modulate brain state to abort seizures is exciting to clinicians and researchers alike (Afshar et al., 2013; Stacey & Litt, 2008; Stanslaski et al., 2012). However, the best targets for chronic devices remain elusive, partly because functional brain networks, including the epileptic network, reorganize dynamically (Bassett et al., 2011; Bassett et al., 2006; Burns et al., 2014; Khambhati et al., 2015; Rummel et al., 2013). Such reorganization appears to follow a specific progression through network states unique to the patient's seizures (Burns et al., 2014; Khambhati et al., 2015; Wulsin et al., 2013). The mechanisms that drive seizures through network states can inform neural control paradigms that aim to stop or contain propagation of seizure activity. Such a capability is vital, clinically, because epileptogenic regions cause symptoms not only through their own dysfunction, but also through their ability to recruit and disrupt healthy brain tissue (Kutsy et al., 1999). Understanding and translating network mechanisms of seizure evolution to identify targets for therapy requires further intellectual dissection of functional epileptic network architecture.
Conventional thinking divides epileptic brain into clinically-defined regions where seizures presumably originate (Rosenow and Luders, 2001) and surrounding regions in which seizures do not originate. Recent models describe connectivity between seizure-onset and surrounding brain regions in the framework of a broader, dysfunctional epileptic network, where network nodes are neural populations measured by intracranial sensors and network connections are statistical relationships between neural activation patterns (Burns et al., 2014; Khambhati et al., 2015; Kramer et al., 2010; Nair et al., 2004; Warren et al., 2010; Wilke et al., 2011) (Figure 1A). For example, partial seizures that begin in the seizure-onset zone can evolve, spreading spatially as they modulate in dominant frequency via local connections to the surrounding tissue, implicating a distributed epileptic network (Khambhati et al., 2015; Korzeniewska et al., 2014; Mark A. Kramer et al., 2010; Nair et al., 2004; Spencer, 2002). In the extreme case, these seizures can generalize and eventually encompass the entire brain.
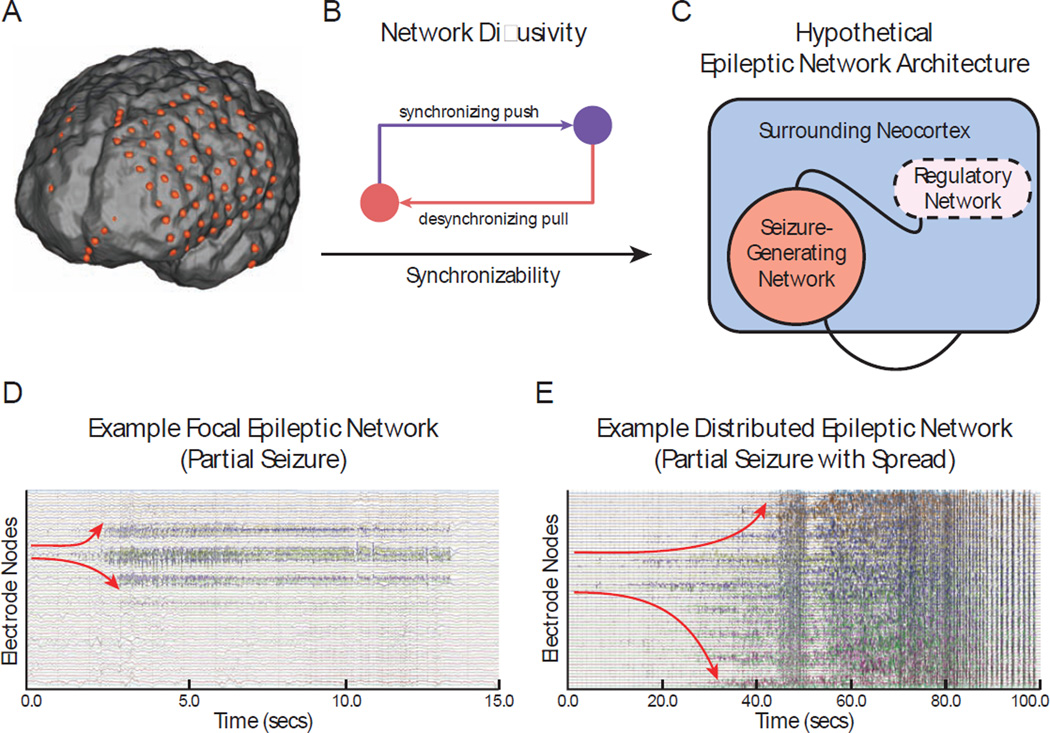
Figure 1. Hypothesized Mechanism of Seizure Regulation.
(A) We created functional networks from intracranial electrophysiology of patients with neocortical epilepsy. Each sensor is a network node, and weighted functional connectivity between sensors, or magnitude coherence, is a network connection. (B) Diagram demonstrates push-pull control, where opposing synchronizing and desynchronizing forces (nodes) shifts overall network synchronizability. (C) Schematic of the epileptic network composed of a seizure-generating system and a hypothesized regulatory system that controls the spread of pathologic seizure activity. (D) Example partial seizure that remains focal: the seizure begins at a single node and evolves to and persists within a focal area. (E) Example partial seizure that generalizes to surrounding tissue: the seizure begins at two nodes and evolves to the broader network. We hypothesize that these two types of dynamics are determined by differences in the regulatory system.
Given the distributed nature of epileptic activity, it is critical to isolate underlying propagation mechanisms. Leading hypotheses suggest that either (i) seizure evolution is driven by strong, synchronizing activity from the seizure-generating network impinging outward on the surrounding tissue (Jiruska et al., 2013; Kramer and Cash, 2012; Kramer et al., 2010; Schindler et al., 2008), or (ii) seizure evolution is caused by a diminished ability of the surrounding tissue to regulate, or contain, abnormal activity (Bower et al., 2012; Nair et al., 2004). While little evidence exists to determine which of these hypotheses accurately reflect seizure dynamics, both mechanisms can be succinctly summarized as abnormalities of synchronizability, a description of how easily neural processes, such as rhythmic activity, can diffuse through a network. Fundamental work has demonstrated that the distance over which neural populations can synchronize is dependent upon the dominant rhythmic frequency of neural oscillations (Kopell et al., 1999). Gamma-band (30–70 Hz) activity tends to synchronize neural populations over shorter distances, while beta-band activity (12–29 Hz) tends to synchronize neural populations over longer distances. However, a direct relationship between frequency-dependent neural activity and the synchronization dynamics of seizure propagation has not been explored and may highlight critical mechanisms of how seizures spread.
Theoretical work in the fields of physics and engineering demonstrates that diffusion of dynamics through the network can be regulated through a push-pull control mechanism, where desynchronizing and synchronizing nodes operate antagonistically in a “tug-of-war”. When synchronizing nodes exert greater push than desynchronizing nodes, synchronizability increases and dynamic processes may diffuse through the network more easily (He et al., 2014) (Figure 1B). Such mechanisms are particularly successful in heterogeneous networks like the brain, where some regions are sparsely connected and other regions are densely connected (Wang & Chen, 2002). Does the brain utilize such a control mechanism for seizure regulation? And if so, what regions of the brain affect this control?
To address these questions, we present a novel method we call virtual cortical resection, which offers a statistically robust means to pinpoint putative control regions in the epileptic network that may regulate seizure dynamics, based on the network's response to simulated lesioning. Importantly, while other groups have studied the effects of removing structural brain regions and connections (also called virtual lesioning or virtual dissection) on dynamics of simulated neural processes (Alstott et al., 2009; Honey and Sporns, 2008) and on probabilistic tractography (Rafal et al., 2015), our virtual cortical resection approach uniquely applies node removal to functional brain regions to uncover network control regions that regulate network properties of synchronization. We use this method to test the hypothesis that the epileptic network contains a native regulatory system (Figure 1C) whose connectivity to the seizure-generating area accounts for differential seizure dynamics, including (i) the constrained dynamics observed in partial seizures that remain focal (Figure 1D), and (ii) the unconstrained dynamics observed in partial seizures that generalize to surrounding tissue (Figure 1E).
More specifically, using electrocorticography recorded from 10 patients diagnosed with drug-resistant neocortical epilepsy undergoing routine pre-surgical evaluation, we constructed time-evolving functional networks across events, each of which included a seizure epoch preceded by a pre-seizure epoch. The seizure epoch spanned the period between the clinically-marked earliest electrographic change (Litt et al., 2001) and seizure termination, while the pre-seizure epoch was identical in duration to the seizure and ended immediately prior to the earliest electrographic change. In each epoch, we divided the ECoG signal into Is non-overlapping time-windows and estimated functional connectivity in α/θ (5–15 Hz), β (15–25 Hz), low-γ (30–40 Hz), and high-γ (95–105 Hz) frequency bands using multitaper coherence estimation (see Experimental Procedures). We implemented virtual cortical resection on this dynamic epileptic network by independently removing electrode sites from the network model. This was done to assess the synchronizability of (i) the distributed epileptic network in partial seizures that generalize to surrounding tissue, versus (ii) the focal epileptic network in seizures that do not generalize to surrounding tissue. By removing electrode sites from the network model, we were able to probe the importance of brain regions, in their presence and absence, to seizure generation and propagation.
Results
Network Homogeneity Improves Synchronizability
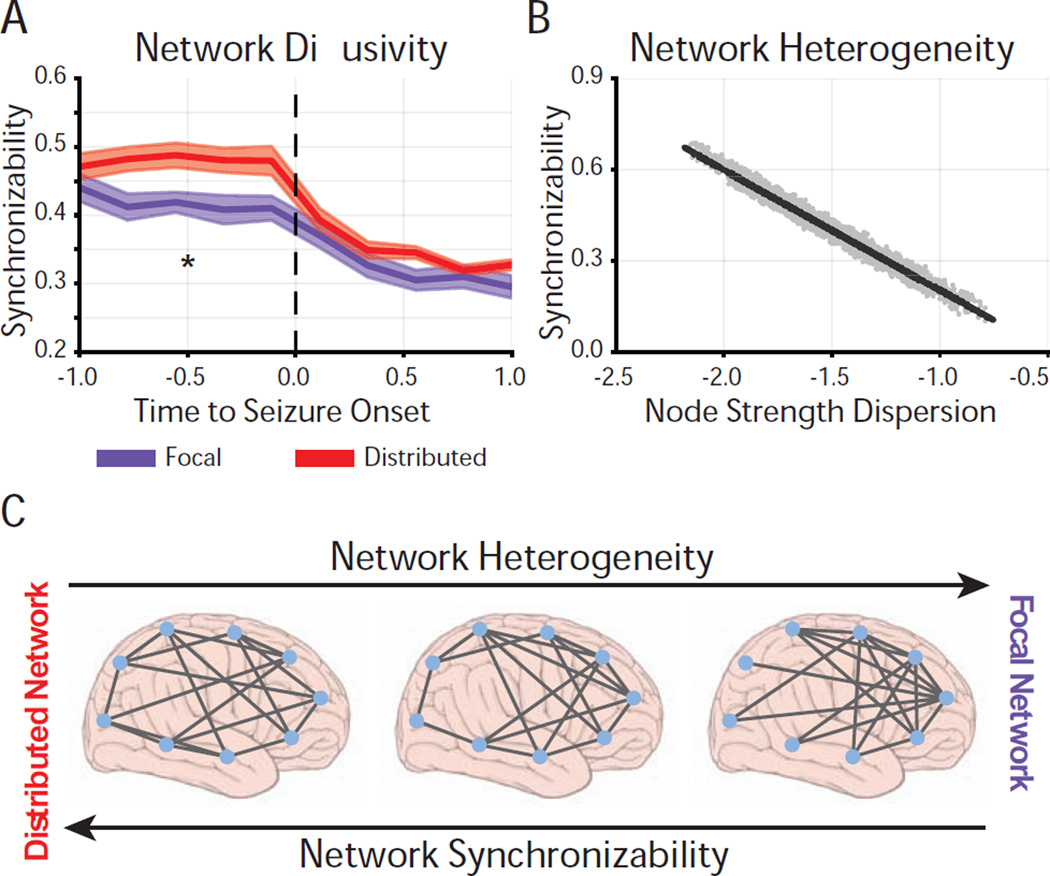
We first asked the question, “How easily do seizures diffuse through the distributed or focal network?” We hypothesized that seizure spread, the dynamical process whereby neural activity becomes increasingly synchronous, is facilitated by network topology. To relate network dynamics and network topology, we estimated the time-varying Laplacian matrix L(t), whose entries lij(t) quantify how easily information can diffuse between nodes i and j, from the time-varying functional connectivity matrix (see Experimental Procedures). Using the time-varying Laplacian matrix, we computed synchronizability, a dynamical network property that quantifies how easily neural activity, in our case seizures, can synchronize, or diffuse through, the network. Synchronizability measures the spread of eigenvalues of the Laplacian matrix through the ratio , where λ2 and λmax are the second-smallest eigenvalue and the largest eigenvalue, respectively, of L(t) (see (Barahona and Pecora, 2002) and Supplemental Information). Intuitively, greater network synchronizability results from a smaller spread between eigenvalues, which is caused by increases in the second-smallest eigenvalue or decreases in the largest eigenvalue, and implies greater ease for neural populations to synchronize their dynamics – such as during seizures. We observed significantly greater synchronizability in the distributed network than in the focal network during the pre-seizure epoch, suggesting that high-γ networks have a greater potential to synchronize prior to seizures that spread than prior to seizures that do not spread (Figure 2A). In contrast, we observed synchronizability in low-γ and β networks effectively captured spread through the distributed network after seizure-onset (see Supplemental Information and Figure S1). We observed no differences in synchronizability between the focal and distributed networks, before or during seizures, in the α/θ-band. For the remainder of our main analysis, we focus on high-γ networks because of their tendency to differentiate seizure spread before the seizure begins.
Figure 2. Differential Pre-Seizure Synchronizability Predicts Seizure Spread.
(A) Time-dependent synchronizability captures the potential for seizure spread through high-γ functional networks. The distributed network describes seizures with secondary generalization (N=16), the focal network describes seizures without secondary generalization (N=18). Analyzed epileptic events spanned the clinically-defined seizure and period of time equal in duration to the seizure, immediately preceding seizure-onset. Events were time-normalized with each pre-seizure and seizure period divided into 5 equally-spaced time bins (10 bins per event). Synchronizability was averaged within each bin. Synchronizability was significantly greater in the distributed network than in the focal network prior to seizure onset (functional data analysis, ppre-seizure = 1–56 * 10−2pseizure = 5–01 * 10−2). Thick lines represent mean, shaded area represents standard error around mean, p-values are obtained via the statistical technique known as functional data analysis (FDA) where event labels (two seizure types) were permuted uniformly at random (see Experimental Procedures): *p < 0.05. (B) Relationship between synchronizability and log-scaled dispersion of node strengths in high-γ functional networks across all distributed and focal events. Each point represents average synchronizability and dispersion of average node strengths from a single time-window (N=3560). Greater synchronizability was strongly related to greater network heterogeneity, or lower node strength dispersion (Pearson correlation coefficient; r = −0.964, p < 10−16). (C) Schematic demonstrating that the distributed network has greater synchronizability and more homogeneous topology than the focal network. Seizures may spread more easily in the distributed network due to more homogeneous connectivity between network nodes.
Next, based on theoretical work in physics and engineering, we asked if network synchronizability, or predisposition to seizure spread, might be explained by heterogeneity in network topology. That is, "Does heterogeneity in node strength weaken the network's ability to synchronize?" We expected that the distribution of node strengths would either widen or narrow the gap between the largest and second-smallest eigenvalue of the Laplacian matrix, and consequently, decrease or increase the network synchronizability. To measure heterogeneity, we computed a log-scaled measure of node strength dispersion d(t) based on the standard deviation of node strengths in each time window t (see Experimental Procedures). More heterogeneous network topologies would incur greater node strength dispersion, suggesting nodes might either be highly connected or highly isolated (whereas lower node strength dispersion suggests nodes are more evenly connected in the network). Our results demonstrated a significant linear relationship synchronizability and node strength dispersion (Pearson correlation; r = −0.964, p < 10−16), where greater heterogeneity in node strength lead to lower synchronizability (Figure 2B)
More generally, our results suggest that seizure spread in the distributed network may result from a vulnerability to synchronize easily, a vulnerability that is not present in partial seizures that do not generalize to surrounding tissue. Furthermore, the heightened synchronizability of the distributed network may be driven by homogenous distributions of connectivity amongst network nodes.
Network Controllers of Synchronizability
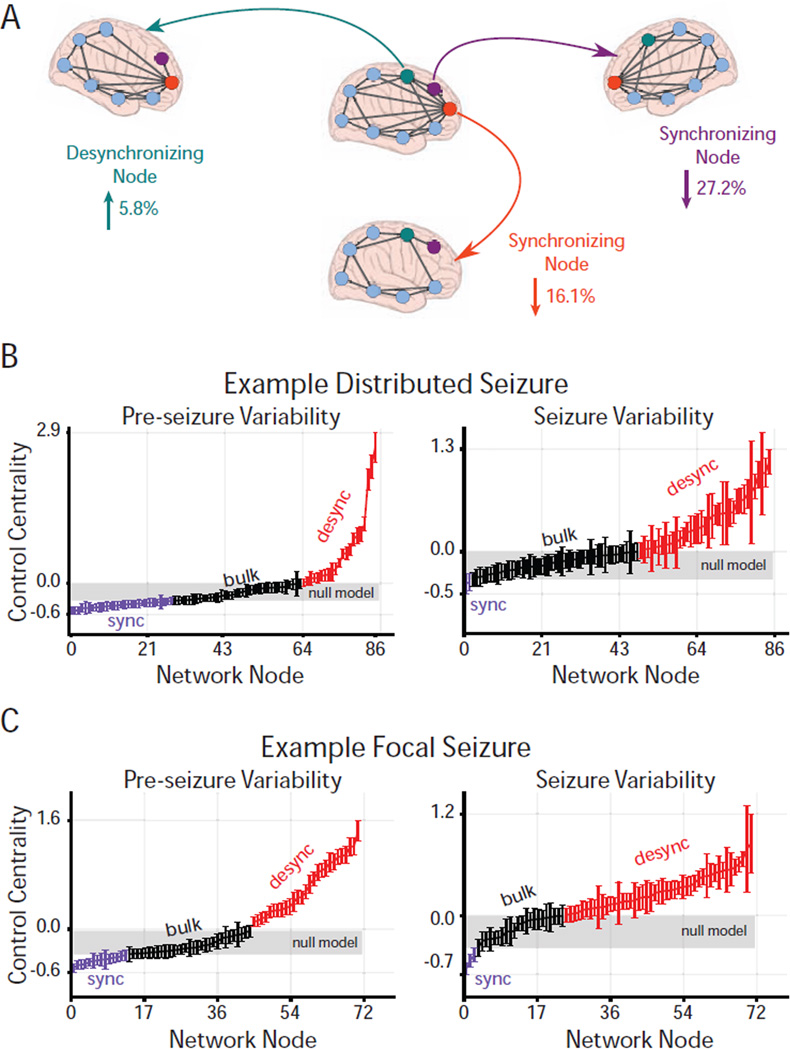
Following our analysis demonstrating that synchronizability is related to the dispersion of node strengths (network topology), we asked “Is synchronizability sensitive to the specific pattern of connections between nodes (network geometry)?” That is, how might network geometry regulate levels of synchronizability? Do a subset of nodes act as key controllers, or do all nodes contribute equally? To answer this question, we developed a novel method to assess the influence of a node on synchronizability. We define the control centrality ci of node i to be the fractional change in synchronizability following removal of node i from the network (Figure 3A): where s is the original synchronizability and si is the synchronizability after node removal (see Experimental Procedures). The magnitude of ci can be interpreted as the overall strength of the node as a controller of synchronizability. If ci is positive, then synchronizability increases upon node removal, and the node is said to be a desynchronizing node. If ci is negative, then synchronizability decreases upon node removal, and the node is said to be a synchronizing node. As illustrated in Figure 3A, both desynchronizing and synchronizing network controllers are characteristic of heterogeneous networks. We expected that independently removing nodes from the network would affect node strength dispersion non-trivially, as node removal affects the overall distribution of node strengths in the network (see Supplemental Information). We observed a low correlation between control centrality and node strength (Pearson correlation coefficient; r = 0.221, p < 10−16), suggesting control centrality is sensitive to the network geometry, or the specific relationships between nodes rather than just the strength of a node (see Supplemental Information and Figure S2).
Figure 3. Virtual Cortical Resection Localizes Network Controllers.
(A) Effect of node removal on network synchronizability (control centrality) in a toy network. Highlighted node removals resulting in increased synchronizability (desynchronizing node; green) or decreased synchronizability (synchronizing nodes; purple and orange). The strongest desynchronizing node increased synchronizability by 5.8% and was present in the network periphery, while the strongest synchronizing nodes decreased synchronizability by 27.2% and 16.1% and were located in the network core. The magnitude and direction of change upon removing a node is called its control centrality. (B) Virtual cortical resection applied to example distributed ((C) and focal) high-γ epileptic network event in a pre-seizure (left) and associated seizure (right) epoch yields a time-varying control centrality for each node. Network nodes are ordered by increasing mean control centrality during the epoch. We assigned each node as a desynchronizing, synchronizing, or bulk controller type using a null distribution of control centrality, constructed by randomly permuting functional connection strength 100 times for each network time window and applying virtual cortical resection to every node from every rewiring permutation. Nodes with mean control centrality in the upper or lower-tail of the null distribution (p < 0.05) were assigned as desynchronizing (red) or synchronizing (purple) nodes, respectively, otherwise, nodes with mean control centrality within the null distribution (range highlighted in gray) were assigned to the bulk (black). Error bars represent standard error of control centrality computed over time windows during the pre-seizure or seizure epoch.
We used control centrality to assess the presence of desynchronizing and synchronizing controllers in the epileptic network, and to define their putative role in regulating synchronizability, a hallmark of seizure spread. To identify groups of statistically significant desynchronizing and synchronizing controllers in the network, we generated a null distribution of control centrality by randomly permuting connections between network nodes 100 times for each time window of the time-varying functional network and re-computing control centrality on each permuted network. Network nodes whose mean control centrality over the pre-seizure or seizure epoch was greater than 97.5% (or less than 2.5%) of the mean null control centrality values were considered desynchronizing (or synchronizing) nodes. Nodes with mean control centrality within the null distribution were considered bulk nodes. We identified desynchronizing and synchronizing brain regions, independently, for each focal and distributed functional network (Figure 3B, C and Figure S3).
Next, we used the node controller type and magnitude control centrality to ask “How are synchronizing and desynchronizing regions distributed in the epileptic network?” Furthermore, can the spatial and temporal distributions of control nodes differentially explain seizure spread?
Regulatory System Controls Seizure Dynamics
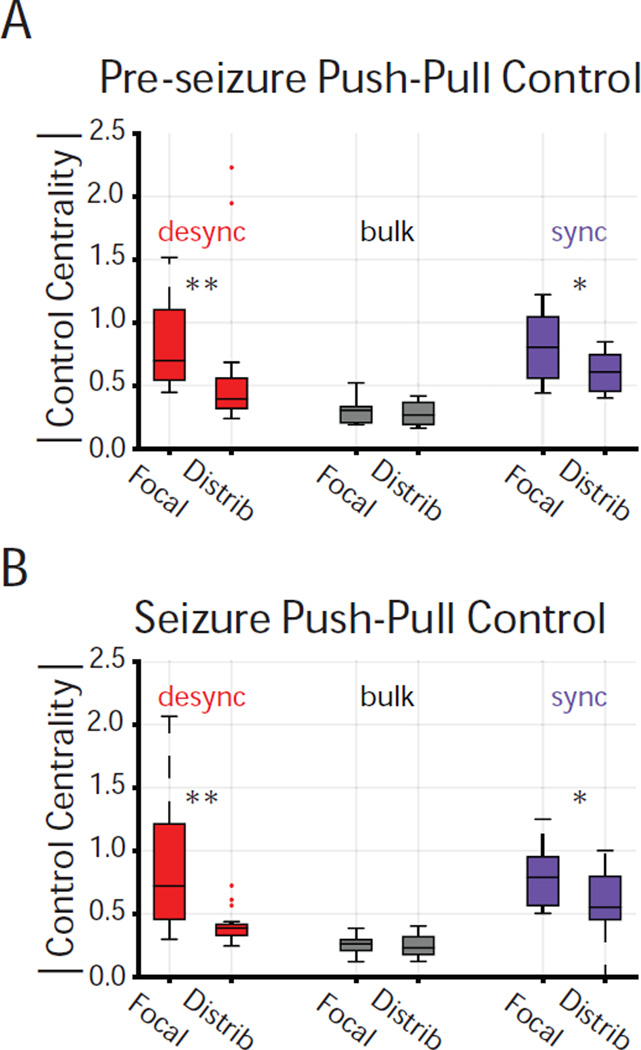
First, we tested whether the control centrality of synchronizing and desynchronizing regions differentiate focal and distributed seizures in high-γ functional networks. During pre-seizure epochs, we observed that: (i) desynchronizing regions of the focal network exhibited greater magnitude control centrality than desynchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.86, p = 4.18 * 10−3), (ii) bulk regions exhibited similar magnitude control centrality between the focal and distributed networks (Wilcoxon rank-sum; z = 0.52, p = 0.60), and (iii) synchronizing regions of the focal network exhibited greater magnitude control centrality than synchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.00, p = 4.54 * 10−2) (Figure 4A). Similarly, during seizure epochs, we observed that: (i) desynchronizing regions of the focal network exhibited greater magnitude control centrality than desynchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.97, p = 3.00 * 10−3), (ii) bulk regions exhibited similar magnitude control centrality between focal and distributed networks (Wilcoxon rank-sum; z = 0.517, p = 0.60), (iii) synchronizing regions of the focal network exhibited greater magnitude control centrality than synchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.10, p = 3.53 *10−2).
Figure 4. Desynchronizing and Synchronizing Control Differentiate Seizure Type.
(A) Distribution of average magnitude control centrality for each controller type across the focal (N=18) and distributed (N=16) networks during the pre-seizure epoch. Magnitude control centrality for each event was averaged across regions of same controller type and across time windows. Desynchronizing regions are stronger in the focal network than in the distributed network, pre-seizure (Wilcoxon rank-sum; z = 2.86, p = 4.18 * 10−3). Synchronizing regions are stronger in the focal network than in the distributed network, pre-seizure (Wilcoxon rank-sum; z = 2.00, p = 4.54 * 10−2). Bulk regions have similar strength in the focal and distributed networks, pre-seizure. (B) Distribution of average magnitude control centrality for each controller type across the focal (N=18) and distributed (N=16) networks during the seizure epoch. Magnitude control centrality for each event was averaged across nodes of same controller type and across time windows. Desynchronizing regions are stronger in the focal network than in the distributed network, during the seizure (Wilcoxon rank-sum; z = 2.97, p = 3.00 * 10−3). Synchronizing regions are stronger in the focal network than in distributed network, during the seizure (Wilcoxon rank-sum; z = 2.10, p = 3.53 * 10−2). Bulk regions have similar strength in the focal and distributed networks, during the seizure. *p < 0.05, **p < 0.01.
These findings suggest that both desynchronizing and synchronizing controllers are stronger in the focal network than the distributed network. Moreover, the differential effect of synchronizing controllers on magnitude control centrality between seizure types increased during the transition from pre-seizure to seizure epochs.
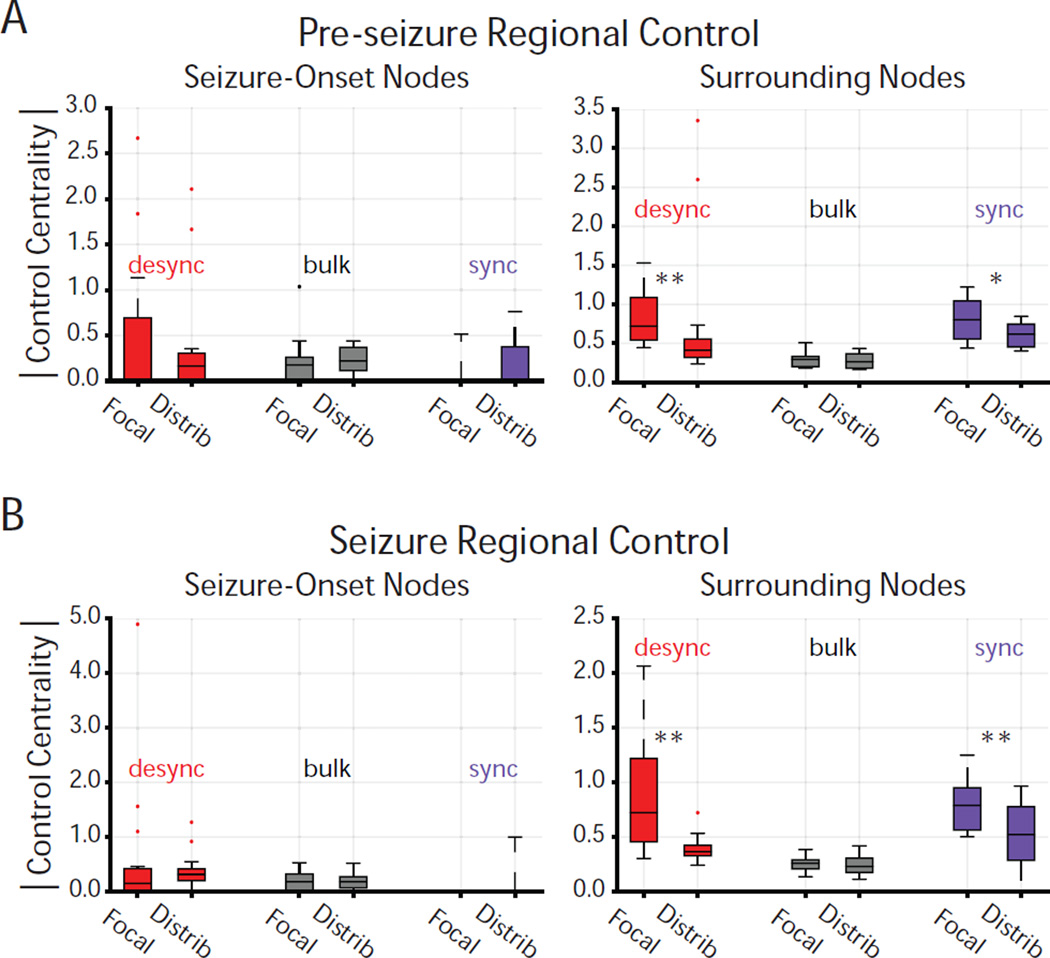
Next, we explored regional control of seizure spread in high-γ functional networks. To assign network regions, a team of neurologists successfully identified the sensors on the seizure-onset zone (SOZ) based on visual inspection of the intracranial recordings. Sensors within the SOZ were grouped as the seizure onset region, while sensors outside the SOZ were labelled as the surrounding region. First, we compared magnitude control centrality of nodes within the seizure-onset region (Figure 5). Both before and during the seizure, we observed no significant difference in magnitude control centrality of synchronizing, desynchronizing, or bulk node types within the SOZ between the focal and distributed networks. Next, we compared magnitude control centrality of nodes outside the seizure-onset region. During pre-seizure epochs, we observed that: (i) desynchronizing regions of the focal network exhibited a greater magnitude control centrality than desynchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.72, p = 6.42 * 10−3), (ii) bulk regions exhibited similar magnitude control centrality between the focal and distributed networks (Wilcoxon rank-sum; z = 0.52, p = 0.60), and (iii) synchronizing regions of the focal network exhibited greater magnitude control centrality than synchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.00, p = 4.54 * 10−2). Similarly, during seizure epochs, we observed that: (i) desynchronizing regions of the focal network exhibited greater magnitude control centrality than desynchronizing regions of the distributed network (Wilcoxon rank-sum; z = 3.07, p = 2.13 * 10−3), (ii) bulk regions exhibited similar magnitude control centrality between the focal and distributed networks (Wilcoxon rank-sum; z = 4.83, p = 0.63), and (iii) synchronizing regions of the focal network exhibited greater magnitude control centrality than the synchronizing regions of the distributed network (Wilcoxon rank-sum; z = 2.59, p = 9.67 * 10−3).
Figure 5. Regional Control Centrality Differentiates Seizure Type.
(A) Distribution of average magnitude control centrality for each controller type across the focal (N=18) and distributed (N=16) networks during the pre-seizure epoch amongst seizure-onset (left) and surrounding (right) regions. Magnitude control centrality was averaged across regions of same controller type, location (seizure-onset or surround), and across time windows. No significant difference in desynchronizing, synchronizing, or bulk magnitude control was observed between seizure-onset regions of the focal and distributed networks, pre-seizure. Surrounding regions exhibit greater desynchronizing control in the focal network than in distributed network, pre-seizure (Wilcoxon rank-sum; z = 2.73, p = 6.42 * 10−3). Surrounding regions exhibit greater synchronizing control in the focal network than in the distributed network, pre-seizure (Wilcoxon rank-sum; z = 2.00, p = 4.54 * 10−2). No significant difference in bulk magnitude control was observed between surrounding regions of the focal and distributed networks, pre-seizure. (B) Distribution of average magnitude control centrality for each controller type across the focal (N=18) and distributed (N=16) networks during the seizure epoch amongst seizure-onset (left) and surrounding (right) regions. Magnitude control centrality was averaged across nodes of same controller type, location (seizure-onset or surround), and across time windows. No significant difference in desynchronizing, synchronizing, or bulk magnitude control was observed between seizure-onset regions of the focal and distributed networks, during the seizure. Surrounding regions exhibit greater desynchronizing control in the focal networks than in the distributed networks, during the seizure (Wilcoxon rank-sum; z = 3.07, p = 2.13 * 10−3). Surrounding regions exhibit greater synchronizing control in the focal network than in the distributed network, during the seizure (Wilcoxon rank-sum; z = 2.59, p = 9.67 * 10−3). No significant difference in bulk magnitude control was observed between surrounding regions of focal and distributed events, during the seizure. *p < 0.05, **p < 0.01.
These findings suggest that the focal and distributed networks are most differentiated in the magnitude of desynchronizing and synchronizing control, localized to areas outside the seizure-onset zone. In contrast, we did not observe a difference in magnitude of desynchronizing or synchronizing control between seizure types in the clinically-defined seizure-onset zone.
Overall, virtual resection of network nodes revealed putative controllers of synchronizability before and during seizures. We observed that network regions outside of the seizure-onset zone that may play a mechanistic role in the regulation of seizure spread by lowering network synchronizability and simultaneously engaging strong, antagonistic, desynchronizing and synchronizing controllers. Furthermore, we identified that desynchronizing controllers are members of a network core, whose organization may be fundamentally different between focal and distributed functional networks and persistent over time. On the other hand, synchronizing controllers are members of a network periphery, whose differential effect on magnitude control centrality between focal and distributed networks grows stronger during the transition from pre-seizure to seizure epochs (see Supplemental Information and Figure S3).
Discussion
In this work we asked, “Is there a network-level control mechanism that regulates seizure evolution?” To answer this question, we designed and applied a novel computational tool – virtual cortical resection – to predict network response to removing regions in the epileptic network. We showed network topology pre-emptively facilitates seizure spread by regulating the synchronizability of epileptic activity. Specifically, synchronizing and desynchronizing network regions competitively modulate network synchronizability and constrain seizure spread beyond seizure-generating regions, effectively forming a push-pull control system. Our results not only significantly extend our understanding of the putative mechanisms of seizure evolution, but also provide a model ripe for further investigation in other brain network disorders and cognition.
Synchronization of the Epileptic Network
Epilepsy researchers have long desired an answer to the question of “Which brain regions drive seizure generation and evolution?” The literature frequently describes the epileptic brain as one that displays an imbalance of excitatory and inhibitory neural populations, leading to instabilities in synchronization that drive seizure dynamics. Clinical observation has informed the development of a dictionary of electrophysiological biomarkers believed to manifest as a result of dysfunctional imbalances in neural populations. However, the variability among epileptologists's descriptions of epileptic events often leads to poor performance of algorithms that seek to mimic the clinical characterization.
In this work, we studied synchronizability: an objective measure of the ability for neural populations to synchronize in the network. We used this measure to describe mechanistic differences between seizures that either remain focal or that spread throughout the network. Prior work has explored differences in seizure semiology to describe primary and secondary zones of dysfunction (Nair et al., 2004; Rosenow and Luders, 2001). Others have identified strong, tightly connected network hubs localized in areas outside of the seizure-generating region that indicate a wider extent of network damage (Rummel et al., 2013; Schevon et al., 2007; Zaveri et al., 2009). Our results support the view that tissue surrounding the seizure-generating area displays abnormalities that support seizure evolution. Specifically, we observe the presence of putative control nodes within a broader heterogeneous network that may serve to oppose seizure spread by limiting synchronizability of healthy activity states.
Our findings support the existence of a control system that manages the degree of synchrony in the cortical network, and therefore may have important neurobiological implications. They raise questions such as, “What is the neuroanatomical substrate for network nodes that drive or contain seizures?” Might there be direct anatomical dysfunction such as loss of inhibitory inter-neurons, aberrant fiber-sprouting or changes in local gap junctions or ion channel expression that correlate with desynchronizing or synchronizing functional regions? Recent work at the cellular level indicates that seizure generation is complex, involving interactions between many neuronal subtypes both within and surrounding seizure-generating regions (Toyoda et al., 2015; Truccolo et al., 2011). Studies establishing a link between macroscale network structure and microscale neuroarchitectonics have demonstrated that heterogeneity of macroscale structure, such as regions of high and low node strengths often associated with the seizure-onset zone (Khambhati et al., 2015; Rummel et al., 2013; Schevon et al., 2007; Warren et al., 2010; Zaveri et al., 2009), is related to increasing complexity in the morphological structure of pyramidal neurons, a common post-synaptic site of excitatory neural activity (Scholtens et al., 2014; van den Heuvel et al., 2015). Prior work has demonstrated that strong γ-band activity at the site of interneurons can transition to β-band activity that is mediated by excitatory, pyramidal neuron activity through changes in excitatory synapses and potassium conductance (Kopell et al., 2000).
Through these data, we propose a mechanistic explanation for our observation that distributed seizures exhibited (i) greater pre-seizure network synchronizability in the high-γ-band and (ii) greater mid-seizure network synchronizability in the β-band compared to focal seizures. Put simply, strong high-γ-band activity, that is perhaps localized to interneurons, during the pre-seizure epoch drives excitatory, pyramidal neuron activity that then induces a mid-seizure transition towards β-band activity in interneurons, which can extend over long distances and facilitate seizure propagation. Moreover, differences in pre-seizure synchronizability of high-γ-band functional interactions can be explained by studies of brain chemoarchitecture that have demonstrated a relationship between the strength of functional connectivity between brain regions and the ratio of excitatory and inhibitory neurotransmitters in underlying neuron populations (Buzsáki and Wang, 2012; Kopell et al., 1999; Turk et al., 2016). From these studies and our own findings, we infer that increased excitatory, high-γ activity in pyramidal neurons, which drives the subsequent transition to β-band activity during seizure spread, is driven by desynchronizing controllers that are weaker in distributed networks than focal networks. Consequently, desynchronizing controllers are stronger when there is a presumably greater inhibition relative to excitation in the network. This theory would also explain how strong desynchronizing controllers of focal networks might increase inhibition in interneurons and limit transitions of interneuron rhythmic activity to the β-band and thereby contain seizure spread. These results may underpin a neurobiological role for desynchronizing and synchronizing network controllers in modulating imbalances in neural excitation and inhibition before and during seizures. Relating correlates of dysfunction from node resection and electrophysiologic studies to underlying neuroanatomy in applications of targeted drug-delivery remains a promising area of epilepsy research.
Push-Pull Control Titrates Network Synchronizability
Controllability of brain networks is a burgeoning area of network neuroscience, particularly in the study of large-scale brain areas and the distributed circuits that they constitute (Bassett et al., 2006; Gu et al., 2014; Taylor et al., 2015). However, an understanding of the principles of brain network control may have even greater impact in the context of meso-scale brain networks, where local neural populations frequently switch between a wide variety of normal and abnormal rhythmic neural processes. Using virtual cortical resection, we observed the presence of specific nodes whose placement in the wider network suggests their critical role in controlling synchronization and desynchronization in seizure dynamics. These key areas display antithetical potential for controlling activity dynamics, and therefore we speculate that they may employ an antagonistic, push-pull control mechanism similar to that described in theoretical work in other systems (He et al., 2014). Mechanistically, synchronizing controllers theoretically pull the network towards a particular synchronous state, and, conversely, desynchronizing controllers push the network away from these states. Such a potential neurobiological mechanism also aligns with the recently proposed Epileptor model of seizure dynamics, where any brain network might be capable of seizure generation depending on its vulnerability to crossing a critical separatrix barrier (Jirsa et al., 2014; Naze et al., 2015). In the framework of the Epileptor, our results suggest that synchronizing and desynchronizing nodes might regulate a critical level of network synchronizability and prevent the extent to which the network crosses a separatrix.
Relevance to Basic and Translational Neuroscience
We speculate that dysfunction of neural circuits in other brain network disorders might also be explained by irregularities in cortical push-pull control mechanisms. For instance, in healthy brain the excitatory and inhibitory pathways of the basal ganglia operate in concert as a push-pull system to control neural activity in the neocortex and brainstem for executive motor function (Graybiel, 1996; Uhlhaas and Singer, 2006). Imbalances in either of these pathways may lead to hypo- or hyperkinetic dysfunction of the basal ganglia in Parkinson's Disease. The tools we present may provide a convenient way to vet new circuit targets in this disorder, when applied to multi-unit or local field recordings across these networks. Surgical lesioning of direct or indirect pathways via deep brain stimulation is a common method for re-balancing the putative push-pull control system and treating Parkinson's. It is intuitively plausible that virtual cortical resection of the basal ganglia network may provide an opportunity to improve localization of control hubs as targets for stimulation.
Imbalances in synchronization have also been found in separate studies of patients with schizophrenia, autism, and Alzheimer's disease (Uhlhaas and Singer, 2006). Brain networks in schizophrenia may be unable to achieve a sufficient degree of synchronization between distant brain networks through corticothalamocortico loops. As a result of decreased control in local brain regions, significant local synchronization may underlie common symptoms such as hallucinations. Similar mechanisms of imbalances that result in hyperexcitation in autism and reduction of synchronization in Alzheimer's disease have been suggested (Uhlhaas and Singer, 2006). The virtual cortical resection method we describe here might point to important network control regions as the source of dysfunction in adequate regulation of network synchronization.
While our results support push-pull mechanisms in meso-scale cortical networks, competitive binding strategies that the brain employs for internally coordinating dynamics in distributed networks through synchronization and desynchronization bear striking similarity to push-pull control mechanisms (Singer, 1999). Push-pull relationships have also explained cognitive control in large-scale brain networks. Antagonistic interactions between internally oriented processing in default mode network and a more distributed external attention system may support the notion that push-pull control assists in dynamically balancing metabolic resources geared towards introspective and extrospective processing (Fornito et al., 2012). And, evidence for an error correction system that mediates goal-directed tasks has been found in network interactions between prefrontal brain regions (Cavanagh et al., 2009). Further work has posited that the flexibility of connections that drives network reorganization may also explain how the brain regulates the degree of competition between opposing cognitive systems (Cocchi et al., 2013). From the perspective of push-pull control, network flexibility might help titrate synchronizability within a critical boundary of order and disorder in distributed networks (Bassett et al., 2006; Bassett et al., 2015). By exploring applications of virtual resection to brain networks during cognitive tasks, we may pinpoint brain areas that coordinate widespread interactions in the brain via push-pull control strategies.
In more basic science applications, our methods could have a role in decomposing network interactions in a variety of circuit investigations. One important feature of our methods is that they can be applied across scales and modalities, as network measures can be applied to signals as diverse as videos from optogenetic recordings, to “inscopix” videos of large numbers of neuronal calcium images, to more standard multi-electrode array studies distributed spatially across the brain. Applying our virtual resection technique across modalities could provide a unique approach to characterize circuit behavior across multiple scales and its components without a priori knowledge of functional divisions.
Methodological Considerations
An important clinical consideration related to this work is the sampling error inherent in any intracranial implantation procedure. Any of the techniques used to map epileptic brain usually yield incomplete representations of the epileptic network. It is not possible to fully record from the entirety of cortex in affected patients, at least not with technologies currently available. In some cases, this might mean that neither seizure onset zones nor all regions of seizure spread are fully delineated. These are problems that are limitations of epilepsy surgery, though usually clinical symptoms, brain imaging and video recording of seizures steer recordings to reasonably target the epileptic network. If successful, at least for superficial neocortical networks, magnetoencephalography (MEG) studies may provide a non-invasive method to delineate the epileptic network without invasive electrode placement. Even with some degree of sampling error, in this work we apply virtual cortical resection to study a single topological metric: network synchronizability. This will guide recordings at least to regions coupled to networks, in worst case, and we expect to rapidly understand signature of main seizure generators that will help guide us to identify and interpret under-sampled studies.
“The terms that we have used throughout the development of this work have important similarities and differences to other related terms used in the neuroscience, mathematics, and physics literature. For a careful description of these similarities and differences, see the Supplemental Information, and for a broader description of some of these concepts in the physics and mathematics literature, see these two books (Pikovsky et al., 2003; Strogatz, 2003).
Clinical Impact
Isolating the natural control mechanisms of brain function is critical for clinical translation. Enhancing and disrupting these natural control mechanisms could be a viable approach for introducing therapy with implantable devices for network disorders like epilepsy, in addition to resective surgery. Current methods of treating drug-resistant epilepsy rely on surgical resection or, more recently, implantable devices. However, predicting network response to therapy remains challenging. The virtual cortical resection technique is a novel, objective method of probing robustness and fragility upon removing components of the epileptic network. Using this method, we pinpointed putative network controllers that may be crucial for seizure evolution - suggesting that resection of these regions may compromise key mechanisms to contain seizure activity.
This technique will require careful retrospective, and then prospective, trials to validate its utility. Critical challenges include: (i) how to target functional connections based upon removal of cortical tissue? And, (ii) to determine if network models can account for neural plasticity after node removal, such as unmasking of latent cortical connectivity (Jacobs and Donoghue, 1991). By honing network models to better capture structural and functional relationships in the brain, virtual cortical resection may allow clinicians to predict response to therapy and provide a quantitative guide to what is now a process guided by manual interpretation of ECoG recordings.
Finally, the clinical implications of this technique may reach beyond guided electrode placement for anti-epileptic devices. In particular, these studies might open the way towards more accurate electrophysiologically-guided cortical resection or perhaps pinpointed thermal ablation to specific network regions, similar to procedures performed by cardiac electrophysiologists. These potential applications, while not immediately possible, offer considerable clinical advantages over the large cortical resections performed currently, with modest seizure-freedom rates. It is also likely that they will open the door to a host of other applications in movement, cognitive, affective and psychiatric disorders.
Experimental Procedures
Patient Data Sets
Ethics Statement
All patients included in this study gave written informed consent in accordance with the Institutional Review Board of the University of Pennsylvania.
Electrophysiology Recordings
Ten patients undergoing surgical treatment for medically refractory epilepsy believed to be of neocortical origin underwent implantation of subdural electrodes to localize the seizure onset zone after presurgical evaluation with scalp EEG recording of ictal epochs, MRI, PET and neuropsychological testing suggested that focal cortical resection may be a therapeutic option. Patients were then deemed candidates for implantation of intracranial electrodes to better define the epileptic network. De-identified patient data was retrieved from the online International Epilepsy Electrophysiology Portal (IEEG Portal) (Wagenaar et al., 2013).
ECoG signals were recorded and digitized at 500 Hz sampling rate using Nicolet C64 amplifiers and pre-processed to eliminate line noise. Cortical surface electrode (Ad Tech Medical Instruments, Racine, WI) configurations, determined by a multidisciplinary team of neurologists and neurosurgeons, consisted of linear and two-dimensional arrays (2.3 mm diameter with 10 mm inter-contact spacing) and sampled the neocortex for epileptic foci (depth electrodes were first verified as being outside the seizure onset zone and subsequently discarded from this analysis). Signals were recorded using a referential montage with the reference electrode, chosen by the clinical team, distant to the site of seizure onset and spanned the duration of a patient's stay in the epilepsy monitoring unit. See Table 1 for demographic and clinical information.
Table 1. Patient information.
Patient data sets accessed through IEEG Portal (http://www.ieeg.org). Age at first reported onset and at phase II monitoring. Localization of seizure onset and etiology is clinically-determined through medical history, imaging, and long-term invasive monitoring. Seizure types are SP (simple-partial), CP (complex-partial), CP+GTC (complex-partial with secondary generalization). Counted seizures were recorded in the epilepsy monitoring unit. Clinical imaging analysis concludes L, Lesion; NL, non-lesion. Surgical outcome was based on Engel score (scale: I-IV, seizure freedom to no improvement; NR, no-resection). M, male; F, female.
| Patient (IEEG Portal) |
Sex | Age (Onset) |
Age (Surgery) |
Seizure Onset |
Etiology | Seizure Type (#) |
Imaging | Outcome |
|---|---|---|---|---|---|---|---|---|
| HUP64_phaseII | M | 03 | 20 | Left frontal | Dysplasia | CP+GTC (1) |
L | I |
| HUP65_phaseII | M | 02 | 36 | Right temporal |
Auditory reflex |
CP+GTC (3) |
N/A | I |
| HUP68_phaseII | F | 15 | 26 | Right temporal |
Meningitis | CP (1), CP+GTC (4) |
NL | I |
| HUP70_phaseII | M | 10 | 32 | Left perirolandic |
Cryptogenic | SP (8) | L | NR |
| HUP72_phaseII | F | 11 | 27 | Bilateral left |
Mesial temporal sclerosis |
CP+GTC (1) |
L | NR |
| HUP73_phaseII | M | 11 | 39 | Anterior right frontal |
Meningitis | CP+GTC (5) |
NL | I |
| HUP78_phaseII | M | 00 | 54 | Anterior left temporal |
Traumatic injury |
CP (5) | L | III |
| HUP79_phaseII | F | 11 | 39 | Occipital | Meningitis | CP (2) | L | NR |
| HUP86_phaseII | F | 18 | 25 | Left temporal |
Cryptogenic | CP+GTC (2) |
NL | II |
| HUP87_phaseII | M | 21 | 24 | Frontal | Meningitis | CP (2) | L | I |
Description of Epileptic Events
We analyzed 18 partial seizures (simple and complex) and 16 partial seizures that generalized to surrounding tissue, forming a population of the focal and distributed epileptic networks, respectively. Of the 10 epilepsy patients in the study cohort, 5 patients exhibited strictly complex-partial seizures that secondarily generalized (distributed events), 4 patients exhibited strictly simple-partial or complex-partial seizures that did not secondarily generalize (focal events), and 1 patient exhibited 4 distributed events and 1 focal event (see Table 1). Seizure type, onset time, and onset localization were marked as a part of routine clinical workup.
The seizure state spanned the period between clinically-marked earliest electrographic change (EEC) (Litt et al., 2001) and termination; and the pre-seizure state spanned a period equal in duration to the seizure state and ended immediately prior to the EEC. Note that we refer to each pair of pre-seizure and seizure states as an event.
Clinical Marking of the Seizure Onset Zone
Seizure onset zone was marked on the Intracranial EEG (IEEG) according to standard clinical protocol in the Penn Epilepsy Center. Initial clinical markings are made on the IEEG the day of each seizure by the attending physician, always a board certified, staff epileptologist responsible for that inpatient's care. Each week these IEEG markings are vetted in detail, and then finalized at surgical conference according to a consensus marking of 4 board certified epileptologists together. These markings on the IEEG are then related to other multi-modality testing, such as brain MRI, PET scan, Neuropsychological testing, ictal SPECT scanning and Magnetoenecephalographic findings to finalize surgical approach and planning. This process is standard of clinical care at National Association of Epilepsy Centers (NAEC) - certified Level-4 epilepsy centers in the United States.
Functional Network Construction
Pre-Processing
ECoG signals from each event were divided into 1s, non-overlapping, weakly stationary time-windows in accord with related studies (Kramer et al., 2010). To measure functional interactions between ECoG signals in each time window, we computed spectral coherence (i.e. a measure of correlation between the power spectra of two signals within a frequency range). Prior studies have shown that coherence is largely independent of the shape of the power spectrum in ECoG signals (Bullock et al., 1995a; Bullock et al., 1995b; Towle et al., 1999), that high-γ-band interactions can describe phenomena of seizure generation (Warren et al., 2010; Worrell et al., 2008) and seizure spread (Korzeniewska et al., 2014; Weiss et al., 2013; Weiss et al., 2015), and that coherence in high-γ-band is sensitive to neural interactions at distances greater than 2 cm (Towle et al., 1999). While signal artifact related to muscle contraction of eye movement is not commonly observed in the electrocorticogram, because the electrodes lay on the subdural surface of the brain, closer to the source, rather than on the surface of the scalp as in EEG (Kern et al., 2009), it is addressed, in addition to other potential sources of correlated noise (e.g. power line noise (60 Hz), instrumentation noise, thermal noise, biological noise, and volume conduction) using common average referencing (Ludwig et al., 2009). Conventional referencing techniques involve subtracting neural signals with respect to a single reference source, which presumably retains correlated noise due to differences in electrode impedance, which secondarily affect signal amplitude, and differences in distance to the noise source generator. Therefore, more recent studies have begun using a common average referencing technique (Burns et al., 2014; Khambhati et al., 2015; Kramer et al., 2010; Kramer et al., 2011; Towle et al., 1999), the current state-of-the-art, to reduce noise by at least 30% and to improve the yield of discernible neuronal activity by ~60% (Ludwig et al., 2009). Specifically, this technique is shown to mitigate the effects of correlated noise such as motion artifact and volume conduction (Ludwig et al., 2009; Towle et al., 1999). Another study that has explored the reliability of using coherence to estimate functional interactions at the scale of ECoG, concludes that coherence between brain regions has very low coefficient of variation (~0.5%, computed over 20 minute baseline epochs) and is highly robust to surrogate models where coherence is computed after randomizing phase relationships between sensors (Towle et al., 1999).
Coherence Estimation
We constructed functional networks in each time-window using multitaper coherence estimation, which defines a network connection between electrode pairs as the power spectral similarity of signal activity over a specific frequency band. We applied the mtspec Python implementation (Prieto et al., 2009) of multitaper coherence estimation with time-bandwidth product of 5 and 8 tapers in accord with related studies (Kramer et al., 2011). This procedure resulted in a symmetric adjacency matrix A(t) with size N x N, where N is the number of network nodes, or electrode sensors. Based on a vast literature implicating high-frequency oscillations and γ-band activity as drivers of epileptic activity, we primarily studied functional connectivity in the high-γ-band band (95–105 Hz). This frequency range represents relatively local neural population dynamics that are largely unaffected by volume conduction. See the Supplemental Information for complementary results in the α/θ (5–15 Hz), β (15–25 Hz), and low-γ (30–40 Hz) bands.
Metrics of the Time-Varying Functional Network
Network Topology
In our network analysis, we refer to heterogeneity of network architecture in the context of node strength, also known as weighted degree. Node strength D(t) is computed as the average connection strength of all functional connections of a particular node in a given time window t. To measure the time-varying quantity of network heterogeneity d(t): the dispersion of the node strengths in each time window, we computed the log10 of the standard deviation of node strengths.
Network Synchronizability
A recent trend in studying functional networks is to model dynamic geometric structure that evolves through system states (Burns et al., 2014; Khambhati et al., 2015; Rummel et al., 2013; Wulsin et al., 2013). Building on the classical notion of stability of the synchronized state in static networks, we fit a popular synchronizability model for weighted, dynamic networks (Gómez et al., 2013) to account for time-varying structure of the functional networks in our study. As a simplification for our analysis, we analyze each time-window separately.
To quantify synchronizability, we first estimated the weighted, time-varying Laplacian matrix L(t) for each time-window t of the functional network (Gómez et al., 2013). The Laplacian matrix is computed as the difference between the diagonal matrix of node strength and the adjacency matrix, such that: L(t) = D(t) – A(t). Intuitively, each entry lij(t) of L(t) can be interpreted as a measure of how easily information could diffuse between nodes i and j based on the relative connectivities of both nodes to all other nodes in the network. Next, we computed the eigenspectrum of L(t) and calculated the ratio of the second-smallest eigenvalue λ2 to the largest eigenvalue λmax for each t, resulting in time-varying network synchronizability (larger values of s(t) correspond to greater state stability) (Barahona and Pecora, 2002). The Supplemental Information provides details of the master stability function formalism behind synchronizability and its relationship to state stability.
Virtual Cortical Resection
To model potential effects of resecting or lesioning regions of brain networks, we develop a virtual cortical resection technique. Generally, the approach allows us to ask how network topology might change upon removing one or more nodes or connections in the network. In time-varying networks, virtual cortical resections may be useful in patterned lesioning schemes for implantable devices that continuously modulate brain state away from seizures (Afshar et al., 2013; Stanslaski et al., 2012).
Here, we tailored virtual cortical resection to study putative controllers that regulate synchronizability in the epileptic network. We measure the control centrality, the contribution of a node to network synchronizability, by applying virtual cortical resection to each node in each time window of the functional network. The control centrality identifies a node as a desynchronizing (ci > +ε), synchronizing (ci < −ε), or bulk (−ε < ci < +ε) controller. To determine the boundaries posed by ε, we computed a null model of control centrality by generating 100 randomly rewired functional networks with uniformly permuted connections, for each time-window t, and applying virtual cortical resection to each node. The upper 97.5% and lower 2.5% of control centrality values of the null distribution were taken as +ε and −ε, respectively. The Supplemental Information explores the relationship between control centrality and other topological properties of networks.
Functional Data Analysis
We compared time-varying network metrics between partial seizures that remain focal and partial seizures that generalize to surrounding tissue. We performed this comparison by (i) normalizing each seizure event into 10 sequential time-bins spanning the pre-seizure and seizure epochs and (ii) employing functional data analysis to statistically test differences in temporal dynamics between seizure type, independently in each state. We assigned p-values to each state by re-assigning events uniformly at random to seizure types up to 1,000,000 times and computing the mean area between the resulting functional curves.
Supplementary Material
Highlights.
Khambhati et al. (2016) ask: “How does the human epileptic brain control seizure spread?” They find a network control mechanism that regulates dynamics of neural synchronization in advance of seizures – providing critical insight into the mechanisms of brain self-regulation.
Functional network synchronizability predicts spread of seizures, before they begin
Virtual cortical resection reveals network regions that control synchronization
Control regions strongly synchronize or desynchronize network dynamics
Weakened push-pull antagonism between control region explains why seizures spread
Acknowledgments
ANK and BL acknowledge support from the National Institutes of Health through awards #R01-NS063039, #1U24 NS63930-01A1, Neil and Barbara Smit, the Citizens United for Research in Epilepsy (CURE) through Julie's Hope Award, and the Mirowski Foundation. DSB acknowledges support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the Army Research Laboratory and the Army Research Office through contract numbers W911NF-10-2-0022 and W911NF-14-1-0679, the National Institute of Child Health and Human Development (1R01HD086888-01), the Office of Naval Research, and the National Science Foundation (BCS-1441502 and BCS-1430087). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Author Contributions
ANK, KAD, BL, DSB conceived and designed the experiments. KAD, THL, BL collected the data. ANK performed the experiments. ANK, BL, DSB analyzed the data. ANK, KAD, THL, BL, DSB wrote the paper.
References
- Afshar P, Khambhati AN, Stanslaski S, Carlson D, Jensen R, Linde D, Denison T. A translational platform for prototyping closed-loop neuromodulation systems. Frontiers in Neural Circuits. 2013;6:1–15. doi: 10.3389/fncir.2012.00117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alstott J, Breakspear M, Hagmann P, Cammoun L, Sporns O. Modeling the impact of lesions in the human brain. PLoS Computational Biology. 2009;5(6) doi: 10.1371/journal.pcbi.1000408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barahona M, Pecora LM. Synchronization in Small-World Systems. Physical Review Letters. 2002;89(5) doi: 10.1103/PhysRevLett.89.054101. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Brown JA, Deshpande V, Carlson JM, Grafton ST. Conserved and variable architecture of human white matter connectivity. NeuroImage. 2011;54(2):1262. doi: 10.1016/j.neuroimage.2010.09.006. [DOI] [PubMed] [Google Scholar]
- Bassett DS, Meyer-Lindenberg A, Achard S, Duke T, Bullmore E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proceedings of the National Academy of Sciences. 2006;103(51):19518–19523. doi: 10.1073/pnas.0606005103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, Yang M, Wymbs NF, Grafton ST. Learning-Induced Autonomy of Sensorimotor Systems. Nature Neuroscience. 2015;18(5):744–751. doi: 10.1038/nn.3993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bower MR, Stead M, Meyer FB, Marsh WR, Worrell GA. Spatiotemporal neuronal correlates of seizure generation in focal epilepsy. Epilepsia. 2012;53(5):807–816. doi: 10.1111/j.1528-1167.2012.03417.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullock TH, Mcclune MC, Achimowicz JZ, Iragui-Madoz VJ, Duckrow RB, Spencer SS. EEG coherence has structure in the millimeter domain: subdural and hippocampal recordings from epileptic patients. Electroencephalography and Clinical Neurophysiology. 1995;95(3):161–177. doi: 10.1016/0013-4694(95)93347-a. [DOI] [PubMed] [Google Scholar]
- Bullock TH, McClune MC, Achimowicz JZ, Iragui-Madoz VJ, Duckrow RB, Spencer SS. Temporal fluctuations in coherence of brain waves. Proceedings of the National Academy of Sciences of the United States of America. 1995;92(25):11568–11572. doi: 10.1073/pnas.92.25.11568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burns SP, Santaniello S, Yaffe RB, Jouny CC, Crone NE. Network dynamics of the brain and influence of the epileptic seizure onset zone. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(49):E5321–E5330. doi: 10.1073/pnas.1401752111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G, Wang X-J. Mechanisms of Gamma Oscillations. Annual Review of Neuroscience. 2012;35:203–225. doi: 10.1146/annurev-neuro-062111-150444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanagh JF, Cohen MX, Allen JJB. Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2009;29(1):98–105. doi: 10.1523/JNEUROSCI.4137-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocchi L, Zalesky A, Fornito A, Mattingley JB. Dynamic cooperation and competition between brain systems during cognitive control. Trends in Cognitive Sciences. 2013;17(10):493–501. doi: 10.1016/j.tics.2013.08.006. [DOI] [PubMed] [Google Scholar]
- Fornito A, Harrison BJ, Zalesky A, Simons JS. Competitive and cooperative dynamics of large-scale brain functional networks supporting recollection. Proceedings of the National Academy of Sciences. 2012;109(31) doi: 10.1073/pnas.1204185109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gómez S, Díaz-Guilera A, Gómez-Gardeñes J, Pérez-Vicente CJ, Moreno Y, Arenas A. Diffusion Dynamics on Multiplex Networks. Physical Review Letters. 2013;110(2):028701. doi: 10.1103/PhysRevLett.110.028701. [DOI] [PubMed] [Google Scholar]
- Graybiel AM. Basal ganglia: New therapeutic approaches to Parkinson’s disease. Current Biology. 1996;6(4):368–371. doi: 10.1016/s0960-9822(02)00497-9. [DOI] [PubMed] [Google Scholar]
- Gu S, Pasqualetti F, Cieslak M, Grafton ST, Bassett DS. Controllability of Brain Networks. arXiv Preprint arXiv:1406.5197. 2014;14 [Google Scholar]
- He Z, Wang X, Zhang G-Y, Zhan M. Control for a synchronization-desynchronization switch. Physical Review E. 2014;90(1):012909. doi: 10.1103/PhysRevE.90.012909. [DOI] [PubMed] [Google Scholar]
- Honey CJ, Sporns O. Dynamical consequences of lesions in cortical networks. Human Brain Mapping. 2008;29(7):802–809. doi: 10.1002/hbm.20579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacobs KM, Donoghue JP. Reshaping the cortical motor map by unmasking latent intracortical connections. Science (New York, N.Y.) 1991;251(4996):944–947. doi: 10.1126/science.2000496. [DOI] [PubMed] [Google Scholar]
- Jirsa VK, Stacey WC, Quilichini PP, Ivanov AI, Bernard C. On the nature of seizure dynamics. Brain. 2014;137(Pt 8):2210–2230. doi: 10.1093/brain/awu133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiruska P, de Curtis M, Jefferys JGR, Schevon CA, Schiff SJ, Schindler K. Synchronization and desynchronization in epilepsy: controversies and hypotheses. The Journal of Physiology. 2013;591(Pt 4):787–797. doi: 10.1113/jphysiol.2012.239590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kern M, Ball T, Lahr J, Mutschler I, Aertsen A, Schulze-Bonhage A. Signal Quality of Simultaneously Recorded ECoG and Non-Invasive EEG: Results from Analysis of Spontaneous Eye Blinks and Saccades. NeuroImage. 2009 May;47:S126. doi: 10.1016/j.neuroimage.2009.02.028. 2016. [DOI] [PubMed] [Google Scholar]
- Khambhati AN, Davis KA, Oommen BS, Chen SH, Lucas TH, Litt B, Bassett DS. Dynamic Network Drivers of Seizure Generation, Propagation and Termination in Human Neocortical Epilepsy. PLOS Computational Biology. 2015;11(12):e1004608. doi: 10.1371/journal.pcbi.1004608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kopell N, Ermentrout GB, Whittington MA, Traub RD. Gamma rhythms and beta rhythms have different synchronization properties. Proceedings of the National Academy of Sciences of the United States of America. 2000;97(4):1867–1872. doi: 10.1073/pnas.97.4.1867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korzeniewska A, Cervenka MC, Jouny CC, Perilla JR, Harezlak J, Bergey GK, Crone NE. Ictal propagation of high frequency activity is recapitulated in interictal recordings: Effective connectivity of epileptogenic networks recorded with intracranial EEG. NeuroImage. 2014;101:96–113. doi: 10.1016/j.neuroimage.2014.06.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MA, Cash SS. Epilepsy as a Disorder of Cortical Network Organization. The Neuroscientist. 2012;18(4):360–372. doi: 10.1177/1073858411422754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MA, Eden UT, Kolaczyk ED, Zepeda R, Eskandar EN, Cash SS. Coalescence and fragmentation of cortical networks during focal seizures. The Journal of Neuroscience : The Official Journal of the Society for Neuroscience. 2010;30(30):10076–10085. doi: 10.1523/JNEUROSCI.6309-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MA, Eden UT, Lepage KQ, Kolaczyk ED, Bianchi MT, Cash SS. Emergence of Persistent Networks in Long-Term Intracranial EEG Recordings. Journal of Neuroscience. 2011;31(44):15757–15767. doi: 10.1523/JNEUROSCI.2287-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutsy RL, Farrell DF, Ojemann GA. Ictal patterns of neocortical seizures monitored with intracranial electrodes: correlation with surgical outcome. Epilepsia. 1999;40(3):257–266. doi: 10.1111/j.1528-1157.1999.tb00702.x. [DOI] [PubMed] [Google Scholar]
- Litt B, Esteller R, Echauz J, D’Alessandro M, Shor R, Henry T, Vachtsevanos G. Epileptic seizures may begin hours in advance of clinical onset: A report of five patients. Neuron. 2001;30(1):51–64. doi: 10.1016/s0896-6273(01)00262-8. [DOI] [PubMed] [Google Scholar]
- Ludwig KA, Miriani RM, Langhals NB, Joseph MD, Anderson DJ, Kipke DR. Using a common average reference to improve cortical neuron recordings from microelectrode arrays. Journal of Neurophysiology. 2009;101(3):1679–1689. doi: 10.1152/jn.90989.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvid R, Ruiz A, Komotar RJ, Jagid JR, Ivan ME, Quencer RM, Desai MB. Current Applications of MRI-Guided Laser Interstitial Thermal Therapy in the Treatment of Brain Neoplasms and Epilepsy: A Radiologic and Neurosurgical Overview. American Journal of Neuroradiology. 2015 doi: 10.3174/ajnr.A4362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrell MJ. Responsive cortical stimulation for the treatment of medically intractable partial epilepsy. Neurology. 2011;77(13):1295–1304. doi: 10.1212/WNL.0b013e3182302056. [DOI] [PubMed] [Google Scholar]
- Nair DR, Mohamed A, Burgess R, Lüders H. A critical review of the different conceptual hypotheses framing human focal epilepsy. Epileptic Disorders: International Epilepsy Journal with Videotape. 2004;6(2):77–83. [PubMed] [Google Scholar]
- Naze S, Bernard C, Jirsa V. Computational modeling of seizure dynamics using coupled neuronal networks: factors shaping epileptiform activity. PLoS Computational Biology. 2015;11(5):e1004209. doi: 10.1371/journal.pcbi.1004209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pikovsky A, Rosenblum M, Kurths J. Synchronization: a universal concept in nonlinear sciences. Vol. 12. Cambridge university press; 2003. [Google Scholar]
- Prieto Ga, Parker RL, Vernon FL. A Fortran 90 library for multitaper spectrum analysis. Computers and Geosciences. 2009;35(8):1701–1710. [Google Scholar]
- Rafal RD, Koller K, Bultitude JH, Mullins P, Ward R, Mitchell AS, Bell AH. Connectivity between the superior colliculus and the amygdala in humans and macaque monkeys: virtual dissection with probabilistic DTI tractography. Journal of Neurophysiology. 2015;114(3):1947–1962. doi: 10.1152/jn.01016.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenow F, Luders H. Presurgical evaluation of epilepsy patients. Brain. 2001;124:1683–1700. doi: 10.1093/brain/124.9.1683. [DOI] [PubMed] [Google Scholar]
- Rummel C, Goodfellow M, Gast H, Hauf M, Amor F, Stibal A, Schindler K. A systems-level approach to human epileptic seizures. Neuroinformatics. 2013;11(2):159–173. doi: 10.1007/s12021-012-9161-2. [DOI] [PubMed] [Google Scholar]
- Schevon CA, Cappell J, Emerson R, Isler J, Grieve P, Goodman R, Gilliam F. Cortical abnormalities in epilepsy revealed by local EEG synchrony. NeuroImage. 2007;35(1):140–148. doi: 10.1016/j.neuroimage.2006.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindler KA, Bialonski S, Horstmann M-T, Elger CE, Lehnertz K. Evolving functional network properties and synchronizability during human epileptic seizures. Chaos (Woodbury, N.Y.) 2008;18(3):033119. doi: 10.1063/1.2966112. [DOI] [PubMed] [Google Scholar]
- Scholtens LH, Schmidt R, de Reus Ma, van den Heuvel MP. Linking macroscale graph analytical organization to microscale neuroarchitectonics in the macaque connectome. Journal of Neuroscience. 2014;34(36):12192–1205. doi: 10.1523/JNEUROSCI.0752-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singer W. Neuronal Synchrony: A Versatile Code for the Definition of Relations? Neuron. 1999;24 doi: 10.1016/s0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
- Spencer SS. Neural Networks in Human Epilepsy: Evidence of and Implications for Treatment. Epilepsia. 2002;43(3):219–227. doi: 10.1046/j.1528-1157.2002.26901.x. [DOI] [PubMed] [Google Scholar]
- Stacey WC, Litt B. Technology insight: neuroengineering and epilepsy-designing devices for seizure control. Nature Clinical Practice. Neurology. 2008;4(4):190–201. doi: 10.1038/ncpneuro0750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stanslaski S, Afshar P, Cong P, Giftakis J, Stypulkowski P, Carlson D, Denison T. Design and validation of a fully implantable, chronic, closed-loop neuromodulation device with concurrent sensing and stimulation. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2012;20(4):410–421. doi: 10.1109/TNSRE.2012.2183617. [DOI] [PubMed] [Google Scholar]
- Strogatz S. Sync: The emerging science of spontaneous order. Hyperion; 2003. [Google Scholar]
- Taylor PN, Thomas J, Sinha N, Dauwels J, Kaiser M, Thesen T, Ruths J. Optimal control based seizure abatement using patient derived connectivity. Frontiers in Neuroscience. 2015 Jun;9:1–10. doi: 10.3389/fnins.2015.00202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tovar-Spinoza Z, Carter D, Ferrone D, Eksioglu Y, Huckins S. The use of MRI-guided laser-induced thermal ablation for epilepsy. Child’s Nervous System. 2013;29(11):2089–2094. doi: 10.1007/s00381-013-2169-6. [DOI] [PubMed] [Google Scholar]
- Towle VL, Carder RK, Khorasani L, Lindberg D. Electrocorticographic coherence patterns. Journal of Clinical Neurophysiology: Official Publication of the American Electroencephalographic Society. 1999 doi: 10.1097/00004691-199911000-00005. [DOI] [PubMed] [Google Scholar]
- Toyoda I, Fujita S, Thamattoor AK, Buckmaster PS. Unit Activity of Hippocampal Interneurons before Spontaneous Seizures in an Animal Model of Temporal Lobe Epilepsy. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2015;35(16):6600–6618. doi: 10.1523/JNEUROSCI.4786-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Truccolo W, Donoghue Ja, Hochberg LR, Eskandar EN, Madsen JR, Anderson WS, Cash SS. Single-neuron dynamics in human focal epilepsy. Nature Neuroscience. 2011;14(5):635–641. doi: 10.1038/nn.2782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turk E, Scholtens LH, van den Heuvel MP. Cortical chemoarchitecture shapes macroscale effective functional connectivity patterns in macaque cerebral cortex. Human Brain Mapping. 2016 Aug;1865 doi: 10.1002/hbm.23141. 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhlhaas PJ, Singer W. Neural Synchrony in Brain Disorders: Relevance for Cognitive Dysfunctions and Pathophysiology. Neuron. 2006;52(1):155–168. doi: 10.1016/j.neuron.2006.09.020. [DOI] [PubMed] [Google Scholar]
- van den Heuvel MP, Scholtens LH, de Reus MA, Kahn RS. Associated Microscale Spine Density and Macroscale Connectivity Disruptions in Schizophrenia. Biological Psychiatry. 2015:1–9. doi: 10.1016/j.biopsych.2015.10.005. [DOI] [PubMed] [Google Scholar]
- Wagenaar JB, Brinkmann BH, Ives Z, Worrell A, Litt B, Member S. A Multimodal Platform for Cloud - based Collaborative Research. 6th Annual International IEEE EMBS Conference on Neural Engineering; IEEE; 2013. pp. 6–8. [Google Scholar]
- Wang XF, Chen G. Synchronization in scale-free dynamical networks: Robustness and fragility. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications. 2002;49(1):54–62. [Google Scholar]
- Warren CP, Hu S, Stead M, Brinkmann BH, Bower MR, Worrell GA. Synchrony in normal and focal epileptic brain: the seizure onset zone is functionally disconnected. Journal of Neurophysiology. 2010;104(6):3530–3539. doi: 10.1152/jn.00368.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss SA, Banks GP, McKhann GM, Goodman RR, Emerson RG, Trevelyan AJ, Schevon CA. Ictal high frequency oscillations distinguish two types of seizure territories in humans. Brain: A Journal of Neurology. 2013;136(Pt 12):3796–3808. doi: 10.1093/brain/awt276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss SA, Lemesiou A, Connors R, Banks GP, McKhann GM, Goodman RR, Schevon CA. Seizure localization using ictal phase-locked high gamma: A retrospective surgical outcome study. Neurology. 2015;84(23):2320–2328. doi: 10.1212/WNL.0000000000001656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke C, Worrell G, He B. Graph analysis of epileptogenic networks in human partial epilepsy. Epilepsia. 2011;52(1):84–93. doi: 10.1111/j.1528-1167.2010.02785.x. http://doi.org/10.1111/j.1528-1167.2010.02785.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worrell GA, Gardner AB, Stead SM, Hu S, Goerss S, Cascino GJ, Litt B. High-frequency oscillations in human temporal lobe: simultaneous microwire and clinical macroelectrode recordings. Brain: A Journal of Neurology. 2008;131(Pt 4):928–937. doi: 10.1093/brain/awn006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wulsin DF, Fox EB, Litt B, Fox EB. Parsing Epileptic Events Using a Markov Switching Process Model for Correlated Time Series-Supplementary Materials. ICML. 2013;2013:1–15. [Google Scholar]
- Zaveri HP, Pincus SM, Goncharova II, Duckrow RB, Spencer DD, Spencer SS. Localization-related epilepsy exhibits significant connectivity away from the seizure-onset area. Neuroreport. 2009;20(9):891–895. doi: 10.1097/WNR.0b013e32832c78e0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.