Neural signatures of experience-based improvements in deterministic decision-making

Abstract

Feedback about our choices is a crucial part of how we gather information and learn from our environment. It provides key information about decision experiences that can be used to optimize future choices. However, our understanding of the processes through which feedback translates into improved decision-making is lacking. Using neuroimaging (fMRI) and cognitive models of decision-making and learning, we examined the influence of feedback on multiple aspects of decision processes across learning. Subjects learned correct choices to a set of 50 word pairs across eight repetitions of a concurrent discrimination task. Behavioral measures were then analyzed with both a drift-diffusion model and a reinforcement learning model. Parameter values from each were then used as fMRI regressors to identify regions whose activity fluctuates with specific cognitive processes described by the models. The patterns of intersecting neural effects across models support two main inferences about the influence of feedback on decision-making. First, frontal, anterior insular, fusiform, and caudate nucleus regions behave like performance monitors, reflecting errors in performance predictions that signal the need for changes in control over decision-making. Second, temporoparietal, supplementary motor, and putamen regions behave like mnemonic storage sites, reflecting differences in learned item values that inform optimal decision choices. As information about optimal choices is accrued, these neural systems dynamically adjust, likely shifting the burden of decision processing from controlled performance monitoring to bottom-up, stimulus-driven choice selection. Collectively, the results provide a detailed perspective on the fundamental ability to use past experiences to improve future decisions.

1. Introduction

Decision-making is fundamentally influenced by past experiences. On a daily basis, we face numerous decisions requiring us to draw upon learned information to optimize our choice selection. This underlying information is acquired through experience, often by using feedback to assess the quality of decisions. Feedback thus provides a critical link between decision outcomes and mnemonic information that influences future choices. However, the processes and neural substrates that translate feedback into improved decision-making remain poorly understood.

The present study investigated how the neural systems that process feedback can influence subsequent decision-making behavior. Specifically, we used computational models of learning and choice selection to investigate how feedback influences decision-making in the context of repeated choice experiences with deterministic outcomes. In such contexts, feedback from a single choice can provide sufficient information to optimize future decisions involving the same choice. For example, if a student guesses that Harrisburg is the capital of Pennsylvania and is then told this answer is correct, the student gains valuable information that may help for later choices. In practice, however, the retrieval of learned information can be faulty, so repetition is typically required to attain optimum performance. These considerations, wherein outcome feedback and choice selection are conceptually linked, suggest that feedback processing and decision-making share a common set of neural substrates. We sought to characterize these substrates using functional magnetic resonance imaging (fMRI) combined with model-informed data analysis.

This work is guided by a literature on perceptual decisions and the impact of noisy sensory input, such as in tasks wherein subjects decide whether a noisy image depicts a face or a house (Heekeren et al., 2004; Dunovan et al., 2014; Tremel and Wheeler, 2015) or whether a cloud of dots with partial motion coherence is drifting leftward or rightward (Shadlen and Newsome, 2001). These perceptual decision processes are well characterized by sequential sampling models, such as the drift-diffusion model (Ratcliff, 1978; Ratcliff and McKoon 2008). In this class of model, a decision-variable accumulates evidence for or against a choice—when this value reaches a threshold, a decision is executed. As one makes a perceptual choice, competing sensory evidence is evaluated until a stopping criterion is reached. This process has been conceptually mapped onto physiological measures, wherein the firing rate of neurons modulates in a manner analogous to parameters within drift-diffusion models (Hanes and Schall, 1999; Shadlen and Newsome, 2001; Ratcliff et al., 2007; Roitman and Shadlen, 2002; Glimcher, 2003). Parallel neuroimaging work in humans has identified fMRI signatures of comparable processes (Ploran et al., 2007, 2011; Wheeler et al., 2008; Kayser et al., 2010a, 2010b) and connected these signatures directly to drift-diffusion parameters (Bowman et al., 2012; Tremel and Wheeler, 2015). Thus, the processes encapsulated by drift-diffusion models are neurally plausible and carry specific cognitive interpretations for underlying neural correlates based on past work.

Importantly, under the drift-diffusion framework, the source of information to be evaluated for a decision can derive from any of a number of systems (e.g., sensory, memory, etc.). Since the underlying information being evaluated is the the distinguishing characteristic of mnemonic versus perceptual decisions, the predictions of drift-diffusion models should hold for decisions wherein evidence is based on information gathered from experience. To support this extension, Yang and Shadlen (2007) trained monkeys to associate shapes with reward probabilities, and using a modified weather prediction task, linked changes in the firing rates of parietal neurons to the integration of probabilistic decision evidence acquired from training. In humans, Wheeler and colleagues (2014) demonstrated similar modulations of fMRI activity in occipital, temporal, and parietal regions that corresponded to sequences of presented probabilistic evidence. In both cases, decision evidence derived directly from arbitrary stimulus-response associations acquired through learning, supporting the link between drift-diffusion principles and decision-making in non-perceptual domains. On top of this, Frank et al. (2015) offered a direct connection by showing that changes in estimates of outcome reward (via probabilistic reinforcement learning) correlated with changes in model-estimated decision thresholds and that this relationship could be traced to activity in thalamic and medial frontal regions. The study’s approach, however, focused on specific cortico-striatal connections and did not directly consider the broader influence of feedback on decision processes or a feedback-based learning framework. Taken together, key findings from simple perceptual decisions seem to translate to the mnemonic domain, but the larger intersection between memory and decision-making remains unclear.

One fundamental unknown is how feedback influences decision-making processes and improves later behavior. This is especially applicable for deterministic or quasi-deterministic decisions, where the available choices always or nearly always produce the same outcome. Tricomi and Fiez (2008, 2012) made progress on this front by examining decision-making across multiple rounds of a paired-associate learning task. They found that feedback influenced both explicit and implicit memory, which together seemed to drive learning and subsequent decision-making. However, the Tricomi and Fiez work did not consider model-based connections between behavioral and neuroimaging data, and therefore could not draw inferences in the context of computationally defined feedback and decision-making processes.

The current study takes this next step by investigating the influence of feedback on decision processes during a concurrent discrimination learning task. In this task, subjects are presented with a pair of items, wherein one is arbitrarily designated as the correct choice, and the other as incorrect. After selecting an item, subjects see feedback that indicates the value of the choice (i.e., a correct or incorrect choice). With repeated experience of the items, subjects accrue mnemonic information and gain proficiency in making correct choices. At the same time, subjects could also accrue all of the mnemonic information necessary for perfect performance from a single decision experience. Thus, concurrent discrimination offers a meaningful framework with which to study how the encoding and accrual of past experiences translate into improved decision-making.

To capture these feedback-based learning influences, we implemented a reinforcement learning model alongside the drift-diffusion model. Reinforcement learning describes how a history of outcomes, built up for individual choices, creates a prediction of an outcome’s value that can be used to drive choice selection. Errors between the expected versus observed outcomes (reward prediction error, RPE) are used to adjust the expected value of a choice (EV) toward a more accurate representation of the actual result. Thus, measures derived from reinforcement learning can explain aspects of feedback processing in terms of a learning signal (RPE) and the consequence of that learning (EV). Neurally, these signals have been shown to be distinct and separable: in the context of probabilistic learning, each signal tends to localize to different areas, such as sub-regions of the basal ganglia and orbitofrontal cortex (Schultz et al., 1998, 2000). In the case of deterministic learning, such as concurrent discrimination, reinforcement learning should be equally applicable. In an extreme case, where mnemonic encoding and retrieval processes are entirely noise-free, the RPE signal from an initial choice should drive sufficient learning to ensure optimal choice selection for a future episode. Reinforcement learning can capture this type of single-trial learning, such that the initial RPE updates the EV to ensure future accuracy. While deterministic learning can be plausibly captured by reinforcement learning models, the extent to which estimates of RPE and EV exhibit the same neural localization and dissociations compared to probabilistic choice learning remains an open question. Regardless, like the drift-diffusion model, reinforcement learning has a set of distinct cognitive predictions that correspond to a set of distinct neural correlates.

Thus, the two models each describe aspects of learning and decision-making that, when combined, could offer unique leverage for understanding how feedback influences decision-making behavior, and how this influence is implemented neurally. The drift-diffusion model describes how information is evaluated to drive decision-making, whereas reinforcement learning describes how feedback shapes that information. As such, each model can distinguish between performance-related effects (e.g., boundary in the diffusion model and RPE in reinforcement learning) and evidence-related effects (e.g., drift-rate in the diffusion model and EV in reinforcement learning). When applied to neural data, these two models can be leveraged to identify regions associated with performance and evidence monitoring, versus regions that provide evidence to decision-making processes.

To investigate these relationships, we acquired behavioral and functional neuroimaging (fMRI) data during a concurrent discrimination task. Drift-diffusion and reinforcement learning models were fit to the learning behavior to describe separable aspects of decision-making and feedback processing. We then localized brain regions whose activity tracked with changes in the model parameters and tested for regional overlap in sensitivity to parameter changes across the two models. Overall, our goal was to meaningfully connect the neural substrates and cognitive processes related to the processing of outcome feedback with those related to decision-making.

2. Materials and Methods

2.1 Subjects

Twenty healthy, right-handed, fluent English speakers participated in a 1-hour behavioral and functional MRI session. Four subjects were excluded for excessive movement during scanning (N = 3) or incomplete data due to technical problems (N = 1), leaving 16 (12 female) subjects contributing to the final analyses. These subjects aged 19–31 years (mean 22.1) and had normal or corrected-to-normal vision. Informed consent was obtained from all subjects according to procedures approved by the University of Pittsburgh Institutional Review Board. Subjects were compensated $75 for their time.

2.2 Task

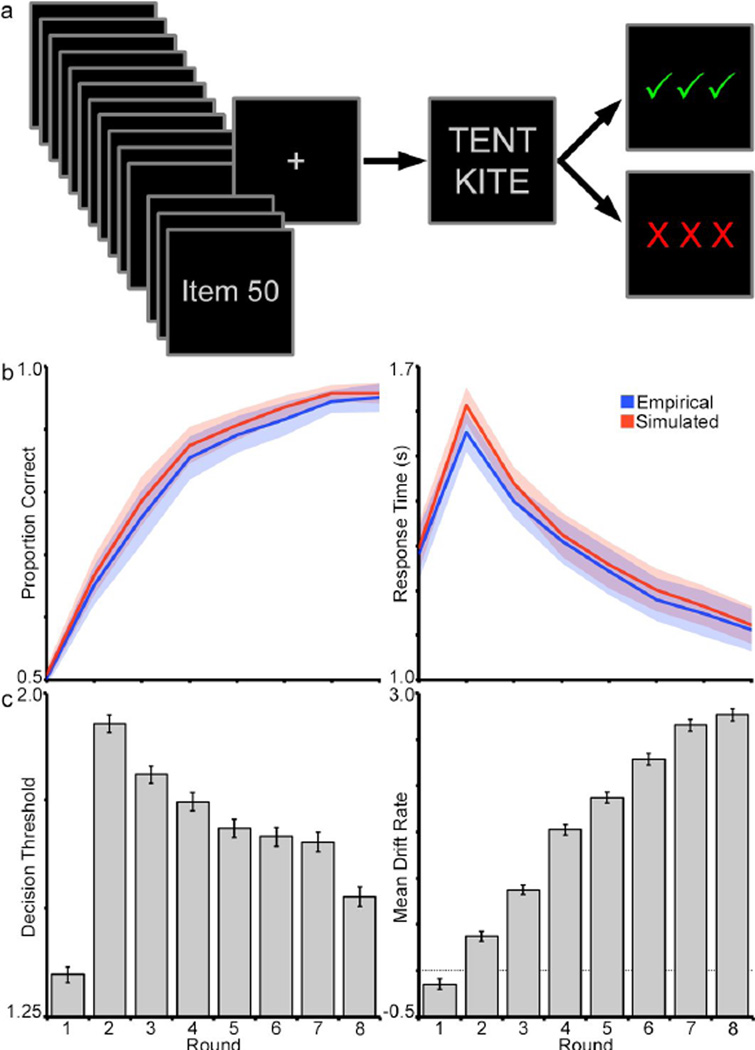
Subjects performed a 50-item concurrent discrimination learning task during the scanning session (Fig. 1a). In each trial, a pair of words was presented in the center of a screen in a single column for three seconds. In each of these pairs, one word was designated as the correct (positive) choice and the other as the incorrect (negative) choice. During the display period, subjects selected one of the words, indicating their selection with a button press, and received feedback about their decision. Feedback was displayed for 1.5 s and indicated either a correct choice (green checkmarks) or an error (red Xs). Trials were separated by a variable inter-stimulus interval of 1.5–7.5 s selected from a distribution positively skewed toward the shorter intervals (1.5 s increments, mean trial separation = 2.91). This served as jitter between trials to facilitate later deconvolution of the fMRI signal (Dale, 1999). After all 50 word pairs in the set were presented, subjects were allowed to rest for one minute before beginning the next Round, in which subjects saw the same set of word pairs again in a randomized presentation sequence and again made choices for each pair. Over the course of eight Rounds (in which each discrimination was presented once), subjects learned which item in each pair was associated with positive feedback (i.e., was “correct”) and which was associated with negative feedback.

Figure 1.

a, Concurrent discrimination task. In a set of 50 items, subjects are presented with a pair of words, one of which is designated the target (i.e., correct). Subjects choose the word and receive visual feedback. The set of 50 items is repeated 8 times total (8 Rounds), during which subjects learn the correct choices. b, Average accuracy across rounds (left panel) and response time across rounds (right panel) is plotted for the task participants (empirical) and for simulations of a drift-diffusion model (simulated) (see Table 1). Shaded area reflects standard error of the means. c, Threshold (left) and drift-rate (right) parameters across rounds of the drift-diffusion model fit from task behavior (see Table 1).

The discrimination learning task was presented using E-prime and projected onto a screen at the head of the magnet bore using a BrianLogics MRI Digitial Projection System. Subjects viewed the screen via a mirror attached to the radio frequency coil and indicated their responses via a fiber optic response glove on their right hand connected to a desktop computer with a serial response box (Brain Logics, Psychology Software Tools, Pittsburgh, PA). Earplugs were provided to minimize discomfort due to scanner noise.

2.3 Stimuli

Word stimuli were pulled from the MRC Psycholinguistic Database (Coltheart, 1981). All words were one syllable, three to five letters, three or four phonemes, and had a log HAL frequency of at least 7.0. Stimuli had concreteness, imageability, and familiarity measures of at least 400. Additional word frequency data were obtained from the English Lexicon Project (Balota et al., 2007). For each subject, a list was generated by randomly selecting two pre-made lists from a set of eight 50-word lists balanced and matched for frequency and number of letters. These two lists were individually randomized and then paired, ensuring that each subject had a unique set of word pairs balanced for selected psycholinguistic criteria.

2.4 Image Acquisition

Images were acquired on a Siemens Allegra 3-Tesla system. T1-weighted anatomical images were obtained using an MP-RAGE sequence (repetition time, TR = 1540 ms; echo time, TE = 3.04 ms; flip angle, FA = 8 degrees; inversion time, TI = 800 ms; 1 mm isotropic voxels acquired in 192 sagittal slices). T2-weighted anatomical images were obtained with a spin-echo sequence (TR = 6000 ms, TE = 73 ms, FA = 150 degrees, 0.78 mm² in-plane resolution; 38 axial slices spaced 3.2 mm apart). Functional images sensitive to the BOLD contrast were acquired using a whole-brain echo-planar T2^*-weighted series (TR = 1500 ms, TE = 25 ms, FA = 60 degrees, 3.125 mm² in-plane resolution, 29 axial slices spaced 3.5 mm apart). The first four images of each run were discarded to allow for net magnetization and RF equilibration.

2.5 Functional Imaging Preprocessing

Image preprocessing and analysis was carried out using FIDL, a software package developed at Washington University in St. Louis. Imaging data were preprocessed to address noise and image artifacts, including within-TR slice-time acquisition correction, motion correction using a rigid-boy translation and rotation algorithm (Snyder, 1996), within-run voxel intensity normalization of 1000 to facilitate cross-subject comparisons (Ojemann et al., 1997), and computation of a Talairach atlas space transformation matrix (Talairach and Tournoux, 1988). Single-subject analyses were performed in data space. For group analysis, data were resampled to 2 mm isotropic voxels and transformed into Talairach atlas space.

2.6 Behavioral analysis

Behavioral accuracy and response time (RT) measures were assessed across Rounds (repetitions of the 50-item set) using repeated-measures ANOVAs. Round was entered as an eight-level (Round 1–8) within-subjects factor. For all ANOVA analyses, the Greenhouse-Geiser sphericity correction was applied when Mauchly’s test indicated a violation of the sphericity assumption.

2.7 Drift-diffusion modeling

The drift-diffusion model is a robust model of decision-making behavior that describes variations in behavioral response time distributions on the basis of several parameters. Of interest for this study were mean drift-rate (v), corresponding to the mean rate of evidence accumulation for a condition, and decision threshold (a), corresponding to decision criteria or the amount of evidence needed before committing to a decision (Ratcliff, 1978; Ratcliff and McKoon, 2008). We expected that as subjects learned, their decision-making would become more proficient. In a drift-diffusion model, an increase in the drift-rate and decrease in the threshold parameters would correspond to faster and more confident decisions. Changes in behavior, as captured by changes in the model parameters, should thus map onto changes in the activity of brain regions associated with evidence accumulation (modeled by drift rate parameter) and decision criteria (modeled by the threshold parameter). It is important to note that because regional activity might correlate with changes in a parameter does not necessarily mean that particular region is responsible for the computation itself (e.g., if a region correlates with changes in drift-rate, this region does not necessarily function as an evidence accumulator). Rather, the correlation is a marker of the cognitive process—the region is associated in some way with what the parameter represents. For instance, a region whose activity correlates with drift-rate may not be responsible for computing a decision variable itself, but rather is associated with that process, either responding to other regions computing the variable or providing signals that feed into the computation. Regardless, however, the region would be associated with drift-rate, while not necessarily computing it.

Drift-diffusion models were fit to subject reaction time and choice data using the HDDM software package (Wiecki et al., 2013). HDDM fits models using hierarchical Bayesian methods wherein subject-level and group-level parameters are estimated at the same time using Markov-chain Monte-Carlo (MCMC). To examine changes in key parameter estimates across learning, two parameters, mean drift rate (v) and decision threshold (a), were allowed to vary across the eight Rounds of the task (i.e., eight repetitions of the 50-item discrimination set). Thus, there was one value per Round for each of drift-rate and threshold, allowing the model to fit changes in behavior across learning in terms of these two parameters. The non-decision time (t_er) and starting point (z) were estimated at the subject- and group-levels, while variance parameters (variance in drift, sv, non-decision time, st, and starting point, sz) were estimated only at the group level. Data were accuracy-coded, such that the upper threshold (a) of the model corresponded to a correct choice (i.e., the subject chose the positive item), whereas the lower bound (0) corresponded to errors (i.e., the subject chose the negative item). Round-wise parameter estimates for drift-rate and threshold were used as covariates in the imaging analyses.

Model parameters were estimated using three MCMC chains of 10,000 samples each. The first 1,000 samples of each chain were discarded to ensure that the chain stabilized. After sampling, model convergence was evaluated visually by inspecting the traces of the model posteriors and statistically by computing the Gelman-Rubin statistic, which compares inter- and intra-chain variance with an ANOVA approach. This statistic was near 1.0 (maximum deviance from 1.0 was 0.007) for all parameters, suggesting that the models converged properly. For a third check, the Geweke statistic, which compares variance at the starts and ends of chains, also indicated proper convergence.

Model fits to the data were evaluated by simulating choice and reaction time data from the model posterior distributions and comparing to the observed data. One hundred datasets were generated from each subject’s model. The mean of these 100 sets was then used to compare against the empirical data to ensure that model-derived data can reproduce key patterns of accuracy and response time in the observed behavioral data. Figure 1b illustrates the relationship of the model-simulated versus empirical behavior. These were assessed for differences across conditions using 2 × 8 repeated measures ANOVA including factors of Dataset (observed, model-derived) and Round (Round 1–8).

Two alternative models were also constructed to assess whether the aforementioned model indeed provided the best fit to the data. One alternative model allowed only threshold to vary by Round, while the other allowed only drift-rate to vary by Round. Primary and alternative models were assessed with the deviance information criterion (DIC), which measures the lack of fit of model estimates and penalizes for complexity (i.e., degrees of freedom) (Spiegelhalter et al., 2002; Spiegelhalter et al., 2014). A lower DIC indicates a better fit, typically by a magnitude of 10 or more (Burnham and Anderson, 2004; Zhang and Rowe, 2014).

2.8 Reinforcement learning agent

In order to capture the dynamics of feedback-based experience across Rounds as subjects performed the concurrent discrimination learning task, a reinforcement learning agent was used. This agent used an off-policy temporal difference control algorithm (Q-learning) to estimate reward-prediction error (RPE) signals and item-level expected values (EV) from subjects’ choice selection behavior across learning (Watkins and Dayan, 1992; Sutton and Barto, 1998). The agent computed an EV (quality measure or Q-value) for selecting each of two actions in a given state. Here, a state was defined as a word pair. A subject, then, could take two possible actions—choosing one or the other word in the pair. The agent updated the EV based on the human subjects’ choices by incrementing the value with an RPE (multiplied by a constant learning rate). EVs of each action were instantiated with random values ranging from 0 to 1 selected from a uniform distribution. Through learning, these initial values should approach the observed value for that action. The RPE was calculated as the difference between the observed outcome (1 for a correct response, 0 for an error) versus the EV for a given action. Thus, the agent updated its values based on the experiences of the human subject.

In contrast to the drift-diffusion model, the reinforcement learning agent learned at the trial-level and learned only from the choice data (i.e., did not address variance in response times). Thus, RPE and EV estimates derived from the model were trial-by-trial estimates and not round-level averages (cf. threshold and drift-rate in the drift-diffusion model). EVs were entered into a softmax logistic function to compute response probabilities for the chosen action. From these probabilities, we computed a log likelihood estimate reflecting the likelihood that a given subject would respond a particular way across the task session. An agent was considered to be optimal when its learning rate parameter produced the maximum likelihood. The models and optimization routine were implemented within Matlab (The MathWorks, Natick, MA). The input learning rate parameter was sampled across a range of possible values from 0.0 to 1.0. Trial-wise model estimates of RPE and EV were extracted from the model running with the optimal learning rate. These estimates were used as covariates in the imaging analyses. The extent of model fit was measured with pseudo-R² statistics computed as (LL_model − LL_null)/LL_null, wherein LL_model is the log-likelihood estimate of the fitted agent and LL_null is that of a chance-performance model (i.e., response probabilities are 0.5 for all trials). These statistics are presented in Table 2.

Table 2.

Estimated model fits and learning rates for the reinforcement learning model. Pseudo R², statistic illustrating degree of model fit (0.20 is generally a well-fit model); α, learning rate parameter.

Subject	Pseudo R2	α
1	0.52	0.86
2	0.17	0.79
3	0.40	0.68
4	0.50	0.93
5	0.50	0.87
6	0.40	0.82
7	0.49	0.85
8	0.23	0.85
9	0.24	0.57
10	0.41	0.76
11	0.32	0.93
12	0.62	0.79
13	0.51	0.83
14	0.46	0.88
15	0.11	0.67
16	0.17	0.86

2.9 Voxelwise imaging analysis

Subject-level neuroimaging data were analyzed using a voxel-by-voxel general linear model (GLM) approach. In the GLM, each time point is computed as the sum of coded effects, produced by model events and by error (Friston et al., 1994; Glover, 1999; Miezin et al., 2000; Ollinger et al., 2001). The GLM approach makes no assumptions about the underlying shape of the blood-oxygen-level-dependent (BOLD) response, but assumes that component signals, described by the coded events, will sum linearly to produce the observed BOLD signal. Within each Round, a linear term was included to capture signal drift, and a constant term captured baseline signal. A high-pass filter at 0.009 Hz was added to the models to reduce the influence of low-frequency fluctuations in the BOLD response. Each trial was modeled with a series of finite impulse response (FIR) basis functions, wherein each time point of a trial was described by a delta function. The sequence of these functions corresponded to trial-level time series averages. Event-related effects were described as an estimate of the percent of BOLD signal change relative to the baseline constant.

For each subject, two GLMs were created which separately modeled effects related to diffusion model parameters and effects related to reinforcement learning measures. In both GLMs, accuracy was entered as a categorical event-related regressor, which coded each decision trial as correct or incorrect, modeled to 11 time-points (16.5 s). In the diffusion model GLM, two additional covariates were entered to describe changes in the drift-rate and decision threshold parameters across Rounds. These were modeled as continuous measures across the entire task and thus captured correlation between the modeled measure and the underlying BOLD signal. On a trial-level, these covariates were modeled with 11 FIR basis functions (11 time-points totaling 16.5 seconds) to describe changes in correlation within a trial epoch. Importantly, the diffusion model parameters captured choice and response time behavior on the level of Round (i.e., all trials in Round 1 had the same parameter values, all trials in Round 2 had the same parameter values, etc.) (Table 1). Modulations in these parameters therefore reflected modulations by Round.

Table 1.

Estimated group-level parameters for drift diffusion models. a, decision threshold values (subscript indicates the Round number); v, mean-drift rate values; t_er, mean non-decision time; z, starting point; st, cross-trial variance in non-decision time; sv, cross-trial variance in drift-rate; sz, cross-trial variance in starting point; SE, standard error of the mean estimates across subjects.

Param	Group Mean	SE
a1	1.347	0.018
a2	1.924	0.020
a3	1.807	0.020
a4	1.745	0.021
a5	1.683	0.021
a6	1.664	0.022
a7	1.652	0.023
a8	1.526	0.021
v1	−0.144	0.056
v2	0.370	0.055
v3	0.875	0.056
v4	1.525	0.059
v5	1.871	0.060
v6	2.281	0.062
v7	2.653	0.065
v8	2.766	0.065
ter	0.845	0.022
z	0.556	0.012
st	0.495	--
sv	0.556	--
sz	0.037	--

The other GLM modeled covariates derived from the reinforcement learning models. RPE and EV measures were entered as covariates to model trial-by-trial modulations across the entire task in a manner similar to the diffusion model GLM. In contrast to the diffusion model parameters (modeled Round-by-Round), the positive RPE and EV measures were continuous such that each trial had a unique value (modeled trial-by-trial). Round was not coded in either GLM since the covariate measures derived from both computational models capture variances due to Round (i.e., measures inherently modulate across Rounds, thus changes in the measures reflect changes across Round).

Importantly, only positive RPEs were entered. There are several reasons for this analysis choice. The first is theoretical. Specifically, positive RPEs are thought to capture learning signals derived from feedback and correlate with phasic increases in the firing rates of dopamine neurons in the brainstem and striatum (Schultz et al., 1997; O’Doherty et al., 2003; Bayer and Glimcher, 2005; Daw and Doya, 2006; Oyama et al., 2010). In contrast, negative prediction errors seem to correspond to different processes than positive ones and localize to different regions in the brain (Spoormaker et al., 2011). If negative RPEs were included in the analysis, it could potentially complicate interpretations and under-power results related to the more dominant positive prediction errors that seem to drive most of the learning in this task (i.e., negative prediction errors are relatively rare in this task, especially in late rounds). Second, very few of the total trials were associated with negative RPEs. Across subjects, a median of 8% of the total trials (~32 trials) were negative RPE trials. Given the single-subject regression design of the GLMs, this is considered to be too few trials to get reliable estimates from a single regressor (Green, 1991). Indeed, the observed power for detecting a moderate effect size for a linear multiple regression or ANCOVA with this design and number of trials would be about 0.20. In contrast, the observed power for the same analysis for the positive RPE regressor would be at least 0.95 for all subjects. Thus, while negative RPE signals have clear theoretical value, this phenomenon was not adequately sampled in the present study.

A critical concern about this regression-style approach to the imaging analysis is that the covariates between the two GLMs are not necessarily orthogonal. Indeed, the correlations between the four covariates of interest are generally high on a subject level, meaning the models will attempt to parse variance based on the uncorrelated components. This suggests that separating the effects attributable to each of the covariates is difficult and should be considered with a degree of caution (for example, Hare et al., 2008; Hunt, 2008). While these concerns should be kept in mind, there are a few factors that may partly assuage these issues. First, since the covariates of interest are derived from computational models that offer strong predictions regarding neural substrates, results from each covariate (Figs. 2 and 3) can be compared against the prior literature. Replication of prior findings bolsters confidence in the present findings. Second, between the two models, our analysis seeks to associate parameters between the models rather than parse them (e.g., examining overlap of regions that track drift-rate with those that track EV). In contrast to much other work, our objective is not to explain effects solely in terms of decision-making or reinforcement learning, but rather in terms of associations between the models to gain insight into the neural substrates that are shared between decision-making and learning. Establishing such associations between these two models is an important step in identifying possible neural substrates that mediate the influence of feedback on decision-making.

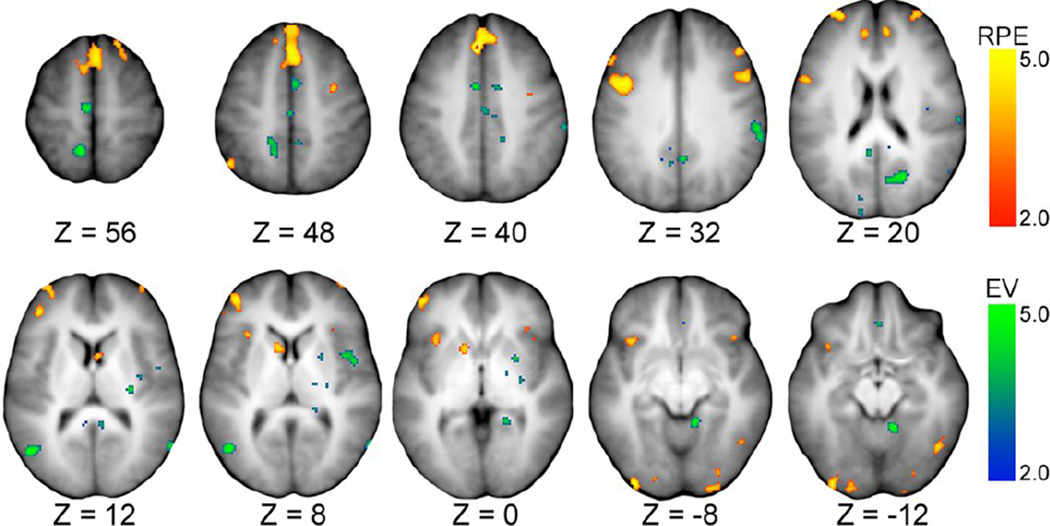
Figure 2.

Activation map illustrating effects of reward prediction error (RPE) and expected value (EV) covariates derived from the reinforcement learning model. Z value indicates offset in mm from anterior commissure/posterior commissure atlas in Talairach space. Heat map scales for RPE (red to yellow) and EV (blue to green) reflect magnitude of the z-transformed t-statistic. Tables 3 and 4 list details of these illustrated regions.

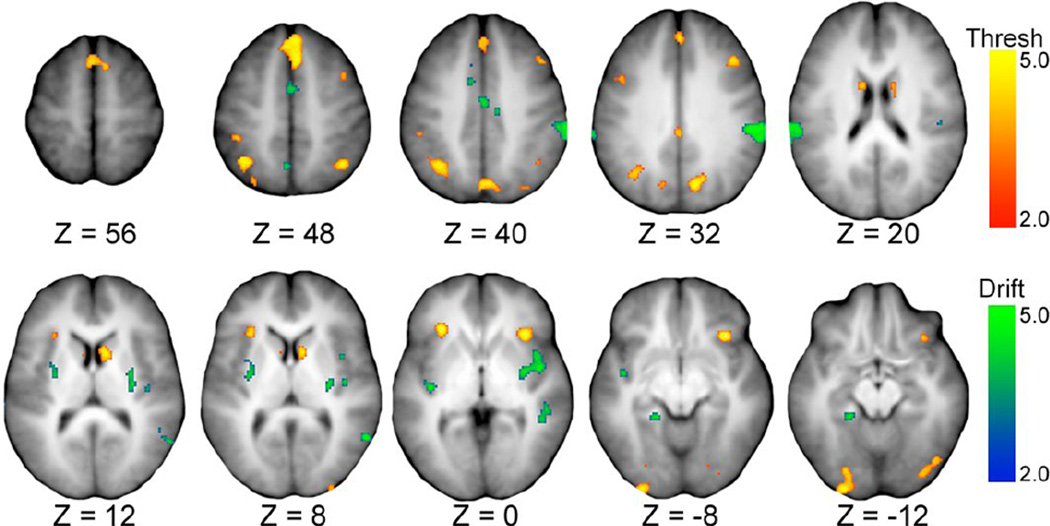
Figure 3.

Activation map illustrating effects of decision threshold and drift-rate covariates derived from the drift-diffusion model. Z value indicates offset in mm from ACPC axis in Talairach space. Heat map scales for decision threshold (red to yellow) and drift-rate (blue to green) reflect magnitude of the z-transformed t-statistic. Tables 5 and 6 list details of these illustrated regions.

2.10 Separating neural effects of within-model parameters

Since the measures within each model are related both behaviorally and conceptually, our focus was on regions that predominantly track one or the other within-model measure (e.g., RPE more than EV or vice-versa). To statistically separate the effects modeled within each GLM, voxel-by-voxel paired t-tests were computed to identify voxels that differentially correlated with the parameters from the diffusion model, or with the parameters from the reinforcement learning agent. For the diffusion model GLM, the drift-rate covariate was tested against the decision threshold covariate. Voxels in the resulting image with a positive t-statistic indicated underlying activity that correlated to a significantly greater degree with modulations in decision threshold than drift-rate. In other words, voxels with statistically larger correlation coefficients for threshold were indicated by significantly positive t-statistics in the activation map. Likewise, voxels with a negative t-statistic indicated activity that correlated to a significantly greater degree with modulations of drift-rate than decision threshold. As such, this t-test separated activity that was statistically more attributable to modulations in either parameter, as computed by the linear models. The analysis was restricted to time points 4–7 (of the 11 modeled time-points), which captured the bulk of trial-related activity and excluded biologically irrelevant time points (e.g., first and last time points of the series). An identical approach was taken with the reinforcement learning measures for the other GLM, separating activity that was statistically more attributable to modulations in either RPE or EV.

Images resulting from the t-tests were corrected for multiple-comparisons using a cluster-extent threshold and adjusted for sphericity (minimum z-transformed t-statistic of 2.5, p = 0.01, 42-voxel contiguity). These corrected images were then smoothed with a two-voxel (4 mm) full width at half maximum (FWHM) Gaussian kernel. A threshold was applied to the smoothed, corrected images at a Z-statistic of 2.0 to eliminate any sub-threshold bleed-over resulting from the smoothing procedure (i.e., from the tails of the Gaussian kernel).

These maps were used to define regions of interest whose activity correlated with the individual covariates (e.g., regions whose activity correlated with modulations in positive RPE signals). Z-statistics that exceeded an alpha of 0.001 were tagged as peaks, around which spherical regions (12 mm radius) were grown. Voxels within the spheres that were absent from the corrected maps were then excluded from the region (i.e., voxels that did not pass the multiple comparisons and sphericity tests). The coordinates of the peaks of each of the resulting regions were used to identify approximate anatomic locations in Talariach space (Talairach and Tournoux, 1988). Regions were defined for each covariate, resulting in a set of regions of interest that corresponded to effects related to drift-rate, decision threshold, RPE, and EV. The purpose of this region identification procedure was to examine regions related to each covariate and to relate it to previous literature. Thus, this level of analysis was independent of the following intersection analysis.

2.11 Intersection of model effects

To establish meaningful links between the two computational approaches and the neural signatures of each, an analysis of the intersection of significant effects, similar to multi-experiment conjunctions, was performed. This analysis identified regions corresponding to the functional overlap between diffusion model and reinforcement learning parameters. First, for each measure of interest (RPE, EV, decision threshold, and drift-rate), a binary mask was created that marked any above-threshold (i.e., significant) voxel with a 1 and any below-threshold voxel with a 0. These masks were computed from the corrected statistical images that resulted from the t-tests described above. Thus, each mask contained information identifying which voxels correlated with each of the four measures at a relatively rigorous threshold corrected for multiple comparisons and adjusted for sphericity.

The resulting masks for the diffusion model parameters were then compared to the masks of the reinforcement learning measures. There were, thus, four possible combinations: Threshold + RPE, Threshold + EV, Drift-rate + RPE, and Drift-rate + EV. For each combination, a logical “AND” computation identified voxels that exhibited above-threshold effects in both source masks (e.g., a given voxel’s activity correlated significantly with threshold modulations and correlated significantly with RPE modulations in separate analyses). This computation is analogous to the minimum t-field computation (or minimum statistic) of multi-experiment conjunctions, which ensures that a given voxel shows a reliable effect independently for both covariate and not just for one. The null hypothesis for this statistic is that a voxel’s activity across subjects correlated with at most, one of the covariates. Therefore, rejecting the null hypothesis would mean that a voxel’s activity correlated with both covariates. For each combination, the result was an image of voxel clusters that were functionally correlated with both model parameters. This analysis, then, related functionally identified regions of reinforcement learning to regions associated with specific aspects of a decision-making processes. We computed the center of mass for each region in the intersections to identify approximate anatomical locations in Talairach space (Talairach and Tournoux, 1988).

The choice of threshold for this analysis is, to an extent, arbitrary. There is a considerable compromise that must be made with respect to false positives and false negatives: by changing the threshold, the results could change appreciably. Our approach is reasonably cautious with false positives and favors a higher threshold at the risk of potentially excluding overlapping regions by mistake. The maps presented in Figs. 2 and 3 show the statistical values of the individual covariates that may help assess the extent to which this tradeoff might impact the results.

3. Results

3.1 Behavioral performance

Subjects overall learned quickly, reaching 80% accuracy in three to four repetitions (Figure 1b). This improvement in accuracy across rounds was indicated by a significant main effect of Round in a repeated measures ANOVA (F[2.58, 38.65] = 83.35, p < 0.001, η_p² = 0.85) and significant rank-order correlation (ρ = 0.99, p < 0.001). Likewise, response time (Figure 1c) decreased across rounds beginning at the first recall round (i.e., Round 1 was exposure only and required no retrieval of learned information), indicated by a significant Round effect on response times (F[2.16, 32.33] = 19.12, p < 0.001, η_p² = 0.56) and negative rank order correlation (ρ = −0.93, p < 0.001). Altogether, the increase in accuracy across rounds suggests that subjects were able to successfully optimize their choice selections with repeated experience. Likewise, the decrease in response times suggests that decision-making becomes more automatized through learning.

3.2 Drift-diffusion modeling

The primary goal of the diffusion model analysis was to attempt to capture behavioral improvements across rounds and describe those changes in terms of decision-making processes. If these changes can be captured successfully, model parameters could be used to inform neuroimaging analysis and thus examine the neural underpinnings of improvements to decision processes across learning. Of specific interest were the threshold and drift-rate parameters, which were free to vary across Round. The model was able to produce parameters that could accurately describe the behavioral data (Fig. 1b). The mean group parameters for the final model are enumerated in Table 1.

In terms of decision processes, improvements in choice selection behavior across rounds manifested as an overall decrease in decision thresholds coupled with an overall increase in driftrates across rounds. Figure 1c illustrates decision threshold changes, which increased from Round 1 to Round 2, and then gradually decreased over subsequent Rounds. These variations reached statistical significance, indicated by a main effect of Round (F[3.26, 48.98] = 10.784, p < 0.001, η_p² = 0.42). The changes in the parameter progressively decreased across Rounds, as indicated by a negative rank order correlation, excluding Round 1 in which decision thresholds had to be formed without prior experience of the experimental context (ρ = −0.99, p < 0.001). Figure 1c also illustrates changes in drift-rates across Round. Drift-rate increased steadily with repetitions of the item set, indicated by a significant effect of Round (F[1.71, 25.57] = 81.97, p < 0.001, η_p² = 0.84) and positive rank order correlation (ρ = 0.99, p < 0.001). Altogether, decreases in threshold and increases in drift-rate are intuitive patterns for a learning task such as this, wherein subjects gain confidence in their choices through repetition and learn to make fast and accurate decisions. Moreover, while the pattern of changes across both parameters is intuitive, it is not requisite; it is equally plausible, for instance, that behavior might be described solely based on changes to one parameter or the other. This was not the case. Two alternative models, wherein either drift-rate or threshold was fixed while the other was free to vary by round, produced poorer fits (DIC 10,325 and 9,324) to the observed data than the primary model (DIC 8,927). It is also worth noting that, while parameters in Round 1 do not reflect experience-related computations, the model seems to account for this, as observed in the increase in threshold and change in sign for drift-rate from Round 1 to Round 2. Conceptually, subjects approach Round 1 with trial-and-error guessing and subsequently switch to a controlled retrieval strategy at Round 2.

To assess the fit of the model, choice and response time data were simulated from the posterior distribution of the final model. Data produced by simulation mapped onto the empirical data with little error for both accuracy (Round × Dataset interaction, F[2.43, 77.84] = 0.06, p = 0.96, η_p² = 0.002) and RT measures (F[2.03, 64.86] = 0.12, p = 0.89, η_p² = 0.004). These null ANOVA results indicate that the empirical and simulated datasets were not different and suggest that data generated from the model posteriors could reproduce key behavioral patterns within the empirical dataset, on average (Fig. 1b).

3.3 Reinforcement learning agent

In parallel with the diffusion model analysis, a reinforcement learning approach was taken to characterize changes in choice selection behavior across rounds in terms of feedback processing and mnemonic prediction strength. Accuracy data for the concurrent discrimination task indicated gradual improvements to performance as choices were repeatedly experienced. As such, the reinforcement learning agent should produce trial-level EV estimates that gradually increase across rounds (reflecting better outcome predictions) and RPE estimates that gradually decrease in magnitude and frequency across rounds (reflecting fewer unexpected outcomes).

Overall, the pseudo-R² statistic of the reinforcement learning models was 0.37 on average, indicating the models fit the human behavior quite well compared to a chance-performance model (Table 2). Learning rates of the models were generally high, at a mean of 0.81 (0.02), corresponding to the rapid climb of the learning curve (Fig. 1b). This indicates that, according to the models, subjects strategically placed a high importance on new information in learning the choice-outcome values. It is worth noting that, while reinforcement learning is typically applied to tasks with probabilistic choice-outcome relationships (in which learning is typically slow), it was successfully applied here to concurrent discrimination learning, which features deterministic choice-outcome relationships and relatively rapid learning. A key result here is in the learning rate for our deterministic task, which is considerably higher than learning rates in probabilistic learning tasks (Rieskamp, 2006; Doll et al., 2009; Cavanagh et al., 2010; Gläscher et al., 2010). Importantly, this high learning rate determines the relative influence of EV and RPE values and how important individual choice experiences are to a particular subject.

3.4 Effects of single model covariates

Regions of interest corresponding to activity that correlated with the model parameters were identified from the covariate activation maps. Tables 3–6 enumerate regions whose activity correlated with modulations in positive RPEs, EV, decision threshold, and drift-rate, respectively. The correlation maps are presented in Figures 2 and 3. Briefly, the results run parallel to many findings in the literature. Positive RPE signals correlated with activity in regions such as the pre-supplementary motor area (pre-SMA), caudate nucleus, cingulate gyrus, and dorsolateral prefrontal cortex (dlPFC), among other regions (Table 3) (Gläscher et al., 2010; Glimcher, 2011; Daw et al., 2011). EV correlated with activity in regions such as the parahippocampal gyrus, orbitofrontal cortex, and the putamen (Table 4) (Frank and Claus, 2006; Hare et al., 2008). Decision thresholds varied with activity in cognitive control regions such as the pre-SMA, anterior insula, and frontoparietal regions (Table 5) (Mulder et al., 2012; Frank et al., 2015). Drift-rates varied with activity in memory regions such as the parahippocampal gyrus and putamen, as well as control regions like supplementary motor areas (SMA) (Table 6) (Badre et al., 2014).

Table 3.

Regions of interest whose activity correlated with modulations in Reward Prediction Errors. x,y,z, Talairach atlas coordinates of center of mass; BA, approximate Brodmann area; Vx, region volume (in voxels); R, right; L, center; G, gyrus; S, sulcus; C, cortex; Ant, anterior; Inf, inferior; Med, medial; Mid, middle; Sup, superior; dlPFC, dorsolateral prefrontal cortex.

ROI	Anatomic Location	x	y	z	BA	Vx
1	Med Frontal G, pre-SMA	0	33	43	8	458
2	L Inf Occipital G	−24	−89	−12	19	237
3	L Inf Frontal G	−40	40	8	45	264
4	L Mid Frontal G	−32	53	16	46	202
5	L Med Frontal G, pre-SMA	−6	24	51	8	472
6	L Inf Frontal G	−48	4	25	44	427
7	R Ant Cingulate C	6	41	23	32	86
8	R Mid Frontal G, dlPFC	46	26	31	9	154
9	R Sup Frontal G	19	23	58	6	125
10	L Inf Frontal G	−49	14	27	44	233
11	L Caudate Head	−11	8	3	--	137
12	R Mid Frontal G	32	−3	45	6	83
13	L Ant Insula	−33	16	−1	13	260
14	R Inf Frontal G	48	8	32	44	149
15	R Fusiform G	27	−88	−9	19	189
16	R Fusiform G	45	−62	−11	19	122
17	L Inf Parietal Lobule	−45	−58	48	40	64
18	R Ant Insula	37	20	−1	13	177
19	R Mid Frontal G	34	54	12	10	216
20	L Cingulate G	−10	38	19	32	100
21	R Caudate Head	4	4	12	--	76
22	L Angular G	−40	−54	35	39	40

Table 6.

Regions of interest whose activity correlated with modulations in Drift-rate. x,y,z, Talairach atlas coordinates of center of mass; BA, approximate Brodmann area; Vx, region volume (in voxels); R, right; L, center; G, gyrus; S, sulcus; C, cortex; Ant, anterior; Post, posterior; Inf, inferior; Med, medial; Mid, middle; Sup, superior; OFC, orbitofrontal cortex.

ROI	Anatomic Location	x	y	z	BA	Vx
1	R Inf Parietal Lobule	52	−29	27	40	570
2	L Inf Parietal Lobule	−56	−38	24	40	434
3	R Mid Temporal G	56	−58	9	39	88
4	R Mid Insula	38	−2	2	13	264
5	R Mid Temporal G	47	−38	−1	21	101
6	R Ant Cingulate C	4	−14	41	32	145
7	R Putamen	32	−16	9	--	249
8	L Post Insula	−38	−15	−1	13	190
9	L Parahippocampal G	−21	−39	−13	35	128
10	L Putamen	−28	−9	11	--	129
11	L Cingulate G	−7	1	45	24	174
12	L Precuneus	−4	−60	49	7	73

Table 4.

Regions of interest whose activity correlated with modulations in the Expected Value covariate. x,y,z, Talairach atlas coordinates of center of mass; BA, approximate Brodmann area; Vx, region volume (in voxels); R, right; L, center; G, gyrus; S, sulcus; C, cortex; Ant, anterior; Post, posterior; Inf, inferior; Med, medial; Mid, middle; Sup, superior; OFC, orbitofrontal cortex.

ROI	Anatomic Location	x	y	z	BA	Vx
1	L Mid Occipital G	−45	−66	10	19	119
2	R Mid Occipital G	15	−70	22	19	325
3	L Precuneus	−12	−48	51	7	228
4	R Parahippocampal G	15	−44	−4	30	207
5	R Cingulate G	1	−4	45	24	267
6	R Inf Parietal Lobule	59	−33	30	40	402
7	L Post Cingulate C	−2	−49	22	30	372
8	R Paracentral Lobule	1	−20	48	7	227
9	R Mid Insula	44	1	7	13	134
10	R Putamen	32	−16	15	--	127
11	R Mid Temporal G	52	−59	14	39	145
12	R Putamen	24	1	5	--	86
13	L Cuneus	−10	−87	23	19	129
14	R Precuneus	9	−42	45	7	64
15	R Med Frontal G, OFC	2	28	−12	11	56
16	R Thalamus	18	−20	6	--	59

Table 5.

Regions of interest whose activity correlated with modulations in Decision Threshold. x,y,z, Talairach atlas coordinates of center of mass; BA, approximate Brodmann area; Vx, region volume (in voxels); R, right; L, center; G, gyrus; S, sulcus; C, cortex; Ant, anterior; Post, posterior; Inf, inferior; Med, medial; Mid, middle; Sup, superior; OFC, orbitofrontal cortex.

ROI	Anatomic Location	x	y	z	BA	Vx
1	R Ant Insula	33	19	−4	13	239
2	L Ant Insula	−29	23	2	13	188
3	R Precuneus	7	−71	36	7	337
4	R Med Frontal G, pre-SMA	2	27	44	8	701
5	L Fusiform G	−31	−85	−8	19	353
6	L Inf Parietal Lobule	−31	−58	43	40	535
7	R Sup Parietal Lobule	38	−57	50	7	149
8	R Mid Frontal G	41	12	41	9	290
9	L Precuneus	−17	−71	32	7	216
10	R Caudate Head	11	3	17	--	244
11	L Post Cingulate C	−1	−28	29	31	199
12	R Mid Occipital G	32	−79	−9	19	253
13	L Caudate Head	−8	2	12	--	138
14	R Angular G	30	−75	38	39	75
15	L Inf Parietal Lobule	−44	−37	45	40	90
16	L Mid Frontal G	−47	8	34	9	77
17	R Mid Occipital G	30	−94	7	19	54

3.5 Intersection of model-defined neural effects

To link together the cognitive processes captured by the drift-diffusion model and reinforcement learning, along with their neural substrates, a conjunction analysis was performed. The overlap of voxels corresponding to learning-related modulations in drift-diffusion model and reinforcement learning parameters were examined using a 2 × 2 design of evaluation (Threshold, Drift-rate by RPE, EV). Each intersection image contained voxels that were significantly active for both of the two parameters in the intersection (e.g., Threshold and RPE). Importantly, these intersections should not be interpreted as indicating dependence between measures (i.e., interactions), but rather that present voxels exhibited activity that correlated with both modulations of a diffusion model parameter and also to modulations of a reinforcement learning measure. Moreover, to keep interpretations as clean as possible, the intersections were created by separating within-model effects (i.e., effects due to positive RPE signals were statistically separated from those due to EV; the same applied to drift-rate and threshold effects). This method thus prevented any overlap between parameters of the same model, namely between RPE and EV and between drift-rate and threshold.

The intersections of Drift-rate + RPE and of Threshold + EV produced no overlapping voxels and were thus excluded from further consideration. The two remaining intersections produced sets of 11 and 5 regions corresponding to intersections of Threshold + RPE and Driftrate + EV covariates, respectively. The overlap of effects related to positive RPE modulations and to changes in decision threshold localized to 11 regions (Table 7), encompassing territory in the caudate head, anterior insula, medial frontal gyrus (pre-SMA), fusiform gyrus, anterior cingulate cortex, right inferior occipital gyrus, and middle frontal gyrus (dlPFC). The other intersection, corresponding to the overlap of drift-rate and EV effects, identified five regions that clustered in the putamen, inferior parietal lobe, SMA, middle insula, and middle temporal lobe (Table 8).

Table 7.

Regions of interest defined by the intersection of Decision Threshold and Reward Prediction Error effects. x,y,z, Talairach atlas coordinates of center of mass; BA, approximate Brodmann area; Vx, region volume (in voxels); R, right; L, center; G, gyrus; S, sulcus; Ant, anterior; Inf, inferior; Med, medial; Mid, middle.

ROI	Anatomic Location	x	y	z	BA	Vx
1	R Ant Insula	38	20	−3	13	61
2	L Ant Insula	−29	23	2	13	67
3	R Med Frontal G, pre-SMA	3	16	53	6	187
4	R Med Frontal G, pre-SMA	1	30	46	8	258
5	L Fusiform G	−29	−86	−11	19	100
6	R Caudate Head	8	7	12	--	24
7	R Ant Cingulate C	1	35	34	32	39
8	R Fusiform G	36	−76	−15	19	12
9	L Caudate Head	−8	2	12	--	18
10	R Inf Occipital G	24	−83	−5	19	25
11	L Mid Frontal G, dlPFC	−44	6	33	9	43

Table 8.

Regions of interest defined by the intersection of Drift-rate and Expected Value effects. x,y,z, Talairach atlas coordinates of center of mass; BA, approximate Brodmann area; Vx, region volume (in voxels); R, right; L, center; G, gyrus; Inf, inferior; Mid, middle; Sup, superior; Ant, anterior.

ROI	Anatomic Location	x	y	z	BA	Vx
1	R Inf Parietal Lobule	56	−31	33	40	269
2	R Mid Temporal G	50	−57	12	39	22
3	R Mid Insula	37	−2	3	13	45
4	R Paracentral Lobule, SMA	4	−14	41	7	18
5	R Putamen	29	−15	9	--	47

It is important to note that while these overlaps can be interpreted with respect to the computational models that provide the covariates, a positive overlap result does not necessarily indicate that the contained regions are performing the same function or exhibit shared processing. For instance, a given region that exhibits a conjunction effect across two particular conditions might exhibit dissociable patterns of activity (Woo et al., 2014) or connectivity (Smith et al., 2015) between those conditions. However, because the analysis is testing correlation based on results from computational models that attach specific interpretations to the parameters, we can speculate how processing related to changes in these parameters might overlap conceptually. In this way, these correlations do not necessarily implicate the regions in the computation of the parameter itself, but rather link it to the conceptual processes represented by the parameter in the models. For instance, RPE signals seem to be computed by brainstem dopamine neurons (Schultz et al., 1997) and subsequently broadcast diffusely to other regions throughout the brain. Though activity in these other regions frequently correlates with RPE signals, it is unlikely that they participate in the computation of RPE. Rather, the correlation marks a process that results from or is associated with the RPE signal, not performing of the computation itself. It is in this spirit that conceptual interpretations of the parameter-correlated overlap regions are discussed in the following section.

4. Discussion

In this study, we used a dual model approach to investigate how different aspects of decision-making were influenced by feedback about decision performance and how the neural correlates of feedback processing and decision-making relate to each other. Behavioral data from a concurrent discrimination task were fit using a drift-diffusion model to characterize decision-making processes and a reinforcement-learning model to describe the influence of feedback. Parameters from these models were regressed onto neural data to localize brain regions whose activity varied with changes in the parameters. Correlations between modulations in the parameters across Rounds and modulations in fMRI activity served as markers of the processes described by the computational models. The intersection of the regions localized across the two models was then examined: brain regions common between the two models should correspond to putative substrates of feedback influences on decision-making.

The patterns of overlap between regions localized by both drift-diffusion and reinforcement-learning model parameters support two primary inferences. First, frontal, fusiform, anterior cingulate, and caudate nucleus regions behave like performance monitors, seeming to reflect errors in performance predictions that signal the need for changes in decision-making control. Second, temporoparietal, SMA, and putamen regions behave like evidence storage and accumulation sites, seeming to reflect differences in learned item values that inform optimal decision choices. As information about optimal choices is accrued, these neural systems dynamically adjust as decision-making becomes more skilled (i.e., faster and more accurate). Figure 4a provides a graphical depiction of these inferred intersections, which are discussed in detail below.

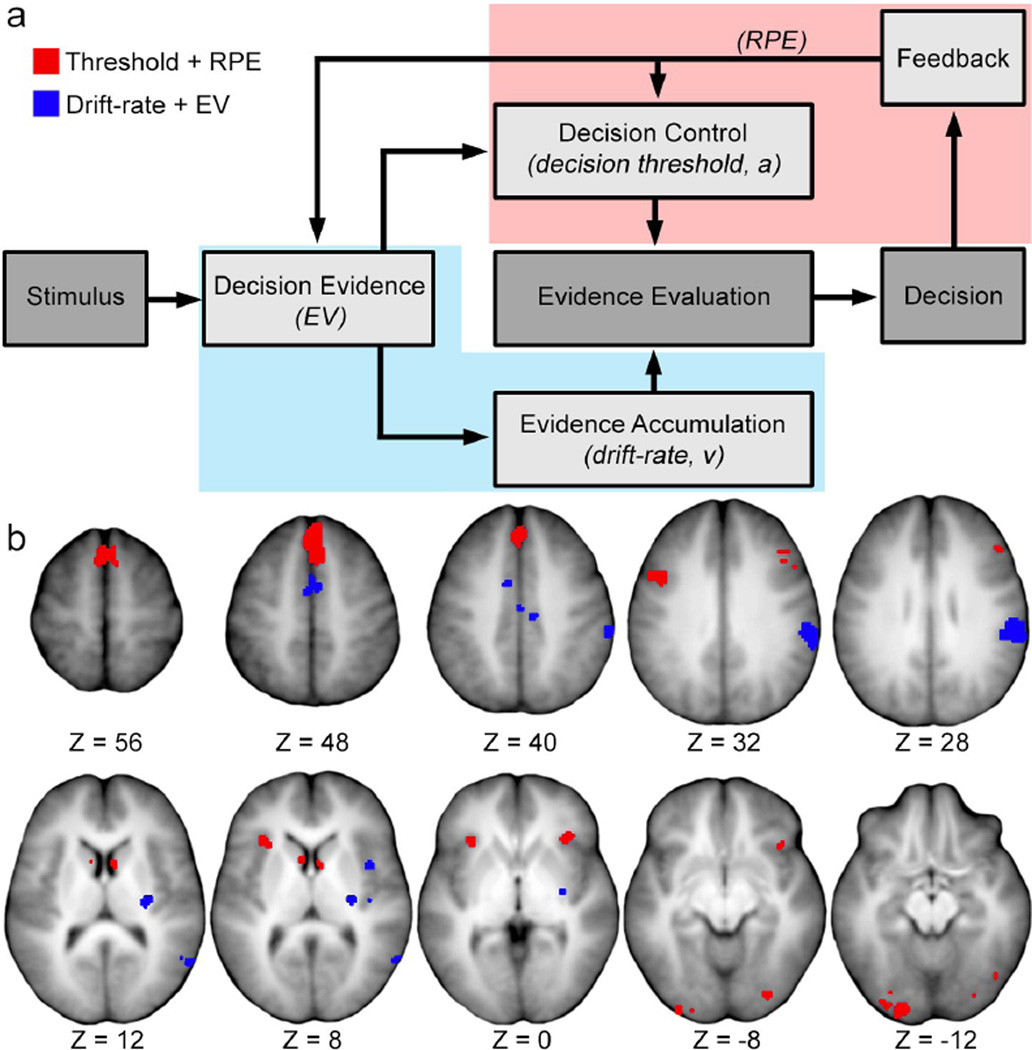
Figure 4.

a, Schematic illustrating the influences of feedback on a decision process. The lighter grey boxes indicate a theoretical process that is a specific focus of the present study, with a corresponding measure of interest indicated in parentheses (e.g., EV is a measure of decision evidence). The color-shaded areas represent a theoretical mapping of the two intersections of reinforcement learning and drift-diffusion parameters in the present study. EV, expected value; RPE, reward prediction error. b, Regions of interest corresponding to the Threshold + RPE (red) and Drift-rate + EV (blue) intersections. Z coordinates indicate the position of the axial slice in mm from ACPC line in Talairach space.

4.1 Outcome feedback influences decision thresholds via performance monitoring

Feedback about choice outcomes provides direct information about whether or not a given behavior met one's performance expectations. In the concurrent discrimination task, an accurate choice in an early round might signal that a chosen memory retrieval strategy worked surprisingly well, whereas an inaccurate choice in later rounds might indicate that a choice was made too quickly. More generally, outcome feedback provides critical information about whether control over the decision-making process is appropriately matched to performance expectations. Outcome feedback can therefore indicate that controlled processing for a subsequent decision can be safely reduced without jeopardizing performance, or that it should be increased so that more or better evidence can be gathered to support a given choice option.

Feedback about such performance discrepancies can be conceptualized as differences between predicted versus observed outcomes. These differences are captured by RPE signals in reinforcement learning models. Similarly, changes in controlled processing can be conceptualized as changes in the amount of evidence needed before a choice can be made; these are captured by the threshold parameter in drift-diffusion models. Thus, the neural substrates corresponding to the influence of outcome feedback on performance monitoring can be derived from the intersection of regions localized by the positive RPE and threshold parameters.

Activity in the anterior insula, pre-SMA, dlPFC, anterior cingulate cortex, fusiform and inferior occipital gyri, and dorsal caudate head (Table 7) was sensitive to changes in positive RPE signals and decision thresholds. These regions might therefore be important for performance monitoring and adjustments in controlled processing in response to unexpected outcomes. It is worth noting that for perceptual decisions, similar regions have been found to exhibit sensitivity to outcome information (Wheeler et al., 2008). This suggests that the control exerted by these regions is not exclusive to decisions based on retrieved information or to decisions with explicit feedback, and thus might reflect some degree of domain-general functionality.

Consistent with this interpretation, each of these regions has been more broadly implicated in performance monitoring. For example, the anterior insula has been associated with the conscious perception of errors (Ullsperger et al., 2010), while the anterior cingulate and dorsolateral prefrontal regions seem to be important in conflict monitoring and cognitive control (Botvinick, 1999; MacDonald et al., 2000). Furthermore, the identification of the dorsal striatum (particularly the dorsal caudate head) is consistent with anatomical models that distinguish between the dorsomedial and dorsolateral striatum, with the former associated with cognitive performance evaluation, goal achievement, and action-reward associations (Tricomi and Fiez, 2008, 2012) and the latter associated with sensorimotor learning and the encoding of implicit reward representations (cf. putamen in the Drift-rate + EV intersection) (Poldrack et al., 2005; Williams and Eskandar, 2006; Seger et al., 2010). Regions in the fusiform and inferior occipital gyrus might reflect an executive influence from prefrontal regions to sensory regions or an attentional biasing on perceptual representations. Additionally, some of the regions are associated with behavioral speed-accuracy tradeoffs, including the pre-SMA, dlPFC, striatum, and perceptual regions in the ventral stream (Bogacz et al., 2010). Thus, the wider literature supports the idea that regions identified from the Threshold + RPE intersection mediate the influence of external performance signals on adjustments to decision-making control.

4.2 Feedback history influences the rate of evidence accumulation

High quality decision evidence is critical to optimal choice selection performance. As noted above, in deterministic decisions, outcome feedback can provide unambiguous information about optimal choices. Experience-based improvements in decision-making should therefore reflect the degree to which this information is encoded into memory and successfully retrieved. In the concurrent discrimination task, mnemonic information deemed relevant to a choice episode can be gathered from various sources and integrated as evidence for or against a given option. For instance, a subject might rely heavily on contextual or associative information from declarative memory in the medial temporal lobe to make an accurate choice on some trials. For other trials (or for other subjects), implicit value information (i.e., familiarity) might drive choice selection, via procedural memory in the basal ganglia. In most cases, it seems likely that a combination of these influences drives optimal decision-making in deterministic contexts (Tricomi and Fiez, 2008, 2012).

Since EV is an analogue of evidence quality, it can be used to localize the neural substrates of mnemonic information that guide choice selection. In parallel, drift-rate provides a measure of the rate of evidence accumulation during a decision. Because EVs are updated based on feedback at the end of each trial and reflect a history of prior experience, the overlap between effects related to this history described by EVs and those related to drift-rate of the current trial reflects the influence of the accrued experience of feedback from previous trials on evidence accumulation. In this intersection, regions were found in inferior parietal lobe, middle temporal gyrus, middle insular cortex, SMA, and the putamen (Table 8).

At its simplest, the concurrent discrimination task requires a mapping of a particular visual item (here, a word) to a motor output (which can change from trial to trial and Round to Round). The SMA, then, may be involved in creating such a mapping on the fly, along with other regions in this intersection, such as the middle insular cortex, which has been implicated in motor control related to habit learning (Poldrack et al., 1999). Importantly, coactivation of similar collections of regions has been reported in studies examining practice-related sensorimotor coordination, timing of movements, and task repetition (Jantzen et al., 2002; Jantzen et al., 2004; Smith et al., 2004). This suggests that the regions in this intersection might contribute to building strong stimulus-driven response behavior over the course of the task. The role of the dorsolateral striatum (putamen) seems to be particularly important in this type of procedural habit and motor learning (Yin et al., 2004, 2006; Tricomi et al., 2009). For instance, if an EV on a particular trial has been well-learned, drift-rate will be high, suggesting strong functional connections between the representation of the EV and the necessary motor mapping to enact the correct response given the orientation of the stimuli for that trial. Taken together, this suggests that corticostriatal circuits similar to those implicated in procedural memory or habit learning might partly underlie performance on a concurrent discrimination task. Such a system supported by the putamen would be well suited to contribute salient value information about each choice option. This information could be built up over repeated outcome experiences, establishing a sense of item-level familiarity (Poldrack et al., 1999; Poldrack et al., 2001; Seger and Cinotta, 2005). EV, thus, carries information about a particular stimulus, such that stronger EVs can lead to easier choices (i.e., better discriminability). Drift-rate can therefore be directly influenced by the quality of an EV, such that stronger EVs can speed up a decision process by providing higher quality evidence. A procedural memory system could work to build strong EVs to be used as evidence for a choice.

4.3 Repeated feedback encourages a shift toward stimulus-driven decision-making

In the concurrent discrimination task, subjects select randomly on the first exposure of an item, having no initial valid information that can be used to predict the choice outcome. With repetition, information is continuously gathered regarding the correct and incorrect outcomes and subsequently used to improve performance. After multiple rounds, this improved performance is manifested as faster and more accurate selection of the rewarded item in each pair (Fig. 1b). In a sense, decision-making becomes proceduralized.

The apparent increase in decision-making efficiency that arises from repeated encoding could be seen as a result of the integrated functioning of the performance monitoring and evidence storage systems discussed above, as illustrated in Figure 4. Early in the task, when choice accuracy is low and response times are slow (Fig. 1b), adequate decision evidence might not yet have been encoded to drive confident choice selection. This is reflected in the high decision thresholds and low drift-rates for the earlier rounds of the task, signifying a need to gather and evaluate better (or more) evidence (Fig. 1c). Correspondingly, RPEs are frequent early on, since EVs are unreliable (i.e., low quality evidence). Control regions such as the dorsal caudate, anterior insula, anterior cingulate, and pre-SMA might monitor these frequent error signals (RPE) to prospectively determine the degree of cognitive oversight needed to ensure optimal performance based on recent performance history.

As experience with the choices builds, accuracy begins to climb and RTs decrease (Fig. 1b), accompanied by a relaxation of decision thresholds and an increase in drift-rates (Fig. 1c). Thus, EVs become more reliable, representing improvements to evidence quality. Consequently, unexpected outcomes become less frequent. After sufficient repetition, bottom-up information from putative evidence providers and accumulators in the putamen, temporoparietal regions, and SMA becomes reliable enough to guide decisions under relatively lenient decision criteria. The skill that potentially develops through repeated choice selection places an emphasis on stimulus-driven information (e.g., outcome predictions), which builds as a result of earlier control (e.g., high decision thresholds). Learning through feedback might therefore enhance the quality of contributing decision evidence, so that bottom-up signals become more salient and reliable, and thus sufficient to enact a choice without burdensome goal, strategy, and error monitoring.

The striatum seems to play a particularly important role in this process. These roles are well characterized by reinforcement learning (Knutson et al., 2005), wherein the caudate and putamen contribute separately to learning processes (Seger and Cincotta 2005) and in the formation of value-driven stimulus-response associations (Yin et al., 2004, 2006; Tricomi et al., 2009). In the present study, EV and RPE relate to different aspects of decision-making. EV captures a history of the feedback experienced on prior trials. RPE captures momentary learning signals that reflect the outcome of the current trial. We found that the putamen seems to capture EV (i.e., predicted outcome value), whereas the caudate seems to capture positive RPE signals (i.e., learning signals). Thus, information held by the putamen is drawn upon as decision evidence (reflected in drift-rate), supporting the development of habit-like responses as information becomes well-learned. These stimulus-response associations arise as a result of computations in the caudate. For instance, microstimulation of the caudate at the time of reward (i.e., post-response feedback) can enhance the rate of associative learning (Williams and Eskandar, 2006). Moreover, the caudate head is sensitive to flexible, short-term changes in learning that might reflect errors between predictions and outcomes (Kim and Hikosaka, 2013). Our findings suggest that the caudate might not directly influence decisions (via drift-rate), but rather seems to respond to or monitor post-decision events. Between the dorsomedial and dorsolateral striatum, then, learning is a process of outcome signaling and subsequent information updating (Miyachi et al., 2002). Information about errors in outcome predictions might be processed in the caudate and might subsequently influence the function of the putamen related to information updating or utilization of a history of outcomes to inform choice-selection.

It is worth noting that a key limitation to these interpretations is the exclusion of negative RPE trials from the analysis. While these trials have clear theoretical value, they were undersampled in this study’s design. Thus, the present task cannot be leveraged with a regression analysis to produce reliable and confident results related to these negative RPE signals. A task that features frequent errors as a critical part of learning would be much better suited for investigating negative RPEs with confidence. Concurrent discrimination, however, wherein many subjects have perfect performance in later rounds, is more about repetition of positive choices.

4.4 Contributions of the medial temporal lobe

Given the nature of the task, it was expected that declarative memory regions such as the hippocampus and medial temporal lobe would map onto the EV and drift-rate intersection. While these regions were absent in this intersection, it should be noted that the parahippocampal gyrus was present in both the drift-rate and EV maps. It would make sense that declarative memory would play a role in concurrent discrimination learning. Such a system would be well suited to supply key contextual information about episodic associations between items in a present pair to support encoding for individual decision events (Burgess et al., 2002; Kirschoff et al., 2000). There are several possible explanations for the apparent absence of the influence of a declarative memory system on improvements in deterministic decision-making. First, given that the parahippocampal regions on each map were in different hemispheres (albeit at homologous locations), it is possible that the thresholds used to define the regions were too strict and washed out any overlapping effects (i.e., false negative). This is an unfortunate tradeoff for the selection of any threshold value. Second, it is possible that reinforcement learning algorithms cannot capture behavior related to hippocampal memory. This seems unlikely given that we did identify parahippocampal regions whose activity correlated with EV and that the learning rate of the model was high (i.e., single-trial learning was possible within the model). However, it is possible that the model-free algorithm we chose for our analyses was not an adequate choice to fully capture hippocampal influences and instead a model-based reinforcement learning approach would be more appropriate (Doll et al., 2015; Johnson and Redish, 2005). A third possibility is that the context of the task overburdens declarative memory and places emphasis on more traditional reinforcement learning circuits (such as striatal procedural memory). For instance, our task used 50 items, which is far more than the typical 8–12 items used in the work with human amnesics (for example, Hood et al., 1999; Bayley et al., 2005). Memorizing associations for 8 items can be supported by declarative memory, but it is less clear how such a system might behave in the context of 50 items. Moreover, feedback or reward context might play a role in the engagement of the hippocampal memory system, since our task featured salient visual feedback while other permutations of discrimination learning tasks have used physical monetary feedback, such as dimes (Hood et al., 1999).

These issues of task context and of tradeoffs between declarative and procedural memory have been highlighted in much of the literature on concurrent discrimination learning. For instance, performance on concurrent discrimination tasks with a compromised declarative memory system can sometimes be spared (Ridley et al., 1989; Gaffan et al., 1991). This might be influenced by task design factors, such as including long retention intervals between decision episodes (Malamut et al., 1984). Moreover, preserved performance ability seems to be mediated, at least in part, by the striatum (Teng et al., 2000). However, when larger areas of the temporal lobe are damaged (such as the parahippocampal gyrus), performance is almost entirely abolished, suggesting that some aspects of declarative, associative, or recognition memory are necessary for learning to occur (Buffalo et al, 1998; Buffalo et al., 1999; Chudasama et al., 2008). Similar mixed results can be found in humans, wherein robust habit learning seems to support learning in amnesics in some instances (Bayley et al., 2005) but not in others (Hood et al., 1999). Likewise, patients with deficient procedural learning capacity due to Parkinson’s disease, seem to require a declarative awareness of cue-reward relationships in order to succeed on concurrent discrimination learning (Moody et al., 2010). This underscores the importance of the basal ganglia for this type of learning, but also highlights the idea that multiple systems can and may interact. In the end, it seems that concurrent discrimination learning is a product of interactions between both hippocampal and basal ganglia systems, but these interactions are modulated by contextual and structural elements of the task (e.g., Turchi et al., 2010).

4.5 Conclusions

In an integrative approach to investigating the neural substrates of feedback and decision-making, our findings outline the cognitive processes and neural correlates that support an intersection of feedback-based learning and decision-making. Feedback carries critical outcome information that influences subsequent decision-making in numerous ways (Fig. 4). Outcome monitoring regions in the pre-SMA, anterior insula, anterior cingulate, dlPFC, and dorsal caudate nucleus help to translate external information about whether behavior is meeting expectations into appropriate adjustments to control over decision-making. At the same time, evidence-providing regions in the putamen, temporoparietal regions, and SMA allow mnemonic information gathered from past decisions to be applied to a current decision-making episode. Taken together, these findings highlight the critical influence of feedback on performance monitoring and the accrual of mnemonic information about choice value. In particular, the findings outline an intersection of neural substrates that are important to both feedback-based learning and decision-making. As this learning occurs, evidence quality improves, leading to a shift in processing from controlled, top-down decision-making to proceduralized, stimulus-driven choice selection, each mediated by separable neural substrates.

Highlights.

1. Covariates derived from decision and learning models identify common neural regions.

2. Feedback provides performance information monitored by a prefrontal network.

3. Choice-outcome learning improves decision evidence via the basal ganglia.

4. Choice-outcome learning drives a shift toward stimulus-driven decision-making.