Abstract
Motivation: Recent experimental studies have suggested that proteins fold via stepwise assembly of structural units named ‘foldons’ through the process of sequential stabilization. Alongside, latest developments on computational side based on probabilistic modeling have shown promising direction to perform de novo protein conformational sampling from continuous space. However, existing computational approaches for de novo protein structure prediction often randomly sample protein conformational space as opposed to experimentally suggested stepwise sampling.
Results: Here, we develop a novel generative, probabilistic model that simultaneously captures local structural preferences of backbone and side chain conformational space of polypeptide chains in a united-residue representation and performs experimentally motivated conditional conformational sampling via stepwise synthesis and assembly of foldon units that minimizes a composite physics and knowledge-based energy function for de novo protein structure prediction. The proposed method, UniCon3D, has been found to (i) sample lower energy conformations with higher accuracy than traditional random sampling in a small benchmark of 6 proteins; (ii) perform comparably with the top five automated methods on 30 difficult target domains from the 11th Critical Assessment of Protein Structure Prediction (CASP) experiment and on 15 difficult target domains from the 10th CASP experiment; and (iii) outperform two state-of-the-art approaches and a baseline counterpart of UniCon3D that performs traditional random sampling for protein modeling aided by predicted residue-residue contacts on 45 targets from the 10th edition of CASP.
Availability and Implementation: Source code, executable versions, manuals and example data of UniCon3D for Linux and OSX are freely available to non-commercial users at http://sysbio.rnet.missouri.edu/UniCon3D/.
Contact: chengji@missouri.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 Introduction
Computationally predicting protein structure from its amino acid sequence, the so called ‘de novo’ structure prediction problem, remains to be largely unsolved owing to the challenges associated with efficiently navigating huge conformational space accessible to proteins as well as due to the difficulties in accurately capturing physical forces behind protein folding in silico (Bradley et al., 2005).
Recent experimental studies based on equilibrium and kinetic hydrogen exchange (Hu et al., 2013; Maity et al., 2005) have theorized that protein folding proceeds by stepwise assembly of protein structural units known as ‘foldons’. Previously formed foldon units cooperate to sequentially stabilize subsequent foldons to gradually build the native structure in a process known as sequential stabilization (Rumbley et al., 2001). Alongside, encouraging process has been made on computational side with development of probabilistic graphical models (Bhattacharya and Cheng, 2015; Bhuyan and Gao, 2011; Boomsma et al., 2008; Boomsma et al., 2014; Hamelryck et al., 2006; Harder et al., 2010; Zhao et al., 2008) to perform conformational search from a continuous space that is free from discretized database-driven search strategies as employed in fragment assembly based structure prediction methods (Simons et al., 1997; Xu and Zhang, 2012). These methods adopt different representations to parameterize protein conformational space and employ a diverse set of machine learning methods to model it. For instance, FB5-HMM (Hamelryck et al., 2006) adopts a coarse-grained (Cα only) representation and trains a generative Hidden Markov Model (HMM) to capture local structural preferences. A discriminative learning method CRFSampler (Zhao et al., 2008), on the other hand, trains a Conditional Random Field (CRF) by utilizing Cα only representation. TorusDBN (Boomsma et al., 2008) and CS-TORUS (Boomsma et al., 2014) uses Dynamic Bayesian Network (DBN) to capture structural bias of proteins’ backbone whereas FUSION (Bhattacharya and Cheng, 2015) relies on Input-Output Hidden Markov Model (IOHMM) for modeling local preferences of backbone conformational space. Furthermore, methods relying on Markov random field (MRF) have been proposed (Bhuyan and Gao, 2011) to generate protein side chain rotamer library (χ dihedral angles) conditioned on backbone conformation. DBN based models such as BASILISK (Harder et al., 2010) also exist to capture backbone-dependent and backbone-independent structural preferences of side chain χ angles. Despite showing promising direction, these approaches follow several conventions that can be circumvented. First, starting from an extended polypeptide conformation of the whole protein, these approaches attempt to predict the folded structure by replacing random stretches of the chain using probabilistic sampling and optimizing a potential energy function. These probabilistic graphical model methods, like current fragment assembly based methods, therefore, do not apply experimentally suggested stepwise protein folding paradigm during structure prediction. Second, these methods do not consider the influence of side chains during structure modeling and typically add side chain conformation conditioned on backbone after the backbone geometry is predicted.
Motivated by experimental hypothesis, we develop UniCon3D, a de novo protein structure prediction method that performs stepwise synthesis and assembly of foldon units via conditional sampling from a novel united-residue probabilistic model, which captures local conformational bias of backbone and side chain simultaneously in a united residue representation. The rationale for choosing united-residue representation is to integrate both backbone and side chain during structure modeling. It is found that (i) stepwise sampling produces lower energy conformations with higher accuracy than random sampling when everything else remains the same; (ii) UniCon3D attains comparable performance with top five automated methods of CASP11 and CASP10 in a dataset of 30 and 15 difficult target domains, respectively; and (iii) UniCon3D outperforms a baseline counterpart of UniCon3D that performs traditional random sampling as well as GDFuzz3D (Pietal et al., 2015) and FT-COMAR (Vassura et al., 2008), two state-of-the-art approaches for de novo protein structure prediction aided by residue-residue contacts in a dataset containing 45 CASP10 targets.
2 Methods
2.1 Parameterization of united-residue model of polypeptide chains
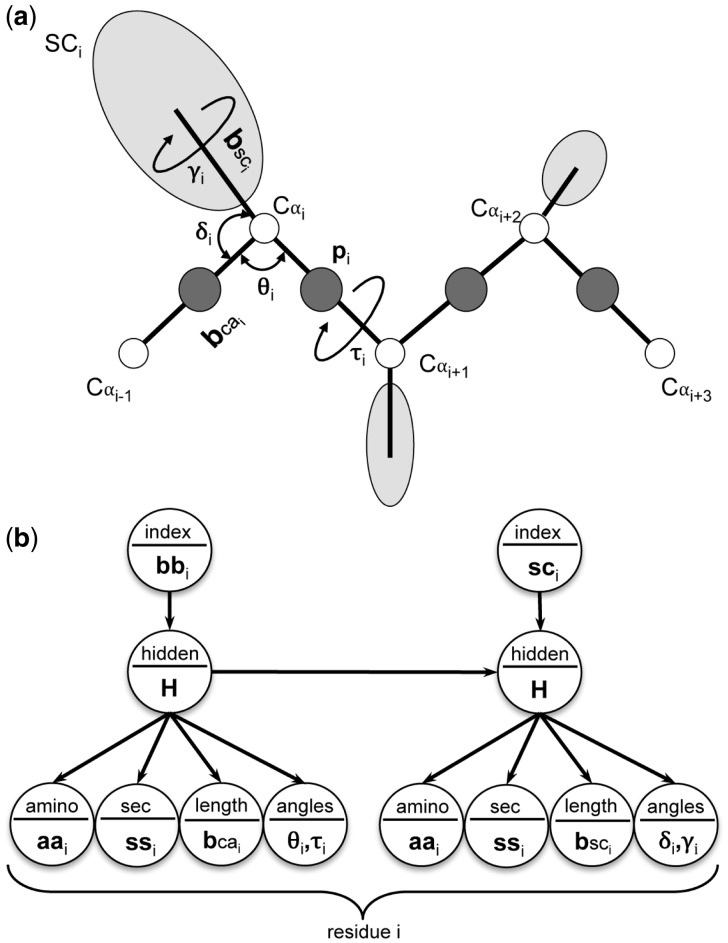
We adopt a united-residue representation, similar to that used in the UNRES model (Liwo et al., 1997), in order to parameterize the conformational space associated with protein molecules. In a united-residue model, the geometry of a polypeptide chain is represented by sequence of alpha-carbon (Cα) atoms linked by virtual bonds with attached united side chains (SC) and united peptide groups (p) located in the middle of two consecutive Cα atoms. The united peptide groups and the united side chains serve as interaction sites, while Cα atoms assist in defining the geometry (Fig. 1a). We parameterize the alpha-carbon positioning of residue i (Cαi) in a polypeptide chain using virtual bond length (bcai) between Cαi-1–Cαi atoms, virtual bond angle (θi) formed by Cαi-1–Cαi–Cαi + 1 atoms, and virtual dihedral angle (τi) formed by Cαi-1–Cαi–Cαi + 1–Cαi + 2 atoms. The united side chain positioning of residue i (SCi) is specified using virtual bond length (bsci) between Cαi–SCi atoms, virtual bond angle (δi) formed by Cαi-1–Cαi–SCi atoms, and virtual dihedral angle (γi) formed by SCi–Cαi–Cαi-1–Cαi + 1 atoms. The united peptide group corresponding to residue i (pi) can be derived using the Cα geometry. In order to compute the geometry of the terminal residues, we extend the chain by adding dummy residue(s) to the terminal amino (N-terminus) and carbonyl groups (C terminus). Following UNRES model, we used orientation dependent anisotropic side chains (Liwo et al., 1997), represented by ellipsoids of revolution with the centers of the ellipsoids at the centers of mass of the side chains, the long axes being assumed to be collinear with the Cα-SC axes. It should be noted that our model, unlike earlier approaches based on a united-residue representation (Levitt, 1976; Liwo et al., 1993, 1997), does not assume ideal values for virtual bond lengths or bond angles and therefore captures united-residue polypeptide geometry in the highest possible granularity.
Fig. 1.
Parameterization and modeling of united-residue polypeptide conformational space. (a) United-residue polypeptide chain parameterized using virtual lengths and virtual angle pairs for backbone and side chain. (b) Conditional dependency graph of UniCon IOHMM. Circular nodes represent stochastic variables and arrows in the graph specify the conditional independence relationships among variables
2.2 Formulating a generative, probabilistic model of united-residue polypeptide conformational space
We encapsulate the abovementioned parameterization into the framework of a Markovian model to formulate UniCon3D, a generative, probabilistic model to capture the local preferences of the united-residue conformational space accessible to protein. In particular, we use Input-Output Hidden Markov Model (IOHMM) (Bengio and Frasconi, 1996) in conjunction with statistical distributions to describe the united-residue protein geometry in a natural, continuous space. A slice of the proposed model is presented in Figure 1b. For each slice, an input node (I) indicates whether backbone or side chain geometry is being modeled. It is a discrete variable that can adopt only two values (0 for backbone, 1 for side chain). The internal structural states of the backbone and side chain geometry are represented by two hidden nodes H, respectively. Two discrete emission nodes, A and S, represent twenty standard amino acid residue types and eight-class secondary structure types (α-helix, isolated β-bridge, extended strand, 310 helix, π-helix, hydrogen bonded turn, bend and random coil) respectively, while two continuous emission nodes, B and V, specify virtual bond lengths and pairs of virtual angles and virtual dihedral angles respectively. All the discrete nodes are modeled using conditional probability tables. We use mixture of Gaussian distributions to capture the preferences of the virtual bond lengths and mixture of bivariate von Mises distributions (Mardia et al., 2007) to model the virtual angles and virtual dihedral angles pairs. The dependencies between the input nodes (which alternates between backbone and side chain as indicated by I) and the output emission nodes (which specify the conformational features as indicated by A, S, B and V) are mediated by a sequence of interconnected, discrete hidden nodes H. Its purpose is to model the dependencies between the input and output nodes and the sequential dependencies between the features. In other words, depending on the value of the input node I, the hidden node H specifies which mixture component is chosen among the possible emission distributions. The optimal number of hidden nodes is found to be 115 after parameter estimation and model selection as described in next section. The values of these hidden nodes are never observed: their sole purpose is to model the dependencies between the input and output nodes in addition to capturing the sequential dependencies between the output nodes. The hidden nodes are, therefore, the so-called nuisance variables that are integrated during parameter estimation, sampling and inference. It should be noted that the hidden nodes introduce dependencies between all residues by means of a transition probability matrix, and not just between two consecutive residues (Harder et al., 2010).
UniCon3D has several advantages over other recently developed probabilistic models (Bhattacharya and Cheng, 2015; Boomsma et al., 2008, 2014; Hamelryck et al., 2006; Harder et al., 2010; Zhao et al., 2008) for capturing local structural bias of protein conformational space. First, it combines backbone and side chain conformational space in a single framework using united-residue representation that allows simultaneous sampling of backbone and side chain conformation. The presence of side chains enables any folding simulation to account for the energetic contribution of hydrophobic (hydrophilic) interactions between side chains as well as interactions of side chains with solvent, which is believed to be one of the major driving forces behind protein folding (Dill, 1990). Second, UniCon3D adopts eight-class secondary structure categorization that is more informative than three-class secondary structure grouping. Third, the model makes it possible to condition side chain sampling upon backbone conformation, which has been shown to have strong influence on side chain's conformation (Dunbrack and Karplus, 1993). Modeling backbone and side chain in continuous space also avoids the problems associated with discretized libraries of fragments (Hegler et al., 2009; Kim et al., 2009) or rotamers (Petrella and Karplus, 2001; Schrauber et al., 1993). Additionally, like other generative model, UniCon3D can be used to generate a sequence of virtual bond lengths and pair of virtual bond angles of any length (even for the whole protein sequence) given an amino acid sequence and secondary structure sequence using the forward-backtrack (FwBt) algorithm (Cawley and Pachter, 2003; Hamelryck et al., 2006). The FwBt algorithm can also be used to conditionally resample any segment of the polypeptide chain given a previously sampled conformation, thereby rebuilding part of a previously generated structure seamlessly.
2.3 Training data, parameter estimation and optimal model selection
UniCon model is trained on a large dataset of protein structures using a training dataset curated to train SSpro/ACCpro 5 (Magnan and Baldi, 2014) containing 5772 nonredundant, high-resolution protein chains. We exclude 240 proteins from training that have more than 25% sequence identity with any of the test proteins used during benchmark experiment using Blastclust (Altschul et al., 1997). The training set finally contains 5532 proteins with sequence lengths ranging from 30 residues to 1264 residues. Amino acid sequences, virtual bond lengths and virtual bond angle pairs are derived directly from the protein structures, whereas eight-class secondary structures are assigned using DSSP (Kabsch and Sander, 1983). The training dataset contains 1 932 712 observations corresponding to 966 356 residues (two observations per residue: one for backbone and the other for side chain).
Parameter learning for UniCon is done via stochastic expectation maximization (S-EM) algorithm (Nielsen, 2000) as implemented in the Mocapy ++ toolkit (Paluszewski and Hamelryck, 2010) using the aforementioned training dataset. In order to determine the number of hidden node values (i.e. the size of the hidden node), a crucial hyperparameter that governs the tradeoff between underfitting and overfitting and hence influences the performance of the model, we perform the training by varying hidden node size from 10 to 120 (with a step size of 5). On one core of an Intel E7-L8867 (2.13 GHz), training one model takes between 10 and 96 h for hidden node size 10 and 120, respectively. Since the nature of the S-EM algorithm is stochastic, parameter estimation for each hidden node size is repeated four times with different starting conditions to lower the chance of selecting a model that got stuck in a local optima. The ideal hidden node size is estimated using Akaike Information Criterion (AIC) (Burnham and Anderson, 2003), a widely used model selection measures. For a model with hidden node size 115, AIC value reaches the minimum value (Supplementary Fig. S1), indicating optimal model. We select this model as the optimal one with 30 707 parameters.
2.4 Conformational sampling via stepwise synthesis and assembly of foldon units
Motivated by recent experimental studies (Hu et al., 2013; Maity et al., 2005) hypothesizing that protein folds by stepwise addition of foldon units (roughly corresponding to one or more secondary structural elements of the native structure), we use conditional resampling capability of UniCon model to simulate stepwise buildup of protein structure (Fig. 2). Starting from a target protein sequence, we first predict eight-class secondary structure using SSpro 5 (Magnan and Baldi, 2014) and locate the secondary structure elements (SSE) comprising of α-helix, isolated β-bridge, extended strand, 310 helix and π-helix. Starting from the N-terminus, we sequentially define foldon units that terminate at the end of SSEs until we reach the C-terminus. We also require that the size of a foldon unit should be at least 20 residues. The minimum size of foldon unit is chosen based on an earlier study (Hamelryck et al., 2006) showing that majority of SSE lengths in naturally occurring proteins are within 20 residues for strands and coils and is slightly longer for helices. In case the size of a SSE is less than 20 residues, we extend the foldon unit to include the following SSEs or up to the C-terminus. Once the foldon units are identified, conformational sampling is performed sequentially from N to C-terminus in a stepwise manner with each step aiming to stabilize one foldon unit at a time. This is achieved via two stages: synthesis and assembly.
Fig. 2.
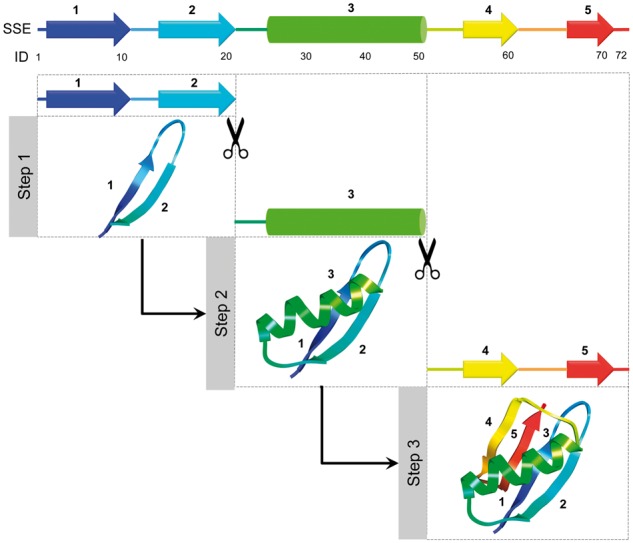
Visualization of stepwise sampling protocol. Foldon units are identified from the SSEs with a size restriction of at least 20 residues. Each foldon unit is then sequentially synthesized and assembled from N to C-terminus via probabilistic sampling conditioned on previously formed conformation
In the synthesis stage, which corresponds to the extrusion of a foldon unit at the C-terminal end of an existing polypeptide conformation, the emission nodes of the already formed structure is marked as observed in addition to fixing the sequence and secondary structure of the extruded foldon unit to specific values. The FwBt algorithm (Cawley and Pachter, 2003; Hamelryck et al., 2006) is subsequently used to sample the virtual bond lengths and virtual angle pairs of backbone and side chain conformation for the entire stretch of the extruded foldon unit conditioned on the existing polypeptide geometry using the trained UniCon model. For the synthesis of the first foldon unit, the sampling is performed solely based on its sequence and secondary structure.
The next stage is the assembly stage that stabilizes the nascent foldon unit with respect to the rest of the structure. First, amino acid sequence and secondary structure emission nodes are marked as observed for both backbone and side chain for the whole structure including the nascent foldon unit. Then, random stretches of 1–15 residues are resampled from the existing polypeptide conformation by flagging all the backbone emission nodes as observed for all the SSEs (i.e. helices and strands) except for those present in the current foldon unit. Emission nodes for virtual bond lengths and virtual angle pairs of the backbone conformation for the rest of the structure (e.g. coils/loops) are marked as hidden. Side chain virtual bond lengths and virtual angle pairs are flagged as hidden for the whole structure. This allows side chain sampling conditioned on backbone for the previously stabilized SSEs, while simultaneously sampling backbone and side chain conformation for the nascent foldon unit as well as for the linker regions (e.g. coils/loops) between previously stabilized SSEs (hydrogen bonded turn, bend and random coil). Flexible backbone conformation in the linker regions may help the conformation to come out of a false local entrapment that may have been caused by premature folding of earlier foldon units before the rest of the foldons have emerged. In order to allow further flexibility, each of the virtual angles associated with the backbone conformation for the previously stabilized SSEs are perturbed randomly by up to 1°.
2.5 Energy function by combining united-residue physics-based force field with knowledge-based information
We use a basic implementation of UNRES physics-based force field (Liwo et al., 1993, 1997) aided by knowledge-based information on residue–residue contacts. The energy of a united-residue polypeptide chain is calculated as:
The term ESCiSCjaccounts for the mean free energy of the hydrophobic (hydrophilic) interactions between the side chains and implicitly includes the energetic contributions from the interactions of the side chain with the solvent. The term ESCipjrepresents excluded-volume potential of the side chain and peptide groups interactions. The term Epipj denotes the peptide-group interaction potential and primarily accounts for the electrostatic interactions (i.e. propensity to form backbone hydrogen-bonds) between peptide groups pi and pj. The details of the parameterization of these terms are provided in the earlier publications of UNRES (Liwo et al., 1997). The final term Erirj accounts for energetic contribution due to residue-residue contacts adopted from previously published FRAGFOLD with RRCON methodology (Kosciolek and Jones, 2014). This is a square well function with exponential decay and is defined as:
where P is the probability of residue i and residue j to be in contact. In united-residue representation, we consider a contact is fully formed when the distance d between the united side chains of the participating residues (SCi–SCj) are within a cutoff distance of d0. We fix d0 at 8 Å. This function strives to avoid false positives by penalizing non-satisfied contacts proportional to P with the penalty decaying with d. It should be noted that the source of residue-residue contact is not fixed in our study. Contacts can be experimentally derived or predicted from the sequence using evolutionary sequence variation (Jones et al., 2012; Marks et al., 2011; Seemayer et al., 2014; Skwark et al., 2013) or machine learning based methods (Cheng and Baldi, 2007; Eickholt and Cheng, 2012; Tegge et al., 2009; Wang and Xu, 2013) or a combination of both covariation techniques and machine learning (Jones et al., 2015; Kosciolek and Jones, 2015). When true contacts are known, all P values can be set to 1. On the other hand, to exclude the influence of contact energy altogether, all P values can be set to 0.
We set the weights of the UNRES energy terms in accordance with the 4P force field (Oldziej et al., 2004; Oldziej et al., 2004), where wSC = 1.00000, wSCp = 2.73684 and wel = 0.06833. The value of wrr depends on the accuracy of residue-residue contacts and should be weighted higher for experimentally derived contacts or contacts predicted using covariation techniques with deep multiple sequence alignment than contacts predicted using pure machine learning methods. After experimenting with several weights for wrr, we select wrr = 3.00000.
2.6 Energy minimization
Simulated annealing (SA) algorithm (Aarts and Korst, 1988) is employed to minimize the potential energy of a united-residue polypeptide conformation. The conformational sampling proceeds by stepwise synthesis and assembly. Given the conformation of an extruded foldon unit generated in the synthesis stage, we propose a new conformation in the assembly stage and accept it with a probability proportional to:
where ΔE is the difference between energy of the new conformation and the energy of the old conformation and t is the annealing temperature. We set the initial temperature to 1000 K based on earlier studies of UNRES force field (Liwo et al., 1993) and gradually decrease it to 298 K using an exponential cooling schedule.
2.7 UniCon3D and B03D
We combine the stepwise sampling and composite energy function to devise UniCon3D, a united-residue de novo protein structure prediction protocol. Given a protein sequence, predicted secondary structure and optionally residue-residue contacts, foldon units are sequentially synthesized and assembled using simulated annealing energy minimization. The number of Monte Carlo (MC) cycles for each step in the stepwise sampling is set to the number of residues times 100. At the end of MC cycles, the lowest-energy conformation is selected as the prediction to be used in the next step or as the final predicted structure (a.k.a. decoy) if all the foldon units are consumed. The procedure can be repeated multiple times in order to generate multiple decoys for the target protein. It should be noted that we set all parameters related to UniCon3D using the training proteins only.
We also implement a baseline sampler (B03D) that does not perform stepwise sampling. It first samples the conformation for the entire polypeptide chain from amino acid and predicted secondary structure sequence using UniCon3D IOHMM model and subsequently resamples the conformation of random stretches of 1–15 residues using FwBt algorithm. This kind of random conformational sampling strategy resembles discretized fragment assembly approaches (Simons et al., 1997; Xu and Zhang, 2012) or their probabilistic equivalents using generative models (Bhattacharya and Cheng, 2015; Boomsma et al., 2008; Hamelryck et al., 2006; Zhao et al., 2008). Using the same energy function and simulated annealing energy minimization with the same number of MC cycles and temperature schedule as used in UniCon3D, the baseline sampler gives rise to a comparable structure prediction approach, which we name B03D. A direct comparison between UniCon3D and B03D may, therefore, reveal the strengths and weaknesses of stepwise sampling over traditional random sampling.
2.8 Ranking decoys and performance assessment
In addition to internal UniCon3D scoring, we also use two external single model quality assessment programs (MQAPs): ProQ2 (Ray et al., 2012) and Qprob (Cao and Cheng, 2016); and two clustering-based MQAPs: APOLLO (Wang et al., 2011) and MUFOLD-CL (Zhang and Xu, 2013) in order to rank decoys produced by UniCon3D. ProQ2 uses support vector machine to predict the quality of a decoy based on its structural features and evaluated to be the best single-model method in CASP11 (Uziela and Wallner, 2016). Qprob predicts a decoy’s quality by estimating the errors of structural, physiochemical and energy-based features using probability density distributions and shown to have achieved state-of-the-art performance in CASP11 (group name MULTICOM-NOVEL). APOLLO is based on full pair-wise comparison approach after optimal structural superposition between each pair of decoys. MUFOLD-CL uses a superposition-independent distance matrix comparison strategy for clustering decoy population. Since both ProQ2 and Qprob require full-atom representation of decoys, we convert united-residue decoy pools produced by UniCon3D into all-atom level using PULCHRA software (Rotkiewicz and Skolnick, 2008). APOLLO and MUFOLD-CL, on the other hand, requires only Cα atoms. We select top 100 decoys by UniCon3D energy function and re-rank them using APOLLO while all decoys produced by UniCon3D are supplied directly for clustering to MUFOLD-CL. After ranking all decoys using a specific MQAP, the top-ranked decoy (or the centroid of the largest cluster in case of MUFOLD-CL) is subsequently selected and compared with its native structure using TM-score program (Zhang and Skolnick, 2004) to compute its Cα-rmsd and TM-score. Residues present in the sequence but not observed in the experimental structure, although modeled, are ignored during the comparison.
3 Results and discussion
3.1 UniCon3D versus B03D
In order to compare UniCon3D with our baseline approach, B03D, we collect six small proteins ranging in length from 43 to 76 residues that have been subject of previous studies (Simons et al., 1997; Zhao et al., 2008). We then predict eight-class secondary structure using SSpro 5, extract true residue-residue contacts from the native structures, and employ UniCon3D and B03D protocol to generate 100 decoys for each protein. The rationale for using true contacts as opposed to predicted contacts is to ensure that the contact energy Erirj during sampling is not dominated by the presence of false positive contacts since the sole purpose of this experiment is to compare stepwise sampling performed in UniCon3D with traditional random sampling done in B03D. Table 1 reports the average energy of the decoy population and the TM-score of the lowest-energy decoy for each protein in the dataset along with energies of the native state. The average energy sampled by UniCon3D (−449.18) is 4.9% lower than the average energy sampled by B03D (−428.25); albeit the average energy of the native state is significantly lower (−723.58). The difference between sampled and native energy indicates that the composite physics and knowledge-based energy function used in UniCon3D is able to distinguish native state from decoys. The energy distributions produced by UniCon3D is consistently skewed towards lower energy regions compared to B03D (Supplementary Fig. S2). This generally results in a higher accuracy decoy compared to its native structure with average TM-score of the lowest-energy decoy for UniCon3D (0.57) outperforming that of B03D (0.53) by 7.5%, demonstrating superiority of stepwise sampling protocol compared to traditional random sampling.
Table 1.
Average energy of 100 decoys and TM-scores of lowest-energy decoy for six small proteins
| Native |
UniCon3D |
B03D |
|||
|---|---|---|---|---|---|
| Protein, PDB code | Energy | Energy | TM-score | Energy | TM-score |
| Protein A, 1FC2 | −459.03 | −419.99 | 0.66 | −403.61 | 0.63 |
| Homeodomain, 1ENH | −550.08 | −473.70 | 0.73 | −446.61 | 0.67 |
| Protein G, 2GB1 | −688.10 | −479.72 | 0.50 | −453.39 | 0.51 |
| Cro repressor, 2CRO | −794.04 | −454.45 | 0.51 | −432.18 | 0.44 |
| Protein L7/L12, 1CTF | −899.18 | −447.23 | 0.41 | −430.11 | 0.43 |
| Calbidin, 4ICB | −951.04 | −419.99 | 0.62 | −403.61 | 0.54 |
| Mean | −723.58 | −449.18 | 0.57 | −428.25 | 0.53 |
We also calculate the Mean Absolute Error (MAE) of virtual backbone angles of the lowest-energy decoys (Adecoy) generated by UniCon3D and B03D with respect to that of the native conformation (Anative). Due to the periodicity of angles, we consider the smaller value of (d = |Adecoy − Anative|) and (360 – d) when calculating MAE. Furthermore, we use SPIDER2 (Heffernan et al., 2015; Lyons et al., 2014) to predict the virtual backbone angles from sequence using machine learning in order to compare MAE of sampled decoy to sequence-based prediction. SPIDER2 employs an iterative deep learning methods and is shown to achieve state-of-the-art performance (Heffernan et al., 2015). Although a reduced MAE in backbone virtual angle pair does not necessarily guarantee a better structure, the comparison offers some interesting insights. Average MAE of the virtual bond angles formed by Cαi−1−Cαi−Cαi + 1 atoms of the decoys produced by UniCon3D is 8.7°, slightly higher than that of B03D (7.8°) and SPIDER2 (6.8°). Average MAE of the virtual dihedral angle for UniCon3D (29.7°) is lower than that of B03D (33.2°) and slightly higher than that of SPIDER2 (26.7°). Overall, average MAE of backbone virtual angle pair for the lowest-energy decoys produced by UniCon3D is 6.5% lower than that of B03D and 14.5% higher than that of SPIDER2. In terms of the ability to sample more accurate backbone virtual angle pairs UniCon3D outperforms B03D, underlining the effectiveness of stepwise sampling. On the other hand, higher average MAE compared to SPIDER2 indicates that UniCon3D sampling could be further improved, possibly by generating more number of decoys or by carrying out longer simulation. It should be noted that SPIDER2 predicts virtual dihedral angle formed by Cαi−2−Cαi−1−Cαi−Cαi + 1 atoms and we adopt the same definition during MAE calculation for fair comparison.
3.2 Performance of UniCon3D in CASP11 free modeling targets
We assess the performance of UniCon3D using 24 single or multi-domain protein targets released during CASP11 experiment with length from 110 to 470 residues with at least one domain classified as free modeling (FM) targets (Kinch et al., 2016). To replicate a blind de novo prediction scenario, we first obtain the sequences of these proteins from CASP11 and predict their eight-class secondary structures using SSpro 5. We choose to use residue-residue contacts submitted by the CONSIP2 predictor (group 021) during CASP11, a method combining both covariation techniques and machine learning techniques (Jones et al., 2015; Kosciolek and Jones, 2015) and evaluated to be the top performing contact predictor during CASP11(Monastyrskyy et al., 2015). For each target, we run UniCon3D using 20 threads in parallel with independent random seeds to generate a decoy pool with a maximum of 2000 decoys within 48 h, thereby adhering to blind prediction mode as performed in CASP. Decoy with the lowest energy in the decoy pool is subsequently predicted to be top-ranked model. After the prediction phase, we evaluate the accuracy of top-ranked model after filtering them based on 30 native domains as defined by CASP11 assessors (Kinch et al., 2016). We also compare the accuracy of UniCon3D with five top-performing servers participated in CASP11 namely QUARK and Zhang-Server (Zhang et al., 2015), RBO_Aleph (Mabrouk et al., 2015), nns (Joung et al., 2015) and BAKER-ROSETTASERVER (Kinch et al., 2015).
In Table 2, we show the average TM-score and Cα-rmsd over the entire dataset for these methods along with P-value of a one-sample t-test of TM-score and Cα-rmsd difference of each method compared to UniCon3D (Supplementary Table S1). In terms of TM-score, Table 2 reveals that UniCon3D is comparable to the state-of-the-art servers with an average TM-score of 0.25; 0.04 and 0.03 TM-score points worse than the best serves QUARK and Zhang-Server respectively. Average TM-scores of UniCon3D is same as RBO_Aleph and 0.02 TM-score points better than nns and BAKER-ROSETTASERVER although their difference is statistically insignificant. With respect to Cα-rmsd, however, UniCon3D performs 10 and 12% better than nns and BAKER-ROSETTASERVER respectively within 95% significance interval while being comparable with other top-performing servers. The results demonstrate that UniCon3D attains performance comparable to the top automated methods worldwide. It should be noted that unlike top-performing servers, UniCon3D operates at coarse-grained representation with a very simple energy function and does not employ any expensive all-atom refinement or relaxation step. Moreover, the stepwise sampling circumvents the error-prone domain splitting and recombination step, typically used in most top-performing methods.
Table 2.
Comparison between UniCon3D and top-performing servers based on average TM-scores and Cα-rmsds of top-ranked model in 30 CASP11 FM domainsa
| Group name |
TM-score (P-value*) | Cα-rmsd (P-value**) |
|---|---|---|
| QUARK | 0.29 (0.015) | 14.83 (0.102) |
| Zhang-Server | 0.28 (0.014) | 15.39 (0.563) |
| UniCon3Db | 0.25 (–) | 15.82 (–) |
| RBO_Aleph | 0.25 (0.306) | 16.67 (0.198) |
| nns | 0.23 (0.372) | 17.41 (0.003) |
| BAKER-ROSETTASERVER | 0.23 (0.181) | 17.71 (0.001) |
* P-value of a one-sample t-test of TM-score difference to UniCon3D TM-scores.
** P-value of a one-sample t-test of Cα-RMSD difference to UniCon3D Cα-rmsds.
a The groups are sorted by descending TM-scores then by ascending Cα-RMSD.
b Not a participating group in CASP11 experiment.
To further investigate whether the performance of UniCon3D can be improved by using other MQAPs, we use ProQ2, Qprob, APOLLO and MUFOLD-CL to re-rank the whole decoy pool and identify top-ranked decoys for each target to compute their accuracies compared to the native domains. Table 3 summarizes the average TM-scores and Cα-rmsds of the top-ranked decoys selected by different MQAPs (Supplementary Table S2). UniCon3D’s energy function performs best as indicated by 0.01, 0.01, 0.02 and 0.02 higher average TM-score compared to APOLLO, Qprob, ProQ2 and MUFOLD-CL respectively and 0.06, 0.46, 0.52 and 0.81 Å lower average Cα-rmsd compared to APOLLO, ProQ2, Qprob and MUFOLD-CL respectively. The comparable performance of the internal energy function of UniCon3D with the state-of-the-art single model and clustering-based MQAPs demonstrates the effectiveness of the composite physics and knowledge-based energy function used in UniCon3D.
Table 3.
Average TM-scores and Cα-rmsds of top-ranked decoys based on different MQAPs in 30 CASP11 FM domains*
| MQAP | TM-score | Cα-rmsd |
|---|---|---|
| UniCon3D | 0.25 | 15.82 |
| APOLLO | 0.24 | 15.88 |
| Qprob | 0.24 | 16.34 |
| ProQ2 | 0.23 | 16.28 |
| MUFOLD-CL | 0.23 | 16.63 |
* MQAPs are sorted by descending TM-scores then by ascending Cα-rmsd.
3.3 Performance of UniCon3D in CASP10 free modeling targets
We further access the performance of UniCon3D using 14 single or multi-domain protein targets released during CASP10 experiment with length varying from 165 to 770 residues with at least one domain classified as free modeling (FM) target (Taylor et al., 2014). We follow the same modeling protocol as described for CASP11 by first predicting eight-class secondary structures using SSpro 5 and residue-residue contacts using MetaPSICOV (Jones et al., 2015; Kosciolek and Jones, 2015) and subsequently executing 20 parallel threads of UniCon3D simulations to generate up to 2000 decoys within 48 hours. The lowest-energy decoy is then compared to 15 native domains as defined by CASP10 assessors after filtering. Just like CASP11, we compare the accuracy of UniCon3D with five top-performing CASP10 servers namely Zhang-Server and QUARK (Zhang, 2014), PMS (Joo et al., 2014), MUFold_CRF (Zhang et al., 2010) and BAKER-ROSETTASERVER.
Table 4 reports the average TM-score and Cα-rmsd together with P-value of a one-sample t-test of TM-score and Cα-rmsd difference of each method compared to UniCon3D (Supplementary Table S3). With respect to TM-score, UniCon3D is 0.03 TM-score points worse than both Zhang-Server and QUARK, same as PMS, 0.01 TM-score points better than both MUFold_CRF and BAKER-ROSETTASERVER. Nevertheless, except for the top-performing method Zhang-Server, TM-score difference between UniCon3D and other methods are statistically insignificant at 95% significance interval. Likewise, in terms of Cα-rmsd, UniCon3D performs slightly worse than Zhang-Server and QUARK and better than PMS, MUFold_CRF and BAKER-ROSETTASERVER; although their difference is statistically insignificant. Once again, UniCon3D achieves performance comparable to the top groups worldwide underscoring its consistency and robustness.
Table 4.
Comparison between UniCon3D and top-performing servers based on avarage TM-scores and Cα-rmsds of top-ranked model in 15 CASP10 FM domainsa
| Group name | TM-score (P-value*) | Cα-rmsd (P-value**) |
|---|---|---|
| Zhang-Server | 0.25 (0.035) | 16.14 (0.164) |
| QUARK | 0.25 (0.056) | 16.42 (0.226) |
| UniCon3Db | 0.22 (–) | 17.45 (–) |
| PMS | 0.22 (0.981) | 18.04 (0.565) |
| MUFold_CRF | 0.21 (0.565) | 18.70 (0.365) |
| BAKER-ROSETTASERVER | 0.21 (0.393) | 22.09 (0.103) |
* P-value of a one-sample t-test of TM-score difference to UniCon3D TM-scores.
** P-value of a one-sample t-test of Cα-RMSD difference to UniCon3D Cα-rmsds.
a The groups are sorted by descending TM-scores then by ascending Cα-RMSD.
b Not a participating group in CASP10 experiment.
3.4 De novo prediction of CASP10 template-based modeling targets using UniCon3D
Next, we examine the performance of UniCon3D’s de novo structure prediction protocol coupled with a machine learning based contact predictor in the context of template based modeling (TBM). This is done using a dataset containing 45 single-domain protein targets from CASP10 experiment (Moult et al., 2014) that are classified as TBM or TBM-hard targets with sequence length from 71 to 390 residues. We select residue–residue contacts generated by MULTICOM predictor (group 489), the top contact predictor according to CASP10 assessment (Monastyrskyy et al., 2014). MULTICOM employs a conformation ensemble approach (Eickholt et al., 2011) to combine different machine learning based contact predictors (Cheng and Baldi, 2007; Eickholt and Cheng, 2012; Tegge et al., 2009). The average sensitivity of predicted contact map by MULTICOM over the entire dataset is 0.3 with 10 targets having sensitivity >0.5. Once again, we replicate a blind prediction scenario and generate up to 2000 decoys for each target using 20 parallel threads within a limited time of 48 hours. The same dataset with the same contact maps produced by MULTICOM has been recently used to evaluate the performance of GDFuzz3D (Pietal et al., 2015). The method predicts distance maps from predicted contact maps using graph distance map coupled with multidimensional scaling and subsequently employ coarse-grained modeling followed by all-atom refinement for de novo structure prediction. GDFuzz3D is compared with FT-COMAR (Vassura et al., 2008), a popular method to predict 3D structures from noisy contact maps, and shown to predict more accurate models. This dataset, therefore, allows a head-to-head comparison between UniCon3D with GDFuzz3D as well as with FT-COMAR. Furthermore, the realistic accuracy of predicted contact maps in this dataset permits a fair performance comparison between UniCon3D and B03D in a large dataset. We compute the accuracy of predictions made by UniCon3D and B03D by comparing them directly with the native structures while the accuracy of GDFuzz3D and FT-COMAR is adopted from the published work of GDFuzz3D method (Pietal et al., 2015).
As reported in Table 5, on an average over the entire dataset, decoys generated by UniCon3D are more accurate with an average TM-score of 0.45 compared to 0.41 and 0.31 for GDFuzz3D and FT-COMAR respectively (Supplementary Table S4). Average Cα-rmsd of UniCon3D is 10.73 Å, comparable to GDFuzz3D (10.75 Å) and lower than FT-COMAR (14.81 Å). Considering the 10 targets with reasonably accurate contact maps (sensitivity > 0.5), UniCon3D generates 8 models with TM-score > 0.5 indicating correct folds (Xu and Zhang, 2010), while GDFuzz3D produces 6 models with TM-score > 0.5 and FT-COMAR returned only 4 models (Supplementary Table S5). The average TM-score for UniCon3D for these targets is 0.54 compared to 0.51 for GDFuzz3D and 0.39 for FT-COMAR (average Cα-rmsd of UniCon3D is 5.66 versus 6.15 Å for GDFuzz3D and 11.02 Å for FT-COMAR). The results suggest the ability of UniCon3D to more consistently predict the correct fold of a protein given reasonably accurate contact maps than GDFuzz3D and FT-COMAR. Furthermore, the higher average accuracy of UniCon3D demonstrates that stepwise sampling combined with united-residue composite energy function can outperform a modeling protocol such as GDFzz3D that integrates coarse-grained modeling with all-atom refinement or a fault tolerant 3D structure reconstruction algorithm from noisy contact map like FT-COMAR. It should be noted, however, that the accuracy of UniCon3D is much worse compared to the best CASP10 server prediction (measured by highest TM-score model among all submitted server models) that leverages available template information via homology modeling or threading techniques. This is expected because UniCon3D is a de novo modeling approach that neither employs template identification nor incorporates template-derived restraints during structure modeling. Nevertheless, the best CASP10 server prediction serves as reference and reveals the gap between TBM and FM when template information is available.
Table 5.
Comparison of average TM-scores and Cα-rmsds between UniCon3D, B03D, GDFuzz3Da and FT-COMARa in CASP10 TBM targets. Best CASP10 results are also provided as a reference
| All 45 targets present in the dataset |
10 targets with reasonable contact maps |
|||
|---|---|---|---|---|
| Method | TM-score | Cα-rmsd | TM-score | Cα-rmsd |
| UniCon3D | 0.45 | 10.73 | 0.54 | 5.66 |
| B03D | 0.42 | 11.86 | 0.50 | 7.26 |
| GDFuzz3D | 0.41 | 10.75 | 0.51 | 6.15 |
| FT-COMAR | 0.31 | 14.81 | 0.39 | 11.02 |
| Best CASP10b | 0.82 | 3.61 | 0.88 | 1.93 |
aPerformance of GDFuzz3D and FT-COMAR adopted from the published work of GDFuzz3D.
b Highest TM-score among all submitted server models during CASP10.
Table 5 (Supplementary Table S5) also shows that UniCon3D outperforms B03D over the entire dataset in terms of both average TM-score (0.45 for UniCon3D versus 0.42 for B03D) and average Cα-rmsd (10.73 Å for UniCon3D versus 11.86 Å for B03D). Out of the 10 targets with reasonably accurate contact maps (sensitivity > 0.5), B03D is able to generate only 5 models with TM-score >0.5 compared to 8 in case of UniCon3D (Supplementary Table S5). Moreover, average TM-score and Cα-rmsd for these targets are 0.5 and 7.26 Å for B03D respectively, worse than that of UniCon3D (average TM-score and Cα-rmsd are 0.54 and 5.66 Å respectively). Better accuracy of UniCon3D over B03D once again demonstrates that average accuracy of models produced via stepwise sampling is better than traditional random sampling strategy even with sequence based predicted contact map that is inherently noisy. Furthermore, when reasonably an accurate contact map is available, stepwise sampling consistently predicts correct fold compared to random sampling, underscoring superiority of stepwise sampling.
4 Conclusion
Here, we show that experimentally motivated stepwise, probabilistic sampling can lead to improvements during de novo conformational sampling of united-residue polypeptide chains by generating lower energy conformation with higher accuracy than traditional random sampling approaches. Moreover, stepwise sampling strategy naturally avoids domain splitting and reassembly during multi-domain protein modeling and can be directly applied to predict structures of relatively larger proteins. Combined with a basic implementation of united-residue physics based force field aided by predicted residue–residue contacts, the method attains accuracy comparable with the top automated approaches worldwide in a dataset of difficult protein targets. Furthermore, with sufficiently accurate predicted contacts, the method can consistently predict correct overall folds of proteins with higher average accuracy than two state-of-the-art approaches. Our results, obtained purely based on coarse-grained sampling and scoring, could be further enhanced by focusing future work on all-atom refinement and improved scoring function.
Supplementary Material
Funding
This work has been supported by the US National Institutes of Health (NIH) grant (R01GM093123) to JC.
Conflict of Interest: none declared.
References
- Aarts E., Korst J. (1988) Simulated annealing and Boltzmann machines.
- Altschul S.F. et al. (1997) Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res., 25, 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengio Y., Frasconi P. (1996) Input-output HMMs for sequence processing. IEEE Trans. Neural Netw., 7, 1231–1249. [DOI] [PubMed] [Google Scholar]
- Bhattacharya D., Cheng J. (2015) De novo protein conformational sampling using a probabilistic graphical model. Sci. Rep., 5, 1–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhuyan M.S., Gao X. (2011) A protein-dependent side-chain rotamer library. BMC Bioinformatics, 12, 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boomsma W. et al. (2008) A generative, probabilistic model of local protein structure. Proc. Natl. Acad. Sci., 105, 8932–8937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boomsma W. et al. (2014) Equilibrium simulations of proteins using molecular fragment replacement and NMR chemical shifts. Proc. Natl. Acad. Sci. U. S. A., 111, 13852–13857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bradley P. et al. (2005) Toward high-resolution de novo structure prediction for small proteins. Science, 309, 1868–1871. [DOI] [PubMed] [Google Scholar]
- Burnham K.P., Anderson D.R. (2003) Model Selection and Multimodel Inference: A Practical information-Theoretic Approach. Springer Science & Business Media, New York. [Google Scholar]
- Cao R., Cheng J. (2016) Protein single-model quality assessment by feature-based probability density functions. Sci. Rep., 6, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cawley S.L., Pachter L. (2003) HMM sampling and applications to gene finding and alternative splicing. Bioinformatics, 19, ii36–ii41. [DOI] [PubMed] [Google Scholar]
- Cheng J., Baldi P. (2007) Improved residue contact prediction using support vector machines and a large feature set. BMC Bioinformatics, 8, 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dill K.A. (1990) Dominant forces in protein folding. Biochemistry, 29, 7133–7155. [DOI] [PubMed] [Google Scholar]
- Dunbrack R.L., Karplus M. (1993) Backbone-dependent rotamer library for proteins application to side-chain prediction. J. Mol. Biol., 230, 543–574. [DOI] [PubMed] [Google Scholar]
- Eickholt J., Cheng J. (2012) Predicting protein residue–residue contacts using deep networks and boosting. Bioinformatics, 28, 3066–3072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eickholt J. et al. (2011) A conformation ensemble approach to protein residue-residue contact. BMC Struct. Biol., 11, 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamelryck T. et al. (2006) Sampling realistic protein conformations using local structural bias. PLoS Comput. Biol., 2, e131.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harder T. et al. (2010) Beyond rotamers: a generative, probabilistic model of side chains in proteins. BMC Bioinformatics, 11, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heffernan R. et al. (2015) Improving prediction of secondary structure, local backbone angles, and solvent accessible surface area of proteins by iterative deep learning. Sci. Rep., 5, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegler J.A. et al. (2009) Restriction versus guidance in protein structure prediction. Proc. Natl. Acad. Sci. U. S. A., 106, 15302–15307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu W. et al. (2013) Stepwise protein folding at near amino acid resolution by hydrogen exchange and mass spectrometry. Proc. Natl. Acad. Sci. U. S. A., 110, 7684–7689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones D.T. et al. (2012) PSICOV: precise structural contact prediction using sparse inverse covariance estimation on large multiple sequence alignments. Bioinformatics, 28, 184–190. [DOI] [PubMed] [Google Scholar]
- Jones D.T. et al. (2015) MetaPSICOV: combining coevolution methods for accurate prediction of contacts and long range hydrogen bonding in proteins. Bioinformatics, 31, 999–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joo K. et al. (2014) Protein structure modeling for CASP10 by multiple layers of global optimization. Proteins Struct. Funct. Bioinf., 82, 188–195. [DOI] [PubMed] [Google Scholar]
- Joung I. et al. (2015) Template‐free modeling by LEE and LEER in CASP11. Proteins Struct. Funct. Bioinf., doi: 10.1002/prot.24944. [DOI] [PubMed] [Google Scholar]
- Kabsch W., Sander C. (1983) Dictionary of protein secondary structure: pattern recognition of hydrogen‐bonded and geometrical features. Biopolymers, 22, 2577–2637. [DOI] [PubMed] [Google Scholar]
- Kim D.E. et al. (2009) Sampling bottlenecks in de novo protein structure prediction. J. Mol. Biol., 393, 249–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinch L.N. et al. (2015) Evaluation of free modeling targets in CASP11 and ROLL. Proteins Struct. Funct. Bioinf., doi: 10.1002/prot.24973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinch L.N. et al. (2016) CASP 11 target classification. Proteins Struct. Funct. Bioinf., doi: 10.1002/prot.24982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosciolek T., Jones D.T. (2014) De novo structure prediction of globular proteins aided by sequence variation-derived contacts. PloS One, 9, e92197.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kosciolek T., Jones D.T. (2015) Accurate contact predictions using covariation techniques and machine learning. Proteins Struct. Funct. Bioinf, doi: 10.1002/prot.24863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt M. (1976) A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol., 104, 59–107. [DOI] [PubMed] [Google Scholar]
- Liwo A. et al. (1997) A united‐residue force field for off‐lattice protein‐structure simulations. I. Functional forms and parameters of long‐range side‐chain interaction potentials from protein crystal data. J. Comput. Chem., 18, 849–873. [Google Scholar]
- Liwo A. et al. (1993) Prediction of protein conformation on the basis of a search for compact structures: test on avian pancreatic polypeptide. Protein Sci., 2, 1715–1731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons J. et al. (2014) Predicting backbone Cα angles and dihedrals from protein sequences by stacked sparse auto‐encoder deep neural network. J. Comput. Chem., 35, 2040–2046. [DOI] [PubMed] [Google Scholar]
- Mabrouk M. et al. (2015) Analysis of free modeling predictions by RBO aleph in CASP11. Proteins Struct. Funct. Bioinf., doi: 10.1002/prot.24950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Magnan C.N., Baldi P. (2014) SSpro/ACCpro 5: almost perfect prediction of protein secondary structure and relative solvent accessibility using profiles, machine learning and structural similarity. Bioinformatics, 30, 2592–2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maity H. et al. (2005) Protein folding: the stepwise assembly of foldon units. Proc. Natl. Acad. Sci. U. S. A., 102, 4741–4746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardia K.V. et al. (2007) Protein bioinformatics and mixtures of bivariate von Mises distributions for angular data. Biometrics, 63, 505–512. [DOI] [PubMed] [Google Scholar]
- Marks D.S. et al. (2011) Protein 3D structure computed from evolutionary sequence variation. PloS One, 6, e28766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monastyrskyy B. et al. (2014) Evaluation of residue–residue contact prediction in CASP10. Proteins Struct. Funct. Bioinf., 82, 138–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monastyrskyy B. et al. (2015) New encouraging developments in contact prediction: assessment of the CASP11 results. Proteins Struct. Funct. Bioinf., doi: 10.1002/prot.24943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moult J. et al. (2014) Critical assessment of methods of protein structure prediction (CASP)—round x. Proteins Struct. Funct. Bioinf., 82, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen S.F. (2000) The stochastic EM algorithm: estimation and asymptotic results. Bernoulli, 6, 457–489. [Google Scholar]
- Oldziej S. et al. (2004a) Optimization of the UNRES force field by hierarchical design of the potential-energy landscape. 3. Use of many proteins in optimization. J. Phys. Chem. B, 108, 16950–16959. [Google Scholar]
- Oldziej S. et al. (2004b) Optimization of the UNRES force field by hierarchical design of the potential-energy landscape. 2. Off-lattice tests of the method with single proteins. J. Phys. Chem. B, 108, 16934–16949. [Google Scholar]
- Paluszewski M., Hamelryck T. (2010) Mocapy ++-A toolkit for inference and learning in dynamic Bayesian networks. BMC Bioinformatics, 11, 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrella R.J., Karplus M. (2001) The energetics of off-rotamer protein side-chain conformations. J. Mol. Biol., 312, 1161–1175. [DOI] [PubMed] [Google Scholar]
- Pietal M.J. et al. (2015) GDFuzz3D: a method for protein 3D structure reconstruction from contact maps, based on a non-Euclidean distance function. Bioinformatics, 31, 3499–3505. [DOI] [PubMed] [Google Scholar]
- Ray A. et al. (2012) Improved model quality assessment using ProQ2. BMC Bioinformatics, 13, 1.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rotkiewicz P., Skolnick J. (2008) Fast procedure for reconstruction of full‐atom protein models from reduced representations. J. Comput. Chem., 29, 1460–1465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rumbley J. et al. (2001) An amino acid code for protein folding. Proc. Natl. Acad. Sci., 98, 105–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schrauber H. et al. (1993) Rotamers: to be or not to be? An analysis of amino acid side-chain conformations in globular proteins. J. Mol. Biol., 230, 592–612. [DOI] [PubMed] [Google Scholar]
- Seemayer S. et al. (2014) CCMpred—fast and precise prediction of protein residue–residue contacts from correlated mutations. Bioinformatics, 30, 3128–3130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons K.T. et al. (1997) Assembly of protein tertiary structures from fragments with similar local sequences using simulated annealing and Bayesian scoring functions. J. Mol. Biol., 268, 209–225. [DOI] [PubMed] [Google Scholar]
- Skwark M.J. et al. (2013) PconsC: combination of direct information methods and alignments improves contact prediction. Bioinformatics, 29, 1815–1816. [DOI] [PubMed] [Google Scholar]
- Taylor T.J. et al. (2014) Definition and classification of evaluation units for CASP10. Proteins Struct. Funct. Bioinf., 82, 14–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tegge A.N. et al. (2009) NNcon: improved protein contact map prediction using 2D-recursive neural networks. Nucleic Acids Res., 37, W515–W518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uziela K., Wallner B. (2016) ProQ2: estimation of model accuracy implemented in Rosetta. Bioinformatics, btv767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vassura M. et al. (2008) FT-COMAR: fault tolerant three-dimensional structure reconstruction from protein contact maps. Bioinformatics, 24, 1313–1315. [DOI] [PubMed] [Google Scholar]
- Wang Z. et al. (2011) APOLLO: a quality assessment service for single and multiple protein models. Bioinformatics, 27, 1715–1716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Z., Xu J. (2013) Predicting protein contact map using evolutionary and physical constraints by integer programming. Bioinformatics, 29, i266–i273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J., Zhang Y. (2010) How significant is a protein structure similarity with TM-score = 0.5? Bioinformatics, 26, 889–895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu D., Zhang Y. (2012) Ab initio protein structure assembly using continuous structure fragments and optimized knowledge‐based force field. Proteins Struct. Funct. Bioinf., 80, 1715-1735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. (2014) Interplay of I‐TASSER and QUARK for template‐based and ab initio protein structure prediction in CASP10. Proteins Struct. Funct. Bioinf., 82, 175–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang J. et al. (2010) MUFOLD: A new solution for protein 3D structure prediction. Proteins Struct. Funct. Bioinf., 78, 1137–1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2004) Scoring function for automated assessment of protein structure template quality. Proteins Struct. Funct. Bioinf., 57, 702–710. [DOI] [PubMed] [Google Scholar]
- Zhang J., Xu D. (2013) Fast algorithm for population‐based protein structural model analysis. Proteomics, 13, 221–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W. et al. (2015) Integration of QUARK and I‐TASSER for Ab Initio Protein Structure Prediction in CASP11, Proteins Struct. Funct. Bioinf, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao F. et al. (2008) Discriminative learning for protein conformation sampling. Proteins Struct. Funct. Bioinf., 73, 228–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.