Paradoxical signaling regulates structural plasticity in dendritic spines

Significance

The basis for learning and memory formation is in tiny $(1-2$ μm) membranous protrusions along short branched extensions (dendrites) of nerve cells (neurons) called dendritic spines. Recently, common themes have begun to emerge in identifying the cellular basis of many conditions associated with learning and memory, mainly through the observation of dynamic changes to the dendritic spine. The ability of the dendritic spine to grow, shrink, and change shape has long been associated with synaptic plasticity, learning, and memory. We develop a mathematical model that couples the biochemical signaling machinery and the actin remodeling events to provide insight into the dynamics of the dendritic spine.

Abstract

Transient spine enlargement (3- to 5-min timescale) is an important event associated with the structural plasticity of dendritic spines. Many of the molecular mechanisms associated with transient spine enlargement have been identified experimentally. Here, we use a systems biology approach to construct a mathematical model of biochemical signaling and actin-mediated transient spine expansion in response to calcium influx caused by NMDA receptor activation. We have identified that a key feature of this signaling network is the paradoxical signaling loop. Paradoxical components act bifunctionally in signaling networks, and their role is to control both the activation and the inhibition of a desired response function (protein activity or spine volume). Using ordinary differential equation (ODE)-based modeling, we show that the dynamics of different regulators of transient spine expansion, including calmodulin-dependent protein kinase II (CaMKII), RhoA, and Cdc42, and the spine volume can be described using paradoxical signaling loops. Our model is able to capture the experimentally observed dynamics of transient spine volume. Furthermore, we show that actin remodeling events provide a robustness to spine volume dynamics. We also generate experimentally testable predictions about the role of different components and parameters of the network on spine dynamics.

The ability of the brain to encode and store information depends on the plastic nature of the individual synapses. The increase and decrease in synaptic strength, mediated through the structural plasticity of the spine, are important for learning, memory, and cognitive function (1–3). Dendritic spines are small structures that contain the synapse. They come in a variety of shapes (stubby, thin, or mushroom-shaped) and a wide range of sizes that protrude from the dendrite (4, 5). These spines are the regions where the postsynaptic biochemical machinery responds to the neurotransmitters (1). Spines are dynamic structures, changing in size, shape, and number during development and aging (3, 6–8).

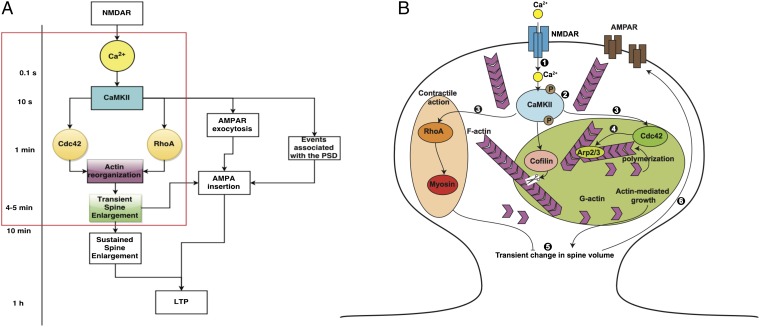
Recent advances in imaging techniques have allowed neuroscientists to study the dynamics of the change in spine volume and identify the role of different molecular components in mediating the structural plasticity of the spine. One way to induce long-term potentiation (LTP) is through N-methyl-d-aspartate (NMDA) receptor-mediated signaling. The resultant transient and sustained changes in the size of the dendritic spine are important for LTP. Recently, a protein–protein interaction network analysis of the early steps in LTP was constructed, and it highlights the complexities of the signaling processes underlying LTP (9). However, kinetic data of a few select species, such as calmodulin-dependent protein kinase II (CaMKII) and RhoGTPases, coupled with the dynamics of spine volume change have been recorded for single spines (10, 11). Thus, LTP is a complex phenomenon, but the events underlying this phenomenon can be summarized as a multiple timescale process as shown in Fig. 1A. In this study, we focus on the events occurring in the 3- to 5-min timescale that is shown in the red box in Fig. 1A. The early events in LTP can be summarized and schematically represented (Fig. 1B). Our goal is to devise a mathematical model to capture the complexity of this process and gain insight into fundamental mechanisms that link signaling to cytoskeletal remodeling in the spine.

Fig. 1.

Ca²⁺–CaMKII regulation of short- and long-term events in LTP. (A) The timescales associated with the events leading up to LTP are shown here. N-methyl-d-aspartate receptor (NMDAR) activation leads to Ca²⁺ release at the millisecond timescale. CaMKII activation by Ca²⁺ is rapid and occurs within tens of seconds. The small RhoGTPases, Cdc42 and RhoA, are activated within a minute or so and lead to actin reorganization events, resulting in transient enlargement of the spine in 4–5 min. Other events include alpha-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid (AMPA) receptor (AMPAR) exocytosis and insertion in the plasma membrane of the synapse, reorganization of the post synaptic density (PSD), and LTP that takes place at the timescale of an hour. Our focus is on the events leading up to the transient spine enlargement as highlighted by the red box. Modified from ref. 16. (B) The events associated with transient spine enlargement are shown in the schematic. The numbers correspond to the following events. (1) Binding of NMDA to NMDA receptor results in a Ca²⁺ influx. (2) Ca²⁺ influx induces a rapid and transient activation of Ca²⁺–CaMKII. (3) CaMKII activation is followed by local and persistent activation of RhoGTPases in the spine. (4) Rapid remodeling of the actin cytoskeleton takes place in response to CaMKII and RhoGTPase activation. (5)These signaling cascades result in a transient increase in spine volume. (6) Synaptic strength is enhanced and made long-lasting by the insertion of functional AMPA receptors in the spine membrane.

The dynamics of CaMKII, RhoGTPases, and spine volume in the 3- to 5-min timescale exhibits a similar profile but with different timescales (10, 11). Essentially, there is a timescale associated with activation and a timescale associated with inhibition, which results in the observed kinetics (a summary is given in figure 1D in ref. 11). A biexponential function can be used to fit these curves, wherein one exponent corresponds to the timescale of activation and one corresponds to the timescale of inhibition. Hart and coworkers (12, 13) identified that network motifs with bifunctional enzymes, which control activation and inhibition, can be thought of as paradoxical, because the same stimulus seems to control the activation and the inhibition in response to the same stimulus. This circuit is a special case of the incoherent feedforward loop (13). Paradoxical signaling has been identified in different contexts; examples include cellular homeostasis, cell population control, and actin dynamics through Arp2/3 and Arpin (12–15). In these studies, the simple idea that the same component can both activate and inhibit a response, resulting in robustness, was applied to many different systems. Here, we consider the same design principle for the dynamics of the dendritic spine and apply it to the core signaling network that regulates early LTP (16).

The initial stimulus is the NMDA receptor inward calcium current in response to electrical and chemical stimulation. The NMDA receptor inhibitor R-2-amino-5-phosphopentanoate (AP 5) blocks both current and LTP. Influx of calcium is tightly coupled to spine expansion 1 min or so later followed by partial compaction over the next 3–4 min (17). Remodeling of the actin spine cytoskeleton coupled to spine expansion is triggered by CaMKII, which is activated by calcium calmodulin. This activation has two consequences. First, activated CaMKII dissociates from F actin and associates with the postsynaptic density (PSD) (18, 19). There is an influx of CaMKII, cofilin, drebrin, and Arp 2/3 from dendrites to the stimulated spine, presumably because of F-actin sites vacated by the activated CaMKII. Free G actin is recruited for polymerization (20). Second, activated CaMKII phosphorylates multiple targets. These targets include the small GTPases-Rho and Cdc42, which in turn, initiate phosphorylation cascades. The effects of Rho are localized to the stimulated spine, whereas Cdc42 phosphorylates targets in adjacent spines to facilitate later stages of LTP (16). Phosphorylated CaMKII has a limited half-life, because calcium calmodulin also activates protein phosphatase 1 (PP1) that dephosphorylates CaMKII, albeit with a slower timescale (21).

Myosin IIb isoforms are involved in maintenance of spine morphology as established by studies with the myosin IIb inhibitor blebbistatin and siRNA (22, 23). Nonmuscle and sarcomeric myosin IIb isoforms play distinct roles in early LTP (24, 25). The nonmuscle isoform localizes at the spine base, where it might stabilize the actin cytoskeleton. The sarcomeric isoform associates with SynGap1 at the PSD. Its contractile activity triggered by myosin light-chain kinase (MLCK) could drive spine head compaction that produces the subsequent decrease in spine volume. The volume decrease does not reach prestimulated levels. One attenuating factor could be partial disassembly of the compacted F-actin cytoskeleton.

Experiments have revealed that different molecules and their complex interactions regulate synaptic plasticity (26, 27). Although the temporal response of the spine volume change and the associated molecular events are well-documented (11, 16, 28), the dynamics of these processes has not been linked. Computational models can provide insight into the nonlinear molecular interactions, identify network motifs, and also, generate experimentally testable predictions. Dynamical modeling using ordinary differential equations approaches has been used to test hypotheses in silico, generate time courses, and identify emergent properties that would be hard to investigate experimentally. This approach has been used in neuroscience successfully to study different aspects of structural plasticity (21, 29, 30). In this study, using computational models, we seek to answer the following questions. (i) How are the dynamics of CaMKII, RhoA, and Cdc42 regulated in response to Ca²⁺ influx? (ii) How does biochemical signaling interface with actin remodeling to control the transient expansion of the spine? In what follows, we outline the construction of the signaling network and the associated mathematical model, compare model outcomes against experimentally observed dynamics of various components, and finally, generate experimentally testable predictions.

Model Development

Modular Construction of the Reaction Network.

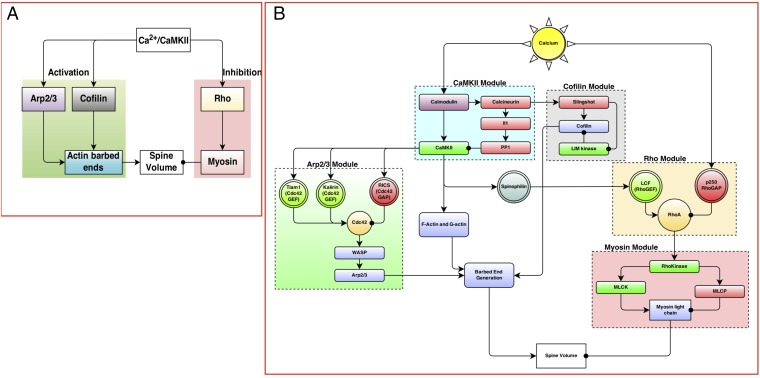
Our first step was to analyze the experimental time course of CaMKII, Rho, Cdc42, and spine volume to predict a network motif based on the principles of chemical reaction engineering. Then, a biochemical signaling network was constructed (31, 32). CaMKII (28), small RhoGTPases (11), actin, and related components (10, 18, 24, 33–35) play important roles in the transient volume change in the spine. Based on these studies, we identified the main components that regulate spine dynamics as CaMKII, Arp2/3, cofilin, Rho, actin, and myosin (Fig. 2A). In the model presented below, myosin II will refer to the sarcomeric myosin IIb isoform (36). We note here that, although there are many more biochemical components involved in the signaling network in the single spine, our choice of components was based on experimentally measured dynamics. The expanded network is shown in Fig. 2B, and the complete tables of reactions for each module are given in SI Appendix, Tables S3–S7. We assumed that the components were present in large-enough quantities that concentrations could be used to represent the amounts of the different molecular species. This assumption allowed us to generate a deterministic dynamical model. We also assumed that the spine is a well-mixed compartment so that we could follow the temporal evolution of the concentrations of the different components. Each interaction was modeled as a chemical reaction using either mass action kinetics for binding–unbinding reactions or Michaelis–Menten kinetics for enzyme-catalyzed reactions (29, 37). The network of interactions was constructed using the Virtual Cell modeling platform (http://www.vcell.org).

Fig. 2.

(A) The events regulating transient spine enlargement can be thought of as modules that regulate key components. (B) The detailed biochemical network shows the interaction between different biochemical species. The network is constructed in modules, where each module contains one key component recognized as a key regulator of dendritic spine volume dynamics. The detailed tables of reactions and parameters are provided in SI Appendix. LCF, lymphocyte chemoattractant factor; MLCK, myosin light chain kinase; MLCP, myosin light chain phosphatase; WASP, Wiskott Aldrich Syndrome protein.

In response to the Ca²⁺–CaMKII activation, the F and G actins released from CaMKII are free to undergo actin polymerization events (18, 33, 38). Because Cdc42 and Rho are activated downstream of CaMKII, we hypothesize that these lead to Arp2/3, cofilin, and myosin activation. This module is built based on the evidence of the role of Arp2/3, cofilin, and myosin in the dendritic spine. We linked the Cdc42 activation to Arp2/3 and actin barbed ends production using a modified version of the model presented by Tania et al. (39). In our model, we included both G and F actins. After the CaMKII-bound actin is released, it undergoes remodeling to generate a large number of barbed ends catalyzed by Arp2/3 and cofilin (34, 39).

Comparison with Experimental Data.

The experimental data were extracted from figure 1D in the work by Murakoshi et al. (16) using the digitize package in the statistical software R. Complete details of the digitize package and how to use it are provided in ref. 40. Because the experimental data were normalized, we also normalized the simulation data to the maximum. Experimental and simulation data were compared for goodness of fit using rms error.

Dynamic Parametric Sensitivity Analysis.

We conducted a local parametric sensitivity analysis of the model to identify the set of parameters and initial concentrations that govern model robustness. The log sensitivity coefficient of the concentration of the ith species $C_i$ with respect to parameter $k_j$ is given by (41, 42)

$$S_{i,j}=\frac{\partial \hspace{0.17em}\text{ln}\hspace{0.17em}{C}_i}{\partial \hspace{0.17em}\text{ln}\hspace{0.17em}{k}_j}.$$ [1]

Because we are dealing with a dynamical system and not steady-state behavior, we computed the change in log sensitivity over time ($d{S}_{i,j}/dt$). The resulting time course gives us information about the time dependence of parametric sensitivity coefficients for the system. The variable of interest, $C_i$, is said to be robust with respect to a parameter $k_j$ if the log sensitivity is of the order of one (41). We conducted dynamic sensitivity analyses for not only all of the kinetic parameters in the system but also, the initial concentrations of the various species in the model.

Results

Paradoxical Signaling.

A summary of the key experimental observations for transient activity in the dendritic spine is given in figure 1D of ref. 16. Two qualitative features of these dynamics are important. (i) They can be fit to biexponential functions, where one exponent controls the timescale of activation and the other controls the timescale of deactivation (SI Appendix, Fig. S1A). (ii) A series of nested biexponential functions can be tuned so as to move the peak activation time of the different components relative to one another (SI Appendix, Fig. S1B). Consider the differential equation

$$\frac{df}{dt}=\frac{ab}{a-b}\left(\underset{\text{activation}}{\underbrace{a{e}^{-at}}}-\underset{\text{inhibition}}{\underbrace{b{e}^{-bt}}}\right),$$ [2]

where a and b are constants. The activation of f is governed by $e^{-at}$, and the inhibition is governed by $e^{-bt}$. The solution to this equation for constants a and b is given by the biexponential function

$$f\left(t\right)=\frac{ab}{a-b}\left(e^{-bt}-e^{-at}\right).$$ [3]

When $a=b$, the function is given by $f\left(t\right)=a^{2}t{e}^{-at}$. In general, the coefficients a and b need not be constant but can be functions of time or other component concentrations. This function produces the profile observed for the dynamics of CaMKII, Rho, Cdc42, and spine volume for different values of a and b (SI Appendix, Fig. S1A).

The dynamics of a simple activation–inhibition scheme driven by the same stimulus is shown in SI Appendix, Fig. S2A. In response to the calcium input (stimulus), concentrations of both the activators and the inhibitors of spine volume are increased. The net change in spine volume is then a balance between the effect of the activator and the inhibitor. The structure of the network in SI Appendix, Fig. S2A suggests that the same stimulus $S\left(t\right)$ both activates and inhibits the response $R\left(t\right)$ by controlling the level of $A\left(t\right)$ and $I\left(t\right)$ simultaneously (SI Appendix, Fig. S2B). In this study, we propose that Ca²⁺-mediated activation of CaMKII results in a paradoxical signaling structure, where CaMKII regulates both the expansion and contraction of the spine volume by regulating actin dynamics through intermediaries, such as Rho, Cdc42, and other actin-related proteins.

Multitier Model of Paradoxical Signaling.

Biological signaling networks are quite complex and have multiple interconnected motifs. These interconnections play an important role in regulating the dynamics of different components in a signaling cascade. One way to alter the timescale of the response in the one-tier model of paradoxical signaling is to change the kinetic parameters of the model shown in SI Appendix, Fig. S1B. Another way to change the timescale of the process is to add multiple tiers to slow down the flow of information from the stimulus to the response.

Although a simple model of paradoxical signaling provides insight into the basic structure of the network, we know that many proteins work in concert to regulate early LTP. By adding a series of activators (activators 1 and 2 to mimic the actin-related proteins and actin barbed end generation) and inhibitors (inhibitors 1 and 2 to represent Rho and myosin) (SI Appendix, Fig. S2C), we can control the response dynamics (spine volume) (SI Appendix, Fig. S2D). The full set of associated ordinary differential equations and parameters along with analytical solutions are given in SI Appendix, Table S2.

The modules in Fig. 2A can be further expanded to construct the biochemical reaction network in Fig. 2B, and the corresponding details are presented in SI Appendix. An emergent property of this network is that, despite its biochemical complexity, each module within this network (CaMKII, Arp2/3, etc.) also exhibits the same structure as in SI Appendix, Fig. S2 A and B. As a result, we suggest that a series of nested paradoxical signaling loops controls the response of the spine volume to the calcium influx and that the nesting of these loops serves to control the timescale of the response to a calcium influx (SI Appendix, Fig. S2 C and D).

One of the key differences between the modular representations in Fig. 2A is the cross-talk between components that participate in the activation and inhibition loops. The cross-talk between the RhoGTPases and other signaling molecules has been well-documented in cell motility and wound healing (43–45). For example, Rho activates Rho-kinase (ROCK), which then regulates cofilin activity through LIM domain kinase and MLCK activity. These interactions, which cannot be represented in the simple modular structure in Fig. 2A, are important features of the complexity of biological signal transduction in the spine. However, these interactions are included in our model, and they are shown in SI Appendix, Tables S5 and S7.

The complete table of reactions for each module along with kinetic parameters, initial concentrations, model assumptions, and references are in provided in SI Appendix.

CaMKII Activation Is Regulated by Autophosphorylation and an Ultrasensitive Phosphatase Cascade.

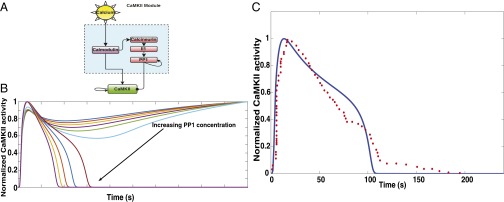
In response to glutamate binding to NMDA receptors, a Ca²⁺ pulse is released in the postsynaptic dendrite (28). This Ca²⁺ binds with calmodulin, a calcium binding messenger protein. Calcium–calmodulin activates CaMKII by cooperative binding. CaMKII can undergo autophosphorylation, leading to a higher activity level (2, 46). CaMKII is dephosphorylated by PP1 through a series of phosphatases. In this module, the stimulus is calcium, activators for CaMKII phosphorylation are calcium–calmodulin and CaMKII itself, and the inhibitors are PP1. PP1 can also undergo autodephosphorylation (2). The module structure is shown in Fig. 3A. Model simulations show that CaMKII dynamics is very sensitive to the concentration of PP1, and the autophosphorylation of CaMKII coupled with the ultrasensitive phosphatase cascade and PP1 autodephosphorylation result in a bistable response (SI Appendix, Fig. S3) (47, 48), similar to the observations made earlier (49). By changing the amount of PP1 in the system, we obtain either sustained activation of CaMKII, which is undesirable, or a transient activation, which is the desired response (Fig. 3B). Our model matched the experimentally observed time course of CaMKII activation when the concentration of PP1 was 0.36 μM (Fig. 3C).

Fig. 3.

(A) CaMKII module: CaMKII is activated by Ca²⁺–calmodulin. Calmodulin also activates an ultrasensitive phosphatase cascade, which includes calcineurin, Il1, and PP1. As a result, the temporal dynamics of CaMKII activation is tightly regulated by both Ca²⁺–calmodulin-led CaMKII autophosphorylation and PP1-mediated dephosphorylation. (B) The coupling between the phosphatase cascade and the autophosphorylation events results in a bistable response of CaMKII. The different curves in the plot are CaMKII dynamics in response to increasing PP1 concentration. PP1 concentration was varied from 0 to 1 μM. Increasing PP1 concentration results in switching from sustained CaMKII activation to transient CaMKII activation. (C) In our model, PP1 initial concentration of 0.36 μM results in CaMKII dynamics that matches closely with experimental data. The blue solid line is the simulation data, and the red filled circles are the experimental data. The experimental data were extracted from figure 1D in the work by Murakoshi et al. (16). The rms error was 0.11 for n = 63 data points from experiments.

Cdc42 and Rho Are Regulated by CaMKII-Mediated Paradoxical Signaling.

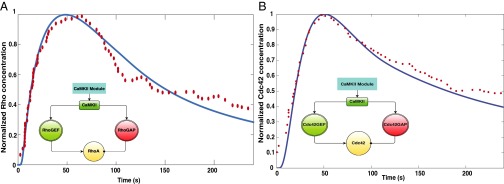
Cdc42 and Rho are small GTPases that have activity that is regulated by guanine nucleotide exchange factors (GEFs) to convert them from the GDP-bound form to the GTP-bound form and GTPase-activating proteins (GAPs) to hydrolyze the bound GTP to GDP, subsequently inactivating the G protein. This GTPase switch has been well-studied in different systems (50, 51). In the case of spine volume change, we modeled the regulation of both the GEF and GAP activity as being controlled by the CaMKII activity (18). As a result, the paradoxical signaling network loop that controls Rho and Cdc42 activity is the one shown in Fig. 4. The time course of normalized activation of Rho and Cdc42 matches with the experimental data (Fig. 4), suggesting that the temporal control of spine dynamics depend on the network structure.

Fig. 4.

CaMKII activates the small RhoGTPases, RhoA and Cdc42, by regulating the activation of the GEFs and the GAPs. The resulting network structure within these modules is similar to the activation–inhibition module of paradoxical signaling shown in SI Appendix, Fig. S2A. (A) Comparison of experimental data from figure 3D in the work by Murakoshi et al. (16) with model simulations for RhoGTP. Inset shows the modular network structure for RhoGTP activation. The blue solid line is the simulation data, and the red filled circles are the experimental data. The rms error was 0.04 for n = 65 data points. (B) Comparison of experimental and simulation data for Cdc42. Inset shows the modular network structure for Cdc42 activation. The blue solid line is the simulation data, and the red filled circles are the experimental data. The experimental data were obtained from figure 1D of ref. 16. The rms error was 0.25 for n = 58 data points from experiments.

Spine Volume Change in Response to Calcium Influx as a Nested Paradoxical Signaling Network.

Transient change in the spine volume is critical to LTP (17). The relationship between pushing barbed ends, $B_p$, and the membrane velocity, $V_{mb}$, has been derived in refs. 39 and 52 and is used here to calculate the radius of the growing spine in response to the actin remodeling events. This relationship is given as

$$V_{mb}=V_0\frac{Bp}{Bp+\mathrm{\varphi }\exp \left(\frac{\omega }{Bp}\right)}.$$ [4]

Here, we used the values of $\mathrm{\varphi }=10/\mu \text{m}$, $V_0=0.07\hspace{0.17em}\mu \text{m/s}$, and $\omega =50/\mu \text{m}$ (39); ϕ is the geometric parameter used in computing membrane protrusion rate, and ω is the physical parameter describing the membrane resistance (39, 52). This density–velocity relationship has a biphasic behavior—for a small number of barbed ends, the membrane resistance limits the velocity, explained as the “decoherent” regime in ref. 52, and for large barbed end density or the “coherent” regime, the protrusion rate is not sensitive to the number of barbed ends.

We also assume that the Rho-activation leads to the activation of ROCK and myosin phosphorylation (53). We then propose that the increase in spine size is proportional to the increase in actin barbed ends (similar to the leading edge pushing velocity) and that the decrease is proportional to the amount of phosphorylated myosin. The rate of change of spine radius, R, is given by the equation

$$\frac{dR}{dt}=\underset{\text{actin}-\text{dependent}\hspace{0.17em}\text{growth}\hspace{0.17em}\text{velocity}}{\underbrace{V_{mb}}}-\underset{\text{myosin}-\text{mediated}\hspace{0.17em}\text{contractility}}{\underbrace{k_{\text{shrink}}\left[ML{C}^{\text{∗}}\right]R}}.$$ [5]

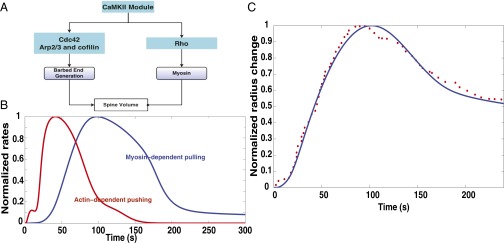
Although spine volume is not a concentration of chemical species, the structure of Eq. 5 indicates the paradoxical nature of the dynamics. The normalized change in spine radius with time is compared between model and experiment in Fig. 5. The paradoxical structure shown in Fig. 5A leads to the actin barbed end-based pushing velocity and myosin-mediated pulling rates as shown in Fig. 5B. The actin-mediated pushing occurs earlier than the myosin-mediated pulling, resulting in spine volume change as shown in Fig. 5C. The rms error between the experimental data and the simulation results was 0.04, indicating that the model is able to capture experimentally observed dynamics quite well. Using our model, we have identified a simple and intuitive network structure that controls the dynamics of the transient dendritic spine volume change. The large concentration of actin in the spine ensures that the number of barbed ends generated is large and that the system is in its coherent state (52).

Fig. 5.

Spine size regulation by Ca²⁺–CaMKII can be represented as a multitier activation–inhibition loop of paradoxical signaling as shown in SI Appendix, Fig. S2C. (A) Spine size regulation module showing the interaction between the upstream signaling modules CaMKII, Rho, and Cdc42 and the barbed end generation and myosin activation. (B) Normalized rates of actin-dependent spine growth caused by pushing of barbed ends and myosin-dependent spine volume decrease. (C) Comparison of experimental and simulation data for normalized spine volume. The blue solid line is the simulation data, and the red filled circles are the experimental data. The experimental data were obtained from figure 1D in ref. 16. The rms error is 0.046 with n = 62 data points.

Actin Nucleation and Severing.

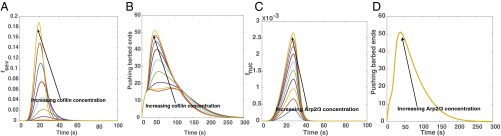
Actin barbed ends can be generated by both branching (Arp2/3-mediated) and severing (cofilin-mediated). To identify the contributions of these two components to barbed end generation, we varied the concentrations of Arp2/3 and cofilin and studied their effect on pushing barbed end generation. For a fixed Arp2/3 concentration of 2 μM, increasing cofilin concentrations leads to a sharp increase in the severing rate, $f_{sev}$ (Fig. 6A). As a result, the generation of pushing barbed ends depends strongly on cofilin concentration (Fig. 6B). However, increasing Arp2/3 concentration, with fixed cofilin concentration of 2 μM , increases the nucleation rate $f_{nuc}$ only to a small extent (Fig. 6C), and therefore, there is no appreciable difference in pushing barbed end production for increasing Arp2/3 concentration (Fig. 6D). These results suggest that, when cofilin is present in sufficient quantities, it dominates the pushing barbed end generation, driving the system to the coherent regime, and Arp2/3 concentration plays a small role in controlling barbed end generation. However, when cofilin concentrations are small, Arp2/3 contribution to barbed end generation will be significant.

Fig. 6.

Effect of cofilin and Arp2/3 concentrations on pushing barbed end generation. (A) Increasing cofilin concentration leads to a cooperative increase in severing rate, $f_{sev}$, and (B) subsequently, an increase in pushing barbed end production. (C) Increasing Arp2/3 concentration, however, does not lead to a cooperative increase in nucleation rate, $f_{nuc}$, and (D) the impact of Arp2/3 concentration on pushing barbed end concentration is negligible, noted by all lines collapsing on to one another.

Sensitivity to Initial Conditions.

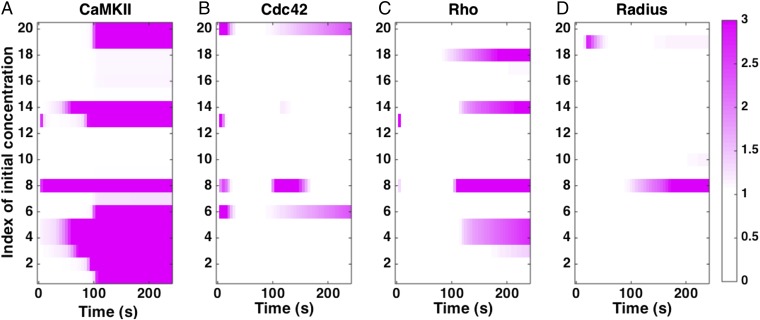
Using dynamic sensitivity analysis, we analyzed the sensitivity of CaMKII, Cdc42, Rho, and spine radius dynamics to the initial concentrations of the different components (Fig. 7 and SI Appendix, Table S10). In Fig. 7, white is no sensitivity, and the pink-purple shades show increasing sensitivity. As listed in SI Appendix, Table S10, the biochemical regulation of CaMKII through the network of components shown in Fig. 2 means that it is sensitive to many initial concentrations at both early and later time stages. Similarly, Cdc42 and Rho show sensitivity to many initial conditions; whereas Cdc42 shows sensitivity at both early and later times, Rho shows sensitivity to the initial conditions listed in SI Appendix, Table S10 at later times. However, the radius of the spine behaves in a robust manner and shows sensitivity to fewer components. Predominant among those are the phosphatases that regulate CaMKII dynamics (and therefore, actin binding to inactive CaMKII) and ROCK, which is responsible for myosin activity. These results suggest that the spine radius is quite robust to changes in initial concentrations of the different species, although the biochemical regulation of protein components shows a larger sensitivity.

Fig. 7.

Sensitivity to initial conditions. We calculated the local sensitivity coefficient (Eq. 1) with respect to the initial concentrations of the different components in the model for (A) CaMKII concentration, (B) Cdc42–GTP concentration, (C) RhoGTP concentration, and (D) spine radius as a function of time. White in the plots indicates that the sensitivity is zero. Any colors toward the purple end of the color range can be interpreted as high sensitivity. The color maps show the absolute scale of $S_{i,j}$. The index of concentrations is given in SI Appendix, Table S10.

Sensitivity to Kinetic Parameters.

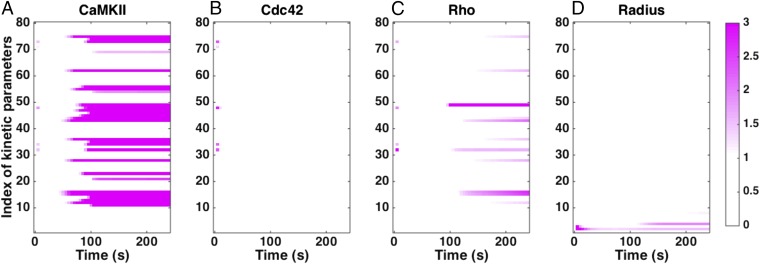
We conducted sensitivity analysis to identify the kinetic parameters to which the model is most sensitive (Fig. 8 and SI Appendix, Table S11). We found that the model is mostly robust to small changes in many parameters. CaMKII was mostly sensitive to parameters that govern the autophosphorylation activity, whereas Cdc42 dynamics was mostly robust to all parameters; Rho-activity was sensitive to parameters associated with CaMKII activation and inactivation. Most interestingly, the radius of the spine showed sensitivity only to the actin dynamics parameters $V_0$ and $k_{cap}$. Thus, the spine volume change is robust to changes in the biochemical events preceding the actin remodeling as long as sufficient barbed ends can be generated.

Fig. 8.

Sensitivity to kinetic parameters. We calculated the local sensitivity coefficient (Eq. 1) with respect to the kinetic parameters in the model for (A) CaMKII concentration, (B) Cdc42-GTP concentration, (C) RhoGTP concentration, and (D) spine radius as a function of time. Note that the model is robust to changes in many kinetic parameters. White in the plots indicates that the sensitivity is zero. Any colors toward the purple end of the color range can be interpreted as high sensitivity. The color maps show the absolute scale of $S_{i,j}$. The index of kinetic parameters is given in SI Appendix, Table S11.

Discussion

The role of dendritic spine dynamics in development and learning is well-established. The presence of contractile actin in these dynamic structures was shown in the 1970s and provided a link between motility, memory, and learning. Length and timescale changes to spine shape and size are now known to impact higher-order synaptic, neural, and brain functions, including many pathologies and age-related mental disorders. Advances in microscopy allow study of spine dynamics in different experimental settings from in vitro cell culture to in vivo animal models. However, there remain unanswered questions on how transient changes to spine volume are regulated by the molecular components. In this work, we propose that the transient dynamics of the spine volume are regulated by a simple paradoxical signaling module.

The dynamics of CaMKII, Cdc42, Rho, and spine volume all follows similar dynamics but at different timescales (Figs. 3, 4, and 5). Because each of these curves can be fit to a biexponential function with different timescales of activation and inhibition, we wondered if these different phenomena can be explained by a simple regulatory structure. We showed that paradoxical signaling network (SI Appendix, Fig. S2A) and multiple tiers within this network (SI Appendix, Fig. S2B) allowed for temporal control of peak activities.

On Ca²⁺ influx, CaMKII is activated and further autophosphorylated, resulting in a “molecular switch” that renders CaMKII active, even after the Ca²⁺ pulse has dissipated (21). Autophosphorylation of CaMKII coupled with the Calcineurin-I1-PP1–mediated dephosphorylation events give rise to a paradoxical signaling network structure that can exhibit bistability (Fig. 3A). The bistability of CaMKII activation is shown in SI Appendix, Fig. S3; the steady-state CaMKII activity depends on the concentration of PP1. CaMKII can exhibit transient or long-term activation as shown in Fig. 3B. For low concentrations of PP1, CaMKII activity is sustained, whereas for high concentration of PP1, CaMKII activity is transient (21). In the spine, we find that GEF and GAP regulation by CaMKII results in a paradoxical network structure that controls the temporal activation of these components (Fig. 4).

Actin remodeling mediates spine volume regulation (54, 55). Although the different aspects of actin regulation are coming to light, to date, there is no comprehensive model of how actin remodeling can affect the dendritic spine volume. We applied a previously published model of actin remodeling in cell motility (39) to spine dynamics (Fig. 5). We further linked the Rho-activity to myosin activity and assumed that spine volume increase was proportional to the generation of new actin barbed ends and that spine volume decrease was proportional to the myosin activity. The net result is spine volume increase and decrease that mimic the experimentally observed behavior (10, 11, 16).

Sensitivity analyses reveal the role of different components and parameters in the system (Fig. 7 and SI Appendix, Table S10). There are two main sources of robustness in our model, despite the large number of parameters. The first source arises from the paradoxical network structure, which is robust to sloppiness (12, 13). The other source of robustness comes from the interplay between the signaling and the cytoskeleton (56). Although the biochemical model is constrained by many unknown parameters and displays parametric sensitivity (Fig. 8 A–C), the spine radius shows limited sensitivity to parameters (Fig. 8D), which indicates that the large number of actin filaments involved in the process provides some robustness to the system.

A problem unique to large biochemical networks is parameter estimation. Recently, a comprehensive analysis of parametric sensitivity applied to many different systems biology models showed that there is a universal sloppiness associated with individual parameters in any model (57). However, we find that the interface between biochemical signaling and actin remodeling can be a source of robustness. Although the signaling dynamics is critical for initiating the actin remodeling events associated with spine dynamics, the actin remodeling events operate in the coherent regime, thereby reducing sensitivities to parameter changes in the signaling network (Fig. 8 and SI Appendix, Table S11). Previously, integrin signaling was shown to be required to initiate the actin remodeling for cell spreading, but the spreading velocity and cell shape were primarily controlled by the actin–membrane interaction through the elastic Brownian ratchet (56). Here, we propose a similar mechanism for spine dynamics, where the Ca²⁺–CaMKII signaling is required to initiate the biochemical activity associated with actin remodeling, but the large concentrations of actin ensure that there is a robust response of the spine dynamics. The recent experimental work by Bosch et al. (17) has made the case that the “synaptic tag” designation is defined by the “increased binding capacity of the actin cytoskeleton” rather than any single molecule (17). This idea is in resonance with the central message of our study established by the sensitivity analysis that F-actin barbed ends ensure a robust response in the coherent regime because of their abundance.

We outline below a set of predictions from our model, which can be tested experimentally using a combination of silencing RNAs, gene KOS, and pharmacological inhibitors. We also identify the model limitations and scope for future work.

CaMKII Dynamics.

CaMKII dynamics are sensitive to many different components but primarily, the phosphastases. Phosphatases are often thought to be ubiquitous in their role in turning off phosphorylation-mediated signaling activity. Here, we find that phosphatases, acting as an ultrasensitive cascade, coupled with autophosphorylation of CaMKII and autodephosphorylation of PP1 result in a bistable-phase profile (also seen in ref. 49). Sensitivity analysis shows that the dynamics of CaMKII is sensitive to PP1 and calcineurin. The model predicts that the timescale of CaMKII transience is extremely sensitive to phosphatase concentration (SI Appendix, Fig. S3) and that the volume change of the spine is sensitive to the concentrations of calmodulin (SI Appendix, Fig. S4B) and calcineurin (SI Appendix, Fig. S4C). Inhibition of PP1, which is associated with sustained CaMKII activation, is thought to prolong memory (47). Although there are many intermediate steps between CaMKII dynamics and memory formation, it is possible that the interaction between CaMKII and PP1 is a small but important step in governing learning and memory formation.

Cdc42 Dynamics.

Sensitivity analysis shows that Cdc42 dynamics is affected primarily by the concentrations of GEFs. The model predicts that depletion of Cdc42 will alter the dynamics of spine volume (SI Appendix, Fig. S5) only slightly. This robustness is because the barbed end generation is in the coherent regime (52). However, Kim et al. (10) showed that loss of Cdc42 may lead to defects in synaptic plasticity. Our model only focuses on single-spine dynamics; the actual dynamics at the neuron and tissue level may be quite different from what we observe in the model.

Rho And Myosin Modification.

Because Rho modulates the myosin, Rho-KO leads to lack of myosin activity, resulting in a situation where the spine volume increases but decreases slowly or not at all (SI Appendix, Fig. S6). Although the role of myosin IIb has been tested using blebbistatin (23), we predict that upstream regulators of myosin activity will also alter spine compaction rates. The role of ROCK has been explored in refs. 58 and 59, where the experiments show that Rho, ROCK, and myosin IIb are required for stable expression of LTP, but the role of these components in the early change in spine volume has not yet been tested.

Cofilin Regulation.

In our model, cofilin plays an important role in spine dynamics through its roles in actin severing and depolymerization. Our model predicts that a cofilin KO will result in impaired actin dynamics that will disrupt the balance of actin remodeling during spine volume change (Fig. 6 and SI Appendix, Fig. S5) (17, 60). The effect of actin-mediated pushing is through barbed end generation, and the loss of cofilin removes the ability to sever existing filaments and generate new barbed ends. Experiments inhibiting cofilin showed that cofilin is highly enriched in the spine within 20 s after stimulation and that inhibition of cofilin using shRNA leads to a smaller enlargement of the spine (17).

Actin Modulators.

To model actin dynamics, we have extended a model developed by Tania et al. (39) to include both G- and F-actin dynamics. The model allows us to study the impact of pharmacological inhibitors on actin, such as latrunculin and cytochalasin. The model predicts that latrunculin (which binds to G actin and limits polymerization) will lead to a smaller increase in spine volume (SI Appendix, Fig. S5D). Indeed, experiments showed that latrunculin A, when applied within 30 s to 2 min, disrupts F-actin increases that are usually observed in spine expansion (59). However, removing actin capping also affects spine dynamics, resulting in increased barbed end production and larger spine volume (SI Appendix, Fig. S7A). Therefore, filament capping is an important step in governing spine dynamics. Similar to Arp2/3, the kinetic parameter for the nucleation of new barbed ends had only a small effect, because barbed ends are also generated by severing (SI Appendix, Fig. S7 B and D).

To summarize, we present a dynamical systems model of the events that affect the transient spine dynamics. We identified that a simple module of paradoxical signaling can be used to explain the dynamics of CaMKII, the RhoGTPases-Rho and Cdc42, actin remodeling, and spine volume change. We found that, after the barbed end generation is in the coherent regime, spine dynamics is robustly controlled by actin remodeling. Thus, the interface between signaling and actin barbed end generation is a source of natural robustness, despite model sensitivity to kinetic parameters.

Although our model explains the dynamics of spine volume change in the 4- to 5-min timescale, it can be enhanced in future versions. Currently, our model represents well-mixed dynamics, which is a good starting point for modeling spine dynamics, because the spine is a small compartment with an average submicrometer diameter and subfemtoliter volume and acts as an isolated compartment for signaling in the 4- to 5-min timescale (1). As shown in refs. 11 and 61, the degree of compartmentalization is determined by the distance that a molecule diffuses before it is inactivated. The dynamics of activity of small GTPases increases rapidly with a timescale of 1 min and decays within 3–5 min, indicating that, for this timescale, a well-mixed assumption is justified.

Spatial regulation of the RhoGTPases and other components, including cofilin and myosin IIb, in the postsynaptic and neighboring spines has been observed in many studies (11). Development of a spatiotemporal model that accounts for diffusive transport along the dendrite with shape change of the spine is an important direction in our future work. Spatial compartmentalization of signaling and shape can affect the dynamics of the activity of different signaling molecules in cell motility (30, 62–64). Membrane mechanics studies have shown that protein interaction with the membrane cannot only induce a curvature but also, change membrane properties (65). The role of these factors in spine dynamics is as yet unknown. Additionally, more complex models will be needed to identify cross-talk between different signaling components, antagonistic activities displayed by the same component at different concentrations and spatial compartments, as well as coupling between the spine and the dendritic shaft.