The Role of Resonant Vibrations in Electronic Energy Transfer

Abstract

Nuclear vibrations play a prominent role in the spectroscopy and dynamics of electronic systems. As recent experimental and theoretical studies suggest, this may be even more so when vibrational frequencies are resonant with transitions between the electronic states. Herein, a vibronic multilevel Redfield model is reported for excitonically coupled electronic two‐level systems with a few explicitly included vibrational modes and interacting with a phonon bath. With numerical simulations the effects of the quantized vibrations on the dynamics of energy transfer and coherence in a model dimer are illustrated. The resonance between the vibrational frequency and energy gap between the sites leads to a large delocalization of vibronic states, which then results in faster energy transfer and longer‐lived mixed coherences.

1.  Introduction

Excitation energy transfer in electronic systems, such as photosynthetic pigment–protein complexes, has been experimentally studied by increasingly faster time‐resolved techniques over the years. The latest nonlinear spectroscopy tool is two‐dimensional electronic spectroscopy (2DES).1 In 2007, this technique was applied to the Fenna–Matthews–Olson (FMO) complex of purple bacteria, in which, among other dynamics, long‐lived coherent oscillations were observed.2 This observation sparked interest in coherent phenomena in such systems. 2DES was used to observe in more detail FMO,3 antenna complexes of marine algae,4 the major light‐harvesting antenna LHCII,5 and the reaction centers (RCs)6, 7 of higher plants, to name a few examples. In all cases, the omnipresent, robust oscillations were found at cryogenic and even at room temperature.

Accordingly, much of the following work was devoted to investigating the origin of these long‐lived oscillations and their relation to energy transfer in the system. Originally, they were associated with electronic coherences.8 One proposed mechanism was that correlated bath fluctuations at different sites could result in long‐lived coherence between the corresponding states. However, no evidence for such correlations was found through modeling based on molecular dynamics simulations.9 Also, direct separation of the coherences into electronic and vibrational is not possible, as can be seen by comparing the oscillation frequencies with known vibrational modes.7 Gradually, the consensus has been reached that the oscillation longevity and frequencies must be explained by mixing of electronic and vibrational coherences.10, 11, 12, 13, 14, 15 In particular, vibrational modes with frequencies resonant with electronic energy gaps were suggested to be important for both spectroscopic signals and energy‐transfer dynamics.7, 16, 17, 18, 19, 20

To investigate the role of the vibrations in the electronic system dynamics, several ingredients have to be present in the model. These include the interaction between the pigments, a few explicitly quantized vibrational modes, and interaction with an external phonon bath. There are several levels of description of such a situation with increasing complexity. The first level involves N interacting pigments with a few quantized vibrational modes and one corresponding generalized coordinate for every vibrational mode. In other words, the configuration space for every vibrational mode is one‐dimensional.

The interaction with the external bath can then be described by second‐order perturbation theory. Such a description by multilevel Redfield theory was developed by Jean et al.21, 22 They derived the equations of motion for such a system and showed the equivalence of weak‐ and strong‐coupling limits to the Fermi golden rule and Landau–Zener regime, respectively. Later Egorova et al. investigated the range of validity of multilevel Redfield theory by comparison with other methods and concluded that it was appropriate for the description of coherent ultrafast dynamics.23 More importantly for our study, they also calculated the dynamics of the vibrational wavepacket after photoexcitation.24 They showed that the vibrational wavepacket evolved coherently and that coherence survived several nonadiabatic transfers between excited‐state potentials. The model was later successfully applied to describe primary charge separation in the photosynthetic reaction center of purple bacteria by Novoderezhkin et al.25 It was concluded that vibrational modes were important for the formation of the charge‐separated state.

The next complexity level keeps the one‐dimensional description of the quantized vibrational modes, but uses an exact model for the treatment of the phonon bath. Such a description is provided by the hierarchical equations of motion (HEOM). HEOM in the presence of quantized vibrational modes were derived by Tanaka and Tanimura,26 and later extended for the presence of underdamped vibrational modes by Tanimura.27 The advantage of this method is its validity for different strengths of coupling to the bath, the disadvantage is the relatively high computational demand. These equations were applied to larger systems, such as FMO (7 pigments)12 and LHCII (14 pigments),18 with several vibrational modes, by using massively parallel calculations on graphics cards.28 Finally, the HEOM were used by Fuller et al. to simulate the coherent dynamics of the photosystem II reaction center, as observed by 2DES.7 Of particular interest for our study is their examination of the effect of the vibrations on charge‐transfer (CT) state formation. First, almost all vibrational modes present are in resonance with some energy gap between the states in the system. The authors then described the vibrational modes as sharp and broader peaks in the phonon spectral density. They showed that, in the sharp case, which they called coherent, charge separation was faster than that in the broad case. As we discuss later, this can be explained by the resonance mechanism described herein.

Another exact approach which describes the bath by polaron transformation was developed by Kolli et al.29 On a FMO‐inspired four‐site model they demonstrated the effects of nonequilibrium bath and illustrated the distinction between the electronic and vibrational components of the oscillatory features. Later the authors applied this approach to a larger PE545 antenna system of cryptophyte algae to investigate the role of quantized vibrations quasi‐resonant with excitonic energy gaps.11

Yet another possibility was explored by Plenio et al.30, 31 They used a time‐dependent density‐matrix renormalization group method together with the orthogonal polynomials technique (TEDOPA method), which allowed them to follow the dynamics of the system and bath. The key principle is the unitary transformation of the oscillator bath into an infinite one‐dimensional chain of harmonic oscillators. In the context of photosynthetic complexes, the authors applied TEDOPA to a FMO‐inspired dimer.17 They demonstrated that the presence of a vibrational mode resonant with the excitonic energy gap could result in longer‐lived coherences and even led to a coherence revival.

The one‐dimensional description of the quantized vibrational mode has, however, some disadvantages. Because all pigments effectively interact with the same vibrational mode, fluctuations along its coordinate will be correlated for all of them. This can lead to unrealistic behavior, such as prolongation of coherence lifetime. Also, nonequilibrium vibrational dynamics of this mode, such as dynamic Stokes shifts, cannot be correctly reproduced. The more complex level of description uses one generalized coordinate for each vibrational mode and for each pigment, that is, independent vibrational modes for each pigment. The dimension of the configuration space for every mode is then N. As is immediately apparent, the scaling of the problem with the number of pigments and/or quantized modes increases dramatically. This description was actually originally proposed by Förster in 1965.32 It was then recently rediscovered in the context of coherent dynamics of photosynthetic complexes by Christensson et al.10 and independently by Tiwari et al.16 In the latter work, a “symmetric” dimer, that is, with equal excited‐state displacements, was investigated. In this special case, dissipative dynamics occurs only along the correlated nuclear motion direction, which permits effective treatment of the energy‐transfer dynamics as a one‐dimensional problem. The special case of a symmetric dimer was also used to discuss the bath correlation33 and 2DES oscillatory features.34 Butkus et al. have also investigated in detail the signatures of the vibrational and electronic degrees of freedom (DOF) in the 2DES spectra.15, 35 An excellent review on the subject of the interplay of electronic and vibrational DOF, presenting HEOM and multiconfiguration time‐dependent Hartree (MCTDH), another method capable of dealing with explicit vibrations, was written by Schröter et al.36 Whereas these studies were of mostly a qualitative nature, Novoderezhkin et al. used the same multidimensional configuration space description to obtain a quantitative fit of experimental 2DES frequency maps. This enabled them to characterize the observed coherences in the B820 subunit of the LH1 complex of purple bacteria37 and in the reaction center of photosystem II of higher plants.20

Herein, we describe the interaction of a system that includes independent quantized vibrational modes on every pigment with a phonon bath. This allows us to observe the interplay of coherent and dissipative dynamics. Our work is thus a logical continuation of the theory development outlined above. The paper is structured as follows: First, we formulate the theoretical description of the interacting pigments with explicitly quantized vibrational modes and in interaction with the phonon bath. We show that the electronic and vibrational modes effectively feel two baths, albeit those arising from the same environmental modes. Using such system–bath interactions, we derive expressions for Redfield theory dynamics. Then we apply this description to a model vibronic dimer of pigments with one vibrational mode on each of them. We study the influence of the vibrations on the system dynamics, in particular the role of the resonance of the vibrational frequency with the energy gap between the pigment electronic transitions.

2.  Results and Discussion

2.1.  Theoretical Description

2.1.1.  The System and Bath

In the traditional open quantum systems approach, the electronic DOF are treated explicitly in the system Hamiltonian, H _S, and all vibrations are included in the bath H _B. These two are then coupled by the interaction Hamiltonian, H _SB, which factorizes into the system part and bath part, $\Phi$ . Because our goal is to study the role of resonant vibrations, let us include one vibrational mode from the bath explicitly quantized in the system Hamiltonian. Originally, the bath modes were typically considered as being independent and noninteracting. However, when a specific vibrational mode is included in the system, not only the electronic DOF, but also this vibrational mode, will be linearly coupled to the rest of the bath modes, which remain to be treated perturbatively. The mathematical procedure for this mode transformation can be found in the Supporting Information. As a result, there are two system–bath interaction terms: one coupling the bath modes to the electronic DOF and the other to the quantized vibrational mode. There are thus effectively two baths, although they originate from the same vibrational modes in the environment. According to the DOF they act on, we call these baths “electronic”, with operator ${\Phi }^{\left(2\right)}$ , and “vibrational”, with operator ${\Phi }^{\left(1\right)}$ . The Hamiltonian of one pigment can be written as Equation (1):

$$H_{\mathrm{pigment}}=H_{\mathrm{B}}+\left[e_g+H_{\mathrm{vib}}\left(Q\right)\right]\left|g\right.〉\left.〈g\right|+\left[e_e+\lambda +H_{\mathrm{vib}}(Q-Q_0)+{\Phi }^{\left(2\right)}\right]\left|e\right.〉\left.〈e\right|$$ (1)

in which H _vib(Q) is given by Equation (2):

$$H_{\mathrm{vib}}\left(Q\right)=\frac{ħ\Omega }{2}\left(P^2+Q^2\right)+Q\sqrt{2}{\Phi }^{\left(1\right)}$$ (2)

in which $\left|g\right.〉$ and $\left|e\right.〉$ are the ground and excited electronic states of the pigment, respectively, with energies e _g,e; λ is the reorganization energy; H _vib is the Hamiltonian of the quantized vibration; Ω is the vibrational frequency; Q is the vibrational coordinate, displaced by Q ₀ in the excited state; and P is the canonical momentum.

The motivation for separating the two baths is not only mathematical. Physically, the two baths correspond to different processes. Because of the DOF it couples to, the electronic bath ${\Phi }^{\left(2\right)}$ causes fluctuations of the electronic energy gap. In contrast, the interaction with the vibrational bath ${\Phi }^{\left(1\right)}$ , coupled linearly to the quantized coordinate, causes transitions between the vibrational states. One can perform a linear absorption measurement. The width of the zero‐phonon line (ZPL) at low temperature is then given by the electronic bath ${\Phi }^{\left(2\right)}$ only, which causes dephasing of the optical coherence between the ground and excited states. One can also perform a time‐resolved measurement, such as transient absorption, to observe a dynamic Stokes shift, that is, intramolecular vibrational relaxation. The relaxation rate is then given only by the vibrational bath ${\Phi }^{\left(1\right)}$ . It is thus, in principle, possible to obtain the parameters of these two baths from different experiments.

Let us proceed to the description of an aggregate of interacting pigments. The total Hamiltonian is then given by Equation (3):

$$H=\sum _n{H}_n{\otimes }_{m\ne n}{1}_m+\sum _{n\ne m}{J}_{nm}{\otimes }_{l\ne n,m}{1}_l$$ (3)

in which H_n is the Hamiltonian of one pigment defined above and J_nm is the element of the operator of interaction between the pigments.

In the Born–Oppenheimer approximation, the electronic and nuclear DOF are independent. The basis functions for the ground and excited states of each pigment can then be written as a product of their vibrational and electronic parts [Eq. (4)]:

$$\left|g_n^{{\nu }_n}\right.〉=\left|{\chi }_n^{\left(g\right){\nu }_n}\right.〉\left|g_n\right.〉,\left|e_n^{{\nu }_n}\right.〉=\left|{\chi }_n^{\left(e\right){\nu }_n}\right.〉\left|e_n\right.〉$$ (4)

in which $n\in 1...N$ counts the pigments and the greek indeces ${\nu }_n\in 1...N_V$ count the vibrational levels. To shorten the notation, we occasionally make use of multi‐indices $\nu ={\nu }_1...{\nu }_N$ in the text below.

The collective states of an aggregate of these N pigments are given by Equation (5):

$$\left|g^{\nu }\right.〉=\left|g_1^{{\nu }_1}\right.〉...\left|g_N^{{\nu }_N}\right.〉={\otimes }_n\left|g_n^{{\nu }_n}\right.〉,\left|e_n^{\nu }\right.〉=\left|g_1^{{\nu }_1}\right.〉...\left|e_n^{{\nu }_n}\right.〉...\left|g_N^{{\nu }_N}\right.〉={\otimes }_{m\ne n}\left|g_m^{{\nu }_m}\right.〉\left|e_n^{{\nu }_n}\right.〉$$ (5)

in which $\left|g^{{\nu }_1...{\nu }_n}\right.〉$ are the ground state levels and $\left|e_n^{{\nu }_1...{\nu }_n}\right.〉$ are the singly excited states. Now we write the explicit elements of the Hamiltonian in this basis.

We again separate the total Hamiltonian into system part H _S, bath part H _B, and system–bath interaction H _SB. Let us write the system Hamiltonian in the exciton‐vibrational basis. The ground state block is (setting e_g=0) given by Equation (6)

$$\left.〈g^{\nu }\right|H_{\mathrm{S}}\left|g^{\mu }\right.〉=\left({\Pi }_n{\delta }_{{\nu }_n{\mu }_n}\right)\left(\sum _m{\nu }_mħ{\Omega }_m\right)$$ (6)

in which ${\Omega }_n$ is the vibrational frequency at the nth pigment. The matrix elements of the one exciton block read as shown in Equation (7):

$$\left.〈e_n^{\nu }\right|H_{\mathrm{S}}\left|e_m^{\mu }\right.〉={\delta }_{nm}\left({\Pi }_l{\delta }_{{\nu }_l{\mu }_l}\right)\left(e_n+\sum _l{\nu }_lħ{\Omega }_l+{\lambda }_n\right)+\left(1-{\delta }_{nm}\right)J_{nm}^{{\nu }_n{\nu }_m{\mu }_n{\mu }_m}$$ (7)

in which λ_n is the reorganization energy and the coupling terms are given by the electronic coupling J_nm and the vibrational wavefunction overlap [Eq. (8)]:

$$J_{nm}^{{\nu }_n{\nu }_m{\mu }_n{\mu }_m}=J_{nm}\left.〈{\chi }_n^{\left(e\right){\nu }_n}\right|{\chi }_n^{\left(g\right){\mu }_n}〉\left.〈{\chi }_m^{\left(g\right){\nu }_m}\right|{\chi }_m^{\left(e\right){\mu }_m}〉$$ (8)

The electronic bath is independent of the vibrational DOF and causes fluctuations of the electronic levels. The vibrational bath causes ${\nu }_k\to {\nu }_k\pm 1$ transitions between the vibrational levels. We can write the system–bath interaction separately for the ground‐state block [Eq. (9)]:

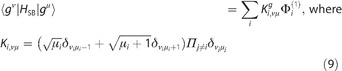
and for the one‐exciton block [Eq. (9)]:

$$\left.〈e_n^{\nu }\right|H_{\mathrm{SB}}\left|e_m^{\mu }\right.〉={\delta }_{nm}\left({\Pi }_l{\delta }_{{\nu }_l{\mu }_l}\right){\Phi }_n^{\left(2\right)}+{\delta }_{nm}\sum _i{K}_{i,\nu \mu }{\Phi }_i^{\left(1\right)}$$ (9)

We introduced the index tensor $K_{i,{\nu }_{1..N}{\mu }_{1..N}}$ to shorten the notation of ${\nu }_i={\mu }_i\pm 1$ transitions.

The system–bath interaction is treated by second‐order perturbation theory, in which the bath is fully described by its correlation function (that is, the spectral density in the frequency domain). We have the vibrational correlation function given by Equation (10):

$$C_n^{\left(1\right)}\left(\Omega \right)=\frac{2}{{ħ}^2}Re{\int }_0^{\infty }{e}^{i\Omega t}〈{\Phi }_n^{\left(1\right)}\left(t\right){\Phi }_n^{\left(1\right)}\left(0\right)〉$$ (10)

the electronic correlation function given by Equation (11):

$$C_n^{\left(2\right)}\left(\Omega \right)=\frac{2}{{ħ}^2}Re{\int }_0^{\infty }{e}^{i\Omega t}〈{\Phi }_n^{\left(2\right)}\left(t\right){\Phi }_n^{\left(2\right)}\left(0\right)〉$$ (11)

and the cross‐correlation term given by Equation (12):

$$C_n^{\left(12\right)}\left(\Omega \right)=\frac{2}{{ħ}^2}Re{\int }_0^{\infty }{e}^{i\Omega t}〈{\Phi }_n^{\left(1\right)}\left(t\right){\Phi }_n^{\left(2\right)}\left(0\right)〉=C^{\left(21\right)}\left(\Omega \right)$$ (12)

In the following calculations, we set these baths as formally uncorrelated for now, that is, $C_n^{\left(12\right)}\left(\Omega \right)=0\forall n$ . We also consider baths coupled to different pigments to be uncorrelated, in accordance with Ref. 38.

The interaction of the system with light, H _SL, is treated in the dipole approximation given by Equation (13):

$$H_{\mathrm{SL}}=-\mu E\left(t\right)$$ (13)

in which μ is the dipole moment operator. In the Condon approximation, the dipole moment operator is independent of the vibrations [Eq. (14)]:

$$\mu =\sum _n\left|e_n\right.〉{\mu }_n\left.〈g\right|+h.c.$$ (14)

If we consider the case when coupling between the pigments is stronger than coupling to the bath (strong coupling regime), the preferred basis is the exciton basis. This is obtained by diagonalization of the one‐exciton block of the system Hamiltonian with an orthogonal transformation $H\to C^{†}HC$ . The resulting states are superpositions of the electron‐vibrational states, so they are called vibronic states [Eq. (15)]:

$$\left|{\varepsilon }_i\right.〉=\sum _{n=1}^N\sum _{\mu }{c}_{n,\mu }^i\left|e_n^{\mu }\right.〉$$ (15)

According to this transformation, the system–bath interaction and dipole moment operators are also transformed into the excitonic basis. The particular expressions can be found in the Supporting Information.

2.1.2.  The Dynamics

In the reduced description, the system dynamics can be calculated by using a master equation in the following form given by Equation (16):

$$\frac{\partial \rho }{\partial t}=-\frac{i}{ħ}[H_{\mathrm{S}},\rho ]-R\left(t\right)\rho +\frac{i}{ħ}[\mu ,\rho ]E\left(t\right)$$ (16)

in which $R\left(t\right)$ is a rank four tensor that arises from the perturbative treatment of the system–bath interaction. The solution of this equation is then formally expressed by a propagator: $\rho \left(t\right)=U\left(t\right)\rho \left(0\right)$ . Herein, we use time‐independent Redfield theory, in which the relaxation tensor (also called Redfield tensor) can be expressed as follows: let us define, similar to the description given in Ref. 39, the auxiliary operators for the electronic and vibrational bath [Eq. (17)]:

$$Y_{ijkl}^{\left(2\right)}=\frac{1}{2}\sum _{n=1}^N\sum _{\nu ,\mu }{c}_{n,\nu }^i{c}_{n,\nu }^j{c}_{n,\mu }^k{c}_{n,\mu }^l{C}_n^{\left(2\right)}\left({\omega }_{ki}\right),Y_{ijkl}^{\left(1\right)}=\frac{1}{2}\sum _{n=1}^N\sum _{m=1}^N\sum _p\sum _{\nu ,\mu ,\kappa ,\lambda }{c}_{n,\nu }^i{c}_{n,\mu }^j{c}_{m,\kappa }^k{c}_{m,\lambda }^l{K}_{p,\nu \mu }{K}_{p,\kappa \lambda }{C}_p^{\left(1\right)}\left({\omega }_{ki}\right)$$ (17)

In the one‐exciton block, we separate the Redfield tensor into the electronic and vibrational bath terms: $R_{ij,kl}^{\left(e\right)}=R_{ij,kl}^{\left(1\right)}+R_{ij,kl}^{\left(2\right)}$ , as given by Equation (18):

$$R_{ij,kl}^{\left(o\right)}=-\left(Y_{ijkl}^{\left(o\right)}+Y_{jilk}^{\left(o\right)}\right)+{\delta }_{jl}\sum _s{Y}_{siks}^{\left(o\right)}+{\delta }_{ik}\sum _s{Y}_{sjls}^{\left(o\right)}o=1,2$$ (18)

In the ground state, there is only the vibrational bath. Defining the auxiliary operator as Equation (19):

$$Y_{\nu \mu \kappa \lambda }^{\left(g\right)}=\sum _n{K}_{n,\nu \kappa }{K}_{n,\lambda \mu }{C}_n^{\left(1\right)}\left({\Omega }_{\kappa \nu }^n\right)$$ (19)

we can write the Redfield tensor as Equation (20):

$$R_{\nu \mu ,\kappa \lambda }^{\left(g\right)}=-\left(Y_{\nu \mu \kappa \lambda }^{\left(g\right)}+Y_{\mu \nu \lambda \kappa }^{\left(g\right)}\right)+{\delta }_{\mu \lambda }\sum _{\sigma }{Y}_{\sigma \nu \kappa \sigma }^{\left(g\right)}+{\delta }_{\nu \kappa }\sum _{\sigma }{Y}_{\sigma \mu \lambda \sigma }^{\left(g\right)}$$ (20)

Herein, we denote the vibrational frequency differences as ${\Omega }_{\mu \nu }^n=\left({\mu }_n-{\nu }_n\right){\Omega }_n$ .

It is also possible to describe the evolution of the optical coherences, that is, ${\rho }_{i{g}_{\nu }}\left(t\right)$ , by Redfield theory, but in the time‐independent case this leads to unrealistic Lorenzian lineshapes. We therefore use a second‐order cumulant expansion, which is even exact for our case of a harmonic oscillator bath. There are again two lineshape functions corresponding to the two baths [Eq. (21)]:

$$g_n^{\left(o\right)}\left(t\right)={\int }_0^{t}d\tau {\int }_0^{\tau }d\tau {}^{\text{'}}{C}_n^{\left(o\right)}\left(\tau {}^{\text{'}}\right)o=1,2$$ (21)

The transformed g functions can be expressed by considering the dynamics of the energy gap, that is, $〈H_{\mathrm{SB}ii}^e-H_{\mathrm{SB}\nu \nu }^g〉$ for the one‐exciton–ground state coherences, leading to Equation (22):

$$g_i^e\left(t\right)=\sum _n\sum _{\nu \mu }|c_{n\nu }^i{|}^2{\left|c_{n\mu }^i\right|}^2{g}_n^{\left(2\right)}\left(t\right)+\sum _{n=1}^N\sum _{m=1}^N\sum _p\sum _{\nu \mu \kappa \lambda }{c}_{n,\nu }^i{c}_{n,\mu }^i{c}_{m,\kappa }^i{c}_{m,\lambda }^i{K}_{p,\nu \mu }{K}_{p,\kappa \lambda }{g}_p^{\left(1\right)}\left(t\right)$$ (22)

The evolution of the optical coherences is then given by Equation (23):39, 40

$$U_{i{g}_{\nu }}\left(t\right)=exp\left\{-g_i^e\left(t\right)-\frac{1}{2}\left(R_{ii,ii}+R_{g_{\nu }{g}_{\nu },g_{\nu }{g}_{\nu }}\right)t\right\}$$ (23)

in which R are the Redfield tensor elements that express population transfer from the respective states leading to lifetime dephasing.

2.1.3.  Spectroscopy

The spectra can be calculated by the response function formalism as a response to the electric field.40 The nth order polarization is then given by Equation (24):

$$P^{\left(n\right)}={\int }_{-\infty }^{\infty }d{t}_1...{\int }_{-\infty }^{\infty }d{t}_n{S}^{\left(n\right)}(t_n,t_{n-1}...t_1)E(t-t_n-t_{n-1}-...-t_1)...E(t-t_1),S^{\left(n\right)}(t_n,t_{n-1}...t_1)=Tr\{\mu U\left(t_n\right)[\mu ,...U\left(t_1\right)[\mu ,{\rho }_{eq}]\}$$ (24)

in which $U\left(t\right)$ is the system “free” propagator without the electric field. In our case, $U\left(t\right)$ is obtained by solving Equation (17) without the electric field. The signal is then connected to the polarization through the Maxwell equations. We thus get the absorption spectrum [Eq. (25)]:

$$\alpha \left(\omega \right)\propto \omega \sum _i\sum _{\nu }{\left|{\mu }_{i,g_{\nu }}\right|}^{2}Re{\int }_0^{\infty }dt{e}^{i\omega t}{U}_{i,g_{\nu }}\left(t\right){\rho }^{\mathrm{eq}}$$ (25)

2.2.  Numerical Simulations

2.2.1.  System Description

In this section, we present the application of the theory presented above for a coupled dimer of pigments, N=2. Unless different values are explicitly given, the parameters used for simulation can be found in Table 1. The vibrational frequency, Ω=340 cm⁻¹, was chosen because it corresponds to a known vibration of chlorophyll and was observed in the experimental 2DES spectra.6, 7 The transition dipole moments of the pigments are parallel‐oriented (head‐to‐head) and are of the same size. To characterize the excited states, we use the Huang–Rhys factors, which relate to the dimensionless displacement as $S_n=d_n^2/2$ ($d_n$ is denoted $Q_0$ in the theory section above). Because we have two pigments and one quantized vibrational mode on each of them, we describe the excited‐state potential in a space of two generalized coordinates (Figure 1). Such a potential surface in the exciton picture and its influence on the exciton delocalization was studied in detail by Beenken et al.41

Table 1.

System parameters used for a simulation of a coupled dimer of pigments.

Parameter	Value
ZPL energy difference	ΔE=e 2−e 1=300 cm−1
electronic coupling	J 12=75 cm−1
Huang–Rhys factor	S 1=0.7, S 2=0.25
vibrational frequency	Ω=340 cm−1
temperature	77 K (k B T=53.7 cm−1)
bath reorganization energy	λ 1=20 cm−1, λ 2=50 cm−1
bath inverse correlation time	Λ=100 cm−1

Figure 1.

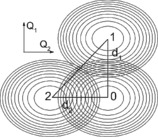
The configuration space with the parabolic potentials of the ground (0) and excited states of the pigments. The excited states are displaced from the ground state along the respective generalized coordinates.

Except for the resonance study, see below, we use an overdamped Brownian oscillator (BO) for the model of the bath [Eq. (26)]:

$$C\left(\omega \right)=\left[1+coth\left(\frac{\omega }{2k_{\mathrm{B}}T}\right)\right]\frac{2\lambda \omega \Lambda }{{\omega }^2+{\Lambda }^2}$$ (26)

(We measure frequencies and energy in wavenumbers, that is, $ħ=1$ , $\left[\omega \right]=\left[E\right]=$  cm⁻¹.) Because both effective baths arise from the same environmental modes, we use the same bath correlation time, ${\tau }_{\mathrm{corr}}={\Lambda }^{-1}\approx 50$  fs, for both. We then vary only the strength of the system–bath coupling, that is, the reorganization energy. For uncoupled pigment at 77 K, these bath parameters give a vibrational relaxation time of approximately 250 fs: ${\tau }_{\mathrm{R}}=k_{\mathrm{R}}^{-1}={\left(C^{\left(1\right)}\left(\Omega \right)\right)}^{-1}$ and 55 cm⁻¹ wide ZPL (3–4 nm in the typical wavelength range). This form of a bath and parameters in this range are commonly used in photosynthetic light‐harvesting complexes.39 High‐frequency modes are sometimes included in the bath spectrum, but these would be represented herein by the explicitly quantized modes. The procedure of including the quantized modes in the bath was investigated by Roden et al.42

In the calculations, four vibrational levels on each pigment were used as a diabatic site basis. After diagonalization, the levels were truncated to 13 lowest levels in the one‐exciton manifold. This restriction is valid because the higher energy vibronic states have negligible oscillator strength and lie out of the Franck–Condon region. Thus, they are neither populated by interaction with light nor by system dynamics. Numerically it was checked that the increase in both the basis size (4→6 states) and number of levels (13→16) did not produce an appreciable difference in the calculated quantities.

To discuss our system, we use the following quantities: absorption spectrum with peak designations, vibronic (excitonic/vibrational) population dynamics with level characterization, vibronic coherence dynamics with coherence characterization, site populations, and intersite coherence. For illustration, we also plot the vibronic wavepacket in the configuration space. We would like to emphasize at this point that the absorption spectra are experimental quantities and the vibronic coherence and population dynamics can be, to a large extent, followed by 2DES.

The absorption spectrum is calculated from the diagonalized Hamiltonian by using a second‐order cumulant expansion [see Eq. (26)]. Peak designations are read from the origin of the corresponding transitions. It turns out that 77 K is a temperature low enough for only the transitions from the vibrational ground state, $\left|g_1^0\right.〉\left|g_2^0\right.〉$ , to be visible in the linear spectrum due to the Boltzmann distribution of the ground‐state populations in thermal equilibrium.

The vibronic states are directly populated by interactions with light and their population dynamics are calculated by using Redfield master Equation (17). Corresponding to experimental conditions in nonlinear spectroscopy, such as 2DES or broadband transient absorption, the initial condition is excitation by a spectrally broad δ‐pulse (two interactions with the field), as given by Equation (27):

$${\rho }_{ij}\left(0\right)=\sum _{\nu }{\mu }_{i{g}_{\nu }}{\rho }_{g_{\nu }{g}_{\nu }}^{eq}{\mu }_{g_{\nu }j}$$ (27)

The system is considered to be in thermal equilibrium before excitation, ${\rho }_{g_{\nu }{g}_{\nu }}^{eq}=\frac{e^{-{\Omega }_{\nu }/k_{\mathrm{B}}T}}{{\sum }_{\nu }{e}^{-{\Omega }_{\nu }/k_{\mathrm{B}}T}}.$

To characterize the vibronic levels in the one‐exciton manifold, we calculate their localization on the respective sites (pigments) from Equation (28):

$$l_i=\left(l_1\left(i\right),l_2\left(i\right)\right),l_n\left(i\right)=\sum _{\nu }{\left|c_{n,\nu }^i\right|}^2$$ (28)

As well as the dynamics of the vibronic populations, we calculate the evolution of the vibronic coherences, called plainly coherences herein. Quantum mechanical coherences are defined as coherent superpositions of states. As such, the system eigenstates, called vibronic states herein, are also coherent superpositions of the diabatic, site states. However,we denote only the superpositions between the vibronic states as coherences, that is, the off‐diagonal elements of the system density matrix in the eigenstate (vibronic) basis. Our motivation is that exactly these coherences are observed by 2DES as oscillations in the population time.

Similar to vibronic populations, coherences are also directly created by light. We describe them by their vibronic levels origin and the “intersite mixing” ratio [Eq. (29)]:

$${\xi }_{ij}=\sum _{\nu ,\mu }\left(|c_{1\nu }^i{|}^2|c_{2\mu }^j{|}^2+|c_{1\nu }^j{|}^2{\left|c_{2\mu }^i\right|}^2\right)$$ (29)

which determines how much the two sites are mixed in the particular coherence, ${\rho }_{ij}$ . This can be also expressed by the state localization, ${\xi }_{ij}=l_1\left(i\right)l_2\left(j\right)+l_1\left(j\right)l_2\left(i\right)=1-l_1\left(i\right)l_1\left(j\right)-l_2\left(i\right)l_2\left(j\right)$ ; in another words, ${\xi }_{ij}$ corresponds to the probability that states i and j are localized on different pigments. This measure helps to distinguish the prevailing character of the coherence. Purely vibrational coherences, that is, superpositions of different vibrational states on the same pigment, have ${\xi }_{ij}=0$ . In contrast, the electronic coherences, namely, superpositions of electronic excitation on different pigments, have ${\xi }_{ij}=1$ . The value of ${\xi }_{ij}$ reaches these extreme values only if the states constituting the coherence correspond to the diabatic states. In practice, this occurs only in the case of uncoupled pigments (see below). In the general, coupled case, if ${\xi }_{ij}$ is close to zero (one), the coherence ${\rho }_{ij}$ is of prevailing vibrational (electronic) character. Depending on the chosen basis, different measures with similar functions can be used, such as those discussed in Refs. 15, 37.

Site populations are calculated as overall population of a particular site (pigment), including all vibrational states, that is, $P_n={\sum }_{\nu }{\sum }_{i,j}{c}_{n\nu }^i{\rho }_{ij}{c}_{n\nu }^j$ .

Intersite coherence is calculated as the coherence between the two sites traced (i.e. averaged) over the vibrations [Eq. (30)]:

$$P_{12}=T{r}_{vib}{\rho }_{1\nu ,2\mu }=\sum _{i,j}\sum _{\nu \mu }{c}_{1,{\nu }_1{\nu }_2}^i{\rho }_{ij}{c}_{2,{\mu }_1{\mu }_2}^j\left.〈{\chi }_{{\mu }_1}^g\right|{\chi }_{{\nu }_1}^e〉\left.〈{\chi }_{{\mu }_2}^e\right|{\chi }_{{\nu }_2}^g〉$$ (30)

In contrast to vibronic coherences, intersite coherence is calculated in the diabatic, site basis. The real part of P ₁₂ measures the delocalization of excitation between the two sites, whereas its imaginary part reflects the amount of dynamic coherence between the two sites.

The vibronic wavepacket is calculated as the probability of the system at a given time to be at a given point, $𝐐=(Q_1,Q_2)$ , of the configuration space [Eq. (31)]:

$$wp(𝐐,t)={\left|\Psi (𝐐,t)\right|}^2=\left.〈𝐐\right|\rho \left(t\right)\left|𝐐\right.〉$$ (31)

2.2.2.  Uncoupled Pigments—Quantities and Measures

First, to get a feeling about the role of the two baths and measures defined above, we show the case of two uncoupled pigments, that is, J=0 cm⁻¹ (Figure 2). In the absorption spectrum in Figure 2 A, we can see the ZPLs of the two pigments and the two vibrational progressions. The width of the ZPLs is determined only by the electronic bath; for higher vibrational peaks, the lifetime broadening caused by the vibrational relaxation also partially contributes. Because this effect is comparatively small, we can say that the linewidth is determined by pure dephasing due to electronic level fluctuations. On the other hand, the vibronic population dynamics (Figure 2 B) is given purely by the vibrational bath. For λ ₁=0 cm⁻¹, the populations would be stationary because there would not be transfer between the pigments, and thus, the electronic fluctuations would be absolutely correlated for all states at a given pigment. Because there is no mixing between the sites, all states are fully localized (i.e. site basis⇔vibronic basis). Small oscillations of the vibronic populations are given by population↔coherence transfer and disappear in the strict secular approximation (see below). Because there is no transfer between pigments, the site populations (not shown) stay constant. In Figure 2 C, the real part of the five most intense coherences (sorted by initial amplitude) are shown. It is apparent from the ${\xi }_{ij}$ measure that we have two kinds of coherences: purely vibrational, with ${\xi }_{ij}=0$ , and electronic, with ${\xi }_{ij}=1$ . The electronic ones dephase quickly due to the electronic bath. The vibrational ones are long‐lived and dephase only by lifetime dephasing given by the vibrational bath. This is best seen by setting λ ₁=0 cm⁻¹, in which case the electronic coherences will decay rapidly, while the vibrational ones will live forever. Finally, the intersite coherence (Figure 2 D) is affected mostly by the electronic bath. As mentioned above, its imaginary part corresponds to the amount of dynamic coherence in the system, whereas its real part reflects the amount of intrinsic delocalization between the pigments due to their coupling. In the J=0 cm⁻¹ case, they both decay to zero.

Figure 2.

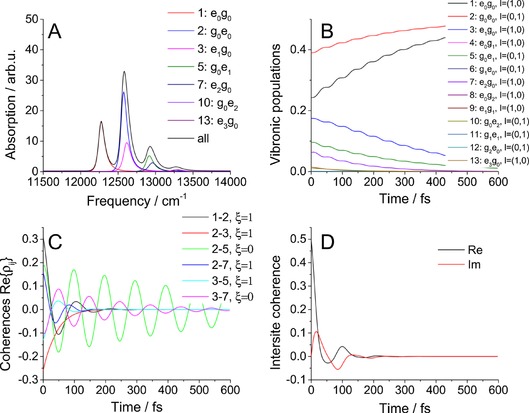
Results for uncoupled pigments: A) absorption spectrum, B) vibronic population dynamics, C) coherence dynamics, and D) intersite coherence. Coupling: J=0 cm⁻¹; other parameters are those given in Table 1.

2.2.3.  Coupled Pigments

Let us now switch on the coupling, setting J=75 cm⁻¹ (intermediate coupling regime), and study the dependence of the system properties on the energy detuning, ΔE. All studied properties are depicted in Figure 3 for three different energy gaps. We remind the reader that the vibrational frequency is Ω=340 cm⁻¹. In the absorption spectra in Figure 3 A–C, we can see the peaks shift and the oscillator strength is redistributed. As the states become delocalized, one‐exciton states consist of several diabatic states and a simple transition designation, as in Figure 2 A, is no longer possible. As expected, different vibronic states are initially populated with increasing ΔE (Figure 3 D–F). For smaller energy gaps, the lowest vibronic state (which is almost the pure ZPL of the lower pigment) is populated faster than that for larger ΔE.

Figure 3.

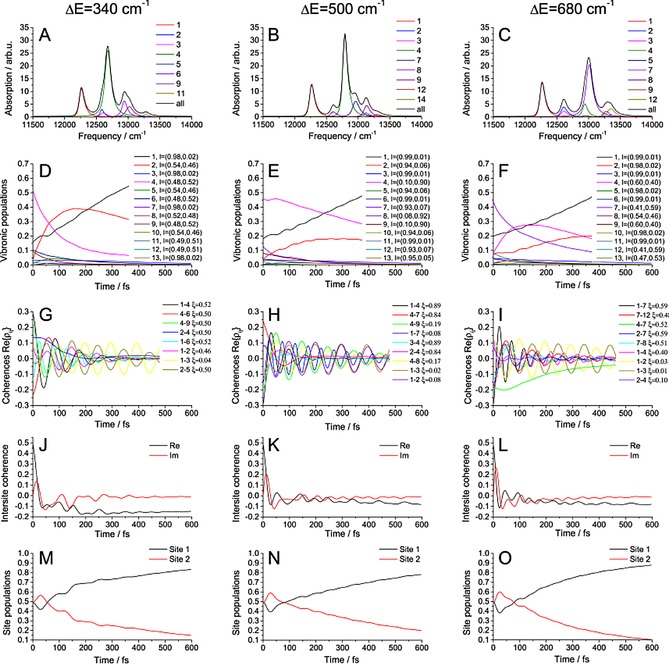
Results for coupled pigments. The properties of the system are calculated for three different energy gaps, ΔE; other parameters are given in Table 1. A–C) Absorption spectrum, states sorted by their energy. d–F) Dynamics of the vibronic states population. G–I) Vibronic coherence dynamics, ordered by their initial amplitude. J–L) Intersite coherence dynamics. M–O) Site population dynamics.

The coherences (Figure 3 G–I) are sorted by initial amplitude, including the five most intense ones, the ones between the strongly populated states and the long‐lived ones. All “localized” coherences with small ${\xi }_{ij}$ are again long‐lived. On the other hand, not all long‐lived coherences have small ${\xi }_{ij}$ : for near‐resonant energy gaps, there can be delocalized coherences with ${\xi }_{ij}\in \left(0.4...0.6\right)$ , which can be also long‐lived. The reason for this is that they are delocalized between the sites in exactly the same way, that is, $l_i=l_j$ , and therefore, the fluctuations that the constituent states feel are correlated, which decreases dephasing. An example is the coherence 2–5 with ${\xi }_{25}=0.5$ for $\Delta E=\Omega$ . To gain an insight into the actual structure of the coherences and the constituent states, the participation ratios, $|c_{n,\nu }^i{|}^2$ , of states 2 and 5 in the site basis states are given in Table 2. We can see that these two vibronic states are composed of completely different exciton‐vibrational states. However, because the electronic bath fluctuations are the same for different vibrational states on the same pigment and it is this electronic bath that mostly causes the decay of coherence 2–5, only total localization on the respective pigments, given by l_i, is important in determining the coherence lifetime. This demonstrates the usefulness of the introduced measures. One more remark is in order. Naively, we would expect the mixed coherences to be easily recognizable in the experiment because their frequencies generally differ from the frequency of the vibrational mode characteristic for purely vibrational coherences. However, as we see from coherences 2–5, even such a mixed coherence can oscillate on frequency ${\varepsilon }_5-{\varepsilon }_2=341\mathrm{cm}{}^{-1}$ , that is, practically at Ω. Indeed, much attention has been given to distinction of the kinds of coherences in recent years.10, 15, 37

Table 2.

Participation ratios of states 2 and 5 from Figure 3 D in specific pigment states. These states constitute the long‐lived mixed coherences 2–5 in Figure 3 G.

Site	State 2	State 5
basis	ɛ 2=12607 cm−1	ɛ 5=12948 cm−1
$\left|e_1^0\right.〉\left|g_2^1\right.〉$	0.14	0.01
$\left|e_1^1\right.〉\left|g_2^0\right.〉$	0.39	0.00
$\left|g_1^0\right.〉\left|e_2^0\right.〉$	0.45	0.00
$\left|e_1^0\right.〉\left|g_2^2\right.〉$	0.00	0.21
$\left|e_1^1\right.〉\left|g_2^1\right.〉$	0.00	0.14
$\left|e_1^2\right.〉\left|g_2^1\right.〉$	0.00	0.18
$\left|g_1^0\right.〉\left|e_2^1\right.〉$	0.00	0.35
$\left|g_1^1\right.〉\left|e_2^0\right.〉$	0.00	0.10

For higher energy gap resonances, the effect of longer coherence lifetime will be obscured by lifetime dephasing because the delocalized states near the potential energy surface (PES) intersections have higher energy and undergo rapid relaxation. A good example is coherences 1–4 in the $\Delta E=2\Omega$ case. The effect of lifetime dephasing alone can be nicely seen on the purely vibrational coherences 3–7 in Figure 2. Notably, the effect of mixed coherence longevity is absent in the off‐resonant ΔE=500 cm⁻¹ case, in which the only long‐lived coherences are purely vibrational.

The intersite coherence (Figure 3 J–L) oscillates because of the coherences from which it originates: with increasing detuning, the overall delocalization (corresponding to the real part of the intersite coherence) decreases as expected.

To show the presence of long‐lived mixed coherences, we calculate the total amplitude of coherence present in the system, $A_{\mathrm{coh}}\left(t\right)={\sum }_{i,j>i}{\left|{\rho }_{ij}\left(t\right)\right|}^2$ , for different energy gaps (see Figure 4 A). Surprisingly, the amount of coherence present in the system decays in almost the same way for all given energy gaps. From the results presented in Figures 2 and 3, we know that for off‐resonant cases there are long‐lived vibrational coherences present, whereas in the resonant cases the coherences become mixed, that is, the constituent states become delocalized. Putting these two pieces of knowledge together, we must conclude that there are longer‐lived mixed coherences when the energy gap is in resonance with vibrational frequency. In other words, a redistribution of the dynamic coherence lifetime between the vibrational and mixed coherences takes place.

Figure 4.

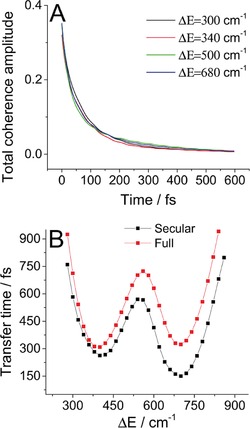
A) Total coherence amplitude present in the system calculated for four different energy detunings. B) Comparison of the “secular” and full Redfield calculations of the transfer time dependence on energy detuning.

Finally, the site populations (Figure 3 M–O) show transient oscillatory behavior when the delocalized states are populated and then more monotonous evolution when the excitation becomes more localized. Most importantly, they show a clear trend of faster dynamics in the resonant $\Delta E=k\Omega$ cases, for which the energy gap is a multiple of the vibrational frequency. This indicates that the direction of resonant vibrations increases population transfer, which is investigated in the next sections.

2.2.4.  Role of Resonance

To quantify the effective rate of population transfer between sites, we fit the first 600 fs of the higher site population dynamics with an exponential decay to obtain the effective transfer time. Let us study the effect of changing the energy gap on this transfer time. Because the Redfield rates also depend on the value of spectral density at the transition frequency and we are only interested in the effect of the resonance at the moment, let us use a flat spectral density [Eq. (32)]:

$$C\left(\omega \right)=\left\{\begin{array}{cc}T\frac{\lambda }{\Lambda },& \omega >0\\ e^{\omega k_{\mathrm{B}}T}T\frac{\lambda }{\Lambda },& \omega <0\end{array}\right.$$ (32)

in which the $\omega >0$ value coincides with the $\omega \to 0$ limit of the BO [Eq. (27)] and the negative frequencies are exponentially damped to preserve the detailed balance, that is, correct thermodynamics. In Figure 5, we study the transfer time for two cases of interpigment coupling and four different lower site displacements. For both strong and weak coupling, there are clear minima around the resonant $\Delta E=k\Omega$ detunings. The slight shift of the minima from the exact resonance is caused by fitting the oscillating higher energy pigment population with an exponential decay. This procedure performed more poorly for more oscillating populations, which correspond to delocalized states. The shifts are therefore present mainly for small displacements and strong coupling.

Figure 5.

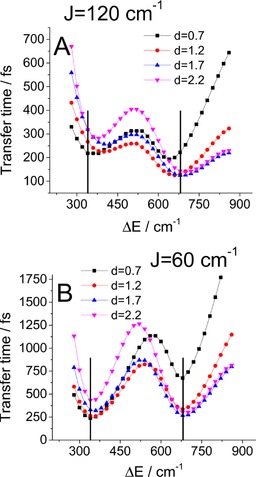
Influence of detuning on transfer time: the role of resonance. The dependence is calculated for four different state 1 displacements and for couplings of A) 120 and B) 60 cm⁻¹. The black vertical lines mark the resonant $\Delta E=k\Omega$ energy gaps.

We would like to emphasize that in traditional Redfield theory the resonance of an energy gap in the excitonic basis with a peak in phonon spectral density speeds up population transfer between excitons. This is caused by a larger density of available phonons. This is a different effect than that observed herein, in which the resonance is in the site basis and speeds up energy transfer between the pigments, leaving the vibronic population dynamics practically unaffected. In our case, this is a consequence of increased delocalization of the vibronic states composed of the resonant states. This delocalization then leads to leaking of the vibrational wavepacket through the excited‐state PES intersection to the lower energy site. We discuss this mechanism in more detail in later sections.

Another point to mention is the significant width of these resonances. This agrees with results in the literature for the multidimensional configuration space14, 16 and is in contrast with the one‐dimensional studies.19, 20 Our results should then better correspond to experimental observations.43 The advantage of wide resonances becomes apparent when realizing that the considered biological systems are dynamically fluctuating and highly energetically disordered.44 Under such conditions, a wider range of quasi‐resonant regimes of fast energy transfer becomes a necessity.

To demonstrate that the resonance speeds up transfer, even for higher multiples of the vibrational frequency, we increased the number of states in the vibronic manifold to 18 (to maintain accuracy) and calculated the population transfer for larger energy gaps (Figure 6 B). For very small energy gaps, the low‐lying states are delocalized, which results in large site population oscillations and makes the fitting unreliable. For large energy gaps the transfer is very slow. However, the effect of accelerated population transfer clearly persists, even for large energy gaps.

Figure 6.

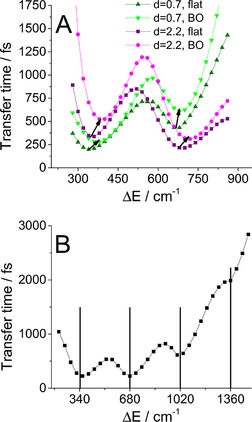
The dependence of the transfer time on energy detuning. A) Comparison of the BO and flat spectral density for two different state 1 displacements. The arrows indicate the shift of the resonance minima from the flat to the case of the BO spectral density. B) Occurrence of multiple resonances for a higher energy gap, as calculated with a flat spectral density (33). The black vertical lines mark the resonant $\Delta E=k\Omega$ energy gaps.

In the case of a more realistic overdamped BO spectral density, we expect these minima to experience only a minor shift because of the slope of the spectral density. As demonstrated in Figure 6 A, this is indeed the case. We can see the minima shift to higher frequencies, which reflects the positive slope of the spectral density in the relevant region of small phonon frequencies.

Knowing that the effect of the BO bath is just an energy shift, we can investigate the role of the baths on the transfer time and resonance conditions (Figure 7). The effect of the vibrational bath is straightforward: weaker coupling to this bath slows down population transfer, which makes resonance more important. This is because in the resonant case excitation “leaks” to the lower site through delocalized states at the excited‐state PES intersection. On the other hand, the effect of the electronic bath is more subtle. Increasing coupling to this bath speeds up transfer in the lower detuning minimum and slows down transfer in the higher detuning minimum. This can be understood intuitively when considering that this bath reduces delocalization of the excitation: in the large detuning case, the population leaks to the lower site at the PES crossing through the delocalized states and relaxation at the upper site is a competing channel. Thus, delocalization is preferable in this case. In the small energy detuning case, even the low upper site states are delocalized and a lack of bath‐induced localization permits coherent oscillations between the sites, which slows down directional transfer.

Figure 7.

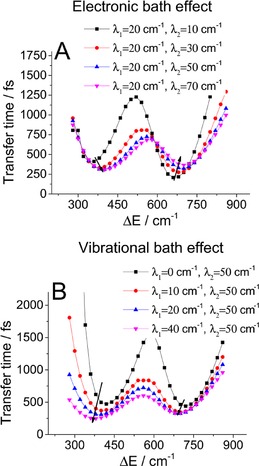
The dependence of the transfer time on energy detuning. The influence of the A) electronic and B) vibrational bath coupling strengths is calculated for four different state 1 displacements. The arrows indicate the shift of the resonance minima with increasing strength of coupling to the respective bath.

To appreciate the role of delocalization of the vibronic states in speeding up energy transfer, consider the evolution of the vibronic populations in Figure 2 for the off‐resonant ΔE=500 cm⁻¹ and resonant ΔE=680 cm⁻¹ cases. Clearly, in the latter, faster case, state 4, which serves as an intermediate state, is of importance. From the localization l ₄ measure, we can see that this state is highly delocalized between the two sites, which provides the means for the vibronic wavepacket to leak into the lower pigment. In contrast, in the off‐resonant case, there are no such states: all vibronic states are highly localized.

Another means of visualizing the actual evolution of the system after excitation is the motion of the vibronic wavepacket (Figure 8). We can observe the actual motion of the excitation, including the initial coherent evolution followed by leaking of the excitation through the potential intersection and final relaxation in the lower energy site 1. Comparing off‐resonant ΔE=500 cm⁻¹ with resonant ΔE=340 and 680 cm⁻¹ energy gaps, we can see that in the resonant cases the excitation clearly reaches the relaxed state at site 1 much faster. Leaking between the potentials occurs along the correlated nuclear motion direction, that is, in the direction of the line between the excited PES minima. The full video of the evolution can be found in the Supporting Information, together with the projection of the vibronic wavepacket on the abscissa connecting the PES minima, which is shown in Figure S1.

Figure 8.

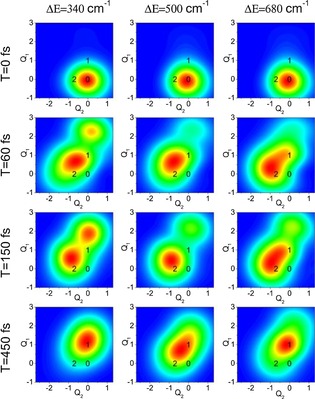
Snapshots of the motion of the vibronic wavepacket for different energy detunings. Black numbers denote the minima of respective PES states, see Figure 1. At T=0 fs, after the Franck–Condon transition, the wavepacket has the position and shape it had in the ground‐state equilibrium. At later times, the excitation coherently oscillates around the minima of states 2 and 1, while leaking through the potential intersections, eventually relaxing to lower energy state 1.

2.2.5.  Secular Approximation

Finally, to further investigate the effect of dynamic localization and to address the much discussed question of dynamic coherences “helping” the energy transfer, let us study the influence of these coherences on population dynamics and transfer time. To this end, we set ΔE=Ω=340 cm⁻¹ and compared the full Redfield dynamics presented above with the case in which terms of type $R_{ii,jk},R_{ij,kk}$ , connecting the populations with the coherences, were set to zero (this is called the secular approximation herein). In this situation, the coherences and populations evolve independently and the eigenenergies of the system are fixed by the transformation of the Hamiltonian to the vibronic basis. For direct comparison of the system dynamics, see Figure S2 in the Supporting Information; in most aspects the two cases are barely distinguishable. The only significant difference can be seen in the site populations, for which the secular case is evidently faster than the full dynamics. Let us then compare the role of resonance in the full and secular cases (Figure 4 B). Interestingly, the energy transfer is actually faster when the populations and coherences evolve independently; the difference is larger for the higher detuning resonance. This further supports the dynamic localization argument presented above, since in the secular approximation the vibronic basis is the fixed preferred basis and there is no localization. This is advantageous for energy transfer because in the original vibronic basis the lowest state is always localized on the lower energy pigment, and thus, dynamic localization in the low states of the higher energy pigment is undesirable.

3.  Conclusions

We derived an expression for the Redfield theory dynamics of a system of interacting pigments in the presence of a vibrational bath and explicit quantization of a few prominent vibrational modes. The resulting description includes two effective baths that correspond to experimentally observable quantities, namely, the spectral line width and dynamic Stokes’ shift. This enabled us to study the effects of the resonance of the quantized vibrational frequency with the energy gap between the two pigments on energy transfer. Moreover, our realistic two‐dimensional configuration space of the vibrational coordinates allowed us to follow the motion of the vibronic wavepacket in the excited state.

The results showed that the system exhibited strong mixing of the vibrational and electronic states, leading to vibronic states. The resonance of the vibrational frequency with the energy gap then resulted in significant delocalization of the vibronic wavefunctions between the two pigments. This caused fast leaking of the vibrational wavepacket in the excited state through the intersection between the excited‐state PESs. The overall energy transfer between the sites was then faster than that in the off‐resonant case. We investigated this effect and found that it persisted over a broad range of physically relevant parameters. The resonance minima were not very sharp, so the mechanism would also work in energetically disordered systems, such as natural photosynthetic pigment–protein complexes.

Furthermore, we tested the effect of the mentioned resonance on the evolution of dynamic coherences, which is, in principle, directly experimentally observable by 2DES. We presented evidence that, although in the off‐resonant case only vibrational coherences can be long‐lived, in the resonant case mixed coherences can also have a long lifetime. The observed presence of long‐lived coherences, which are not of a purely vibrational origin, then acts as a signature of a resonance of typically intrapigment vibrations with electronic energy levels.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

Supplementary

P. Malý, O. J. G. Somsen, V. I. Novoderezhkin, T. Mančal, R. van Grondelle, ChemPhysChem 2016, 17, 1356.