Abstract
The mechanical behavior of a prototype touch panel display, which consists of two layers of CVD graphene embedded into PET films, is investigated in tension and under contact-stress dynamic loading. In both cases, laser Raman spectroscopy was employed to assess the stress transfer efficiency of the embedded graphene layers. The tensile behavior was found to be governed by the “island-like” microstructure of the CVD graphene, and the stress transfer efficiency was dependent on the size of graphene “islands” but also on the yielding behavior of PET at relatively high strains. Finally, the fatigue tests, which simulate real operation conditions, showed that the maximum temperature gradient developed at the point of “finger” contact after 80 000 cycles does not exceed the glass transition temperature of the PET matrix. The effect of these results on future product development and the design of new graphene-based displays are discussed.
Keywords: CVD graphene, touch panel displays, mechanical performance, wrinkles, Raman spectroscopy
Introduction
Touch screen technology acts as an interface between computers and users, providing them a strong control of the device (PCs, smartphones, mobile phones, tablets, and in many other information devices) and an easy and accessible visual experience. Its simplicity and popularity gives impetus to a highly promising market,1 which seems to have tremendous growth potential.2−4 In fact, the industrial production of touch panels has developed rapidly over the past two years; already the first capacitive touch panel has been marketed, and several companies have built up or expanded production lines with annual capacity of several million touch screens.5
Over the last five years, extensive research efforts have shown that polymer-based touch panel displays consisting of transparent conductive films (TCFs) that incorporate graphene (or carbon nanotubes) are considered as key components in current and future optoelectronics such as in flexible, stretchable, and wearable devices.1,6−10 As in many other fields, however, in which graphene is looked upon as a replacement material for future applications, significant challenges must be tackled, and further work is needed to understand fully the performance of these devices in field applications.
Graphene, as a transparent conductor, shows a multitude of advantages such as mechanical stretchability, flexibility, and integrity,11 chemical stability,12 a wealth of fabrication methods (wet or dry processes),13−15 various doping strategies,16 low values of sheet resistance,17 and low absorption in a wide spectral range.18 Large area continuous polycrystalline graphene, synthesized by chemical vapor deposition (CVD) on metal substrates, shows the best performance as a conductive transparent film.8,19 Moreover, turbostratically stacked few-layer graphene is generally favored for low sheet resistance Rs of conductive films, because Rs is inversely proportional to the number of layers.
The fabrication of touch panels requires the transfer of graphene layers onto a transparent and flexible substrate. Various transfer techniques20,21 for large area graphene films onto polymer substrates (e.g., PMMA, PET, PDMS) have been developed with the aim of minimizing any induced structural distortions (wrinkles, cracks, or even holes) on the graphene membranes. Recently, the direct transfer of transparent conductive graphene films (TCF) of more than 100 m in length that exhibit Rs values in the region of 500 Ω/□ has been achieved in an industrial environment.19 Up to now, two methods have been employed to minimize the Rs value of a TCF, the layer-by-layer monolayer stacking22 and the direct growth of few layer films.23 The former strategy is time-consuming and results in the dramatic increase of the production costs with the number of layers. The second strategy suffers from the lack of uniformity regarding number of layers, but, despite that, it seems to be a more favorable fabrication method.
Touch panels over their lifetime (typically a few years) are subjected to bending stresses, as well as to dynamic contact stresses transmitted by forces exercised by the operator’s finger or commercial styluses. Thus, it is of paramount importance to examine in depth the overall mechanical performance of a touch panel display. In this Article, we monitor the mechanical response of a prototype display, which is comprised essentially of two layers of CVD graphene embedded into PET, by means of Raman spectroscopy, tensile loading, and contact-point fatigue measurements. The static mechanical experiments involve the cyclic loading under applied uniaxial tension up to 3%, while measuring the strain transfer efficiency from the PET matrix to the graphene by monitoring the shift of the 2D Raman peak.19 Alterations of the graphene morphology are examined by Raman mapping and thermomechanical testing of the display over frequency and temperature ranges of 0.1–100 Hz and 25–60 °C, respectively, which are analogous to the conditions encountered in real-life applications.
Results and Discussion
Tensile Strain Application in Graphene-Based Prototype Display
Figure 1a shows an image of the prototype graphene flexible display kindly supplied by Bluestone Global Tech (see Experimental Methods for details). A representative spectrum in the G and 2D peak regions from the embedded double graphene films incorporated in the prototype is shown in Figure 1b. Because of the high Raman scattering intensity of PET at about 1614 cm–1, the G peak is partially masked.24 Thus, it was necessary to use the strain sensitivity of the 2D peak for the mechanical assessment of the touch panel.
Figure 1.
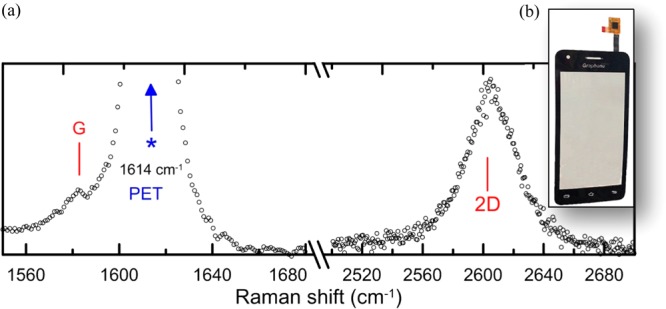
(a) A characteristic spectrum of the embedded graphene films within the prototype display. The G peak of graphene overlaps with a strong peak at 1614 cm–1 from PET and appears as a weak shoulder. (b) Image of the prototype display.
Because of its high strain sensitivity and high intensity, the 2D peak is an ideal phonon mode to follow the evolution of strain.25 To minimize the background signal arising from the surrounding PET matrix, a detailed Raman depth profile analysis of the screen has been carried out. The plot of the 2D Raman spectral intensity recorded by scanning across a section of the display (step size ∼1 μm) is shown in Figure S1; the maximum signal of 2D peak is found to be recorded at a depth of 115 μm from the top surface (z = 0, Figure S1) of the display panel.
Because of the design of the devices employed in display panels such as in mobile phones, bending forces can subject the top graphene/polymer layer to either tension or compression. Here, we have chosen to conduct tensile measurements to understand how stresses are transferred to the graphene layer and to monitor possible failure mechanisms upon loading. The experiments were performed using a microtensionmeter integrated to a confocal Raman microscope, which allowed us to perform simultaneous Raman measurements. Characteristic Raman spectra of the 2D peak for various applied strain levels using the 785 nm excitation wavelength are presented in Figure S2. A double peak feature is apparent mainly at higher strain levels. The most intense component at 2605 cm–1 corresponds to the intrinsic 2D response of CVD graphene and the weaker one at 2622 cm–1 to an overtone Raman mode of PET that does not shift with strain.24
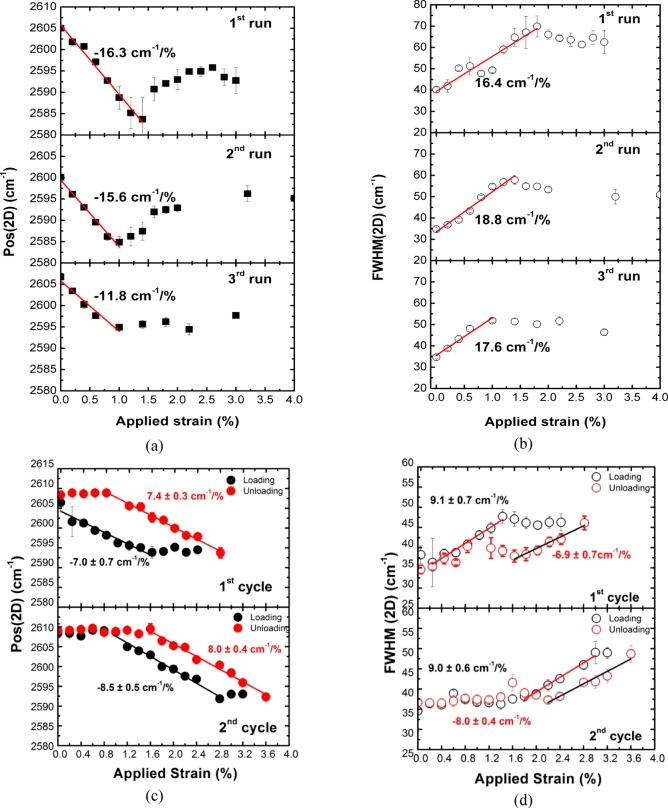
In Figure 2a (first run), the fitted 2D peak frequency position, Pos(2D), versus the applied axial strain is plotted (characteristic Raman spectra are presented in Figure S2). The Pos(2D) of the embedded graphene in the as-received (prior to external loading) was ∼2605 cm–1, whereas the stress-free value is located at ∼2595 cm–1, thus indicating the presence of compressive residual prestrain in the area examined. This is mainly attributed to the graphene growth and transfer processes and possibly also to the morphology (roughness) of the underlying substrate.26,27 Considering a value of 154 cm–1/% for the strain sensitivity of the 2D mode of a flat monolayer under biaxial deformation, which is the same for free-hanging and embedded graphene,28 an initial biaxial compression of about −0.07% is estimated.
Figure 2.
(a) Pos(2D) and (b) the corresponding FWHM(2D) for the CVD graphene incorporated into the flat panel display as a function of applied uniaxial strain for three different runs (same sampling area). (c) Pos(2D) and (d) the corresponding FWHM(2D) for two consecutive deformation cycles as a function of applied uniaxial strain.
In tension, the Pos(2D) red-shifts linearly at a rate of −16.3 cm–1/% for applied strain up to 1.4%, whereas at higher loadings the wavenumber is observed to relax back reaching the value of 2593 cm–1 at 3%. Similar results are depicted in Figure S4 where the strain evolution of the 2D peak position and its corresponding full-width-at-half-maximum (FWHM) were captured from another sampling area. In this case, the initial biaxial compression is estimated to be 0.13%. The 2D wavenumber red-shifts at a rate of −18.9 cm–1/% up to the onset of sliding (∼0.8%), while for greater strains a relaxation toward its initial value is observed.
In previous studies,29−38 it was demonstrated that the loading of exfoliated graphene/polymer model composites results in the development of a shear stress at the interface between graphene and the surrounding polymer matrix, which is responsible for the transfer of stress/strain to the inclusion. To transfer the applied load efficiently from the polymer to graphene, a specific critical transfer length (Lt) along the axial direction is required. As is well-known in composites mechanics,36 if the graphene length (L) along the axial direction is smaller than 2Lt, then the graphene flake is not stressed efficiently and only a fraction of load is transmitted through the polymer to the membrane. Recently, the overall required length for efficient load transfer in similar graphene/polymer systems was estimated to be ∼4 μm.32
In a recent study39 concerning the uniaxial deformation of CVD graphene onto a PET substrate, we showed that the transferred CVD graphene has a characteristic wrinkled morphology comprised of flat isolated graphene islands separated by out-of-plane wrinkles, which are sticking up above the PET substrate; thus a hollow region within the wrinkles is formed in which there can be no stress transfer, giving rise to the mechanically isolated graphene “islands” (Figure S5). The mean size of the graphene “islands” is about 1.5 μm, while the height of the accompanied wrinkles is of the order of 15 nm.39 Inside the “islands”, the transferred graphene is nearly flat, suggesting that good CVD graphene/PET adhesion in these areas is plausible.39 A downshift of the 2D peak position under uniaxial tensile strain at a rate of 12.8 cm–1/% is recorded, which is significantly lower than that obtained for flat exfoliated graphene embedded into polymer.28,32,40 In particular, in a recent work by some of the authors40 concerning the deformation of CVD graphene that exhibited fewer wrinkles supported on a PMMA substrate, it was shown that if the area of the graphene island increases at the expense of the folds, then a more efficient stress transfer (around 50% in that case) can be accomplished.
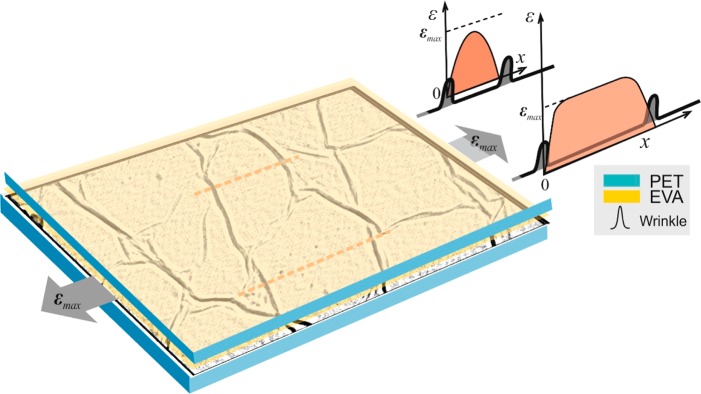
Because of their formation, wrinkles are mechanically free because of the absence of interface with the substrate.39 The buildup of normal stress takes place from the edges of the islands and reaches a maximum value at some distance of Lt away from the edges, whereas the interfacial shear stresses exhibit a maximum at the edges and die away as one moves into the specific island. Figure 3 depicts schematically the proposed stress transfer mechanism. Therefore, due to the relatively small size of the graphene islands, the buildup of strain within them is small because the size along the axial direction is smaller than the critical length (L < Lc).
Figure 3.
(Left) Schematic representation of the wrinkled morphology and the formation of “islands” in the embedded graphene system; (Right) Predicted stress transfer profiles across the graphene flat regions. PET: poly(ethylene terepthalate) EVA: ethylene vinyl acetate.
To further investigate the topography of embedded CVD graphene, we have performed polarized Raman measurements based on a recent work by some of the authors.41 Because of the double or even triple resonant nature41,42 of the Raman scattering in graphene, a relatively intense Raman signal can be obtained from the transverse sections of graphene monolayer. The inset in Figure 4 explains the specimen geometry relative to the incident linear polarized light. Raman spectra were collected from sections of the display in the backscattering geometry with the direction of laser propagation along the x-axis (parallel to the plane of display). For these polarization arrangements, fixed spectra were taken by rotating the display to different angles with regard to the angle Φx (inset of Figure 4) and at steps of 10°. The results for the 2D peak intensity are presented in Figure 4.
Figure 4.
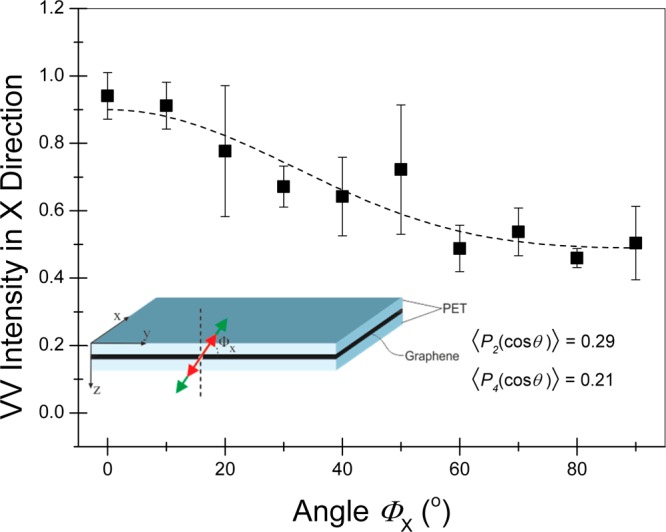
2D peak intensity variation of the display’s CVD graphene with the angle Φx (laser beam direction along the x-axis). The inset presents the chosen Cartesian coordinate system relative to the surface of the display. The laser beam direction and the polarization vectors of the incident and scattered beams are shown.
According to the analysis presented in ref (41), the orientation distribution function, which describes the spatial orientation of embedded graphene in nonpolar materials such as graphene, can be analyzed in even degree Legendre polynomials Pi(cos(θ)) having the corresponding ⟨Pi(cos(θ))⟩ as order parameters.41 Polarized Raman spectroscopy has the ability to determine only the ⟨P2(cos(θ))⟩ and ⟨P4(cos(θ))⟩. The extracted values for the ⟨P2(cos(θ))⟩ and ⟨P4(cos(θ))⟩ are 0.29 and 0.21, respectively. These values are smaller than those determined from graphene deposited onto PET film and mounted in polymer resin, being 0.86 and 0.79, respectively. The results show sharp deviation of the graphene membranes from in-plane orientation, which can be attributed to the wrinkled morphology of the graphene inside the display. Moreover, we have calculated the Krenchel factor,43 referring to orientation effects on stress transfer efficiency, for the display as 0.66. This would predict a 2D peak shift rate of around 38 cm–1/% (=0.66 × (−57.5) cm–1/%, where −57.5 cm–1/% is the reference slope of 2D peak for 514 nm) for uniaxial deformation, which is much higher than the measured shift rates (see below). As mentioned earlier, the further reduction of the shift rate per strain is attributed to the size of the flat region (islands) of the flake, which is not sufficiently large to allow efficient load transfer.
Very recently, we have established44 a simple correction method to convert the nominal applied strain (εappl) to actual graphene strain (εCVD) in cases where the flake length is smaller than the critical length. This is based on the comparison of the measured wavenumber shift per strain to the reference slope (−57.5 cm–1/% for 514.5 nm), which yields εCVD (%) = εappl(%)(−16.3 cm–1/%)/(−57.5 cm–1/%) = εappl (%)·0.30 or approximately 30% efficiency. Pertinent values of 2D strain sensitivity as a function of excitation wavelength and the Poisson ratio of the encapsulating polymer matrix have been given elsewhere.44
In the case of a continuous embedded membrane, the length L ≫ Lc = 8 μm, which does not have grains or discontinuities, all of the applied strain should have been transmitted to graphene. Provided that the two materials are in perfect contact, no relaxation of graphene strain should have been observed up to polymer failure. The observed wavenumber plateau and subsequent relaxation for applied strains higher than 1.4% (∼0.4% on graphene) indicates that beyond that strain level the polymer yield point has been exceeded and no further stress is transferred to graphene (Figure 2a).
Raman linewidths give complementary information regarding doping, strain, disorder, number of layers, and morphology of different types of graphene.45,46 For graphene grown on copper, the FWHM(2D) varies between 28 and 40 cm–1.45,47,48 CVD synthesized graphene exhibits a larger FWHM at rest as compared to exfoliated flakes (∼24 cm–1)49 as a result of the growth-induced strain, doping from the metal substrate,50 thermally and topographically induced folding and rippling of the membrane, as well as being due to the presence of grain boundaries and annealing twins.51 In our case, the presence of two CVD grown graphene films transferred sequentially, one on top of the other, is another source of peak broadening, because it amplifies the out-of-plane instabilities of the graphene membranes and the inhomogeneities of the in-plane strain.
In Figure 2b (first run), the FWHM of the 2D peak is plotted as a function of applied strain. The initial FWHM (2D) is about 40.2 cm–1. It is evident that 2D broadens considerably at a rate of 16.4 cm–1/% for applied (actual) strains up to ∼1.8% (∼0.4%), reaching the value of 70 cm–1 after which a smooth decrease is observed. The variability in the 2D strain sensitivity of the individual grains due to the different size distribution and crystallographic orientation of the grains within the laser spot can merely explain the observed FWHM strain dependence.39 Another important broadening factor relates to the double resonant nature of 2D peak.46 As has been shown recently,52 the application of uniaxial strain in exfoliated graphene results in a pronounced splitting of the 2D mode excited with 785 nm radiation. The 2D peak broadening is found to be ∼8 cm–1 for strains up to 0.4%. The overall 2D peak uniaxial strain response depends on the induced asymmetry of the Brillouin zone (BZ) and the direction of the incident laser polarization with respect to the strain axis along with the contribution of the inner and outer double-resonance scattering mechanisms.53
Rapid retraction of the PET substrate upon specimen unloading subjects the graphene to compression again (the Pos(2D) reverts to 2602.7 ± 0.4 cm–1, which corresponds to a strain of −0.05%). The observed decrease of the residual compressive strain at the end of the cycle is possibly due to graphene relaxation during PET plastic deformation over 1.4% of strain. Further loading/unloading of the display (second and third runs, Figure 2a) leads to lower values of shifts of Pos(2D) with strain, which indicates gradual deterioration of the stress/strain efficiency as a result of PET plastic deformation (see also Figure S6).
Deformation of the Graphene Display during Loading and Unloading Cycles
To capture the changes occurring during mechanical deformation of the graphene/PET system, we have conducted Raman measurements on a different area of the display during both loading and unloading cycles. The results presented in Figure 2c show that the 2D peak red shifts linearly at a rate of −7.0 cm–1/% for applied strain up to 1.6%, whereas at higher uniaxial loadings the Pos(2D) is found to fluctuate around the stress-free value of ∼2595 cm–1 up to 2.8% of applied strain (see also Figure S3).
During the decrease of the applied strain on PET (unloading), a linear blue shift of the 2D peak at a rate of 7.6 cm–1/% is observed for deformations up to 0.8%. It is important to point out that within experimental error, the slopes of Pos(2D) per strain are identical for both the loading and the unloading regimes. As was also postulated earlier, the Pos(2D) are related to the stress values in the tensile stress–strain curve of pure PET, which is shown in Figure S6 for quasi-static deformation that emulates the conditions of the Raman experiment. As shown, a linear relationship between stress and strain is observed for both specimens (pure and prototype PET) up to 1.5%, whereas beyond that strain level plastic yielding seems to be initiated, leading to a significant decrease in slope.
Hence, the Pos(2D) of graphene seems to be dependent on the stress that material experiences and does not follow the strain of the host matrix. In other words, when the substrate is yielding due to plastic deformation, the 2D phonon position is “locked” as the graphene inclusion cannot be loaded any further. The Raman shift captures perfectly this effect as it is only sensitive to the presence of “stress” in the graphene material and not “plastic strain”.54 During unloading, both films examined follow a typical hysteresis curve. When the external load has reached almost a zero value, both films appeared to have a residual strain in the range of 1.6–1.7%, proving that when a polymeric material is stretched beyond the point of plastic deformation, then it acquires a certain degree of permanent deformation upon unloading. The latter is a well-established mechanical behavior of thermoplastic polymers such as PET, where the level of permanent strain depends clearly on how far the polymer is deformed beyond its yield point.54,55 The presence of plastic yielding for PET upon high tensile strains can be actually seen in the stress–strain curve of pure PET given in Figure S6. Loading and unloading curves for pure PET are also presented therein to verify the conclusions above.
Recently, similar spectroscopic measurements were performed in simply supported mechanical exfoliated graphene lying on the top of PET.31 The efficiency of stress transfer was analyzed using a nonlinear shear–lag model. The authors observed, upon unloading when PET was stretched up to 7%, a nonlinear behavior similar to that encountered here, the development of compressive stress/strain and reverse sliding along the interface.31 AFM measurements showed that for tensile strains higher than 2%, buckling ridges are imposed upon the graphene on unloading. As the applied tensile strain to PET increases, the compressive strain that graphene experiences on unloading and then buckling ridges of higher density are observed.31
This behavior is also very important for practical applications and can affect the efficient operation of flexible displays. Indeed, this is further corroborated by the second loading of the same sampling area (Figure 2c,d). As seen, graphene retains its residual compressive strain up to 1%, which corresponds to the permanent deformation of the PET matrix and then exhibits a similar shift of about 8.5 and 8.0 cm–1/% for the loading and unloading stages, respectively. Finally, it is worth noting that in the area examined, the slopes of the plots of Pos(2D) and FWHM(2D) versus strain obtained are significantly lower than in other areas examined such as those of Figure 2a,b and Figure S4, which is again attributed to the variability observed in the size of the graphene “islands” that take up the stress during PET loading.
Thermomechanical Response of Prototype Display
To assess fully the integrity of the displays in a real-life operational environment, we have subjected the panels to dynamic mechanical analysis (DMA) at different frequency sweeps (0.1, 1, 10, 100 Hz) over a temperature range 25–60 °C for each frequency. At the lowest frequency (0.1 Hz) of the applied sinusoidal stress, the storage modulus is found to be 4.1 GPa. As the frequency increases, the storage modulus at 25 °C slightly increases, reaching the value of 4.4 GPa for both 1 and 10 Hz as well as 4.6 GPa for 100 Hz. The observed stiffness enhancement of the display specimens is typical for PET films.56
Also, the temperature dependence is quite similar for all of the sweeps examined. The influence of the mechanical loading on the morphology of embedded graphene is examined by detailed postloading Raman mapping at ambient conditions at the end of 1 and 100 Hz frequency sweeps. In Figure S7, contour maps of the Pos(2D) and FWHM(2D) before and after the 100 Hz/25–60 °C cycle are presented. Initially, the mean Pos(2D) (FWHM(2D)) over the 100 spectra taken in the 10 × 10 μm2 area examined is located at 2602.2 ± 0.5 cm–1 (45 ± 2 cm–1). After the 0.1 and 1 Hz sweeps followed by the temperature scans, the mean values increase to 2606.3 ± 0.5 cm–1 (43.0 ± 1.5 cm–1), respectively. At the end of 100 Hz/25–60 °C cycle, the corresponding value was 2604.9 ± 0.3 cm–1 (41 ± 1 cm–1).
These results indicate that the initial residual compressive strain of 0.13% increases to 0.2% after the 1 Hz/25–60 °C cycle, and it relaxes to 0.17% at the end of the multifrequency sweeps. Regarding the FWHM(2D), the peak seems to narrow by about 9% relative to its initial value. This might suggest a more homogeneous strain field imparted to the embedded large-area graphene sheets due to the partial unfolding of wrinkles and the subsequent flattening of the graphene films.
Functional Fatigue Behavior of the Prototype Display
Further as to the DMA experiments described above, we conducted functional fatigue experiments on the touch display by simulating the finger force of an average user via a mobile stylus over a tapped area of 20 × 20 μm2 on the specimen (experimental setup is shown in Figure S8 and in the corresponding video). The effect of fatigue on graphene was evaluated by taking Raman maps within the tapped area.
The initial position of the 2D peak of the embedded CVD graphene is 2603.2 ± 0.5 cm–1. As compared to its stress-free value of ∼2595 cm–1 (exfoliated monolayer graphene), it corresponds to a small compressive strain (assuming biaxial stress) of about −0.055%. Figure S9 shows the evolution of the resulting force as a function of time, during the deflection controlled functional fatigue experiment. The results of the functional fatigue behavior and the blue-shift of 2D phonon position, corresponding to compressive residual strains, prior to and after the cycling experiment as obtained by means of Raman measurements are presented in Figure 5.
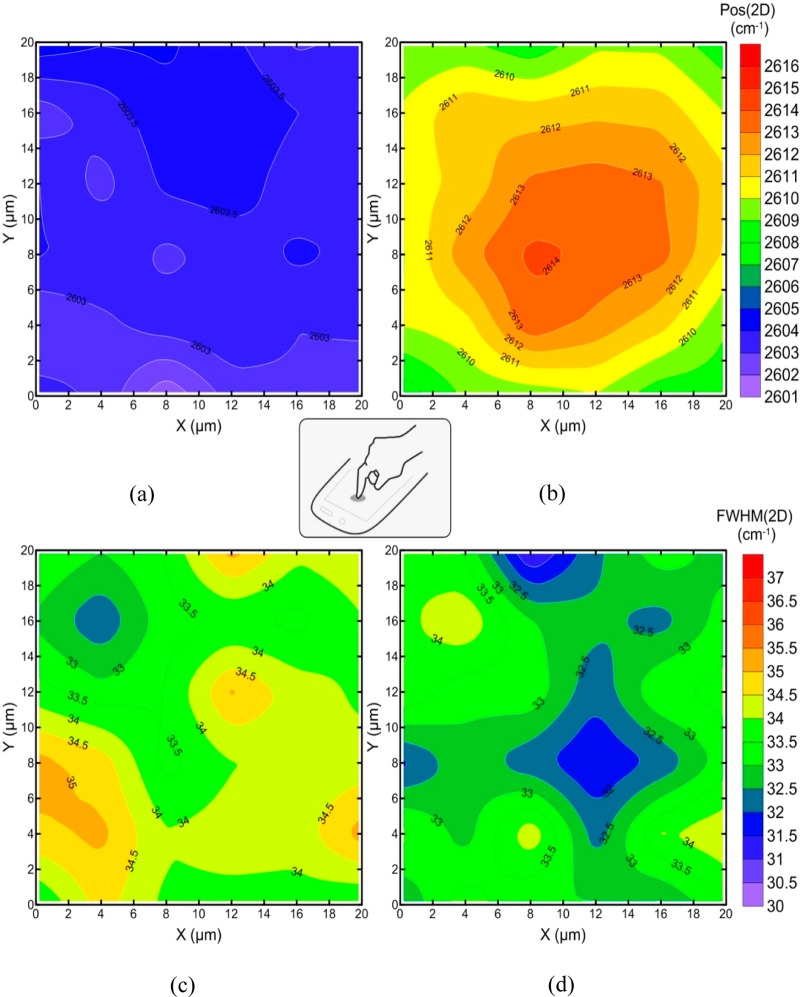
Figure 5.
Contour maps of Pos(2D) and FWHM(2D) before (a,c) and after (b,d) the implementation of functional fatigue.
The mechanical experiments (Figure S10) show that there is a gradual relaxation of the imposed maximum compressive force, which is actually depicted by the diminishing maximum compressive values of contact force with the applied loading cycles. The mapping of Pos(2D) after the functional fatigue experiment within the tapped area of an area of 20 × 20 μm2 (Figure 5) implements a high residual compression exactly at the precise point of contact corresponding to a wavenumber shift of 10 cm–1, which gradually decreases concentrically to a value of 4 cm–1 (Figure 5b).
If we assume biaxial loading due to the conditions of the experiment, then the permanent compressive strain after the fatigue is of the order of −0.07% at the position of the tip of the stylus. Because the initial compressive strain (see above) was estimated to be about 0.055%, then we expect that on the completion of the experiment the embedded graphene is experiencing a compressive strain of ∼ –0.12% due to the contraction upon cooling. Taking into account that the linear thermal expansion coefficient of pure PET is αL = 19 × 10–6 °C–1 (see Experimental Methods), the variation of temperature ΔT relative to room temperature (23 °C) is given by the relation ΔT = 2αLεb, where εb is the biaxial strain (0.0012) and the factor of 2 comes from the fact that in isotropic materials the area thermal expansion coefficient is twice the linear coefficient.
Hence, the maximum temperature induced at the point of contact value is estimated to be 58 °C, which is a quite reasonable value for the type of experiment described here. According to differential scanning calorimetry (DSC) measurements (see Figure S11), a weak glass transition at about 80 and 78 °C for the pure PET and the prototype display, respectively, is observed, indicating that the functionality of the display is still maintained after the fatigue experiments were conducted. Further discussion regarding the optimal design for stretchable and flexible electronics, as the case study reported in this Article, is presented in the Supporting Information, where an extension of the de Saint Venant and Kirchhoff theories is implemented.57
Conclusions
We have examined the application of axial tension to a prototype touch panel display. Such studies had not been conducted previously and are important because they can assist in product improvement and the design of new graphene-based displays. The microstructure of the CVD synthesized graphene plays a key role upon the suggested mechanism of stress transfer also in the case of embedded graphene examined here. The external stress is transferred solely by the graphene grains exhibiting strain variation along the tensile strain axis similar to that encountered in discontinuous exfoliated graphene flakes. At a certain level of applied strain, no further stress is transferred to graphene due to the plastic yielding of the polymer matrix.
Thermomechanical tests close to real operational conditions followed by Raman mapping revealed that the display is mechanically robust. The functional fatigue performance of the display showed that the maximum temperature developed is well below the glass transition temperature of the display. The results reveal how graphene films respond to moderate external loads and may have important implications in the fabrication of next generation flexible touch panel displays. Finally, it becomes clear that the observed graphene microstructure as a result of the CVD growth on specific substrates controls the stress transfer efficiency, which is a prerequisite for good conduction through finger contact.
Experimental Methods
Fabrication of Flexible Graphene-Based Display
The prototype display was manufactured by Bluestone Global Tech (New York). The two layers of CVD graphene transferred on PET to effectively reduce the influence of defects as well as nonuniformity. Because of the small size of the display prototype (less than 4″), external doping is not required. A thin ethylene vinyl acetate (EVA) adhesive was used to adhere the graphene to the PET. A highly stable (5W) Nd:YAG laser operated at 1064 nm was used to directly write onto the polymer to fabricate one-dimensional patterns. Finally, copper plating onto the predefined patterns took place.
Mechanical Tensile Tests
A. Cyclic Deformation
Rectangular strips of the display prototype with total length of 60 mm and width of 5 mm were carefully cut and mounted on an in-house microtensile tester. Axial deformations with a step of 0.2 μm can be applied. The microtensile tester was attached onto an XYZ piezoelectric translation stage (Thorlabs Inc.) with extremely high accuracy in positioning on the three axes, and the whole system was placed under a Raman microscope. For samples with a gauge length of 30 mm, the strain was applied at steps of 0.2%, which corresponds to an extension step of 60 μm. Two different cyclic tensile deformation tests were carried out to study the stress transfer and the strain sensitivity of the graphene within the display prototype.
I. Rapid Release of Loading
Three different tensile loading cycles at a maximum applied strain of 3.0%, 4.0%, and 3.0% were performed sequentially. In each cycle, the maximum strain level is reached then the specimen is released and allowed to relax rapidly to its zero strain state.
II. Gradual Release of Loading
Two deformation cycles at a maximum applied strain level of 2.8% and 3.6% were performed. For each cycle, a maximum tensile strain level was reached, and then the specimen was gradually released to its zero strain state.
B. Functional Fatigue
The experiment was conducted on a Universal Servohydraulic Testing Apparatus (model: MTS mini Bionix) controlled by a MTS Test Star 40 processing unit. The maximum force capability of the machine was 250 N with an accuracy of 10–3 N. A specimen with total length of 60 mm and width of 5 mm was placed horizontally on the bottom grip of the MTS where an assembly was supported.
The assembly was a “sandwiched” structure designed to ensure the rigidity of the specimen and to secure the polymer surface from defects that may be caused by the contact of the surface with the grip surface during the fatigue experiment. The assembly consisted of a metallic plate at the bottom and a Teflon plate on the top, both with the same thickness of 10 mm. The specimen was placed and secured on the Teflon surface using adhesive tape at both edges. On the upper grip of the testing frame, a commercially available stylus, with a 7 mm diameter and suitable for capacitive screens, was mounted. The contact tip of the stylus was covered with soft elastomeric material. A photograph of the experimental setup is given in Figure S8.
The experimental procedure involves sinusoidal movement of the upper grip, ensuring that the specimen contacts with the stylus every 1 s. The vertical displacement of the stylus was carefully adjusted so that the applied force on the specimen was within the range that a human fingertip applies on the screen of a cell phone. The resulting force during the whole procedure was varied within the range of 7–17 N, on the same contact point located in the middle of the specimen. The overall duration of the experiment was 23.2 h, which corresponds to 83 639 successive loading cycles. A video presenting a glimpse of the corresponding experimental procedure is given in the Supporting Information. A postfatigue Raman mapping of residual strains within the affected zone by the stylus was carried out, and the results were compared to the strain distribution of the same area prior to fatigue testing.
C. Stress–Strain Curves
The influence of the external applied strain on the specimen was studied by designing a mechanical test, which simulated the quasi static tensile loading conditions that took place in the microtensile tester in terms of strain and time. The experiment was conducted on the same unit where the fatigue tests took place. The overall duration of the test, as well as the final strain level, were determined by the corresponding testing conditions during the Raman spectra acquisition.
The applied quasi-static consisted of a full strain-controlled loading–unloading cycle at a maximum strain of 4%. The displacement rate was calculated to be 0.005 mm/min. Two different types of specimens were used: (a) rectangular stripes of pure PET film (MELINEX ST506) with dimensions 60 mm in length, 10 mm in width, and 0.17 mm in thickness; and (b) rectangular stripes of the display prototype with dimensions 60 mm in length, 10 mm in width, and 0.30 mm in thickness.
All specimens were tabbed at the edges using glass/epoxy material to ensure a uniform stress–strain transfer and also to avoid local damage to the specimen due to excessive pressure at gripping points. The glass/epoxy tabs were attached to the specimen using fast-curing adhesive.
D. Thermomechanical Measurements
The thermomechanical response of the graphene prototype display was investigated by means of Dynamic Mechanical Analysis (DMA) on a Q800, TA Instruments system. Rectangular stripes of 20 mm in length, 10 mm in width, and 0.30 mm in thickness were tested at various frequencies (0.1, 1, 10, 100 Hz) over a temperature range from 25–60 °C in each frequency. The heating rate was 1 °C/min, for all temperature scans. Raman mapping in a window of 10 × 10 μm2 (step of 1 μm) on each specimen was performed before and after the DMA tests to investigate any concomitant morphological alterations of graphene membrane that might have been taken place.
Raman Spectroscopy Measurements
The Raman maps during the tensile test were conducted in an area 15 × 15 μm2 with a step of 3 μm in each direction. Depth profile analysis was performed by recorded Raman spectra at different depths from the display surface with increment of 1 μm. Raman spectra were collected using an excitation laser line at 785 nm (1.58 eV), using a MicroRaman (InVia Reflex, Renishaw, UK) spectrograph. The laser was focused on the sample using a 100× objective, while the laser power was kept below 1.5 mW on the sample to eliminate laser-heating effects on the probed materials. The polarization test was carried out using a Renishaw 1000 system with 514 nm laser excitation.
Differential Scanning Calorimetry
To verify the thermal transitions of PET film (MELINEX ST506) and the display prototype, differential scanning calorimetry (DSC) was applied (Q100, TA Instruments). Both pure PET film and the display prototype specimens were circular in shape with a diameter of 5 mm and weight 4.7 and 8.7 mg, respectively. The pans used were standard aluminum, and nitrogen was used as a dynamic purge gas to flush the samples chamber during the tests. According to DuPont Teijin Films, pure PET film (MELINEX ST506) had a coefficient of thermal expansion of αL = 19 × 10–6 C–1.
Acknowledgments
The research leading to these results has received funding from the European Union Seventh Framework Programme under grant agreement no. 604391 Graphene Flagship, EPSRC (award no. EP/I023879/1), and the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 696656-Graphene Core 1. C.G., K.P., J.P., and G.A. also acknowledge the support of the ERC Advanced Grant “Tailor Graphene” (no: 321124). P.-N.P. also acknowledges the support of the European Commission with funding from the EC Seventh Framework Programme (FP7-2007-2013) under the FP7-NMP.2013.2.1-1 NEWSPEC project Grant agreement no. 604168. N.P. is supported by the European Research Council (ERC StG Ideas 2011 BIHSNAM No. 279985 on Bio-Inspired hierarchical supernanomaterials, ERC PoC 2013-1 REPLICA2 No. 619448 on Largearea replication of biological antiadhesive nanosurfaces, ERC PoC 2013-2 KNOTOUGH No. 632277 on Supertough knotted fibers), by the European Commission under the Graphene Flagship (WP10 “Nanocomposites”, no. 604391), and by the Provincia Autonoma di Trento (“Graphene Nanocomposites”, no. S116/2012-242637 and delib. reg. no. 2266).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.6b05227.
Further experimental data and explanations are given upon (a) depth profile mapping, (b) spectra evolution of 2D peak for various types of loading, (c) the dependence of Pos(2D) and the corresponding FWHM(2D) with the applied strain for another sampling area of the flexible display, (d) description of wrinkled graphene network, (e) stress–strain curves for PET and display film, (f) thermomechanical response of prototype display, (g) experimental setup of the functional fatigue test, (h) differential scanning calorimetry, and (i) optimal design (PDF)
A typical user finger force simulation via mobile stylus (AVI)
The authors declare no competing financial interest.
Supplementary Material
References
- Du J.; Pei S.; Ma L.; Cheng H. M. 25th anniversary article: carbon nanotube- and graphene-based transparent conductive films for optoelectronic devices. Adv. Mater. 2014, 26 (13), 1958–91. 10.1002/adma.201304135. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Bonaccorso F.; Fal’ko V.; Novoselov K. S.; Roche S.; Boggild P.; Borini S.; Koppens F. H. L.; Palermo V.; Pugno N.; Garrido J. A.; Sordan R.; Bianco A.; Ballerini L.; Prato M.; Lidorikis E.; Kivioja J.; Marinelli C.; Ryhanen T.; Morpurgo A.; Coleman J. N.; Nicolosi V.; Colombo L.; Fert A.; Garcia-Hernandez M.; Bachtold A.; Schneider G. F.; Guinea F.; Dekker C.; Barbone M.; Sun Z.; Galiotis C.; Grigorenko A. N.; Konstantatos G.; Kis A.; Katsnelson M.; Vandersypen L.; Loiseau A.; Morandi V.; Neumaier D.; Treossi E.; Pellegrini V.; Polini M.; Tredicucci A.; Williams G. M.; Hee Hong B.; Ahn J.-H.; Min Kim J.; Zirath H.; van Wees B. J.; van der Zant H.; Occhipinti L.; Di Matteo A.; Kinloch I. A.; Seyller T.; Quesnel E.; Feng X.; Teo K.; Rupesinghe N.; Hakonen P.; Neil S. R. T.; Tannock Q.; Lofwander T.; Kinaret J. Science and technology roadmap for graphene, related two-dimensional crystals, and hybrid systems. Nanoscale 2015, 7 (11), 4598–4810. 10.1039/C4NR01600A. [DOI] [PubMed] [Google Scholar]
- Chae S. H.; Lee Y. H. Carbon nanotubes and graphene towards soft electronics. Nano Convergence 2014, 1, 1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arthur D.; Silvy R. P.; Wallis P.; Tan Y.; Rocha J.-D. R.; Resasco D.; Praino R.; Hurley W. Carbon nanomaterial commercialization: Lessons for graphene from carbon nanotubes. MRS Bull. 2012, 37 (12), 1297–1306. 10.1557/mrs.2012.276. [DOI] [Google Scholar]
- Ren W.; Cheng H. M. The global growth of graphene. Nat. Nanotechnol. 2014, 9 (10), 726–30. 10.1038/nnano.2014.229. [DOI] [PubMed] [Google Scholar]
- Bonaccorso F.; Sun Z.; Hasan T.; Ferrari A. C. Graphene photonics and optoelectronics. Nat. Photonics 2010, 4 (9), 611–622. 10.1038/nphoton.2010.186. [DOI] [Google Scholar]
- Ahn J.-H.; Hong B. H. Graphene for displays that bend. Nat. Nanotechnol. 2014, 9 (10), 737–738. 10.1038/nnano.2014.226. [DOI] [PubMed] [Google Scholar]
- Bae S.; Kim H.; Lee Y.; Xu X.; Park J.-S.; Zheng Y.; Balakrishnan J.; Lei T.; Ri Kim H.; Song Y. I.; Kim Y.-J.; Kim K. S.; Ozyilmaz B.; Ahn J.-H.; Hong B. H.; Iijima S. Roll-to-roll production of 30-in. graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5 (8), 574–578. 10.1038/nnano.2010.132. [DOI] [PubMed] [Google Scholar]
- Novoselov K. S.; Fal’ko V. I.; Colombo L.; Gellert P. R.; Schwab M. G.; Kim K. A roadmap for graphene. Nature 2012, 490 (7419), 192–200. 10.1038/nature11458. [DOI] [PubMed] [Google Scholar]
- Lee H.; Kim M.; Kim I.; Lee H. Flexible and Stretchable Optoelectronic Devices using Silver Nanowires and Graphene. Adv. Mater. 2016, 28 (22), 4541–4548. 10.1002/adma.201505559. [DOI] [PubMed] [Google Scholar]
- Geim A. K. Graphene: Status and Prospects. Science 2009, 324 (5934), 1530–1534. 10.1126/science.1158877. [DOI] [PubMed] [Google Scholar]
- Loh K. P.; Bao Q.; Ang P. K.; Yang J. The chemistry of graphene. J. Mater. Chem. 2010, 20 (12), 2277–2289. 10.1039/b920539j. [DOI] [Google Scholar]
- Bonaccorso F.; Lombardo A.; Hasan T.; Sun Z.; Colombo L.; Ferrari A. C. Production and processing of graphene and 2d crystals. Mater. Today 2012, 15 (12), 564–589. 10.1016/S1369-7021(13)70014-2. [DOI] [Google Scholar]
- Yazyev O. V.; Chen Y. P. Polycrystalline graphene and other two-dimensional materials. Nat. Nanotechnol. 2014, 9 (10), 755–767. 10.1038/nnano.2014.166. [DOI] [PubMed] [Google Scholar]
- Park S.; Ruoff R. S. (REVIEW) Chemical methods for the production of graphenes. Nat. Nanotechnol. 2009, 4 (4), 217–224. 10.1038/nnano.2009.58. [DOI] [PubMed] [Google Scholar]
- Lv R.; Terrones M. Towards new graphene materials: Doped graphene sheets and nanoribbons. Mater. Lett. 2012, 78, 209–218. 10.1016/j.matlet.2012.04.033. [DOI] [Google Scholar]
- Bae S.; Kim H.; Lee Y.; Xu X.; Park J. S.; Zheng Y.; Balakrishnan J.; Lei T.; Kim H. R.; Song Y. I.; Kim Y. J.; Kim K. S.; Ozyilmaz B.; Ahn J. H.; Hong B. H.; Iijima S. Roll-to-roll production of 30-in. graphene films for transparent electrodes. Nat. Nanotechnol. 2010, 5 (8), 574–8. 10.1038/nnano.2010.132. [DOI] [PubMed] [Google Scholar]
- Nair R. R.; Blake P.; Grigorenko A. N.; Novoselov K. S.; Booth T. J.; Stauber T.; Peres N. M.; Geim A. K. Fine structure constant defines visual transparency of graphene. Science 2008, 320 (5881), 1308. 10.1126/science.1156965. [DOI] [PubMed] [Google Scholar]
- Kobayashi T.; Bando M.; Kimura N.; Shimizu K.; Kadono K.; Umezu N.; Miyahara K.; Hayazaki S.; Nagai S.; Mizuguchi Y.; Murakami Y.; Hobara D. Production of a 100-m-long high-quality graphene transparent conductive film by roll-to-roll chemical vapor deposition and transfer process. Appl. Phys. Lett. 2013, 102 (2), 023112. 10.1063/1.4776707. [DOI] [Google Scholar]
- Song J.; Kam F. Y.; Png R. Q.; Seah W. L.; Zhuo J. M.; Lim G. K.; Ho P. K.; Chua L. L. A general method for transferring graphene onto soft surfaces. Nat. Nanotechnol. 2013, 8 (5), 356–62. 10.1038/nnano.2013.63. [DOI] [PubMed] [Google Scholar]
- Martins L. G.; Song Y.; Zeng T.; Dresselhaus M. S.; Kong J.; Araujo P. T. Direct transfer of graphene onto flexible substrates. Proc. Natl. Acad. Sci. U. S. A. 2013, 110 (44), 17762–7. 10.1073/pnas.1306508110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y.; Tong S. W.; Xu X. F.; Özyilmaz B.; Loh K. P. Interface Engineering of Layer-by-Layer Stacked Graphene Anodes for High-Performance Organic Solar Cells. Adv. Mater. 2011, 23 (13), 1514–1518. 10.1002/adma.201003673. [DOI] [PubMed] [Google Scholar]
- Sun Z.; Raji A.-R. O.; Zhu Y.; Xiang C.; Yan Z.; Kittrell C.; Samuel E. L. G.; Tour J. M. Large-Area Bernal-Stacked Bi-, Tri-, and Tetralayer Graphene. ACS Nano 2012, 6 (11), 9790–9796. 10.1021/nn303328e. [DOI] [PubMed] [Google Scholar]
- Štokr J.; Schneider B.; Doskočilová D.; Lövy J.; Sedláček P. Conformational structure of poly(ethylene terephthalate). Infra-red, Raman and n.m.r. spectra. Polymer 1982, 23 (5), 714–721. 10.1016/0032-3861(82)90057-X. [DOI] [Google Scholar]
- Ferrari A. C.; Meyer J. C.; Scardaci V.; Casiraghi C.; Lazzeri M.; Mauri F.; Piscanec S.; Jiang D.; Novoselov K. S.; Roth S.; Geim A. K. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 97, 187401. [DOI] [PubMed] [Google Scholar]
- Liu N.; Pan Z.; Fu L.; Zhang C.; Dai B.; Liu Z. The origin of wrinkles on transferred graphene. Nano Res. 2011, 4 (10), 996–1004. 10.1007/s12274-011-0156-3. [DOI] [Google Scholar]
- Obraztsov A. N.; O E. A.; Tyurnina A. V.; Zolotukhin A. A. Chemical vapor deposition of thin graphite films of nanometer thickness. Carbon 2007, 45 (10), 2017–2021. 10.1016/j.carbon.2007.05.028. [DOI] [Google Scholar]
- Mohiuddin T. M. G.; Lombardo A.; Nair R. R.; Bonetti A.; Savini G.; Jalil R.; Bonini N.; Basko D. M.; Galiotis C.; Marzari N.; Novoselov K. S.; Geim A. K.; Ferrari A. C. Uniaxial strain in graphene by Raman spectroscopy: G peak splitting, Gruneisen parameters, and sample orientation. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 205433. [Google Scholar]
- Xu C.; Xue T.; Guo J.; Qin Q.; Wu S.; Song H.; Xie H. An experimental investigation on the mechanical properties of the interface between large-sized graphene and a flexible substrate. J. Appl. Phys. 2015, 117 (16), 164301. 10.1063/1.4918899. [DOI] [Google Scholar]
- Xu C.; Xue T.; Guo J.; Kang Y.; Qiu W.; Song H.; Xie H. An experimental investigation on the tangential interfacial properties of graphene: Size effect. Mater. Lett. 2015, 161, 755–758. 10.1016/j.matlet.2015.09.088. [DOI] [Google Scholar]
- Jiang T.; Huang R.; Zhu Y. Interfacial Sliding and Buckling of Monolayer Graphene on a Stretchable Substrate. Adv. Funct. Mater. 2014, 24 (3), 396–402. 10.1002/adfm.201301999. [DOI] [Google Scholar]
- Anagnostopoulos G.; Androulidakis C.; Koukaras E. N.; Tsoukleri G.; Polyzos I.; Parthenios J.; Papagelis K.; Galiotis C. Stress Transfer Mechanisms at the Submicron Level for Graphene/Polymer Systems. ACS Appl. Mater. Interfaces 2015, 7 (7), 4216–4223. 10.1021/am508482n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong L.; Kinloch I. A.; Young R. J.; Riaz I.; Jalil R.; Novoselov K. S. Interfacial stress transfer in a graphene monolayer nanocomposite. Adv. Mater. 2010, 22 (24), 2694–7. 10.1002/adma.200904264. [DOI] [PubMed] [Google Scholar]
- Gong L.; Young R. J.; Kinloch I. A.; Riaz I.; Jalil R.; Novoselov K. S. Optimizing the Reinforcement of Polymer-Based Nanocomposites by Graphene. ACS Nano 2012, 6 (3), 2086–2095. 10.1021/nn203917d. [DOI] [PubMed] [Google Scholar]
- Young R. J.; Gong L.; Kinloch I. A.; Riaz I.; Jalil R.; Novoselov K. S. Strain mapping in a graphene monolayer nanocomposite. ACS Nano 2011, 5 (4), 3079–84. 10.1021/nn2002079. [DOI] [PubMed] [Google Scholar]
- Young R. J.; Kinloch I. A.; Gong L.; Novoselov K. S. The mechanics of graphene nanocomposites: A review. Compos. Sci. Technol. 2012, 72 (12), 1459–1476. 10.1016/j.compscitech.2012.05.005. [DOI] [Google Scholar]
- Tsoukleri G.; Parthenios J.; Papagelis K.; Jalil R.; Ferrari A. C.; Geim A. K.; Novoselov K. S.; Galiotis C. Subjecting a Graphene Monolayer to Tension and Compression. Small 2009, 5 (21), 2397–2402. 10.1002/smll.200900802. [DOI] [PubMed] [Google Scholar]
- Frank O.; Tsoukleri G.; Parthenios J.; Papagelis K.; Riaz I.; Jalil R.; Novoselov K. S.; Galiotis C. Compression Behavior of Single-Layer Graphenes. ACS Nano 2010, 4 (6), 3131–3138. 10.1021/nn100454w. [DOI] [PubMed] [Google Scholar]
- Li Z.; Kinloch I. A.; Young R. J.; Novoselov K. S.; Anagnostopoulos G.; Parthenios J.; Galiotis C.; Papagelis K.; Lu C.-Y.; Britnell L. Deformation of Wrinkled Graphene. ACS Nano 2015, 9 (4), 3917–3925. 10.1021/nn507202c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raju A. P. A.; Lewis A.; Derby B.; Young R. J.; Kinloch I. A.; Zan R.; Novoselov K. S. Wide-Area Strain Sensors based upon Graphene-Polymer Composite Coatings Probed by Raman Spectroscopy. Adv. Funct. Mater. 2014, 24 (19), 2865–2874. 10.1002/adfm.201302869. [DOI] [Google Scholar]
- Li Z.; Young R. J.; Kinloch I. A.; Wilson N. R.; Marsden A. J.; Raju A. P. A. Quantitative determination of the spatial orientation of graphene by polarized Raman spectroscopy. Carbon 2015, 88, 215–224. 10.1016/j.carbon.2015.02.072. [DOI] [Google Scholar]
- Tan P.; Hu C.; Dong J.; Shen W.; Zhang B. Polarization properties, high-order Raman spectra, and frequency asymmetry between Stokes and anti-Stokes scattering of Raman modes in a graphite whisker. Phys. Rev. B 2001, 64, 214301. [Google Scholar]
- Krenchel H.Fibre Reinforcement: Theoretical and Practical Investigations of the Elasticity and Strength of Fibre-reinforced Materials; Akademisk Forlag, 1964. [Google Scholar]
- Androulidakis C.; Tsoukleri G.; Koutroumanis N.; Gkikas G.; Pappas P.; Parthenios J.; Papagelis K.; Galiotis C. Experimentally derived axial stress–strain relations for two-dimensional materials such as monolayer graphene. Carbon 2015, 81, 322–328. 10.1016/j.carbon.2014.09.064. [DOI] [Google Scholar]
- Wood J. D.; Schmucker S. W.; Lyons A. S.; Pop E.; Lyding J. W. Effects of Polycrystalline Cu Substrate on Graphene Growth by Chemical Vapor Deposition. Nano Lett. 2011, 11 (11), 4547–4554. 10.1021/nl201566c. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Basko D. M. (REVIEW) Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 2013, 8 (4), 235–246. 10.1038/nnano.2013.46. [DOI] [PubMed] [Google Scholar]
- Huang P. Y.; Ruiz-Vargas C. S.; van der Zande A. M.; Whitney W. S.; Levendorf M. P.; Kevek J. W.; Garg S.; Alden J. S.; Hustedt C. J.; Zhu Y.; Park J.; McEuen P. L.; Muller D. A. Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature 2011, 469 (7330), 389–392. 10.1038/nature09718. [DOI] [PubMed] [Google Scholar]
- Frank O.; Vejpravova J.; Holy V.; Kavan L.; Kalbac M. Interaction between graphene and copper substrate: The role of lattice orientation. Carbon 2014, 68, 440–451. 10.1016/j.carbon.2013.11.020. [DOI] [Google Scholar]
- Malard L. M.; Pimenta M. A.; Dresselhaus G.; Dresselhaus M. S. Raman spectroscopy in graphene. Phys. Rep. 2009, 473 (5–6), 51–87. 10.1016/j.physrep.2009.02.003. [DOI] [Google Scholar]
- He R.; Zhao L.; Petrone N.; Kim K. S.; Roth M.; Hone J.; Kim P.; Pasupathy A.; Pinczuk A. Large Physisorption Strain in Chemical Vapor Deposition of Graphene on Copper Substrates. Nano Lett. 2012, 12 (5), 2408–2413. 10.1021/nl300397v. [DOI] [PubMed] [Google Scholar]
- Yu Q.; Jauregui L. A.; Wu W.; Colby R.; Tian J.; Su Z.; Cao H.; Liu Z.; Pandey D.; Wei D.; Chung T. F.; Peng P.; Guisinger N. P.; Stach E. A.; Bao J.; Pei S.-S.; Chen Y. P. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10 (6), 443–449. 10.1038/nmat3010. [DOI] [PubMed] [Google Scholar]
- Frank O.; Mohr M.; Maultzsch J.; Thomsen C.; Riaz I.; Jalil R.; Novoselov K. S.; Tsoukleri G.; Parthenios J.; Papagelis K.; Kavan L.; Galiotis C. Raman 2D-Band Splitting in Graphene: Theory and Experiment. ACS Nano 2011, 5 (3), 2231–2239. 10.1021/nn103493g. [DOI] [PubMed] [Google Scholar]
- Mohr M.; Papagelis K.; Maultzsch J.; Thomsen C. Two-dimensional electronic and vibrational band structure of uniaxially strained graphene from ab initio calculations. Phys. Rev. B 2009, 80, 205410. [Google Scholar]
- Tarantili P. A.; Andreopoulos A. G.; Galiotis C. Real-Time Micro-Raman Measurements on Stressed Polyethylene Fibers. 1. Strain Rate Effects and Molecular Stress Redistribution. Macromolecules 1998, 31 (20), 6964–6976. 10.1021/ma961498l. [DOI] [Google Scholar]
- Young R. J.; Eichhorn S. J. Deformation mechanisms in polymer fibres and nanocomposites. Polymer 2007, 48 (1), 2–18. 10.1016/j.polymer.2006.11.016. [DOI] [Google Scholar]
- Thompson A. B.; Woods D. W. The transitions of polyethylene terephthalate. Trans. Faraday Soc. 1956, 52, 1383–1397. 10.1039/tf9565201383. [DOI] [Google Scholar]
- Carpinteri A.; Pugno N.. Extension of the de Saint Venant and Kirchhoff Theories to Functionally Graded Materials; IOS Press: 2009; pp 53–62. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.