Conformational Dynamics on the Extracellular Side of LeuT Controlled by Na⁺ and K⁺ Ions and the Protonation State of Glu²⁹⁰

Abstract

Ions play key mechanistic roles in the gating dynamics of neurotransmitter:sodium symporters (NSSs). In recent microsecond scale molecular dynamics simulations of a complete model of the dopamine transporter, a NSS protein, we observed a partitioning of K⁺ ions from the intracellular side toward the unoccupied Na2 site of dopamine transporter following the release of the Na2-bound Na⁺. Here we evaluate with computational simulations and experimental measurements of ion affinities under corresponding conditions, the consequences of K⁺ binding in the Na2 site of LeuT, a bacterial homolog of NSS, when both Na⁺ ions and substrate have left, and the transporter prepares for a new cycle. We compare the results with the consequences of binding Na⁺ in the same apo system. Analysis of >50-μs atomistic molecular dynamics and enhanced sampling trajectories of constructs with Glu²⁹⁰, either charged or neutral, point to the Glu²⁹⁰ protonation state as a main determinant in the structural reconfiguration of the extracellular vestibule of LeuT in which a “water gate” opens through coordinated motions of residues Leu²⁵, Tyr¹⁰⁸, and Phe²⁵³. The resulting water channel enables the binding/dissociation of the Na⁺ and K⁺ ions that are prevalent, respectively, in the extracellular and intracellular environments.

Introduction

Transmembrane (TM)² proteins belonging the neurotransmitter:sodium symporter (NSS) family are key regulators of neuronal signaling, because they terminate neurotransmission by uptake of their respective substrates from the synapse (1–3). The process of substrate transport into the presynaptic neuron against its concentration gradient is powered by co-transport of Na⁺ ions, and in most eukaryotic NSS is Cl⁻-dependent (4). Members of the NSS family, which among others include transporters for dopamine (DAT), serotonin (SERT), and norephinephrine, have been implicated in a number of psychiatric and neurological disorders, making them primary targets for antidepressant medications, psychostimulants (5–7), and the subject of intensive studies.

Recently determined x-ray structures of NSS DAT from Drosophila in complex with various ligands (8–10) revealed the same TM domain architecture originally identified in LeuT (leucine transporter), a bacterial NSS ortholog (11–20). In the TM domain composed of a 12-helix bundle, both LeuT and DAT from Drosophila harbor a centrally located primary substrate binding site, S1, and two Na⁺ ions bound at sites termed Na1 and Na2 (supplemental Fig. S1). Unlike the mammalian NSSs, transport in LeuT and other bacterial homologs is independent of Cl⁻ (21) and was shown to be stimulated by a proton-antiport mechanism (22). Indeed, mutagenesis studies have revealed that the dependence on Cl⁻ can be mimicked in LeuT by regulating the protonation state of Glu²⁹⁰ (4, 21, 23), and as predicted, the DAT structures from Drosophila were found to contain a Cl⁻ ion bound in the corresponding site.

The general role of ions in controlling the gating dynamics in the LeuT-fold Na⁺ symporters has been addressed in a large number of mechanistic studies, both experimental (24–30) and computational (20, 27–48). In particular, the role of Na⁺ in the functionally important allosteric coupling between the intracellular (IC) and extracellular (EC) vestibules in LeuT (49, 50) had been investigated with single molecule FRET (27) and ensemble measurements using double electron-electron resonance (30). Free energy calculations and measurements of substrate and ion binding in LeuT (32) yielded a mechanistic model for the conformational transition from the Na⁺-stabilized substrate-occluded state to the inward facing state that precedes substrate translocation; the transition is triggered by Na⁺ release from the Na2 site. Extensive MD simulations of DAT (51), SERT (46), and LeuT (37, 38, 47, 48) have demonstrated how water penetration from the intracellular side releases the Na2-bound Na⁺ and connects the inward opening of the transporter to destabilization of the substrate in the S1 site. For DAT, electrophysiology and computations revealed the role of the Na2 site occupancy in controlling the permeation of cations and showed that Li⁺ binding in the Na2 site is regulated by Cl⁻ (45).

Assessing the conformational changes associated with substrate and ion binding, MD simulations (31) initiated from the outward occluded state of LeuT with Na⁺ in the Na1 and Na2 sites but without substrate in the S1 site revealed a gradual widening of the EC vestibule as the transporter converged to a conformation similar to that seen crystallographically for the substrate-free LeuT (16). The outward opening was further enhanced in MD simulations carried out without Na⁺ in Na1 and found to be modulated by the protonation state of Glu²⁹⁰ (31).

In microsecond scale, unbiased MD simulations of a full-length model of human DAT (hDAT) described recently (51), we found great similarity between the conformational rearrangements of DAT and those described previously for LeuT (based on results for both transporters obtained from simulations as well as experiments that were shown to be in excellent agreement (30)). However, in the simulations of the DAT system, we also observed for the first time a strong tendency for K⁺ ions to partition from the solution, through the IC vestibule, into the Na2 site of the transporter following the release of the Na2-bound Na⁺.³ Given the similarity in conformational transitions of DAT and LeuT, we reasoned that K⁺ would partition similarly into inward facing LeuT once the water penetration on the intracellular side connects the protein to the high physiological concentrations of K⁺ ions in the cytoplasm. Here we investigate the consequences of K⁺ presence in the Na2 site on the structure and conformational dynamics of the prototypical NSS transporter LeuT, because this may represent a general feature of this family of transporters when they have transitioned toward the inward facing conformation. The intriguing possibility that K⁺ binding in an apo structure that should be ready for a return to the start of a transport cycle could play a functional role prompted the detailed comparative investigation of the effects of K⁺ and Na⁺ in the Na2 site of the LeuT transporter, for which a role of ions in controlling the gating dynamics has been elucidated in a number of experimental and computational studies. In particular, two questions were suggested by the recent findings for DAT (51) regarding the possible involvement of K⁺ in the return step of transport cycle of LeuT-fold NSS: 1) What are the consequences of K⁺ in Na2 when both the Na⁺ ions and substrate have left the transporter? and 2) How does this compare with the state of the system when a Na⁺ ion binds in that same site under the same conditions? We present here the results of a computational investigation of these conditions with microsecond scale unbiased atomistic MD simulations and enhanced sampling with ensemble MD and relate the findings regarding the various constructs to experimentally measured affinities under corresponding conditions.

We show here that simulations of apo LeuT with/without K⁺ in Na2 indicate a strong dependence of the outcomes on the protonation state of Glu²⁹⁰ (see supplemental Fig. S1 for structural details). The effects of changes in the charge carried by the Glu²⁹⁰ residue in LeuT have been shown (4, 21) to correspond to those produced by the presence or absence of Cl⁻ in the eukaryotic NSS homologs such as DAT and SERT. We find that when Glu²⁹⁰ is in its charged (deprotonated) form, K⁺ appears relatively stable in the Na⁺ binding region. In contrast, when Glu²⁹⁰ is protonated (neutral) K⁺ is destabilized and released from the Na2 site to the aqueous the solution on the extracellular side. This release of K⁺ is enabled by the formation of a continuous water channel connecting the EC vestibule to the functional sites (S1, Na1, and Na2) and leads to a widening of the EC vestibule of the transporter. Importantly, our analysis shows that the penetration of water into the channel formed when Glu²⁹⁰ is protonated is accompanied by a rearrangement of residues associated with the substrate-binding S1 site, specifically Leu²⁵ and Tyr¹⁰⁸ and eventually Phe²⁵³; together these residues are proposed to constitute a “water gate” (see supplemental Fig. S1 for the relative positions of these key residues).

In parallel MD simulations addressing the second question, regarding the comparison with Na⁺-bound states, we find that the same repositioning of Leu²⁵ and Tyr¹⁰⁸ is required for the partitioning of Na⁺ ions from the extracellular solution into the ion binding sites of LeuT and that this occurs only when Glu²⁹⁰ is negatively charged (deprotonated). These mechanistic findings point to the protonation state of Glu²⁹⁰ as a determinant factor in the structural reconfiguration of the extracellular vestibule of LeuT. This reconfiguration results in the opening of the water gate to enable the transporter to bind the Na⁺ and K⁺ ions under the physiological conditions prevalent, respectively, in the extracellular and the intracellular environments.

Results

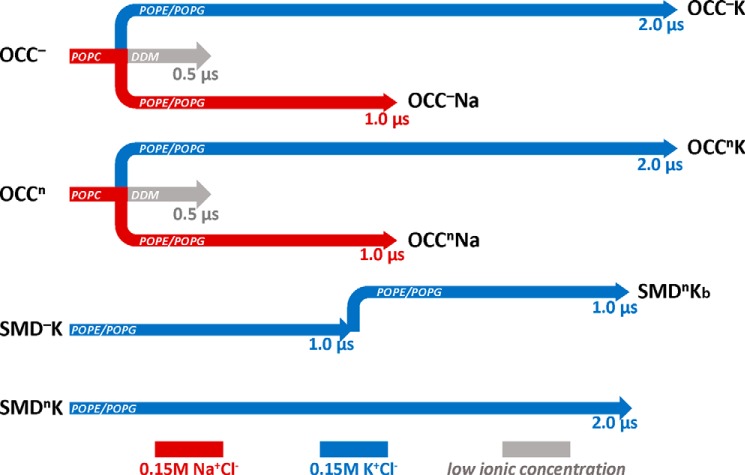
In microsecond scale atomistic MD simulations (51) of the NSS hDAT, we found that after the Na2-bound Na⁺ had been released inward and the hDAT had transitioned toward an inward facing conformation, one K⁺ ion at a time could partition into the Na2 site of the transporter through the cytoplasmic vestibule (51). The putative involvement of K⁺ binding in an apo structure before the return to the start of the transport cycle of DAT could not be fully understood from these computations, however, because the system had not yet reached the substrate release state, and both the S1 and the Na1 sites were still occupied. Therefore we carried out the analysis of the effects of K⁺ in the Na2 site for LeuT, the prototypical NSS in which the general role of ions in controlling the gating dynamics has been elucidated in a number of experimental and computational studies. To this end, we constructed, as described under “Experimental Procedures,” a number of apo models of LeuT into which a K⁺ ion was docked in the Na2 site for subsequent evaluation of conformational dynamics. The series of MD simulations performed in this study for the various constructs described under “Experimental Procedures” is summarized in Fig. 1.

FIGURE 1.

Schematic representation of the atomistic MD simulations carried out in this work. OCC denotes runs performed with LeuT models based on the x-ray structure of the occluded state (Protein Data Bank code 2A65 (12)). SMD indicates trajectories with LeuT model developed as described under “Experimental Procedures” from the earlier SMD simulation (32). Superscripts n and − indicate respectively the “neutral” (protonated) or negatively charged state of the Glu²⁹⁰ residue in the LeuT structures. Designations K and Na indicate whether Na2 site in the initial model was occupied by K⁺ or Na⁺, respectively. Simulations in detergent are shown in gray and labeled. Trajectories accumulated in the different lipid membranes are indicated in the respective arrows. Red and blue denote simulations in Na⁺Cl⁻ and K⁺Cl⁻ ionic solution, respectively. SMDnKb is a continuation of SMD⁻K trajectory after Glu²⁹⁰ residue was protonated in the last frame of the SMD⁻K run.

Conformational Switch of Leu²⁵ and Repositioning of Tyr¹⁰⁸ in the apo LeuT

In the first unbiased MD simulations of the apo LeuT models shown in Fig. 1, the Glu²⁹⁰ residue is either charged (OCC⁻ in Fig. 1) or protonated (OCCⁿ) (see legend of Fig. 1 for definitions, and see “Experimental Procedures” for the description of the constructs). The 200 ns of the simulations were carried out in the absence of the K⁺, in POPC lipid membranes (see Fig. 1 and “Experimental Procedures”). Monitoring the local dynamics of the residues that comprise the substrate and ion binding sites, we found that only one residue that contacts the substrate leucine in the occluded state LeuT structure (12), namely Leu²⁵, had dramatically changed its orientation in these simulations. Thus, during the OCC⁻ trajectory, the conformation of the Leu²⁵ side chain changes from one initially pointing toward TM3 (in close proximity to residue Ile¹¹¹; Fig. 2A) and away from the S1 site (termed “OUT” orientation), to one in which its side chain is inserted into the S1 site into a position that invades the substrate binding S1 site (termed “IN” orientation). This conformational switch was enabled by a parallel repositioning of residue Tyr¹⁰⁸ (in the S1 site) toward the TM1 segment (see Tyr¹⁰⁸–Gly²⁴ distance measures in Fig. 2A). A similar rearrangement of Leu²⁵ and Tyr¹⁰⁸ was observed as well in the OCCⁿ simulation (data not shown), and the IN positioning of Leu²⁵ was maintained during the subsequent ∼300 ns of MD simulations of both OCC⁻ and OCCⁿ models in DDM micelles (supplemental Fig. S2).

FIGURE 2.

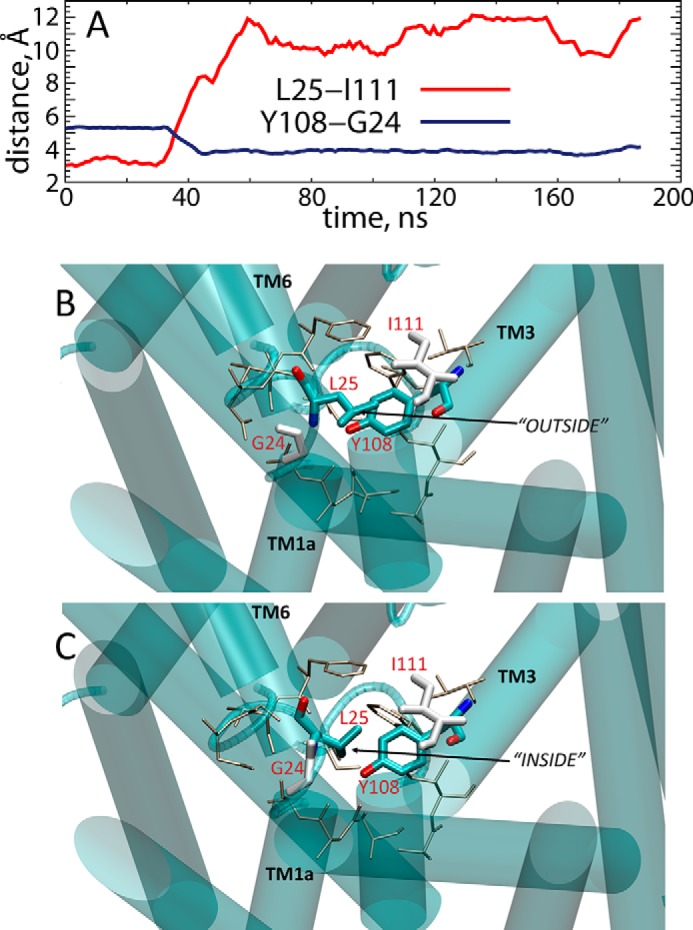
A, time evolution of distances between Leu²⁵–Ile¹¹¹ (red) and Tyr¹⁰⁸–Gly²⁴ (blue) pairs of residues in the OCC simulation. B and C, snapshots in the initial and final frames of the OCC trajectory in POPC lipids (see also Fig. 1) showing conformational switch in Leu²⁵ residue. Leu²⁵ and Tyr¹⁰⁸ residues are shown in licorice rendering; Gly²⁴ and Ile¹¹¹ are depicted in white. The residues lining the primary substrate binding site in LeuT are rendered as sticks (tan). Relevant TM segments are show in cartoon and labeled.

To examine the effect of the conformational switch of Leu²⁵ between IN and OUT orientations and the concomitant reorientation of Tyr¹⁰⁸, we positioned a K⁺ ion in the Na2 site of the OCC⁻ and OCCⁿ structures from the last frames of the respective trajectories in POPC bilayers and initiated a new set of microsecond scale MD simulations of the K⁺-bound LeuT models in 74:26 POPE/POPG lipid membranes (identified in Fig. 1 as runs OCC⁻K and OCCⁿK). For comparison, we also simulated in the same bilayers the alternative LeuT models derived as described under “Experimental Procedures” from previous SMD/MD trajectories (32) with K⁺ docked into the Na2 site (SMD⁻K and SMDⁿK runs in Fig. 1). Because the starting structures of these models were obtained from previous simulations, the pathways from the S1 site to the IC side were already hydrated, and the Leu²⁵ and Tyr¹⁰⁸ residues were positioned similarly to those in the initial OCC⁻ and OCCⁿ models (Fig. 2B), i.e. Leu²⁵ was in the OUT orientation and the side chain of Tyr¹⁰⁸ pointed away from the TM1 segment and toward the S1 site. The comparison of all these parallel computations enabled an evaluation of conformational transitions related to the presence of K⁺, with statistically independent replicas from various initial models with K⁺ in Na2.

Destabilization and Release of the K⁺ Ion from the Na2 Site of LeuT

Analysis of the OCCⁿK and SMDⁿK trajectories shows that in both trajectories the K⁺ ion is gradually destabilized in the Na2 site and released “outward” into the extracellular environment. This is illustrated in Fig. 3 for the OCCⁿK simulation (gray trace), showing that after ∼160 ns, K⁺ moved from Na2 to an intermediate site partially overlapping with the Na1 site and remained stable there for >1 μs (coordinated by the carbonyl group of Phe²⁵³; Fig. 3), before exiting LeuT to the EC milieu. In the SMDⁿK run, the K⁺ ion moved from Na2 to Na1 very early in the trajectory (within ∼20 ns, red trace in Fig. 3) and remained in the Na1 site for ∼1.2 μs before diffusing out to the solution.

FIGURE 3.

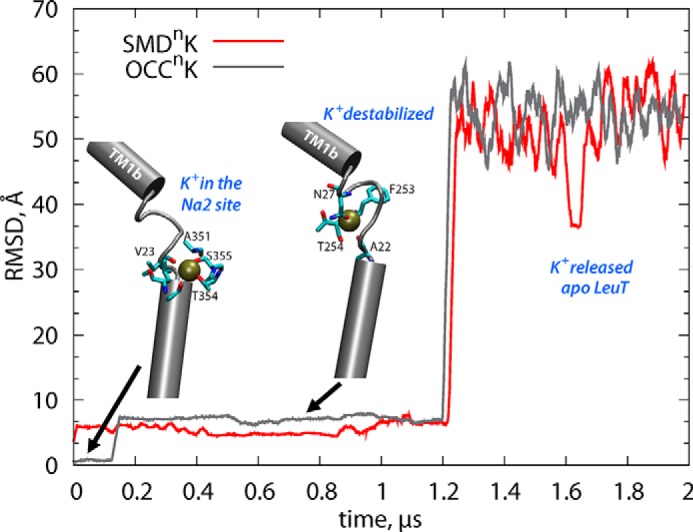
Time evolution of the root mean square deviation of the K⁺ ion in OCCⁿK (gray) and SMDⁿK (red) simulations. The insets are taken from two different time points along the OCCⁿK trajectory (after 0.1 and 0.8 μs) and illustrate the K⁺ ion bound in the Na2 and in the intermediate site the partially overlaps with the Na1 site. The root mean square deviation was calculated with respect to the K⁺ positioning in the initial frame of the respective simulations after the trajectories were aligned using the backbone atoms of the TM helical segments.

In contrast, when Glu²⁹⁰ is negatively charged, the K⁺ ion initially placed in the Na2 site remained protein-bound on the simulation time scales in both the OCC⁻K and SMD⁻K runs. Notably, however, the K⁺ ion became unstable in the Na2 site within the first ∼180 ns interval of the OCC⁻K trajectory (supplemental Fig. S3), but for the remaining part of the simulation it remained confined to the volume between the Na1 and Na2 sites (supplemental Fig. S3, inset). The K⁺ ion also remained stably bound in the Na2 site throughout the entire trajectory of the SMD⁻K run (supplemental Fig. S4). To seek a mechanistic understanding of the observed behaviors of the K⁺ ions in the different conditions, we examined the interactions and dynamics of the residues coordinating the ion.

Structural Rearrangements Leading to the Release of K⁺

Destabilization of the K⁺ Ion Relates to the Conformational Dynamics of Residues Leu²⁵ and Tyr¹⁰⁸

As shown in Fig. 4, the side chains of residues Leu²⁵ and Tyr¹⁰⁸ are reoriented during the initial stage of the OCCⁿK trajectory, so that Leu²⁵ transitions from the IN to the OUT orientation (Leu²⁵–Ile¹¹¹ distance decreases in Fig. 4A, compare with Fig. 2) and concomitantly Tyr¹⁰⁸ moves away from TM1 (Tyr¹⁰⁸–Gly²⁴ distance increases in Fig. 4B). Comparison of the time traces in Fig. 4 (A and B) with the one describing the dynamics of the K⁺ ion in the OCCⁿK simulation (Fig. 3) shows that the destabilization of the K⁺ ion takes place after the conformational switch in Leu²⁵ and Tyr¹⁰⁸ residues is complete.

FIGURE 4.

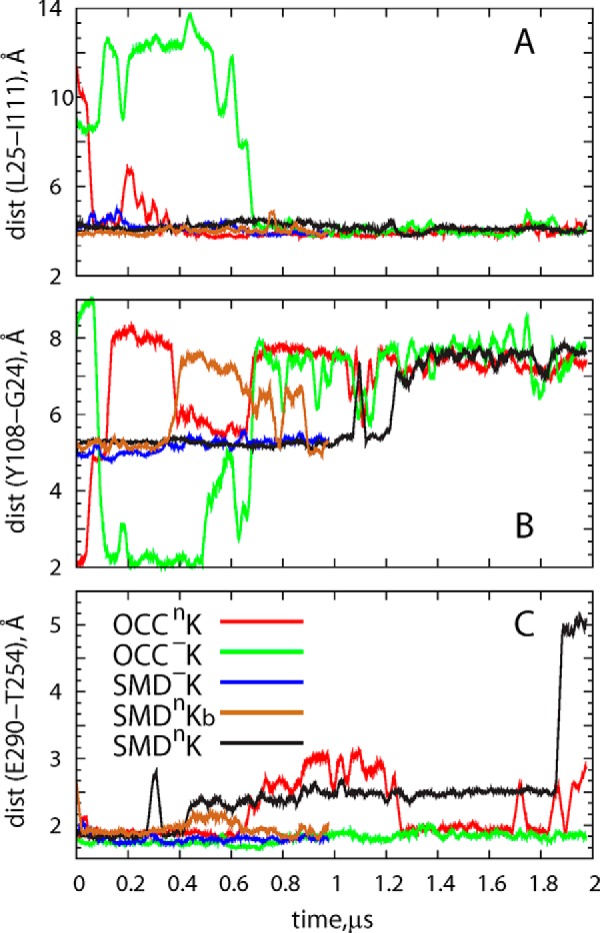
Time evolution of the distance between residue pairs in different simulations. A, Leu²⁵–Ile¹¹¹. B, Tyr¹⁰⁸–Gly²⁴. C, Glu²⁹⁰–Thr²⁵⁴.

The relationship between the dynamics of K⁺ in the Na2 site and the rearrangement of the Leu²⁵ and Tyr¹⁰⁸ side chains is further supported by the developments in the SMDⁿK trajectory (Fig. 4, A and B, black traces) in which Leu²⁵ starts and remains in the OUT orientation (with Tyr¹⁰⁸ being away from TM1) throughout the simulation, and the K⁺ ion leaves the Na2 site at the onset of the trajectory (Fig. 3). However, whereas these data suggest that destabilization of the K⁺ ion in the Na2 site is favorable when the orientation of Leu²⁵ is OUT, the results also suggest that the rearrangement of Leu²⁵ and Tyr¹⁰⁸ residues alone is not sufficient for the full release of K⁺. Indeed, as described above, K⁺ remains LeuT-bound in the OCC⁻K and SMD⁻K runs in which Leu²⁵ either is in the OUT orientation throughout trajectory (as in SMD⁻K; Fig. 4, A and B, blue traces) or transitions to this state during the simulation (as in OCC⁻K; green traces in Fig. 4, A and B). The additional condition for the release of the K⁺ relates to the protonation state of Glu²⁹⁰.

Full Release of K⁺ Requires Water Penetration to the Ion Binding Sites and a Neutral Glu²⁹⁰

Fig. 4C shows the time evolution of the minimal distance between Glu²⁹⁰ and Thr²⁵⁴ (a functional residue in the Na1 site that is seen in different x-ray structures of LeuT to interact closely with Glu²⁹⁰). This interaction prevails in simulations with a negatively charged Glu²⁹⁰ (OCC⁻K and SMD⁻K in Fig. 4C). However, in the runs with protonated (neutral) Glu²⁹⁰, the bond between Glu²⁹⁰ and Thr²⁵⁴ is weakened. In Fig. 4C the loosening of Glu²⁹⁰-Thr²⁵⁴ association is shown for the SMDⁿKb trajectory that was started from the last frame (after 1 μs) of the SMD⁻K simulation, with a neutralized Glu²⁹⁰ (compare brown and blue traces during the 0.4–0.6-μs time interval).

Because the Glu²⁹⁰/Thr²⁵⁴ pair is adjacent to Phe²⁵³, the functionally important residue that acts as a gate between substrate and ion binding sites and the EC vestibule (12, 16, 32), we reasoned that the extent of Glu²⁹⁰-Thr²⁵⁴ association would affect the dynamics of Phe²⁵³. We quantified the sampling of conformational space by the Phe²⁵³ side chain from the evolution of its χ₁ dihedral angle in various trajectories, and the results in Fig. 5 and supplemental Fig. S5 show a strong coupling between the Glu²⁹⁰-Thr²⁵⁴ interactions and the conformational space sampled by the Phe²⁵³ ring. Thus, in the OCC⁻K and SMD⁻K runs (in which Glu²⁹⁰ interacts extensively with Thr²⁵⁴; Fig. 4C), Phe²⁵³ is mostly in a horizontal orientation (χ₁ near 180°). In this position Phe²⁵³ covers the S1 site from the top and prevents water penetration from the EC milieu to the ion/substrate binding sites (Fig. 6A). However, in trajectories in which Glu²⁹⁰-Thr²⁵⁴ interactions are weakened (OCCⁿK, SMDⁿK, and SMDⁿKb in Fig. 4C), Phe²⁵³ samples an alternative orientation (χ₁ distributions in Fig. 5 centered ∼60–70°) in which its ring flips toward the EC vestibule (Fig. 6B). This rearrangement of Phe²⁵³ to this “open” position, together with the side chain rearrangement of Tyr¹⁰⁸ that repositions the -OH group away from TM1 (Figs. 2 and 4B), opens a water gate, allowing water influx and the formation of a continuous water channel that connects the EC vestibule to the functional binding sites (Fig. 6, compare A and B). Indeed, as shown in Fig. 7A, the Tyr¹⁰⁸ residue is the least solvated in the SMD⁻K simulation in which K⁺ is stably bound in Na2, whereas in all the other trajectories Tyr¹⁰⁸ is surrounded by larger numbers of water molecules. Furthermore, the analysis of the overall water count in the EC vestibule of LeuT (performed as described previously (31)), which measures the volume of the EC vestibule (Fig. 7B), yielded a relatively low count in the SMD⁻K simulation compared with the other runs and is similar to that reported in MD simulations of LeuT with both Na1 and Na2 occupied by Na⁺ ions (31). However, release of K⁺ from Na2 leads to an increase in solvation of the EC side. Taken together, these results suggest that destabilization of the K⁺ ion in the Na2 site requires the formation of a water channel linking the EC vestibule with the functional sites in LeuT, which requires the opening of a water gate by specific rearrangements in Phe²⁵³, Leu²⁵, and Tyr¹⁰⁸ when Glu²⁹⁰ is protonated.

FIGURE 5.

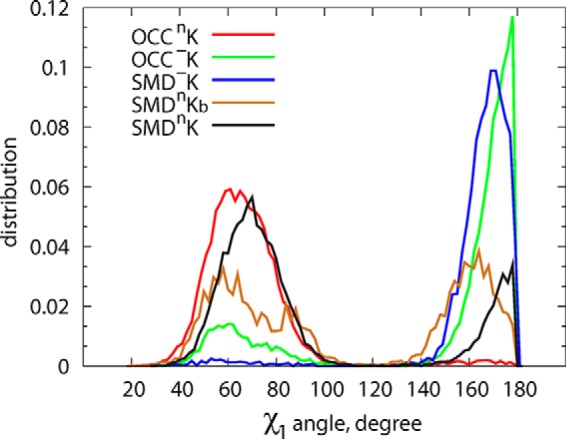
Probability distribution of χ₁ dihedral angle of residue Phe²⁵³ in different trajectories. Open conformation of Phe²⁵³ (χ₁ values close to 180°) is predominantly sampled under conditions of charged Glu²⁹⁰ (blue and green curves).

FIGURE 6.

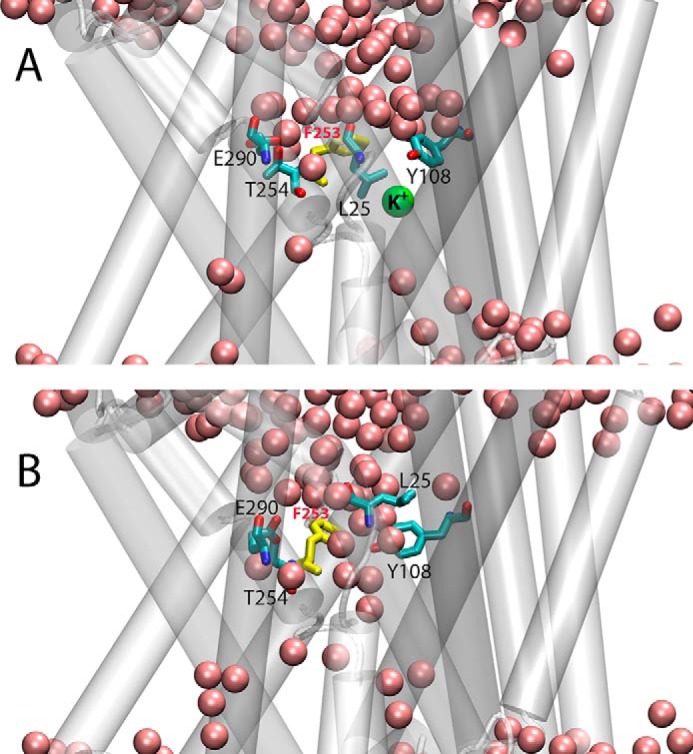
Snapshots from initial (A) and final (B) frames of OCCⁿK trajectory illustrating different orientation of Phe²⁵³ residue (in yellow) and formation of continuous water channel (pink spheres) connecting EC vestibule to the functional sites of LeuT. Glu²⁹⁰, Thr²⁵⁴, Leu²⁵, and Tyr¹⁰⁸ residues are shown in licorice rendering, and K⁺ ion is depicted as a green sphere.

FIGURE 7.

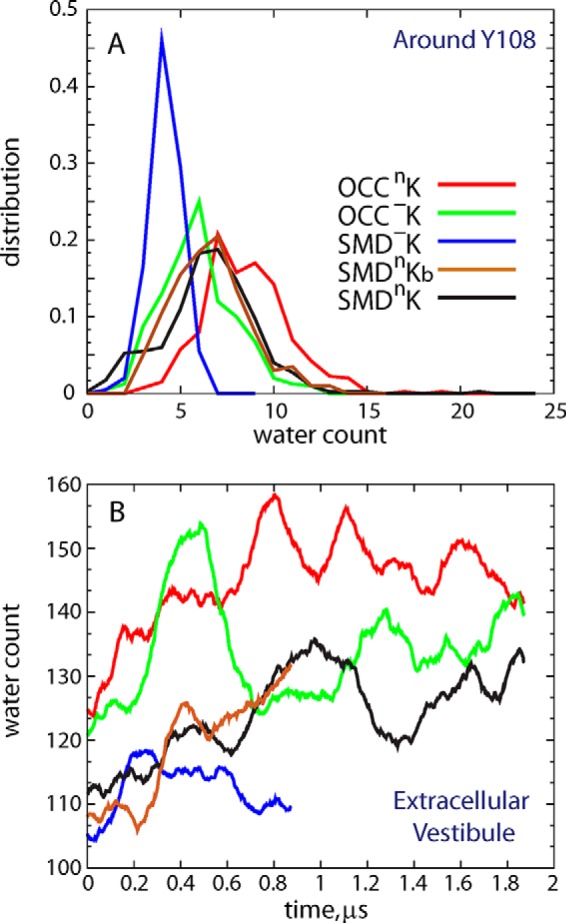
A, distribution of the water molecule count around residue Tyr¹⁰⁸ (i.e. waters within 3 Å of any atom of Tyr¹⁰⁸) in different simulations. B, time evolution of the overall water count in the EC vestibule of LeuT in various simulations.

The K⁺ Ion in the Na2 Site Stabilizes an Outward Occluded Conformation of LeuT

Because all the simulations in which destabilization of K⁺ in the Na2 site was observed also showed an increase in the volume and hydration of the EC vestibule, we analyzed the trajectories for the details of global motions on the extracellular side of LeuT. To describe conformational transitions related to K⁺ ion dynamics in our simulations, we took advantage of EPR studies of conformational dynamics in LeuT (30) and the structurally related Mhp1 (52) transporter that had measured distance changes between specific IC and EC protein segments in response to ion and/or ligand binding. We monitored in the MD trajectories the same pairwise distances in the IC and EC regions that were used in the experiments to monitor the state to state isomerizations in these transporters.

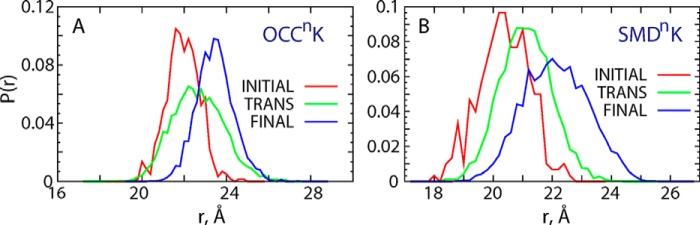
In all the trajectories examined here, the distance changes observed on the IC side of LeuT remained within local fluctuation profiles, as expected from the conditions of the simulations. In contrast, on the EC side the analysis showed larger conformational changes and in particular of extracellular loop 4 (ECL4), which assumed a different position with respect to other EC segments. To establish a connection between the dynamic rearrangements on the EC side of LeuT and the dynamics of K⁺ release, we constructed ECL4-ECL5 distance distributions in the OCCⁿK and SMDⁿK runs, separately for three different parts of these trajectories in which the situation of K⁺ had evolved: 1) the time interval when K⁺ was in the Na2 site (“INITIAL”); 2) when the K⁺ became destabilized and moved toward the Na1 site (“TRANS”); and 3) when K⁺ diffused out of LeuT (“FINAL”). Shown in Fig. 8 (A and B), these distance distributions clearly illustrate a gradual opening of the EC vestibule as the K⁺ ion moves along the EC pathway and diffuses out of the transporter. Taken together, the data presented in Figs. 7 and 8 suggest that the release of K⁺ ion from the Na2 site results in a widening of the EC vestibule.

FIGURE 8.

Distribution of the ECL4-ECL5 distances in OCCⁿK (A) and SMDⁿK (B) simulations. The calculations were performed on three separate parts of the respective 2-μs-long trajectories: 1) the time interval when K⁺ is stably bound in the Na2 site (INITIAL, red curve); 2) the time interval when K⁺ becomes destabilized (TRANS, green curve); and 3) after K⁺ leaves the transporter (FINAL, blue curve).

The Consequences of Extracellular Na⁺ Binding in the Na2 Site of apo LeuT

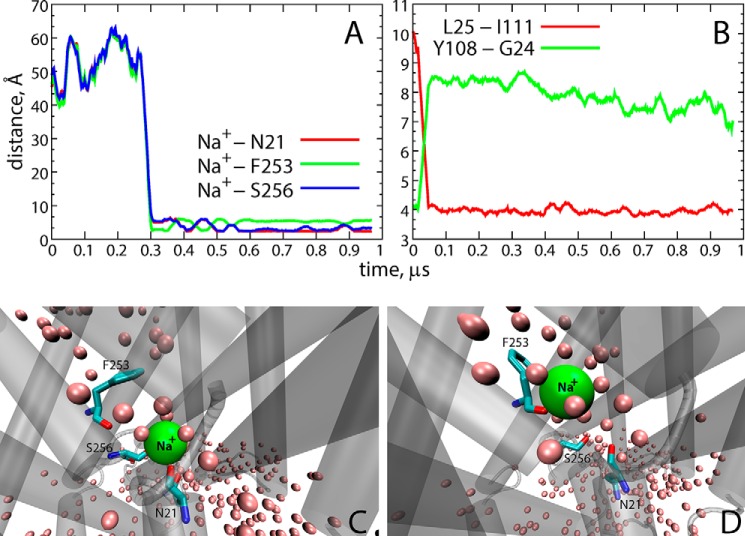
Microsecond-long MD simulations of the apo OCC LeuT models (with charged or neutral Glu²⁹⁰ and initially empty Na1 and Na2 sites equilibrated in POPC membranes; see Fig. 1) were carried out in the presence of 150 mm Na⁺Cl⁻ solution (runs OCC⁻Na and OCCⁿNa in Fig. 1). As shown in Fig. 9A, we observed the partitioning of a Na⁺ ion into LeuT from the EC milieu in the OCC⁻Na trajectory (at ∼0.3 μs). The penetrating Na⁺ was seen to fluctuate between the Na1 site (Fig. 9A, green trace), where it was coordinated by the backbone carbonyl of Phe²⁵³ residue (similar to the coordination of the K⁺ ion in the OCCⁿK simulation; Fig. 3), and a site identified from recent microsecond scale MD simulations of LeuT (33) as an intermediate, Na1″ binding site, where the Na⁺ interacts with the backbone carbonyl group of Asn²¹ and the side chain of Ser²⁵⁶ (blue and red traces in Fig. 9A; see also Fig. 9, C and D).

FIGURE 9.

Environment and coordination of the Na⁺ ion. A, time evolution of the distance between the Na⁺-coordinating residues Asn²¹ (red), Phe²⁵³ (green), and Ser²⁵⁶ (blue), and the Na⁺ ion, in the OCC-Na simulation. B, Leu²⁵-Ile¹¹¹ (red) and Tyr¹⁰⁸–Gly²⁴ (green) distances as a function of time in the OCC-Na trajectory. C and D, snapshots from the OCC-Na simulation showing Na⁺ bound in the Na2 site (C) and in the Na1 site (D). Residues coordinating the Na⁺ ion (Asn²¹, Phe²⁵³, and Ser²⁵⁶) are shown in licorice rendering. Water oxygen atoms within 3 Å of the protein are depicted as pink spheres, and LeuT is shown in cartoon rendering.

It was interesting to find that the binding of Na⁺ entering from the extracellular environment was enabled by the same IN/OUT structural rearrangement of Leu²⁵ that resulted in the release of K⁺ from Na2 (see above). Indeed, as shown in Fig. 9B, we observe that the conformational switch of Leu²⁵ away from the S1 site and the concomitant repositioning of Tyr¹⁰⁸ (Fig. 9B) into the S1 site enable the solvation of the ion binding sites (Fig. 9, C and D) and pari passu freeing the S1 site for substrate binding. The conformational changes and water penetration observed in this Na⁺ binding process occurs under conditions that are the exact reverse of those that favored K⁺ releases, for example, and under conditions created by the negatively charged Glu²⁹⁰. Indeed, in the OCCⁿNa trajectory, we did not observe partitioning of Na⁺ into LeuT, because the side chains of Leu²⁵ and Tyr¹⁰⁸ did not undergo the IN/OUT rearrangement (supplemental Fig. S6). Taken together, these results suggest that binding of a Na⁺ ion from the EC milieu to the Na2 site of LeuT is favorable when Glu²⁹⁰ is negatively charged and involves the same repositioning of Leu²⁵ and Tyr¹⁰⁸ and water penetration observed during the K⁺ release.

Enhanced Sampling of the Conformational Space Recapitulates Structural and Dynamic Rearrangements Observed in Trajectories Leading to K⁺ Release or Na⁺ Binding

We carried out enhanced sampling of the conformational space through ensemble MD simulations of the OCC⁻, OCCⁿ, OCC⁻K, and OCCⁿK LeuT models, as described under “Experimental Procedures.” For each LeuT construct, the enhanced sampling of conformational space involved 10 statistically independent replicates of unbiased MD trajectories (∼950 ns/simulation resulting in combined MD time of 9.5 μs/construct). Release of K⁺ from the Na2 site to the EC solution occurred in 6 of 10 trajectories of the OCCⁿK model and in only 3 of 10 of the OCC⁻K (supplemental Fig. S7). Conversely, partitioning of a Na⁺ ion from the EC side to the ion binding sites in LeuT (see below) was detected in 6 of 10 simulations carried out with the OCC⁻ model, but 0 of 10 Na⁺ binding events were observed in the runs started from the OCCⁿ structure (supplemental Fig. S8).

Furthermore, in agreement with the results presented in Fig. 5, we found that Phe²⁵³ sampled the “closed” conformations (i.e. χ₁ dihedral angle >150°; supplemental Fig. S9A) only when Glu²⁹⁰ was charged. In addition, consistent with the data presented in Figs. 7 and 8, the release of K⁺ from Na2 resulted in a widening of the EC vestibule. This is seen in supplemental Fig. S9B where the extent of the hydration of the EC milieu increases as K⁺ diffuses out from LeuT. Taken together, these results recapitulate the key role of Phe²⁵³ and of the protonation state of Glu²⁹⁰, in connecting through the formation of the water channel the EC vestibule with the functional sites and regulating the movements of the ions.

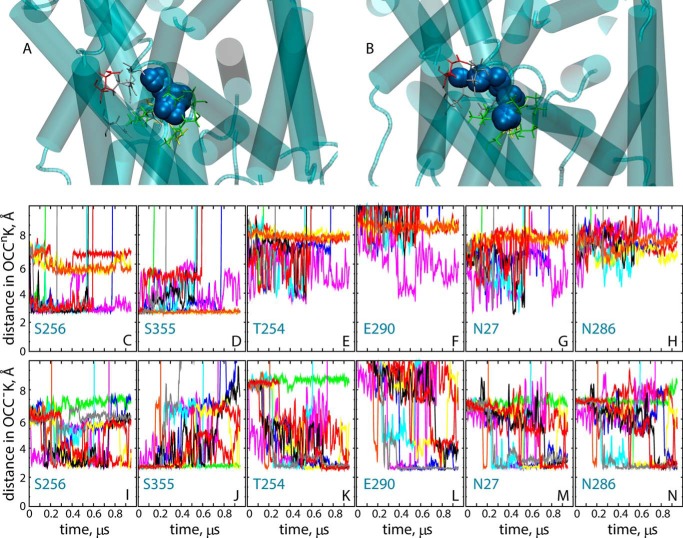
The extensive conformational sampling offered by the ensemble simulations enables a more detailed understanding of the key role that protonation/deprotonation of Glu²⁹⁰ has on the pathways taken by the K⁺ ion upon destabilization in the Na2 site. Thus, K⁺ is unstable in the Na2 site in most of the OCCⁿK and OCC⁻K trajectories (as seen from the increasing the distance between Thr³⁵⁴ and K⁺ in supplemental Fig. S7). However, the path of K⁺ upon release from the Na2 site depends on the protonation state of Glu²⁹⁰. As detailed in Fig. 10, with neutral Glu²⁹⁰ (Fig. 10A), K⁺ is mostly coordinated by residues Ser²⁵⁶ and Ser³⁵⁵ in the region overlapping with the Na1″ site (33) (Fig. 10, C and D). However, when Glu²⁹⁰ is charged (Fig. 10B), the destabilized K⁺ ion diffuses toward the Na1 site (interacts with Asn²⁷ and Asn²⁸⁶ residues; Fig. 10, M–N), visiting both the Na1″ site and another proposed intermediate Na⁺ binding site (31) termed Na1′ (interaction with Glu²⁹⁰ and Thr²⁵⁴; Fig. 10, K–L). We note that the Na1′ and Na1 sites were not explored by K⁺ in OCCⁿK simulations (Fig. 10, E–H) in which K⁺ released from Na2 sampled only the Na1″ site before diffusing out into the EC solution.

FIGURE 10.

Positioning of the K⁺ ion in various trajectories. A and B, trajectories of the K⁺ ion initially bound in the Na2 site in ensemble simulations of OCCⁿK (A) and OCC⁻K (B) models. Snapshots combine positioning of the K⁺ ion (blue spheres) from all 10 replicates accumulated per construct (shown are only trajectory frames in which the K⁺ is within the confines of the Na1 and Na2 sites). In gray are residues comprising the Na1 site (Ala²², Asn²⁷, Thr²⁵⁴, Asn²⁸⁶), and in green those in the Na2 site (G20, V23, A351, T354, S355). In addition, residue Glu²⁹⁰ is shown in red, and residues Asn²¹ and Ser²⁵⁶ are in yellow. Panels C–N, show the time evolution of the minimum distance between K⁺ ion and selected residues from OCCⁿK (C–H) and OCC⁻K (I–N) ensemble simulations. The different trajectory replicas are indicated by the different colors. In C–N, the vertical axis (y) range was truncated at 10 Å for better resolution of distance changes.

The partitioning of Na⁺ from the EC milieu to the ion binding sites in LeuT largely follows the same path as the K⁺ released from Na2 in the OCC⁻K trajectories. As seen from supplemental Fig. S10, B–D, Na⁺ binds to LeuT in a region that largely overlaps with the Na1 site but also involves interactions with Glu²⁹⁰ (the Na1′ site; supplemental Fig. S10, A and E). Furthermore, consistent with our findings from the Anton simulations (Fig. 9), the binding pathway involves transient interactions with residues in the proposed Na1′ site (supplemental Fig. S10, F and G). Collectively, the results from the ensemble MD simulations illustrate how protonation of Glu²⁹⁰ can modulate the pathways of the K⁺ and Na⁺ ions on the EC side of LeuT, controlling the release of K⁺ from the Na2 site and the binding Na⁺ from the EC vestibule in LeuT.

Na⁺ Affinity for LeuT Is pH-dependent and Is Modulated by K⁺ Ions

The observations from the computational analysis that protonation/deprotonation of Glu²⁹⁰ plays a key role in Na⁺ binding and K⁺ release suggests that Na⁺ binding to LeuT is pH-dependent. To test this hypothesis experimentally, we measured Na⁺-dependent [³H]leucine binding to detergent-solubilized LeuT at different pH values using a scintillation proximity assay as described under “Experimental Procedures.” We found that the affinity for Na⁺ decreased significantly with decreasing pH (compare curves with filled symbols in Fig. 11; see also Table 1), consistent with our computational data showing that Na⁺ binding is more favorable when Glu²⁹⁰ is charged (the side chain of Glu²⁹⁰ is much more likely to be charged at pH 8 than at pH 6).

FIGURE 11.

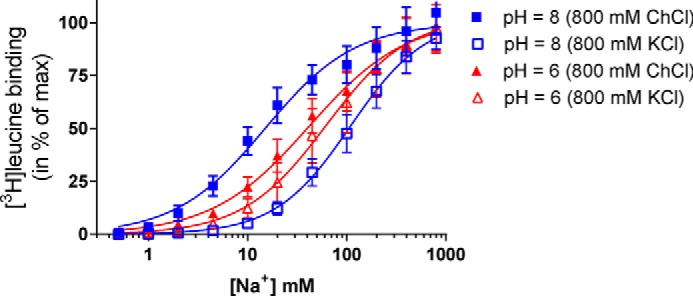
Na⁺ affinity for LeuT is pH-dependent and is modulated by K⁺ ions. Na⁺-dependent [3H]leucine binding to purified LeuT in DDM was assessed with scintillation proximity assay. At pH 8 (blue curves), the IC₅₀ for Na⁺ was significantly (p < 0.0001) reduced when ChCl (800 mm, filled squares) was substituted with KCl (800 mm, open squares). The IC₅₀ value of Na⁺ was not significantly different at pH 6 (red curves) between ChCl and KCl substitution but increases significantly (p = 0.0005) in ChCl when pH is changed from 8 to 6 (Table 1). The data are means ± S.E. (error bars) of four or five individual experiments performed in triplicate. Statistical analysis performed with one-way analysis of variance with Tukey's multiple comparison test (F value: 43.7, p < 0.0001).

TABLE 1.

Effect of pH and K⁺ on Na⁺ affinity for LeuT

The data are shown as mean values calculated from means of pIC₅₀ and the [S.E. interval] from pIC₅₀ ± S.E. based on the means from the triplicates within each experiment.

pH	Salt (800 mm)	Na+ Ki (mm)	n
8	ChCl	15 [14;17]	5
8	KCl	109 [95;125]	5
6	ChCl	42 [40;45]	4
6	KCl	64 [52;79]	4

To assess the effect of K⁺ on Na⁺ affinity, we considered experimental preparations where KCl was substituted for ChCl we found that, at pH 8 (Fig. 11, blue curves), the IC₅₀ for Na⁺ was significantly (p < 0.0001) increased when ChCl (800 mm; Fig. 11, filled squares) was substituted with KCl (800 mm; Fig. 11, open squares). The IC₅₀ value for Na⁺ was not significantly different in pH 6 (red curves) upon ChCl to KCl substitution. Together, these experimental findings suggest that the effect of K⁺ on Na⁺ affinity is stronger at higher pH, when residue Glu²⁹⁰ is likely to be charged, consistent with the involvement of the predicted protonation state of the Glu²⁹⁰ residue in populating the ion binding sites in LeuT.

Discussion

Given the high concentration of K⁺ ions in the cytoplasm, it is not entirely surprising that outward transport of K⁺ ions has been shown to be involved in NSS protein function (e.g. SERT (53)) and that we found in our recent computational studies of membrane-embedded hDAT (51) that K⁺ penetrates from the intracellular environment into the Na2 site after the Na⁺ was released. It was less clear, however, what the parameters and consequences of K⁺ binding would be. The computational simulations of various LeuT constructs presented here showed that a K⁺ in the Na2 site is largely unstable, especially when Glu²⁹⁰ is protonated (corresponding to a state of eukaryotic NSS in which the chloride is not present in the binding site). In contrast, observations from the trajectories in which Glu²⁹⁰ was charged are that in the K⁺ ion escapes less frequently to the EC milieu and its position fluctuates between the Na2 and Na1 ion binding sites in LeuT.

The dependence on the protonation state of Glu²⁹⁰ is interesting in light of the established role of the negative charge on this residue in LeuT as a substitute for Cl⁻ binding in mammalian NSS proteins (4, 21), because we find that the charge of Glu²⁹⁰ also affects strongly the dynamic behavior of the neighboring Phe²⁵³ residue that functions as a gate between binding sites and the EC vestibule. In particular, we showed that a charged Glu²⁹⁰ is hydrogen-bonded to the hydroxyl group of Thr²⁵⁴ and that this interaction favors the “closed” orientation of Phe²⁵³ that shields the functional sites from water penetration in the “occluded” state of the transporter. It is in this configuration that we observe the K⁺ ion diffusing from the Na2 site toward Na1, exploring an area that overlaps the proposed intermediate Na⁺ binding sites Na1′ and Na1″ described in previous studies (31, 33).

Importantly, complete release of K⁺ from binding sites in LeuT is enabled by isomerization of Phe²⁵³ from closed to open conformation. This transition allows water to penetrate and form a continuous channel connecting the EC vestibule to the ion and S1 substrate binding sites. This facilitates the diffusion of any K⁺ that has penetrated to the Na2 site, away from it and into the extracellular environment. Our data also suggest that transition to the open conformation of residue Phe²⁵³ is much more likely when Glu²⁹⁰ is neutral (protonated). Under such conditions, association of Glu²⁹⁰ with neighboring Thr²⁵⁴ is weakened, allowing higher flexibility to Phe²⁵³.

The rearrangements involved in the formation of the water channel that facilitates the escape of K⁺ were observed in the computational study to involve a particular positioning of a pair of residues in the primary S1 substrate binding site, namely Leu²⁵ and Tyr¹⁰⁸. Together, Phe²⁵³, Leu²⁵, and Tyr¹⁰⁸ can be seen to constitute a gate allowing the influx of water into the functional sites. This water channel connects the EC vestibule to the ion and S1 substrate binding sites, suggesting that it facilitates the penetration of extracellular ions and substrate. Indeed, observed in separate simulations, the entrance of Na⁺ ions from the EC solution to the ion binding sites is found to depend on the same network of penetrating water molecules, enabled by the same local conformational rearrangements, but the events in which Na⁺ penetration results in binding were detected only in the simulations with charged Glu²⁹⁰. Given that the negatively charged Glu²⁹⁰ side chain in LeuT mimics the effect of Cl⁻ binding in mammalian NSS transporters, these findings are consistent with the suggested role of Cl⁻ in regulating cation permeation in NSS proteins (45).

The insights from the simulation studies are echoed by results presented here from experimental measurements of Na⁺ ion binding at different pH values and in the presence or absence of K⁺ ions. Indeed, the measured Na⁺ affinity is pH-dependent and is significantly reduced in the presence of K⁺ ions in the high pH regime where the Glu²⁹⁰ is charged. However, at the lower pH values tested, when Glu²⁹⁰ is likely to be protonated, the Na⁺ affinity is unaffected by K⁺ ions. Although these experimental results do not show how the changes in pH modulate the competition between K⁺ and Na⁺ ions, they highlight the involvement of the protonation state of the Glu²⁹⁰ residue in populating the ion binding sites in LeuT in accordance with the molecular mechanisms identified from the computations described in this work. A key role in these mechanisms is played by the local rearrangements that open the water gate and enable the water channel that facilitates both K⁺ release and Na⁺ binding. This agrees with previously suggested roles of local hydration in the outward release, or the binding, of Na⁺ ions to LeuT (31, 33, 36, 38, 47). The connection we describe here between the protonation state of Glu²⁹⁰ and the orientation of residues Leu²⁵ and Tyr¹⁰⁸ emerges as a determinant mechanism for the level of the hydration and the attendant movement of the ions. These mechanistic conclusions are further reinforced by a new crystal structure of an apo LeuT (54) published while our manuscript was being revised. Remarkably, in comparison with the occluded state of LeuT, the new apo structure exhibits a rotation of residue Leu²⁵ into the empty substrate-binding pocket, analogous to that observed in our MD simulations.

The broader implications of the conformational switch we describe and its relation to the state of Glu²⁹⁰ (protonated/unprotonated) warrant further study to establish their specific contribution(s) to the allosteric mechanism of function in LeuT (26, 50, 55) and cognate NSS proteins (49).

Experimental Procedures

Computational Methods

Description of Molecular Systems

Two different starting points were used for generating structural models of apo LeuT. In the first, the initial structure for atomistic MD simulations was constructed from the occluded state (OCC) of LeuT in the crystal structure Protein Data Bank code 2A65 (12), by removing the bound substrate (Leu) from the primary substrate binding (S1) site and the two Na⁺ ions from the Na1 and Na2 binding sites. In the second, we took advantage of available results from a steered MD (SMD) trajectory (32) that followed the transition of LeuT from the occluded to an inward facing state as the substrate Leu was pulled from the S1 site toward the IC vestibule when Na⁺ occupied the Na1 site and a second Leu substrate was in the secondary S2 binding site (see Ref. 32 for more details). In this case, the initial structure for MD simulations of apo LeuT was obtained from the last frame of the SMD trajectory by removing Na⁺ from the Na1 site and the ligand from the S2 site.

In the apo LeuT models we considered both charged and neutral forms of Glu²⁹⁰ (designated as OCC⁻, OCCⁿ, SMD⁻, and SMDⁿ, for the two models generated from different starting points). Protonation states of all other titratable residues were determined for pH 7 with PROPKA 3.0 (56) resulting in neutral Glu¹¹², Glu²⁸⁷, and Glu⁴¹⁹.

The apo OCC⁻ and OCCⁿ structures were equilibrated with atomistic MD simulations first in POPC lipid membranes and then in DDM detergent micelles for a combined simulation time of ∼500 ns, during which both ion binding sites (Na1 and Na2) remained empty (see below and also Fig. 1). Trajectory frames were extracted after 200 ns of these simulations and used to initiate several new sets of extensive atomistic MD simulations. Thus, the extracted LeuT structures were transferred to bilayers containing 74:26 mixture of POPE/POPG lipids and were subjected to microsecond scale atomistic MD simulations containing either K⁺Cl⁻ or Na⁺Cl⁻ in the solution (Fig. 1, blue and red arrows). In the starting protein models for the simulations in K⁺Cl⁻, a K⁺ ion was placed in the Na2 site of the OCC⁻ and OCCⁿ structures to model the result of the penetration observed in hDAT (51), whereas for the simulations in Na⁺Cl⁻ the protein models were kept as apo (i.e. both Na1 and Na2 ion binding sites unoccupied) to explore the binding of Na⁺ from the extracellular side.

In the SMD⁻ and SMDⁿ structures (see above), the K⁺ ion was also docked into the Na2 site, and the K⁺-bound protein models were then embedded into the same 74:26 POPE/POPG lipid membranes and a solution containing K⁺Cl⁻. 1-μs-long atomistic MD simulations were initiated (SMD⁻K and SMDⁿK runs in Fig. 1). Finally, to obtain run SMDⁿKb in Fig. 1, the Glu²⁹⁰ residue was protonated at the end of the SMD⁻K trajectory, and the simulation was continued for an additional 1 μs.

Atomistic MD Simulations

Equilibration of apo OCC⁻ and OCCⁿ LeuT Models

The apo OCC⁻ and OCCⁿ LeuT structures were embedded in a previously equilibrated POPC membrane composed of 204 lipids and equilibrated for ∼200 ns in MD simulations using the protocols described earlier (32). To further assess the stability of the apo LeuT models of the OCC⁻ and OCCⁿ structures in conditions relevant to the experimental measurements (see below), the structures equilibrated for 200 ns of MD were transferred into proteomicelles composed of 160 DDM molecules. As we described in detail previously (57, 58), a 1:160 protein/detergent ratio represents well the experimental conditions under which many in vitro functional and structural studies on LeuT are carried out (25, 27–30, 32). Following the computational protocol established earlier (57, 58), the OCC⁻/DDM and OCCⁿ/DDM proteomicelles were placed in a cubic water box of ∼3 × 10⁶ ų volume (corresponding to ∼0.09 M DDM concentration), and Cl⁻ ions were added for electroneutrality. Each system was then simulated for ∼300 ns with the NAMD 2.9 software (59) and CHARMM36 parameters for proteins (60), ions (61), and detergents (62); the equilibration scheme and run parameters were as described previously (57). The MD simulations described under “Results” were carried out from these starting structures of the LeuT models.

Microsecond Scale MD Simulations of LeuT in POPE/POPG Lipid Membranes

Because lipidic environment can strongly modulate functional mechanisms of LeuT (63), the production simulations for all the LeuT constructs were carried out in native Escherichia coli lipid-like membrane environment containing a 74:26 mixture of POPE/POPG lipids. The bilayer was created with the CHARMM-GUI web interface (64), in which we embedded K⁺-bound OCC⁻ or OCCⁿ (denoted by OCC⁻K and OCCⁿK) or apo OCC⁻ and OCCⁿ LeuT models, as well as K⁺-bound SMD⁻ and SMDⁿ LeuT structures (referred to as SMD⁻K and SMDⁿK). After removing overlapping lipids (while preserving the initial lipid ratio), the bilayer patch contained 296 lipids in total.

The protein-membrane complexes were solvated with the TIP3P water model (∼82 waters/lipid), and the ion environment was set to either 0.15 m K⁺Cl⁻ or 0.15 m Na⁺Cl⁻ ionic (Fig. 1). The final systems, each containing ∼120,000 atoms, were first subjected to a multistep equilibration protocol (for examples see Refs. 32 and 65) with NAMD version 2.9 using CHARMM36 parameters for proteins (60), lipids (67), and ions. Briefly, this phase included: 1) minimization for 5,000 steps and running MD with a 1-fs integration time step for 250 ps, fixing all atoms in the system except for the lipid tails; 2) minimization for 2,500 steps and performing MD with a 1-fs time step for 500 ps with constrained protein backbone and lipid headgroups (force constant of 1 kcal/(mol Ų) and keeping water out of the membrane hydrophobic core; 3) gradual release of the constraints on the protein backbone and lipid headgroup atoms (force constant of 0.5 and 0.1 kcal/(mol Ų)) while still keeping water out of the membrane interior; at each value of the force constant, the system was minimized for 2,500 steps followed by 500-ps MD (with a 1-fs time step); and 4) unbiased MD simulation for 30 ns using a 2-fs time step. These steps implemented PME for electrostatic interactions (68) and were carried out in the NPT ensemble under semi-isotropic pressure coupling conditions, at 310 K temperature. The Nosé-Hoover Langevin piston (59) algorithm was used to control the target p = 1 atm pressure with the LangevinPistonPeriod set to 100 fs and the LangevinPistonDecay set to 50 fs. The van der Waals interactions were calculated applying a cutoff distance of 12 Å and switching the potential from 10 Å.

After this initial phase, the molecular systems were subjected to microsecond scale MD simulations (see Fig. 1 for simulation times) on Anton, a special purpose supercomputer machine (69). These production runs implemented the same set of CHARMM36 force field parameters and were carried out in the NPT ensemble under semi-isotropic pressure coupling conditions (using the Multigrator scheme that employs the Martyna-Tuckerman-Klein barostat (70) and the Nosé-Hoover thermostat (71)), at 310 K temperature, with a 2-fs time step and using PME for electrostatic interactions. All the other run parameters were derived from the Anton guesser scripts based on the system chemistry (69).

Protonation of the Glu²⁹⁰ residue after 1 μs of SMD⁻K trajectory (Fig. 1) was carried out with the psfgen plugin using VMD (72). After this step, the system (SMDⁿKb in Fig. 1) was equilibrated following the protocol described above and was subjected to the production MD run protocol on the Anton machine.

Ensemble MD Simulations of LeuT in POPE/POPG Lipid Membranes

For enhanced sampling of the dynamics of K⁺ release and Na⁺ binding, we carried out ensemble MD simulations of LeuT models in POPE/POPG lipid membranes. Thus, the OCC⁻, OCCⁿ, OCC⁻K, and OCCⁿK LeuT structures were each simulated in 10 independent replicas ∼950 ns long (resulting in combined MD trajectory time of 9.5 μs for each construct). These simulations were carried out on the Titan GPU cluster using ACEMD software (an MD simulation suite developed at Acellera (73) and designed for GPU machine architecture), with CHARMM36 force field parameters for protein and lipids. The simulations with ACEMD implemented the PME method for electrostatic calculations and were carried out according to protocols established previously (73), which included a 4-fs integration time step enabled by standard mass repartitioning procedure for hydrogen atoms. The computations were conducted under the NVT ensemble (at T = 310 K), using the Langevin Thermostat with Langevin Damping Factor set to 0.1. Prior to the ACEMD step, the OCC⁻, OCCⁿ, OCC⁻K, and OCCⁿK models were each subjected to a 30-ns equilibration phase carried out with NAMD version 2.9 and using the same parameters as described above (i.e. CHARMM36 force field for protein and lipids, 2-fs integration time step, and NPT ensemble with semi-isotropic pressure coupling). After this initial phase, statistically independent trajectory replicates were collected by reinitializing velocities. We note that for the ensemble simulations, OCC⁻K and OCCⁿK models were created by placing a K⁺ ion in the Na2 site directly after removing the bound Na⁺ ions and the Leu ligand from the 2A65 structure (contrary to the protocol described above and depicted in Fig. 1 whereby the K⁺ ion was introduced only after initial equilibration of apo LeuT models in POPC membranes).

Experimental Methods

Expression and Purification of LeuT

Expression and purification of LeuT were performed as previously described (66). In short, E. coli strain C41 containing His-tagged LeuT in pET16b expression vector was cultivated in lysogeny broth with 75 μg ml⁻¹ ampicillin at 37 °C shaking at 180 r.p.m. Expression was induced at A₆₀₀ = ∼0.6 by addition of 100 μm isopropyl β-d-1-thiogalactopyranoside and grown for 20 h (20 °C, 180 r.p.m.). The cells were harvested and resuspended in buffer A (100 mm KCl, 50 mm Tris-HCl, pH 8.0, 1 mm EDTA, 0.5 m sucrose). Phenylmethylsulfonyl fluoride (2.5 mm), protease inhibitor mixture, and lysozyme (250 μg/ml) were added and rotated for 30 min at room temperature. The membrane fraction was isolated by two passages through Basic Z Cell Disruptor (Constant Systems) at 2.30 bar (4 °C) and subsequently ultracentrifuged (Beckmann Coulter, 32,000 rpm, 4 °C) for 2 h. The membrane fraction was resuspended in buffer B (50 mm Tris-HCl, pH 8, 30% glycerol (v/v), 300 mm KCl, 5 mm MgCl₂, 0.1 mm tris(2-carboxyethyl)phosphine (TCEP)) and solubilized by addition of 1% (w/v) DDM (Anatrace) with rotation (4 °C for 1 h). LeuT was immobilized on ProBond Ni²⁺-IDA resin (Life Technology) and extensively washed in buffer C (20 mm Tris-HCl, pH 7.5, 200 mm KCl, 100 μm TCEP, 20% glycerol, 0.05% DDM) with increasing imidazole (60–100 mm). LeuT was eluted by addition of buffer C containing 300 mm imidazole. Purity of LeuT was examined by SDS-PAGE. Protein content was quantified by NanoDrop 2000c Spectrophotometer (Thermo Scientific). Samples were stored at −80 °C.

LeuT Equilibrium Binding Assay

LeuT binding was investigated using the scintillation proximity assay. The assay was carried out in clear-bottomed 96-well plates with 100 ng of purified LeuT in DDM (0.05%) and 1.25 mg/ml YSi-Cu His tag scintillation proximity assay beads (PerkinElmer). Na⁺-dependent leucine binding was performed in 100 nm [³H]leucine at pH 8 (100 mm Tris-HCl, pH 8, 100 μm TCEP, 20% glycerol, 0.05% DDM) or pH 6 (100 mm MES-bis-Tris, pH 6, 100 μm TCEP, 20% glycerol, 0.05% DDM) with increasing NaCl concentrations (0–800 mm) substituted with ChCl to maintain ionic strength. The experiment was carried out with either additional 800 mm ChCl or 800 mm KCl to allow determination of the effect of K⁺. The plates were incubated for 30 min at room temperature and were then kept at 4 °C overnight before being counted on 2450 MicroBeta² microplate counter (PerkinElmer).

Data Analysis

All experiments were performed at least three times, each with triplicate determination. The data are shown as mean values calculated from means of pIC₅₀ and the [S.E. interval] from pIC₅₀ ± S.E. based on the means from the triplicates within each experiment. The data from the equilibrium binding assay were analyzed using non-linear regression algorithms. For analysis of variance testing, a significant F ratio and homogeneity of sample variance were required to progress to post hoc tests. Analysis of variance is based on mean pIC₅₀ of the individual experiments. All data were processed using Prism 6.0 (GraphPad Software Inc.).

Author Contributions

G. K., S. G. S., C. J. L., and H. W. designed the experiments. G. K. carried out computations and analysis, S. G. S. did experiments and analyzed the data. All the authors took part in discussing and interpreting the results. G. K. and H. W. wrote the manuscript with participation of S. G. S. and C. J. L. All the authors participated in editing the manuscript and approved the final draft.