Biased and unbiased estimation in longitudinal studies with informative visit processes

Summary

The availability of data in longitudinal studies is often driven by features of the characteristics being studied. For example, clinical databases are increasingly being used for research to address longitudinal questions. Because visit times in such data are often driven by patient characteristics that may be related to the outcome being studied, the danger is that this will result in biased estimation compared to designed, prospective studies. We study longitudinal data that follow a generalized linear mixed model and use a log link to relate an informative visit process to random effects in the mixed model. This device allows us to elucidate which parameters are biased under the informative visit process and to what degree. We show that the informative visit process can badly bias estimators of parameters of covariates associated with the random effects, while allowing consistent estimation of other parameters.

1. Introduction

Calls have been made recently to utilize the wealth of information in large clinical databases to drive biomedical research. For example, the Patient-Centered Outcomes Research Institute (PCORI) recently funded 11 clinical data research networks with the goal (PCORI, 2014) to “...integrate data from ... networks that originate in healthcare systems such as hospitals, health plans, or practise-based networks and securely collect ‘real-time,’ ‘real-world’ health information during the routine course of patient care” in order to have, in part, the “capacity to support large-scale comparative effectiveness trials, as well as observational studies of multiple research questions, including prevention and treatment.” In contrast to well-designed longitudinal studies, the availability of data in clinical databases is often driven by patient characteristics. For example, in a study of decline in kidney function in the elderly, a patient may visit their doctor because they are feeling ill and that visit might generate a measurement of kidney function that would be included in the analysis. If the likelihood of a visit is higher among those with lower kidney function – an informative visit process – then it is clear that standard statistical analyses will yield a biased estimate of the average kidney function in the population served by the clinic. But what about trends over time in kidney function? Or the differences between levels of a covariate in trends over time in kidney function? Can those features reliably be estimated from the clinical database? In general the question we set out to answer is the following: using standard statistical analyses that ignore the informative visit process, which parameters are estimated with bias and which are not? Though our motivation has been clinical databases and biomedical research, the results apply more broadly to data collected longitudinally subject to informative visit processes, e.g., data collected through internet sampling.

Previous work has tended to follow two avenues. First, specification of joint models for the visit process and the outcome process (e.g., Lin et al., 2004; Sun et al., 2007; Wulfsohn and Tsiatis, 1997). These require specification of a model for the visit process (which is not of scientific interest) as well as a model for the association between the outcome and visit processes. The joint models specified in the literature have been quite simple. More realistic models would be problematic because they would require accurate specification of the model for reasons why visits occur or do not occur. The variables that govern the presence of visits are often not measured and attempts to fit models to correct for missing data have typically been extremely sensitive to model specification errors (Kenward, 1998).

The second avenue of argument has appealed to the missing data literature, typically requiring the assumption that the data are “missing at random,” or MAR (e.g., Lipsitz et al., 2002; Rathouz, 2004; Fitzmaurice et al., 2006). In the situations we consider, only a very small percentage of possible visits are present and hence a large percentage of data are “missing.” In such a situation the assumption that the data are MAR becomes less and less tenable with the importance of the assumptions becoming more and more critical, and hence the characterization becomes less and less useful. Intuitively, if we have less than 5% missing data in a well-conducted longitudinal study with yearly visits, then it might be reasonable and innocuous to assume that the data are MAR. Contrast this with a study in which data are also scheduled to be collected approximately yearly, but that patients come in and get measured more frequently when they are feeling ill. Because of the haphazard timing of visits we might consider time on a scale of a week, resulting in 95% of the data being missing.

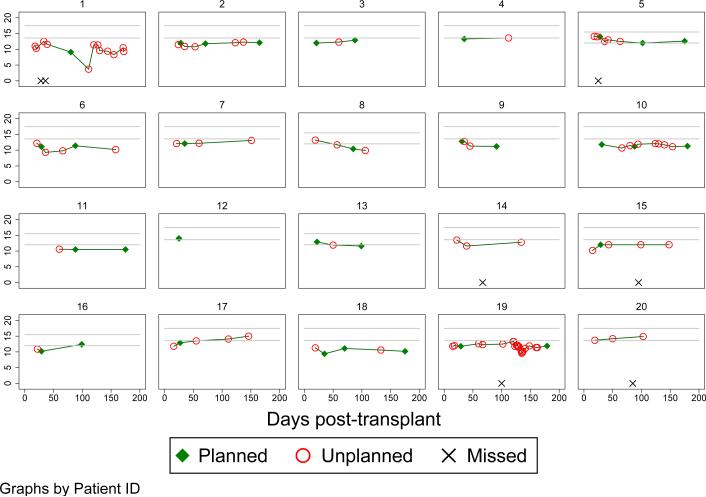
Figure 1 shows the actual visit process from 20 patients being cared for by the University of California, San Francisco bone-marrow transplant clinic. The patients’ hemoglobin levels are being monitored following transplant because of concerns of anemia. The goal is to achieve normal hemoglobin levels (defined as 12 to 15.5 in women and 13.6 to 17.5 in men, as marked on the figure in light gray) and planned follow-up would be scheduled within reasonable windows of 30, 90 and 180 days.

Figure 1.

Hemoglobin levels versus days post bone-marrow transplant with different types of visits.

We fit a linear mixed model to the data in Figure 1 with an outcome of hemoglobin, predictors of sex, days post-transplant, whether a visit fell within the scheduled window or not, interactions of days post-transplant with sex and whether the visit was scheduled, and we allowed for correlated random intercepts and slopes (with days post-transplant). The interaction between days post-transplant and whether the visit fell within the scheduled window was statistically significant (p=0.019) with a statistically-significant decline in hemoglobin of 0.025 per day (95% CI −0.041 to −0.010) for the unscheduled visits and a not-statistically-significant decline of 0.011 per day (95% CI −0.023 to 0.0002) for the scheduled visits. This is suggestive that the unscheduled visits may be concentrated in patients with declining hemoglobin levels.

Several features of the process are noteworthy. First, many of the visits are unplanned and are driven by feeling ill or physician concern. Second, there are missed visits. And third, the inter-visit timing is highly irregular and would be quite difficult to model. In many realistic situations such as this one, there will be little to no information available from which to model the informative data process and hypothesizing simplistic modeling approaches may be more harmful than helpful. Instead, our goal is to study the influence of an informative visit process on longitudinal data analysis and the consequences of naive estimation from such data assuming the data were collected in a non-informative manner.

We begin by assuming the outcome process follows a generalized linear mixed model with random effects, a very flexible class of models for a variety of outcome types. Our approach to modeling the informative visit process starts in a fashion similar to other work (e.g., Sun et al., 2007; Liu et al., 2008). Namely, we build in an association between the outcome process and visit process through shared random effects. Because we wish to avoid assuming a specific model for how the random effects are shared, we model this quite flexibly using a novel, log link relationship and derive general results under a wide class of models. In contrast with previous approaches, we do not use information on the visit time process and instead focus on the impact on the distribution of the outcome process, conditioning on the data being observed. Our log link approximations and simulations evaluate the case where many visit times are possible but only a small fraction of the possible visits are observed and, essentially, all the visits are unplanned as in electronic health record data. Our models and simulations hence generate irregular visit patterns.

After defining our models and notation we derive the distribution of the outcome under informative visit processes and a log link. The next section elaborates the effect for a special case of a random slopes and intercepts model and then we evaluate the effects under a more realistic logistic link visit model via simulations.

2. Models and Notation

2.1 Longitudinal outcome process

We begin by defining the model for the outcome, which is assumed to be a generalized linear mixed model, a commonly used model for longitudinal data analysis. We describe our models in terms of “subjects” for the correlated clusters of data and “times” for the observations within a cluster though, of course, the results apply more broadly.

Let Y_it represent the measurement at time t on subject i. Our model assumes that observations are conditionally independent given the random effects and that our outcome process follows a generalized linear mixed model with normally distributed random effects, b_i:

$$\begin{array}{cc}\hfill Y_{it}\mid b_i& \sim \text{independent}{f}_{Y}i=1,\dots ,m;t=1,\dots ,n_i\hfill \\ \hfill g\left(\mathrm{E}[Y_{it}\mid b_i]\right)& =x_{it}^T\beta +z_{it}^T{b}_i\hfill \end{array}$$ (1)

$$b_i\sim \mathrm{i}.\mathrm{i}.\mathrm{d}.\mathcal{N}(0,{\Sigma }_b),$$ (2)

In this model, x_it represents the covariates associated with subject i at time t, β is the vector of covariate effects, z_it is the model matrix for the random effects, and g(·) is the link function.

2.2 Informative visit process

Let R_it be a binary indicator with R_it = 1 indicating that Y_it is observed and is 0 otherwise. We assume that, conditional on the random effects, Y_it and R_it are independent (and independent from one another) and that the probability that R_it = 1 is dependent on the random effects via a log link:

$$\mathrm{P}(Y_{it}\text{is observed}\mid b_i)\equiv \mathrm{P}(R_{it}=1\mid b_i)=\exp \{{\mu }_{it}+{\gamma }_{it}^T{b}_i\}.$$ (3)

In this model, γ_it governs the strength and directionality of the association between the random effects and whether or not data are observed. The model in (3) is a flexible specification; for example we can allow dependence on where subjects start (i.e., through dependence on their random intercept), their trend over time (i.e., through dependence on a random slope) or on a subject's true mean value (i.e., the mean conditional on the random effects) at the current or previous time points. Importantly, and to allow more realistic models, both μ_it and γ_it can depend arbitrarily on either fixed or time-varying covariates.

Because the visit process depends on the unobserved random effects, it is a “missing not at random” (Fitzmaurice et al., 2001) process and even methods such as maximum likelihood based fits, which are consistent under “missing at random” assumptions, may be biased. In Section 3.6 we extend our results to the case where we allow dependence of the visit process on unobserved previous outcomes. This is often a realistic scenario under which virtually no approaches that attempt to model the joint process can succeed.

There is a technical issue with using a log link in (3) for a probability, along with the specification of a normal distribution for the random effects in (2) since the value of the probability is not constrained to be less than 1. To be technically correct the distribution needs to be truncated so that the probability in (3) is less than or equal to 1, That is, the distribution of the random effects needs to be a multivariate normal, truncated so that ${\gamma }_{it}^T{b}_i<-{\mu }_{it}$. For now we ignore this truncation to exploit the simplification that results in the theoretical calculations. In Section 5 we give simulation results under a logit link informative visit process (which naturally constrains probabilities to be less than one) and in the online supplemental material we give exact calculations under truncation as well as more detailed simulation results under both log and logit link informative visit processes.

3. Observed data model

3.1 Conditional distributions of random effects for the observed data

Our goal is to elucidate the consequences of analyzing the available data, so we are led to consideration of the conditional distribution of the outcome process, given R_it = 1. This, in turn, leads to consideration of the distribution of the random effects conditional on R_it = 1.

From (3) and (2) we can obtain the joint probability of b_i being less than s and R_it = 1:

$$\begin{array}{cc}\hfill \mathrm{P}(R_{it}=1,b_i\le s)& =\mathrm{E}\left[\mathrm{P}(R_{it}=1,b_i\le s\mid b_i=u)\right]\hfill \\ \hfill & =\mathrm{E}\left[\mathrm{P}(R_{it}=1\mid b_i=u)I_{\{u<s\}}\right]\hfill \\ \hfill & ={\int }_{-\infty }^s\exp \{{\mu }_{it}+{\gamma }_{it}^{T}u\}\frac{\exp \{-u^T{\Sigma }_b^{-1}u∕2\}}{{\left(2\pi \right)}^{-q∕2}{\mid {\Sigma }_b\mid }^{-1∕2}}\mathrm{d}u,\hfill \end{array}$$ (4)

where q is the dimension of b_i.

The conditional density of b_i given R_it = 1 can be derived by differentiating (4) with respect to s and dividing by the marginal probability that R_it = 1:

$$f_{b_i\mid R_{it}=1}\left(b\right)=\exp \left\{{\gamma }_{it}^{T}b\right\}\exp \{-b^T{\Sigma }_b^{-1}b∕2\}∕{\int }_{-\infty }^{\infty }\exp \left\{{\gamma }_{it}^{T}u\right\}\exp \{-u^T{\Sigma }_n^{-1}u∕2\}du$$ (5)

The denominator in (5) is constant in b so completing the square in the numerator leads to

$$f_{b_i\mid R_{it}=1}\left(b\right)\propto \exp \{-{(b-{\Sigma }_b{\gamma }_{it})}^T{\Sigma }_n^{-1}(b-{\Sigma }_b{\gamma }_{it})∕2\}.$$ (6)

We thus have that the conditional distribution of b_i given R_it = 1 is given by

$$b_i\mid R_{it}=1\sim \mathcal{N}({\Sigma }_b{\gamma }_{it},{\Sigma }_b).$$ (7)

That is, the distribution is multivariate normal with variance Σ_b (both the same as the unconditional distribution), but with a mean given by Σ_bγ_it instead of 0.

3.2 Conditional distributions for the observed data

We are now in a position to derive the conditional distribution of Y_it, conditional on being observed. Our calculations are for the “marginal” distribution of each individual Y_it (as opposed to the joint distribution of Y). The result concerning the random effects above generalizes to Y_it, namely that the distribution of Y_it conditional on R_it = 1 is the same as the unconditional distribution of Y_it except that the mean of Y_it is affected by the mean of b_i given in (7). To see this, first recall that the distributions of Y_it and R_it are defined independently of one another, conditional on b_i. Therefore, using bracket notation for distributions, we have [Y_it | R_it = 1, b_i] = [Y_it | b_i], and the conditional distribution of Y_it given R_it = 1 is

$$\begin{array}{cc}\hfill [Y_{it}\mid R_{it}=1]=& \int [Y_{it}\mid R_{it}=1,b][b\mid R_{it}=1]\mathrm{d}b\hfill \\ \hfill =& \int [Y_{it}\mid b_i][b_i\mid R_{it}=1]\mathrm{b}{b}_i.\hfill \end{array}$$ (8)

That is, the distribution of Y_it given R_it = 1 is a convolution of the same, non-informative, conditional distribution of Y_it given b from (1) with the conditional distribution of b given R_it = 1. Since the conditional distribution of b given R_it = 1 is the same as its unconditional distribution (except for its mean), the only influence conditioning on R_it = 1 has is to modify the mean of the random effects distribution.

Furthermore, because both the random and fixed effects enter the linear predictor in (1), we can move the mean of the conditional distribution of b_i into the fixed effects portion of the model and re-center the distribution of b_i given R_it = 1 to have mean 0. The importance of this result is that the distribution of the observed data is exactly the same as that of a non-informative visit process with fixed effects given by $x_{it}^T\beta +z_{it}^T{\Sigma }_b{\gamma }_{it}$. This allows calculation of the exact distribution of the outcome or aspects of that distribution in a number of special cases that we consider in the following subsections. One important result is immediate from the form of differences induced in the marginal distribution. Namely that μ_it in (3) does not impact the marginal distribution under the log link informative visit process. Since μ_it can depend arbitrarily on the covariates, dependence of the informative visit process on the covariates alone does not influence the marginal distribution.

3.3 Linear mixed model

Using the result above, and for a linear mixed model with Y_it having a distribution (conditional on b_i) that is normal with variance ${\sigma }_{ϵ}^2$, we immediately have the distribution of Y_it conditional on being observed:

$$Y_{it}\mid R_{it}=1\sim \mathcal{N}(x_{it}^T\beta +z_{it}^T{\Sigma }_b{\gamma }_{it},{\sigma }_e^2+z_{it}^T{\Sigma }_b{z}_{it}).$$

This is practical because we can determine the asymptotic limit of many estimation methods (for example, ordinary least squares or generalized estimating equations with an independence working correlation structure) by simply examining the mean. To determine consistency for estimating β, we can often simply compare $x_{it}^T\beta +z_{it}^T{\Sigma }_b{\gamma }_{it}$ with $x_{it}^T\beta$. Coefficients of covariates that do not enter in the second term, $z_{it}^T{\Sigma }_b{\gamma }_{it}$, may be consistently estimated.

3.4 Mean under log link models

For models with a log link for the outcome and arbitrary distributions (conditional on b_i) we can easily calculate the mean when the random effects are normally distributed. Without selection the mean is given by $\mathrm{E}\left[Y_{it}\right]=\exp \{x_{it}^T\beta +z_{it}^T{\Sigma }_b{z}_{it}∕2\}$. On the other hand, with selection and using the results above, we have $\mathrm{E}[Y_{it}\mid R_{it}=1]=\exp \{x_{it}^T\beta +z_{it}^T{\Sigma }_b{z}_{it}∕2+z_{it}^T{\Sigma }_b{\gamma }_{it}\}$. Therefore the difference in the log of the mean with and without selection is given by $\log \mathrm{E}[Y_{it}\mid R_{it}=1]-\log \mathrm{E}\left[Y_{it}\right]=z_{it}^T{\Sigma }_b{\gamma }_{it}$.

3.5 Probit models

For probit models, the mean of Y_it without selection is (McCulloch et al., 2008) $\mathrm{E}\left[Y_{it}\right]=\Phi \left(\lambda x_{it}^T\beta \right)$, where $\lambda =1∕\sqrt{1+z_{it}^T{\Sigma }_b{z}_{it}}$. With selection we have $\mathrm{E}[Y_{it}\mid R_{it}=1]=\Phi (\lambda x_{it}^T\beta +\lambda z_{it}^T{\Sigma }_b{\gamma }_{it})$. Therefore the difference, on the probit scale, of the mean with and without selection is given by $\Phi \left(\mathrm{E}[Y_{it}\mid R_{it}=1]\right)-\Phi \left(\mathrm{E}\left[Y_{it}\right]\right)=\lambda z_{it}^T{\Sigma }_b{\gamma }_{it}$. Since the outcome is binary, the outcome model under selection is still a probit model but with a shift of the mean (on the probit scale) of $\lambda z_{it}^T{\Sigma }_b{\gamma }_{it}$. Given that probit models closely approximate logistic models, this suggests that logit models will exhibit similar patterns of bias. We report simulation results for a logistic outcome model in Section 5.

3.6 Linear mixed model with dependence on previous outcomes

The results of Section 3.2 can be extended to dependence on previous outcomes by essentially the same arguments in the case of a linear mixed model. Suppose the probability of observing an outcome is dependent on the value of the outcome lagged by τ time units:

$$\begin{array}{cc}\hfill \mathrm{P}(Y_{it}\text{is observed}\mid Y_{i,t-\tau })=& \exp \{\alpha +\delta Y_{i,t-\tau }\}\hfill \\ \hfill =& \exp \{\alpha +\delta (x_{i,t-\tau }^T\beta +z_{i,t-\tau }^T{b}_i+{ϵ}_{i,t-\tau })\},\hfill \end{array}$$ (9)

with ε_it being the error term in the linear mixed model for subject i at time t. Then the joint probability of b_i being less than s, ε_i,t–τ being less than s_ε, and R_it = 1 is given by:

$$\begin{array}{cc}\hfill \mathrm{P}(R_{it}=1,b_i\le s,{ϵ}_{i,t-\tau }\le s_{ϵ})=& \mathrm{E}\left[\mathrm{P}(R_{it}=1,b_i\le s,{ϵ}_{i,t-\tau }\le s_{ϵ}\mid b_i=u,{ϵ}_{i,t-\tau }=ϵ)\right]\hfill \\ \hfill =& \mathrm{E}[\mathrm{P}(R_{it}=1\mid b_i=u,{ϵ}_{i,t-\tau }=ϵ)I\{u\le s,ϵ\le s_{ϵ}\},]\hfill \\ \hfill =& {\int }_{-\infty }^{s_{ϵ}}{\int }_{-\infty }^s\exp \{\alpha +\delta (x_{i,t-\tau }^T\beta +z_{i,t-\tau }^{T}u+ϵ)\}\times \frac{\exp \{-u^T{\Sigma }_b^{-1}u∕2\}}{{\left(2\pi \right)}^{-q∕2}{\mid {\Sigma }_b\mid }^{-1∕2}}\frac{\exp \{-{ϵ}^2∕2{\sigma }_{ϵ}^2\}}{\sqrt{2\pi {\sigma }_{ϵ}^2}}\mathrm{d}u\mathrm{d}ϵ.\hfill \end{array}$$ (10)

Integrating out ε from (10) and using the same argument as before shows that the conditional density of b_i given R_it = 1 is $b_i\mid R_{it}=1\sim \mathcal{N}(\delta {\Sigma }_b{z}_{i,t-\tau },{\Sigma }_b)$.

Also, using assumed independence of errors, ε_it is independent of ε_i,t–τ and b_i, so that the conditional distribution of ε_it is unchanged by conditioning on {R_it = 1}. We thus have the following result for a linear mixed model:

$$Y_{it}\mid R_{it}=1\sim \mathcal{N}(x_{it}^T\beta +\delta z_{it}^T{\Sigma }_b{z}_{i,t-\tau },{\sigma }_e^2+z_{it}^T{\Sigma }_b{z}_{it}).$$

The results derived previously thus carry over to this situation. That is, the marginal distribution of Y_it in the observed data is unchanged except for a modification of the mean which depends on the model matrix of the random effects. So for covariates that are unrelated to the random effects we can expect little or no bias.

4. Consequences of the observed data process for a random intercepts and slopes model

4.1 A random intercepts and slopes linear mixed model

We next consider the impact of selection for a common mixed model used in the longitudinal context: a random intercepts and slopes linear mixed model. In this model Z consists of subject-specific intercepts and slopes for one of the variables in X. To better understand the consequences of the calculations above we work out the details for the random intercept and slope model under three informative visit process models: dependence on random intercept only, random slope only, and conditional mean. In both this section and the next we use a common longitudinal data model, incorporating a subject-specific “time” variable, x₁, a treatment variable, x₂, which is 1 for a treatment group and zero otherwise, and a time by treatment interaction variable, x₃ = x₁ × x₂. We incorporate the random slopes as slopes over time (and so associated with x₁):

$$Y_{it}\mid b_i\sim \text{independent}\mathcal{N}(\mathrm{E}[Y_{it}\mid b_i],{\sigma }_{ϵ}^2)i=1,\dots ,m;t=1,\dots ,n_i$$

$$\begin{array}{cc}\hfill \mathrm{E}[Y_{it}\mid b_i]=& ({\beta }_0+b_{0i})+({\beta }_1+b_{1i})x_{1it}+{\beta }_2{x}_{2i}+{\beta }_3{x}_{3it}\hfill \\ \hfill b_i\sim & \mathrm{i}.\mathrm{i}.\mathrm{d}\mathcal{N}(0,{\Sigma }_b),\hfill \end{array}$$ (11)

with $\mathrm{var}\left(b_{0i}\right)={\sigma }_0^2$, $\mathrm{var}\left(b_{1i}\right)={\sigma }_1^2$, and cov(b_0i, b_1i) = σ₀₁. For this model, the t^th row of of Z_i is given by $z_{it}^T=\left(1x_{1it}\right)$. In most of this section we consider only the linear mixed model given in (11) but indicate generalizations in Section 4.4.

4.2 Dependence on the conditional mean

In this section we consider a model where the probability of observing an observation is dependent on the true state of the subject at time t. In the Supplementary Material we also give results for an informative visit process that depends directly on the random intercepts and slopes. Dependence on the true mean is incorporated through the conditional value of the linear predictor and a log link:

$$\begin{array}{cc}\hfill \mathrm{P}(R_{it}=1\mid b_i)=& \exp \{\mu +\delta \mathrm{E}[Y_{it}\mid b_i]\}\hfill \\ \hfill =& \exp \{\mu +\delta ({\beta }_0+{\beta }_1{x}_{1it}+{\beta }_2{x}_{2i}+{\beta }_3{x}_{3it})+\delta b_{0i}+\delta x_{1it}{b}_{1i}\}\hfill \\ \hfill \equiv & \exp \{{\mu }_{it}+\delta b_{0i}+\delta x_{1it}{b}_{1i}\},\hfill \end{array}$$ (12)

so this fits into the general formulation, (3), with μ_it = μ+δ(β₀+β₁x_1it+β₂x_2i+β₃x_3it), γ_1it = δ, and γ_2it = δx_1it. For this model, the result of Section 3.3 gives the expected value of the linear predictor conditional on being observed as

$$\begin{array}{cc}\hfill x_{it}^T\beta +z_{it}^T{\Sigma }_b{\gamma }_{it}=& {\beta }_0+{\beta }_1{x}_{1it}+{\beta }_2{x}_{2i}+{\beta }_3{x}_{3it}+\delta {\sigma }_0^2+\delta {\sigma }_{01}{x}_{1it}+\delta {\sigma }_{01}{x}_{1it}+\delta {\sigma }_1^2{x}_{1it}^2\hfill \\ \hfill =& ({\beta }_0+\delta {\sigma }_0^2)+({\beta }_1+2\delta {\sigma }_{01})x_{1it}\hfill \end{array}$$ (13)

$$+{\beta }_2{x}_{2i}+{\beta }_3{x}_{3it}$$ (14)

$$+\delta {\sigma }_1^2{x}_{1it}^2.$$ (15)

Under this informative visit model, the results in (13)-(15) indicate that:

• The estimators of β₀ and β₁ will be biased due to the extra terms in (13);

• The functional dependence of the mean on x₂ and x₃ will be unaffected by the informative visit process (from (14));

• An additional functional relationship (quadratic in x₁) is introduced, which could further bias estimation of the βs if it is not accommodated.

Because the functional dependence on x₂ and x₃ is unaffected by the selection process, these results also indicate that the estimation of β₂ and β₃ may be unbiased if the additional spurious relationship with x₁ is accommodated in the model.

4.3 Multiplicative link functions

In this section we show that some of the results hold for more general link functions than that specified by (3). We hypothesize a model where the conditional probability of a visit is the product of two terms with the first term depending on both the random effects and x₁ and any dependence on other covariates is in the second term:

$$\mathrm{P}(R_{it}=1\mid b_i)\equiv p_1(x_{1it},b_i)p_2(x_{2i},x_{3it}).$$ (16)

This class encompasses models that may be more realistic than the log link model, for example both p₁(·) and p₂(·) could be logistic in form, constraining the probabilities to be between 0 and 1. As before, we can obtain the joint probability of b_i being less than s and R_it = 1:

$$\begin{array}{cc}\hfill \mathrm{P}(R_{it}=1,b_i\le s)=& \mathrm{E}\left[\mathrm{P}(R_{it}=1,b_i\le s\mid b_i=u)\right]\hfill \\ \hfill =& \mathrm{E}\left[\mathrm{P}(R_{it}=1\mid b_i=u)I_{\{u<s\}}\right]\hfill \end{array}$$ (17)

$$={\int }_{-\infty }^s{p}_1(x_{1it},u)p_2(x_{2i},x_{3it})f_b\left(u\right)\mathrm{d}u.$$ (18)

The joint density of b_i and R_it = 1 is therefore:

$$f_{b_i,R_{it}=1}\left(b\right)=p_1(x_{1it},b)p_2(x_{2i},x_{3it})f_b\left(b\right),$$ (19)

and the marginal probability of R_it = 1 is the integral of (19) with respect to b. Therefore the conditional distribution of b_i given R_it = 1 is given by

$$\begin{array}{cc}\hfill f_{b_i\mid R_{it}=1}=& p_1(x_{1it},b)p_2(x_{2i},x_{3it})f_b\left(b\right)∕{\int }_{-\infty }^{\infty }{p}_1(x_{1it},u)p_2(x_{2i},x_{3it})f_b\left(u\right)\mathrm{d}u\hfill \\ \hfill =& p_1(x_{1it},b)f_b\left(b\right)∕{\int }_{-\infty }^{\infty }{p}_1(x_{1it},u)f_b\left(u\right)\mathrm{d}u\hfill \end{array}$$ (20)

That is, there is no functional dependence of the conditional distribution of b on either x₂ or x₃. Therefore the mean of Y in a linear mixed model, conditional on R_it = 1 has the same functional dependence on x₂ and x₃ as the unconditional mean. We therefore expect that fitting a model while ignoring the selection process will yield consistent estimation of β₂ and β₃, perhaps after accommodating spurious relationships in x₁.

4.4 Probit and log link outcome models

The results derived in the above subsections for the linear mixed model generalize in a straightforward way to the log and probit link models in Sections 3.4 and 3.5, albeit on the log or probit scales. For example, under the conditional mean dependence of Section 4.2, the probit model will have (on the probit scale) additional terms associated with the intercept and x₁ as well as a spurious quadratic relationship in x₁.

How these results will affect maximum likelihood fitting, which is based on the entire joint distribution rather than the marginal distribution under selection, is not immediate. However, the performance of fitting methods such as generalized estimating equations with a working independence structure will be governed by the marginal mean structure and the bias results from Section 4.2 will apply. This then suggests that maximum likelihood fits will similarly be affected, which we check using simulations, described in the next section.

5. Simulations

Since the log link theoretical results are only an approximation and apply to the marginal distribution, we conducted a simulation study to verify that they held under visit processes with reasonable degrees of informativeness and to compare the results to a more natural logit link instead of the log link in (3), namely

$$\mathrm{P}(R_{it}=1\mid b_i)=1∕[1+\exp \{-({\mu }_{it}+{\gamma }_{it}^T{b}_i)\}].$$ (21)

To do so, we simulated data with two different outcome distributions and used the linear predictor in Section 4.2, namely a model with an intercept (β₀), time effect (β₁), group effect (β₂), and a group by time interaction (β₃) and random intercepts, b_0i, and slopes, b_1i, with time. The first model was a linear mixed model, (11), with covariances for b_0i, b_1i, and ε_it of ${\sigma }_0^2={\sigma }_1^2={\sigma }_{ϵ}^2=1$, σ₀₁ = 0 or 0.5, and fixed effect parameters β_k = k. Using common random numbers, we simulated informativeness using both (3) and (21) and using the informative visit models in Sections 4.2 and 4 of the Supplemental Material. We simulated 3000 subjects with up to 25 visits per subject, though the number of subjects in any simulation replication was much lower because many subjects have no visits.

We also simulated data from a logistic model, that is a logit link and Bernoulli distribution in (1), again under both a logit and log link informative visit process and using parameters β₀ = –1, β₁ = 0.5, β₂ = 1, β₃ = 0.5, ${\sigma }_0^2={\sigma }_1^2=1$, σ₀₁ = 0 or 0.5, and using 3000 subjects and up to 10 visits.

We simulated data ranging from no “informativeness” to a high degree of informativeness. To determine the upper range of informativeness we aimed to have about a five-fold ratio of P(R_it = 1 | b_i) as the random effect distribution in (3) ranged from its 25^th to 75^th percentiles. This would lead to more than a 10-fold ratio going from an observation that is one standard deviation below normal compared to an observation that is one standard deviation above normal and more than a 100-fold ratio comparing observations two standard deviations below to two standard deviations above normal.

Our first informative visit model has dependence on the conditional mean of Y:

$$\log P(R_{it}=1\mid b_i)=\alpha +\delta \mathrm{E}[Y_{it}\mid b_i].$$ (22)

Using the outcome model described above, the standard deviation of E[Y_it|b_i] is a little less than 2.5. To achieve the five-fold ratio would require δ of about 0.6. Accordingly we simulated values of δ of 0, 0.25, 0.5, and 0.75 and used α = –5 for the linear mixed model and α = –1 for the Bernoulli outcome model.

Our second informative visit model, which we used only for the linear mixed model, has dependence directly on the random effects:

$$\log P(R_{it}=1\mid b_i)=\mu +{\gamma }_0{b}_{0i}+{\gamma }_1{b}_{1i}.$$ (23)

In this model, if γ₀ = γ₁ = γ and if the random effects were uncorrelated then the value of γ giving a five-fold difference would be 0.84. Accordingly, for this model we simulated values of γ_l = 0, 0.5 or 1, σ₀₁ = 0 or 0.5 and we used μ = –4.

Under each of these scenarios we fit a random intercepts and slopes model (allowing separate variances and a covariance) using maximum likelihood and also fit an independence generalized estimating equations approach (i.e., ordinary least squares fit for the linear mixed model or logistic regression fit for the Bernoulli model). For the simulations under the conditional mean informative model we also included a quadratic term in x₁ to accommodate the functional dependence noted in Section 4.2. All simulations were conducted in Stata 13.1 (StataCorp, College Station, TX) and used 500 replications. We report illustrative results in figures below, but the full set of simulation results (including standard errors) is available in tabular form in the online supplemental material.

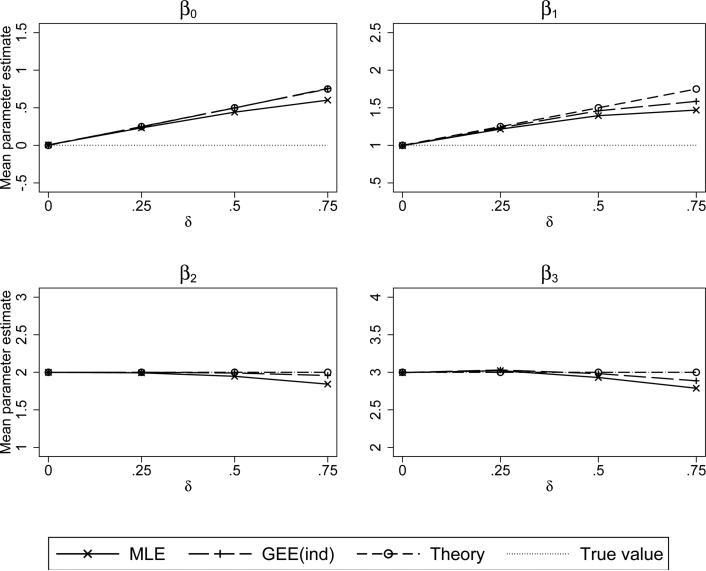
Figure 2 shows the results for the linear mixed model under the conditional mean informative visit model, (22), as well what is predicted by theory based on the log link model (ignoring truncation), and are as expected. The estimators of β₀ and β₁ are badly biased as the degree of informativeness increases. Further, within the range of low to moderate informativeness, the estimators of β₂ and β₃, the parameters unconnected to the random effects, exhibit little bias. There is slight bias at the upper ranges of informativeness for both the mixed model and GEE independence fits. Under strong degrees of informativeness, the approximations needed for the log link theory to apply (namely that the probabilities are less than 1) are violated. For the log link (shown in the supplemental material) there is still slight bias for the mixed model fit under δ = 0.75, but the GEE independence fit does not exhibit bias, as predicted by the theory. The difference between ML and GEE may be because our results apply to the marginal distribution (on which GEE depends) but the ML fits utilize the entire joint distribution.

Figure 2.

Simulated mean values of the maximum likelihood (MLE) and GEE-independence regression coefficient estimators. Simulated under a conditional mean informative visit process with a logit link, i.e., logit(P(R_it = 1)) = –5 + δE[Y | b], and linear mixed outcome model with random intercepts and slopes.

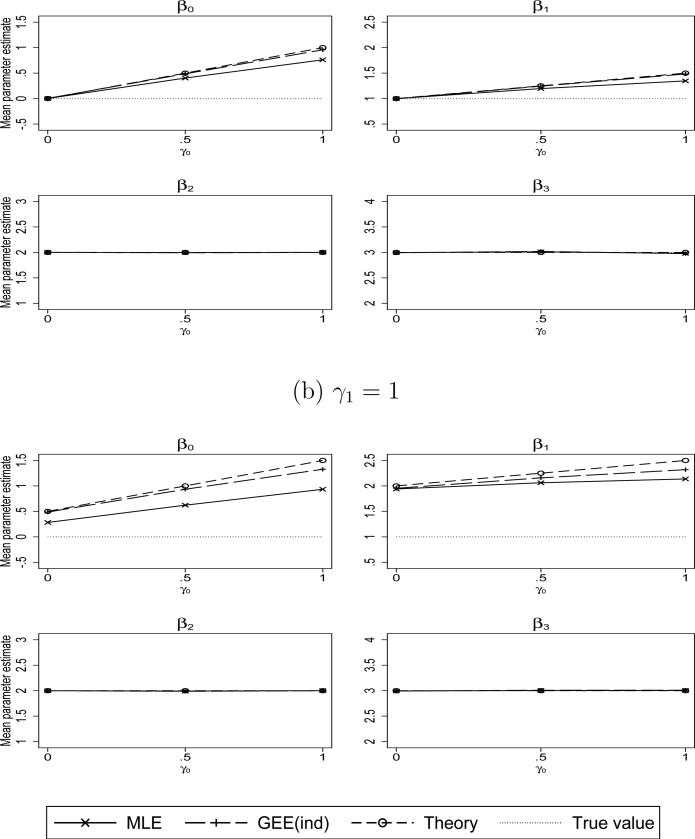
Figure 3 shows the results for the linear mixed model under the random effects informative visit model (23). The results again match well with the theory (see Section 4 of the Supplemental Material), especially qualitatively: large degrees of bias in the estimators of β₀ and β₁ and little or no bias for β₂ and β₃. There are minor discrepancies between the quantitative results predicted by the theory in the most extreme degrees of informativeness (again due to the simulation being conducted under the logit link).

Figure 3.

Simulated mean values of the maximum likelihood (MLE) and GEE-independence regression coefficient estimators. Simulated under a random effects informative visit process with a logit link, i.e., logit(P(R_it = 1)) = –5 + γ₀b₀ + γ₁b₁, and linear mixed outcome model with random intercepts, b₀, and random slopes, b₁.

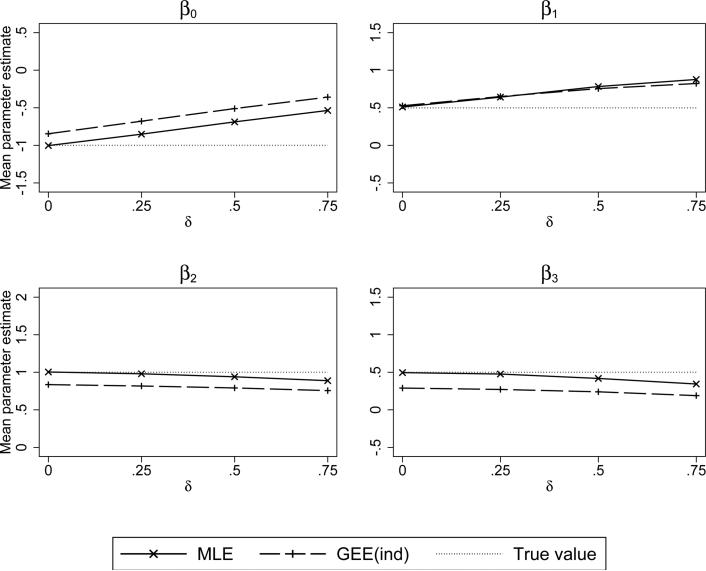
Figure 4 shows the results for the logistic outcome model under the conditional mean informative visit model, (22). The results are similar to that of the linear mixed model. The estimators of β₀ and β₁ exhibit a large degree of bias as the degree of informativeness increases. Further, within the range of low to moderate informativeness, the estimators of β₂ and β₃, the parameters unconnected to the random effects, exhibit little bias. There is slight bias at the upper ranges of informativeness for both the mixed model and GEE independence fits. Note that on Figure 4 the “true” value represents the subject-specific parameter from the generalized linear mixed model and the GEE independence estimator is instead estimating the population-averaged parameter.

Figure 4.

Simulated mean values of the maximum likelihood (MLE) and GEE-independence regression coefficient estimators. Simulated under a conditional mean informative visit process with a logit link, i.e., logit(P(R_it = 1)) = –1 + δE[Y | b], and logistic mixed outcome model with random intercepts and slopes.

As noted at the end of Section 3.2 and under the log link visit model, the marginal distribution of an individual Y_it is unchanged with arbitrary dependence of the visit process on covariates, which can be absorbed as part of μ_it in (3). To check to see if this also held under the logistic link, (21), we redid the simulation of Figure 1 but allowing additional dependence of the visit process on the group variable, x₂. The results were virtually unchanged even under strong dependence on x₂, as predicted by the log link theory. Details are given in the Supplementary Material.

6. Discussion

In this paper we developed theory for the marginal distribution of data generated under a generalized linear mixed model but subject to a novel log link informative visit process. That visit process allowed dependence of the probability of a visit on the random effects in the mixed model. We used the log link because it allowed approximate, theoretical quantification of the bias under the informative visit process; this was supplemented by simulation results using a logit link that gave very similar results.

Broadly speaking, the theory and simulation studies indicate that estimators of parameters associated with the random effects will be badly biased but that those not associated with the random effects will be estimated with little or no bias. The lack of bias with estimated covariate effects unconnected to the random effects is similar to results we and others have demonstrated in the informative cluster size literature (e.g., Williamson et al., 2003; Neuhaus and McCulloch, 2011). However, we did not see the severe degree of bias in that context that we see here.

Our work is similar to the investigation of bias in selection models in the econometric literature. For example, Heckman (1979) studied the effect of selection on the mean in linear models using the equivalent of a probit link instead of our log link. This gives bias for the mean in terms of ratios of normal p.d.f.s and c.d.f.s (inverse Mill's ratios) which are, in turn, complicated functions of the variance components and covariates. Our approach has two main advantages: 1) the log link gives easy to understand bias terms as contrasted with the effects imbedded in inverse Mill's ratios and 2) in dealing with generalized linear mixed models in which the variance-covariance structure influences the marginal mean, we must derive the impact of selection on the entire marginal distribution, not just the mean.

Because the log link visit process does not constrain the visit probabilities to be less than 1 and because the theoretical results apply only to the marginal distribution, we also conducted simulations of the performance of standard analyses (mixed model fits and GEE independence fits) to longitudinal data under a more realistic logit link informative visit process. To a large degree the results mirrored the theory. First, estimators of parameters associated with the random effects were badly biased. Second, under low to moderate degrees of informativeness, the estimators of parameters unassociated with the random effects exhibited little or no bias. However, for large degrees of informativeness, both methods exhibited slight bias.

The results herein indicate that analysis of data that may be subject to informative visit processes should be undertaken with care. Investigation of the random effects structure can provide guidance as to which parameter estimates may be biased (those for covariates associated with the random effects) and therefore interpreted with caution. On the positive side, parameter estimates not associated with the random effects are not likely to be biased due to the informative visit process.