Abstract
Louis Henry Sullivan, the father of skyscrapers, famously stated “Form ever follows function”. In this short review, we will focus on the relationship between form (structure) and function (dynamics) in the brain. We summarize recent advances on the quantification of directed- and weighted-mesoscopic connectivity of mammalian cortex, the exponential distance rule for mesoscopic and microscopic circuit wiring, a spatially-embedded random model of inter-areal cortical networks, and a large-scale dynamical circuit model of money’s cortex that gives rise to a hierarchy of timescales. These findings demonstrate that inter-areal cortical networks are dense (hence such concepts as “small-world” need to be refined when applied to the brain), spatially dependent (therefore purely topological approach of graph theory has limited applicability) and heterogeneous (consequently cortical areas cannot be treated as identical “nodes”).
Keywords: mesoscopic inter-areal connectivity, exponential distance rule, hierarchy of temporal response fields
Introduction
Recent years have witnessed a sea-change in our knowledge of the microscopic local cortical circuits and mesoscopic long-distance connectivity between cortical areas. We recently published a series of papers reporting a new dataset of quantitative- and weighted- inter-areal connectivity in the macaque monkey cortex [1••, 2, 3••]. Moreover, two separate teams reported datasets on the mouse whole-brain connectome [4••, 5••]. The findings revealed that the inter-areal connectivity at the mesoscopic level are dense (more than 50% of all possible connections are present) and dependent on spatial distances between cortical areas. These findings have highlighted limitations of theoretical analysis of brain circuits in terms of purely topological networks with sparse connectivity, and have led to the proposal of an alternative class of spatially embedded random networks which could be more fruitful in Neuroscience [6••, 7]. In this review, we summarize recent advances and discuss to what extent those findings are valid across scales from micro- to mesoscopic cortical circuits, and between primate and rodent.
Whereas structural connectivity is essential for understanding the constraints of brain function, it alone is insufficient to predict the dynamical behavior of neural circuits. Consider two identical neurons interconnected by mutually inhibition. Given this connectome, can one predict the network’s behavior? It turns out that experimentation and theory have uncovered multiple possibilities. First, both neurons may simply remain silent. Second, in response to inputs, the system may behave as a switch, causing only one neuron to be active at any one time. Third, if the neurons are endowed with a slow adaptation, each could take turns to be active leading to a “half-center” oscillator, which is the core of rhythmic central pattern generators. Finally, under certain conditions, the two neurons can be perfectly synchronized, spike by spike: the two neurons fire at the same time, leading to mutual inhibition after a brief delay, and when this inhibition has decayed they can fire again together [8]. This simple example illustrates that dynamical behavior often cannot be deduced from anatomy in a straightforward fashion; physiology and modeling are important for discovering the dynamical operations of neural circuits.
To tackle the brain-wide complex dynamics, which give rise to neuronal function and behavior, several groups have developed large-scale dynamical models [9••, 10, 11••]. In particular, combining monkey interareal connectivity with data on the areal differences in the number of spine counts per pyramidal neuron [12], a new model naturally exhibits a hierarchy of timescales [11••]. These findings exemplify a fruitful interplay between theory and experimentation in discovering general principles of how large-scale brain systems work. This progress has opened the door to tackle complex brain dynamical phenomena including neural avalanches [13] and lognormal distribution of firing rates [14••] in future research.
Spatially embedded microscopic and mesoscopic cortical connectivity
Local neuronal networks in the cortex exhibit non-random configurations with a wide range of synaptic strengths [15]. Because the connections within local areas account for about 80% of the total connections of the cortex [1••], the local circuits constitute a large part of the cortical machine. A recent investigation described the functional organization of synaptic strength in the local circuit thereby making a major contribution to our understanding of the cortex [16••]. In a first instance, these authors used natural images in vivo to look at the correlation of activity in neighboring neurons in the supragranular layers of the mouse visual cortex, before completing whole cell recordings of the same neurons in a slice preparation. These technically challenging experiments revealed the functional organization of the local circuit; the strong reciprocal connections are mostly found between pairs of neurons with high correlated responses whereas neurons with uncorrelated response are infrequently and weakly connected. These findings, extended to showing that cells with similar receptive fields were preferentially connected, are highly significant because they go some way to explaining how recurrent excitation of the supragranular layer neurons amplifies and sharpens weak thalamic inputs [17], or produces self-sustained persistent activity in a number of cortical areas [18]. These results suggest that local circuit neurons may form subnetworks [19, 20, 21, 22], that could provide an important infrastructure supporting global and local integration.
One interpretation of the strongly interconnected neighboring neurons in the supragranular layers is that they constitute cell assemblies. In a sensory area, these cell assemblies not only encode sensory input but also integrate contextual information such as reward, attention and expectation [21]. These contextual interactions are derived largely from the network of long-range inter-areal connections (see Figure 1). The inter-areal graph in macaque has a density of 67%, with individual target areas receiving inputs from between 30 to 80 source areas suggesting high levels of global interactions [2]. The specificity of the inter-areal network is derived from connection weights being highly heterogeneous and conforming to a distance rule, namely the weight of connection between two areas decays exponentially with their wiring distance (Figure 1) [1••]. These findings make it possible to propose a statistical algorithm that predicts many of the observed anatomical features of the inter-areal cortical network including the existence of a network core, the distribution of cliques, global and local weight based communication efficiencies and overall wire-length minimization [3••]. The spatially embedded properties of the interareal network reflect morphological constraints such as folding and the spatial clustering of sensory, motor and cognitive areas. The interareal and local networks share a number of features including lognormal distribution of weights and an exponential decline in connection weight [2, 1••, 15, 23], suggesting that binary connectivity in the brain is rooted in physical and geometrical properties, opening the possibility for a general model of cortical connectivity including local connectivity.
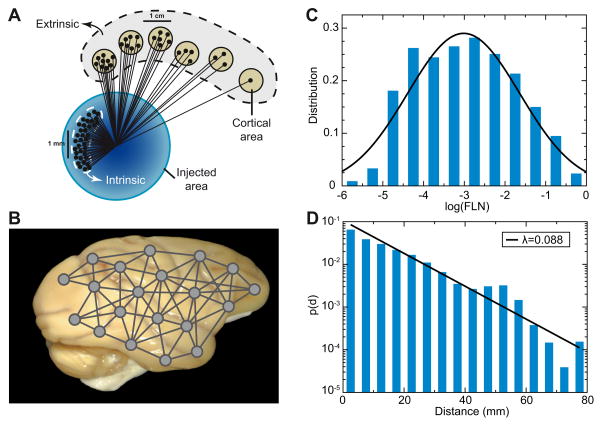
Figure 1.
Inter-areal connections of macaque monkey cortex. (A) A retrograde tracer is injected in a (target) area, and relative weight of connection between a source area and the target area is quantified by the fraction of labelled neurons (FLN), which is the number of labelled neurons in the source area divided by the total number of labelled neurons. (B) The analysis is carried out with a number of cortical areas, leading to a weighted- and directed- inter-areal network connectivity. (C) FLNs span five order of magnitudes and are fit by a lognormal distribution. (D) FLN between a pair of cortical areas is an exponential function of their distance, with the characteristic distance length of ~ 11 mm. Adapted with permission from [1••].
The exponential distance rule stands out from network models applied to the brain connectivity that typically are purely topological and do not take spatial organization into consideration [24•]. Motivated by the recent anatomical findings, Song et al. recently proposed a spatially embedded cortical network model [6••]. In this model the cortex is described as a continuum in space, which is partitioned into a discrete number of areas. Connections are established, point-to-point, using a simple “axonal growth rule” inspired by developmental neurobiology. The model captures the salient quantitative statistics of the monkey data, including the inter-areal connection probability as a function of wiring distance or functional similarity distance between two cortical areas, the five-order of magnitude range of connection weights. Furthermore, the model also reproduces key network properties such as sequence of in- or out-degree, and distribution of three-node motifs (Figure 2). This work suggests a novel class of spatially embedded random networks that are generative and of potential importance for understanding the brain connectomics.
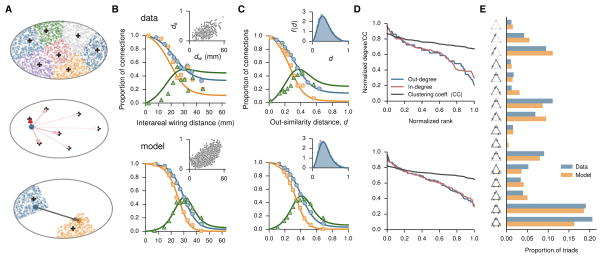
Figure 2.
A spatially embedded random network model of large-scale cortical system. (A) The model cortex is a continuous volume in a 3D Euclidean space in the shape of a spheroid, here represented in 2D as an ellipse for illustration purposes. Top: N areal centers are chosen randomly from the spheroid (plus symbols), and the configuration of the areal centers defines the parcellation of the model cortex into N areas (various colors) through a Voronoi partition of the spheroid, i.e., each area is the set of points closer to a given center than to any other center. Middle: The source of an axon (blue dot) is sampled uniformly from within the spheroid, and the direction of the axon is determined by the sum of the forces which attract the axon to the areal centers. The individual forces decay with the distance to the areal centers (arrows) according to an inverse power law, with the strengths represented here by the red intensity from light (weak) to dark (strong) red. Bottom: With the direction fixed, the axon extends from the source (blue dot) to the target (orange dot); the length is determined by sampling from an exponential distribution. The areas corresponding to the source and target of the axon are assigned according to the parcellation shown at the top. (B) Proportion of directed connections and occurrence of reciprocal and unidirectional pairs as a function of interareal (center-to-center) wiring distance in data (top) and model (bottom). The occurrence of reciprocal (squares) and unidirectional (triangles) connections are compared with p2 (orange line) and 2p(1-p) (green line), respectively, where p is the maximum-likelihood estimate of the proportion of directed connections (blue line). (Insets) Relationship between similarity and wiring distances in the edge-complete subnetwork. (C) Same as B but as a function of output similarity distance. (Insets) Distribution of similarity distances. (D) Normalized in- and out-degree sequences and clustering coefficients (for areas in the edge-complete subnetwork). In-degree represents input from all 91 source areas, for the 29 injected areas; out-degree represents output to the 29 injected areas, from all 91 source areas. (E) Comparison of the triad motif distribution in model and data. Reproduced with permission from [6••].
Similarity and differences between primate and rodent
Much recent work on the functional connectivity of local circuits has been carried out in mice, which is warranted given the high selectivity of cortical receptive fields in this species. Last year two groups reported directed- and weighted-connection data of the mouse brain [4••,5••]. The inter-areal weights of the whole brain span 104 fold, whereas intra-cortical connection weights vary over two orders of magnitude [4••]. While the inter-areal cortical connection weight distribution is well fit by a lognormal distribution in both species, the range of weight values seem to be significantly narrower (102 fold) in mouse compared to monkey (105 fold). Presently it is unclear whether this discrepancy is due to differences in brain size or to rodent primate differences in scaling, as the connection strength measured by both groups depends on neuron number), or technique (intensity of EGFP signals labeled by a anterograde tracer versus count of neurons labeled by a retrograde tracer) used for weight quantification. Regardless, neither technique directly measured the physiological synaptic strengths. While we lack functional data at this level, the synaptic ultrastructure of inter-areal connections show a skewed distribution with a wide range of values [25], suggesting that inter-areal synapses could show a similar range in weight or strength values as do local synapses. Physiological studies [26, 15, 23, 16] revealed synaptic strengths in the microcircuit spanning two orders of magnitude. Note that, at least for nearby pairs of neurons (within a couple of hundreds of microns), the probability of connection decreases with distance but the synaptic strength (measured by the amplitude of excitatory postsynaptic potential) remains constant [15, 23]. It remains to be seen whether the range of physiologically defined synaptic weights are similar for local versus long-distance connections, and across species.
Other important differences between rodent and primate cortical biology need to be considered. First, the scaling rules for rodents and primates are very different [27••], allowing considerable increases in neuron number via increased brain size and neuronal density in primates compared to rodents. Secondly, human and non-human primate corticogenesis shows unique features that could have important structural as well as functional consequences [28•]. A specialized germinal zone named the OSVZ largely generates the supragranular layers of the primate cortex. The precursors of the OSVZ show very different lineage relationships to those observed during mouse corticogenesis. During evolution there is an increase in the number of neurons in the supragranular layers [29], due to the primate-specific high incidence of proliferative divisions of OSVZ precursors.
Recent studies of corticogenesis suggest that members of local assemblies are clonally related [30]. This suggests that the intricate lineages of the primate OSVZ precursors will lead to larger and perhaps more complex interconnected assemblies in the supragranular layers of the primate compared to the rodent. The supra- and infragranular layers differ in their coding strategies; whereas supragranular layers exhibit sparse coding, infragranular layers exhibit dense coding [31]. Sparse coding leads to greater efficiency but at the cost of increased numbers of neurons in agreement with the expansion of the primate supragranular layers. Hence, in the primate, the expanded supragranular layer could argue for an increased role of sparse coding.
Recently it has been suggested that feedback connections could serve to stabilize reliable propagation of information coding in spike times through the cortex [32]. The hierarchical organization of interareal connections and their interaction with the local circuit is thought to implement predictive coding, according to which predictions (i.e. expectations) descend the cortical hierarchy and prediction errors ascend the hierarchy [33]. Would the precision of feedback connections be sufficient to allow the cortical network to learn the statistical regularities of the sensory input? Indeed in the primate this might be relatively more feasible than in the rodent because there is a high precision feedback pathway in the upper part of the primate supragranular layers [2]. In the primate there are two feedback streams, one in the supragranular layers that contains uniquely cortical projecting neurons, and one in the infragranular layer which houses the subcortical projecting neurons [34]. The feedback stream in the supragranular layers is point-to-point, contrasting with the diffuse feedback stream in the infragranular layers. Hence the primate counterstream organization would have a fine grain supragranular feedback system conveying predictions in a sparse coding system and a more classical infragranular course grain feedback system conveying predictions in a dense coding system.
From structure to dynamics: a hierarchy of timescales
The advance of the diffusion tensor imaging (DTI) technique has led to the perspective of non-invasive and quantitatively mapping of connections of the human brain, making it possible to study the structure-dynamics relationship using dynamical “whole-brain” modeling [35•, 9••, 10]. However, DTI has some inherent limitations compared to axonal tracer method [36, 37], and it does not provide directional or hierarchical information about interareal connectivity.
Recently, we developed a dynamical model of the primate cortical system, with inter-areal connections constrained by the recently published weighted- and directed- connectivity data for monkeys [11••]. We assumed that all local areas share an excitatory-inhibitory recurrent architecture described by the same mathematical model. However, certain network properties exhibit heterogeneity quantitatively. In particular, the strength of synaptic excitation varies from area to area, which was calibrated by the anatomical data on the number spines per pyramidal neuron [12]. Interestingly, a hierarchy of timescales emerges in this model system: early sensory areas show brief, transient responses to input (appropriate for sensory processing), whereas higher association areas such as the prefrontal cortex integrate inputs over time and exhibit persistent activity (suitable for decision-making and working memory). Such a hierarchy of “temporal response windows” is supported by fMRI and MEG observations [38,39,40•], our model suggests a large-scale circuit mechanism for this important characteristic of large-scale cortical organizations. It is well known that, in an isolated local circuit, the time constant of dynamics could be larger with strong recurrent excitation [18]. However, the pattern of the timescale hierarchy in the large-scale model has been shown to critically depend on interareal connection loops. For instance, an area with relatively weak local connections may display slow reverberatory dynamics as a result of being part of a large feedback system. This explains why the dominant timescale of a cortical area is not a monotonic function of its position along the brain’s hierarchy (Figure 3D). A theoretical work mathematically identified classes of network architecture that give rise to a hierarchy of disparate timescales differentially localized in different regions of a network [41].
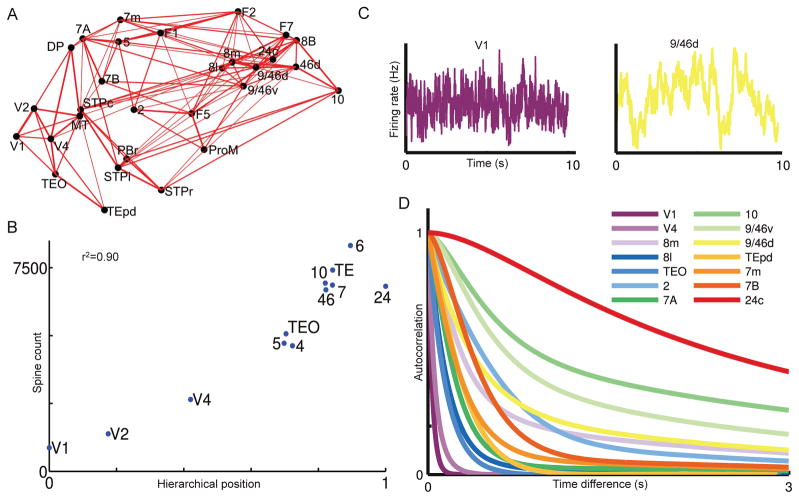
Figure 3.
Hierarchy of timescales in an anatomically-constrained dynamical model of macaque cortex. (A) Connections between 29 areas in the macaque cortex. Strong connections are indicated by lines, with line thickness determined by connection strength. (B) The number of spines on the basal dendrites of pyramidal cells in an area is strongly correlated with the area’s hierarchical position determined by the pattern of laminar projections. This is incorporated into the model, in which the excitation input strength is larger in areas higher in the hierarchy. (C) Stochastic activity fluctuations are fast in Area V1 but much slower in dorsolateral prefrontal cortex area 9/64d. (D) Autocorrelation functions in response to white-noise input to area V1, from which a dominant time constant was extracted for each cortical area. The model shows a hierarchy of timescales, with sensory areas and association areas characterized by short versus long timescales, respectively. Reproduced with permission from [11••].
A segregation of timescales, that are heterogeneously distributed in different parts of the cortical system has a least two conceptual consequences that need to be considered. Spatial differences in neuron response led to a reappraisal of the concept of receptive field by indicating that there are responses beyond the classical receptive field. Similarly, we need to elucidate what is the integration of a signal from a higher area with a long time constant on a neuron with a short time constant in a lower area. Differences in time scales should be contrasted to the idea of scale-free neural dynamics [42,43•,44,45]. Insofar as scale-free dynamics is defined by the lack of a characteristic timescale, does it imply a homogeneity of (however complex) neural dynamics regardless of the cortical location? Future experiments will determine more precisely to what extent neural dynamics differ across cortical areas. At the same time, this question can be investigated in computational modeling constrained by new anatomical data.
Concluding remarks
The quest for the principles of cortical function have to explain the “skeleton of strong connections in a sea of weak connections at the level of the local circuit [15, 46] and the highly skewed distribution of inter-areal connection weights linking areas across different sensory, motor and cognitive modalities [2]. The insight from the recent work [16••] points to an experimental approach to tackle the local aspects of the cortical network, and a similar approach is now becoming technically feasible for the inter-areal cortical network. This work raises many conceptual questions such as the relationship between large-scale population codes and circuit connectivity and the topology of interconnected subnetworks [21]. However, while work in the rodent is in many ways cutting edge, benefitting as it does from numerous technological advantages, we need to keep in mind the important qualitative differences in the rodent and primate brain. The advent of genetic engineering in the primate promises to greatly facilitate future research in this direction. Establishing a firm link from structure to function is essential to understand complex neural dynamics.
We review recent work on mesoscopic, directed- and weighted- connectivity of monkey and rodent.
New data led to the proposal of a spatially-embedded random network model for the mammalian cortex.
Several important differences between primate and rodent are highlighted.
A large-scale dynamical model of the primate cortex gives rise to a hierarchy of timescales.
Acknowledgments
We thank Nikola Markov, Francis Song and Rishi Chaudhuri for their contributions and help with figures. This work was supported by the ONR grant N00014-13-1-0297 and NIH grant R01MH062349 (X.-J.W.) and by ANR-11-BSV4-501 and LABEX CORTEX (ANR-11-LABX-0042) of Université de Lyon, program “Investissements d’Avenir” (ANR-11-IDEX-0007) operated by the French National Research Agency (H.K.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1••.Markov NT, Misery P, Falchier A, Lamy C, Vezoli J, Quilodran R, Gariel MA, Giroud P, Ercsey-Ravasz M, Pilaz LJ, Huissoud C, Barone P, Dehay C, Toroczkai Z, Van Essen DC, Kennedy H, Knoblauch K. Weight consistency specifies regularities of macaque cortical networks. Cereb Cortex. 2011;21:1254–1272. doi: 10.1093/cercor/bhq201. The study reports the first consistent, directed and weighted interareal cortical connectome for macaque, showing that weight heterogeneity and asymmetry are highly characteristic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Markov NT, Ercsey-Ravasz M, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H. Cortical high-density counterstream architectures. Science. 2013;342:1238406. doi: 10.1126/science.1238406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3••.Ercsey-Ravasz M, Markov NT, Lamy C, Van Essen DC, Knoblauch K, Toroczkai Z, Kennedy H. A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron. 2013;80:184–197. doi: 10.1016/j.neuron.2013.07.036. This study shows that the exponential decline of connection weight with distance is a distinctive feature of interareal connectivity and can be used to predict numerous local and global features including a core-periphery structure, global and local efficiency and wire minimization. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4••.Oh SW, Harris JA, Ng L, Winslow B, Cain N, Mihalas S, Wang Q, Lau C, Kuan L, Henry AM, Mortrud MT, Ouellette B, Nguyen TN, Sorensen SA, Slaughterbeck CR, Wakeman W, Li Y, Feng D, Ho A, Nicholas E, Hirokawa KE, Bohn P, Joines KM, Peng H, Hawrylycz MJ, Phillips JW, Hohmann JG, Wohnoutka P, Gerfen CR, Koch C, Bernard A, Dang C, Jones AR, Zeng H. A mesoscale connectome of the mouse brain. Nature. 2014;508:207–214. doi: 10.1038/nature13186. The first report of the mouse whole-brain, cellular-level mesoscopic connectome, including the cortico-thalamic network. The authors used EGFP-expressing adeno-associated viral vectors to anterogradely trace axonal projections, and the connection weights were quantified by the intensity of EGFP-labeling of axons. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5••.Zingg B, Hintiryan H, Gou L, Song MY, Bay M, Bienkowski MS, Foster NN, Yamashita S, Bowman I, Toga AW, Dong HW. Neural networks of the mouse neocortex. Cell. 2014;156:1096–1111. doi: 10.1016/j.cell.2014.02.023. A comprehensive cortico-cortical connectome for the mouse, using both anterograde tracing and retrograde tracing. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6••.Song F, Kennedy H, Wang X-J. Spatial embedding of similarity structure in the cerebral cortex. Proc Natl Acad Sci (USA) 2014;111:16580–16585. doi: 10.1073/pnas.1414153111. The authors proposed a new class of spatially-embedded random network models that explains interareal connectivity in terms of underlying individual axonal projections. The model accounts for the key statistical properties of quantitative- and directed connectivity data from the macaque monkey. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Song F, Wang XJ. Simple, distance-dependent formulation of the Watts-Strogatz model for directed and undirected small-world networks. Phys Rev E. 2014;90:062801. doi: 10.1103/PhysRevE.90.062801. [DOI] [PubMed] [Google Scholar]
- 8.Wang XJ. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol Rev. 2010;90:1195–1268. doi: 10.1152/physrev.00035.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9••.Deco G, Jirsa VK. Ongoing cortical activity at rest: criticality, multistability, and ghost attractors. 2012;32:3366–3375. doi: 10.1523/JNEUROSCI.2523-11.2012. A dynamical model of global cortical network, with symmetrical connectivity based on human diffusion-tensor imaging data, and using a local circuit model adopted from N. Brunel and X.-J. Wang (J Comput. Neurosci. 2001). The ineterareal projections are assumed to be only between pyramidal neurons, the long-range excitation is compensated through adjusting the strength of local inhibitory connections. The model behavior is most similar to human fMRI data at the edge of a bifurcation for multistability. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Deco G, Ponce-Alvarez A, Hagmann P, Romani GL, Mantini D, Corbetta M. How local excitation-inhibition ratio impacts the whole brain dynamics. J Neurosci. 2014;34:7886–7898. doi: 10.1523/JNEUROSCI.5068-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11••.Chaudhuri R, Knoblauch K, Gariel M-A, Kennedy H, Wang X-J. A large-scale circuit mechanism for hierarchical dynamical processing in the primate cortex. Neuron. 2015 doi: 10.1016/j.neuron.2015.09.008. org/10.1016/j.neuron.2015.09.008. A dynamical model based on the new directed- and weighted connectivity of macaque cortex. In the presence of area-to-area heterogeneity, a hierarchy of timescales naturally emerges in this model. This functional hierarchy is not unique, as shown by stimulation of either visual or somatosensory pathway. Slower dynamics of association areas strongly influence the global functional connectivity. [DOI] [PMC free article] [PubMed]
- 12.Elston G. Specialization of the neocortical pyramidal cell during primate evolution. In: Kaass JH, Preuss TM, editors. Evolution of the Nervous Systems: A Comprehensive Reference, Vol. 4 Primates. Amsterdam: Elsevier; 2007. pp. 191–242. [Google Scholar]
- 13.Plenz D, Thiagarajan TC. The organizing principles of neuronal avalanches: cell assemblies in the cortex? Trends Neurosci. 2007;30:101–110. doi: 10.1016/j.tins.2007.01.005. [DOI] [PubMed] [Google Scholar]
- 14••.Buzsaki G, Mizuseki K. The log-dynamic brain: how skewed distributions affect network operations. Nat Rev Neurosci. 2014;15:264–278. doi: 10.1038/nrn3687. A review of scaling properties in the brain, highlighting the widespread observation of lognormal distribution of firing rates. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Song S, Sjöström PJ, Reigl M, Nelson S, Chklovskii DB. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 2005;3:e68. doi: 10.1371/journal.pbio.0030068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16••.Cossell L, Iacaruso MF, Muir DR, Houlton R, Sader EN, Ko H, Hofer SB, Mrsic-Flogel TD. Functional organization of excitatory synaptic strength in primary visual cortex. Nature. 2015;518:399–403. doi: 10.1038/nature14182. A technically superb study showing that the strongly connected neurons in the mouse supragranular layers share highly correlated activity and receptive field properties, the study raises the intriguing question on the role of the weak connections linking with non-correlated activity. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Douglas RJ, Koch C, Mahowald M, Martin KM, Suarez HH. Recurrent excitation in neocortical circuits. Science. 1995;269:981–985. doi: 10.1126/science.7638624. [DOI] [PubMed] [Google Scholar]
- 18.Wang XJ. Synaptic reverberation underlying mnemonic persistent activity. Trends in Neurosci. 2001;24:455–463. doi: 10.1016/s0166-2236(00)01868-3. [DOI] [PubMed] [Google Scholar]
- 19.Perin R, Berger TK, Markram H. A synaptic organizing principle for cortical neuronal groups. Proc Natl Acad Sci USA. 2011;108:5419–5424. doi: 10.1073/pnas.1016051108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bathellier B, Ushakova L, Rumpel S. Discrete neocortical dynamics predict behavioral categorization of sounds. Neuron. 2012;76:435–449. doi: 10.1016/j.neuron.2012.07.008. [DOI] [PubMed] [Google Scholar]
- 21.Harris KD, Mrsic-Flogel TD. Cortical connectivity and sensory coding. Nature. 2013;503:51–58. doi: 10.1038/nature12654. [DOI] [PubMed] [Google Scholar]
- 22.Harris KD, Shepherd GM. The neocortical circuit: themes and variations. Nat Neurosci. 2015;18:170–181. doi: 10.1038/nn.3917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Levy RB, Reyes AD. Spatial profile of excitatory and inhibitory synaptic connectivity in mouse primary auditory cortex. J Neurosci. 2012;32:5609–5619. doi: 10.1523/JNEUROSCI.5158-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24•.Sporns O. Contributions and challenges for network models in cognitive neuroscience. Nat Neurosci. 2014;17:652–660. doi: 10.1038/nn.3690. A highly readable introduction to the concept of networks and their importance in the brain. [DOI] [PubMed] [Google Scholar]
- 25.Anderson JC, Binzegger T, Martin KA, Rockland KS. The connection from cortical area V1 to V5: a light and electron microscopic study. J Neurosci. 1998;18:10525–10540. doi: 10.1523/JNEUROSCI.18-24-10525.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Holmgren C, Harkany T, Svennenfors B, Zilberter Y. Pyramidal cell communication within local networks in layer 2/3 of rat neocortex. J Physiol (Lond) 2003;551:139–153. doi: 10.1113/jphysiol.2003.044784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27••.Herculano-Houzel S. Neuronal scaling rules for primate brains: the primate advantage. Prog Brain Res. 2012;195:325–340. doi: 10.1016/B978-0-444-53860-4.00015-5. The authors review their work using a novel system for making neuron counts that shows unique primate cortical scaling features. [DOI] [PubMed] [Google Scholar]
- 28•.Dehay C, Kennedy H, Kosik KS. The outer subventricular zone and primate-specific cortical complexification. Neuron. 2015;85:683–694. doi: 10.1016/j.neuron.2014.12.060. Review of the unique properties of primate corticogenesis during the generation of the supragranular layers. [DOI] [PubMed] [Google Scholar]
- 29.Cahalane DJ, Charvet CJ, Finlay BL. Modeling local and cross-species neuron number variations in the cerebral cortex as arising from a common mechanism. Proc Natl Acad Sci USA. 2014;111:17642–17647. doi: 10.1073/pnas.1409271111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yu YC, Bultje RS, Wang X, Shi SH. Specific synapses develop preferentially among sister excitatory neurons in the neocortex. Nature. 2009;458:501–504. doi: 10.1038/nature07722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sakata S, Harris KD. Laminar structure of spontaneous and sensory-evoked population activity in auditory cortex. Neuron. 2009;64:404–418. doi: 10.1016/j.neuron.2009.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Moldakarimov S, Bazhenov M, Sejnowski TJ. Feedback stabilizes propagation of synchronous spiking in cortical neural networks. Proc Natl Acad Sci USA. 2015;112:2545–2550. doi: 10.1073/pnas.1500643112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bastos AM, Usrey WM, Adams RA, Mangun GR, Fries P, Friston KJ. Canonical microcircuits for predictive coding. Neuron. 2012;76:695–711. doi: 10.1016/j.neuron.2012.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Markov NT, Vezoli J, Chameau P, Falchier A, Quilodran R, Huissoud C, Lamy C, Misery P, Giroud P, Ullman S, Barone P, Dehay C, Knoblauch K, Kennedy H. Anatomy of hierarchy: feedforward and feedback pathways in macaque visual cortex. J Comp Neurol. 2014;522:225–259. doi: 10.1002/cne.23458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35•.Izhikevich EM, Edelman GM. Large-scale model of mammalian thalamocortical systems. Proc Natl Acad Sci USA. 2008;105:3593–3598. doi: 10.1073/pnas.0712231105. An early large-scale model based on human DTI connectivity data and one of the few large-scale models of the thalamocortical network. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Thomas C, Ye FQ, Irfanoglu MO, Modi P, Saleem KS, Leopold DA, Pierpaoli C. Anatomical accuracy of brain connections derived from diffusion MRI tractography is inherently limited. Proc Natl Acad Sci USA. 2014;111:16574–16579. doi: 10.1073/pnas.1405672111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Reveley C, Seth AK, Pierpaoli C, Silva AC, Yu D, Saunders RC, Leopold DA, Ye FQ. Superficial white matter fiber systems impede detection of long-range cortical connections in diffusion MR tractography. Proc Natl Acad Sci USA. 2015;112:E2820–2828. doi: 10.1073/pnas.1418198112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hasson U, Yang E, Vallines I, Heeger DJ, Rubin N. A hierarchy of temporal receptive windows in human cortex. J Neurosci. 2008;28:2539–2550. doi: 10.1523/JNEUROSCI.5487-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Honey CJ, Thesen T, Donner TH, Silbert LJ, Carlson CE, Devinsky O, Doyle WK, Rubin N, Heeger DJ, Hasson U. Slow cortical dynamics and the accumulation of information over long timescales. Neuron. 2012;76:423–434. doi: 10.1016/j.neuron.2012.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40•.Hasson U, Chen J, Honey CJ. Hierarchical process memory: memory as an integral component of information processing. Trends Cogn Sci (Regul Ed) 2015;19:304–313. doi: 10.1016/j.tics.2015.04.006. An excellent review that marshals empirical evidence in support of a hierarchy of temporal windows in the primate brain and argues for the importance of such a hierarchy for time integration of information over multiple scales. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chaudhuri R, Bernacchia A, Wang X-J. A diversity of localized timescales in network activity. Elife. 2014;3:e01239. doi: 10.7554/eLife.01239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.He BJ, Zempel JM, Snyder AZ, Raichle ME. The temporal structures and functional significance of scale-free brain activity. Neuron. 2010;66:353–369. doi: 10.1016/j.neuron.2010.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43•.Priesemann V, Wibral M, Valderrama M, Propper R, Le Van Quyen M, Geisel T, Triesch J, Nikolić D, Munk MH. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front Syst Neurosci. 2014;8:108. doi: 10.3389/fnsys.2014.00108. A comparison of models with spiking data led to the conclusion that in vivo neural activity does not exhibit self organized criticality but is consistent with a slightly sub-critical state. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Roberts JA, Boonstra TW, Breakspear M. The heavy tail of the human brain. Curr Opin Neurobiol. 2015;31:164–172. doi: 10.1016/j.conb.2014.10.014. [DOI] [PubMed] [Google Scholar]
- 45.Bellay T, Klaus A, Seshadri S, Plenz D. Irregular spiking of pyramidal neurons organizes as scale-invariant neuronal avalanches in the awake state. Elife. 2015;4:e07224. doi: 10.7554/eLife.07224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Barbour B, Brunel N, Hakim V, Nadal JP. What can we learn from synaptic weight distributions? Trends Neurosci. 2007;30:622–629. doi: 10.1016/j.tins.2007.09.005. [DOI] [PubMed] [Google Scholar]