Geodetic measurements reveal similarities between post–Last Glacial Maximum and present-day mass loss from the Greenland ice sheet

Present destabilization of marine-based sectors in Greenland may increase sea level for centuries to come.

Abstract

Accurate quantification of the millennial-scale mass balance of the Greenland ice sheet (GrIS) and its contribution to global sea-level rise remain challenging because of sparse in situ observations in key regions. Glacial isostatic adjustment (GIA) is the ongoing response of the solid Earth to ice and ocean load changes occurring since the Last Glacial Maximum (LGM; ~21 thousand years ago) and may be used to constrain the GrIS deglaciation history. We use data from the Greenland Global Positioning System network to directly measure GIA and estimate basin-wide mass changes since the LGM. Unpredicted, large GIA uplift rates of +12 mm/year are found in southeast Greenland. These rates are due to low upper mantle viscosity in the region, from when Greenland passed over the Iceland hot spot about 40 million years ago. This region of concentrated soft rheology has a profound influence on reconstructing the deglaciation history of Greenland. We reevaluate the evolution of the GrIS since LGM and obtain a loss of 1.5-m sea-level equivalent from the northwest and southeast. These same sectors are dominating modern mass loss. We suggest that the present destabilization of these marine-based sectors may increase sea level for centuries to come. Our new deglaciation history and GIA uplift estimates suggest that studies that use the Gravity Recovery and Climate Experiment satellite mission to infer present-day changes in the GrIS may have erroneously corrected for GIA and underestimated the mass loss by about 20 gigatons/year.

INTRODUCTION

Relative sea-level (RSL) observations and geomorphological constraints on historic ice extent are used to constrain the deglaciation history of Greenland (1–5). However, because the bedrock around Greenland is still responding to deglaciation since the Last Glacial Maximum (LGM), geodetic observations of the present-day rate of uplift can provide information about the temporal and spatial patterns of that deglaciation and Earth’s viscosity profile (5–10). Earlier studies used viscosity profiles that represent a global average. However, in regions close to hot spots or plate boundaries, this may lead to substantial errors in glacial isostatic adjustment (GIA) predictions (11). Hot spot tracks are expressions of tectonic plates moving over upwelling mantle plumes that can alter Earth’s rheological properties. The present-day hot spot under eastern Iceland is thought to have been under eastern Greenland 40 million years ago (12–14). This hot spot would cause a warmer than average upper mantle with reduced viscosity that will significantly affect present-day GIA rates (15). Because previous Greenland GIA models did not consider low viscosity beneath the southern Greenland lithosphere, they will underpredict GIA rates.

RESULTS

Global Positioning System

Here, we use data from the Greenland Global Positioning System (GPS) Network (GNET) (16) (Fig. 1) to constrain past and present-day changes in the Greenland ice sheet (GrIS). The entire network is uplifting in response to a combination of GIA and Earth’s immediate elastic response to contemporary ice mass changes—tectonic deformation is considered negligible. To isolate the GIA signal, we model and remove Earth’s elastic response at each GPS site using satellite and airborne laser and satellite radar altimetry data (see Materials and Methods). The GPS site in southeast Greenland at Kulusuk (KULU; located about 50 km from the ice margin), established in 1996, provides one of the longest records and shows an average uplift rate of 7.7 ± 0.1 mm/year between 1996 and 2015 (Fig. 2A). After the modeled elastic uplift is removed (Fig. 2B), the resulting time series of the residual vertical rate, the GIA (Fig. 2C), is linear over almost two decades of measurements. The resulting time series of GIA at KULU suggests an uplift rate of 4.4 ± 0.1 mm/year. Figure 3A shows inferred GIA uplift rates for the entire GNET.

Fig. 1. Location map.

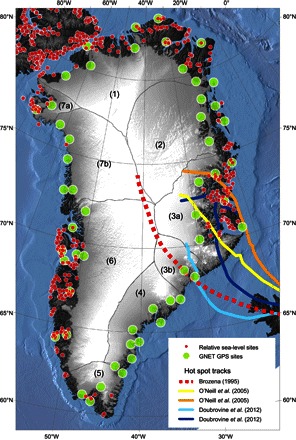
Locations of the GNET GPS stations (red dots) and RSL observations (green dots). Black curves denote the major drainage basins numbered from 1 to 7; drainage 3 is separated into subbasins 3A and 3B (inset), the latter representing the near field of the KUAQ glacier. The yellow curve shows a reconstruction of the Iceland hot spot track (57, 58). Bathymetry is shown over the ocean and surface elevation over the land/ice (25).

Fig. 2. Uplift at KULU.

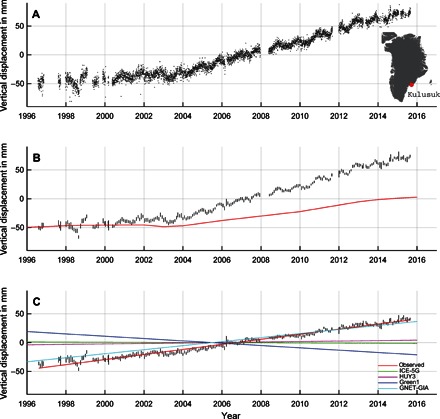
(A) Daily GPS values of the vertical solutions at KULU, southeast Greenland. (B) Monthly mean values of the vertical solutions at KULU. The associated uncertainties are shown as vertical lines. The red curve denotes the estimated elastic vertical displacement based on load changes inferred from radar/laser altimetry observations. (C) Monthly mean values of vertical solutions after removing the annual, semiannual, and elastic vertical displacement, which represents the ongoing GIA vertical displacement from ice load changes following the LGM. Green line, ICE-5G GIA trend; blue, Green1 GIA trend; light blue, GPS inferred GIA trend; purple, HUY3 GIA trend; red, observed.

Fig. 3. Glacial isostatic adjustment.

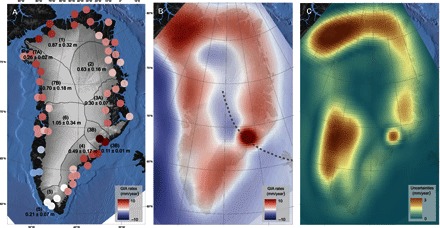
(A) Inferred GIA vertical displacement rates at GNET sites. Gray curves denote major drainage basins, and the numbers represent SLE estimates of each basin. (B) GIA vertical displacement rates from new model entitled “GNET-GIA.” (C) Uncertainties of GIA vertical displacement rates.

We divide the GrIS into seven major drainage basins (Fig. 1), with basins 3 and 7 subdivided further into two parts each [3 (A and B) and 7 (A and B), respectively]. Basin 6 shows negative GIA rates (subsidence), whereas all other basins show positive rates (uplift) (see Fig. 3A). Our measurements show GIA rates of 5 to 8 mm/year in north Greenland (basin 1) and 3 to 5 mm/year in southeast and northwest Greenland (basins 4 and 7). However, the largest GIA rate, ~12 mm/year, is measured in east Greenland (basin 3B) near Kangerdlugssuaq (KUAQ) glacier (Fig. 1). We compare our measured GIA rates with modeled estimates from the Green1 ice load history (2) (fig. S7B), which is constrained by RSL data and includes a glacial readvance during the late Holocene [5 thousand years ago (ka B.P.)]. For ice load variability outside of Greenland, we use the Australian National University ice load history (2). This Green1 reconstruction is optimized considering a lithosphere thickness (LT) of 80 km, upper mantle viscosity (UMV) of 5 × 10²⁰ Pa·s, and a lower mantle viscosity (LMV) of 1 × 10²² Pa·s, and produces relatively large GIA uplift rates in north Greenland and close to zero in the rest of coastal Greenland. The more recent deglaciation models, such as HUY3 (10) and ICE-5G (3, 17), produce similarly large uplift rates in the north and almost zero elsewhere (see Materials and Methods). In general, differences between the three models are of the order of a few millimeters per year. Our measured GIA rates are inconsistent with all three models and suggest that the deglaciation history and/or Earth’s viscosity profiles used by the models are incorrect. Notably, all three models show the largest disagreements with GPS-inferred GIA rates in regions with almost no RSL data (basins 3, 4, and 7), suggesting that the lack of observational constraints may have significantly affected the glacial reconstructions for those regions.

Improving Green1 using GPS observations

To improve the GIA predictions on the basis of Green1, we modify the UMV to 4 × 10²⁰ Pa·s and the LMV to 2 × 10²² Pa·s and reduce the effective elastic lithosphere to 60 km [this profile is denoted as viscosity model–GPS (VM-GPS); table S2]. This modification of Earth model yields uplift rates consistent with rates measured by GPS, particularly in basins with very good spatial distributions of RSL data (basins 1, 2, 3A, and 6; see Fig. 1). The forward model produces GIA rates fully consistent with the GPS-derived GIA rates for a plausible viscosity profile in regions where the deglaciation history is strongly supported by RSL data.

To improve the performance of the GIA modeling in basins with no or few RSL data, we take advantage of the GPS observations. We develop a new glaciation history constrained to the GIA rates inferred from GPS observations by estimating a scaling between the modeled and measured GIA uplift rates for each basin (see Table 1). A scale value close to 1 implies that the model and observations are consistent, >1 means the model underestimates past mass loss, and <1 means the model overestimates past ice loss, assuming, as a first-order approximation, a linear relationship between ice load and GIA response. Table 1 shows our best-fitting scale estimates for the relationship between modeled and inferred GIA. In basins 1, 2, 3A, and 6, estimated scales are close to 1 when accounting for the uncertainties; consequently, for those basins, we adapt the loading history as provided by Green1 with only a slight modification. Basins 4, 5, and 7 (A and B) suggest scaling parameters >2, indicating that past mass loss has been greatly underestimated by more than 100% by the Green1 deglaciation model (Table 1).

Table 1. Scale factors between inferred and predicted GIS rates for each basin and adopted viscosity profile.

The LMV is 2 × 10²² Pa·s for all profiles. The asthenosphere thickness is set to 200 km.

Basin	Scale factor	Viscosity profile			No. of RSL data	No. of GPS sites
		LT (km)	AV (1020 Pa·s)	UMV (1020 Pa·s)
1	1.04 ± 0.45	60	—	5	180	10
2	0.97 ± 0.36	60	—	5	25	6
3A	1.07 ± 0.33	60	—	5	160	7
3B	1.06 ± 0.20	40	0.1	5	0	2
4	5.10 ± 0.41	60	—	5	0	10
5	1.96 ± 0.45	60	—	5	13	3
6	1.14 ± 0.56	60	—	5	281	9
7A	2.28 ± 0.24	60	—	5	56	2
7B	3.45 ± 0.35	60	—	5	1	5
Total	—	—	—	—	716	54

The observed GIA rates in basin 3B are significantly larger and more localized compared to all the other GPS sites. They cannot be reproduced using Green1 in conjunction with the viscosity profile VM-GPS. We therefore explain the large observed uplift as a result of ice loss during the past century in the presence of a comparably weak Earth structure, reflected by a thinner lithosphere and the presence of a low-viscous asthenosphere. Here, the GIA response to the retreat of the KUAQ area assumes full isostatic equilibrium (18) in 1900. We estimate basin-wide elevation changes for the KUAQ area glaciers from 1900 to the present on the basis of termini positions, fresh trimlines, aerial photos, and airborne altimetry data (19–21). Thus, the 19th century loading is well constrained. The retreat of the glacier front position since 1900 is shown in the study by Khan et al. (21). The associated recent load changes are added to Green1. Figure 4 shows present-day GIA uplift rates based on mass loss over the last century for 12 different Earth structures with an LT ranging from 30 to 60 km and asthenosphere viscosity (AV) ranging from 4 × 10¹⁸ to 1 × 10²⁰ Pa·s (asthenosphere thickness is 200 km). The UMV is set to 5 × 10²⁰ Pa·s and LMV is set to 2 × 10²² Pa·s for all 12 combinations. Among the present-day GIA uplift rates shown in Fig. 1, the viscosity profile of AV = 1 × 10¹⁹ Pa·s, UMV = 4 × 10²⁰ Pa·s, LMV = 2 × 10²² Pa·s, and an LT = 40 km match the GIA rates as observed by GPS. The LGM contribution to the GIA is close to zero for AV = 1 × 10¹⁹ Pa·s. Similar low-viscosity asthenosphere values have been reported, for example, in Patagonia (AV = ~4 × 10¹⁸ to 8 × 10¹⁸ Pa·s) (22), Alaska (AV = 1.4 × 10¹⁹ Pa·s) (23), and West Antarctica (AV = ~10¹⁹ Pa·s) (24, 25).

Fig. 4. GIA rates in basin 3B.

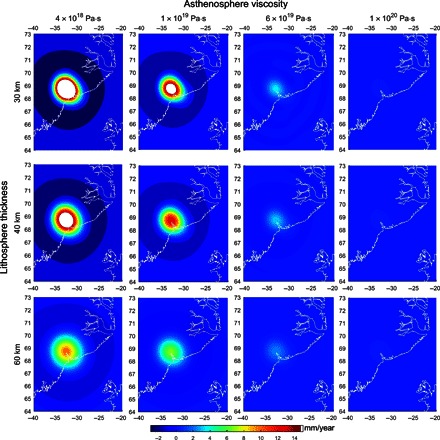
Spatial pattern of GIA-induced uplift by the retreat of the KUAQ glaciers in the past century for different LT and AV; best fit to the measured GIA uplift is achieved for LT = 40 km and AV = 1 × 10¹⁹ Pa·s. The UMV and LMV are constant with 5 × 10²⁰ and 2 × 10²² Pa·s, respectively (VM-GPS).

Sea-level equivalent

From the Green1 glacial reconstruction, we infer the ice mass loss for each basin since the LGM, expressed as sea-level equivalent (SLE) (Table 2). The total SLE contribution of the GrIS since the LGM from the unaltered Green1 deglaciation history is 3.2 m. For comparison, the GrIS at present holds enough ice to raise global sea level by 7.4 m (26). Our improved deglaciation history constrained by GPS suggests an SLE contribution of 4.6 ± 0.7 m since the LGM (44% greater than Green1). The increase of 1.4 m largely originates from basins 4, 5, and 7 (Table 2). The improved deglaciation history suggests that central and southeast as well as northwest Greenland (basins 3, 4, and 7) accounted for a total 1.9-m SLE, which corresponds to 40% of the loss of the GrIS since the LGM. Our SLE estimate is consistent with an independently derived value, obtained from an ice sheet model constrained by RSL data, which estimates a maximum SLE volume of 5.1 m at 16.5 ka B.P. (10). However, the spatial distribution of the mass loss that contributes to SLE estimates is quite different. For example, we estimate more mass loss from basins 4, 5, and 7 and less from basins 1 and 2 than the HUY3 model. These basins are characterized by a high density of marine-terminating outlet glaciers. The coarse grid resolution (20 km) of the ice sheet model used in HUY3 is insufficient to resolve the flow of outlet glaciers (27), thus possibly underestimating mass loss from these areas.

Table 2. SLE mass change per basin.

SLE estimates for each basin from Green1 and the new GPS-based deglaciation model.

Basin	Green 1 SLE (m)	Scaled Green1 SLE (m)	SLE increase (%)
1	0.84	0.87 ± 0.38	4
2	0.65	0.63 ± 0.23	−3
3A	0.28	0.30 ± 0.09	7
3B	0.10	0.11 ± 0.02	10
4	0.10	0.51 ± 0.04	410
5	0.11	0.21 ± 0.05	91
6	0.92	1.05 ± 0.52	14
7A	0.11	0.25 ± 0.03	127
7B*	0.09	0.70 ± 0.18	678
Total	3.21	4.63 ± 0.72	44

*Load distribution modified (see text).

DISCUSSION

Our GPS uplift rates suggest a complex three-dimensional (3D) viscosity structure beneath southeast Greenland, which should be taken into account in the prediction of GIA rates. Extreme uplift rates in southeast Greenland point toward an asthenospheric layer with a viscosity as low as 1 × 10¹⁹ Pa·s (see Fig. 4). The low-viscosity zone, a consequence of the Iceland hot spot and its migration, is supported by seismic tomography and geodynamic modeling (14, 28). In regions with no or few RSL data, geodetic data have been shown to be critical for reliably constraining the deglaciation history and regionally refining the viscosity structure.

A warmer upper mantle in southeast Greenland (and presumably along the past hot spot track) may also have a large influence on ice sheet or glacier flow dynamics, because a greater geothermal heat flux at the base of an ice mass (14, 29) will affect its internal thermal regime and the presence of basal melt water (30). The viscosity of ice has an inverse exponential relationship with temperature. The onset of increasing flow of the northeast Greenland ice stream (the largest flow feature of the ice sheet), for example, has been linked to a geothermal hot spot (14, 31). Geodynamic models suggest that the path of the Iceland hot spot went beneath the interior of the GrIS (12–14), which would potentially reduce the amplitude of the GIA-induced subsidence (Fig. 3B) in the interior caused by enhanced accumulation at the start of the Holocene. We demonstrate the importance of correctly accounting for GIA when using Gravity Recovery and Climate Experiment (GRACE) satellite data, because a proportion of the mass gain in central Greenland reported in several recent studies [for example, Sutterley et al. (32)] using GRACE and predicted by models in a warming climate (33) could be an artifact of an erroneous GIA correction in the interior. The improved deglaciation history constrained by GPS suggests a GIA-induced mass correction for GRACE of 32 gigatons (Gt)/year, compared to 13 Gt/year (ICE-5G) (17). As a consequence, studies will underestimate ice mass loss inferred from GRACE observations by 19 Gt/year when using ICE-5G as a GIA correction.

Mass loss of the GrIS has increased over the last two decades because of an acceleration of glacier flow and enhanced surface melting (34). During this time, the basins of the southeast, east, and northwest of the ice sheet (3, 4, 8) have undergone profound change and have contributed more than 70% of the total ice loss to the ocean. These regions of the ice sheet are dominated by extensive direct contact with the ocean (Fig. 1). A recent study by Kjeldsen et al. (19) shows that the same three basins contributed 77% of GrIS’s total mass loss over the last century (between 1900 and 1981) (see Materials and Methods and table S7), and our study suggests that the east and southeast (basins 3 and 4) and northwest (basin 7) also contributed significantly (40%) to ice mass loss over millennial time scales. Therefore, it seems likely that the present destabilization of these marine-based sectors will continue to provide the majority of Greenland’s contribution to sea-level rise in the future.

Our findings, based primarily on geodetic measurements of crustal motion, suggest that the rheology of the mantle beneath Greenland has been poorly characterized by failing to take into account the tectonic history of the region. The localized GIA signature in southeast Greenland caused by a low-viscosity upper mantle layer has only been unequivocally revealed by the presence of a dense network of GPS stations, suggesting that these measurements are critical for accurately reconstructing GIA. Seismic tomography suggests that similar rheological mischaracterizations are also likely in Antarctic GIA estimates (35). Rheological changes and poorly known ice histories there may have an even larger impact on present-day estimates of ice mass loss inferred from GRACE than in Greenland; however, the sparse GNET in Antarctica will make a comprehensive analysis difficult or impossible.

MATERIALS AND METHODS

GPS data processing

To estimate site coordinates, we followed the procedure of Khan et al. (36). We used the GIPSY OASIS 6.3 software package developed at the Jet Propulsion Laboratory (JPL) and released in March 2014. We used JPL final orbit products, which include satellite orbits, satellite clock parameters, and Earth orientation parameters. The orbit products took the satellite antenna phase center offsets into account. Receiver clock parameters were modeled, and the atmospheric delay parameters were modeled using the Vienna Mapping Function 1 (VMF1) (37, 38), with VMF1 grid nominals. Corrections were applied to remove the solid Earth tide and ocean tidal loading. The amplitudes and phases of the main ocean tidal loading terms were calculated using the automatic loading provider (http://holt.oso.chalmers.se/loading) (39) applied to the FES2004 ocean tide model, including correction for center of mass motion of Earth due to the ocean tides. The site coordinates were computed in the IGS08 frame (40). Table S1 shows the best-fitting uplift rates when taking the temporally correlated noise into account. We used 30-day averages of the daily vertical solutions to take the temporally correlated (non-Gaussian) noise into account. We used the root mean square of those averages to represent their uncertainties σ_GPS.

The observed GIA rates were obtained by removing the elastic response to present-day mass loss from the observed GPS rates. The uncertainty of the observed GIA rates was estimated as the sum in quadrature of the σ_GPS and σ_elastic

$${\mathrm{\sigma }}_{\text{GIA}}=\sqrt{{\mathrm{\sigma }}_{\text{GPS}}^2+{\mathrm{\sigma }}_{\text{elastic}}^2}$$

The uncertainty of the elastic response, σ_elastic, is described in the next section. The locations of the GPS stations used in this study are displayed in fig. S1, and the observed time series of GIA vertical displacements are presented in fig. S2.

Elastic uplift and the associated uncertainty

We first estimated the rate of ice volume change using 1995–2014 NASA’s Airborne Topographic Mapper (ATM) flights (41) derived altimetry, supplemented with laser altimetry observations from the Ice, Cloud, and Land Elevation Satellite (ICESat) (42) during 2003–2009; the airborne Land, Vegetation, and Ice Sensor (LVIS) instrument (43) during 2007–2013; radar altimetry from the CryoSat-2 (44, 45) satellite during 2010–2015; and European Remote-Sensing Satellite–1 (ERS-1) and ERS-2 data during 1995–2003 (46). We converted the volume loss rate into a mass loss rate, taking firn compaction into account, as described by Kuipers Munneke et al. (47). To predict the elastic displacements, we convolved mass loss estimates (from ICESat, ATM, and LVIS) with the Green’s function for vertical displacements derived by Petrov and Boy (48) for the Preliminary Reference Earth Model (49). To predict the associated uncertainty of the elastic response, σ_elastic, we convolved the uncertainty of mass loss estimates with the Green’s function for vertical displacements.

Table S1 shows predicted uplift rates for each GPS site. Figure S3 shows the elevation change rates for 3-year periods between 1997 and 2015, and fig. S4 shows the total mass loss rate during 1997–2015.

GIA: Viscoelastic Earth model

We predicted the GIA with a Maxwell-viscoelastic self-gravitating Earth model on the basis of the spectral finite element method developed by Martinec (50). The code used here provided a spatial resolution up to spherical harmonic degree and order 256 (ca. 80 km) and had recently been benchmarked with other GIA models (51). Earth structure prescribed here was radially symmetric and divided into four layers: an elastic lithosphere, asthenosphere, upper mantle, and lower mantle with the respective viscosities (table S2). It should be noted that Earth model used here assumed elastic incompressibility, leading to a greater effective elastic thickness compared to compressible models. Following Tanaka et al. (52), the elastic LT should be divided by a factor of approximately 0.75 for comparison with compressible models used [for example, by Peltier (17)].

Glacial reconstruction Green1

To estimate the GIA uplift rates, we adopted the Green1 deglaciation history (2), which is a geomorphological reconstruction constrained by RSL data. Figure 1 shows the distribution of RSL data and their spatial subdivision as considered in Green1. Fleming and Lambeck (2) showed that a regional adjustment of the initial load history was necessary to reconcile with the RSL data. However, it is notable that the reconstruction is poorly constrained in southeast and northwest Greenland because of a lack of RSL evidence.

1D viscosity profile for Greenland

Earth structure underneath the GrIS was highly uncertain. For the reconstruction of Green1, a range of plausible viscosities and LT was tested. The preferred profile for Green1 (table S2), referred to as EARTH1 by Fleming et al. (53), reflected the tectonic setting of Greenland being, to a large extent, an old craton. We optimally fit observed present-day GIA uplift rates in basins 1, 2, 3A, and 6 with an LT of 60 km, a UMV of 5 × 10²⁰, and an LMV of 2 × 10²² Pa·s (denoted as VM-GPS). The mantle viscosities and LT were within the limits of EARTH1 and therefore predicted relative sea level consistent with observed values (2, 53). Independently, Nakada et al. (54) suggested very little sensitivity to lower mantle properties when considering the fit to RSL sites in Greenland. The use of a slightly thinner LT of 60 km compared to the nominal value of 80 km was justified by a recent study [for example, Zhao (15)], suggesting a thinner Greenland lithosphere. The higher viscosity for the lower mantle mainly controlled the large-scale, long-wavelength GIA patterns and did not have a significant effect on the regional GIA predictions for Greenland as detected by GPS.

3D viscosity profile for Greenland

Priestley and McKenzie (55) provided evidence for a gradient in LT from north to south and toward Iceland. Therefore, we refined the 1D viscosity structure for Greenland by individually assigning average viscosities to each region (1 to 7) in Fig. 1. We based the parameter estimate of the LT and UMV on Earth model of Priestley and McKenzie (55), which is a global model derived from seismic tomography together with other geophysical and petrological observations. The absolute values of viscosity by Priestley and McKenzie (55) were calibrated to fit 4.2 × 10²⁰ Pa·s within the range of 150 to 300 km, as inferred from GIA inversion analysis of the upper mantle viscosity in Fennoscandia [Zhao et al. (56)]. Moreover, Priestley and McKenzie (55) defined the LT as the change from convective to conductive heat transport. This “thermal” lithosphere definition is thicker than the elastic (or “mechanical”) lithosphere, which is relevant for the viscoelastic rebound calculations presented here.

To adapt the model for our purpose of GIA modeling in Greenland, we calibrated Earth model parameters to the viscosity profile for basins 1, 2, and 6 (VM-GPS): these regions had abundant RSL data and the GIA predictions based on Green1 showed an excellent fit to the GPS rates. First, we defined a threshold of the viscosity above which the deformational behavior was considered purely elastic (here, 10²⁴ Pa·s) and inferred the corresponding average depth within each basin, ${\mathit{h}}_{\mathit{L}}^{*}$. Then, an adjustment factor α was inferred, such that $\mathrm{\alpha }{\mathit{h}}_{\text{LT}}^{*}=60 \text{km}$ (our best-fit LT) within basins 1, 2, and 6. It should be noted that ${\mathit{h}}_{\mathit{L}}^{*}$ is similar in these three basins and also in the model of Priestley and McKenzie (55). We then applied α to the other basins. Next, we similarly calculated a scaling factor for the UMV, such that it equals VM-GPS in basins 1, 2, and 6: β ${\mathrm{\eta }}^{*}$ = 5 × 10²⁰ Pa·s (our best-fit viscosity). It should be noted that the sensitivity to the threshold values for inferring the mechanical LT was low. The resulting values of the LT and UMV are shown in table S3 (rounded to 10 km for ${\mathit{h}}_{\text{LT}}$ and 1 × 10²⁰ Pa·s for the viscosity). Applying separate (1D) viscosity profiles for each region neglected the transmission of stresses across lateral boundaries and was therefore considered a preliminary step toward full 3D Earth modeling.

Sensitivity analysis

We assessed the uncertainty of the scale factor (load magnitude) introduced by the variation in the load and Earth model parameters. For this, we calculated an ensemble of regional GIA responses on the basis of Green1 with different values for VM-GPS (1D and 3D). We fit these to the GIA-induced GPS rates. The ensemble was created by perturbing (i) the termination of the deglaciation in Green1 (Δt_end = ±500 years), as well as (ii) the LT $({\mathrm{\Delta }\mathit{h}}_{\mathit{L}}=\pm 10 \text{km}$) and the asthenosphere mantle viscosity (ΔAV = ± 1 × 10²⁰ Pa·s). The values represent 1-σ parameter uncertainties, which are then propagated to the scale parameter estimates. Table S4 shows the influence of each parameter, as well as their total induced variability. Note that the trade-off between parameters and overlaps between GIA signals of individual regions caused correlated uncertainties of the scale parameter. It is evident that the LT had the greatest influence on the scale factor. Exceptions are regions 5 and 6, which were subject to a neoglaciation, increasing the sensitivity to the timing of the load and the viscosity parameter. The uncertainties were added to the scale factor uncertainties associated with the GPS rates in Tables 1 and 2.

1D versus 3D structure

Overall, the introduction of individual viscosity profiles had only a small effect on the scale factor. Table S5 lists the ratio of the scale factor using 3D versus 1D viscosity profiles. In regions 3A and 4, the scale factor being close to 1 was explained by the trade-off in the GIA response between a thinner lithosphere (larger uplift) and lower viscosity (lower uplift). Region 7 (A and B) showed lower uplift rates because of a much thicker lithosphere, requiring about 20 to 30% larger loads compared to the 1D case. Region 5 showed a strong signature of the neoglacial readvance. In this case, depending on the mantle viscosity, displacement was dominated by the response to the LGM retreat (high viscosity leading to uplift; 1D case) or neoglacial readvance (low viscosity causing subsidence; 3D case). Note that for the 3D case, the scaling factor had a negative sign to accommodate the GPS-measured uplift rates.

Constraining Green1 to GPS observations

To improve the performance of the deglaciation history in basins with no or few RSL data (basins 4, 5, and 7), we developed a new deglaciation history constrained to the GIA rates inferred from GPS. To do this, we estimated the ratio between modeled and inferred GIA rates at GPS sites within a basin and adjusted the Green1 deglaciation history basin-by-basin using this scale factor. Thus, the scaled model predicted GIA rates tuned to fit the inferred GIA rates, accounting for the uncertainties associated with the GPS rates. The scale factors for each basin are shown in table S3. For each basin, we used the viscosity profile VM-GPS, except for basin 3B, where an asthenosphere of thickness 200 km (LT, 160 km) with lower viscosity is introduced.

The results show that the GPS rates confirmed the GIA predictions of Green1 in basins 1, 2, 3A, and 6 with good abundance of RSL data (scaling close to 1). With the 1900 to present mass changes of KUAQ area glaciers and the low-viscosity asthenosphere, the perfections reconciled with GPS also for basin 3B. However, substantial adjustments were necessary in other basins. For example, to reproduce the observed GIA rates in basin 5 (south Greenland), the ice loss from Green1 must be multiplied by a factor of 1.96 ± 0.45. This simple approach provided a first-order adjustment to the LGM ice mass changes of Green1, justified by the linear relationship between loading and GIA response for a fixed temporal evolution.

We adopted the geometry of ice load retreat of Green1 in all basins, except in the northwest (basin 7). Here, the GPS sites indicated GIA-induced uplift along the entire coast of the basin, which is, to some extent, captured by ICE-5G. However, Green1 could not reproduce this signal by simple scaling, because the northern part of basin 7 (henceforth, 7A) experienced greater ice retreat than its southern part (henceforth, 7B). Therefore, we modified the terminal margins of the LGM ice sheet extent in basin 7B, in agreement with studies of glaciological modeling (1). For this, we defined a zone within 50 km of the current coastline with uniformly distributed ice retreat since the LGM. At each time step, the additional ice thickness change was set to the maximum within basin 7B (800 m at LGM) and synchronized to the temporal evolution of this maximum. This modification of Green1 allowed independent scaling for basin 7 (A and B), leading to reconciliation of the scaled predicted GIA pattern with the GPS rates in the entire basin. From the scaling factors, the ice thickness change since the LGM of the scaled model Green1 VM-GPS is shown in fig. S5.

Comparison with ICE-5G

Figure S6 shows present-day GIA uplift rates computed by deglaciation history (VM) from scaled Green1 (VM-GPS) (fig. S6A), Green1 (EARTH1) (fig. S6B) (2), and ICE-5G (VM2) (fig. S6C) (17). The glacial reconstructions Green1, ICE-5G, and HUY3 exhibited very similar uplift rate patterns in north and central east Greenland, with subsidence in southwest Greenland. The scaled Green1 model showed much larger uplift rates along all coastal regions of Greenland, and a localized pattern of extreme uplift associated with the low-viscosity zone in southeast Greenland.

Elastic correction at KUAQ and MIK2

The elastic correction to the observed vertical GPS rates could potentially be erroneous and therefore produce biased inferred GIA rates. Here, we showed that this is not the case. The elastic vertical displacement rates due to ice mass loss, estimated from ICESat, ATM, LVIS, and CryoSat-2 between 2009.6 and 2015.6, are 11.8 ± 1.3 mm/year at KUAQ and 5.1 ± 0.1 mm/year at MIK2 (Miki Fjord) (table S1).

Assuming that basin 3B has the same viscosity profile as the rest of Greenland (VM-GPS) and the load history is correct, we predicted GIA rates at MIK2 and KUAQ of 1.2 mm/year. We now test different scenarios of elastic uplift correction that reconcile with GIA rates of 1.2 mm/year at MIK2 and KUAQ. If we can find an elastic correction where the GPS rate minus the elastic rate is 1.2 mm/year at MIK2 and KUAQ, then we may conclude that basin 3B has the same viscosity as VM-GPS.

If we assume that contemporary mass loss from the KUAQ glacier is underestimated by a huge amount, that is, 20 Gt/year, then weobtain a GIA rate of 1.2 mm/year at KUAQ; however, the rate of 7.0 mm/year at MIK2 is still too rapid, and we may reject this scenario (see table S6).

The KUAQ GPS site is closer to the KUAQ glacier than MIK2; therefore, it is impossible to obtain a residual rate (GPS-elastic) of 1.2 mm/year at both GPS sites simply by assuming greater mass loss from the KUAQ glacier. The elastic signal will be focused at the KUAQ GPS site. An extra mass loss of 20 Gt/year would also result in a total mass loss of more than 35 Gt/year, which is too large for the KUAQ glacier.

To produce a “missing elastic” rate of about 10 mm/year at both GPS sites (see table S1), the missing elastic mass loss must be located approximately the same distance from the two GPS sites. Figure S7 shows five scenarios of mass loss rate that give vertical rate of 10 mm/year at both GPS sites. However, all scenarios require unrealistic mass loss rates between 25 and 45 Gt/year in areas without any major outlet glacier that may potentially be losing mass at such high rate.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/2/9/e1600931/DC1

fig. S1. Locations of the permanent GPS stations in Greenland.

fig. S2. Monthly mean values of vertical GPS solutions after removing the annual, semiannual, and elastic vertical displacement.

fig. S3. Elevation change rate during 1997–2015.

fig. S4. Time series of GrIS mass loss rate.

fig. S5. Ice thickness change since the LGM as represented by the Green1 VM-GPS.

fig. S6. GIA rates.

fig. S7. Landsat image of southeast Greenland.

table S1. Location of GPS sites, data time span, observed uplift rates, predicted elastic uplift rates, and observed GIA uplift rate.

table S2. 1D viscosity profiles for Greenland.

table S3. 1D viscosity profiles assigned to each region in Greenland.

table S4. Uncertainty of the scaling parameter caused by the load and Earth model parameters.

table S5. Ratio of inferred scaling factor for the 3D viscosity profiles versus the 1D viscosity profile (VM-GPS).

table S6. SLE mass change per basin since LGM.

table S7. SLE mass change per basin during 1900–1983.