Abstract
When a moderate number of potential predictors are available and a survival model is fit with regularization to achieve variable selection, providing accurate inference on the predicted survival can be challenging. We investigate inference on the predicted survival estimated after fitting a Cox model under regularization guaranteeing the oracle property. We demonstrate that existing asymptotic formulas for the standard errors of the coefficients tend to underestimate the variability for some coefficients, while typical resampling such as the bootstrap tends to overestimate it; these approaches can both lead to inaccurate variance estimation for predicted survival functions. We propose a two-stage adaptation of a resampling approach that brings the estimated error in line with the truth. In stage 1, we estimate the coefficients in the observed data set and in 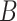 resampled data sets, and allow the resampled coefficient estimates to vote on whether each coefficient should be 0. For those coefficients voted as zero, we set both the point and interval estimates to
resampled data sets, and allow the resampled coefficient estimates to vote on whether each coefficient should be 0. For those coefficients voted as zero, we set both the point and interval estimates to 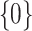 . In stage 2, to make inference about coefficients not voted as zero in stage 1, we refit the penalized model in the observed data and in the
. In stage 2, to make inference about coefficients not voted as zero in stage 1, we refit the penalized model in the observed data and in the 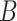 resampled data sets with only variables corresponding to those coefficients. We demonstrate that ensemble voting-based point and interval estimators of the coefficients perform well in finite samples, and prove that the point estimator maintains the oracle property. We extend this approach to derive inference procedures for survival functions and demonstrate that our proposed interval estimation procedures substantially outperform estimators based on asymptotic inference or standard bootstrap. We further illustrate our proposed procedures to predict breast cancer survival in a gene expression study.
resampled data sets with only variables corresponding to those coefficients. We demonstrate that ensemble voting-based point and interval estimators of the coefficients perform well in finite samples, and prove that the point estimator maintains the oracle property. We extend this approach to derive inference procedures for survival functions and demonstrate that our proposed interval estimation procedures substantially outperform estimators based on asymptotic inference or standard bootstrap. We further illustrate our proposed procedures to predict breast cancer survival in a gene expression study.
Keywords: Bootstrap, Ensemble methods, Oracle property, Proportional hazards model, Regularized estimation, Resampling, Risk prediction, Simultaneous confidence intervals, Survival functions
1. Introduction
Many modern medical studies seek to use genomic measurements to predict survival. With a small number of predictors, the standard Cox proportional hazards model (Cox, 1972) can be used to effectively make inference about survival functions. When many potential predictors are available, it is often desirable to build accurate yet parsimonious models that only use a small number of biomarkers. When the number of predictors is moderate, an approach using shrinkage to perform simultaneous variable selection and estimation, such as the lasso, can be effective (Tibshirani, 1996, 1997). Asymptotically, the lasso-penalized estimator is not consistent in variable selection and has non-regular asymptotic distributions, which results in difficulty constructing valid confidence intervals (CIs) (Knight and Fu, 2000). Several alternative penalty functions have been proposed that do possess the so-called oracle properties, in that they are consistent for variable selection and yield estimators with asymptotic normality. These penalty functions, including the adaptive lasso, the smoothly clipped absolute deviation (SCAD), and the adaptive elastic net (aENET), have been adapted to the Cox model (Fan and Li, 2002; Zou, 2006; Zhang and Lu, 2007; Zou and Zhang, 2009; Wu, 2012). There are benefits to each of these approaches; for example, the aENET has good estimation and variable selection performance in situations with correlated predictors whose effects are sparse.
For the regression parameters, denoted by 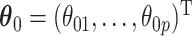 , standard error (SE) formulas for the estimate
, standard error (SE) formulas for the estimate 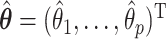 based on asymptotic results have been proposed for the adaptive lasso and SCAD, and could be analogously derived for the aENET (Fan and Li, 2002; Zhang and Lu, 2007). The basis for the derivation of these formulas is the oracle property, which tells us that the penalized estimator is asymptotically equivalent to the oracle estimator, the unpenalized estimator fit with only the “true” signals. The formulas thus rely in part on the accuracy of the variable selection achieved by the penalization: they provide non-trivial SE estimates for
based on asymptotic results have been proposed for the adaptive lasso and SCAD, and could be analogously derived for the aENET (Fan and Li, 2002; Zhang and Lu, 2007). The basis for the derivation of these formulas is the oracle property, which tells us that the penalized estimator is asymptotically equivalent to the oracle estimator, the unpenalized estimator fit with only the “true” signals. The formulas thus rely in part on the accuracy of the variable selection achieved by the penalization: they provide non-trivial SE estimates for 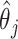 when
when 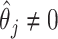 , but set the SE to zero when
, but set the SE to zero when  . This tends to yield accurate SE estimates for non-zero
. This tends to yield accurate SE estimates for non-zero 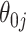 's, but underestimates the SE of
's, but underestimates the SE of 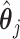 when
when 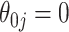 . An alternative approach would be to obtain variance estimates with commonly used resampling methods such as the bootstrap. Unfortunately, standard resampling methods tend to overestimate the variance when the true coefficient is 0, even when the sample size is relatively large. In this paper, we first propose an ensemble voting-based procedure, an adaptation of resampling leveraging the oracle property, to provide accurate point and interval estimates for both zero and non-zero coefficients. Building on top of the ensemble procedure for coefficient estimation, we then propose resampling procedures for making precise inference about predicted survival functions at any given predictor level.
. An alternative approach would be to obtain variance estimates with commonly used resampling methods such as the bootstrap. Unfortunately, standard resampling methods tend to overestimate the variance when the true coefficient is 0, even when the sample size is relatively large. In this paper, we first propose an ensemble voting-based procedure, an adaptation of resampling leveraging the oracle property, to provide accurate point and interval estimates for both zero and non-zero coefficients. Building on top of the ensemble procedure for coefficient estimation, we then propose resampling procedures for making precise inference about predicted survival functions at any given predictor level.
Specifically, our proposed method proceeds in two stages. In stage 1, we fit the penalized model in the observed data set and across resampled data sets, and use this collection of estimated coefficients to vote on which variables belong in the model. For each coefficient  we determine whether the proportion of
we determine whether the proportion of 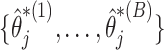 which are 0 is higher than a specified fraction
which are 0 is higher than a specified fraction 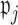 and if so, we set both the point and interval estimate for
and if so, we set both the point and interval estimate for 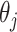 to be
to be 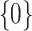 . To make inference about coefficients voted as non-zero in stage 1, in stage 2, we refit the model in both the original and resampled data sets with only those surviving variables. The refit estimates are then used to construct point and interval estimates for these coefficients. This ensemble voting-based method can be viewed as a compromise between making inferences based on the oracle property and resampling. Those voted as zero in stage 1 are deemed as “confidently zero” and hence the oracle property is applied to make inference for these coefficients. Resampling is then used to make inference about the remaining coefficients. Note that our proposed point estimator resembles the relaxed lasso estimator (Meinshausen, 2007), with one main difference being that our method determines the active set based on voting. As shown in numerical studies, the new point estimate does not differ dramatically from the initial aENET estimate, yet it allows the resampling to more accurately capture its variability and hence leads to more precise inference.
. To make inference about coefficients voted as non-zero in stage 1, in stage 2, we refit the model in both the original and resampled data sets with only those surviving variables. The refit estimates are then used to construct point and interval estimates for these coefficients. This ensemble voting-based method can be viewed as a compromise between making inferences based on the oracle property and resampling. Those voted as zero in stage 1 are deemed as “confidently zero” and hence the oracle property is applied to make inference for these coefficients. Resampling is then used to make inference about the remaining coefficients. Note that our proposed point estimator resembles the relaxed lasso estimator (Meinshausen, 2007), with one main difference being that our method determines the active set based on voting. As shown in numerical studies, the new point estimate does not differ dramatically from the initial aENET estimate, yet it allows the resampling to more accurately capture its variability and hence leads to more precise inference.
Our interest lies in inference not only on the coefficients, but also on functions of the coefficients—specifically, the predicted survival function for new patients. With regularized estimation of the regression coefficients, proper inference procedures for the survival function are not currently available. Naively making inference based on asymptotics or the bootstrap can lead to imprecise interval estimation for the survival functions. We propose to construct point and interval estimates for the survival functions building on top of the two-stage procedure for coefficient estimation and resampling. Our procedure, benefiting from more accurate inference for the zero coefficients, can produce pointwise and simultaneous CIs with better finite sample performance than those obtained from naive methods.
Our proposed approach shares a number of features with other recent ensemble-based approaches developed for variable selection. For example, for linear models, the randomized lasso with stability selection (Meinshausen and Bühlmann, 2010) and the bootstrap lasso (Bach, 2008) both fit lasso-type procedures in observed and resampled data, and look across the resampled estimators to identify which variables should and should not be included in the model. They establish results about the consistency of variable selection guaranteed by these approaches, even when the number of potential predictors is quite large. The idea behind our proposed point estimator is similar to what is proposed in these papers, and it does inherit oracle properties from the penalized estimators it uses. However, our goal is to use an ensemble-type approach to produce both a good point estimate and a good collection of resampled estimators that accurately capture the variability of the point estimate in finite samples. This joint goal distinguishes our method from previous work. Furthermore, no existing methods consider downstream inference for survival functions in the presence of regularization for coefficient estimation.
The rest of the paper is organized as follows. In Section 2, we introduce our ensemble voting-based procedure, with the main methodological details provided in Section 2.2 and notes on implementation in Section 2.4. In Section 3.1, we evaluate our method using simulation studies and in Section 3.2, we demonstrate its usage for predicting the probability of breast cancer progression using a set of genes in a candidate pathway. In Section 4, we make some final comments and further situate our method in the context of other existing ensemble approaches.
2. Methods
We consider the setting in which we have a collection of 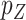 novel genomic or biological predictors
novel genomic or biological predictors 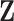 , and wish to use them along with
, and wish to use them along with 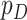 clinical covariates
clinical covariates 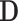 to predict patient survival time
to predict patient survival time  . Due to censoring, we only observe
. Due to censoring, we only observe 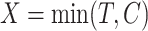 and
and 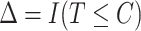 , where
, where 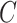 is the censoring time assumed independent of
is the censoring time assumed independent of 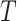 given
given 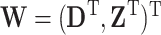 . The observed data consist of
. The observed data consist of 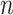 independent and identically distributed (iid) random vectors,
independent and identically distributed (iid) random vectors, 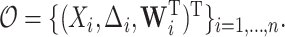 Without loss of generality, we assume that
Without loss of generality, we assume that 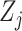 's are standardized to have mean 0 and variance 1. We further assume that
's are standardized to have mean 0 and variance 1. We further assume that 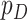 is small and all clinical variables are included in the model; however,
is small and all clinical variables are included in the model; however, 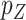 may be of moderate size relative to
may be of moderate size relative to 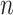 . We assume a Cox proportional hazards model for
. We assume a Cox proportional hazards model for 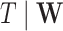 ,
, 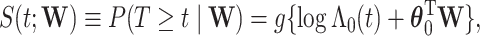 where
where 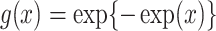 ,
, 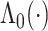 is the unknown baseline cumulative hazard function, and
is the unknown baseline cumulative hazard function, and 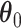 are the unknown log hazard ratio parameters. We let
are the unknown log hazard ratio parameters. We let 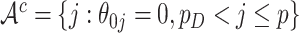 denote the non-active set of the coefficients for
denote the non-active set of the coefficients for 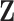 and let
and let  , where
, where 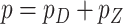 .
.
2.1. Regularized estimation and initial perturbation
Since 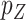 is not small and the coefficient vector may be sparse, we may estimate
is not small and the coefficient vector may be sparse, we may estimate 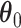 by maximizing a penalized log partial likelihood with a penalty providing simultaneous variable selection and estimation. For clarity, we will use the aENET penalty throughout but identical methods could be pursued using any penalization with oracle properties. Specifically, we focus on the estimator
by maximizing a penalized log partial likelihood with a penalty providing simultaneous variable selection and estimation. For clarity, we will use the aENET penalty throughout but identical methods could be pursued using any penalization with oracle properties. Specifically, we focus on the estimator
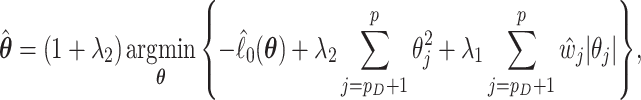 |
where 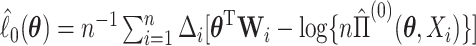 is the log partial likelihood,
is the log partial likelihood, 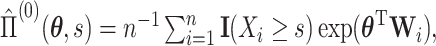
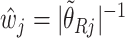 , and
, and 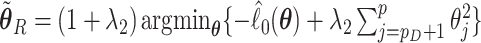 . Here
. Here 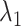 and
and 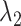 are non-negative tuning parameters controlling the amount of regularization with both tending to 0 as
are non-negative tuning parameters controlling the amount of regularization with both tending to 0 as 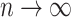 . Further discussion of tuning parameters is given in Section 2.4.
. Further discussion of tuning parameters is given in Section 2.4.
To construct CIs for  , we may rely on asymptotic results similar to those suggested in Fan and Li (2002) and Zhang and Lu (2007), or resampling methods such as the bootstrap. However, the asymptotic-based approach tends to underestimate the variability as shown in, for example, Minnier and others (2011), as well as in the simulation results in Section 3.1. Thus, we turn to resampling to obtain more accurate assessment of the variability. First, we consider the commonly used wild bootstrap approach (Kosorok, 2007). We generate a vector of iid mean-1-variance-1 random variables,
, we may rely on asymptotic results similar to those suggested in Fan and Li (2002) and Zhang and Lu (2007), or resampling methods such as the bootstrap. However, the asymptotic-based approach tends to underestimate the variability as shown in, for example, Minnier and others (2011), as well as in the simulation results in Section 3.1. Thus, we turn to resampling to obtain more accurate assessment of the variability. First, we consider the commonly used wild bootstrap approach (Kosorok, 2007). We generate a vector of iid mean-1-variance-1 random variables, 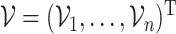 , independently of
, independently of 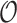 , and calculate
, and calculate
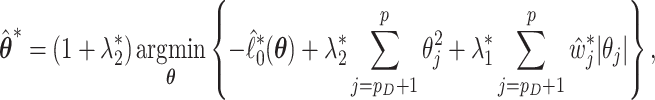 |
where 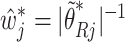 ,
, 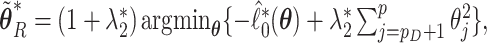
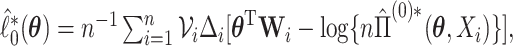 and
and 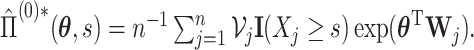 In Appendix A of the Supplementary Material (available at Biostatistics online), we show that
In Appendix A of the Supplementary Material (available at Biostatistics online), we show that 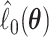 and
and 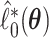 are asymptotically equivalent to objective functions that are the sum of iid terms; thus, arguments similar to those given in Minnier and others (2011) show that
are asymptotically equivalent to objective functions that are the sum of iid terms; thus, arguments similar to those given in Minnier and others (2011) show that 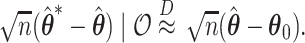 Thus, by producing
Thus, by producing 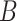 vectors
vectors 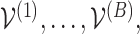 we may find
we may find 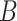 iid estimators
iid estimators 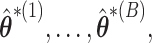 and use the distribution of
and use the distribution of 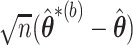 to approximate the distribution of
to approximate the distribution of 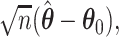 where
where 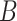 is some large number. In practice, we find good performance when
is some large number. In practice, we find good performance when 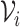 has finite support, such as
has finite support, such as 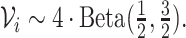 One may directly make inference about
One may directly make inference about 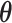 based on
based on 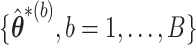 ; however, variance estimators from this approach tend to be overly conservative for
; however, variance estimators from this approach tend to be overly conservative for 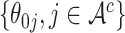 leading to imprecise interval estimation for survival functions. To produce valid inference for all coefficients as well as predicted survival, we instead propose the following two-stage ensemble voting approach.
leading to imprecise interval estimation for survival functions. To produce valid inference for all coefficients as well as predicted survival, we instead propose the following two-stage ensemble voting approach.
2.2. Ensemble voting
In stage 1, we obtain  and
and 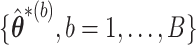 as described in Section 2.1. Then we let the perturbed estimators vote, so that for
as described in Section 2.1. Then we let the perturbed estimators vote, so that for 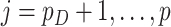 , if at least
, if at least 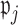 of
of 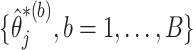 are zero, both the point and interval estimates of
are zero, both the point and interval estimates of 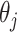 are set to
are set to 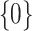 for some
for some 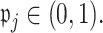 Details on the choice of
Details on the choice of 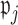 are given in Section 2.4. Let
are given in Section 2.4. Let  be the active set based on voting. Obviously,
be the active set based on voting. Obviously, 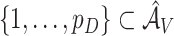 since coefficients for
since coefficients for  are not penalized. In stage 2, we repeat the aENET regularized fitting and resampling using the restricted data
are not penalized. In stage 2, we repeat the aENET regularized fitting and resampling using the restricted data 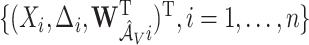 , where, for any
, where, for any 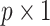 vector
vector 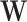 and any set
and any set 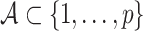 ,
, 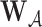 denotes the subvector of
denotes the subvector of 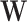 corresponding to
corresponding to 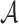 . Let
. Let 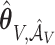 and
and 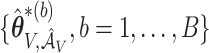 denote the corresponding estimates of the coefficients for
denote the corresponding estimates of the coefficients for  from the observed data and perturbations.
from the observed data and perturbations.
Let 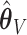 denote the final two-stage point estimator for
denote the final two-stage point estimator for 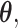 and let
and let 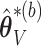 denote the resampled counterpart of
denote the resampled counterpart of 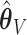 based on
based on 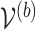 . Then the elements of
. Then the elements of 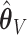 and
and 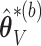 , are set to zero for
, are set to zero for 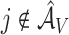 ; and the subvectors of
; and the subvectors of 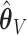 and
and 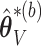 excluding these elements are, respectively, set to
excluding these elements are, respectively, set to  and
and 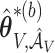 . The variability in
. The variability in  now more closely matches the empirical variability of
now more closely matches the empirical variability of 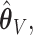 as demonstrated in the simulation studies. Asymptotic oracle properties of these ensemble-based estimators are established in Appendix A of the Supplementary Material (available at Biostatistics online).
as demonstrated in the simulation studies. Asymptotic oracle properties of these ensemble-based estimators are established in Appendix A of the Supplementary Material (available at Biostatistics online).
2.3. Survival functions and CIs
To predict survival probabilities for a future patient with 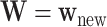 , we may estimate
, we may estimate 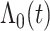 based on Breslow's estimator (Breslow, 1972),
based on Breslow's estimator (Breslow, 1972),  , where
, where 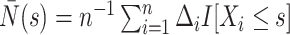 . Subsequently, we estimate the survival function
. Subsequently, we estimate the survival function 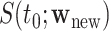 as
as
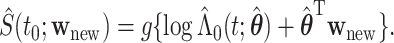 |
(2.1) |
To construct pointwise CIs for 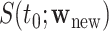 for
for 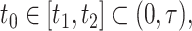 one may estimate the variances based on the asymptotic properties of
one may estimate the variances based on the asymptotic properties of 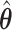 and
and  , where
, where 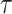 is a time satisfying
is a time satisfying 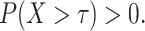 However, such an explicit estimation approach may underestimate the variability as the case for
However, such an explicit estimation approach may underestimate the variability as the case for 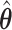 and also is infeasible when the goal is to obtain simultaneous CIs.
and also is infeasible when the goal is to obtain simultaneous CIs.
We propose to employ the resampling method for both pointwise and simultaneous CI estimation. Specifically, for each set of  , we first obtain the perturbed estimate
, we first obtain the perturbed estimate 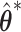 and then calculate
and then calculate 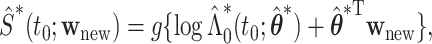 where
where 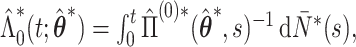 and
and 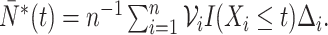 We demonstrate in Appendix B of the Supplementary Materials (available at Biostatistics online) that
We demonstrate in Appendix B of the Supplementary Materials (available at Biostatistics online) that 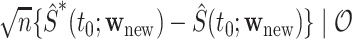 and
and  converge weakly to the same limiting zero-mean Gaussian process. Thus, we may use the observed realizations of
converge weakly to the same limiting zero-mean Gaussian process. Thus, we may use the observed realizations of 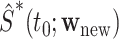 to construct CIs for
to construct CIs for 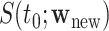 . The variance of
. The variance of  may be estimated as
may be estimated as  A 95% CI at
A 95% CI at 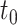 may be calculated as
may be calculated as 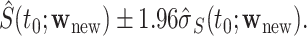 To construct simultaneous CIs, we follow the same strategy as in Lin and others (1994) based on the resampled realizations. A 95% simultaneous CIs over the range
To construct simultaneous CIs, we follow the same strategy as in Lin and others (1994) based on the resampled realizations. A 95% simultaneous CIs over the range 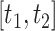 can be obtained as
can be obtained as 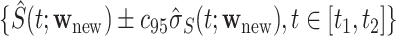 , where
, where 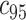 is the 95th percentile of the distribution of
is the 95th percentile of the distribution of 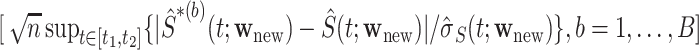 . In finite samples, coverage is improved if we calculate CIs on the logit scale.
. In finite samples, coverage is improved if we calculate CIs on the logit scale.
2.4. Implementation and tuning
To obtain 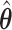 numerically, one may use the algorithm proposed in Wu (2012). Alternatively, one may use a quadratic approximation to the likelihood similar to those proposed in Wang and Leng (2007) and Zhang and Lu (2007) to convert to a penalized least squares problem. Specifically, for a given
numerically, one may use the algorithm proposed in Wu (2012). Alternatively, one may use a quadratic approximation to the likelihood similar to those proposed in Wang and Leng (2007) and Zhang and Lu (2007) to convert to a penalized least squares problem. Specifically, for a given 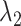 , let
, let 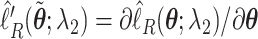 and
and  . We take the Cholesky decomposition of
. We take the Cholesky decomposition of 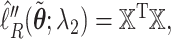 and define
and define 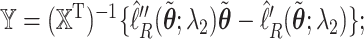 we may check that
we may check that 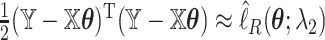 up to constants. Thus, after a preliminary estimate
up to constants. Thus, after a preliminary estimate  is found,
is found, 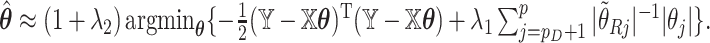 We find that this approximation performs well in finite samples.
We find that this approximation performs well in finite samples.
We need to select tuning parameters to ensure satisfactory performance of the regularized estimation and the resampling methods. To this end, we recommend employing weak 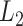 regularization to avoid over-shrinkage which can induce bias. For the
regularization to avoid over-shrinkage which can induce bias. For the 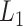 regularization, we follow the same principles as suggested in Minnier and others (2011) and consider a modified BIC. Precisely, we select
regularization, we follow the same principles as suggested in Minnier and others (2011) and consider a modified BIC. Precisely, we select 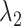 to guarantee
to guarantee 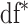 degrees of freedom, using the implemented ridge option of coxph in R with
degrees of freedom, using the implemented ridge option of coxph in R with 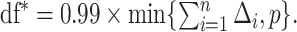 We then select
We then select 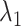 by minimizing a modified BIC penalty,
by minimizing a modified BIC penalty, 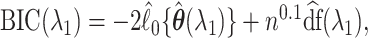 where
where 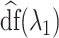 is simply the number of non-zero elements of
is simply the number of non-zero elements of 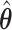 when
when 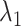 is used for tuning. We repeat tuning parameter selection for each perturbed estimate. When we recalculate the estimates after ensemble voting,
is used for tuning. We repeat tuning parameter selection for each perturbed estimate. When we recalculate the estimates after ensemble voting, 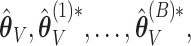 we use the same tuning parameters as used in the initial estimators
we use the same tuning parameters as used in the initial estimators 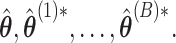
To choose the proportions 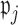 for determining whether
for determining whether 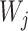 should be excluded, we propose here a data-driven approach that works well in practice, but note that any thresholds
should be excluded, we propose here a data-driven approach that works well in practice, but note that any thresholds 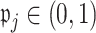 will yield the property that
will yield the property that 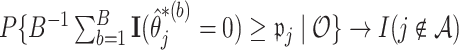 due to the oracle properties of
due to the oracle properties of 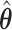 and
and 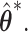 In simulation, the obvious choice
In simulation, the obvious choice 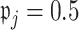 for all
for all 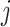 works relatively well; however, we find that an approach that is more tuned to the data yields improved performance in finite samples. Specifically, we use a permutation approach to estimate what the threshold would be under a global null,
works relatively well; however, we find that an approach that is more tuned to the data yields improved performance in finite samples. Specifically, we use a permutation approach to estimate what the threshold would be under a global null, 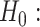
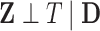 . Since
. Since 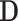 may be both associated with
may be both associated with 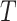 and
and 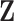 , the standard permutation that breaks the link between
, the standard permutation that breaks the link between 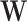 and
and 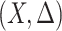 may not be ideal. To account for the correlation, we propose to first regress
may not be ideal. To account for the correlation, we propose to first regress 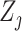 against
against 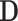 and obtain residuals
and obtain residuals 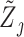 for
for 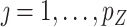 . Let
. Let  be the new covariates. Then
be the new covariates. Then 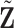 is uncorrelated with
is uncorrelated with 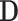 and remains unrelated to
and remains unrelated to  under
under 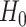 . Next, for each set of permuted data
. Next, for each set of permuted data 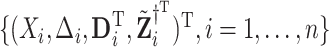 , we fit the aENET regularized Cox model and perform resampling to obtain perturbed estimates of
, we fit the aENET regularized Cox model and perform resampling to obtain perturbed estimates of 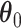 under
under 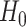 , where
, where 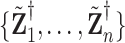 represents permuted
represents permuted 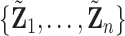 . If we perform
. If we perform 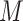 such permutations, and let
such permutations, and let 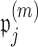 denote the proportion of perturbed values that vote for each
denote the proportion of perturbed values that vote for each 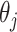 to be 0 from the
to be 0 from the 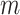 th permutation, we may calculate
th permutation, we may calculate 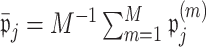 . We then set
. We then set 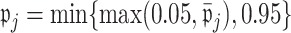 to ensure that
to ensure that 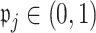 for the ensemble voting. For ease of implementation, one may also simply choose a common threshold
for the ensemble voting. For ease of implementation, one may also simply choose a common threshold 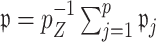 when the covariates are standardized, which is what we adopt in our numerical studies and seems to work well in practice.
when the covariates are standardized, which is what we adopt in our numerical studies and seems to work well in practice.
3. Numerical studies
3.1. Simulation studies
To assess the performance of the proposed procedures, we generated 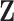 from a multivariate normal distribution with mean 0 and compound symmetry structure with variance 1 and correlation
from a multivariate normal distribution with mean 0 and compound symmetry structure with variance 1 and correlation 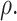 We considered settings with
We considered settings with 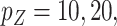 and 30 covariates, and correlations
and 30 covariates, and correlations 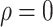 and
and 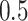 . For simplicity, we did not include any additional clinical covariates. The underlying signal was linear involving only the first five covariates; the structure of this signal was
. For simplicity, we did not include any additional clinical covariates. The underlying signal was linear involving only the first five covariates; the structure of this signal was 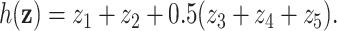 For each setting, we generated survival times under the Cox model
For each setting, we generated survival times under the Cox model 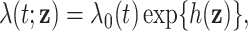 where
where 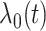 is the hazard function from a
is the hazard function from a 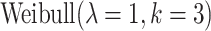 . The censoring was generated from a uniform distribution with range chosen to produce
. The censoring was generated from a uniform distribution with range chosen to produce 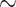 50% censoring. We considered small and moderate sample sizes (
50% censoring. We considered small and moderate sample sizes (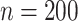 and
and 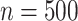 ).
).
For prediction of survival time for future patients, we consider three individuals. One is the “baseline” individual (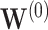 ) who has all covariates equal to 0; for this individual, the estimate
) who has all covariates equal to 0; for this individual, the estimate 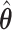 appears only in the estimation of the cumulative baseline hazard
appears only in the estimation of the cumulative baseline hazard 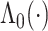 . We also consider two individuals with non-trivial covariates, where
. We also consider two individuals with non-trivial covariates, where  appears twice in the survival function estimate (2.1). The individual
appears twice in the survival function estimate (2.1). The individual 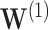 , with covariate pattern
, with covariate pattern  should emphasize difficulties in estimating the smaller signals. The individual
should emphasize difficulties in estimating the smaller signals. The individual 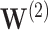 , with covariate pattern
, with covariate pattern 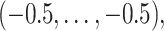 should emphasize overall difficulties in estimating both the non-zero and zero coefficients. We estimate the survival function and calculate CIs in the region
should emphasize overall difficulties in estimating both the non-zero and zero coefficients. We estimate the survival function and calculate CIs in the region 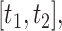 where
where 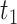 is defined to be the 10th percentile of
is defined to be the 10th percentile of 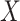 and
and 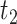 is the 90th percentile of
is the 90th percentile of 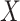 . We present results on the CIs for the conditional survival function at
. We present results on the CIs for the conditional survival function at  as well as simultaneous CIs for
as well as simultaneous CIs for 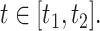
We compare three methods for interval estimation: the bootstrap; our proposed approach using perturbation resampling and voting; and an approach mimicking the asymptotic method. For the asymptotic method, because formulas do not exist for CIs of the survival function, we mimicked the approach of the formula by applying aENET to the observed data, identifying which  are declared non-zero, and restricting to these covariates for estimation using resampling. Resampling methods use
are declared non-zero, and restricting to these covariates for estimation using resampling. Resampling methods use 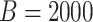 resamples. Results presented are based on 2000 simulations.
resamples. Results presented are based on 2000 simulations.
In Figure 1, we present the biases and the empirical SEs of the two point estimators: the standard aENET estimator 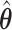 and our voting-based estimator
and our voting-based estimator 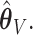 For the coefficients
For the coefficients  the absolute bias is displayed. The data-adaptive voting threshold
the absolute bias is displayed. The data-adaptive voting threshold 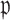 varies between about
varies between about 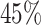 and
and 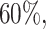 depending on how “informed” the voters are—for example, when
depending on how “informed” the voters are—for example, when 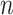 is larger and
is larger and 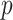 is smaller, a higher proportion of the voters successfully eliminate the true zeros under the global null, so a higher threshold
is smaller, a higher proportion of the voters successfully eliminate the true zeros under the global null, so a higher threshold 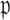 may be used. Both
may be used. Both 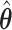 and
and 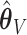 have negligible bias for zero and non-zero coefficients. For the non-zero signals, the bias is slightly upward for the strong signals (
have negligible bias for zero and non-zero coefficients. For the non-zero signals, the bias is slightly upward for the strong signals (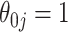 ) when
) when  and
and  or 30. For the weaker signals (
or 30. For the weaker signals ( ), the aENET estimator has a downward bias as expected for any shrinkage estimator, but the voting-based estimator shifts the estimators slightly upward with slightly less bias for the weaker signals.
), the aENET estimator has a downward bias as expected for any shrinkage estimator, but the voting-based estimator shifts the estimators slightly upward with slightly less bias for the weaker signals.
Fig. 1.
Comparison of the SEs, bias, and 95% CI coverage of 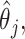 for true model parameters
for true model parameters 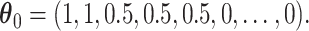 Shown are values when
Shown are values when 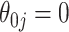 (with absolute bias displayed), as well as
(with absolute bias displayed), as well as 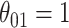 and
and 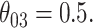 Bias and empirical SEs are compared for the base aENET fit (
Bias and empirical SEs are compared for the base aENET fit (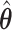 ) and the aENET fit after the voting procedure (
) and the aENET fit after the voting procedure (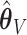 ); the variability for the base aENET fit may be estimated using either the bootstrap or the asymptotic method, while the variability for the voting procedure is estimated using the resampled coefficient estimators after voting.
); the variability for the base aENET fit may be estimated using either the bootstrap or the asymptotic method, while the variability for the voting procedure is estimated using the resampled coefficient estimators after voting.
The empirical SEs for 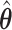 and
and 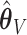 are nearly identical for the non-trivial signals (
are nearly identical for the non-trivial signals ( or 1); when
or 1); when 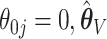 displays a slight increase in variability. This may be because the voting-based estimator actually tends to include covariates with true
displays a slight increase in variability. This may be because the voting-based estimator actually tends to include covariates with true 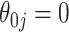 at a slightly higher rate than the standard aENET, although the frequencies of
at a slightly higher rate than the standard aENET, although the frequencies of 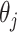 's being set to 0 only differ slightly between
's being set to 0 only differ slightly between 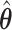 and
and 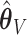 . Under no correlation, when
. Under no correlation, when 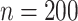 , the percent of zero coefficients set to zero was (69%, 70%, 68%) for
, the percent of zero coefficients set to zero was (69%, 70%, 68%) for 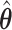 and (60%, 61%, 60%) for
and (60%, 61%, 60%) for 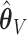 when
when 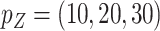 . These frequencies get higher as expected when
. These frequencies get higher as expected when 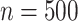 : (77%, 79%, 79%) for
: (77%, 79%, 79%) for  and (66%, 67%, 66%) for
and (66%, 67%, 66%) for 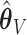 . Under 0.5 correlation, when
. Under 0.5 correlation, when 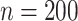 , the percent of zero coefficients set to zero was (70%, 70%, 67%) for
, the percent of zero coefficients set to zero was (70%, 70%, 67%) for  and (69%, 62%, 60%) for
and (69%, 62%, 60%) for 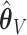 when
when 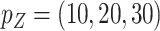 ; when
; when 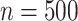 : (78%, 80%, 79%) for
: (78%, 80%, 79%) for 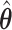 and (66%, 69%, 68%) for
and (66%, 69%, 68%) for 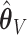 . The slight over-selection of variables for
. The slight over-selection of variables for 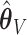 is compensated with a small gain in retaining the true signals. Both methods always include the strong signals (
is compensated with a small gain in retaining the true signals. Both methods always include the strong signals (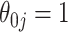 ), but when
), but when 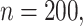 under no correlation
under no correlation 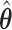 misses moderate signals (
misses moderate signals ( ) (.05%, .06%, .03%) of the time, while
) (.05%, .06%, .03%) of the time, while 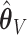 misses them (.03%, 0%, .03%) of the time for
misses them (.03%, 0%, .03%) of the time for 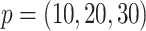 . Under 0.5 correlation, these rates are slightly higher, but with better success again for
. Under 0.5 correlation, these rates are slightly higher, but with better success again for 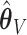 : (1.1%, 1.9%, 2.0%) for
: (1.1%, 1.9%, 2.0%) for  and (0.7%, 1.4%, 1.6%) for
and (0.7%, 1.4%, 1.6%) for 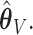
We have two methods to estimate 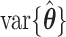 (asymptotic and bootstrap) and one to estimate
(asymptotic and bootstrap) and one to estimate 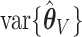 (our proposed resampling with voting method). When
(our proposed resampling with voting method). When 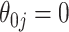 , the variance calculated using asymptotics tends to fall below the empirical variance, while the bootstrap variance is typically higher. When
, the variance calculated using asymptotics tends to fall below the empirical variance, while the bootstrap variance is typically higher. When 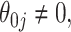 the asymptotic method agrees with the empirical variance, while the bootstrap variance is still inflated when
the asymptotic method agrees with the empirical variance, while the bootstrap variance is still inflated when 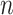 is small. The ensemble-based voting method yields variance estimates that are more consistently in line with the empirical variance for all
is small. The ensemble-based voting method yields variance estimates that are more consistently in line with the empirical variance for all 
Henceforth, we will compare CI coverage and refer to these by the error estimation method (asymptotic, bootstrap, and voting)—noting that asymptotic and bootstrap methods are centered at 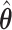 while voting-based methods are centered at
while voting-based methods are centered at 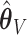 . The coverage for
. The coverage for 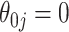 is high for all methods as expected based on the oracle properties. For
is high for all methods as expected based on the oracle properties. For 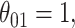 we see that the bootstrap method has substantial over-coverage due to overestimation of the variability, especially when
we see that the bootstrap method has substantial over-coverage due to overestimation of the variability, especially when 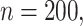 while the asymptotic and voting methods demonstrate near 95% coverage. For the moderate signal
while the asymptotic and voting methods demonstrate near 95% coverage. For the moderate signal  the bootstrap intervals again tend to over-cover, and the asymptotic intervals exhibit some under-coverage when the number of covariates is larger. The ensemble voting method falls between these and maintains levels near 95%. In general, we find that our proposed voting method provides more precise estimation of the sampling variability compared to both the asymptotic based and bootstrap methods.
the bootstrap intervals again tend to over-cover, and the asymptotic intervals exhibit some under-coverage when the number of covariates is larger. The ensemble voting method falls between these and maintains levels near 95%. In general, we find that our proposed voting method provides more precise estimation of the sampling variability compared to both the asymptotic based and bootstrap methods.
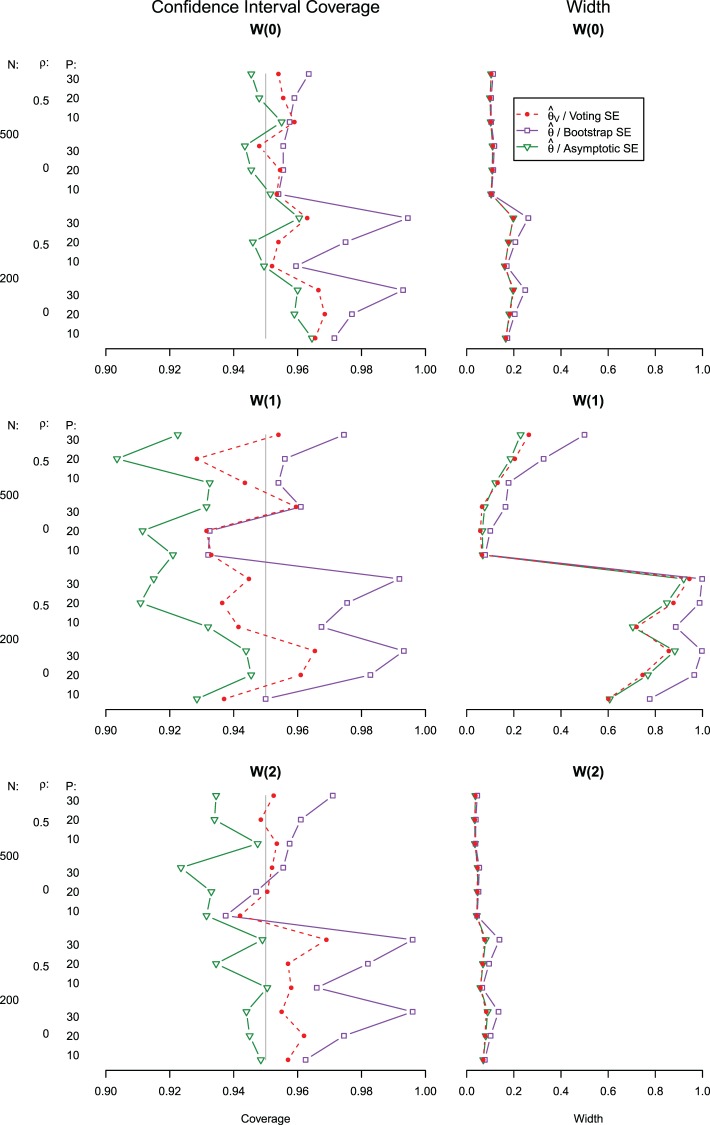
The coverage and width of the CIs for the 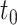 -year survival predictions are compared for the 3 individuals in Figure 2. The conditional survival probabilities at
-year survival predictions are compared for the 3 individuals in Figure 2. The conditional survival probabilities at 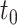 are approximately
are approximately 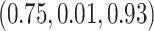 for the three individuals
for the three individuals 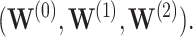 The bootstrap method tends to produce overly conservative CIs with coverage levels much higher than 95% and substantially broader widths. The asymptotic and voting-based CIs have very similar widths, but the voting-based coverage is typically higher. For
The bootstrap method tends to produce overly conservative CIs with coverage levels much higher than 95% and substantially broader widths. The asymptotic and voting-based CIs have very similar widths, but the voting-based coverage is typically higher. For 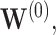 when all coefficients are 0, there is little difference between the asymptotic and voting methods. However, especially for
when all coefficients are 0, there is little difference between the asymptotic and voting methods. However, especially for 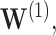 the asymptotic method can under-cover, while the voting-based CI has coverage near 95% across settings.
the asymptotic method can under-cover, while the voting-based CI has coverage near 95% across settings.
Fig. 2.
Under the model with 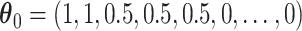 , CI coverage for
, CI coverage for  -year survival, and width, for three covariate levels:
-year survival, and width, for three covariate levels: 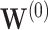 , with all covariates 0;
, with all covariates 0; 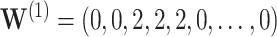 ; and
; and 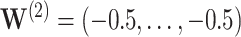 .
.
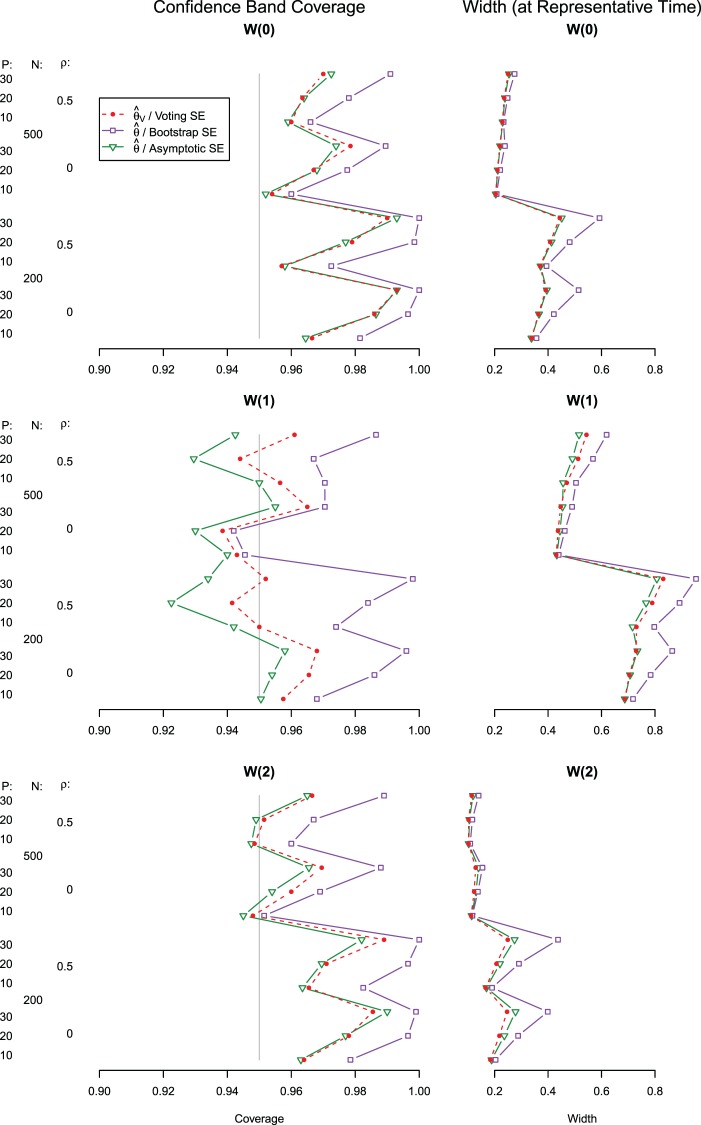
In Figure 3, we present results on the simultaneous CIs including their widths and empirical coverage levels. As with the pointwise intervals, we see that typically the simultaneous CIs based on bootstrap over-cover and are wider, while the asymptotic and voting-based methods are narrower. When  coverage of the voting-based method is in general near 95%; when
coverage of the voting-based method is in general near 95%; when 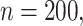 the coverage tends to be over
the coverage tends to be over 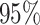 for
for 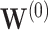 and
and  For
For 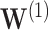 , we see where our voting method most improves over the asymptotic method because the ensemble voting provides more specific knowledge of which
, we see where our voting method most improves over the asymptotic method because the ensemble voting provides more specific knowledge of which 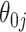 should be set to 0.
should be set to 0.
Fig. 3.
Under the model with 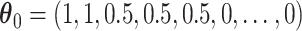 , simultaneous CI coverage for
, simultaneous CI coverage for 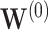 , with all covariates 0;
, with all covariates 0; 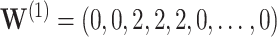 ; and
; and 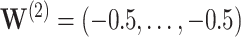 . Also shown are simultaneous confidence widths at representative times.
. Also shown are simultaneous confidence widths at representative times.
The simulations presented above focused on settings where the true non-zero 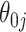 were of large or moderate size, and thus almost always included in the models. We focus on this setting because precise interval estimation based on shrinkage estimators is feasible with moderate sample sizes. When some of the true signals are of order
were of large or moderate size, and thus almost always included in the models. We focus on this setting because precise interval estimation based on shrinkage estimators is feasible with moderate sample sizes. When some of the true signals are of order  , adaptive lasso-type estimators are expected to yield significant bias for such weak signals and it becomes implausible to construct precise CIs as previously shown in Pötscher and Schneider (2009). To further examine the performance of our proposed procedures under such settings, we present additional simulation results in the Online Supplementary Materials (Web Appendix C, available at Biostatistics online) which follow the same structure as those above, but with
, adaptive lasso-type estimators are expected to yield significant bias for such weak signals and it becomes implausible to construct precise CIs as previously shown in Pötscher and Schneider (2009). To further examine the performance of our proposed procedures under such settings, we present additional simulation results in the Online Supplementary Materials (Web Appendix C, available at Biostatistics online) which follow the same structure as those above, but with 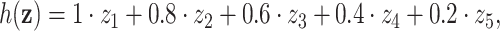 and focus in particular on the small signal
and focus in particular on the small signal  The probability of inclusion of the fifth variable in the support varies between 0.6 and 1.0, and we see that even the voting approach has empirical coverage levels significantly below the nominal level for
The probability of inclusion of the fifth variable in the support varies between 0.6 and 1.0, and we see that even the voting approach has empirical coverage levels significantly below the nominal level for 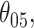 especially when
especially when 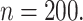 Once
Once 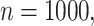 coverage returns to the nominal level for
coverage returns to the nominal level for  (results not shown). For the survival functions, both asymptotic-based and bootstrap-based procedures tend to have difficulty in providing precise CIs under this setting, yielding either too low or too high of coverage levels. On the other hand, the proposed interval estimator for the survival functions based on ensemble and perturbation yields reasonable coverage levels despite the difficulty in making precise inference about the regression coefficients of weak signals. This further demonstrates the advantage of our proposed interval estimation procedures over existing methods based on asymptotic inference or bootstrap.
(results not shown). For the survival functions, both asymptotic-based and bootstrap-based procedures tend to have difficulty in providing precise CIs under this setting, yielding either too low or too high of coverage levels. On the other hand, the proposed interval estimator for the survival functions based on ensemble and perturbation yields reasonable coverage levels despite the difficulty in making precise inference about the regression coefficients of weak signals. This further demonstrates the advantage of our proposed interval estimation procedures over existing methods based on asymptotic inference or bootstrap.
3.2. Data example
To illustrate our approach, we consider a breast cancer gene expression study previously reported in Wang and others (2005) consisting of 286 breast cancer subjects, 37% of whom experience breast cancer progression (107 events). We consider using the 62 genes belonging to the p53 signaling pathway (Subramanian and others, 2005) to predict breast cancer progression; this pathway is known to play an important role in breast cancer progression (Gasco and others, 2002). We build a model predicting survival, and compare the performance of the standard aENET-penalized Cox model with bootstrap-based CIs to our voting-based method of point and interval estimators. We are not presenting results based on the asymptotic formulas because our simulations suggested that they may not always be valid. We standardized each gene to have mean 0 and variance 1, and we included ER status as an unpenalized control covariate. Follow-up ranged between 2 months and 14.3 years; the range of observed deaths was between 2 months and 6.7 years. We provide predictions of survival between 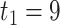 months and
months and  years.
years.
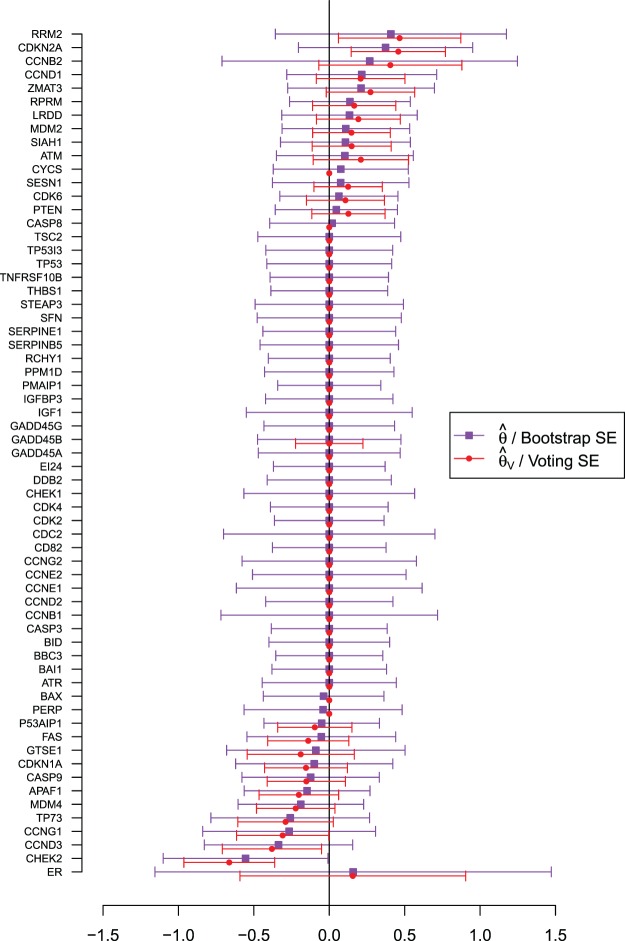
Figure 4 shows the coefficient estimates with 95% CIs from the aENET using the bootstrap, as well the estimates and CIs from our perturbation with voting procedure. Our data-adaptive voting threshold 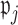 was set to be 36%, so if more than 36% of the perturbations agreed that a coefficient should be 0, the covariate was excluded from the second stage of refitting. The genes in the model and the point estimates differ only slightly between the two methods, as we would expect based on the simulation studies: 28 genes are estimated to have non-zero effects in the initial aENET fit, while the voting-based estimate contains only 24 genes with non-zero effects. The real difference comes in the interval estimation. For example if we identify genes with nominal 95% CIs that exclude 0, we have only one significant gene (CHEK2) using the bootstrap, but five using the voting method (CHEK2, CCND3, CCNG1, CDKN2A, RRM2). CHEK2, a gene included on breast cancer hereditary panels, has been shown to interact with BRCA1 (Economopoulou and others, 2015). The other genes involved in cell cycle control are believed to relate to survival in numerous cancers including breast cancer; for example, CDKN2A was one of seven genes found to be useful for breast cancer progression prediction using a DNA methylation panel (Li and others, 2015). The point estimates of the log hazard ratios for these five genes according to the voting-based estimate are
was set to be 36%, so if more than 36% of the perturbations agreed that a coefficient should be 0, the covariate was excluded from the second stage of refitting. The genes in the model and the point estimates differ only slightly between the two methods, as we would expect based on the simulation studies: 28 genes are estimated to have non-zero effects in the initial aENET fit, while the voting-based estimate contains only 24 genes with non-zero effects. The real difference comes in the interval estimation. For example if we identify genes with nominal 95% CIs that exclude 0, we have only one significant gene (CHEK2) using the bootstrap, but five using the voting method (CHEK2, CCND3, CCNG1, CDKN2A, RRM2). CHEK2, a gene included on breast cancer hereditary panels, has been shown to interact with BRCA1 (Economopoulou and others, 2015). The other genes involved in cell cycle control are believed to relate to survival in numerous cancers including breast cancer; for example, CDKN2A was one of seven genes found to be useful for breast cancer progression prediction using a DNA methylation panel (Li and others, 2015). The point estimates of the log hazard ratios for these five genes according to the voting-based estimate are 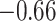 ,
, 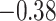 ,
, 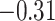 , 0.46, and 0.47, respectively. Thus, up-regularization of the first three genes is protective and of the last two genes is detrimental.
, 0.46, and 0.47, respectively. Thus, up-regularization of the first three genes is protective and of the last two genes is detrimental.
Fig. 4.
In the breast cancer study, estimates of the (unpenalized) coefficient for ER status and the (penalized) coefficients for the variables in the p53 signaling pathway, each with 95% CIs, estimated using the aENET estimate with bootstrap CIs, and the voting-based method for both point estimation and interval estimation.
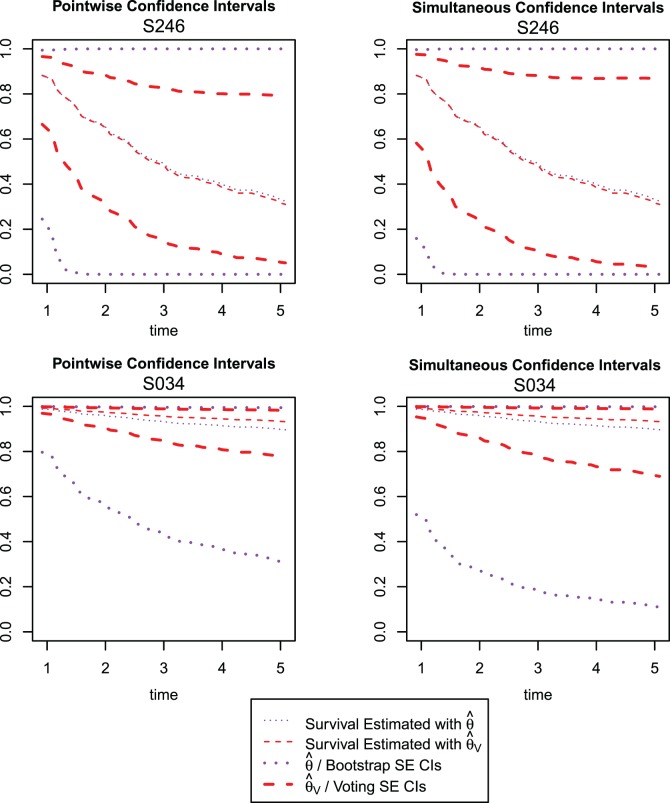
To see how the difference in coefficient-level variability estimation impacts the variability estimation of downstream functions, we calculate the predicted survival function and associated CIs using the two methods for two individuals in the study, whose predicted 3-year survival rates are at the 10th and 90th percentiles; these are displayed in Figure 5. Individual S246 is at the 10th percentile; her predicted three-year survival probability is 0.49 using the aENET, with a 95% bootstrap CI of (0.00, 1.00)—a virtually meaningless interval. Her predicted three-year survival is very similar according to the voting-based estimate—0.48—but the 95% CI is narrower: (0.15, 0.83). The patient's breast tumor is ER positive, and the standardized gene expression values for the five genes (CHEK2, CCND3, CCNG1, CDKN2A, RRM2) are, respectively ( ). Individual S034 is at the 90th percentile; according to the aENET with bootstrap, her predicted three-year survival is 0.93, and a 95% CI is (0.44, 1.00). The voting-based predicted survival estimate is 0.96 with a much narrower 95% CI of (0.85, 0.99). The patient's breast tumor is ER positive, and the gene expression values for the fives genes listed above are (2.13,
). Individual S034 is at the 90th percentile; according to the aENET with bootstrap, her predicted three-year survival is 0.93, and a 95% CI is (0.44, 1.00). The voting-based predicted survival estimate is 0.96 with a much narrower 95% CI of (0.85, 0.99). The patient's breast tumor is ER positive, and the gene expression values for the fives genes listed above are (2.13, 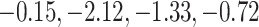 ). The pointwise and simultaneous CIs based on the voting procedure are dramatically narrower than the bootstrap-based limits, demonstrating the ability of our proposed method to give more precise but still accurate inferential information on the predicted survival.
). The pointwise and simultaneous CIs based on the voting procedure are dramatically narrower than the bootstrap-based limits, demonstrating the ability of our proposed method to give more precise but still accurate inferential information on the predicted survival.
Fig. 5.
Pointwise (left-hand column) and simultaneous (right-hand column) CIs for two individuals in the data set (top row: ID S246; bottom row: ID S034). The thin dotted line is the predicted survival from the aENET  ; the thin dashed line is the predicted survival from voting-based estimate
; the thin dashed line is the predicted survival from voting-based estimate 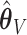 . Thick dotted lines are the bootstrap-based confidence limits around the aENET predicted survival, and thick dashed lines are the voting-based confidence limits around the voting-based predicted survival.
. Thick dotted lines are the bootstrap-based confidence limits around the aENET predicted survival, and thick dashed lines are the voting-based confidence limits around the voting-based predicted survival.
4. Discussion
In this paper, we proposed an adaptation of a resampling approach to use with a penalization method for variable selection, in which we use an ensemble of resampled estimators 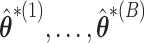 to better inform our knowledge of which
to better inform our knowledge of which 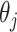 are truly 0, with the goal of improving our estimation of the variability in
are truly 0, with the goal of improving our estimation of the variability in 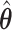 . We use the ensemble to vote out the unimportant covariates, and then by refitting the model in the data set and in resampled data sets, we produce estimators
. We use the ensemble to vote out the unimportant covariates, and then by refitting the model in the data set and in resampled data sets, we produce estimators 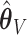 and
and 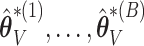 that can be used for valid inference. This not only improves precision of interval estimation for regression coefficients but also provides more precise interval estimation for the survival functions when compared with the standard bootstrap or asymptotic-based calculations. The voting-based perturbation approach tends to be the most robust across simulations, and maintains fairly good coverage levels with smaller interval width than the standard bootstrap. The compromise
that can be used for valid inference. This not only improves precision of interval estimation for regression coefficients but also provides more precise interval estimation for the survival functions when compared with the standard bootstrap or asymptotic-based calculations. The voting-based perturbation approach tends to be the most robust across simulations, and maintains fairly good coverage levels with smaller interval width than the standard bootstrap. The compromise  makes in variable selection enables us to reduce the downward bias for weak shrinkage and provide more accurate estimation of the sampling variability via resampling. In the context of risk prediction, prediction performance measures such as C-statistics (Uno and others, 2011) are often of interest for validating prediction models. Extending the proposed method to make precise inference about prediction accuracy measures warrants further research.
makes in variable selection enables us to reduce the downward bias for weak shrinkage and provide more accurate estimation of the sampling variability via resampling. In the context of risk prediction, prediction performance measures such as C-statistics (Uno and others, 2011) are often of interest for validating prediction models. Extending the proposed method to make precise inference about prediction accuracy measures warrants further research.
The actual mechanics of the voting based on resampling are similar to those proposed in other work. For example, Zhu and Fan (2011) perform stepwise selection on bootstrapped samples of the data, and select variables to be included in the final model based on the bootstrapped samples. Bach (2008) bootstraps the data and performs lasso on each bootstrapped sample, fitting a final model using unconstrained ordinary least squares on the variables that are non-zero in every bootstrap lasso fit. Meinshausen and Bühlmann (2010) subsample the data, perform lasso with a randomized weight, and then include variables that appear in some proportion of these fits. Our proposed method differs in some key details from these—we build around a variable selection method that has oracle properties in order to guarantee good asymptotic behavior and choose the voting threshold in a data-adaptive manner for good finite sample performance—but the general idea is similar. The main difference is that in other ensemble methods, the goal is typically improvement of variable selection and prediction; in contrast, we use the ensemble-derived knowledge to refit the model in both the original and the resampled data, in order to use the resampled data to more accurately assess error; to our knowledge, this has not been done previously. This allows us to achieve our goal of improving inference on potentially complicated functions of the parameter, such as the predicted survival.
Supplementary material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
J.A.S. was supported by the National Institutes of Health (NIH) grant T32 CA09001 and the A. David Mazzone Career Development Award. T. C. was supported by the NIH grants R01 GM079330, R01 HL089778, and U54 H6007963.
Supplementary Material
Acknowledgments
Conflict of Interest: None declared.
References
- Bach F. R. (2008). Bolasso: model consistent lasso estimation through the bootstrap. In: Proceedings of the 25th International Conference on Machine Learning New York: ACM, pp. 33–40. [Google Scholar]
- Breslow N. E. (1972). Contribution to the discussion of the paper by DR Cox. Journal of the Royal Statistical Society, Series B 342, 216–217. [Google Scholar]
- Cox D. R. (1972). Regression models and life tables. Journal of the Royal Statistical Society. Series B 34, 187–220. [Google Scholar]
- Economopoulou P., Dimitriadis G., Psyrri A. (2015). Beyond brca: new hereditary breast cancer susceptibility genes. Cancer Treatment Reviews 411, 1–8. [DOI] [PubMed] [Google Scholar]
- Fan J., Li R. (2002). Variable selection for Cox's proportional hazards model and frailty model. The Annals of Statistics 301, 74–99. [Google Scholar]
- Gasco M., Shami S., Crook T. (2002). The p53 pathway in breast cancer. Breast Cancer Research 42, 70–76. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knight K., Fu W. (2000). Asymptotics for lasso-type estimators. The Annals of Statistics 285, 1356–1378. [Google Scholar]
- Kosorok M. R. (2007) Introduction to Empirical Processes and Semiparametric Inference. Berlin: Springer. [Google Scholar]
- Li Y., Melnikov A. A., Levenson V., Guerra E., Simeone P., Alberti S., Deng Y. (2015). A seven-gene cpg-island methylation panel predicts breast cancer progression. BMC Cancer 151, 417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin D. Y., Fleming T. R., Wei L. J. (1994). Confidence bands for survival curves under the proportional hazards model. Biometrika 811, 73–81. [Google Scholar]
- Meinshausen N. (2007). Relaxed lasso. Computational Statistics & Data Analysis 521, 374–393. [Google Scholar]
- Meinshausen N., Bühlmann P. (2010). Stability selection. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 724, 417–473. [Google Scholar]
- Minnier J., Tian L., Cai T. (2011). A perturbation method for inference on regularized regression estimates. Journal of the American Statistical Association 106496, 1371–1382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pötscher B. M., Schneider U. (2009). On the distribution of the adaptive lasso estimator. Journal of Statistical Planning and Inference 1398, 2775–2790. [Google Scholar]
- Subramanian A., Tamayo P., Mootha V. K., Mukherjee S., Ebert B. L., Gillette M. A., Paulovich A., Pomeroy S. L., Golub T. R., Lander E. S.. and others (2005). Gene set enrichment analysis: a knowledge-based approach for interpreting genome-wide expression profiles. Proceedings of the National Academy of Sciences of the United States of America 10243, 15545–15550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. (1996). Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 581, 267–288. [Google Scholar]
- Tibshirani R. (1997). The lasso method for variable selection in the Cox model. Statistics in Medicine 164, 385–395. [DOI] [PubMed] [Google Scholar]
- Uno H., Cai T., Pencina M. J., D'Agostino R. B., Wei L. J. (2011). On the c-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Statistics in Medicine 3010, 1105–1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y., Klijn J. G. M., Zhang Y., Sieuwerts A. M., Look M. P., Yang F., Talantov D., Timmermans M., Meijer-vanGelder M. E., Yu J.. and others (2005). Gene-expression profiles to predict distant metastasis of lymph-node-negative primary breast cancer. The Lancet 3659460, 671–679. [DOI] [PubMed] [Google Scholar]
- Wang H., Leng C. (2007). Unified lasso estimation by least squares approximation. Journal of the American Statistical Association 102479, 1039–1048. [Google Scholar]
- Wu Y. (2012). Elastic net for Cox's proportional hazards model with a solution path algorithm. Statistica Sinica 22, 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H. H., Lu W. (2007). Adaptive lasso for Cox's proportional hazards model. Biometrika 943, 691–703. [Google Scholar]
- Zhu M., Fan G. (2011). Variable selection by ensembles for the Cox model. Journal of Statistical Computation and Simulation 8112, 1983–1992. [Google Scholar]
- Zou H. (2006). The adaptive lasso and its oracle properties. Journal of the American Statistical Association 101476, 1418–1429. [Google Scholar]
- Zou H., Zhang H. H. (2009). On the adaptive elastic-net with a diverging number of parameters. Annals of Statistics 374, 1733. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.