Stochastic Kinetics of Nascent RNA

Abstract

The stochastic kinetics of transcription is typically inferred from the distribution of RNA numbers in individual cells. However, cellular RNA reflects additional processes downstream of transcription, hampering this analysis. In contrast, nascent (actively transcribed) RNA closely reflects the kinetics of transcription. We present a theoretical model for the stochastic kinetics of nascent RNA, which we solve to obtain the probability distribution of nascent RNA per gene. The model allows us to evaluate the kinetic parameters of transcription from single-cell measurements of nascent RNA. The model also predicts surprising discontinuities in the distribution of nascent RNA, a feature which we verify experimentally.

Transcription, the production of RNA from a gene, is a stochastic process consisting of multiple single-molecule events [1,2]. The inference of transcription kinetics is typically addressed as an inverse problem, using the ergodic assumption that population statistics contain the signature of single-cell kinetics. Specifically, the number of RNA molecules from the gene is measured in many individual cells simultaneously using microscopy-based methods [3–5], and the measured RNA copy-number distribution is then compared to the prediction from a stochastic model for transcription kinetics [6–9]. This approach has been successfully used to demonstrate the bursty, non-Poissonian nature of transcription [6–8] and to examine how transcription kinetics are modulated by transcription factors [10–12].

However, mapping cellular RNA number to the underlying kinetics of transcription is hampered by the fact that this number reflects additional processes downstream of transcription, such as RNA degradation and its partitioning during cell division. The stochasticity of both processes may mask that of the transcription process [13,14]. Moreover, cellular RNA represents the combined contributions from multiple copies of the same gene, whose number changes through the cell cycle [14,15] and whose activity may be correlated [15–18].

In contrast to total cellular RNA, nascent RNA the RNA molecules still actively transcribed at the gene is not subject to these effects, and therefore bears more closely the signature of the transcription process. Recent progress in fluorescence microscopy has allowed measuring the amount of nascent RNA at individual genes in single cells [8,15,16,19–24]. However, the theoretical modeling of nascent RNA kinetics is only at its infancy [8,16,23,25–27]. We still lack a theoretical framework for mapping the single-cell measurements back to the stochastic kinetics of transcription. The goal of this paper is to develop such a framework.

The model

We model the kinetics of nascent RNA as consisting of four steps (Fig. 1(a)): Gene activation, transcription initiation, RNA synthesis (elongation), and release [8,16,23]. The gene fluctuates between two states, active (state 1), where transcription initiation is allowed, and inactive (state 0), where it is forbidden. Transitions between states and the initiation of transcription in the active state are modeled as Poisson processes, with rates k₀₁, k₁₀ and k_INI, respectively [6,9,28,29]. Following initiation, RNA synthesis proceeds with a constant elongation speed V_EL [25,30], to a final length L. The completed RNA molecule remains on the gene for a (deterministic) duration T_S before being released [22,31]. See Supplemental Material [32] for a detailed discussion of model assumptions and of possible extensions to the model.

FIG. 1. A stochastic model of nascent RNA kinetics.

(a) Model schematic. (b) Different experimental observables that can be described by the model: The number of RNA polymerases (RNAPs) on the gene (green), the amount of nascent RNA (red), and the signal from single-molecule fluorescence in situ hybridization (smFISH) probes (blue). (c) The contribution function corresponding to the three observables in panel b. In all cases, T_S = 0.

The state of the system is defined by two random variables, the gene state n ( n= 0, 1) and the amount of nascent RNA m ( m≥ 0 ). m is obtained by summing over all nascent RNA molecules present at the gene, and is measured in units of a single complete (mature) RNA [8,14,16]. Since nascent RNAs may be incomplete [14,22], m can have non-integer values. Here we generalize m to represent the experimentally measured signal from the nascent RNA. The actual value of m thus depends on the specific experimental observable (Fig. 1(b)). For example, in the case of single-molecule fluorescence in situ hybridization (smFISH, [3–5]), commonly used for RNA detection, m corresponds to the fluorescent signal emitted by oligonucleotide probes bound to the RNA. In all cases, the signal m at time t is determined by initiation events happening within a time window T_RES = L V_EL +T_S (the residence time of RNA at the gene) prior to t , and the contribution from each nascent RNA molecule depends only on its length at time t. We define the contribution function G l ( ) to describe the signal from a single RNA of length l [23]. Since l is determined by the difference between the RNA initiation time t and the observation time t , we can rewrite G as a function of this time difference, g(τ) = G(l(τ)), with τ = t_i − t (−T_RES ≤ τ ≤ 0) and l(τ) = min{L, −V_EL τ} [16]. The observed signal is then given by $m(t)={\displaystyle \sum _{t-T_{\text{RES}}\le t_i\le t}}g(t_i-t)$. The form of g(τ) reflects the experimental observable. A few examples are depicted in Fig. 1(c) and discussed in more detail below. In all cases, g(τ) is non-increasing, with the delay T_s in RNA release represented as a time period with g=1.

General approach to solving the model

Because m exhibits a finite deterministic memory (over duration T_RES), we cannot easily write the master equation for the probability distribution P(n, m). To overcome this problem and solve for the state of the system at time t, we first define the pseudo-observables 𝓷(tau;, t) ≡ n(t + τ), which indicates the gene state n at t + τ and $\mathcal{m}(\tau ,t)={\displaystyle \sum _{t-T_{\text{RES}}\le t_i\le t+\tau }}g(t_i-t)$, which describes the accumulation of m over the history from t − T_RES to t + τ. Here, τ varies from −T_RES to 0. Notably, 𝓶 = 0 for τ = −T_RES and 𝓶 = m for τ = 0. Next, we write the master equation for the probability distribution P(𝓷, 𝓶) [16]:

$$\frac{d\mathbf{P}(\mathcal{m})}{d\tau }=(\mathbf{K}-{\mathbf{K}}_{\text{INI}})\mathbf{P}(\mathcal{m})+{\mathbf{K}}_{\text{INI}}\mathbf{P}(\mathcal{m}-g(\tau )).$$ (1)

Here, $\mathbf{K}=\left[\begin{array}{cc}-k_{01}& k_{10}\\ k_{01}& -k_{10}\end{array}\right],{\mathbf{K}}_{\text{INI}}=\left[\begin{array}{cc}0& 0\\ 0& k_{\text{INI}}\end{array}\right]$, and $\mathbf{P}(\mathcal{m})=\left[\begin{array}{c}P(0,\mathcal{m})\\ p(1,\mathcal{m})\end{array}\right]$. Note that we allow 𝓶 to be negative, but Eq. (1) guarantees that P(𝓶< 0) = 0 as long as the initial conditions satisfy that condition. To obtain the distribution of the true observables (n, m) , we solve Eq. (1) for the pseudo-observables (𝓷, 𝓶) and substitute τ = 0 (Alternatively, Eq. (1) can be used to derive an equation for P(n, m), see Supplemental Material [32]).

We focus on the steady-state behavior of P(n, m). Using the definition of 𝓶 and the (easily calculable) steady-state distribution for the gene state n , we obtain the initial condition ${\mathbf{P}}_{\tau =-T_{\text{RES}}}(\mathcal{m})=\frac{\delta (\mathcal{m})}{k_{01}+k_{10}}\left[\begin{array}{c}{k}_{10}\\ k_{01}\end{array}\right]$. To solve Eq. (1), we transform P(𝓷, 𝓶) to its characteristic function $\mathrm{\Psi }(\mathcal{n},\omega )\equiv {\int }_0^{\infty }{e}^{im/\omega }P(\mathcal{n},\mathcal{m})d\mathcal{m}$ [46] to obtain

$$\frac{d\mathbf{\Psi }(\omega )}{d\tau }=(\mathbf{K}+(e^{i\omega g(\tau )}-1){\mathbf{K}}_{\mathbf{INI}})\mathbf{\Psi }(\omega ),$$ (2)

with $\mathbf{\Psi }(\omega )=\left[\begin{array}{c}\mathrm{\Psi }(0,\omega )\\ \mathrm{\Psi }(1,\omega )\end{array}\right]$ and the initial condition ${\mathbf{\Psi }}_{\tau =-T_{\text{RES}}}(\omega )=\frac{1}{k_{01}+k_{10}}\left[\begin{array}{c}{k}_{10}\\ k_{01}\end{array}\right]$. Eq. (2) is analogous to a quantum mechanical spin system with a time-dependent interaction term. Its solution is therefore given by the Dyson series [54]:

$${\mathbf{\Psi }}_{\tau =0}(\omega )=\left\{\mathbf{I}+\sum _{N=1}^{\infty }{\int }_{-T_{\text{RES}}}^{0}d{\tau }_1\cdots {\int }_{-T_{\text{RES}}}^{{\tau }_{N-1}}d{\tau }_N\prod _{{\tau }_1>\cdots {\tau }_i\cdots \ge {\tau }_N}{e}^{i\omega g({\tau }_i)}\mathbf{V}({\tau }_i)\right\}{e}^{(\mathbf{K}-{\mathbf{K}}_{\mathbf{INI}})T_{\text{RES}}}{\mathbf{\Psi }}_{\tau =-T_{\text{RES}}},$$ (3)

where V(τ)= e^{−(K−K_INI)τ}K_INIe^{(K−K_INI)τ.} Applying the inverse transformation, we obtain the steady-state distribution,

$$\begin{array}{l}\mathbf{P}(m)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }{e}^{-im\omega }{\mathbf{\Psi }}_{\tau =0}(\omega )d\omega =\sum _{N=0}^{\infty }{\mathbf{P}}_N(m)\\ =\left\{\delta (m)+\sum _{N=1}^{\infty }{\int }_{-T_{\text{RES}}}^{0}d{\tau }_1\cdots {\int }_{-T_{\text{RES}}}^{{\tau }_{N-1}}d{\tau }_N\delta \left(m-\sum _{i=1}^{N}g({\tau }_i)\right)\mathcal{T}\left[\prod _{i=1}^N\mathbf{V}({\tau }_i)\right]\right\}{e}^{(\mathbf{K}-{\mathbf{K}}_{\mathbf{INI}})T_{\text{RES}}}{\mathbf{\Psi }}_{\tau =-T_{\text{RES}}}.\end{array}$$ (4)

where 𝒯 is the time -ordering operator. ${\mathbf{P}}_N(m)=\left[\begin{array}{c}P(0,m\mid N)\\ P(1,m\mid N)\end{array}\right]$ is the vectorized probability of observing m, given that the number of initiation events in the time interval −T_RES ≤ τ ≤ 0 was exactly N. In the general case, P_N(m) depends on the contribution function g(τ) , and therefore solving Eq. (4) requires knowing the specific form of g(τ). Below we describe the solution for a number of experimentally-relevant examples. A closed-form solution may not be always possible, but P(n m , ) can be calculated numerically using the finite state projection method [16,23,33,47](Supplemental Material [32]). For the purpose of comparing with experimental data, the calculated distribution is typically marginalized over n , i.e. $P(m)={\displaystyle \sum _n}P(n,m)$. The moments of P(m) can be directly calculated from Eq. (2) (Supplemental Material [32]):

$$\begin{array}{l}\langle m^N\rangle =\mathbf{u}·{(-i)}^N\frac{d^N}{d{\omega }^N}{\mathbf{\Psi }}_{\tau =0}(0)\\ =\mathbf{u}·\sum _{I=1}^N\sum _{0=\underset{i=1,\cdots ,I-1}{\underbrace{k_0<k_i<k_I}}=N}{\int }_{-T_{\text{RES}}}^{0}d{\tau }_1\cdots {\int }_{-T_{\text{RES}}}^{{\tau }_{l-1}}d{\tau }_I\mathcal{T}\left[\prod _{i=1}^I\left(\begin{array}{c}{k}_i\\ k_{i-1}\end{array}\right)g{({\tau }_i)}^{k_i-k_{i-1}}\mathbf{W}({\tau }_i)\right]{\mathbf{\Psi }}_{\tau =T_{\text{RES}}}(0),\end{array}$$ (5)

with u = (1,1) and W(τ)= e^−KτK_INIe^Kτ. Below we use these moments to explore the shape of P(m) as a function of model parameters.

Solutions for specific contribution functions

Case 1: g = 1

This corresponds to measuring the number of RNA polymerases (RNAPs) currently transcribing the gene (Fig. 1(c), panel I), or, equivalently, the number of nascent RNA molecules present, irrespective of their lengths [8]. Here and below we assume for simplicity that T_S = 0 (i.e. RNA is released from the gene immediately upon completion [16,19]), and (without loss of generality) set T_RES =1. Since g in this case does not take fractional values, we replace the characteristic functions with generating functions, $F_{\mathcal{n}}(z,\tau )\equiv {\displaystyle \sum _{\mathcal{m}=0}^{\infty }}{z}^{\mathcal{m}}{P}_{\tau }(\mathcal{n},\mathcal{m})$ and F(z, τ) ≡ F₀(z, τ) + F₁(z,τ), and transform Eq. (1) to obtain

$$\ddot{F}+(k_{01}+k_{10}+(1-z)k_{\text{INI}})\stackrel{.}{F}+(1-z)k_{\text{INI}}{k}_{01}F=0,$$ (6)

with the initial conditions F (z, −1) =1, $\stackrel{.}{F}(z,-1)=(z-1)\frac{k_{\text{INI}}{k}_{01}}{k_{01}+k_{10}}$. Solving Eq. (6) and performing the inverse transformation allows us to calculate the marginal probability distribution of m (see Supplemental Material [32]),

$$P(m)=\frac{e^{-\frac{k_{01}+k_{10}+k_{\text{INI}}}{2}}}{m!}{\left(\frac{k_{\text{INI}}}{2}\right)}^m\{\left[\frac{k_{01}+k_{10}+k_{\text{INI}}}{2}-\frac{k_{\text{INI}}{k}_{01}}{k_{01}+k_{10}}\right]\sum _{i=0}^m\left(\begin{array}{c}m\\ i\end{array}\right)M_{1,i}+\sum _{i=0}^m\left(\begin{array}{c}m\\ i\end{array}\right)M_{0,i}+m\frac{k_{01}-k_{10}}{k_{01}+k_{10}}\sum _{i=0}^{m-1}\left(\begin{array}{c}m-1\\ i\end{array}\right)M_{1,i}\},$$ (7)

with $M_{s,i}={\displaystyle \sum _{2l\ge i}}{\displaystyle \sum _{w=max(0,i-l)}^{min(l,i)}}\left(\begin{array}{c}l\\ w\end{array}\right)\left(\begin{array}{c}l\\ i-w\end{array}\right)\frac{{(-1)}^{i}i!}{(2l+s)!}{\left(\frac{k_{\text{INI}}+{\kappa }_1}{2}\right)}^{l-w}{\left(\frac{k_{\text{INI}}+{\kappa }_2}{2}\right)}^{l-i+w},{\kappa }_{1,2}=k_{10}-k_{01}\pm 2i\sqrt{k_{10}{k}_{01}}$ Eq. (7) provides the exact solution for the distribution of the number of transcribing RNAPs at the gene.

Figure 2(a) depicts P(m) , calculated from Eq. (7), for a few parameter values. Stochastic simulations of the model, also shown, agree with the analytical calculation (Supplemental Material [32]). For insight into the shape of P(m) , we first note that gene-state transitions are typically believed to be slow compared to both the rate of initiation and the time to complete one RNA [8,16,55]. Specifically, in the limit (k₀₁& k₁₀) k_INI and (k₀₁ or k₁₀) 1, Eq. (7) can be written as the weighed sum of two Poisson distributions, with rates 0 and k (Supplemental Material [32]). In this limit, P(m) is also identical to the solution for the commonly used two-state model for cellular RNA kinetics [6,8,9,29], if we replace the residence time T_RES with the RNA degradation rate k_D. Outside that limiting case, however (as e.g. in [16]), the two distributions can be quite different (Fig. S1 in the Supplemental Material [32]).

FIG. 2. The probability distribution for the number of RNAPs at the gene.

(a) The exact solution for P(m) (binned to integer values, red) for a few parameter values. Also shown are the results of stochastic simulations (gray). (b) The bimodality coefficient β as a function of k₀₁, k₀ and k _NI was calculated and thresholded (β_th = 5 9 , bottom, red surface) to classify P(m) as either bimodal or unimodal. The unimodal distributions were further classified based on the peak position. Parameter values corresponding to panel a are marked as gray circles.

To map how the shape of P(m) varies with transcription parameters, we defined the bimodality coefficient, β ≡ 1/(κ − γ²) , where γ is the skewness and κ the kurtosis of P(m) [51]. Calculating β over a broad range of kinetic rates, and using a threshold of β_th = 5/9 (corresponding to a uniform distribution, see Supplemental Material [32]), we found that P(m) is bimodal for k₀₁ ~ k₁₀ ≲ and k_INI ≳ 1, and unimodal outside this region (Fig. 2(b)). The unimodal region can be further divided based on the position of the distribution peak, at m= 0 or m> 0 (Fig. 2(b)).

Case 2: g = − τ

This corresponds to measuring the total length of nascent RNA, summed over multiple molecules present at the gene (Fig. 1(c), panel II). Experimentally, this is achieved by using multiple smFISH probes covering the length of the target gene [4]. In contrast to Case 1 above, m is now continuous, and Eq. (2) can be transformed to a single equation for Ψ(1, ω) (Supplemental Material [32]):

$$\ddot{\mathrm{\Psi }}(1,\omega )+\left[k_{01}+k_{10}+k_{\text{INI}}\left(1-e^{-i\omega \tau }\right)\right]\stackrel{.}{\mathrm{\Psi }}(1,\omega )-\left[k_{\text{INI}}\left(k_{01}-i\omega \right)e^{-i\omega \tau }-k_{\text{INI}}{k}_{01}\right]\mathrm{\Psi }(1,\omega )=0,$$ (8)

with the initial conditions ${\mathrm{\Psi }}_{\tau =-1}(1,\omega )=\frac{k_{01}}{k_{01}+k_{10}},{\stackrel{.}{\mathrm{\Psi }}}_{\tau =-1}(1,\omega )=\frac{k_{01}{k}_{\text{INI}}}{k_{01}+k_{10}}(e^{i\omega }-1)$. By solving Eq. (8), we obtain the exact expression for Ψ(ω) ≡Ψ(0, ω) +Ψ (1, ω) as a combination of confluent hypergeometric functions. Since transforming Ψ (ω) back to an analytical form of P(m) is challenging, we proceed to calculate P(m) using finite state projection [16,23,33]. The calculated P(m) exhibits the same three characteristic shapes as in Case 1, but the boundaries in parameter space between regions exhibiting different shapes are shifted by up to 2-fold (Fig. S2 in the Supplemental Material [32]). Thus, the difference in contribution functions can lead to different shapes of P(m) for the same transcription parameters (another example of this effect is described below).

Inferring transcription kinetics from single-cell measurements of nascent RNA

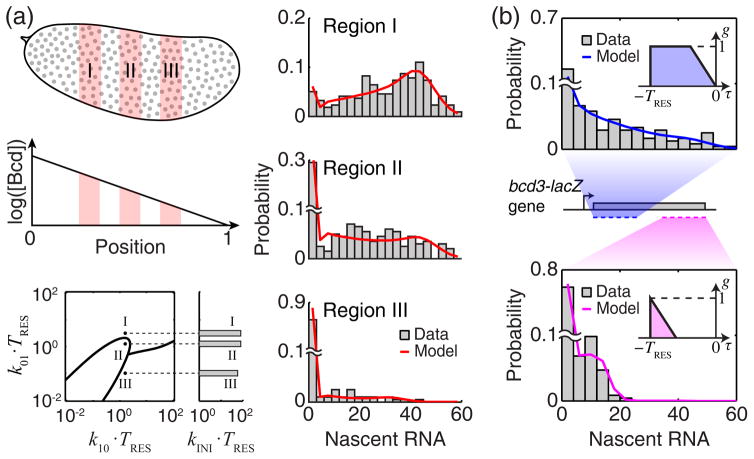
To demonstrate how the model can be used to interpret experimental data, we first examined the transcription of the hunchback (hb) gene in embryos of the fruit fly, Drosophila melanogaster ([16] and Supplemental Material [32]). Early in development, hb is regulated by the transcription factor Bicoid (Bcd), whose concentration forms a gradient along the embryo [56] (Fig. 3(a)). We measured the amount of nascent RNA at individual copies of the hb gene [16], and examined the distribution of nascent RNA over all cell nuclei within a given region of the embryo (corresponding to a given Bcd concentration) (Fig. 3(a)). Next, we solved Eq. (1) using g(τ) that corresponds to the set of smFISH probes used in the experiment [16], and used maximum likelihood estimation to fit the model to the experimental data. The model was able to capture the change in P(m) shape along the embryo (Fig. 3(a)). We found that the regulatory effect of Bcd is to increase k₀₁ (>50 fold along a single embryo) while k₁₀ and k _INI remain almost unchanged (Fig. 3(a)). Thus, the model allowed us to identify what aspect of hb kinetics is modulated during gene regulation [16].

FIG. 3. Estimating transcription kinetics from experimental data.

(a) Regulation of the hb gene by Bcd. Top left, Bcd forms a concentration gradient along the anterior-posterior axis of the Drosophila embryo. Grey circles indicate individual cell nuclei. Three representative regions of the embryo are highlighted in pink, corresponding to high (I), medium (II) and low (III) Bcd concentrations. Right, the measured distribution of nascent hb RNA at each region (smFISH data from a single embryo, >200 data points per histogram, bin width = 3), and the corresponding theoretical fit (red). Bottom left, the estimated transcription parameters (dots), superimposed on the modality phase plane of P(m) calculated as in Fig. 2(b). (b) The effect of smFISH probe positions. Two different sets of probes were designed against the bcd3-lacZ reporter gene, targeting the first half (blue) and second half (magenta) of the gene. The two sets yielded different distributions of nascent RNA (top and bottom, >250 data points from a single embryo, at 0.2–0.3 embryo length, bin width = 4). Using the contribution functions calculated from the probe positions on the gene (insets) yielded a good fit between the model and experimental data.

In the second example, we labeled the two halves of the same gene using two different smFISH probe sets carrying two different fluorescent dyes (Fig. 3(b) and Supplemental Material [32]). In the experiment, the two probe sets yielded very different signal distributions P(m) (both normalized to the signal from a single full-length RNA). In particular, the signal from the first half of the gene was spread ~2 fold wider on the m axis than that from the second half (Fig. 3(b)). Since both probe sets label the same gene, the two data sets should be describable using the same kinetic parameters, the only difference being the form of g(τ) , which we calculated directly from the probe positions on the gene (Fig. 3(b)). In agreement with this hypothesis, we were able to fit the two experimental distributions (as well as the joint distribution) using a single set of transcription parameters (Fig. 3(b) and Supplemental Material [32]).

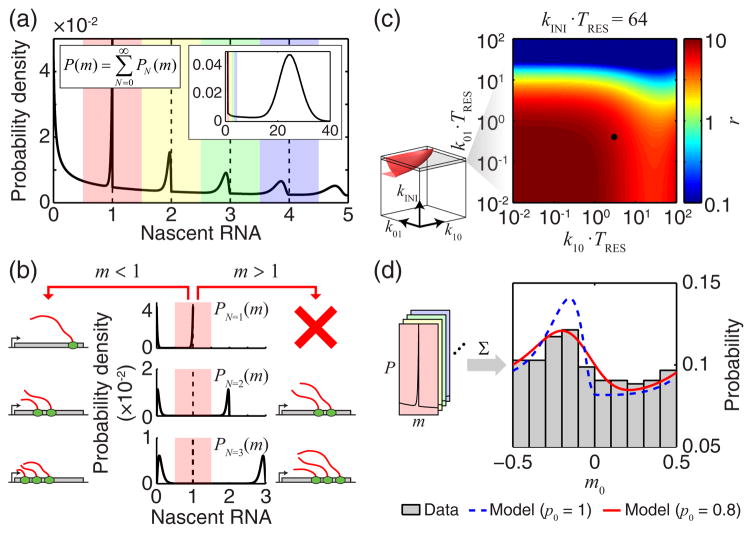
Discontinuities in P(m)

As noted above, a distinctive feature of nascent RNA, in contrast to mature cellular RNA, is that it can be approximated as continuous [4,5,16]. When examining the behavior of our model in the case g=−τ (i.e. measuring the total amount of nascent RNA at the gene), we found that, for multiple parameter choices, P(m) appears discontinuous at integer values of m (insets of Fig. S2(a) in the Supplemental Material [32]). This discontinuity was consistent with the appearance of terms of order 1ω in the characteristic function Ψ(ω) [57]. The source of the discontinuity can be understood by noting that, in Eq. (4), P(m) is written as the sum of P_N(m) , the probabilities of observing m given that the number of initiation events in the time interval −T_RES ≤τ≤ 0 is N (equivalently, the number of RNAPs present at the gene is N ). Since, for a given N , m cannot exceed N , the result may be a discontinuity of P(m) or its derivatives at integer values. Specifically, since P₀(m) ∝δ (m) , P(m) has an infinite discontinuity at m= 0. P₁(m) is nonzero only for m≤1, hence P(m) has a jump discontinuity at m=1. For higher values of N , it can be shown that the (N−1) ^th derivative of P(m) has a jump discontinuity at m = N (Supplemental Material [32]). For each point of discontinuity, the magnitude of the jump is

$$\mathrm{\Delta }{P}_N={\frac{d^{N-1}P(m)}{d{m}^{N-1}}|}_{m=N^{-}}-{\frac{d^{N-1}P(m)}{d{m}^{N-1}}|}_{m=N^{+}}=\frac{{(-1)}^{N-1}}{N!}\mathbf{u}·e^{(\mathbf{K}-{\mathbf{K}}_{\mathbf{INI}})}{\mathbf{K}}_{\text{INI}}^N{\mathbf{\Psi }}_{\tau =-1}.$$ (9)

We explore this feature in Fig. 4. For the parameters used (k₀₁ = k₁₀ = 0.1, k _NI = 50 ), zooming in to the low range of m reveals a sharp drop of P(m) at m=1 (Fig. 4(a)). At higher integer m ’s, the drop becomes smaller and is shifted to the left (Fig. 4(a)). The drop reflects the discontinuity of P(m) (or its derivatives) at integer m ’s. Each drop is preceded by an increase of P(m) , resulting in a peak at m → N⁻ (Fig. 4(b)). This peak, in turn, is due to the fact that, when k_INI ≥ N and gene transitions are slow (k₀₁, k₁₀ ≤ 1), the two most probable ways of observing exactly N initiation events are for the gene to be active only at the beginning ( $\tau \to -T_{\text{RES}}^{+}$) or the end (τ→ 0⁻) of the time window, resulting in maxima of P_N (m) at m → N⁻ and m→ 0⁺ , respectively (Fig. 4(b)).

FIG. 4. Discontinuities in nascent RNA distribution at integer m values.

(a) The calculated distribution of nascent RNA at small values of m , for k₀₁ = k₀= 0.1 , k_INI = 50. A larger range of m is shown in the inset. The range of m was divided into windows covering 0.5 to 0.5 around each integer (colored shading). (b) The origin of discontinuity at m=1. The total probability of observing m is a marginalization over different numbers of RNAPs on the gene (plotted for N=1, 2, 3 ). (c) The discontinuity factor r as a function of k₀₁, k₁₀ and k_INI was calculated and thresholded (r_th = 0.1, left, red surface). Black dot indicates the experimental data analyzed in panel d. (d) The experimental signature of P(m) discontinuity. Nascent RNA from bcd3-lacZ was measured using smFISH (at 0.1–0.3 embryo length, 23 embryos). The distribution of m₀, the deviation of m from the nearest integer, was calculated (gray, 3.5 ≤ m< 6.5, ~500 data points, bin width = 0.1) and compared to model predictions with (red) and without (dashed blue) incorporating the effect of finite probe binding probability p₀.

To ask whether these features of P(m) can be detected experimentally, we first defined the discontinuity factor r ≡ ΔP₁/Pm (=1⁺) to characterize the magnitude of the jump in the distribution of nascent RNA. Calculating r over a wide range of kinetic rates indicated that it would be high (> 0.1) for k₀₁ ≲ 10¹ (Fig. 4(c)). This range covers the estimated parameters in multiple biological systems [16,23,58], including our measurements in Drosophila (Fig. 3 above). To then try and detect this feature in our experimental data, we focused on the small m (< 6.5 ) range, where the peaks in P(m) are expected to be the highest (Fig. 4(a)). To improve data sampling, we defined the variable m₀ = m −[m] (where [·] denotes the nearest integer) such that all m values are mapped into the range [−0.5, 0.5). Using this procedure, we detected a peak to the left of m₀ = 0 , as predicted by the model (Fig. 4(d)). Allowing for the finite binding probability of smFISH probes [16,53], we were able to successfully reproduce the shape of the folded probability distribution (Fig. 4(d), see Supplemental Material [32]). Thus, the experimental data supports the theoretical prediction of discontinuity in the distribution of nascent RNA. The periodic discontinuities can be used to identify the signal intensity corresponding to a single RNA, thus improving the precision of RNA counting using smFISH [3,5,14,16].

Conclusion

We presented a theoretical framework for connecting the stochastic kinetics of transcription with the resulting probability distribution of nascent RNA at the gene. By changing the form of the contribution function g(τ) , the model can be used to describe different experimental observables. The model allowed us to interpret experimental data, extract the kinetic parameters of gene activity, and identify how the kinetics vary under the regulatory influence of a transcription factor. The model also predicted a hitherto unobserved feature of discontinuities and periodic peaks in nascent RNA distribution, which we were able to validate experimentally. To further improve the estimation of transcription parameters, the model for nascent RNA can be combined with one for the total cellular RNA [15] and compared to experimental measurements of both species simultaneously [3,6,8,15] (Supplemental Material [32]). Beyond the steady-state distribution discussed here, solving for the time-dependent behavior of the model (Supplemental Material [32]) can allow a direct comparison with live-cell measurements of nascent RNA [19,21,22].