A semivarying joint model for longitudinal binary and continuous outcomes

Abstract

Semivarying models extend varying coefficient models by allowing some regression coefficients to be constant with respect to the underlying covariate(s). In this paper we develop a semivarying joint modelling framework for estimating the time-varying association between two intensively measured longitudinal response: a continuous one and a binary one. To overcome the major challenge of jointly modelling these responses, namely, the lack of a natural multivariate distribution, we introduce a Gaussian latent variable underlying the binary response. Then we decompose the model into two components: a marginal model for the continuous response, and a conditional model for the binary response given the continuous response. We develop a two-stage estimation procedure and discuss the asymptotic normality of the resulting estimators. We assess the finite-sample performance of our procedure using a simulation study, and we illustrate our method by analyzing binary and continuous responses from the Women’s Interagency HIV Study.

1. INTRODUCTION

Analysis of longitudinal data can be challenging due to intra-subject dependence. When there are multiple responses and the association between those responses is of interest, it is common to model the responses jointly. In applications of joint modelling of longitudinal responses, two challenges may be encountered: (1) the responses may be of different types (such as binary and continuous), in which case no natural multivariate distribution exists, and (2) the data may exhibit a dynamic pattern that cannot be revealed by ordinary models. These issues imply the need for a general statistical procedure for analyzing longitudinal binary and continuous outcomes, a procedure that permits the association between the responses to be time varying while accommodating two types of response–predictor relationships: time varying and time invariant. In this paper we propose such a procedure.

Various methods have been developed for modelling longitudinal binary and continuous responses jointly (Catalano and Ryan, 1992; Cox and Wermuth, 1992; Dunson, 2000; Fitzmaurice and Laird, 1995; Gueorguieva and Agresti, 2001; Kürüm et al., 2014; Liu et al., 2009; Regan and Catalano, 1999; Sammel et al., 1997). The chief difficulty in developing these methods is that there is no natural multivariate distribution for such outcomes. One solution to this problem is to introduce a latent variable underlying the binary response, and assume that the continuous response and the latent variable are jointly normally distributed. This joint distribution is then decomposed in one of two ways: (1) a marginal distribution for the continuous response and a conditional distribution for the binary response given the continuous response, or (2) a marginal distribution for the binary response and a conditional distribution for the continuous response given the binary response.

Another solution to the aforementioned problem is the joint mixed-effects model (Gueorguieva, 2001; Gueorguieva and Agresti, 2001). In this model a random effect is assumed for each response, and the responses are associated through a joint distribution for the random effects. One disadvantage of this approach is that maximum likelihood estimation is possible only when strong assumptions are made (Verbeke et al., 2010). For instance, Roy and Lin (2000) assumed that the random effects are perfectly correlated. Moreover, a mixed-effects model may be confounded (Hodges and Reich, 2010), which may inflate the variance of fixed-effects estimators and thereby prevent the discovery of important response–predictor relationships.

In a longitudinal study the relationship between a response and predictors, or the association between the continuous and binary responses, may vary over time, and ordinary models cannot capture these dynamic patterns. For this reason, unlike the aforementioned joint modelling techniques, Kürüm et al. (2014) proposed time-varying coefficient models (Brumback and Rice, 1998; Hoover et al., 1998) for modelling longitudinal binary and continuous responses jointly. Their method allows all parameters, including association parameters, to be time varying. These nonparametric models relax the restrictive assumptions of parametric models and are very useful in exploring the hidden structure in a data set. A nonparametric approach may, however, lack power when the sample is small, in which case a semivarying model may be more appropriate, especially if the practitioner has reason to believe that some response–predictor relationships are time invariant.

In this paper we introduce a new joint modelling approach for intensively measured longitudinal binary and continuous outcomes. The goals of our approach are to (1) efficiently estimate the time-varying partial association between the responses conditional on predictors of interest, and to (2) reveal both time-varying and time-invariant response–predictor relationships.

To achieve our goals, we employ semivarying coefficient models, which were studied by Fan and Huang (2005) for independent and identically distributed (iid) observations, and were extended to longitudinal data analysis by Fan et al. (2007). These models are extensions of both partially linear models (Härdle et al., 2000) and time-varying coefficient models (Hastie and Tibshirani, 1993; Hoover et al., 1998). The major contribution of this work is that our proposed approach can explore the time-varying partial association between binary and continuous responses while allowing some of the response–predictor relationships to be time invariant, unlike the approach of Kürüm et al. (2014), which posits that all of these relationships are time-varying. To the best of our knowledge, semivarying coefficient models have not been applied for jointly modelling these types of responses in a longitudinal setting. This work will fill this gap in the literature.

We propose an estimation procedure for semivarying coefficient models for joint binary and continuous outcomes. We adopt the above mentioned latent variable approach and then factor the joint distribution into two components. This results in a two-stage estimation procedure. In the first stage we fit the marginal model of the continuous response by using estimation techniques for semivarying coefficient models. In the second stage we use generalized time-varying coefficient models (Cai et al., 2000) (for iid data) to fit the conditional model of the binary response given the continuous response. We use a simulation study to investigate the efficacy of our procedure.

The remainder of this paper is organized as follows. Section 2 introduces our joint model for longitudinal binary and continuous responses, and describes our two-stage estimation procedure. In this section, we also discuss the asymptotic behavior of our estimators. Section 3 presents our simulation study. Section 4 illustrates our proposed methodology by analyzing data from the Women’s Interagency HIV Study. In Section 5 we make concluding remarks.

2. JOINT MODEL FOR BINARY AND CONTINUOUS RESPONSES

2.1. Model Specification

When the joint distribution of two continuous responses is of interest, it may be reasonable to assume that the responses are bivariate normal. There is no analogous joint distribution for the binary–continuous case, however. In order to overcome this challenge, we follow the well-known joint modelling approach described in Catalano and Ryan (1992). That is, we introduce a latent variable underlying the binary response, and assume that the continuous response and the latent variable are jointly normal. We then obtain the desired joint distribution using a two-component factorization: a marginal model for the continuous variable, and a conditional model for the binary variable given the continuous variable. The first component is readily available, and the second component is obtained using the normality of the latent variable along with the relationship defined between the latent variable and the binary response.

Before we describe our modelling scheme, let us introduce some notation. Suppose we have n independent subjects. For subject i, let Q_i(t) and W_i(t) denote the binary and continuous responses, respectively, measured at time points t = t_ij, where j = 1, …, n_i and n_i is the number of observations for subject i. We denote the latent variable as Y_i(t). Let x_i(t) = (x_i1(t), …, x_ip(t))^T and z_i(t) = (z_i1(t), …, z_iq(t))^T be the vectors of predictors for subject i. To simplify our presentation, we use the same set of predictors for both the continuous response and the latent variable, but our method can handle different predictors for the two responses, which we demonstrate in the data application.

Now, consider the bivariate semivarying coefficient model

$$\begin{array}{ll}\hfill W_i(t)& ={\mathbf{x}}_i^{\mathrm{T}}(t){\mathit{\alpha }}_w(t)+{\mathbf{z}}_i^{\mathrm{T}}(t){\mathit{\beta }}_w+{\epsilon }_{wi}(t)\hfill \\ \hfill Y_i(t)& ={\mathbf{x}}_i^{\mathrm{T}}(t){\mathit{\alpha }}_y(t)+{\mathbf{z}}_i^{\mathrm{T}}(t){\mathit{\beta }}_y+{\epsilon }_{yi}(t),\hfill \end{array}$$ (1)

where β_• = (β_•1, …, β_•q)^T and α_•(t) = (α_•1(t), …, α_•p(t))^T are the unknown regression coefficient vector and the nonparametric smooth baseline functions, respectively, and both ε_wi(t) and ε_yi(t) follow normal distributions with mean zero and time-varying variances ${\sigma }_w^2(t)$ and ${\sigma }_y^2(t)$, respectively. Let ρ_w(·, ·) and ρ_y(·, ·) be the correlations between two errors measured at different time points for ε_wi(·) and ε_yi(·), respectively. τ(t) = corr {ε_wi(t), ε_yi(t)} is the partial correlation between W_i(t) and Y_i(t) given x_i and z_i. Thus, we refer to τ(t) as the partial association between the binary and continuous responses. The primary goal of this paper is to develop an accurate estimator of this association.

In our modelling scheme, the relation between the binary variable and the latent variable is defined as: Q_i(t) = 1 if Y_i(t) > 0, and Q_i(t) = 0 if Y_i(t) ≤ 0. Since Y_i(t) follows a normal distribution, the binary response Q_i(t) follows the probit model

$$P\{Q_i(t)=1\mid {\mathbf{x}}_i(t),{\mathbf{z}}_i(t)\}=\mathrm{\Phi }\left\{\frac{{\mathbf{x}}_i^{\mathrm{T}}(t){\mathit{\alpha }}_y(t)+{\mathbf{z}}_i^{\mathrm{T}}(t){\mathit{\beta }}_y}{{\sigma }_y(t)}\right\},$$ (2)

where Φ(·) is the cumulative distribution function of the standard normal distribution.

To obtain the joint distribution, we use the two-component decomposition with a marginal model for the continuous variable W_i(t), and a conditional model for Q_i(t) given W_i(t):

$$f_{q,w}\{q_i(t),w_i(t)\}=f_w\{w_i(t)\}{f}_{q\mid w}\{q_i(t)\mid w_i(t)\}.$$

The first component (the marginal model for the continuous response) was defined in (1). The second component (the conditional model for Q_i(t) given W_i(t)) is derived using the conditional model for Y_i(t) given W_i(t). Normal theory shows that the conditional distribution Y_i(t) | W_i(t) follows a Gaussian distribution, and the mean of this conditional distribution depends on the error from the marginal model of the continuous response. Specifically,

$$Y_i(t)\mid W_i(t)~\mathcal{N}[{\mu }_i(t),{\sigma }_y^2(t)\{1-{\tau }^2(t)\}],$$ (3)

where

$${\mu }_i(t)={\mathbf{x}}_i^{\mathrm{T}}(t){\mathit{\alpha }}_y(t)+{\mathbf{z}}_i^{\mathrm{T}}(t){\mathit{\beta }}_y+\frac{{\sigma }_y(t)}{{\sigma }_w(t)}\tau (t){\epsilon }_{wi}(t)$$

and

$${\epsilon }_{wi}(t)=W_i(t)=\{{\mathbf{x}}_i^{\mathrm{T}}(t){\mathit{\alpha }}_w(t)+{\mathbf{z}}_i^{\mathrm{T}}(t){\beta }_w\}$$

is the error from the marginal model of the continuous response. Combining (3) with the relation defined between the latent variable and the binary response leads to the model

$$P\{Q_i(t)=1\mid W_i(t)\}=\mathrm{\Phi }\left[\frac{{\mu }_i(t)}{\sqrt{{\sigma }_y^2(t)\{1-{\tau }^2(t)\}}}\right].$$ (4)

Note that not all of the parameters in model (4) are estimable. For instance, it is not possible to estimate α_y(t) and σ_y(t) separately, but the ratio ${\mathit{\alpha }}_y(t)/\sqrt{{\sigma }_y^2(t)\{1-{\tau }^2(t)\}}$ is identifiable. Moreover, we might expect practitioners be more interested in the relationship between the predictors and the binary response. Thus we reparameterize the probit model in (4) to arrive at a more parsimonious and fully estimable form:

$$P\{Q_i(t)=1\mid W_i(t)\}=\mathrm{\Phi }\{{\mathbf{x}}_i^{\ast \mathrm{T}}(t)\mathit{\gamma }(t)+{\gamma }_{p+q+1}(t){\epsilon }_{wi}(t)\},$$ (5)

where ${\mathbf{x}}_i^{\ast \mathrm{T}}(t)={({\mathbf{x}}_i^{\mathrm{T}}(t),{\mathbf{z}}_i^{\mathrm{T}}(t))}^{\mathrm{T}}$ and γ(t) = (γ₁(t), …, γ_p+q(t))^T. The conditional form above shows that the continuous response is linked with the binary response in a probit regression model that includes the error from the marginal model as a covariate.

Model (5) and the definition of μ_i(t) lead to

$${\gamma }_{p+q+1}(t)=\frac{1}{{\sigma }_w(t)}·\frac{\tau (t)}{\sqrt{1-{\tau }^2(t)}}$$

and, hence,

$$\tau (t)=\frac{b(t)}{\sqrt{1+b^2(t)}},$$ (6)

where b(t) = γ_p+q+1(t)σ_w(t). According to (6), the partial association τ(t) depends on the regression coefficient of the error term from the marginal model and on the variance of the continuous response. The regression coefficient γ_p+q+1(t) and τ(t) share the same sign and are positively correlated.

2.2. Estimation Procedure

We propose a two-stage estimation procedure. Before presenting the details of our procedure, we give a brief sketch of both stages. In the first stage we fit a semivarying coefficient model (Fan and Huang, 2005; Fan et al., 2007) to the continuous response. At this stage we employ the profile least squares approach proposed by Fan et al. (2007) to obtain efficient estimators of the regression coefficients α_w(t) and β_w. In the second stage we use the residuals from the first stage and the predictors for the binary response, and fit a generalized varying coefficient model for the binary response given the continuous response. At this stage we obtain the components necessary to compute the estimate of τ(t).

Now we turn to the details for the first stage. Fan et al. (2007) suggest using the following formula to estimate the nonparametric smooth baseline functions in (1):

$${\widehat{\mathit{\alpha }}}_w(t)=({\mathbf{I}}_p,{\mathbf{0}}_p){({\mathbf{\Lambda }}^{\mathrm{T}}\kappa \mathbf{\Lambda })}^{-1}{\mathbf{\Lambda }}^{\mathrm{T}}\kappa {\mathbf{W}}^{\ast },$$ (7)

where I_p is the p × p identity matrix, 0_p is the p × p matrix of zeros, Λ = (Λ₁, …, Λ_n)^T, Λ_i = ((1, t_i1 − t) ⊗ x_i1, …, (1, t_ini − t) ⊗ x_ini), and κ is an N × N diagonal matrix with the kernel weights along its diagonal.

Substituting α̂_w(t) in (1) and using weighted least squares yields

$${\widehat{\mathit{\beta }}}_w={\{{\mathbf{z}}^{\mathrm{T}}{({\mathbf{I}}_N-\mathbf{S})}^{\mathrm{T}}\mathbf{R}({\mathbf{I}}_N-\mathbf{S})\mathbf{z}\}}^{-1}{\mathbf{z}}^{\mathrm{T}}{({\mathbf{I}}_N-\mathbf{S})}^{\mathrm{T}}\mathbf{R}({\mathbf{I}}_N-\mathbf{S})\mathbf{W},$$

where $\mathbf{z}={({\mathbf{z}}_1^{\mathrm{T}},\dots ,{\mathbf{z}}_n^{\mathrm{T}})}^{\mathrm{T}},\mathbf{W}={({\mathbf{W}}_1^{\mathrm{T}},\dots ,{\mathbf{W}}_n^{\mathrm{T}})}^{\mathrm{T}}$ with W_i = (W_i(t_i1), …, W_i(t_ini))^T, R is the working covariance matrix, and S is the smoothing matrix of the local linear smoother. Mis-specification of the working covariance matrix affects only the efficiency, not the consistency, of this estimator, whereas the local linear estimator (7) is not significantly affected by the covariance structure since the data are localized in time (Fan et al., 2007). We demonstrate this result by using various covariance structures in our simulation study.

After we fit a semivarying coefficient model to the continuous response and obtain the residuals from this fit, we move to the second stage. In the second stage we fit a generalized time-varying coefficient model for the conditional model (5). Cai et al. (2000) introduced generalized varying coefficient models for independent and identically distributed data. We adapt these models to a longitudinal setting.

We start by locally approximating the functions in a neighbourhood of a fixed point t₀ via the Taylor expansion:

$${\gamma }_r(t)\approx {\gamma }_r(t_0)+{\gamma }_r^{\prime }(t_0)(t-t_0)\equiv a_r^{\ast }+b_r^{\ast }(t-t_0),$$ (8)

for r = 1, …, p + q + 1. Let ${\mathbf{a}}^{\ast }={(a_1^{\ast },\dots ,a_{p+q+1}^{\ast })}^{\mathrm{T}}$ and ${\mathbf{b}}^{\ast }={(b_1^{\ast },\dots ,b_{p+q+1}^{\ast })}^{\mathrm{T}}$. For subject i, let ${\mathbf{x}}_i^{\ast }(t)={({\mathbf{x}}_i^{\mathrm{T}}(t),{\mathbf{z}}_i^{\mathrm{T}}(t),e_i(t))}^{\mathrm{T}}$. We maximize the local likelihood

$${\ell }_n({\mathbf{a}}^{\ast },{\mathbf{b}}^{\ast })=\frac{1}{N}\sum _{i=1}^n\sum _{j=1}^{n_i}\ell \left(g^{-1}\left[\sum _{r=0}^{p+q+1}\{a_r^{\ast }+b_r^{\ast }(t-t_0)\}{x}_{ir}^{\ast }(t)\right],Q_i(t)\right)K_{h_2}(t-t_0),$$ (9)

where g(·) is a link function, which is probit for our procedure, and h₂ is the bandwidth for the second stage. We use an iterative regression algorithm to find the solution that satisfies ℓ′(a^*, b^*) = 0, and the estimators are given by â^* = γ̂(t₀) = (γ̂₁(t₀), …, γ̂_p+q+1(t₀))^T. Details of this algorithm are presented in the supplementary material.

It is necessary to derive pointwise confidence intervals for the nonparametric components in both stages of the estimation procedure, and to do so we need estimates of the asymptotic covariance matrices. We encourage the reader to refer to the supplementary material for details on these estimators. The sampling properties of the estimators obtained in both stages are also discussed in the supplementary material.

Recall that our chief goal is to estimate the partial association τ(t₀) between the continuous and binary responses. According to (6), to obtain τ̂(t₀) we need to estimate γ_p+q+1(t₀) and ${\sigma }_w^2(t_0)$. The estimator of $a_{p+q+1}^{\ast }$ gives us γ̂_p+q+1(t₀). To estimate ${\sigma }_w^2(t_0)$ we propose using the kernel estimator

$${\widehat{\sigma }}_w^2(t_0)=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{e}_i^2(t_{ij})K_{h_1}(t_{ij}-t_0)}{{\sum }_{i=1}^n{\sum }_{j=1}^{n_i}{K}_{h_1}(t_{ij}-t_0)}.$$ (10)

Plugging σ̂_w(t₀) and γ̂_p+q+1(t₀) into (6) gives the estimator for τ(t₀). Based on the relationship between γ_p+q+1(t₀) and τ(t₀) defined in (6), the pointwise asymptotic confidence band for γ_p+q+1(t₀) gives us information regarding the significance of the partial association τ(t₀). Another way of determining the significance of the partial association is to use a nonparametric bootstrapping procedure. As we demonstrate in the data application, the bootstrap and asymptotic confidence bands agree closely.

For methods based on kernel smoothing, selecting a suitable bandwidth and kernel function are important. These issues are addressed in detail in the supplementary material.

3. SIMULATED APPLICATION

In this section we demonstrate the performance of our proposed procedure via a Monte Carlo simulation study that mimics the data application presented in Section 4. For the simulation study we used the K_0.1 bimodal kernel and a set of equidistant grid points {t_k, k = 1, …, n_grid} between 0 and 1 with n_grid = 200. We simulated 500 intensive longitudinal data sets. For the ith subject, the number of observations n_i was randomly selected according to the discrete uniform distribution on [1, 8], and the measurement times T_i = (t_i1, …, t_ini) were drawn from the standard uniform distribution. We used a sample size of n = 300.

Let x_wi(t) = (1, x_w1i(t))^T, x_yi(t) = (1, x_y1i(t))^T, z_wi(t) = (z_w1i(t), z_w2i(t), z_w3i(t))^T, and z_yi(t) = z_y1i(t). We then generated the continuous and latent variables from the following models:

$$\begin{array}{ll}\hfill W_i(t)& ={\mathbf{x}}_{wi}^{\mathrm{T}}(t){\mathit{\alpha }}_w(t)+{\mathbf{z}}_{wi}^{\mathrm{T}}(t){\mathit{\beta }}_w+{\epsilon }_{wi}(t),\hfill \\ \hfill Y_i(t)& ={\mathbf{x}}_{yi}^{\mathrm{T}}(t){\mathit{\alpha }}_y(t)+z_{yi}(t){\beta }_y+{\epsilon }_{yi}(t),\hfill \end{array}$$ (11)

where α_w(t) = (α_w0(t), α_w1(t))^T = (sin(2πt), cos(2πt))^T, β_w = (β_w1, β_w2, β_w3)^T = (0.3, 0.15, −0.10)^T, α_y(t) = (α_y0(t), α_y1(t))^T = (−0.2 sin(2π t), 1 + cos(2π t))^T, β_y = −0.05, and i = 1, …, 300. We simulated the predictors from the standard Gaussian distribution. Both ε_wi(t) and ε_yi(t) follow Gaussian distributions with mean zero and time-varying variance 0.4 + 0.4 sin²(2πt). The correlations between two error terms measured at different time points are ρ_w(t₁, t₂) = 2^{−7|t₁−t₂|} and ρ_y(t₁, t₂) = 5^{−7|t₁−t₂|} for ε_wi(·) and ε_yi(·), respectively. The association between the binary and continuous responses measured at time t is τ(t) = 0.2 + 0.15 sin(2πt). The primary aim of our study was to demonstrate that we can accurately estimate this association.

In Section 2.1 the binary variable was defined as Q_i(t_ij) = 1 if Y_i(t_ij) > 0, and Q_i(t_ij) = 0 if Y_i(t_ij) ≤ 0. However, it is of interest to show that decreasing the percentage of successes in the binary response does not decrease the efficacy of our procedure. Hence, the relation between the latent variable and the binary variable was defined as Q_i(t_ij) = 1 if Y_i(t_ij) > 0.25, and Q_i(t_ij) = 0 if Y_i(t_ij) ≤ 0.25. Therefore, each of our 500 simulated data sets had approximately 40% failure.

In the first stage we fit a semivarying coefficient model to the marginal model of the continuous response. The estimation procedure requires that we choose a covariance structure. According to Fan et al. (2007), the performance of estimators for the parametric and nonparametric components should be similar no matter the chosen structure. To show that this result holds for our approach, we compared results for three covariance structures: the identity matrix, an ARMA(1, 1) structure, and the true within-subject covariance structure of the continuous response. The results were comparable, and so we present the results for the true covariance structure only.

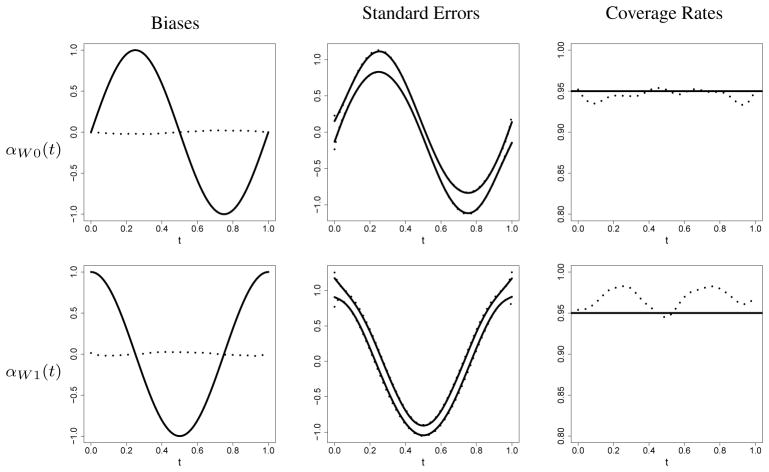
We generated several pilot data sets and used the leave-one-out cross-validation bandwidth selector to obtain the optimal bandwidth. Figure 1 shows the results for h₁ = 0.075: the bandwidth that minimized the cross-validation score. Our estimation procedure for the first stage performed well with respect to bias, as the biases are typically near zero. We used a smaller bandwidth for variance estimation in order to obtain more accurate estimates. Specifically, we used h₀ in O(n^−1/4) since the asymptotically optimal bandwidth is in O(n^−1/5). We see from the plots in Figure 1 that this bandwidth yielded accurate confidence intervals. We estimated parametric components β̂_wj (j = 1, 2, 3) with small biases and mean squared errors of (0.003, 0.001, 0.001) and (0.002, 0.003, 0.002), respectively.

Figure 1.

Results from the first stage of our simulation study. Each row shows three plots for a given time-varying parameter. The first plot shows the true function (solid) and the empirical bias of our estimator (dotted). The second plot shows the empirical pointwise 95% confidence band (solid) and the mean theoretical pointwise 95% confidence band (dotted). The third plot shows the desired coverage rate (solid) and the empirical pointwise coverage rates (dotted).

In the second stage we fit a generalized time-varying coefficient model to the conditional model

$$P\{Q_i(t)=1\mid W_i(t)\}=\mathrm{\Phi }\{{\mathbf{x}}_i^{\ast \mathrm{T}}(t)\mathit{\gamma }(t)+{\gamma }_4(t)e_{wi}(t)\},$$

where γ(t) = (γ₁(t), γ₂(t), γ₃(t))^T is the vector of varying coefficient functions, and ${{\mathbf{x}}_i^{\ast }}^{\mathrm{T}}(t)={({\mathbf{x}}_{yi}^{\mathrm{T}}(t),z_{yi}(t))}^{\mathrm{T}}$ and $e_{wi}(t)=W_i(t)-\{{\mathbf{x}}_{wi}^{\mathrm{T}}(t){\widehat{\mathit{\alpha }}}_w(t)+{\mathbf{z}}_{wi}^{\mathrm{T}}(t){\widehat{\mathit{\beta }}}_w\}$ are the predictors and the residual, respectively, from the first stage, for subject i.

We once again used a pilot study to choose the optimal bandwidth. At this stage we obtain ${\widehat{\gamma }}_k^{\ast }(t)(k=1,\dots ,4)$ at the optimal bandwidth (h₂ = 0.15), and the kernel estimate of ${\sigma }_w^2(t)$ at the optimal bandwidth for the first stage (h₁ = 0.075). We then estimate τ(t) using (6). Figure 2 shows the median estimated time-varying partial association based on 500 Monte Carlo simulation runs, along with the 2.5 and 97.5 percentiles based on 500 bootstrap samples. Judging from this plot, the median estimated time-varying association is close to the true association.

Figure 2.

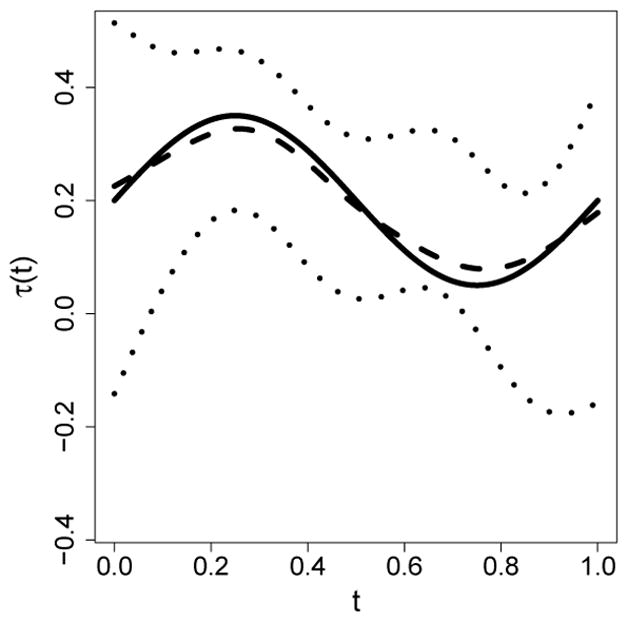
Median estimated time-varying partial association (dashed) overlaying the true function (solid) along with 2.5 and 97.5 percentiles based on 500 bootstrap samples (dotted).

4. APPLICATION TO DATA FROM THE WOMEN’S INTERAGENCY HIV STUDY

We now illustrate our proposed joint modelling methodology via an analysis of data from the Women’s Interagency HIV Study (WIHS). The data are for 372 women recruited from HIV testing sites in Chicago, San Francisco, Los Angeles, New York City (Bronx and Brooklyn), and Washington, DC between 1994 and 1995. Participants were scheduled to have a semiannual interview at a WIHS site. During this interview, participants received physical and oral examinations, gave blood, urine, and gynecological specimens, and also answered a series of questions about their daily activities such as sexual behaviors, tobacco and alcohol use. We restricted our analysis to 292 HIV positive participants aged 25–55. 26%, 45%, and 12% of these subjects self-identified as Latina or Hispanic, African-American non-Hispanic origin, and white non-Hispanic origin, respectively. Among the participants, 66% were smokers, and by the end of the study 8.3% of the smokers quit smoking whereas 8.1% of the non-smokers started smoking. Our data set contains follow-up information on the participants until 2006. Since many participants missed some of their scheduled visits, the number of measurements and measurement times varies from subject to subject. The number of observations for each participant varies from one to eight.

Ferson et al. (1979), Galai et al. (1997), Halonen et al. (1982) and Hughes et al. (1985) demonstrated that cigarette smoking has effects on the immune system, but it is not yet clear whether any of these effects influence the progression of HIV to AIDS. Galai et al. (1997) analyzed data from the Multicenter AIDS Cohort Study of homosexual men in order to investigate the effect of cigarette smoking on development of AIDS. They applied Kaplan–Meier analysis and multivariate Cox regression models, and concluded that smoking was not significantly associated with progression to AIDS. Likewise, Burns et al. (1996) studied the association between cigarette smoking and HIV progression on a cohort of 3,221 HIV-seropositive men and women enrolled in the Terry Beirn Community Programs for Clinical Research on AIDS. Using proportional hazards regression analysis, they found no association between smoking and the overall risk of HIV progression or death. On the other hand, Nieman et al. (1993) showed that in a case series of 84 individuals, smokers progressed to AIDS more rapidly than nonsmokers. They employed life tables and compared median time to develop AIDS for smokers and nonsmokers. Our main interest is to study the relationship between HIV progression (measured by CD4 cell percentage) and smoking status for the women who participated in the WIHS.

There are two important differences between our approach and the above mentioned methods. First, some of the previous analyses excluded subjects who changed their smoking behavior during the study. The drawback of this exclusion is that in a longitudinal study we expect behaviors to change over time, and the inability to take these changes into account may result in biased results. Second, we do not apply survival methods, since our data are not censored. In addition, we are interested in investigating the relationship between CD4 cell percentage and smoking status throughout the study instead of defining a lifetime for a subject that ends when the subject progresses to AIDS.

Based on some preliminary analysis and findings in the HIV literature (Zeger and Diggle, 1994; Obirikorang and Yeboah, 2009), we chose a set of predictors for each response. The predictors for CD4 cell percentage (the continuous response) were: baseline CD4 cell percentage (measured at the first visit), number of sexual partners, hematocrit value (the volume percentage of red cells in the blood), mean corpuscular volume (a measure of average red blood cell size), platelet count, and Center for Epidemiologic Studies Depression (CESD) scale score. For smoking status (the binary response), CESD scale score and race were used as predictors. All predictors except race are continuous variables, and they were centered. Note that the race variable initially had five levels: African American, white, Asian/Pacific Islander, native American/Alaskan native, and other. Since our data set had only two participants in each of the Asian/Pacific Islander and native American/Alaskan native categories, we recategorized race into three levels: African American, white, and other.

We began by determining whether a fully time-varying or a semivarying approach is appropriate for these data. To do so we fit the appropriate time-varying coefficient model to each of the continuous and binary responses. Since some of the effects appeared to be constant over time, we decided to proceed with a semivarying analysis. For the continuous response, we observed that the intercept and baseline CD4 cell percentage have time-varying effects, while the remaining effects are time invariant. For the binary response, CESD and the first dummy variable for race (RACE1), which is equal to 1 if a subject is African American, were time varying, while the second dummy variable for race (RACE2), which is equal to 1 if a subject is white, was time invariant.

In our analysis the K_0.1 bimodal kernel function was used in both stages. We applied the leave-one-out cross-validation method, and chose h₁ = 29.5 and h₂ = 36 as the bandwidths for the first and second stages, respectively.

In the first stage of our estimation procedure, we fit the following semivarying coefficient model to CD4 cell percentage:

$$W_i(t)={\mathbf{x}}_i^{\mathrm{T}}(t){\mathit{\alpha }}_w(t)+{\mathbf{z}}_i^{\mathrm{T}}(t){\mathit{\beta }}_w+{\epsilon }_{wi}(t),$$

where α_w(t) = (α_w0(t), α_w1(t))^T, β_w = (β_w1, β_w2, β_w3, β_w4, β_w5)^T, x_i(t) = (1, x_i1(t))^T with x_i1(t) as the baseline CD4 cell percentage of subject i at the first visit, and z_i(t) = (z_i1(t), z_i2(t), z_i3(t), z_i4(t), z_i5(t))^T with

• z_i1(t) : the number of sexual partners of subject i at time t,

• z_i2(t) : the hematocrit value of subject i at time t,

• z_i3(t) : the mean corpuscular volume of subject i at time t,

• z_i4(t) : the platelet count of subject i at time t,

• z_i5(t) : the CESD scale score of subject i at time t,

and t = t_ij the age of subject i at visit j.

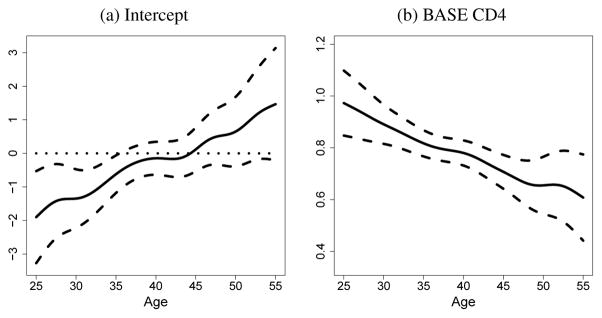
The estimated time-varying functions in the first stage are depicted in Figure 3. The plot in panel (a) shows that the intercept function increases as age increases, and the confidence band suggests that the intercept function is time varying. From the plot in panel (b), we observe that the effect for baseline CD4 is time varying and decreases with age. Furthermore, the confidence intervals suggest that the effect is always significant and positive for ages between 25 and 55.

Figure 3.

The results of our data analysis for the continuous response, CD4 cell percentage. For each panel, the solid curve shows the estimate, the dashed curves show the estimated 95% pointwise confidence band, and the dotted line marks zero.

We next estimate the parametric component β_w. Here we decided to use an ARMA(1, 1) correlation structure. Note that, as we would expect, using a working independence covariance matrix yielded similar results. The resulting estimates along with their corresponding 95% confidence intervals are displayed in Table 1. We see that all of the predictors except number of sexual partners are significantly associated with CD4 cell percentage for the WIHS data. The continuous response (CD4 cell percentage) has a positive relationship with the volume percentage of red cells in the blood (HCT), average red blood cell size (MCV), and the platelet count, and a negative relationship with CESD scale score.

Table 1.

Results for the first stage fit

Variable	β̂	95% CI
PART	0.044	(−0.056, 0.144)
HCT	0.120	(0.008, 0.232)
MCV	0.124	(0.075, 0.173)
PLAT	0.013	(0.007, 0.019)
CESD scale	−0.126	(−0.163, −0.089)

After fitting the marginal model for the continuous response and obtaining the residuals for this fit, in the second stage of the estimation procedure we fit the conditional model for the binary response given the continuous response:

$$P\{Q_i(t)=1\mid W_i(t)\}=\mathrm{\Phi }\{{\mathbf{x}}_i^{\ast \mathrm{T}}(t)\mathit{\gamma }(t)+{\gamma }_5(t)e_{wi}(t)\},$$

where Q_i(t) is the smoking status of subject i at time t, e_wi(t) is the residual from the marginal fit of the continuous response, γ(t) = (γ₁(t), …, γ₄(t))^T is the vector of regression coefficients, and ${{\mathbf{x}}_i^{\ast }}^{\mathrm{T}}(t)={(1,x_{2i}(t),x_{3i}(t),z_{6i}(t))}^{\mathrm{T}}$ with

• x_i2(t) : the CESD scale score of subject i at time t,

• x_i3(t) : the first dummy variable for race (x_i2(t) = 1 if subject i is African American),

• z_i6(t) : the second dummy variable for race (z_i6(t) = 1 if subject i is white).

As mentioned in Section 2.1, $\tau (t)=b(t)/\sqrt{1+b^2(t)}$ with b(t) = γ_p+q+1(t)σ_w(t), where ${\sigma }_w^2(t)$ is the variance of CD4 cell percentage at time t, and τ(t) is the partial association between CD4 cell percentage and smoking status at time t conditional on a set of predictors. We estimate σ_w(t) using kernel estimator (10) with bandwidth h = 29.5. To obtain a pointwise confidence band for τ(t), we generated 500 bootstrap samples by resampling from independent subjects.

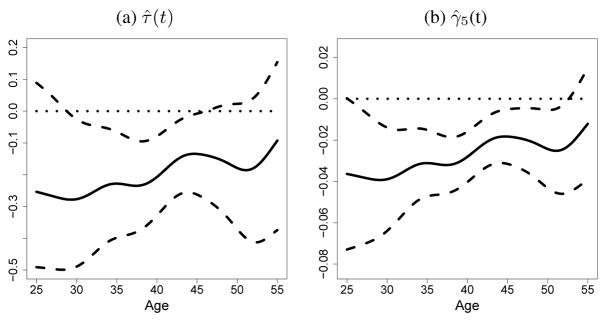
Figure 4 (a) presents the estimated partial association τ̂(t) along with 2.5 and 97.5 percentiles of the bootstrap samples. According to Figure 4 (a) we cannot conclude that the partial association between CD4 cell percentage and smoking status is time varying. However, we can conclude that the partial association is significant and negative for women between the ages of 29 and 46, i.e., for women enrolled in the WIHS, decreased CD4 cell percentage is partially associated with smoking. Based on the relationship between τ(t) and γ₅(t), we can also investigate the significance of the partial association using the estimated confidence intervals for γ₅(t). Figure 4 (b) depicts the estimated regression coefficient γ̂₅(t) along with its confidence band. This plot shows a slightly wider significance region for the association: the association is significant for women aged between 26 and 52, approximately.

Figure 4.

(a) Estimated time-varying partial association and (b) estimated coefficient function for residuals. For each panel, the solid curve shows the estimate, the dotted line marks zero, and the dashed curves show the 2.5 and 97.5 percentiles of 500 bootstrap samples in (a) and the estimated 95% pointwise confidence band in (b).

Smoking is associated with pulmonary complications, decreased adherence to highly active antiretroviral therapy (Feldman et al., 2006), and increased incidence of opportunistic infections (Arcavi and Benowitz, 2004; Crothers et al., 2005; Kohli et al., 2006) for HIV-positive patients. Therefore, the results of our study and others suggest that successful smoking cessation programs are necessary for HIV patients in order to enhance the quality of life and make disease progression more manageable. A detailed review of existing smoking cessation techniques for HIV patients can be found in Niaura et al. (2012) along with ways to improve current research studies so that more effective cessation programs can be designed.

5. DISCUSSION

In this article we developed a new joint modelling approach for longitudinal binary and a continuous responses. In this approach the continuous response and the latent variable underlying the binary response are assumed to follow a semivarying coefficient model. We also proposed a two-stage estimation procedure based on local linear regression, and discussed the asymptotic normality of the resulting estimators in both stages. We demonstrated that our procedure performs well for estimating the time-varying partial association between longitudinal binary and continuous responses. We also applied our methodology to a bivariate response (CD4 cell percentage and smoking status) from the Women’s Interagency HIV Study. We concluded that there is a significant negative partial association between CD4 cell percentage and smoking status for women aged 29–46.

It might seem restrictive that our modelling scheme only considers a semivarying coefficient model for the continuous response but not for the binary response. However, in order to have a semivarying model for the binary response in (2), one has to assume that the coefficient of z_i(t) is proportional to the standard deviation function σ_y(t). Such an assumption seems to be unnatural. Thus, it is more natural to consider a varying-coefficient probit model for the binary variable. Note that, in practice, an association may exist between the binary and continuous outcomes measured at different time points. Ignoring this dependence does not affect the asymptotic behavior of the estimators (Lin and Carroll, 2001; Kürüm et al., 2014).