Heparin's Solution Structure Determined by Small-Angle Neutron Scattering (SANS)

Abstract

Heparin is a linear, anionic polysaccharide that is widely used as a clinical anticoagulant. Despite its discovery 100 years ago in 1916, the solution structure of heparin remains unknown. The solution shape of heparin has not previously been examined in water under a range of concentrations, and here is done so in D₂O solution using small-angle neutron scattering (SANS). Solutions of 10-kDa heparin—in the millimolar concentration range—were probed with SANS. Our results show that when sodium concentrations are equivalent to the polyelectrolyte's charge or up to a few hundred millimolar higher, the molecular structure of heparin is compact and the shape could be well modeled by a cylinder with a length three to four times its diameter. In the presence of molar concentrations of sodium, the molecule becomes extended to nearly its full length estimated from reported x-ray measurements on stretched fibers. This stretched form is not found in the presence of molar concentrations of potassium ions. In this high-potassium environment, the heparin molecules have the same shape as when its charges were mostly protonated at pD ± 0.5, that is, they are compact and approximately half the length of the extended molecules.

INTRODUCTION

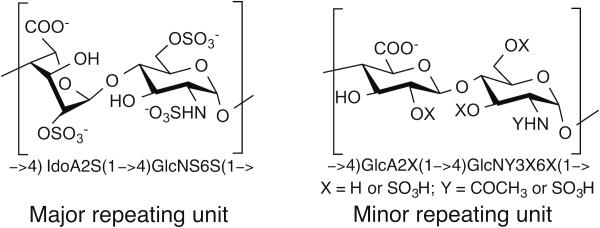
Heparin is a linear, polydisperse, polyanionic polysaccharide with an average molecular weight of 10 kDa to 20 kDa.¹ It is composed of a repeating disaccharide unit of 1-4 glycosidically linked sulfated uronic acid and glucosamine (GlcN) residues (Figure 1). The uronic acid residue can be L-iduronic acid (IdoA) or D-glucuronic acid (GlcA) that can also be substituted with a 2-O-sulfo group. The GlcN residue can be substituted with an N-sulfo or N-acetyl group and with 6-O-sulfo or 3-O-sulfo groups.² While heparin’s sequence is heterogeneous, it is comprised mostly of a trisulfated disaccharide repeating unit of →4) IdoA2S (1→4) GlcNS6S (1→ (where S is sulfo), representing from 60-90% of heparin's structure,³ with the remaining repeating units containing a lower level of sulfation. As a result, the average degree of sulfation for heparin is ~2.7 sulfo groups/disaccharide unit,⁴ and a heparin chain of molecular weight 10 kDa contains ~40 sulfo groups. The pK_a values of heparin's carboxyl, O-sulfo, and N-sulfo groups have been reported to be 2.79 to 3.13, 0.5 to 1.2, and 1.4 to 1.9, respectively,^5,6 so at neutral pH, the anionic groups in heparin will be fully deprotonated. In sodium heparin, the anionic groups are charge neutralized by sodium cations, and this form is consistent with the reported ash content of sodium heparin.⁷

FIGURE 1.

Structure of heparin’s major and minor repeating units.

Although the primary structure or sequence of heparin has been extensively studied, ⁸ no high-resolution x-ray structures revealing the secondary structure have appeared, apparently because heparin's inherent heterogeneity and polydispersity prevents its crystallization. Indeed, the structures of only relatively small heparin oligosaccharides have been solved and then only in complexes with heparin-binding proteins.^4,9-11 Some the earliest physico-chemical characterization of heparin solutions involved small-angle x-ray scattering by Stivala and coworkers.^12-14 In addition, x-ray fiber diffraction was obtained by Nieduszynski and Atkins.¹⁵ More recently, Yamaguchi and coworkers investigated the conformation of heparin in water by intermediate-angle x-ray scattering.¹⁶ These studies, all performed over 30 years ago, while providing insights into heparin structure, afford inconsistencies in structures and fail to take into account more recent advances in our understanding of the molecular structure of polyelectrolytes and their counter-ions.^17,18

NMR solution structure studies have been performed on a number of heparin oligosaccharides to better understand their conformational properties.^19-21 The cited studies have been limited to at most a dozen saccharide units in the chain (3-4 kDa),²² and each study uses only a single, low sodium ion concentration. These are far below the average chain sizes of a full-length heparin polysaccharide and not near the physiological environment of their action.

Heparin was discovered in 1916, and its use as a clinical anticoagulant predates the establishment of the United States Food and Drug Administration.²³ Heparin is required in extracorporeal therapy, in major surgery, and in the treatment of thrombosis, and without its use the practice of modern medicine would be difficult.³ Worldwide, currently about 100 metric tons of heparin are used annually, making it, after insulin, the second most widely used biopolymeric drug.²³ Despite its critical importance, the full primary sequence and secondary structures of heparin remain unknown. This lack of understanding of heparin’s structure was partially responsible for the heparin contamination crisis of 2008 that led to the injury and death of hundreds of patients when heparin was adulterated with the related, toxic semisynthetic polysaccharide, namely oversulfated chondroitin sulfate.^23,24

Here we examine the secondary structures of 10 kDa heparin in water using small-angle neutron scattering (SANS). We have found that the structure changes significantly with the solution conditions, and the shapes that do appear have not been expected previously.^8,25

MATERIALS AND METHODS^‡

Preparation of heparin samples

Sodium heparin (50 mg) was prepared from porcine intestinal mucosa with an average molecular weight of ~16 kDa and a polydispersity (PD) of ~1.5 (Celsus, Laboratories, Cincinnati, OH). The heparin was dissolved in 0.5 mL of 1 mol L⁻¹ (M) sodium chloride and fractionated on a Sephadex G75 column (2.5 cm diameter × 1 m length) with 1 M sodium chloride at a flow rate of 0.2 mL/min. The peak, determined by azure A assay,²⁶ was divided into 5 fractions and then dialyzed (1 kDa molecular weight cut-off in bags) and freeze-dried. Each fraction was similarly reapplied to the same column, and again fractionated, and the central third of the area of the resulting peak collected, dialyzed, and freeze-dried.

A fraction of reduced molecular weight heparin with a smaller PD was used in the current studies: number averaged molecular weight (M_N) 9700, weight averaged molecular weight (M_W) 11000, and PD 1.13. The molecular weight properties of this sample were determined by gel filtration (TSKgel G3000SWxl, Tosoh Bioscience, King of Prussia, PA) at 30 °C with refractive index (RI) detection following the United States Pharmacopeial Convention (USP) guidelines using the USP reference standard as calibrant.²⁷

Heparin solutions in D₂O

The sodium heparin was dissolved in D₂O (99.9 atom% D; Cambridge Isotope Laboratories Inc., Andover, MA) to replace exchangeable protons with deuterium, and subsequently lyophilized. When dissolved in solution at 50 mg/mL, the solution's measured pD ≈ 3.7, which suggests that when the material was dialyzed against pure water, the carboxylic acids were at least partially protonated. This stock solution in D₂O was brought to pD 7 ± 0.2 with concentrated NaOD in D₂O. For the purpose of expressing the Na⁺ concentrations of heparin solutions, we have assumed that the sodium is, then, equivalent to the charges of the heparin molecules.

The pD values were those recorded by a glass electrode standardized in H₂O. No isotope correction was made with the assumption that the unmodified value was more correct since it is likely that the buffer pD and electrode surface’s pK_a shifted in the same direction with changing levels of D₂O/H₂O. After at least 24 h, the solution was filtered through a 0.2 μm pore filter. With the exception of one strongly acidified solution, the final pD values of the samples fell within the range of 6.8 to 7.3.

Stock solutions of the 2-[4-(2-hydroxyethyl)piperazin-1-yl]ethanesulfonic acid (HEPES) buffer were made in D₂O by titrating the acid forms (Acros, ThermoFisher, New Jersey, US) to the desired pD with concentrated NaOD solution. The HEPES was not deuterated, and its single exchangeable proton for a 10 mM solution contributes 0.01% H to the final deuterated solutions. Stock solutions of NaCl and KCl (GFS, Columbus, OH, bio-refined) were prepared from the anhydrous salts dissolved in D₂O. The concentrated D₂SO₄ (Sigma-Aldrich, St. Louis) was added directly to make a 0.3 M solution that, using calculations from the characteristics of H₂SO₄ in light water, were expected to produce a pD ≈ 0.5 solution.

Sodium heparin solutions (10 mM HEPES buffer) with 10, 20, and 30 mg/mL (and assuming fully occupied sulfonate and carboxylate positions) contain 66, 133, and 199 mM Na⁺. As a result, the 10 mg/mL heparin solution with 1.00 M added NaCl had 1.07 M Na⁺. A set of 20, and 30 mg/mL heparin solutions were made with a fixed 200 mM Na⁺ concentration; these were, then, respectively 67, and 0 mM in Cl⁻ once the heparin sodium counter ions were complemented. The 10 mg/mL solution with added 1.00 M KCl retained its original 66 mM Na⁺ in addition to the potassium chloride.

The final solutions were made at least 24 h in advance of the beginning of the scattering experiments and held at 22 °C to allow equilibration. The samples were degassed under vacuum immediately before placing all of them into the instrument's sample holder for temperature equilibration to 25 °C at the beginning of the experiment time. However, unlike the other samples, the strongly acidic solution of heparin was prepared and degassed immediately before its data collection, which was completed within two hours of the solution's preparation. Samples were held in 2.00 mm path length cylindrical quartz cuvettes (NSG Precision Cells, Farmington, NY). Data at the 10 m camera position was collected for 3 h or 4 h with data sets recorded at the end of each one-hour period to monitor any possible structure changes during the experiments. Within the experimental uncertainty, no changes were observed for any of the solutions over those time periods.

SANS Measurements

SANS measurements were obtained on the NG7 30 m SANS instrument at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR) in Gaithersburg, MD.²⁸ The neutron beam wavelength for the data presented here was 5.5 Å with Δλ/λ of 0.115.

Scattered neutrons were detected with a (64 × 64) cm two-dimensional position sensitive detector with (128 × 128) pixels and 0.5 cm resolution per pixel. Data reduction was accomplished using Igor Pro software (WaveMetrics, Lake Oswego, OR) with SANS reduction and SANS analysis macros developed at the NCNR.²⁵ Raw counts were normalized to a common incident beam-monitor count, corrected for empty cell counts, for ambient room background counts, and for non uniform detector pixel response. The incident beam flux monitor running concurrently with the individual sample transmissions allowed normalization to a common absolute scale. Finally, the data were radially averaged to produce the scattering intensity I(q) to plot the log I(q) versus log q curves shown, where q = (4π/λ) sin θ, and 2θ is the scattering angle measured from the axis of the incoming neutron beam. The model fitting additionally corrects for the known, measured beam characteristics due to the neutron optics. These corrections include the geometric smearing, the wavelength spread, and the beamstop’s shadowing.

The scattering from the appropriate buffer solution was subtracted from the scattering of the heparin-containing samples to produce the scattering curves shown here. There remains some incoherent scatter from the non-exchanged protons of the heparin. With, on average, four non-exchangeable protons per saccharide unit, at the highest concentration of 30 mg/mL, where the 10 kDa polymer is 3 mM, a polymer number of 32 means that there is 100 mM of monomer and 400 mM in protons. This increases the solution’s hydrogen equivalent to an additional 0.2% H₂O. The increase is equivalent to 0.07% H₂O for the 10 mg/mL solutions, which we neglect. Following background buffer subtractions, the scattering from the two different sample-to-detector positions, 1 m together with 10 m, were merged using the NCNR SANS reduction software.²⁹

The Models Providing Structural Insight

The resulting SANS curves can be separated into three different ranges of q values that provide different information about the structures of the samples. These are the higher q region (q ≥ 0.08), the middle range (0.01 ≤ q ≤ 0.08), and the low-q range (0.005 ≤ q ≤ 0.01). These ranges provide information about the molecular shape, the nearest-neighbor distances, and the longer-range positions of the molecules in the solution, respectively. However, note that sometimes the curve shape in one of these regions is difficult to model due to interference from scattering in the adjacent region. We have chosen to focus this analysis on the shorter distances from which the shapes of the molecules are modeled.

A commonly used, simple model that provides chemically reasonable structures of the molecule shapes begins with calculating the scattering from elementary geometric shapes that are homogeneous in scattering length density (SLD, the scattering ability per unit volume, usually in units of Å⁻²). Here we have tried spheres, cylinders, and parallelepipeds. The equations for these models can be found in the classic book by Guinier and Fournet.³⁰ The equations applicable to the homogeneous circular cylinder model are shown below.

In the middle range of q in the scattering curves—as can be observed in many of the curves shown below—a low, broad peak appears. The position of the peak in q results from the average distance between independent, separate polymer structures. These are often called Bragg peaks, but their origin is not due to a Bragg reflection such as a unit cell in an extended crystal. It arises instead from pairs of scatterers and is more properly called a paracrystalline peak. Paracrystal has a number of different meanings, and here it is used in the sense that the structure is not a true crystal but has some degree of order at shorter distances. For a set of scatterers that are equally spaced in solution, the first-neighbor distance that causes this peak is related to the concentration by d = 12.70 Å/(Molar concentration)^1/3.³¹

When the solute molecules are, on average, randomly distributed throughout the solution, the scattering curve resulting from the molecular shape levels off and remains horizontal until it reaches the lowest q values in the range. However this environment is not present for heparin under any of the conditions that were run here. In the heparin solution, because of interactions between the molecules, the solutes have a more or less fixed intermolecular structure throughout the solution. As a result, the scattering curves continue to rise over the low q range. Often such scattering curves can be fit well on the log log plot by a sloping straight line as is seen here for the heparin data. The slope is negative, and the log-log fit can have meaningful, non-integral values from −1 to −4 (its fractal slope), which informs us about the kinds of structures appearing within that range of lengths.³² Mathematical details relating the slope to the fractal dimension can be found elsewhere.^33,34 However, the presence of the scattering from the molecular structures of the heparin add great uncertainty to these slopes. Again, as a result, we shall analyze only the molecular structures here.

One additional value is needed to understand heparin's structure—its density. Based on flotation of sodium heparin fibers, a density 1.72 was found.¹⁵ The amount of water in the structure was not ascertained. As a calculational alternative to use for an aqueous solution, we employed the MOPAC2012 computational chemistry code (Stewart Computational Chemistry, Colorado Springs, CO) on heparin's protonated constituent dimer. Its volume not accessible by a 1.3 Å sphere (the commonly accepted protocol) was 596 ų. With a formula mass of 637.5, the density is calculated to be 1.77 g cm⁻³, which we accept as the molecular density.

The Equations for Scattering from Randomly Oriented Circular Cylinders

The function to fit the scattering P(q) from a set of randomly oriented, monodisperse, right circular, rigid cylinders of radius r and length L is calculated as:

$$P(q)=\frac{\text{scale}}{V_{\mathrm{cyl}}}\underset{0}{\overset{\pi ∕2}{\int }}{f}^2\left(q,\alpha \right)\sin \alpha d\alpha$$

where

$$f\left(q,\alpha \right)=2\left({\text{SLD}}_{\mathrm{cyl}}-{\text{SLD}}_{\mathrm{solv}}\right)V_{\mathrm{cyl}}{j}_0\left(\frac{\mathit{qL}\cos \alpha }{2}\right)\frac{J_1\left(\mathit{qr}\sin \alpha \right)}{\left(\mathit{qr}\sin \alpha \right)}$$

Here,

$$V_{\mathrm{cyl}}=\pi r^{2}L,j_0(x)=\sin (x)∕x,J_1(x)=\sum _{m=0}^{\infty }\frac{{(-1)}^m}{m!\Gamma \left(m+2\right)}{\left(\frac{x}{2}\right)}^{2m+1},\text{and}\Gamma (z)=\underset{0}{\overset{\infty }{\int }}{w}^{z-1}{e}^{-w}\mathit{dw}$$

J₁(x) is the first order Bessel function. Γ(z) is the gamma function. α is defined as the angle between the cylinder axis and q, the scattering vector. The integral over α averages the form factor P(q) over all possible orientations of the cylinder with respect to q. The returned value is in units of cm⁻¹ on an absolute scale, which is the scale of units for all the scattering curves shown in the figures.

RESULTS AND DISCUSSION

The overall concentrations of heparin and the conditions under which they were held are organized in Table I. The high salt and acid conditions are shown shaded. As can be seen, when the sodium concentration in the solution is the equivalent of the polyanions and when it is mammalian isotonic, the heparin assumes a compact structure. (This is contrary to the generally held view on heparin aqueous solution structure.) Such a phenomenon is called polyelectrolyte collapse, which has been treated theoretically by various groups.^17,35-37 Nevertheless, this behavior in the presence of small ions was not expected to occur in aqueous solutions.

Table I.

Heparin scattering entity sizes and volumes modeled as homogeneous cylinders^a,^b

Heparin concentration Description	Ion Concentrations/mM	Homogeneous cylinder shape dimensions
		Radius (Å)	Length (Å)	Volume (103•Å3)
10 mg/mL Equivalent Na	66 Na	6.8 ± 0.8	54 ± 8	8 ± 3
20 mg/mL Equivalent Na	133 Na	5.4 ± 0.5	39 ± 2	4 ± 1
20 mg/mL Low pD	133 Na 300 D2SO4 (pD 0.5)	6.9 ± 0.5	76 ± 6	12 ± 3
20 mg/mL 1.1 M Na	1133 Na 1000 Cl	4 ± 2	116 ± 14	8 ± 7
10 mg/mL 1 M K	66 Na 1000 K 1000 Cl	7 ± 1	75 ± 18	11 ± 4
20 mg/mL 200 mM Na	200 Na 66 Cl	3 ± 4	47 ± 6	5 ± 4
30 mg/mL 200 mM Na	200 Na 0 Cl	6.6 ± 0.5	31 ± 3	4 ± 1

^aUncertainties are ±σ for the curve fitting process alone.

^bAll length measures are for nucleus-to-nucleus distances.

Also contrary to expectations, in the presence of molar sodium ions, the chain is extended. In addition, for the low-pH solution, in which we expect that the ionized groups are protonated, a compact but less extended confirmation appears. In molar potassium solution, the heparin appears to form the same shape as in the acid. Details about these general results appear next.

Scattering from the Compact Solute Heparin and the Solution's Longer Range Structures under Conditions of Lower Sodium

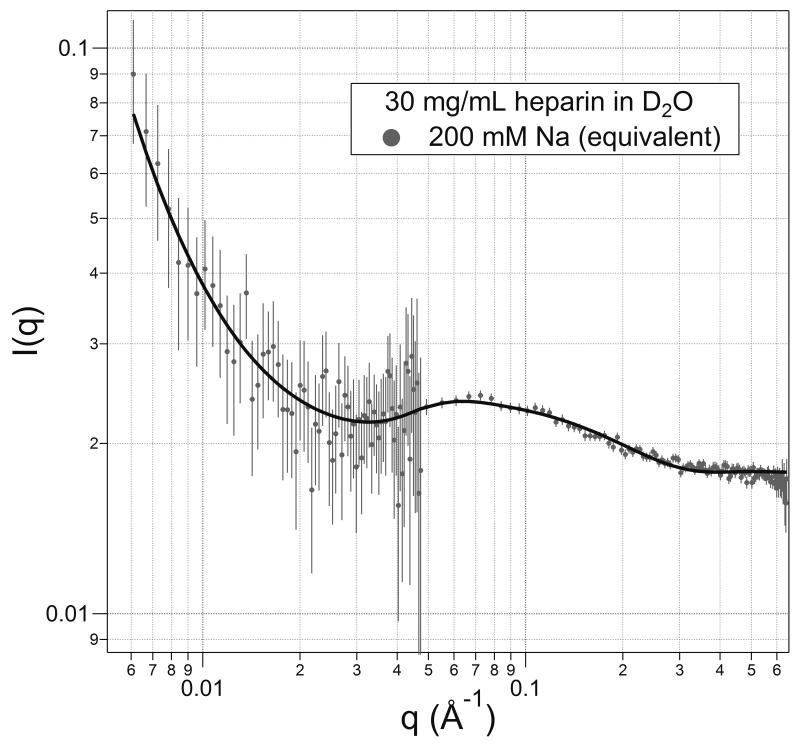
A scattering curve for heparin at 30 mg mL⁻¹ with 200 mM sodium, which is the Na⁺ concentration equivalent to the polyanion's charge at this concentration, is shown in Figure 2. The curve fitting results from a model that has homogeneous spherical scatterers with paracrystalline order in the solution with a certain amount of heterogeneity of positions within that paracrystalline order. The fit is quite good except at the left side (low-q, long distance). The homogeneous sphere has its best fitting radius of (11.6 ± 0.03) Å, where the uncertainty is ±σ with the other variables held constant. A sphere of this radius has a volume of 6370 ų. This volume can be compared with that expected from a M_w 11 kDa heparin molecule with the density of heparin (1.77 g cm³); the heparin would occupy about 10,750 ų, almost double the measured volume. (A homogeneous sphere of 10,750 ų has a radius of 13.7 Å.)

FIGURE 2.

Scattering from 30 mg/mL heparin in the presence of 200 mM Na⁺. The model is that for a paracrystalline array of homogeneous spheres. Error bars indicate the uncertainties for the counting statistics only in all the figures.

This discrepancy between the volume of a molecule and the volume of the modeled sphere may be explained in a few possible ways. One is that the structure is not spherical, which the data and model fitting indicates is the fact as will be described later. However, experience has shown that volumes modeled optimally with different geometric shapes, e.g., spheres and cylinders, have volumes that remain similar (~20%).

Another explanation is that approximately half the chain is packed, and the other half is disordered in the same region. However when models of such structures were tried and optimized, the disordered regions shrank to provide negligible contributions to the scattering. So such disorder is unlikely.

With the sphere model, as seen in Figure 2, the best-fit line lies above the data points in the range 0.1 < q < 0.2 but below them within 0.06 < q < 0.1. This misfit is eliminated with the cylinder model that is used to fit the structures under the rest of the solution conditions. The cylinder shapes do, in fact, fit the data quite well for q > 0.3. As a result, a third possibility for the diminished volume is that when a dimension such as a cylinder's diameter is small (d < 8 Å), which is at or beyond the right end of the data. The uncertainty of that dimension can be greater than the stated uncertainty of the scattering-curve fit alone. This occurs because that length is determined by the slope and second derivative of the curve in a region of the data with relatively high uncertainty. In addition, neutron scattering occurs at the nuclei of atoms, and does not encompass the van der Waals radii of atoms. In all cases, it may be reasonable to add an extra two Ångstroms to a diameter to conform to the chemical dimensions. Such an addition would make a 7 Å internuclear distance into a 9 Å diameter, and increase a calculated volume by over 60%. Such two-Ångstrom additions generally lie within the uncertainties of the modeled lengths however. (Adding 1 Å to the radius of the model sphere, the 11.6 Å is changed to a chemical radius of 12.6 Å, which still differs from the 13.7 Å expected.)

This discrepancy in volumes cannot be resolved by the SANS data and modeling alone, and the meaning of a scattering shape that has a volume about half that expected for a 10 kDa heparin molecule remains an open question. Nevertheless, the lengths of the cylinders when such discrepancies appear will not be as inaccurate as a factor of two.

In the middle of the scattering curve—around q = 0.7 Å⁻¹ — a low peak appears. This is explained by another paracrystal parameter, which is the nearest-neighbor separation for a structure that is equivalent to placements on, e.g., a simple cubic lattice in space. It is more likely that the dispositions of the molecules are, on average, evenly spaced from each other, and so an assumed cubic framework does not yield the correct distance. Instead, spacing for equally separated molecules can be found by recasting the position of the peak into its equivalent distance (d = 2π/q), which here for a q-value of 0.07 Å⁻¹ yields d = 90 Å. Then, for evenly spaced M_n ≈ 9700 Da molecules at 30 mg/mL, we expect their first-neighbor distances to be³¹ d(Å) = 12.7 Å/(Molar concentration)^1/3. Here, for the 3.1 mM solution, that distance is 87 Å, which is in agreement within the measurement uncertainties. The data says, then, that in this solution with 200 mM sodium, the heparin polymers are relatively compact molecules, and are separated by an average distance that is larger than the compacted molecule.

However, this set of characteristics does not apply under conditions where the molecules are extended. In that case, the average intermolecular distance can be about the same as the length of the extended 10 kDa chain. This situation will be discussed next: where a clear separation into individual, isolated molecules is not present.

Heparin shapes in solution with 133 mM Na⁺ and 1.1 M Na⁺

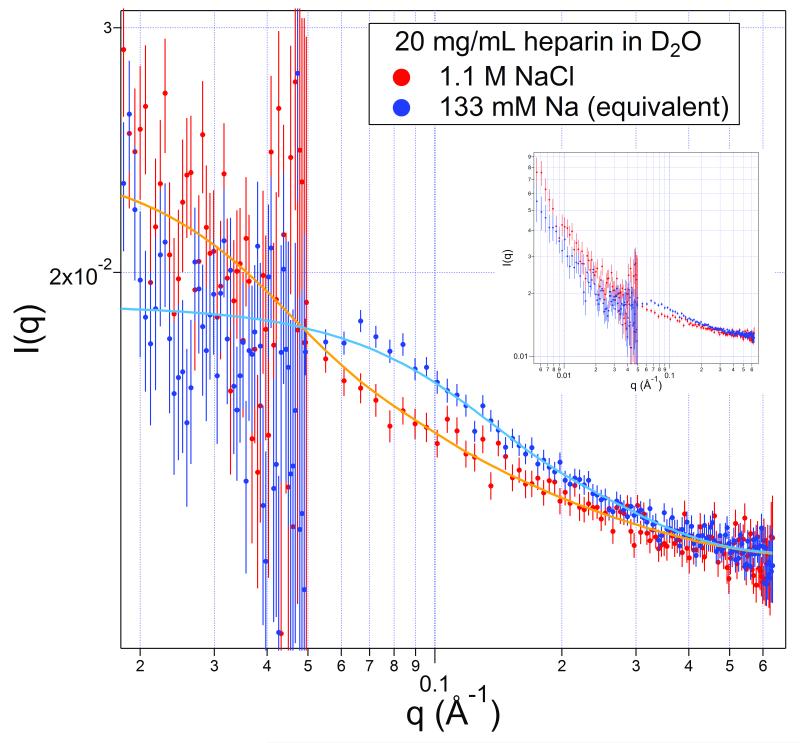
We next analyze and compare the scattering from 20 mg/mL heparin (2 mM) with 133 mM sodium present (a concentration equivalent to the polymer charge) and another with ≈ 1.1 M Na⁺. Parts of the two scattering curves are shown in Figure 3, with curves over the entire measured range appearing in the inset. Again, note that the cylinder shape model does not apply to the lower q range, unlike the paracrystal model that includes the whole q range.

FIGURE 3.

Scattering from 20 mg/mL heparin in the presence of 133 mM sodium (upper points, blue) and 1.1 M sodium (lower points, red) with model curves. The scattering over the entire range is shown in the inset, which more clearly shows the scattering data crossover.

From x-ray studies of stretched heparin fibers at 76% humidity,³⁸ a component dimer length within the polymer was measured to be 8.4 Å. The 9.7 kDa heparin consistent with that measure would, then, extend ≈130 Å.

Under the low-sodium conditions (blue), the scattering curve is fit well by a homogeneous cylinder with a diameter of (11 ± 1) Å and a length of (39 ± 2) Å. See Table I. The nominal volume of the cylinder is 3800 ų, significantly smaller than the volume of a 10 kDa heparin, and smaller than the best-fit cylinder for heparin in 200 mM Na⁺ (Figure 2). In comparison, for a lower concentration, 10 mg/mL sodium heparin, which has 66 mM Na⁺, the best-fit diameter is larger (13.6 ± 1.6) Å, and, perhaps, slightly longer (54 ± 8) Å. Its molecular volume is close to that of a tightly packed, single heparin molecule. The lengths of the 20 mg/mL (133 mM Na⁺) and the 10 mg/mL (66 mM Na⁺) solutions are one-half to one-third of a fully extended molecule. (Top two entries in Table I.)

The high-sodium sample (red) has the range 0.02 < q < 0.6 fit well with a homogeneous cylinder with a cross section approximately the molecular diameter of (8 ± 4) Å, and a length of (116 ± 14) Å. We may say from the fitting that in the presence of the 1.1 M Na⁺, the heparin is extended in its confirmation, and its length is close to that calculated from stretched fiber diffraction of 130 Å. The molecule is essentially fully extended.

In comparison, Pavlov et al.³⁹ investigated heparin using x-ray scattering over the range 0.01 Å⁻¹ < q < 0.27 Å⁻¹ together with hydrodynamic methods on a 9.4 kDa heparin fraction (their fraction 11) in 200 mM Na⁺ in light water. They found a cross-sectional radius of gyration of 4.3 Å. For a homogeneous circle, the radius of gyration and the radius are related by R_g = R/√2, which produces a diameter of 12 Å for the heparin under these conditions. This value agrees with the diameter found here under the lower-sodium conditions. In addition, the hydrodynamics suggested that the chain was stiff over the full length of these 10 kDa heparins.

Why is the Heparin Extended in a Molar Sodium Solution?

As mentioned above, in the presence of equivalent and slightly higher sodium (66 mM, 133 mM, 200 mM) the heparin is found in a compact or folded form. Why, then, does it extend in the presence of molar sodium ion? A chemically reasonable explanation is that the sulfonate and carboxylate groups are, as is typical for larger anions, only weakly hydrated. Then, at molar sodium concentrations, the sodium ions are forced into proximity with these anions forming either ion pairs or solvent-separated ion pairs at the anion sites along the chain. Together with the sodium ions come an excess of five water molecules for each, and so the cation-anion binding brings 15 to 20 additional, relatively strongly bound water molecules into proximity with each 8 Å- to 10 Å-long section of the heparin chain. This extra water acts like filling a balloon with water, and the chain extends as it is pushed out by the attached water sheath surrounding and bound to the chain. As a result, the chain is pushed out into an extended form due to the extra, crowded waters now attached in an annular sheath surrounding the polyanion.

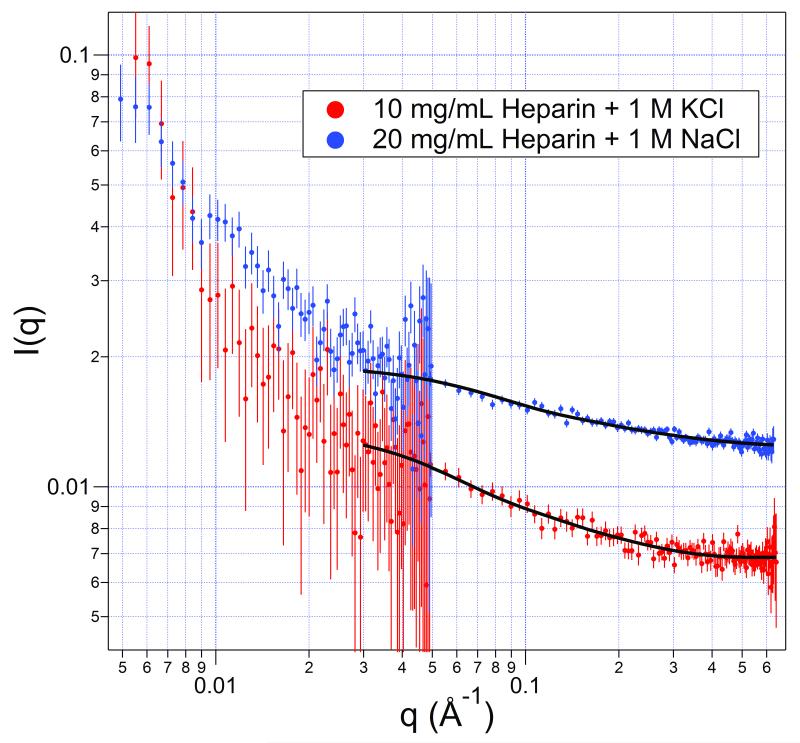
To test this hypothesis, a solution of the less strongly hydrated cation K⁺ was added at 1.0 M to a 10 mg/mL heparin solution with the equivalent sodium still present. The results of the scattering are shown in Figure 4 along with the curves of the best fits by homogeneous-cylinder models. The parameters are listed in Table II (and Table I). The heparin in the presence of potassium is much less extended, and its diameter larger than in the presence of sodium, in concordance with the assumption of the chain extension being caused by the amount of extra, strong hydration linked with the associating sodium ions. Apparently the chemistry of the cation does influence the degree of chain extension that occurs and not just the presence of cation charges.

FIGURE 4.

A solution of 10 mg/mL heparin sodium with 1.0 M KCl added (red, bottom) and a 20 mg/mL solution with 1.0 M NaCl added (blue, top). The fits are of homogeneous cylinders with dimensions shown in Table 2 (and Table 1). Note that the curves are not congruent, which would occur if the scatterers were the same shape.

Table II.

Fitting parameters for solutions with molar added salt^a,^b

Solution	Cyl Radius (Å)	Cyl Length (Å)	Cyl Vol (103•Å3)
10 mg/mL + 1 M KCl	7 ± 1	75 ± 18	11 ± 4
20 mg/mL + 1 M NaCl	4 ± 2	116 ± 14	8 ± 7

^aUncertainties are ±σ for the curve fitting process alone.

^bAll length measures are for nucleus-to-nucleus distances

From NMR data and theoretical calculations for a heparin trisaccharide, Hricovíni, et al.²⁰ has suggested that the sodium ions bind to one or more sulfate groups with each sulfate bidentate with two oxygens binding the sodium and forming a four-member chelate ring. If the sodium ions are shared at low concentrations, the cross-linking from sharing would aid the polyelectrolyte collapse. However, at high sodium, the sodium ions would not be shared, and the extra bound waters would force the chain extension. This straightforward change in sodium ion bonding agrees with the observed structures found in the low and high sodium conditions.

The Structure with Acid Neutralization of the Heparin Charge

Another question about the structure is, "What happens when the charge is neutralized by protonation?" To decide on the conditions for an experiment, we note that the experimental pK_a values of the heparin carboxyl groups are found in the range 2.79 to 3.13.⁵ However, the pK_a values of the N-sulfo and O-sulfo have been estimated only by theoretical calculation.⁶ Results are derived from gas phase values and projected semi-empirically into water to estimate the pK_a: for the O-sulfo group, 0.5 to 1.2, and for the N-sulfo group, 1.4 to 1.9. The possible variations in these values because they are within a highly charged region of a polyelectrolyte were not evaluated.

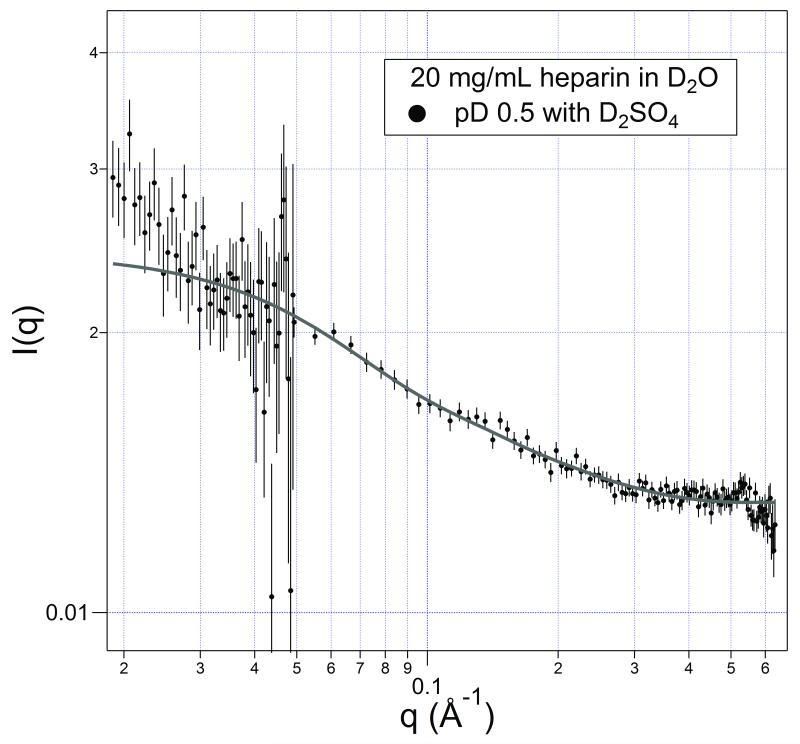
A solution of heparin was prepared in 0.3 M in deuterosulfuric acid to address the question raised in this section; the solution had a pD ≈ 0.5. These conditions should completely protonate the carboxylates and leave at most only a minority of the N-sulfo and O-sulfo groups unprotonated. At least 3/4 of the charge should be neutralized by protonation. The results are shown in Figure 5, and the best-fit cylinder parameters are listed in Table I. As can be observed, the shape of the molecules are essentially the same as in the presence of molar-level potassium; the molecule has a length about half that of its extended form with a volume expected for a packed heparin molecule.

FIGURE 5.

Scattering from a 20 mg/mL heparin solution with pD ≈ 0.5 (0.3 M D₂SO₄ added). The fit is a homogeneous cylinder model with the dimensions listed in Table 1.

CONCLUSIONS

The results of small angle neutron scattering on 10 kDa heparin solutions in the millimolar concentration range show that when sodium concentrations are equivalent to the polyelectrolyte's charge and up to a few hundred millimolar higher, the molecular structure is compact and the shape is well modeled by a cylinder with a length three to four times its diameter.

When molar level sodium is present, the molecule becomes extended to nearly its full length as estimated from reported x-ray measurements on stretched fibers. However, this stretched form is not found in the presence of molar potassium ions, and in that high-potassium environment, the heparin molecules have the same shape as when its charges are mostly protonated at pD ≈ 0.5, a structure that is compact and approximately half as long as the stretched molecule.