Abstract
Objective
The purpose of the present study is to model the dynamics of lobular Ca2+ wave propagation induced by an extracellular stimulus and to analyze the effect of spatially systematic variations in cell-intrinsic signaling parameters on sinusoidal Ca2+ response.
Methods
We developed a computational model of lobular scale Ca2+ signaling that accounts for receptor-mediated initiation of cell-intrinsic Ca2+ signal in hepatocytes and its propagation to neighboring hepatocytes through gap junction-mediated molecular exchange.
Results
Analysis of the simulations showed that a pericentral-to-periportal spatial gradient in hormone sensitivity and/or rates of IP3 synthesis underlies the Ca2+ wave propagation. We simulated specific cases corresponding to localized disruptions in the graded pattern of these parameters along a hepatic sinusoid. Simulations incorporating locally altered parameters exhibited Ca2+ waves that do not propagate throughout the hepatic plate. Increased gap junction coupling restored normal Ca2+ wave propagation when hepatocytes with low Ca2+ signaling ability were localized in the mid-lobular or the pericentral region.
Conclusion
Multiple spatial patterns in intracellular signaling parameters can lead to Ca2+ wave propagation that is consistent with the experimentally observed spatial patterns of Ca2+ dynamics. Based on simulations and analysis, we predict that increased gap junction-mediated intercellular coupling can induce robust Ca2+ signals in otherwise poorly responsive hepatocytes, at least partly restoring the sinusoidally oriented Ca2+ waves.
Significance
Our bottom-up model of agonist-evoked spatial Ca2+ patterns can be integrated with detailed descriptions of liver histology to study Ca2+ regulation at the tissue level.
Index Terms: Biology, Biological Systems Modeling, Biomedical Engineering, Computational Biology, Ca2+ dynamics, Liver, Cell-cell interactions
I. Introduction
The liver performs a wide variety of physiological functions such as regulation of intermediary metabolism, lipid synthesis, bile production and xenobiotic detoxification. Normal liver function requires both tight regulation of intracellular processes as well as intercellular coordination. Free Ca2+ in the intracellular domain participates in the regulation of hepatocyte functions such as glucose metabolism, bile secretion, proliferation and apoptosis[1], [2], [3]. Regulation of cytosolic Ca2+ is particularly important in hepatocytes, the cells responsible for the bulk of metabolic and detoxification activities in the liver. Consequently, disruption of Ca2+ dynamics can potentially lead to pathological conditions (for example cholestasis [4]).
Hepatocytes are polarized cells arranged in quasi-linear structures called hepatic cords alongside the sinusoids, the blood vessels that provide the cells with access to the circulation across the hepatic plate. The basolateral membranes of hepatocytes are in indirect contact with blood whereas the apical membranes open into bile canaliculi. Ca2+ oscillations are induced in hepatocytes by a wide range of chemical signals [5], [6], [7]. In the case of growth factors and many hormones, binding of the ligand to cell surface receptors on the basolateral membrane elicits a signaling cascade involving phospholipase C (PLC) activation, inositol triphosphate (IP3) synthesis, opening of Ca2+ channels in the endoplasmic reticulum (ER) store, and subsequent efflux of Ca2+ from the ER into the cytosol, resulting in a transient spike in cytosolic Ca2+ concentration. Upon hormone stimulation, hepatocytes in intact rat livers typically exhibit Ca2+ spikes with inter-spike intervals of about 100 seconds [8]. However, many factors can lead to variations in spike frequencies, for example, hepatocytes respond to an increase in extracellular stimulus by increasing the Ca2+ spike frequency [8].
Variations in Ca2+ spike frequencies have been shown to lead to differential expression of several downstream genes [9]. In order to obtain a coherent lobular scale response to extracellular stimuli, the Ca2+ signals in hepatocytes across the lobule must be coordinated. Gap junctions are believed to play a role in coordinating this response across cells, leading to synchronized cytosolic Ca2+ spikes across the liver lobule in response to G-protein coupled receptor agonists [10]. Cytosolic Ca2+ as well as IP3 synthesized within a hepatocyte can migrate to neighboring hepatocytes, inducing synchronization of Ca2+ spikes across the liver lobule [11]. Another mechanism of long-range coordination is the release of paracrine signals such as ATP into the extracellular region, which then elicits Ca2+ spiking in the neighboring hepatocytes by purinergic receptor activation[12]. Thus, induction of Ca2+ spikes in one hepatocyte can propagate through the lobule in well-defined spatial patterns.
In liver lobules, Ca2+ signals commonly manifest as traveling waves [9], [13]. Ca2+ waves usually start at the pericentral (PC) region of the lobule and propagate toward the periportal (PP) region [14]. The direction of Ca2+ signal propagation is opposite to the general direction of blood flow, which is from PP to PC. This observation indicates an organized spatial heterogeneity in the Ca2+ signaling capacity of cells. This phenomenon of liver zonation has been observed in many other physiological functions in liver lobules [15], [16].
A systematic propagation of Ca2+ signals from PC to PP lobular regions is commonly observed, and gap junctions have been identified as being responsible for the orchestration of Ca2+ signal propagation at the lobular scale. However, the contribution of hepatocyte-specific Ca2+ signaling components to the lobular scale Ca2+ wave propagation are mostly unknown. In this study, we present a computational model of spatio-temporal Ca2+ signal propagation at the lobular scale, through hepatocytes aligned alongside a sinusoid. We demonstrate synchronization of intracellular Ca2+ spiking in our model due to gap junction-mediated IP3 transfer. We identify spatial patterns in intracellular Ca2+ signaling parameters that can lead to propagation of Ca2+ waves from PC to PP lobular regions, and simulate Ca2+ wave propagation changes under disruption of zonation. We also investigate the effect of localized incapacity of hepatocytes within hepatic plates on Ca2+ wave propagation.
II. MODEL DEVELOPMENT
Our model is based on the IP3-Ca2+ cross coupling model proposed in [17, 18] with the following modifications: we retain the kinetic equations for intracellular fluxes and IP3 receptor dynamics, but our treatment of IP3 synthesis relies on hormone receptor dynamics instead of the constant receptor activation value used in [17, 18]; we account for intercellular interactions by including gap junctions connecting the adjacent hepatocytes (Figure 1). Hepatocyte gap junctions are primarily composed of Connexins 32 and 26[19]. While Connexin 32 expression is evenly distributed throughout the liver, Connexin 26 is preferentially expressed in the periportal hepatocytes[20]. Although permeability of gap junctions to IP3 depends upon the constituent Connexin type[21], we assume that all gap junctions are uniformly permeable to IP3 transfer in the present model formulation. While the number of hepatocytes aligned across the lobule is variable and arrangement of sinusoids in lobules is complex, we considered a representative lobular axis consisting of 15 successive hepatocytes connected in a sequence via gap junctions.
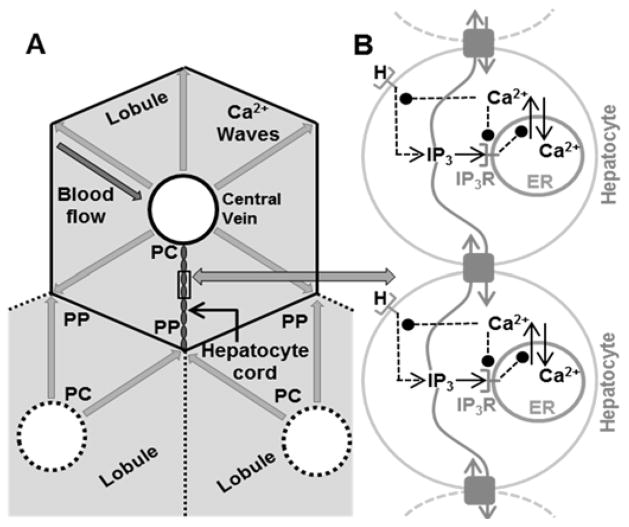
Figure 1.
A – Hepatocyte cords and Ca2+ wave propagation in liver lobules. At the microscopic scale, the liver consists of roughly hexagonal shaped lobules. The area surrounding the central vein is the pericentral region (PC), whereas the outer extremities are the periportal (PP) region. Blood flows from the PP region towards the PC region in lobules. Hepatocytes lie roughly radially between the PC and PP regions along quasi-linear structures in the hepatic plate. Each hepatocyte is connected to its neighbors by gap junctions. Ca2+ waves originate near the PC region and propagate radially outward along all hepatocyte cords. B - Network model of Ca2+ wave propagation along hepatocytes in a sinusoid induced by the agonist.
We characterize the signaling state of every hepatocyte by the concentrations of 4 species – cytosolic Ca2+ (CaI), cytosolic IP3 (IP3), ratio of inactive to total IP3R (g), and the ratio of free to total receptor levels (r). Sustained Ca2+ spiking over long durations can cause loss of oscillatory Ca2+ response due to ER store depletion. In response to decreasing store Ca2+, store operated Ca2+ channels are activated, allowing Ca2+ influx from the extracellular domain and stable Ca2+ spiking behavior [22]. We assume active Ca2+ replenishment by such mechanisms so that total intracellular store Ca2+ content, CaT, remains constant. Ryanodine receptors (Ryr) can act as independent regulators of intracellular Ca2+ dynamics and are expressed in hepatocytes[23]. However, intercellular Ca2+ waves cannot be initiated by Ryr-specific stimuli in hepatocytes. Ryr activation can only modulate the frequency and amplitude of intracellular Ca2+ spikes[23]. In the current model, we only consider IP3R activation for simplicity.
We consider cytosolic Ca2+ spikes induced by vasopressin, a well-studied G-protein coupled receptor agonist known to induce Ca2+ oscillations in hepatocytes. We assume vasopressin levels to be constant, such that binding of vasopressin to the receptor does not decrease the circulating agonist concentration. This corresponds to typical in vivo experiments involving steady perfusion of the liver with vasopressin at a fixed concentration. The model will now be discussed in greater detail in the following sections, with the parameter and species definitions compiled in Table 1.
TABLE I.
Model Species and Parameters
| Symbol | Quantity; Value |
|---|---|
| A | Maximal rate of Ca2+ release from ER store; 0.20μM /s |
| B | Maximal rate of cytosolic Ca2+ pump to ER; 0.082μM/s |
| CaIi | Cytosolic Ca2+ concentration; μM |
| CaTi | Total Ca2+ concentration; μM |
| D | IP3 degradation rate; 1.6/s |
| E | IP3R deactivation rate; 1/(μM)4-s |
| F | IP3R activation rate; 0.01/s |
| G | Mass transfer coefficient between cells i and j; 0–5/s |
| gi | Ratio of free to total IP3R |
| H | Hormone concentration; 1.8 ×10−10 M |
| IP3i | IP3 concentration; μM |
| k1 | IP3 concentration for half maximal rate of catalysis of store Ca2+ release; 0.5μM |
| k2 | Cytosolic Ca2+ concentration for half maximal pump rate; 0.15μM |
| k3 | Cytosolic Ca2+ concentration for half maximal rate of IP3 production catalysis; 1μM |
| kcat | Bound receptor ratio for half-maximal IP3 production rate; 0.45 |
| kd | Hormone independent agonist receptor binding rate;0.34/s |
| kHr | Hormone-receptor binding rate; 1 /10−10 M-s |
| kIP3i | Saturation IP3 synthesis rate; 0.7 – 0.9 μM /s |
| kri | Agonist receptor recycling rate; 1 – 2/s |
| L | Ca2+ leakage flux from store to cytosol; 0.00015μM /s |
| ri | Ratio of free to total agonist receptors in cell i |
A. Vasopressin Receptor (r) dynamics and IP3 synthesis
Binding of extracellular vasopressin to the cognate receptors on the cell membrane leads to Ca2+ spiking in hepatocytes. While receptor internalization is possible, we assume that the total receptor number is a constant for the duration of typical experiments considered here (approximately 60 minutes). Denoting the extracellular vasopressin concentration by H, the free (not agonist-bound) receptor concentration balance is represented as:
| (1) |
We consider the rate of increase in fraction of free receptors to be proportional to the bound receptor fraction. We assume that the decrease in free receptor fraction occurs in a vasopressin-dependent as well as in a vasopressin-independent manner (e.g., binding to competitive substrates, inactivation etc.). Dividing both sides of equation (1) by Rtotal, yields the following equation for the balance for the fraction of free (inactive) vasopressin receptors denoted by r:
| (2) |
where kr, kd, and kHr represent the rate constants for increase of unbound receptor fraction, vasopressin-independent decrease in unbound receptor fraction, and vasopressin-dependent receptor activation rate, respectively. Binding of vasopressin to the cell surface receptors leads to PLC activation and the synthesis of IP3. We assume saturation kinetics for vasopressin induced IP3 synthesis. PLC activity-induced IP3 synthesis is further enhanced by cytosolic Ca2+ [24]. Ca2+-mediated enhancement of PLC activity is represented by a Hill-like function. While IP3 deactivation is known to occur through multiple mechanisms[25], we consider an integrated IP3 deactivation term proportional to the cytosolic IP3 concentration. The net IP3 balance is given by:
| (3) |
B. Intracellular Ca2+ transport
Binding of cytosolic IP3 with the heterotetrameric IP3 receptors on the ER membrane activates Ca2+ channels and releases the ER-stored Ca2+ into the cytosol. Cytosolic Ca2+ balance is modeled as:
| (4) |
Equation (4) includes an additional Ca2+ leakage term from ER Ca2+ stores into the cytosol, denoted by L. The increase in cytosolic Ca2+ initiates active transport mechanisms to pump Ca2+ back into the ER store at the expense of ATP, described by the second order Hill function in equation (4).
C. IP3 receptor dynamics
Cytosolic Ca2+ operates synergistically with IP3 to regulate IP3 receptor activity residing on the ER membrane. Studies have reported a nonlinear effect of cytosolic Ca2+ on IP3 receptor activation, where low levels of cytosolic Ca2+ promote and high levels of cytosolic Ca2+ inhibit IP3 receptor activity [26]. IP3 receptor activity balance is modeled as a Ca2+ assisted inactivation and a constitutive activation rate yielding:
| (5) |
We extended the single hepatocyte model to include a hepatocyte cord spatial context by introducing gap junction coupling between adjacent hepatocytes. Following [27], we modeled IP3 exchange between gap junction-coupled hepatocytes as a mass transfer term. Although Ca2+ can be exchanged through gap junctions, we ignore this process based on studies reporting substantially lower rates of Ca2+ diffusion through the cells compared to the intercellular transfer of IP3[28]. The rate of IP3 exchange between gap junction-coupled hepatocytes is proportional to the coupling parameter G and the instantaneous difference between their respective IP3 concentrations. Upon incorporating gap junction coupling, the resulting hepatocyte cord model is given by the following equations:
| (6) |
| (7) |
| (8) |
| (9) |
Subscript i represents the cell index for hepatocyte-specific species and parameters. The summation term in equation (7) describes the IP3 exchange between adjacent gap junction-coupled hepatocytes, where the adjacency set for hepatocyte i along a sinusoid consisting of N cells is defined by:
III. Results
We focused on two hepatocyte-specific parameters: kr and kIP3, and examined the effects of altering the spatial patterns of these parameters on Ca2+ wave propagation. Differential expression of vasopressin receptor between PP and PC regions of lobules has been demonstrated experimentally [29], [30], [31], [32]. Spatial variations of kr for each hepatocyte served as a proxy for inhomogeneous vasopressin receptor expression in our model. In addition, we considered spatial inhomogeneity in IP3 production rates because of the role of IP3 as the key species controlling Ca2+ oscillations in individual hepatocytes. Model parameters were tuned to match typical Ca2+ spiking dynamics observed experimentally in hepatocytes. Nominal parameter values and ranges used to initialize each hepatocyte in our model are listed in Table 1. The dependence of the inter-spike interval of Ca2+ oscillations in a single hepatocyte on select model parameters is shown in Figure S1A (Supplementary Material). Ca2+ spike frequency ranges in hepatocytes obtained using our model for varying kr and kIP3 values (Figure S1B) are in agreement with experimental data for the agonist ranges examined [8]. For each simulation, the initial concentration of each species was considered to be uniform across all the hepatocytes. In each of the following simulations, the concentration of vasopressin was set to zero for the initial 200 seconds and was subsequently increased to a non-zero value at 200 seconds. This allows all intracellular species concentrations to reach a steady state by 200 seconds. All simulations were performed using the ode15s integrator in MATLAB 2013a (MathWorks, Natick, MA, see supplement S7 for the MATLAB code and supplement S8 for the SBML model; the SBML model is available online on the Biomodels database[18] (https://www.ebi.ac.uk/biomodels-main/).
A. Cytosolic Ca2+spiking and the effect of gap junctions along a hepatocyte cord comprised of identical hepatocytes
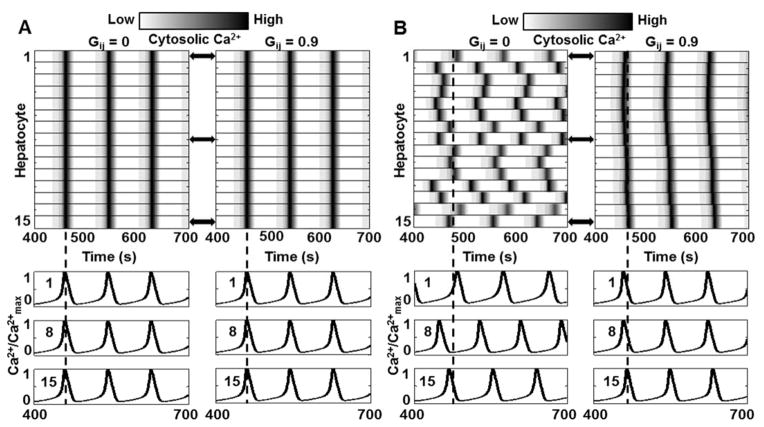
We simulated Ca2+ signal propagation in the case where kr and kIP3 were the same for all hepatocytes along a sinusoid. The resulting simulations are shown in Figure 2A. All hepatocytes showed Ca2+ spikes at the same time, a synchrony that is inconsistent with experimental observations. Furthermore, gap junction coupling did not alter Ca2+ spikes in the hepatocytes, as can be seen in Figure 2A, upon comparing the results for Gij = 0/s and 0.9/s. Simultaneous Ca2+ spiking in identical hepatocytes with or without gap junction coupling can be attributed to identical intracellular IP3 dynamics. Since IP3 concentrations in every gap junction coupled hepatocyte pair are the same at all times during the simulation, no IP3 exchange occurs. However, when kr and kIP3 were varied across hepatocytes, inter-spike periods for a given vasopressin concentration were different. In this case, gap junction coupling led to synchronization in Ca2+ spikes along the hepatocyte cord (Figure 2B).
Figure 2.
Role of gap junctions in lobular Ca2+ wave propagation. Hepatocytes were numbered from 1 to 15 starting at the hepatocyte closest to the PC region and assigned identical intracellular signaling parameters. There is no Ca2+ wave under this condition with or without gap junction coupling (Gij = 0 or 0.9) since all hepatocytes exhibit simultaneous rise and fall in Ca2+ levels. Corresponding Cytosolic Ca2+ traces for cells 1, 8, and 15 are shown to demonstrate concurrence of Ca2+ spikes; B - Gap junction coupling causes synchronization in hepatocytes with different intrinsic signaling parameters. Without gap junction coupling (Gij =0), cytosolic Ca2+ spikes appear in hepatocytes are distinct times, as seen in the corresponding cytosolic Ca2+ traces for cells 1, 8, and 15. When the hepatocytes are coupled through gap junctions (Gij = 0.9); Ca2+ spikes in each hepatocyte are synchronized. Note that there is a phase lag between Ca2+ spikes, however, the number of spikes within the 300 second period is the same for all hepatocytes, unlike the Gij = 0 case. (See Table S3 for parameter values for each hepatocyte.)
B. Ca2+ waves generated by spatial parameter gradients
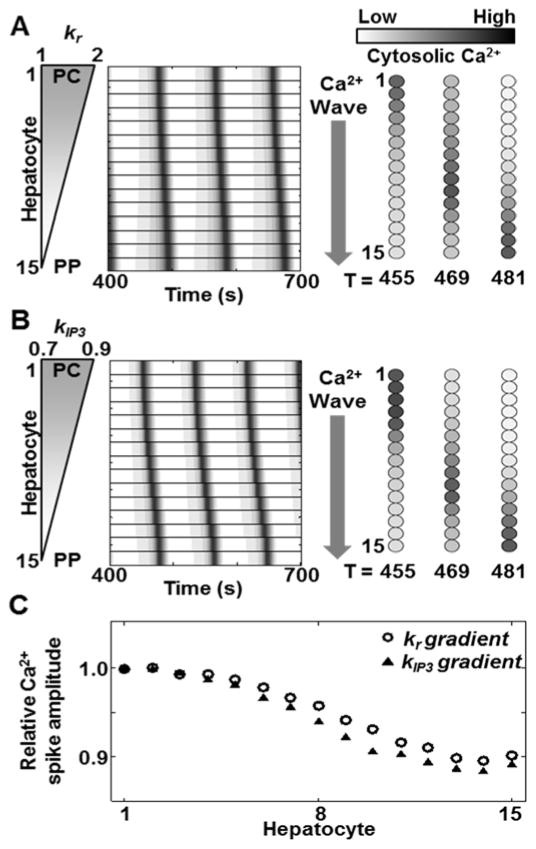
Next we simulated the effects of a spatial gradient of kr or kIP3, independently and in combination. In the first set of simulations (investigating the independent effects of kr and kIP3), we initialized the hepatocytes with either kr or kIP3 specified by a linear PC to PP gradient ranging between the values in Table 1, while the other parameter was held constant at the nominal value (kr = 1.5/s; kIP3 = 0.8μM/s). A constant vasopressin concentration was used in the simulations (H = 1.8×10−10M). Both cases correspond to the highest responsiveness of PC hepatocytes towards vasopressin, which decreases progressively toward the PP region. PC to PP Ca2+ waves were observed in each case (Figure 3A and B). PC to PP propagation of Ca2+ signals observed in the case of a graded kr along the hepatocyte cord is consistent with expectations based on experimental results[29]. Studies have reported that although dependent on the specific agonist, IP3 synthesis dynamics are strongly correlated with the receptor number [33]. Relative overexpression of vasopressin receptors in the PC region compared to the PP region therefore suggests higher IP3 synthesis and Ca2+ mobilization in PC hepatocytes. Ca2+ signals are thus initiated near the PC region and propagate toward the PP region. Additionally, as shown in Figure 3B, PC to PP Ca2+ waves were observed with a PC to PP linear gradient of kIP3 suggesting that Ca2+ wave propagation can be regulated by spatial inhomogeneity in IP3 production rates. The amplitude of the cytosolic Ca2+ spikes was a near constant along the lobular axis with ~10% decrease (Figure 3C), consistent with previous findings[34]. We simulated Ca2+ wave propagation along the liver plate with combined spatial inhomogeneity in kr as well as kIP3. A linear two-fold gradient of kr was maintained consistent with experimentally reported differential expression of vasopressin receptors. Four distinct spatial patterns of kIP3 were considered in combination with the two-fold kr gradient – (1) a linear PC to PP gradient, (2) a constant value across the lobule, (3) a linear PP to PC gradient, and (4) a randomly chosen value for all hepatocytes. We estimated the speed of wave propagation along a hepatocyte cord, by considering a nominal hepatocyte diameter of ~20μm. In each case, kIP3 values for all hepatocytes ranged between 0.7 – 0.9μM/s. To simulate the fourth case with random kIP3 for all hepatocytes, a 15-step linear gradient from 0.7 – 0.9 was generated, and a random permutation of the obtained vector was assigned as kIP3 values for the 15 hepatocytes. Vasopressin concentration was held constant (H = 1.8×10−10M) after t = 200 seconds (Figure 4A).
Figure 3.
PC to PP Ca2+ waves can be observed due to gradients of vasopressin receptor recycling rate as well as IP3 synthesis rate independently. Simulation results for PC to PP Ca2+ waves obtained with a (A) linear PC to PP kr gradient (2 to 1/s) with a constant kIP3 value (0.8μM/s), and (b) linear PC to PP kIP3 gradient (0.9 to 0.7μM/s) with a constant kr value (1.5/s) for all hepatocytes. Hepatocytes were numbered from 1 to 15 starting at the hepatocyte closest to the PC region. Either case resulted in diminishing Ca2+ spike amplitude from the PC to PP region. (See Table S4 for all parameters values).
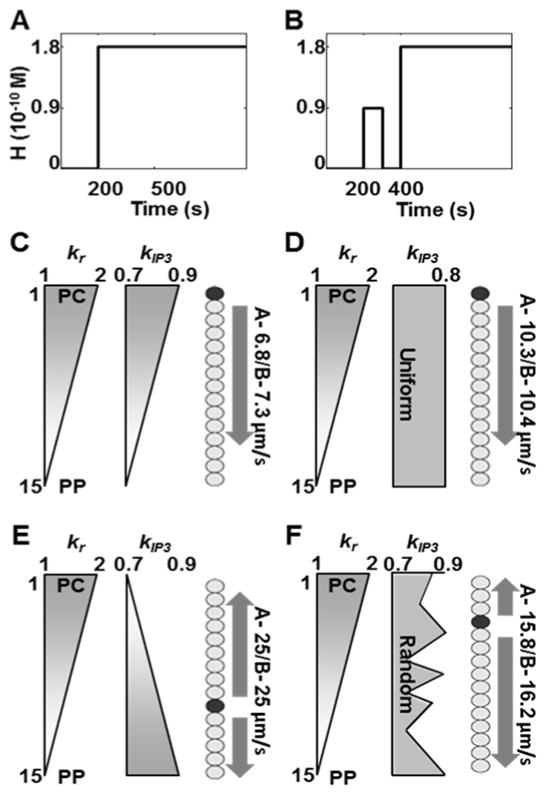
Figure 4.
Ca2+ wave direction, start site and speed for PC to PP vasopressin receptor production gradient (kr) and different IP3 synthesis patterns (kIP3) under sustained stimulus shown in A, and under a preconditioning stimulus prior to a sustained stimulus shown in B. Wave speeds were estimated assuming typical hepatocyte diameter of 20 μm. Estimations were based on spike time difference between the wave start site (dark circle) and the hepatocyte in the hepatocyte cord farthest away from it. C - Both gradients from PC to PP yield a PC to PP Ca2+ wave starting at the hepatocyte closest to the PC region. Wave propagation speed is 6.8 μm/s; D - kr gradient superimposed with constant kIP3 gives PC to PP propagation with a wave speed of 10.3 μm/s; E - Opposing gradients result in faster wave propagation speed (25 μm/s), however, the start site is closer to the PP region. Waves propagate in either direction from the start site; F - Random variations of kIP3 within the specified range result in waves starting close to the PC region and propagating in both directions. (See Table S5 for parameter values used in the simulations).
The simulation results for different spatial patterns of kr as well as kIP3 are shown in Figure 4. When both parameters had PC to PP gradients, Ca2+ waves propagated from the PC towards the PP region (Figure 4C). PC to PP wave propagation was also observed when kIP3 was held constant (Figure 4D). In each case, the hepatocyte lying closest to the PC region was the start site of Ca2+ waves. However, Ca2+ waves traversed the hepatic plate slower (6.8μm/s) when kr as well as kIP3 had PC to PP gradient, as compared to the case with uniform kIP3 (10.3μm/s). Opposing gradients of kr and kIP3 yielded faster Ca2+ wave traversal speeds (25μm/s) (Figure 4E). However, Ca2+ waves started in the mid-lobular region and propagated in either direction. When kIP3 values ranging between 0.7–0.9 μM/s were chosen randomly, waves started closer to the PC region and propagated towards the PP region. Ca2+ wave propagation speed was 15.8μm/s (Figure 4F).
C. Pre-conditioning with short-lived stimulus pulse sensitizes hepatocytes to subsequent agonist stimulus
We simulated our model to observe whether wave propagation velocities along a hepatic cord are altered due to a short agonist pulse prior to a sustained high agonist concentration under the spatial kr and kIP3 patterns shown in Figure 4B. An agonist pulse lasting 100 second (H = 0.9 × 10−10 M) was applied at t = 200 seconds. After a 100 second refractory period with no stimulus, a constant stimulus (H = 1.8 × 10−10 M) was applied starting t = 400 seconds. The Ca2+ wave start site was then recorded and propagation speed along the sinusoid was estimated as described above.
Simulation results for the altered agonist profile are shown in Figure 4 with new estimates of Ca2+ wave propagation rate reported in green for each case. Preconditioning with a short-lived stimulus pulse did not alter the wave start site for any of the cases considered. However, Ca2+ wave propagation speed was altered due to the initial agonist pulse. A small increase in wave propagation speed was observed in three out of the four spatial kIP3 patterns considered - a PC to PP kIP3 gradient, a constant kIP3 value throughout the hepatocyte cord, and randomly chosen kIP3 values. Ca2+ wave propagation speed did not change in case of PC to PP kr gradient along with PP to PC kIP3 gradient. Within our modeling framework, the trend of increased Ca2+ wave propagation speed can be attributed to accumulated cytosolic IP3 in all hepatocytes due to the initial pulse. While our analysis pointed to a potential sensitization trend, additional simulations are needed to exhaustively explore the parameter space considering the effects of amplitude and duration of the initial pulse, refractory period prior to the second pulse, relative amplitudes between the first and second pulse, etc. on lobular Ca2+ wave dynamics.
D. Effects of localized Ca2+ signaling insufficiency along the sinusoid
We considered Ca2+ wave propagation under gap junction coupling where a limited number of hepatocytes along the liver plate show very low signaling responses to extracellular vasopressin. We assigned kr values of 0.5/s to 5 consecutive hepatocytes while the remaining hepatocytes had a linear PC to PP gradient with kr values from 1 – 2/s. All hepatocytes were initialized with kIP3 = 0.8 μM /s. We considered three cases with local vasopressin insensitivity in (1) PC, (2) mid-lobular, and (3) PP regions. The simulation results are shown in Figure 5.
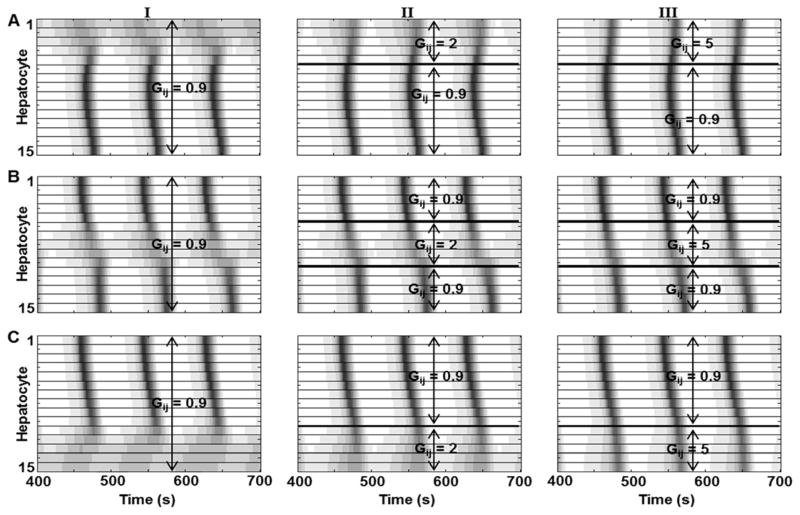
Figure 5.
Effect of local hepatocyte incapacities w.r.t. Ca2+ signaling in the sinusoid on Ca2+ wave propagation. Local increase in IP3 exchange is sufficient to re-establish Ca2+ waves across the sinusoid. Low response to vasopressin was implemented by decreasing vasopressin sensitivity (kr); A - five hepatocytes closest to the PC region were initialized with low vasopressin sensitivity. Ca2+ waves start in the mid-lobular region and propagate in both directions. However, propagation towards the PC region is disrupted by low hepatocyte response when mass transfer coefficient between all hepatocyte pairs is kept at 0.9 (I). Increasing mass transfer coefficients for these hepatocytes (II and III) results in more robust Ca2+ oscillations in hepatocytes in the PC region. Similarly, B and C represent cases where mid-lobular and PP hepatocytes have low vasopressin sensitivity. In both cases, local increase in IP3 exchange rates rescues Ca2+ wave propagation. Similar effects were seen when mass transfer coefficients were changed for all hepatocytes in the sinusoid (not shown). (See Table S6 for parameter values used)
PC hepatocyte insensitivity results in Ca2+ waves starting in the mid-lobular region and propagating in either direction. With Gij = 0.9/s for all hepatocyte pairs, we observed a damped Ca2+ spiking response in the PC hepatocytes (Figure 5A, column I). We increased the mass transfer parameter, Gij, to analyze its effects on the response of PC hepatocytes. Increasing the mass transfer coefficient values for only the 5 vasopressin insensitive PC hepatocytes (Gij = 2 or 5 for i=1..5, and j=2..6) yielded relatively robust cytosolic Ca2+ spikes and Ca2+ wave propagation (Figure 5A, columns II and III). Similarly, increased Ca2+ spiking and synchronized waves were observed when Gij was increased to 2/s and 5/s for all hepatocyte pairs (data not shown).
Mid-lobular hepatocyte insensitivity with Gij = 0.9/s for all gap junction-connected hepatocyte pairs led to discontinuous PC to PP Ca2+ waves owing to the low vasopressin sensitivity and hence IP3 synthesis in this region. Local increase in the mass transfer coefficients resulted in a continuous Ca2+ wave across the sinusoid (Figure 5B). Ca2+ waves propagated from the PC to the PP region when the PP hepatocytes were set up with low vasopressin sensitivity, and the cytosolic Ca2+ spiking improved with increased local mass transfer coefficient, similar to the previous cases (Figure 5C).
IV. Discussion
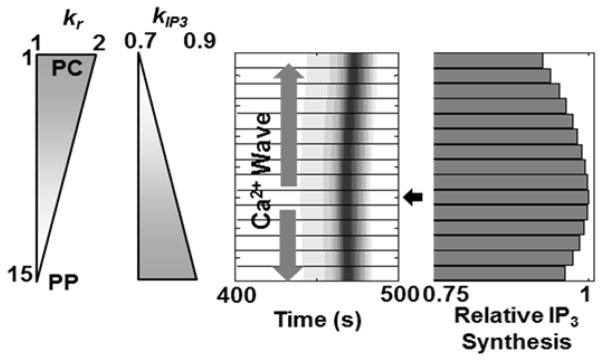
Our simulations suggested that wave-like propagation of Ca2+ signals is dependent on the spatial heterogeneity of the intrinsic vasopressin sensitivities and/or IP3 synthesis rates. In vivo stochasticity or regulated gradients in intracellular Ca2+ signaling parameters at the cellular level processes may yield such spatially non-uniform sensitivities to shape the lobular patterns of Ca2+ dynamics. Based on simulations, we predict that this cell-to-cell heterogeneity may be countered by gap junction coupling, to yield a systematic, synchronous lobular scale Ca2+ response to the extracellular stimuli. Our simulations provide insight into the underlying spatial patterns of two hepatocyte-specific Ca2+ signaling parameters – differential expression of vasopressin receptors (accounted for by kr in the model), and IP3 production rate (accounted for by kIP3) – which can lead to a PC to PP Ca2+ wave propagation. Linear gradients of these parameters from PC to PP hepatocytes can lead to Ca2+ wave patterns that are consistent with the experimental observations. In addition, PC to PP wave propagation in the case of a uniform kr in conjunction with a PC to PP linear gradient of kIP3 indicated that the start site of Ca2+ waves could be related to the rate of IP3 synthesis in the hepatocytes. We examined the coincidence of Ca2+ wave start site with the hepatocyte synthesizing the most IP3 for the specific case of a PC to PP gradient of kr and a PP to PC gradient of kIP3 (Figure 6). Ca2+ waves started in the mid-lobular region and propagated in either direction, even though neither the vasopressin sensitivity nor the IP3 production rate of the mid-lobular hepatocytes was the highest compared to the other hepatocytes along the sinusoid but the total IP3 synthesized in mid-lobular hepatocytes was the highest for a 5000 second simulation. Our model suggests that the first-responder hepatocytes, i.e., the hepatocytes initiating the Ca2+ spikes, are those with the highest IP3 synthesis capacity, which is determined by a combination of vasopressin sensitivity and IP3 synthesis rate, but not by either parameter independently. Note that we do not explicitly consider differential rates of IP3 degradation along the hepatocyte cord. If considered, it is easy to appreciate that IP3 degradation rate will also modulate Ca2+ wave propagation along the liver plate.
Figure 6.
Ca2+ wave start site coincides with the cell that synthesizes the highest amount of IP3. Opposing gradients of kr and kIP3 were chosen. The wave starts at hepatocyte 10 (arrow), which has intermediate values of kr and kIP3, and propagates in both directions. Hepatocyte 10 synthesizes the highest amount of IP3. The relative IP3 production values shown were integrated over a 5000 second simulation. (Parameter values used were identical to those in Figure 4E).
Our simulations and findings may have physiological implications in the context of regulation of bile flow in the liver. Bile acid synthesis is an important function of hepatocytes linked with cholesterol homeostasis. By-products of cholesterol metabolism are aggregated in the form of bile acids and secreted into the bile canaliculi from the apical regions of hepatocytes. Cytosolic Ca2+ spikes have been shown to induce hepatocyte microfilament contractions driving bile secretion. Vasopressin stimulation has been demonstrated to cause hepatocyte contraction and concomitant bile secretion from hepatocytes [35]. Disruption of spatially coordinated Ca2+ signals can therefore cause aberrations in cholesterol and bile flow homeostasis, potentially predisposing the liver to pathological conditions such as cholestasis.
In a healthy liver, bile flows from the PC to the PP region. This is believed to be a consequence of sequential hepatocyte contractions along the liver lobule starting in the PC region and progressing towards the PP region which push the secreted bile towards bile ducts in the PP region [27]. Our model-based approach identified multiple spatial patterns of intracellular signaling components that can lead to PC to PP Ca2+ waves, with likely consequences on successive PC to PP hepatocyte contractions. Independent as well as simultaneous PC to PP gradients of vasopressin sensitivity (kr) and (kIP3) led to PC to PP Ca2+ waves. A PC to PP vasopressin sensitivity gradient coupled with non-uniform but tightly controlled IP3 synthesis rates was also a favorable scenario for normal bile trafficking.
Among the spatial patterns tested, two scenarios were not favorable to normal PC to PP bile flow – (1) hepatocytes with identical signaling and Ca2+ regulation, and (2) opposing kr and kIP3 gradients in the hepatocytes along a sinusoid. While all intrinsic signaling parameters being identical for all hepatocytes may be unrealistic due to known zonated functions and molecular expression gradients, such a scenario provides insight into possible bile flow dynamics when hepatocytes are very similar in their molecular properties. An extracellular hormone challenge could potentially lead to near-simultaneous hepatocyte contractions along a sinusoid, which may cause disruption in the overall PC to PP bile flow. The PC to PP gradient of kr, coupled with PP to PC gradient of kIP3, yielded Ca2+ waves starting in the mid-lobular region and propagating in both directions. This, again, is expected to be unfavorable for draining hepatocyte-secreted bile into the PP bile duct.
Finally, we considered the impact of localized hepatocyte insensitivities to vasopressin on Ca2+ waves along a sinusoid, and its likely consequences to bile movement through liver lobules. Short-range insensitivity of hepatocytes to external stimuli could represent a cholestatic condition where local intracellular signaling insufficiencies may lead to bile accumulation. Increase in Ca2+ spiking in low-responsive hepatocytes upon a local or a global increase in the gap junction mediated IP3 transfer could translate to robust contractility, enhancing bile secretion from those hepatocytes. When vasopressin insensitive hepatocytes were close to the PC region, Ca2+ wave propagation occurred outward in both directions from the mid-lobular region. In this case, a local or global increase in gap junction mediated IP3 transfer, while sufficient to generate more robust Ca2+ spikes in the low-responsive hepatocytes, was not able to rectify the directionality of Ca2+ wave propagation. In contrast, the disruptions in Ca2+ waves due to low vasopressin sensitivity of hepatocytes in the mid-lobular or PP regions could be rescued by a local or a global increase in gap junction coupling. These results provide new predictions on the significant role of regulation of the gap junction-mediated molecular exchange in the maintenance of normal liver function.
Our computational model provides a framework for examining the impact of intracellular signaling components and intercellular coupling on the sinusoidal and lobular scale Ca2+ wave propagation under the influence of a G-protein coupled receptor agonist. The complexity of liver lobular organization presents many challenges and avenues for exploration. For instance, intracellular calcium signaling parameters, entrainment burden of hepatocytes to drive Ca2+ spikes in their neighbors and spiking frequencies could be a function of the spatial location of the hepatocyte within the lobule. Another intriguing possibility is determining what spatiotemporal information is inferable along the lobular axis based on calcium signaling patterns within each hepatocyte and its neighbors. While periportal and pericentral hepatocytes exhibit location dependent intrinsic molecular profiles, the molecular correlates of the spatial address are not clear within the mid-lobular zone. Decoding of spatial location based on cues from neighbors such as calcium spike frequency and phase shift could be a determinant in shaping hepatocyte phenotype in the mid-lobular zone.
The present model, based on a one-dimensional approximation of hepatocytes lying along a sinusoid could be extended to account for the complexity of hepatocyte arrangement in the three-dimensional lobular geometry. Such an extension is enabled by the recent improvements in imaging and image processing technologies that were utilized to develop a high-resolution visualization of the three-dimensional hepatic histology [36], [37]. Integrating our model with such detailed histological reconstructions will enable novel simulations that are likely to provide insights into tissue-scale coordination of Ca2+ signals underlying normal and pathophysiological conditions in the liver.
V. Conclusions
In the present study, we developed a computational model of Ca2+ wave propagation elicited in hepatocytes by extracellular stimulus by a G-protein coupled receptor agonist. Analysis of our simulations suggested that gradients of hormone sensitivity as well as intracellular Ca2+ signaling parameters together contribute to yield a wave-like propagation of Ca2+ signals along the lobular axis. Our model provides a computational platform for exploring lobular response shaped by gap junction mediated intercellular interactions as well as paracrine signaling in more detailed spatial models of liver lobules.
Supplementary Material
Acknowledgments
This work was supported by NIH/NIAAA under grant R01 AA018873.
Contributor Information
Aalap Verma, Department of Biomedical Engineering, University of Delaware, Newark, DE and the Department of Pathology, Anatomy and Cell Biology, Thomas Jefferson University, Philadelphia, PA.
Hirenkumar Makadia, Department of Pathology, Anatomy and Cell Biology, Thomas Jefferson University, Philadelphia, PA.
Jan B. Hoek, Department of Pathology, Anatomy and Cell Biology, Thomas Jefferson University, Philadelphia, PA
Babatunde A. Ogunnaike, Department of Chemical and Biomolecular Engineering, University of Delaware, Newark, DE
Rajanikanth Vadigepalli, Department of Pathology, Anatomy and Cell Biology, Thomas Jefferson University, Philadelphia, PA.
References
- 1.Exton JH. Mechanisms of hormonal regulation of hepatic glucose metabolism. Diabetes/metabolism reviews. 1987;3(1):163–183. doi: 10.1002/dmr.5610030108. [DOI] [PubMed] [Google Scholar]
- 2.Canaff L, et al. Extracellular calcium-sensing receptor is expressed in rat hepatocytes coupling to intracellular calcium mobilization and stimulation of bile flow. Journal of Biological Chemistry. 2001;276(6):4070–4079. doi: 10.1074/jbc.M009317200. [DOI] [PubMed] [Google Scholar]
- 3.McConkey DJ, Orrenius S. The role of calcium in the regulation of apoptosis. Biochemical and biophysical research communications. 1997;239(2):357–366. doi: 10.1006/bbrc.1997.7409. [DOI] [PubMed] [Google Scholar]
- 4.Kruglov EA, et al. Type 2 inositol 1, 4, 5-trisphosphate receptor modulates bile salt export pump activity in rat hepatocytes. Hepatology. 2011;54(5):1790–1799. doi: 10.1002/hep.24548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Woods NM, et al. Repetitive transient rises in cytoplasmic free calcium in hormone-stimulated hepatocytes. Nature. 1986;319:600–602. doi: 10.1038/319600a0. [DOI] [PubMed] [Google Scholar]
- 6.Woods NM, et al. Agonist-induced oscillations in cytoplasmic free calcium concentration in single rat hepatocytes. Cell calcium. 1987;8(1):79–100. doi: 10.1016/0143-4160(87)90038-8. [DOI] [PubMed] [Google Scholar]
- 7.Serradeil-Le Gal C, et al. Endothelin action in rat liver. Receptors, free Ca2+ oscillations, and activation of glycogenolysis. Journal of Clinical Investigation. 1991;87(1):133. doi: 10.1172/JCI114962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Robb-Gaspers LD, et al. Coordination of Ca2+ signaling by intercellular propagation of Ca2+ waves in the intact liver. Journal of Biological Chemistry. 1995;270(14):8102–8107. doi: 10.1074/jbc.270.14.8102. [DOI] [PubMed] [Google Scholar]
- 9.Dolmetsch RE, et al. Calcium oscillations increase the efficiency and specificity of gene expression. Nature. 1998;392(6679):933–936. doi: 10.1038/31960. [DOI] [PubMed] [Google Scholar]
- 10.Tordjmann T, et al. Coordinated intercellular calcium waves induced by noradrenaline in rat hepatocytes: dual control by gap junction permeability and agonist. The EMBO Journal. 1997;16(17):5398–5407. doi: 10.1093/emboj/16.17.5398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Saez JC, et al. Hepatocyte gap junctions are permeable to the second messenger, inositol 1, 4, 5-trisphosphate, and to calcium ions. Proceedings of the National Academy of Sciences. 1989;86(8):2708–2712. doi: 10.1073/pnas.86.8.2708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schlosser SF, et al. Isolated rat hepatocytes can signal to other hepatocytes and bile duct cells by release of nucleotides. Proceedings of the National Academy of Sciences. 1996;93(18):9948–9953. doi: 10.1073/pnas.93.18.9948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Thomas AP, et al. Spatial and temporal aspects of cellular calcium signaling. The FASEB Journal. 1996;10(13):1505–1517. [PubMed] [Google Scholar]
- 14.Nathanson MH, et al. Ca2+ waves are organized among hepatocytes in the intact organ. American Journal of Physiology-Gastrointestinal and Liver Physiology. 1995;269(1):G167–G171. doi: 10.1152/ajpgi.1995.269.1.G167. [DOI] [PubMed] [Google Scholar]
- 15.Jungermann K. Metabolic zonation of liver parenchyma: significance for the regulation of glycogen metabolism, gluconeogenesis, and glycolysis. Diabetes/metabolism reviews. 1987;3(1):269–293. doi: 10.1002/dmr.5610030112. [DOI] [PubMed] [Google Scholar]
- 16.Gebhardt R, Mecke D. Heterogeneous distribution of glutamine synthetase among rat liver parenchymal cells in situ and in primary culture. The EMBO journal. 1983;2(4):567. doi: 10.1002/j.1460-2075.1983.tb01464.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Meyer T, Stryer L. Calcium spiking. Annual review of biophysics and biophysical chemistry. 1991;20(1):153–174. doi: 10.1146/annurev.bb.20.060191.001101. BIOMD0000000224. [DOI] [PubMed] [Google Scholar]
- 18.Chelliah V, et al. BioModels: ten-year anniversary. Nucleic acids research. 2014 doi: 10.1093/nar/gku1181. gku1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kumar NM, Gilula NB. Cloning and characterization of human and rat liver cDNAs coding for a gap junction protein. The Journal of cell biology. 1986;103(3):767–776. doi: 10.1083/jcb.103.3.767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sakamoto H, et al. Differential changes in expression of gap junction proteins connexin 26 and 32 during hepatocarcinogenesis in rats. Japanese journal of cancer research. 1992;83(11):1210–1215. doi: 10.1111/j.1349-7006.1992.tb02747.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Niessen H, et al. Selective permeability of different connexin channels to the second messenger inositol 1, 4, 5-trisphosphate. Journal of Cell Science. 2000;113(8):1365–1372. doi: 10.1242/jcs.113.8.1365. [DOI] [PubMed] [Google Scholar]
- 22.Vanderheyden V, et al. Regulation of inositol 1, 4, 5-trisphosphate-induced Ca 2+ release by reversible phosphorylation and dephosphorylation. Biochimica et Biophysica Acta (BBA)-Molecular Cell Research. 2009;1793(6):959–970. doi: 10.1016/j.bbamcr.2008.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pierobon N, et al. Ryanodine receptors in liver. Journal of Biological Chemistry. 2006;281(45):34086–34095. doi: 10.1074/jbc.M607788200. [DOI] [PubMed] [Google Scholar]
- 24.Jones Bertina F, et al. Calcium influx mechanisms underlying calcium oscillations in rat hepatocytes. Hepatology. 2008;48(4):1273–1281. doi: 10.1002/hep.22461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Thore S, et al. Feedback activation of phospholipase C via intracellular mobilization and store-operated influx of Ca2+ in insulin-secreting β-cells. Journal of cell science. 2005;118(19):4463–4471. doi: 10.1242/jcs.02577. [DOI] [PubMed] [Google Scholar]
- 26.Finch EA, et al. Calcium as a coagonist of inositol 1, 4, 5-trisphosphate-induced calcium release. Science. 1991;252(5004):443–446. doi: 10.1126/science.2017683. [DOI] [PubMed] [Google Scholar]
- 27.Höfer T. Model of intercellular calcium oscillations in hepatocytes: synchronization of heterogeneous cells. Biophysical journal. 1999;77(3):1244–1256. doi: 10.1016/S0006-3495(99)76976-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Swann Karl, Whitaker Michael. The part played by inositol trisphosphate and calcium in the propagation of the fertilization wave in sea urchin eggs. The Journal of cell biology. 1986;103(6):2333–2342. doi: 10.1083/jcb.103.6.2333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tordjmann T, et al. Receptor-oriented intercellular calcium waves evoked by vasopressin in rat hepatocytes. The EMBO journal. 1998;17(16):4695–4703. doi: 10.1093/emboj/17.16.4695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Benhamouche S, et al. Apc tumor suppressor gene is the “zonation-keeper” of mouse liver. Developmental cell. 2006;10(6):759–770. doi: 10.1016/j.devcel.2006.03.015. [DOI] [PubMed] [Google Scholar]
- 31.Serrière V, et al. Vasopressin receptor distribution in the liver controls calcium wave propagation and bile flow. The FASEB Journal. 2001;15(8):1484–1486. doi: 10.1096/fj.00-0659fje. [DOI] [PubMed] [Google Scholar]
- 32.Braeuning A, et al. Differential gene expression in periportal and perivenous mouse hepatocytes. FEBS Journal. 2006;273(22):5051–5061. doi: 10.1111/j.1742-4658.2006.05503.x. [DOI] [PubMed] [Google Scholar]
- 33.Lynch CJ, et al. The relationships between receptor binding capacity for norepinephrine, angiotensin II, and vasopressin and release of inositol trisphosphate, Ca2+ mobilization, and phosphorylase activation in rat liver. Molecular pharmacology. 1985;28(2):93–99. [PubMed] [Google Scholar]
- 34.Motoyama K, et al. Effect of Ca2+ agonists in the perfused liver: determination via laser scanning confocal microscopy. American Journal of Physiology-Regulatory, Integrative and Comparative Physiology. 1999;276(2):R575–R585. doi: 10.1152/ajpregu.1999.276.2.R575. [DOI] [PubMed] [Google Scholar]
- 35.Nathanson MH, Burgstahler AD. Coordination of hormone-induced calcium signals in isolated rat hepatocyte couplets: demonstration with confocal microscopy. Molecular biology of the cell. 1992;3(1):113–121. doi: 10.1091/mbc.3.1.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hammad S, et al. Protocols for staining of bile canalicular and sinusoidal networks of human, mouse and pig livers, three-dimensional reconstruction and quantification of tissue microarchitecture by image processing and analysis. Archives of toxicology. 2014;88(5):1161–1183. doi: 10.1007/s00204-014-1243-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Drasdo D, et al. How predictive quantitative modelling of tissue organisation can inform liver disease pathogenesis. Journal of hepatology. 2014;61(4):951–956. doi: 10.1016/j.jhep.2014.06.013. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.