Abstract
Breaking signals of secondary structure put strong limitations on the tertiary structures of proteins. In addition to proline and glycine clusters, which are well-known secondary structure breakers, clusters of amphiphilic residues were found to be a novel type of secondary structure breaker. These secondary structure breakers were found to depend on specific environmental factors. Such conditions included the average hydrophobicity, the helical periodicity, the density of serine and threonine residues, and the presence of tryptophan and tyrosine clusters. Principal component analysis of environmental factors was conducted in order to identify candidate breakers in the secondary structure breaking regions. Predicted breakers were located in breaking regions with an accuracy of 72%. Taking the loop core into consideration, almost 90% of the predicted breakers were located in the loop segments. When the migration effect of the breaking point was taken into account, the loop segments with the predicted breakers covered two thirds of all loop segments. Herein, the possibility of secondary structure prediction based on secondary structure breakers is discussed. The system of the present method is available at the URL: http://bp.nuap.nagoya-u.ac.jp/sosui/sosuibreaker/sosuibreaker_submit.html.
Keywords: secondary structure, secondary structure breaker, soluble proteins, structure prediction, amphiphilicity
The amino acid sequences of proteins contain various signals for structural stability and function. Membrane proteins have clear signals for helical structures. These signals are characterized by a cluster of hydrophobic residues sandwiched between clusters of amphiphilic residues1,2. However, the distinct physicochemical signals for secondary structures in soluble proteins remain unclear. Therefore, despite a long history of investigation, the accuracy of secondary structure prediction is not sufficiently high3. Chou and Fasman4 developed a very simple method that attained an accuracy of prediction above 50%. However, currently the accuracy of prediction remains below 80%, even after the modern introduction of information technologies3,5.
In contrast, very clear signals for secondary structure breakers have been established. These signals include the presence of proline residues, glycine residues, or clusters of a combination of proline and glycine residues4,6. In fact, most proline and glycine residues are located at the termini of secondary structures or within loop segments. However, the reason that the secondary structures are broken differs for proline and glycine residues; proline is structurally too rigid to be incorporated into a local ordered structure, whereas glycine is so flexible that the entropy effect drives a structural change from a defined secondary structure to a loop.
Recently, intrinsically disordered segments in proteins have been reported to have important functions in molecular recognition and regulation7–10. Dunker et al. developed a model to predict the disordered regions on the basis of the likelihood that specific amino acids are present in ordered and disordered segments7. The amino acid composition profiles of the disordered regions revealed that proline and glycine enhance the occurrence of disordered structures. In addition to these residues, amino acids with amphiphilic side chains having both a polar group and a flexible hydrocarbon (arginine, lysine, histidine, glutamic acid, and glutamine)11 were more likely to be present in disordered regions7,8.
Previously, these amphiphilic residues were determined to commonly exist at the terminal regions of transmembrane helices. The combination of high hydrophobicity at the center and high amphiphilicity in the neighboring regions led to an accurate model for the prediction of transmembrane helices1,2. The amino acid composition profiles of disordered regions in soluble proteins, together with those at the terminal regions in membrane proteins, strongly suggest that clusters of amphiphilic residues generally correlate with breaking points for secondary structures. Specifically, amphiphilic amino acids are thought to be a new type of secondary structure breaker. However, some of these residues are also abundant in the secondary structure regions of soluble proteins. Glutamic acid, for example, is frequently found in helical regions4,6. These apparently contradictory observations may be reconciled by the idea that the local structures are determined not only by the intrinsic properties of amino acids, but also by their interaction with their environment.
Herein, the distribution of the amphiphilicity together with proline and glycine clusters in the amino acid sequences of soluble proteins was examined in order to determine the environment that drives the formation of a segment loop. Proline clusters were determined to occur mostly in the loop segments. However, regions of high amphiphilicity were found both in the loops and the secondary structures. The glycine clusters showed an intermediate distribution between the proline clusters and amphiphilic peaks; many glycine residues are located in the loop segments, however the existence of glycine residues in the secondary structure regions cannot be neglected. The amphiphilic peaks in the loop segments exhibited lower helical periodicity and a higher density of serine and threonine than those in the secondary structure regions. The same trend was also observed for glycine clusters. This finding indicates that the amphiphilic peaks and glycine clusters are significant in breaking secondary structures, however, several other environmental factors are necessary to determine the fate of the clusters. Principal component analysis of several environmental factors was performed in order to discriminate potential breakers in loop segments from secondary structure regions. Finally, the possibility of creating a novel algorithm for secondary structure prediction based on information about the presence and location of secondary structure breakers is discussed.
Principle of determining secondary structure breakers
Proline and glycine are known secondary structure breakers4,6. However, the molecular structures of several proteins have revealed that the presence of numerous glycine residues in the central region of secondary structures does not break the secondary structures. Further, this trend was also observed in some cases for proline residues. This indicates that the final structure is determined by a combination of numerous factors. The environmental factors in amino acid sequences, such as the average hydrophobicity and helical periodicity, also contribute to local disordered structures.
In order to identify secondary structure breakers, three main features were first evaluated: the presence of proline, the presence of glycine, and the peak of the amphiphilicity index. The amphiphilicity index was previously defined for the development of a membrane protein prediction system, SOSUI1,11. Finite amphiphilicity index values were calculated for lysine (3.67), arginine (2.45), histidine (1.45), glutamic acid (1.27), glutamine (1.25), tryptophan (6.93), and tyrosine (5.06). The amphiphilicity index was determined as the transfer energy of the hydrophobic stem group based on accessible surface. The first five residues bear very polar side chains, whereas the last two residues are only weakly polar. The amphiphilicity index for strongly polar residues was named the A-index, and that for weakly polar residues was named the A′-index. The seven residues listed above are abundant in the end-regions of transmembrane helices, indicating that they break the secondary structures of membrane proteins1,2,11. Recent analysis by Dunker et al. also revealed that the amino acid composition of disordered regions contains many amphiphilic side chains, bearing both a polar group and a flexible hydrocarbon7,8. The three features evaluated result in similar structural features in proteins, namely, breakage of the secondary structure. However, the features function to break the secondary structures in different ways. Proline is too rigid and glycine is too flexible to be incorporated into the secondary structure. Finally, the peak of amphiphilicity index has a strong preference to be located at the interface between the aqueous phase and nonpolar moieties, and the segments on both sides of the amphiphilic segment are nonpolar moieties of the protein, breaking the secondary structure.
Herein, the three primary features of secondary structure breakers, as well as the environmental factors involved in secondary structure breakers were evaluated in three steps. First, the potential breakers were enumerated according to the peaks of the main features. Next, the potential breakers were classified into several categories according to the position relative to the termini of the secondary structures. Finally, an average of the environmental factors in several regions was compared, and a discrimination function for the secondary structure breakers was determined by primary component analysis. Results of this analysis revealed the predicted secondary structure breakers.
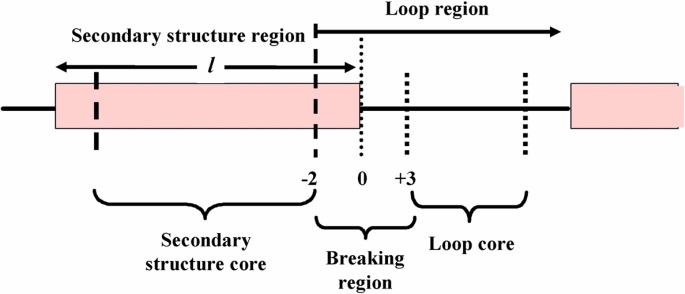
Three regions around the termini of secondary structures were defined for statistical analysis of the main features in the first step; the breaking region, the secondary structure core, and the loop core (Fig. 1). The breaking region is defined in this work by six residues containing the three terminal residues of the secondary structure or the three terminal residues of a loop. Branching of the same potential breakers to different local structures is thought to be due to the different environmental conditions present in the amino acid sequence. Therefore, all potential breakers were classified into the three regions and the difference in the environments of the potential breakers was investigated.
Figure 1.
Definition of secondary structure core, breaking region, and loop core for statistical analysis of various amino acids.
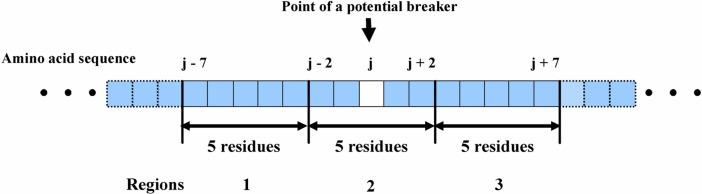
In order to reveal the difference between the potential breakers in the breaking regions and those in the secondary structure core, a segment around a potential breaker numerated according to the primary features was divided into three regions with a fixed length of five residues (Fig. 2). Then, the averages of various physicochemical parameters in the three regions in Figure 2 were calculated for both the potential breakers in the breaker regions (true data) and those in the secondary structure core (false data). A number of physicochemical properties may contribute to the environmental conditions around the breaking point of secondary structures. Approximately ten types of physicochemical parameters were investigated. Four of these parameters that were selected were found to be different between the true and false data: the average hydrophobicity, the helical periodicity score, the density of small polar residues, and the average A′-index (defined in the Methods). Because these parameters have their own physical meanings, the results of analysis reveal which property supports or hampers the local structures. Moreover, the difference in the environmental parameters may be used to predict secondary structure breakers. The similarity in the profiles of the environmental factors around the potential breakers with the typical profiles of real breakers became a good score to predict the true secondary structure breakers based solely on amino acid sequences.
Figure 2.
Three regions around a potential breaker with a length of five residues used for analysis of environmental factors.
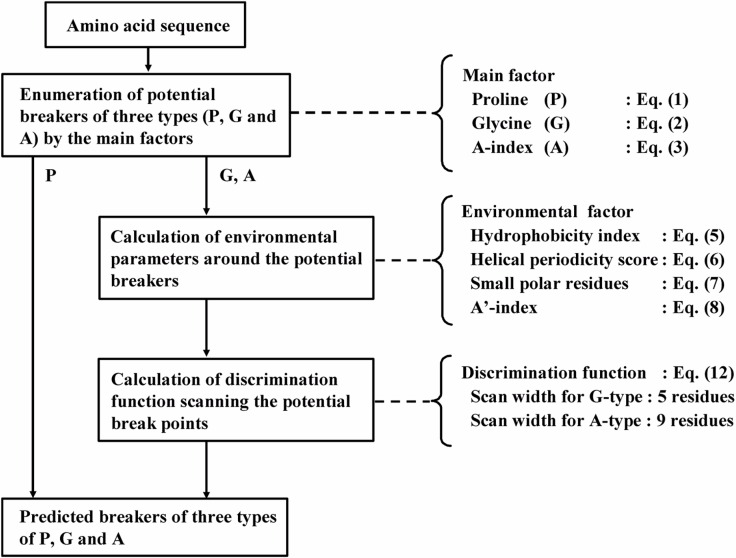
In order to obtain the best fit of the profiles for the potential breakers with typical breakers, the position of the potential breakers was scanned for several residues: 5 residues for glycine clusters and 9 residues for amphiphilic residues. This final step of the prediction improved its accuracy by several percent. A flow chart of prediction of secondary structure breakers is shown in Figure 3, in which the equations for the parameters and a discrimination function given in the next section are related to the corresponding processes.
Figure 3.
Flow chart of prediction of secondary structure breakers.
Methods
Physicochemical parameters for discrimination
The parameters representing the primary features of secondary structure breakers were defined by the following equations (1)–(3).
| (1) |
| (2) |
where P(i) and G(i) indicate the existence of proline and glycine, respectively. A value of one for P(i) represents the existence, and a value of zero represents the absence of proline at the i-th residue. G(i) represents the corresponding parameter for glycine.
| (3) |
| (4) |
where <<A(k)>> is the double average of the amphiphilicity index, A(i). A moving average was calculated in order to smooth the graphs, however, plots of the single average of amphiphilicity <A(j)> remained irregular. Therefore, the double average of the amphiphilicity index was calculated in order to identify significantly large peaks. The A′-index was not used to evaluate the three primary features of secondary structure beakers, but was used to evaluate the environmental factors. The maxima values obtained for the three parameters, <P(j)>, <G(j)>, and <<A(k)>>, were identified as candidates for secondary structure breakers. The thresholds for <P(j)> and <G(j)> were zero and that for <<A(k)>> was 0.4.
The parameters used to evaluate the environmental factors include; the average hydrophobicity index <H(j)>, the helical periodicity score <HPS (j)>, the density of small polar residues <ST(j)>, and the average A′-index <A′(j)> which are given in the following equations.
| (5) |
| (6) |
where <HP(j)> = [H(j+5)−H(j+3)+H(j+1)−H(j)+H(j−2) − H(j − 4)]/5. This score, introduced for the first time in this work, is a very simple index, but effectively represents the α-helical periodicity. The hydropathy index, H(i), was developed by Kyte and Doolittle12. The density of small polar residues <ST(j)> and the average A′-index <A′(j)> are defined by equations 7 and 8, respectively.
| (7) |
| (8) |
where ST(i) represents the existence of small polar residues (serine or threonine) and A′(i) is the amphiphilicity index for weakly polar aromatic residues (tryptophan and tyrosine).
Dataset of secondary structures, loops, and breaking regions
In an effort to develop a method to discriminate the secondary structure breakers, amino acid sequences for proteins with known tertiary structures were collected. Data for the four differenttypes ofproteinfolds were selected from the SCOP database, including 239 datasets for all-α-proteins, 249 for all-β-proteins, 251 for α/β proteins, and 292 for α+β proteins. Sequences with greater than 30% homology were eliminated. The total number of sequences was 1,031.
As shown in Figure 1, the breaking region of secondary structures was defined by six residues at the end of a secondary structure. Therefore, a secondary structure region is composed of a secondary structure core and two breaking regions. Similarly, a loop region is composed of two breaking regions and a loop core, assuming the loop is long enough. A total of 11,600 secondary structure regions were obtained from 1,031 amino acid sequences. However, because short secondary structures have properties similar to loop regions, secondary structure regions longer than or equal to seven residues were used for the analyses, resulting in a total of 5,657 secondary structure regions. There were 5,943 secondary structures present that were shorter than seven residues. Further, a total of 3,932 α-helix regions and 1,725 β-sheet regions were present. A total of 8,731 loop regions, containing both N- and C-terminal regions, were present. However, some loop regions located between short secondary structure regions were omitted. Hence, the total number of breaking regions was 11,314, which is twice the number of secondary structures. It is important to note that many loop regions were shorter than six residues. Therefore, there were fewer loop cores (2,425 total) than loop regions. These results are summarized in Table 1.
Table 1.
Numbers of regions obtained from the tertiary structures of 1031 proteins
| Regions | Number | |
|---|---|---|
| Secondary structure | l ≤ 6 | 5943 |
| l ≥ 7 | 5657 | |
| α-helix | 3932 | |
| β-sheet | 1725 | |
|
| ||
| Loop region | Loop region | 8731 |
| Breaking region | 11314 | |
| Loop core | 2425 |
Primary component analysis of environmental parameters
In the current work, four environmental parameters were evaluated in order to identify true breakers; <H(l)>, <HPS(l)>, <ST(l)>, and <A′(l)>. The parameter l defines the position of a potential breaker in the amino acid sequence. Hereafter, these parameter are defined as zk(l) (k = 1, 2, 3, 4) for convenience of simple formulation, where z1(l) = <H(l)>, z2(l) = <HPS (l)>, z3(l) = <ST(l)>, and z4(l) = <A′(l)>. We hypothesized that a local structure is influenced by the environmental properties of its neighboring regions. Further, we assumed that three regions with a length of five residues constitute the environment of a secondary structure breaker. The three regions are numbered from 1 to 3, and expressed in the properties by the superscript i in . The center of the second region was set to the position of a potential breaker. The environmental segments were divided into three regions, because at least three regions (the secondary core, the breaking region and the loop core) are necessary in order to characterize the breaking points.
The basis of the discrimination is the difference in the environmental properties of the true and false potential breakers. The average values of property k at region i are calculated for true data as well as for false data .
| (9) |
| (10) |
where M and N represent the total number of true and false data, respectively.
Next, the deviation Δzk(l), weighted by the average difference between the true and false data, was calculated for a potential breaker at position l.
| (11) |
Finally, a set of deviations {Δz1(l), Δz2(l), Δz3(l), Δz4(l)} was defined as the environment of a potential secondary structure breaker. Primary component analysis was carried out for the discrimination of two categories of data: potential breakers in the breaking region and those in the secondary structure core. This resulted in the coefficients ak (k=0, 1, 2, 3, 4) for the discrimination score S(l).
| (12) |
Results
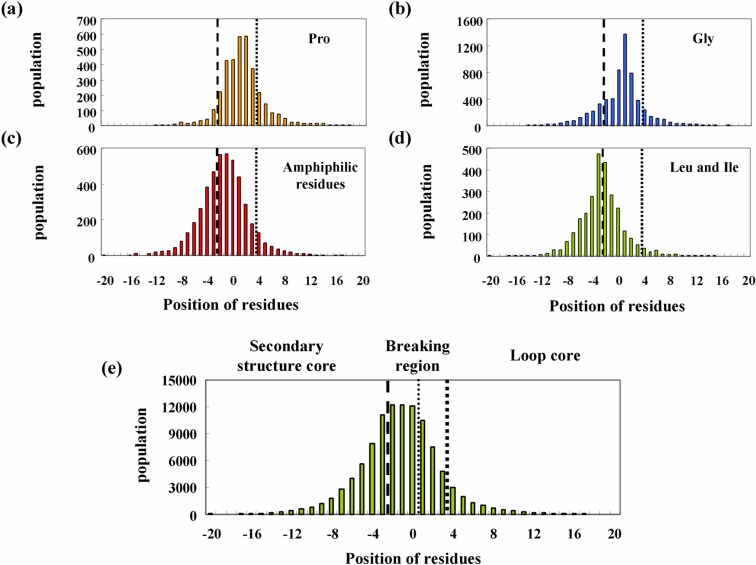
Proline and glycine are well-known secondary structure breakers4,6. Furthermore, amphiphilic residues are known to form clusters at disordered regions of soluble proteins7,8 as well as at the ends of transmembrane helices1,2,11. Figures 4a, 4b, and 4c show histograms of the locations of proline, glycine, and clusters of amphiphilic residues around the termini of secondary structures, respectively. The histograms of hydrophobic residues, leucine and isoleucine, and all residues are shown in Figures 4d and 4e as control data. As can be seen in the figures, all histograms have a bell shape. The histogram showing all of the residues is related to the length of the secondary structures and the loop regions. Analysis was only conducted on secondary structures longer than seven residues. Further, a residue was counted only once at the terminal position of the nearest secondary structure. Therefore, the number of all residues at positions −2 to 0 was constant at 11,314. The number of residues was observed to gradually decrease on the negative side beyond position −3, according to the length distribution of the secondary structures, and on the positive side depending on the length distribution of the loop regions.
Figure 4.
Histograms of four types of amino acid clusters as a function of position relative to termini of secondary structures: proline (a), glycine (b), amphiphilic residues (c), and leucine and isoleucine (d). A histogram of all residues is also plotted as a control (e).
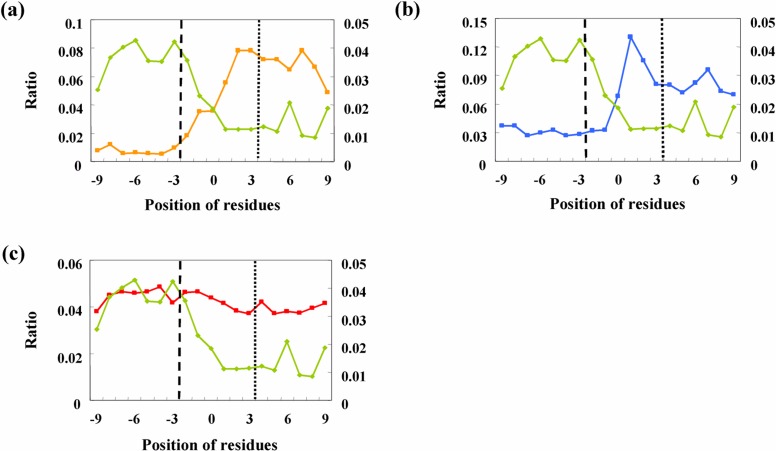
The maximum number of proline and glycine residues in the histograms is located in the loop region, whereas that of leucine and isoleucine is located in the secondary structure core. The shape of the histogram of amphiphilic residues is very similar to that for all of the residues. The histograms of various amino acids are determined by two factors: the histogram of all residues and the ratio for a type of amino acid at all positions. Figures 5a–c show the ratios of four types of amino acids at every position. These values were calculated by dividing the number of a type of amino acid by the total number of residues. As a control for secondary structure breakers, the ratio of leucine and isoleucine in all three graphs for proline (Fig. 5a), glycine (Fig. 5b), and the amphiphilic residues (Fig. 5c) was plotted. The ordinate on the right side indicates the ratio of leucine and isoleucine.
Figure 5.
Ratio of number of amino acid clusters to that of all amino acid residues: proline (a), glycine (b), and amphiphilic residues (c). The plot for leucine and isoleucine is shown in all graphs for comparison with potential breakers.
The ratios were almost constant in the region of the secondary structure core and the loop core. Moreover, transitions were observed only in the breaking regions. The ratios of typical breakers, proline and glycine, were observed to suddenly increase in the breaking region, whereas the ratio of leucine and isoleucine decreased like a mirror image of the plot for proline. The results shown in Figure 5a indicate that almost all proline residues are in the loop region, including the loop core and the breaking regions. Further, leucine and isoleucine residues were localized primarily in the secondary structure regions. The level of proline in the secondary structure core was less than 10% of that in the loop core. This indicates that proline is a good secondary structure breaker.
Figures 5b and 5c show plots of the ratio of glycine and amphiphilic residues to all residues, respectively. The plot for glycine is similar to that for proline. However, the ratio of glycine in the secondary structure core was about 30% of that localized in the loop core. This value is significantly larger than the corresponding value for proline (<10%). A similar trend is also observable for amphiphilic peaks. The plot of the ratio for the amphiphilic peaks in Figure 5c shows that the level in the secondary structure core region is as high as that in the loop core region. These observations indicate that the existence of glycine clusters and amphiphilic peaks in an amino acid sequence is not crucial for the breakage of the secondary structure. Branching of these residues into the secondary structure and loop regions is an important problem involved in predicting secondary structure breakers. The mechanism for branching is thought to be that glycine clusters and amphiphilic peaks act to trigger the secondary structure breakers, but the final structures may be α-helices or β-sheets, depending on the physicochemical properties of the surrounding regions. Thus, the physicochemical environments of amino acid segments within 15 residues of glycine clusters and amphiphilic peaks were evaluated using the primary component analysis method.
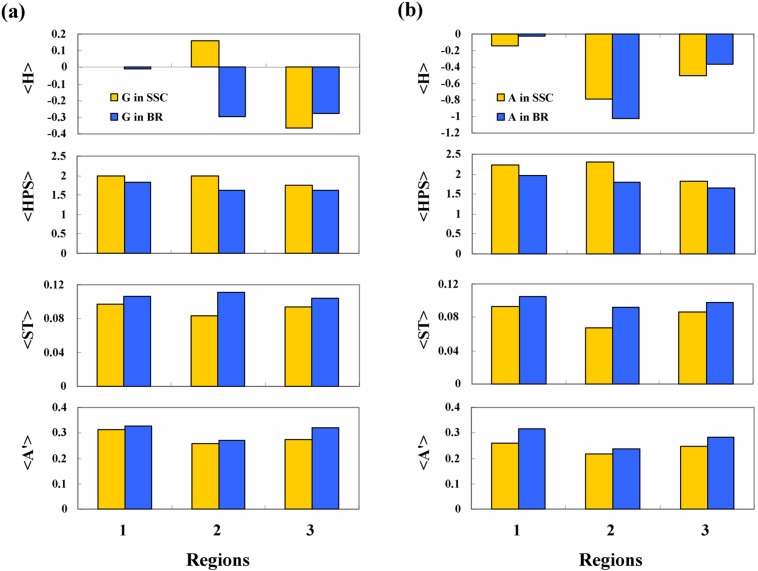
The averages of the four physicochemical properties surrounding the potential breakers were plotted in histograms for glycine residues (Fig. 6a) and amphiphilic clusters (Fig. 6b).The propertiesare averaged over alldataineach dataset, therefore, a general trend can be obtained from the histograms. The hydrophobicity of the segments surrounding the potential breakers in the breaking region is lower than in the secondary structure core. Similarly, the helical periodicity in the breaking region is lower than that in the secondary structure core. These statistical trends seem physically reasonable. Because most disordered segments stick to the outside of proteins, the hydrophobicity of disordered segments must be low in order to have an affinity for water, and the periodicity due to the local order in the secondary structure region is lost in the loop region. The small polar residues, serine and threonine, are found with higher frequency in the breaking region than in the secondary structure core. This type of residue is thought to have the same effect as glycine, because of the small size of the side chains. Further, bulky amino acids with polar groups, such as tryptophan and tyrosine, are also more abundant in the breaking region. The bulkiness of the side chain may hinder ordering of the structure due to an excluded volume effect.
Figure 6.
Levels of averages of four kinds of properties, <H(l)>, <HPS(l)>, <ST(l)>, and <A′(l)>, in three regions were compared between potential breakers in secondary structure core (SSC) and breaking regions (BR). The potential breakers glycine (a) and amphiphilic peaks (b) showed similar patterns despite average hydrophobicity.
The difference in the four properties is not large, however, a combination of these effects may lead to accurate identification of secondary structure breakers. Computational analysis was conducted by calculating the deviations using equation (11) for all data, including the true breakers in the breaking regions and the false potential breakers in the secondary structure core. Primary component analysis of the deviations was also conducted so that the true and false data could be accurately discriminated. The coefficients of the discrimination score were as follows: a1= 2.01, a2= 1.90, a3= 32.9, a4= 5.30, and a0=−0.68 for glycine breakers; and a1= 3.15, a2= 1.36, a3= 42.5, a4= 2.40, and a0=−1.71 for amphiphilic peak breakers. Coefficient a3 for the index of small polar residues <ST> is larger than the other coefficients by an order of magnitude. This apparent difference is due to the small deviation in <ST>, as shown in Figure 6. The contribution of the parameters to the discrimination functions may be easily estimated by multiplying the coefficient by the deviation of the parameters. The contributions of <H>, <HPS> and <ST> were observed to be almost the same. Only the index for tyrosine and tryptophan exhibited a smaller contribution. These findings for primary component analysis seem reasonable: the hydrophobic core of a protein with high hydrophobicity <H> is generally formed by secondary structures, and the helical structure at the interface region shows high periodicity <HPS>. Small polar residues give high flexibility and polarity to polypeptides, which tend to break the secondary structures. These correlations between the deviations of parameters and the secondary structure forming tendencies result in a high accuracy of discrimination.
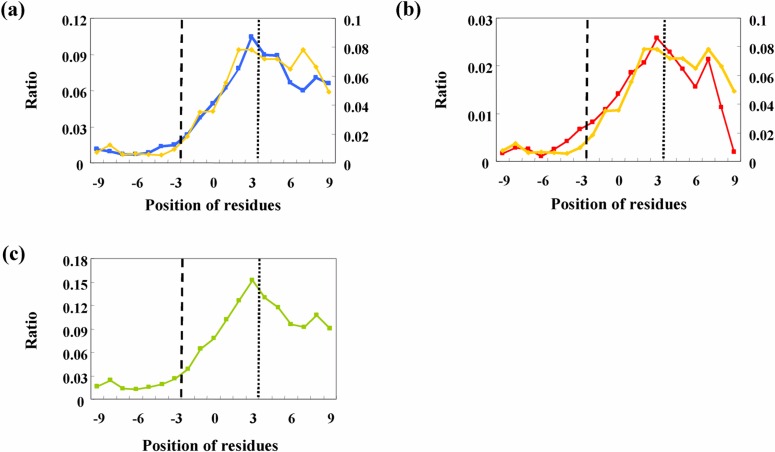
Results of the discrimination of potential breakers are shown in Figure 7. A profile of the ratio of proline around the termini of the secondary structure is plotted as the standard profile of the breaker. The profiles of both glycine and amphiphilic peaks after discrimination in Figures 7a and 7b are very similar to that of proline, strongly suggesting that the effect of the environmental parameters are substantial for the final local structures. The profile of unified secondary structure breakers is plotted in Figure 7c. Approximately 10% of all residues at each position in the loop region have the activity to break the secondary structure.
Figure 7.
Ratio of the number of predicted secondary structure breakers to that of all amino acid residues after discrimination by primary component analysis: glycine (a) and amphiphilic residues (b). The plot for proline is shown in both graphs. A combination of the three types of predicted breakers is also plotted (c).
The accuracy of discrimination using this method is summarized in Tables 2a and 2b. Table 2a shows the statistics for the three regions. Half of the breaking regions and the loop cores contain the predicted breakers, however, the potential breakers in the secondary structure core represent only 10% of the total. A number of very short loops exist; therefore, 739 predicted breakers in the breaking regions in Table 2a are double-counted. However, the definition of the breaking regions for very short loops should have been changed so that two breaking regions are merged into a single breaking region. This does not change the ratio of predicted breakers to the breaking regions significantly.
Table 2.
Numbers and ratios of loop region and secondary structure core containing predicted secondary structure breakers (a); and numbers and accuracy of predicted breakers in loop region, breaking region, and secondary structure core (b)
| (a) | |||||
|
| |||||
| Regions | Total number | Number of regions with predicted breakers | Ratio | ||
|
| |||||
| Loop region | 8731 | 5774 | 0.66 | ||
| Breaking region | 11314 | 5699 | 0.50 | ||
| Loop core | 2425 | 1282 | 0.53 | ||
| Secondary structure core | 5657 | 626 | 0.11 | ||
|
| |||||
| (b) | |||||
|
| |||||
| P | G | A | PGA | Accuracy of prediction (%) | |
|
| |||||
| Total predicted breakers | 3619 | 3937 | 1197 | 6841 | – |
| Loop region | 3343 | 3578 | 1047 | 6110 | 89.3 |
| Breaking region | 2622 | 2871 | 875 | 4960 | 72.5 |
| Loop core | 721 | 707 | 172 | 1150 | 16.8 |
| Secondary structure core | 276 | 395 | 150 | 731 | 10.7 |
Table 2b shows the statistics for predicted breakers. Three-fourths of the predicted breakers are actually located in the breaking region, and 90% are located in the loop region containing the loop core region. The secondary structure breakers exist in the loop core region with almost the same ratio as in the breaking region. However, as many as 72% of predicted breakers are located in the breaking region. On the other hand, the loop core contains only 17% of predicted breakers. This is because there are significantly fewer long loops with loop cores than short loops. Therefore, the present method can actually discriminate the secondary structure breakers.
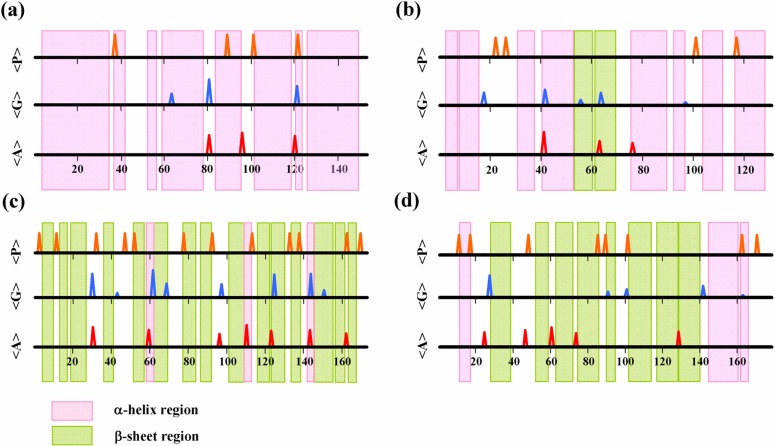
The present method is applicable to breakers of both α-helices and β-sheets. Figure 8 shows a number of examples. The results of all-α-type proteins, myoglobin (1a6m) and cytochrome-C552 (1c52), and all-β-type proteins, FC-γ RIIB ectodomain (2fcbA) and human neutrophil gelatinase (1dfvB) are shown in Figures 8a–d. The α-helices and the β-sheets are effectively terminated by the predicted breakers, irrespective of the types of folds.
Figure 8.
Predicted secondary structure breakers by proline, glycine, and amphiphilic peaks: (a) myoglobin 1a6m (all α-type); (b) cytochrome-C552 1c52 (all α-type); (c) FC-γ RIIB ectodomain 2fcbA (all β-type); (d) human neutrophil gelatinase 1dfvB (all β-type).
Discussion
Secondary structures are the most basic element of protein structures, therefore, secondary structure prediction is one of the most important technologies for protein engineering. However, because of the enormous variety of amino acid sequences that generate the same local structures, the physical mechanisms of secondary structure formation are not yet understood. Herein, the conditions for secondary structure breakers were investigated with a focus on clusters of proline, glycine, and amphiphilic residues.
Three key observations were made based on this investigation: (1) the same local structure, secondary structure breakers, is caused by more than three completely different mechanisms; (2) not only local, but also environmental sequences are important in order to determine the local structure; and (3) as far as the secondary structure breakers are concerned, a combination of several physicochemical properties of amino acid fragments is enough to determine the local structures.
The first observation is well known and indicates that completely different types of amino acids, namely proline and glycine, act as secondary structure breakers. In this work, a novel type of secondary structure breaker, amphiphilic residue clusters, was also identified. The first evidence that these could be breakers in soluble proteins resulted from an analysis of membrane proteins. Clusters of amphiphilic residues were found to stabilize the ends of transmembrane helices, and also to have the ability to break the secondary structure. These clusters of amphiphilic residues break transmembrane helices due to the strong preference of these residues for the aqueous phase. In the current work, amino acid sequences of soluble proteins were analyzed assuming that the amphiphilic residues therein had the same ability to act as breakers. This novel class of breaker covers only 12% of all loop segments (see Table 2). However, the strong preference for amphiphilic residues to lie at an interface with hydrophilic moieties determines the characteristics of this type of breaker and puts strong limitations on the tertiary structure of proteins. Furthermore, the mechanism for this class of breakers was found to differ from that for proline and glycine clusters. Proline is too rigid to be incorporated into a secondary structure, whereas glycine is so flexible that the local structure becomes unstable in a cluster. Proline and glycine residues do not have a preference for the interface with the aqueous phase; therefore, they can function as secondary structure breakers at any location in the tertiary protein structure. Although the proportion of amphiphilic clusters in the secondary structure breakers is small, they put more strain on molecular structures than other types of breakers.
The second observation, the importance of environmental factors, is not surprising, because a local structure interacts with and is stabilized by its neighboring segments. For an unknown protein, however, the tertiary structure of the neighboring segments is not known. Therefore, the effect of the environment on the local structures is not taken into consideration in typical secondary structure prediction methods. Herein, the properties of neighboring segments were considered the most important environment for a local structure. In fact, breaker candidates in the loop segments showed different levels of hydrophobicity and helical periodicity than those in secondary structures. Taking the differences in these environments into consideration enabled accurate prediction of secondary structure breakers.
The present method of sequence analysis differs from those typically employed in modern information technology. Coarse graining of physical properties, the essence of the third observation, is related to the robustness of the molecular structure to mutations during the process of evolution. If the local structure is determined by a combination of average values for various physicochemical properties, the allowance of mutations becomes very large, thus explaining the robustness of the tertiary structure against mutations of amino acid sequences.
However, three problems still remain to be solved. The first interesting problem is that the secondary structures are effectively terminated by the predicted breakers, irrespective of the types of folds. However, the cause of this observation remains unclear. The most plausible reason is that the positions of the breaks in the secondary structure are determined before the local structures are formed. Secondly, 66% of loop regions contain the predicted breakers, and the accuracy was as good as 90%. The mechanism of breaking the secondary structures in the remaining loop regions remains unclear. One possibility is that the entire tertiary structure of a protein facilitates breaking of the secondary structure. Another possibility is that when the secondary structure is predicted by an alternative method, additional termini may be predicted. The third problem that remains to be solved is prediction of secondary structure using the present approach. Current investigations in our laboratories involve the analysis of amino acid sequences for secondary structure prediction assuming more than one mechanism13–15, investigation of the effects of environmental sequences, and coarse graining of physical properties. The results of these analyses and a method for secondary structure prediction will be published elsewhere.
The system of the method for predicting secondary structure breakers is available at the URL: http://bp.nuap.nagoya-u.ac.jp/sosui/sosuibreaker/sosuibreaker_submit.html.
Acknowledgments
This work was supported in part by a Grant-in-Aid from the National Project on Protein Structural and Functional Analysis from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
References
- 1.Hirokawa T, Boon-Chieng S, Mitaku S. SOSUI: Classification and secondary structure prediction system for membrane proteins. Bioinformatics. 1998;14:378–379. doi: 10.1093/bioinformatics/14.4.378. [DOI] [PubMed] [Google Scholar]
- 2.Tsuji T, Mitaku S. Features of transmembrane helices useful for membrane protein prediction. CBIJ. 2004;4:110–120. [Google Scholar]
- 3.Rost B. Prediction in 1D: Secondary structure, membrane helices, and accessibility. Methods Biochem. Anal. 2003;44:559–587. [PubMed] [Google Scholar]
- 4.Chou PY, Fasman GD. Prediction of the secondary structure of proteins from their amino acid sequence. Adv. Enzymol. Relat. Areas Mol. Biol. 1978;47:45–148. doi: 10.1002/9780470122921.ch2. [DOI] [PubMed] [Google Scholar]
- 5.Huang JT, Wang MT. Secondary structural wobble: the limits of protein prediction accuracy. Biochem. Biophys. Res. Commun. 2002;294:621–625. doi: 10.1016/S0006-291X(02)00545-4. [DOI] [PubMed] [Google Scholar]
- 6.Levitt M. Conformational preferences of amino acids in globular proteins. Biochemistry. 1978;17:4277–4285. doi: 10.1021/bi00613a026. [DOI] [PubMed] [Google Scholar]
- 7.Dunker AK, Lawson JD, Brown CJ, Williams RM, Romero P, Oh JS, Oldfield CJ, Campen AM, Ratliff CM, Hipps KW, Ausio J, Nissen MS, Reeves R, Kang C, Kissinger CR, Bailey RW, Griswold MD, Chiu W, Garner EC, Obradovic Z. Intrinsically disordered protein. J. Mol. Graph. Model. 2001;19:26–59. doi: 10.1016/s1093-3263(00)00138-8. [DOI] [PubMed] [Google Scholar]
- 8.Dunker AK, Brown CJ, Lawson JD, Iakoucheva LM, Obradovic Z. Intrinsic disorder and protein function. Biochemistry. 2002;41:6573–6582. doi: 10.1021/bi012159+. [DOI] [PubMed] [Google Scholar]
- 9.Jones DT, Ward JJ. Prediction of disordered regions in proteins from position specific score matrices. Proteins. 2003;53:573–578. doi: 10.1002/prot.10528. [DOI] [PubMed] [Google Scholar]
- 10.Ward JJ, Sodhi JS, McGuffin LJ, Buxton BF, Jones DT. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004;337:635–645. doi: 10.1016/j.jmb.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 11.Mitaku S, Hirokawa T, Tsuji T. Amphiphilicity index of polar amino acids as an aid in the characterization of amino acid preference at membrane-water interfaces. Bioinformatics. 2002;18:608–616. doi: 10.1093/bioinformatics/18.4.608. [DOI] [PubMed] [Google Scholar]
- 12.Kyte J, Doolittle RF. A simple method for displaying the hydropathic character of a protein. J. Mol. Biol. 1982;157:105–132. doi: 10.1016/0022-2836(82)90515-0. [DOI] [PubMed] [Google Scholar]
- 13.Mitaku S, Hoshi S, Kataoka J. Spectral analysis of amino acid sequence. II. Characterization of α-helices by local periodicity. J. Phys. Soc. Jpn. 1985;54:2047–2054. [Google Scholar]
- 14.Mitaku S, Hirokawa T. Physicochemical factors for discriminating between soluble and membrane proteins: hydrophobicity of helical segments and protein length. Protein Eng. 1999;12:953–957. doi: 10.1093/protein/12.11.953. [DOI] [PubMed] [Google Scholar]
- 15.Uchikoga N, Takahashi S, Ke R, Sonoyama M, Mitaku S. Electric charge balance mechanism of extended soluble proteins. Protein Sci. 2005;14:74–80. doi: 10.1110/ps.04984505. [DOI] [PMC free article] [PubMed] [Google Scholar]