Transparallel processing by hyperstrings

Abstract

Human vision research aims at understanding the brain processes that enable us to see the world as a structured whole consisting of separate objects. To explain how humans organize a visual pattern, structural information theory starts from the idea that our visual system prefers the organization with the simplest descriptive code, that is, the code that captures a maximum of visual regularity. Empirically, structural information theory gained support from psychological data on a wide variety of perceptual phenomena, but theoretically, the computation of guaranteed simplest codes remained a troubling problem. Here, the graph-theoretical concept of “hyperstrings” is presented as a key to the solution of this problem. A hyperstring is a distributed data structure that allows a search for regularity in O(2^N) strings as if only one string of length N were concerned. Thereby, hyperstrings enable transparallel processing, a previously uncharacterized form of processing that might also be a form of cognitive processing.

In the 1960s, Leeuwenberg (1) initiated structural information theory (SIT), which is a theory that aims at explaining how humans perceive visual patterns. A visual pattern can always be interpreted in many different ways, and SIT starts from the idea that the human visual system has a preference for the interpretation with the simplest descriptive code. In the 1950s, this idea had been proposed by Hochberg and McAlister (2), with an eye on Shannon's work (3) as well as on early 20th century Gestalt psychology (ref. 4; see also ref. 5). To this idea, SIT adds a concrete visual coding language (see below), thus specifying the search space within which the simplest codes are to be found.

In interaction with empirical research, SIT developed into a competitive theory of visual structure. Leeuwenberg et al. (6–18) applied SIT to explain a variety of perceptual phenomena such as judged pattern complexity, pattern classification, neon effects, judged temporal order, assimilation and contrast, figure-ground organization, beauty, embeddedness, hierarchy, serial pattern segmentation and completion, and handedness. SIT started with a classification model, but nowadays it also contains comprehensive models of amodal completion (19, 20) and symmetry perception (21–24).

For object perception, SIT proposes an integration of viewpoint-independent and viewpoint-dependent factors quantified in terms of object complexities (19). A Bayesian translation of this integration, using precisals (i.e., probabilities p = 2^–c derived from complexities c), suggests that fairly veridical vision in many worlds is a side effect of the preference for simplest interpretations (25). This idea, which challenges the traditional Helmholtzian idea that vision is highly veridical in only the one world in which we happen to live, is sustained by findings in the domain of algorithmic information theory (AIT), also known as the domain of Kolmogorov complexity or the domain of the minimal description-length (MDL) principle.

During the past 40 years, SIT and AIT showed similar developments. These developments, however, occurred in a different order, and until recently, SIT and AIT developed independently (see ref. 26 for an overview of AIT and ref. 25 for a comparison of SIT and AIT). Currently, noteworthy are the following two differences between SIT and AIT.

One difference applies to the complexity measurement. Unlike AIT, SIT takes account of the perceptually relevant distinction between structural and metrical information (27). For example, the simplest codes of metrically different squares may have different algorithmic complexities in AIT but have the same structural complexity in SIT. By the same token, an AIT object class consists of objects with the same algorithmic complexity (ignoring structural differences), whereas an SIT object class consists of objects with the same structure (and hence with the same structural complexity) (25, 28). This might be a temporary difference, by the way. Since recently, AIT also seems to recognize the relevance of structures (29).

The other difference applies to the search space within which simplest codes are to be found. In both SIT and AIT, the simplest code of an object is to be obtained by “squeezing out” a maximum amount of regularity in a symbol string that represents a reconstruction recipe for the object; one might think of computer programs (binary strings) that produce certain output (an object). To formalize this idea, AIT did not focus on concrete coding languages that squeeze out specific regularities but instead provided (incomputable) definitions of randomness (30) to specify the result of squeezing out regularity. SIT, conversely, focused on a (computable) definition of “visual regularity,” which yielded a concrete coding language that squeezes out only transparent holographic regularities (for details, see ref. 31).

The transparent holographic character of these regularities has shown to be relevant in human symmetry perception (21–24). It also gave rise to the concept of “hyperstrings” that, in this article, is presented as a key to the computation of guaranteed simplest SIT codes. I begin by specifying the coding language of SIT and the related minimal-encoding problem.

SIT Coding Language

Basically, there are only three transparent holographic regularities, namely, iterations, symmetries, and alternations, which are described by, respectively, I-forms, S-forms, and A-forms (for short, ISA-forms), as given in the following definition of SIT's coding language.

Definition 1: An SIT code 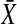of a string X is a string t₁t₂...t_m such that X = D(t₁)...D(t_m), where the decoding function D:t → D(t) takes one of the following forms:

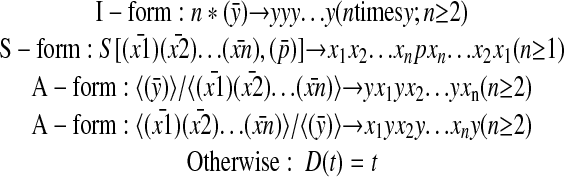[1]

for strings y, p, and x_i (i = 1, 2,..., n). The code parts (ȳ), (p̄), and 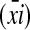are called “chunks”; the chunk (ȳ) in an I-form or A-form is called a “repeat”; the chunk (p̄) in an S-form is called a “pivot,” which, as a limit case, may be empty; the chunk string 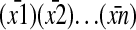in an S-form is called an “S-argument” consisting of “S-chunks” 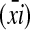; and the chunk string 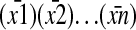inanA-form is called an “A-argument” consisting of “A-chunks” .

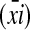Hence, an SIT code may involve not only encodings of strings inside chunks [that is, from (y) into (ȳ)] but also hierarchically recursive encodings of S-arguments or A-arguments 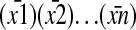into 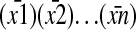. As I specify in the next section, this hierarchically recursive search for regularity creates the problem that, to compute simplest SIT codes, a superexponential amount of time seems to be required (see also ref. 32). The following sample of SIT codes of one and the same symbol string may give a gist of this problem.

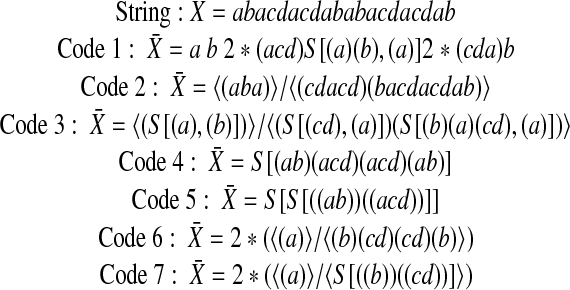[2]

Code 1 is a code with six code terms, namely, one S-form, two I-forms, and three symbols. Code 2 is an A-form with chunks containing strings that may be encoded as given in code 3. Code 4 is an S-form with an empty pivot and illustrates that, in general, S-forms describe broken symmetry (33); mirror symmetry then is the limit case in which every S-chunk contains only one symbol. Code 5 gives a hierarchically recursive encoding of the S-argument in code 4. Code 6 is an I-form with a repeat that has been encoded into an A-form with an A-argument that, in code 7, has been encoded hierarchically recursively into an S-form.

SIT's Minimal-Encoding Problem

As said, the coding language of SIT specifies the search space within which simplest codes are to be found. To search this space for simplest codes, one of course needs a measure of code complexity, but this is a subordinate problem in this article. SIT has known complexity measures that were either empirically supported or theoretically plausible (28), but since about 1990, SIT uses a measure that is both (ref. 15; see also ref. 25). For any complexity measure, however, the question is whether one can ever be sure that a given code is indeed a simplest code. In other words, the fundamental problem of computing guaranteed simplest codes is to take account of all possible codes of a given string.

It is expedient to note that the SIT minimal-encoding problem differs from context-free grammar (CFG) problems such as finding the smallest CFG for any given string, for which fast approximation algorithms exist (e.g., see refs. 34 and 35). SIT starts from a particular CFG, namely, the coding language given in Definition 1, which was designed specifically to capture perceptually relevant structures in strings. The minimal-encoding problem of SIT then is to compute, for any given string, a guaranteed simplest code (i.e., no approximation) by means of the specific coding rules supplied by this perceptual coding language.

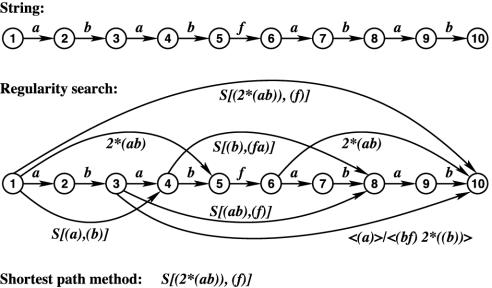
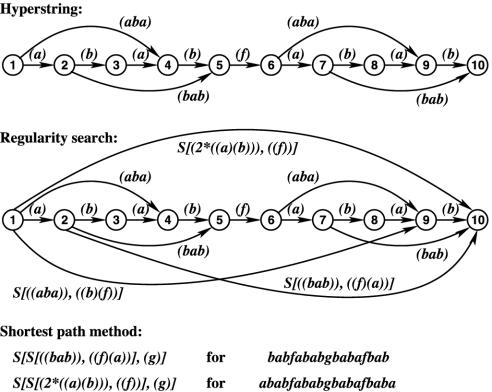
A part of SIT's minimal-encoding problem can be solved as follows by means of Dijkstra's (36) shortest-path method (SPM). Suppose that for every substring of a string of length N, one already has computed a simplest covering ISA-form, that is, a simplest substring code among those that consist of only one ISA-form. Then, Dijkstra's O(N²) SPM can be applied to select a simplest code for the entire string from among the O(2^N) codes that then still are possible (see Fig. 1; see ref. 37 for details on this application).

Fig. 1.

Suppose for the string 𝒫 = ababfabab that the regularity search has yielded simplest covering ISA-forms for the substrings of 𝒫 (only a few of these ISA-forms are shown). Then, the SPM yields S[(2*(ab)), (f)] as the simplest code of 𝒫. (Note: the number of string symbols in a code is taken to quantify its structural complexity.)

This, however, leaves open the much harder part of computing simplest covering ISA-forms for every substring. In general, as one may infer from Definition 1, a substring of length k can be encoded into O(2^k) covering S-forms and O(k2^k) covering A-forms. To pinpoint a simplest covering S-form or A-form, a simplest code for every one of the O(2^k) S-arguments and O(k2^k) A-arguments has to be computed as well, and so on, with O(logN) recursion steps. Hence, an algorithm that would process each and every S-argument and A-argument separately would require a superexponential O(2^{N logN}) amount of computing time.

In the next sections, I show that the concept of hyperstrings provides a key to the solution of this daunting problem. First, I define and illustrate hyperstrings in a graph-theoretical setting (for an extensive course on graph theory, see ref. 38; for a brief course, see Appendix 1, which is published as supporting information on the PNAS web site). Then, I show that A-arguments and S-arguments group by nature into hyperstrings. Finally, I evaluate the fact that hyperstrings allow for what I call “transparallel processing,” that is, they allow a search for regularity in O(2^N) A-arguments or S-arguments as if only one A-argument or S-argument of length N were concerned.

Hyperstrings

The concept of hyperstrings is a generalization of the concept of strings. To identify context-free string structures, the only usable property is the identity of substrings. As I specify next, a generalization of this property holds for the hypersubstrings of a hyperstring.

Definition 2: A hyperstring is a simple semi-Hamiltonian directed acyclic graph (V, E) with a labeling of the edges in E such that for all vertices i, j, p, q ∈ V:

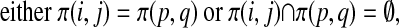[3]

where a substring set π(v₁, v₂) is the set of label strings represented by the paths (v₁,..., v₂) in an edge-labeled directed acyclic graph. In a hyperstring, the subgraph formed by the vertices and edges in these paths (v₁,..., v₂) is called a “hyper-substring.”

It can easily be verified that a hyperstring is an st-digraph (i.e., a directed acyclic graph with only one source and only one sink) with only one Hamiltonian path from source to sink (i.e., a path that visits every vertex only once). The label string represented by this Hamiltonian path is what I call the “kernel” of the hyperstring.

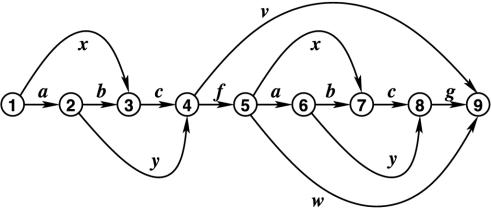
For example, the graph in Fig. 2 is a simple semi-Hamiltonian directed acyclic graph with 13 source-to-sink paths that each represent some string consisting of some number of symbols. For instance, the path (1,2,4,5,7,8,9) represents the string ayfxcg, and the path (1,3,4,5,9) represents the string xcfw. Furthermore, the substring sets π(1, 4) and π(5, 8) are identical: The paths (1,...,4) and the paths (5,...,8) represent the same set of substrings, namely, abc, ay, and xc. In fact, for this graph, all substring sets are pairwise either identical or disjunct, so that this graph is a hyperstring. The kernel of this hyperstring is the string abcfabcg, which is represented by the unique Hamiltonian path (1,2,3,4,5,6,7,8,9).

Fig. 2.

A hyperstring. The paths from vertex 1 to vertex 4 represent the same substrings as those represented by the paths from vertex 5 to vertex 8; that is, the substring sets π(1, 4) and π(5, 8) are identical.

In general, as in Fig. 2, a hyperstring represents a collection of strings that have a common structure but that, for the rest, may be unrelated. In other words, the common structure of the strings is the crucial property that allows the strings to be seen as one hyperstring, and depending on particular applications, the strings may or may not have further things in common. In this article, I focus on hyperstrings representing strings that are related further in that they are derived from one underlying string.

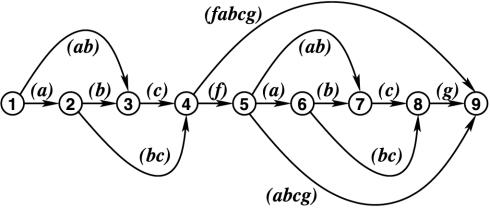
For example, in Fig. 3, the graph from Fig. 2 has been given an edge-labeling such that, this time, the source-to-sink paths represent “chunkings” of the string abcfabcg, that is, partitionings into successive substrings. For instance, in Fig. 3, the path (1,3,4,5,9) represents the chunking (ab)(c)(f)(abcg), that is, it represents a string consisting of four chunks. A string of length N can be chunked in 2^N–1 different ways, which is also the maximum number of source-to-sink paths (i.e., represented strings) in a hyperstring with kernel length N. Not all collections of chunkings of a string form hyperstrings, but as I show next, A-arguments and S-arguments are chunkings that group by nature into hyperstrings.

Fig. 3.

A hyperstring that represents 13 chunkings of the string abcfabcg. Just as in Fig. 2, the substring sets π(1, 4) and π(5, 8) are identical.

Alternation Hyperstrings

A full account of alternation hyperstrings would involve code-technical details that are beyond the scope of this article. For instance, one would have to distinguish between A-forms 〈(y)〉/〈(x₁)(x₂...(x_n)〉 and 〈(x₁)(x₂)...(x_n)〉/〈(y)〉, and in both cases one would have to distinguish further between repeats y of different lengths. The role of hyperstrings for all these cases, however, is essentially the same as for A-forms 〈(y)〉/〈(x₁)(x₂...(x_n)〉 with repeat y consisting of just one element. Therefore, I consider the latter case only here.

There are two ways to verbalize the encoding of a string yx₁yx₂...yx_n into the A-form 〈(y)〉/〈(x₁)(x₂)...(x_n)〉. First, because the x_i are substrings of arbitrary lengths, the A-form can be said to specify repeats y at arbitrary positions in the string. Second, however, the A-form can also be said to specify the string as consisting of substrings yx_i, that is, substrings with identical prefixes y. The latter verbalization triggered the following definition.

Definition 3: For a string T = s₁s₂...s_N, the A-graph is a simple directed acyclic graph (V, E) with V = {1, 2,..., N + 1} and, for all 1 ≤ i < j ≤ N, edges (i, j) and (j, N + 1) labeled with, respectively, the chunks (s_i...s_j–1) and (s_j...s_N) if and only if s_i = s_j.

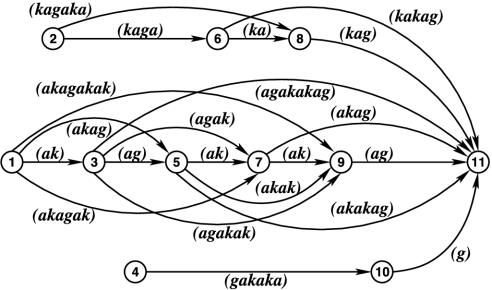
Fig. 4 illustrates that an A-graph contains a corresponding path for every A-form 〈(y)〉/〈(x₁)(x₂...(x_n)〉 that covers a suffix of T. For example, in Fig. 4, the path (3,7,9,11) represents the chunk string (agak)(ak)(ag). After extraction of the first symbol from each chunk, this chunk string corresponds to the A-argument in the A-form 〈(a)〉/〈(gak)(k)(g)〉, which covers the suffix agakakag of T = akagakakag.

Fig. 4.

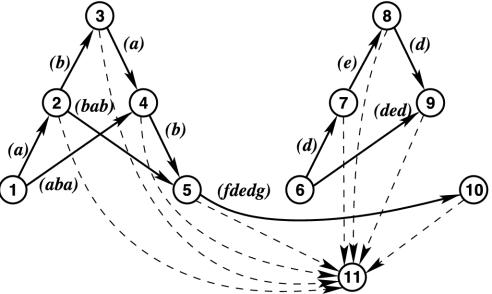
The A-graph for the string T = akagakakag, with three independent hyperstrings and with, among others, identical substring sets π(1, 5) and π(7, 11).

Furthermore, an A-graph may contain edges [like edge (10, 11) in Fig. 4] that represent a repeat only, that is, edges that do not correspond to an A-chunk in some A-form. (In the case of repeats of more than one element, edges may even represent only a part of a repeat.) During the computation of simplest SIT codes, such “pseudo A-chunk” edges are excluded from ending up in codes (see later in the article), but until then, they are needed to maintain the integrity of the hyperstrings of which, as I establish next, an A-graph is composed.

Theorem 1. The A-graph 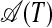for a string T = s₁s₂...s_N consists of at most N + 1 disconnected vertices and at most ⌊N/2⌋ independent subgraphs (i.e., subgraphs that share only the sink vertex N + 1) each of which is a hyperstring.

Proof: See Appendix 2, which is published as supporting information on the PNAS web site.

For instance, the A-graph in Fig. 4 consists of three independent hyperstrings. Before I elaborate on the relevance of Theorem 1, I show that a similar finding holds for S-arguments.

Symmetry Hyperstrings

By Definition 1, a string T = x₁...x_npx_n...x₁ can be covered by an S-form S[(x₁)...(x_n), (p)]. By the same token, for 1 ≤ i ≤ j ≤ n, every substring x_i...x_npx_n...x_i of T can be covered by an S-form S[(x_i)...(x_j–1), (x_j...x_npx_n...x_j)]. The substrings x_i...x_npx_n...x_i are all centered around the midpoint of T and form what I next define to be “diafixes.” The notion of diafixes is convenient in the subsequent elaboration of how S-arguments group into hyper-strings.

Definition 4: A diafix of a string T = s₁s₂...s_N is a substring s_i+1...s_N–i (0 ≤ i < N/2).

Definition 5: For a string T = s₁s₂...s_N, the S-graph 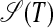is a simple directed acyclic graph (V, E) with V = {1, 2,..., ⌊N/2⌋ + 2} and, for all 1 ≤ i < j < ⌊N/2⌋ + 2, edges (i, j) and (j, ⌊N/2⌋ + 2) labeled with, respectively, the chunk (s_i...s_j–1) and the possibly empty chunk (s_j...s_N–j+1) if and only if s_i...s_j–1 = s_N–j+2...s_N–i+1.

Fig. 5 illustrates that an S-graph 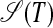may contain several independent subgraphs and that every S-form covering a diafix of T is represented by a path in 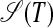. For instance, the path (2,5,10,11) represents the S-form S[(bab)(fdedg), (p)] covering the diafix babfdedgpfdedgbab. Thus, in Definition 5, the edges (j, ⌊N/2⌋ + 2) represent all possible pivots in such S-forms, and the edges (i, j) represent all possible S-chunks in such S-forms.

Fig. 5.

The S-graph 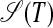for the string T = ababfdedgpfdedgbaba, with two independent subgraphs. Dashed edges and bold edges represent pivots and S-chunks, respectively, in S-forms covering diafixes of T.

Hence, without its pivot edges, an S-graph 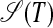represents the S-arguments of all S-forms covering diafixes of T. As I establish next, these S-arguments group into hyperstrings.

Theorem 2. The S-graph 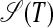for a string T = s₁s₂...s_N consists of at most ⌊N/2⌋ + 2 disconnected vertices and at most ⌊N/4⌋ independent subgraphs that, without the sink vertex ⌊N/2⌋ + 2 and its incoming pivot edges, form one disconnected hyperstring each.

Proof: See Appendix 2.

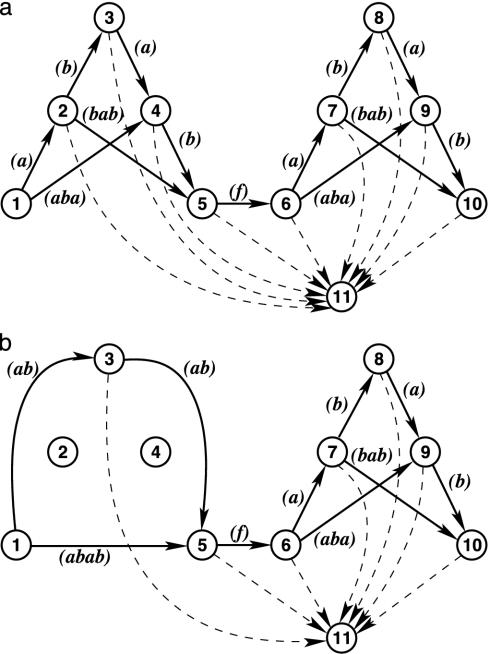
For instance, Fig. 6 shows two S-graphs 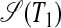and , which each consist of one independent subgraph that, without the pivot edges, forms a hyperstring. Although in Fig. 6 the two strings T₁ and T₂ are near identical, the substring sets π(1, 5) and π(6, 10) are identical for T₁ but disjunct for T₂. This illustrates the crucial hyperstring property that substring sets are either completely identical or completely disjunct (see Definition 2).

Fig. 6.

(a) The S-graph for the string T₁ = ababfababgbabafbaba, with, among others, identical substring sets π(1, 5) and π(6, 10). (b) The S-graph for the nearly identical string T₂ = ababfababgbabafabab, in which the substring sets π(1, 5) and π(6, 10) are disjunct.

The Computability of Simplest SIT Codes

Within AIT, guaranteed minimal encoding is not feasible, because without a definition of regularity, one can never be sure that one has extracted a maximum of regularity. Within SIT, regularity is defined as being constituted by transparent holographic configurations, but even then, guaranteed minimal encoding did not seem feasible: The required hierarchically recursive search for regularity seemed to imply that every S-argument and A-argument has to be processed separately, which would consume superexponential computing time.

The previous two sections, however, show that S-arguments and A-arguments group by nature into hyperstrings. More specifically, A-arguments group into independent hyperstrings, and S-arguments group into disconnected hyperstrings. As I discuss next, this paves the way for an encoding algorithm that determines guaranteed simplest SIT codes.

My quest for such an algorithm started in the mid-1980s, by developing an approximation algorithm (37). In the mid-1990s, I completed an algorithm that already used S-graphs and A-graphs without pseudo A-chunk edges (31). This algorithm is available on request; it determines guaranteed simplest SIT codes under the restriction that pseudo A-chunks do not occur (at the time, the need to include pseudo A-chunks was not yet evident). The upcoming upgrade (see below) removes this restriction by using hyperstrings as defined in this article. For the rest, the available algorithm deals with the hierarchically recursive search for regularity in A-arguments and S-arguments as outlined in the next overview of the upgrade.

Step 1: The search for simplest covering ISA-forms for the substrings of a string 𝒫 of length N can be embedded in an O(N³) all-pairs SPM (see ref. 39) that selects a simplest SIT code for every substring of 𝒫, proceeding from small to large substrings, the largest substring being the entire string 𝒫. That is, a simplest covering ISA-form for some substring of 𝒫 has to be computed only once all smaller substrings of 𝒫 have already been assigned a simplest code. This implies that the search for simplest covering I-forms is “peanuts,” and that the hierarchically recursive search for regularity in A-arguments and S-arguments can start from A-forms and S-forms with simplest codes ȳ, p̄, and for the smaller substrings inside the chunks.

Step 2: An A-graph 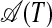or an S-graph 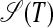for a substring T = s₁s₂...s_M of 𝒫 represents O(2^M) individual chunk strings, but it can be constructed in only O(M²) computing steps. For 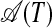, one only has to check for every substring of T whether this substring and the subsequent suffix have identical prefixes (see Definition 3). [In an O(N²) preprocess, every substring of 𝒫 can be assigned an integer that is the same for all and only all identical substrings.] Similarly, for 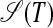, one only has to check for every substring s_i...s_j–1 in the left-hand half of T whether it is identical to its symmetrical counterpart s_M–j+2...s_M–i+1 in the right-hand half of T (see Definition 5). Every edge in 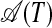and 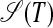can be given a complexity on the basis of the already processed content of the represented A-chunk, S-chunk, or pivot (see Step 1). At this point, pseudo A-chunks can be given an “infinite” complexity to prevent them from ending up as real A-chunks.

Step 3: Hierarchically recursively, the hypersubstrings in 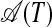and 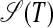can be processed starting with Step 1. That is, by Definition 2, a hyperstring with kernel length n can be conceived of as one string 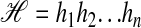in which a substring h_i...h_j stands for the substring set π(i, j + 1) in the hyperstring. For instance, the hyperstring in Fig. 2 can be conceived of as a string 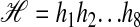in which, among others, substrings h₁...h₃ and h₅...h₇ are identical. This identity stands for the identity of the substring sets π(1, 4) and π(5, 8), which in one go captures the abc, ay, and xc identities in strings represented in the hyperstring. Inversely, one such substring identity already implies that the substring sets are identical. Hence, the ISA-forms in this single string ℋ account for all ISA-forms in all strings represented in the hyperstring, so this single string ℋ can be taken as the input of Step 1. In other words, Step 1 can take the hyperstring as if it were only one string (namely, the hyperstring kernel) with, for various substrings, various a priori given alternatives that all but one will be dismissed during the all-pairs SPM (see Fig. 7).

Fig. 7.

For the hyperstring in the S-graph 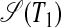from Fig. 6a, with T₁ = ababfababgbabafbaba, the hierarchically recursive regularity search yields simplest covering ISA-forms for the hypersubstrings (only a few of these ISA-forms are shown). By including the pivots, the all-pairs SPM then yields simplest covering S-forms for the diafixes of T₁ (only a few of these S-forms are shown). Note that the number of string symbols in a code is taken to quantify its structural complexity, and for clarity the substrings aba and bab inside chunks are shown uncoded but should be read as S[(a), (b)] and S[(b), (a)], respectively.

Step 4: The argument of an A-form or S-form in a substring T of 𝒫 contains at most ⌊N/2⌋ chunks, so the recursion depth is at most log₂N. The recursion ends when Step 2 yields A-graphs and S-graphs without identical substring sets. For these graphs and, backtracking, eventually for 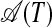and 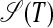, the all-pairs SPM selects a simplest code for every hypersubstring, and by including repeats and pivots, respectively, it selects simplest covering A-forms and S-forms for, eventually, all suffixes and diafixes of T. These A-forms and S-forms are used in the all-pairs SPM that eventually selects a simplest code for 𝒫.

As indicated in Step 4, the all-pairs SPM yields eventually simplest covering A-forms and S-forms for all suffixes and diafixes of T. Therefore, each pass, Step 2 has to yield only O(N) A-graph and S-graphs. Hence, Step 2 yields O(N^log N) such graphs during the entire hierarchically recursive search for regularity. Furthermore, because of the all-pairs SPM, the algorithm requires O(N³) computing steps per A-graph or S-graph. Hence, in total, it requires O(N^3+logN) steps to compute a simplest SIT code for a string of length N.

It is true that this still implies a weakly exponential computing time, but it contrasts, in any case, very favorably with the uncomputability of a simplest AIT code and with the superexponential computing time that beforehand seemed to be required to compute a simplest SIT code. Furthermore, the weakly exponential factor logN is due to the number of hierarchical recursion steps in the worst case. Only few strings have a deep hierarchical structure, so in the average case, this weakly exponential factor hardly seems a problem.

Be that as it may, the central issue in this article is not this algorithm as a whole but rather the role of hyperstrings in it. As outlined in Step 3, hyperstrings imply that O(2^N) S-arguments or A-arguments do not have to be searched serially or in parallel for regularity but can be processed as if only one S-argument or A-argument were concerned. I propose to call this a form of transparallel processing, which may be qualified as follows.

Transparallel Processing

To be clear, I do not use the term “transparallel” in the sense that Nelson (40) proposed it in the 1960s following Bush's idea (41) to display related items in correspondence with the way humans think. Nelson used it in “transparallel displays,” which means so much as that connected items are shown together with their connections. Nowadays, such data structures are better known as “distributed representations,” and this is the term I use here as a leg up to what I call transparallel processing. To Nelson, a typical example of a distributed representation is a display showing two related stories side by side, with visible links between the corresponding parts. A more everyday example is a road map in which routes between places are not displayed separately but such that common parts are effectively displayed as common parts. Likewise, hyperstrings are distributed representations of strings.

A process that effectively exploits a distributed representation of items can be said to perform “distributed processing.” This is often taken to mean that the process is distributed over many processors, but here I take it to mean primarily that the items are processed simultaneously in the sense that every common part is processed only once. Different common parts can then be processed serially by one processor or in parallel by many processors. A classical example of serial distributed processing is Dijkstra`s SPM (ref. 36; see also Fig. 1). Generally, such a one-processor implementation can be converted into a many-processors implementation performing parallel distributed processing (see Appendix 3, which is published as supporting information on the PNAS web site).

Nowadays, distributed processing is a standard in many applications in computer science and in many models in cognitive science. For instance, in computer science, a deterministic finite automaton (DFA) is a distributed representation of the sentences in a regular language, which enables a quick serial distributed processing check on whether a given string is a sentence in this language (42). Furthermore, in cognitive science, distributed representations called networks are used in parallel distributed processing models of cognitive processes that, given certain input, select quickly a best matching item from among the items represented in the network (43). The items in the network could be words to be recognized in written or spoken language, for instance.

In the minimal-encoding algorithm outlined in the previous section, hyperstrings are subjected to all-pairs SPMs and, thereby, to distributed processing. In this respect, hyperstrings do not differ from deterministic finite automatons and networks: These data structures all allow stored items to be processed simultaneously in the sense that every common part is processed only once. Hyperstrings, however, allow in addition for what I call transparallel processing, which, as I specify next, goes one step beyond distributed processing.

First, as said, in distributed processing, different common parts still have to be processed serially by one processor or in parallel by many processors. Second, in the minimal-encoding algorithm, a hyperstring is subjected not only to an all-pairs SPM but also to a search for regularity in the strings represented in the hyperstring. During this regularity search, different common parts do not have to be processed serially by one processor or in parallel by many processors but can, by one processor, be processed as if only one part were concerned. As outlined in Step 3 in the previous section, this form of processing is due to the hyperstring property that substring sets are either completely identical or completely disjunct (see Definition 2), and this is the form of processing I call transparallel processing.

Conclusions

In cognitive science, our brain is typically supposed to be attuned to relevant regularities in the world. Symmetry, for instance, is doubtlessly relevant: It is a regularity that is visible in the shape of virtually every living organism. In this article I showed that such visually relevant regularities lend themselves for transparallel processing. Hence, if our brain is indeed attuned to relevant regularities, then, just as distributed processing, transparallel processing might well be a form of cognitive processing.