Tension Amplification in Tethered Layers of Bottle-Brush Polymers

Abstract

Molecular dynamics simulations of a coarse-grained bead–spring model have been used to study the effects of molecular crowding on the accumulation of tension in the backbone of bottle-brush polymers tethered to a flat substrate. The number of bottle-brushes per unit surface area, Σ, as well as the lengths of the bottle-brush backbones N_bb (50 ≤ N_bb ≤ 200) and side chains N_sc (50 ≤ N_sc ≤ 200) were varied to determine how the dimensions and degree of crowding of bottle-brushes give rise to bond tension amplification along the backbone, especially near the substrate. From these simulations, we have identified three separate regimes of tension. For low Σ, the tension is due solely to intramolecular interactions and is dominated by the side chain repulsion that governs the lateral brush dimensions. With increasing Σ, the interactions between bottle-brush polymers induce compression of the side chains, transmitting increasing tension to the backbone. For large Σ, intermolecular side chain repulsion increases, forcing side chain extension and reorientation in the direction normal to the surface and transmitting considerable tension to the backbone.

Graphical abstract

1. INTRODUCTION

Bottle-brush polymers are a special case of comb-like polymers, which consist of two principal components: a central linear polymer backbone and linear side chains grafted to the backbone. In bottle-brush polymers, the chemical composition of each component can be controlled independently. The immense number of possible combinations of chemistry, physical properties, and variations of architecture within these polymers thus creates a highly versatile framework for a number of applications. Such versatility is readily apparent in nature, ranging from versicans acting on cell proliferation and adhesion^1,2 to aggrecans, which form a major component of articular cartilage surfaces,^3–5 to the bottle-brush-like trans-membrane mucins of the periciliary layer of human lungs, which facilitate airway clearance by acting as an osmotic barrier to mucus and contaminants.⁶ Among these, aggrecans have perhaps been studied most extensively in recent years, both experimentally and theoretically,^7–13 in the hopes of applying an understanding of the properties that lead to the low coefficient of friction and high strength of synovial joints to replicating these properties synthetically.

The primary factor separating bottle-brush polymers from comb polymers is the grafting density of side chains along the backbone. In comb polymers, this grafting density is low enough that backbone flexibility is largely unaffected by the presence of side chains. As side chain density increases, the number of monomers in the spacer between adjacent side chains along the backbone becomes smaller than the square root of the degree of polymerization of the side chains, and steric repulsion between side chains begins to overwhelm the conformational entropy of the backbone. This forces the backbone to straighten at intermediate length scales and the side chains to stretch away from the backbone.^14,15 The amount of stretching depends on the molecular weight of the side chains, the degree of polymerization of the spacers between side chains, and interactions with the backbone. These characteristics of bottle-brush polymers have generated special interest because they give rise to properties not often seen in linear polymers.^16,17

Studies of bottle-brush polymers have largely focused on structural properties and conformations in specific environments. The main goal being to manipulate the interactions between specific components in layered or bulk systems in order to tailor self-assembly to desired applications. Grubbs and co-workers were able to precisely control the lamellar width of microphase-separated regions in bulk systems of bottle-brushes with two types of side chains by controlling side chain arrangement and degree of polymerization.^18,19 More recent work has incorporated theoretical predictions of bottle-brush block copolymers with state-of-the-art synthesis to better understand the self-assembly and morphology of bottle-brush materials.^20,21 Such work has been extended to the fabrication of large-feature nanopatterns on untreated substrates.²² Others have used similar synthetic methods to create multicomponent nanocapsules,²³ core–shell cylindrical brushes,^24,25 nano-wires,²⁶ and wire-shaped nanoparticle assemblies.²⁷ Further, multicomponent brushes have been studied as potential routes to Janus particles and Janus-type polymers, resulting in an increasing number of studies of bottle-brush polymers.^14,28–34

Bottle-brush polymers are also important in the design of biological devices, such as those involving surfaces that resist fouling by certain classes of molecules or biomolecules. Dense tethered layers of poly(oligoethylene glycol) bottle-brushes have been shown to exhibit remarkable resistance to protein adsorption^35–38 and can be altered, by manipulating grafting density and component dimensions, to create porous surfaces capable of transporting or trapping nonprotein molecules via size exclusion.³⁹ Other functionalized surfaces with this type of chemistry have been used in applications from support for protein arrays^40,41 to surfaces that improve the acceptance of biometallic implants⁴² to wastewater remediation via brush-functionalized magnetic nanoparticles.⁴³

Recently, it was demonstrated that the steric repulsion between side chains that restricts backbone conformations also transmits significant tension from the side chains to the backbone.^44–48 This tension can be amplified by enhancing the crowding of side chains, which can be accomplished by tethering the backbone to a substrate or by allowing adhesion of the side chains to an attractive surface.^44–48

The accumulation of tension in linear polymer brushes has been an area of interest for years. Early scaling theories of linear polymer brushes^49–51 set the stage for the study of conformational change in the linear chains of dense polymer brushes. The loss of conformational entropy associated with increased grafting density is the main source of tension in linear brush chains. However, this tension is limited in magnitude, even at high coverages.⁵² For additional analysis of theoretical concepts regarding the properties of polymer brushes grafted to flat and curved surfaces, the reader is referred to a review by Binder and Milchev⁵³ in which the concepts behind the expected conformations, sizes, and shapes of polymer brushes are discussed.

Panyukov et al. examined the connections between backbone tension amplification and polymer conformations for branched polymers such as stars, pom-poms,⁵⁴ and bottle-brushes in solution and adsorbed on surfaces⁵⁵ and star and bottle-brush polymers tethered to surfaces.⁵² The two latter cases provide the starting point of the current investigation. In those works, the authors demonstrated the importance of the two primary length scales in individual bottle-brushes: D, the cross-section diameter of the brush as determined by the equilibrium conformations of the side chains, and L, the contour length of the bottle-brush, which is dependent on intramolecular steric repulsion. In general, bottle-brushes can be divided into two key classes based on the values of D and L: “hairy” bottle-brushes (D ≫ L), which are comparable to star polymers tethered or strongly adsorbed on surfaces⁵⁶ and exhibit progressively increasing backbone tension as a function of distance from the backbone free end, and “crew-cut” bottle-brushes (D ≪ L), cylindrical molecules that have more in common with linear polymer brushes but exhibit backbone tension generation beyond that of linear brushes due to side chains in the region near the free end of the backbone.

Tethering bottle-brush polymers to a substrate introduces a third important length scale: the distance between nearest-neighbor tethering sites, d. This gives a measure of grafting density equivalent to the molecular coverage (Σ), defined by the number of bottle-brush molecules per unit of surface area. The grafting of bottle-brushes to the substrate can then be divided into three regimes⁵² based on the comparison between d, the bottle-brush diameter D, and the radius R_f of the “footprint”—the projection of the bottle-brush backbone and side chains onto the grafting plane. The mushroom regime corresponds to grafting densities Σ below the overlap of footprints Σ* ≈ 1/R_f² with the inter-brush spacing d greater than R_f. The individual bottle-brushes in the mushroom regime do not interact with each other and the backbone tension is purely intramolecular in nature. In the so-called “loosely-grafted” regime at intermediate grafting densities Σ* < Σ < Σ**, where Σ** ≈ 1/D², the fluctuations of bottle-brush backbones away from the normal to the substrate are suppressed, but no significant additional backbone tension is predicted.⁵² In the “densely-grafted” regime at high grafting densities Σ > Σ** the separation between bottle-brushes is smaller than their thickness (d < D) and significant additional backbone tension is expected. In the current study, we use coarse-grained molecular dynamics simulations to investigate how changes in side chain conformations at different molecular coverages are reflected in the amplification and accumulation of tension in the bottle-brush backbone.

Previous computational simulations of bottle-brush polymer systems can be broadly divided into two categories: simulations of bottle-brush polymers with limited side chain lengths (N_sc ≤ 50)^{10–13,28,30,32,48,57,58} and limited numbers of bottle-brush molecules and simulations of single bottle-brush polymers modeled using periodic boundary conditions along a fixed backbone to represent an effectively infinite-length, perfectly rigid backbone to study the dependence of the radial density and side chain conformations on number of backbone monomers between side chains.^28,29,31,33 The current work seeks to study multiple bottle-brushes with a significant density of moderately long side chains (50–200 units) grafted to backbones with lengths from 50 to 200 monomeric units in order to examine a broader class of bottle-brush polymers. To the best of our knowledge, this represents the first simulation study directed toward refining and complementing the existing theory regarding tension accumulation in dense bottle-brush tethered layers while offering more detailed information regarding the changes in chain conformations that give rise to backbone tension accumulation and amplification.

2. SIMULATION MODEL

Many bottle-brush simulations focusing on properties arising from molecular architecture have been performed at a coarse-grained level using Monte Carlo (MC) methods^{28–30,59–61} and molecular dynamics (MD).^{10–13,31–33,57,62} Here we use the bead–spring model of Kremer and Grest,^63,64 in which the interactions between pairs of beads are represented by a truncated and shifted Lennard-Jones 12–6 potential:

$$U_{\text{LJ}}(r)=\{\begin{array}{ll}4{\mathrm{\epsilon }}_{\text{LJ}}\left[{\left(\frac{{\sigma }_{\text{LJ}}}{r}\right)}^{12}-{\left(\frac{{\sigma }_{\text{LJ}}}{r}\right)}^6\right]+\mathrm{C}\hfill & r\le r_{\mathrm{c}}\hfill \\ 0\hfill & r>r_{\mathrm{c}}\hfill \end{array}$$

where r is the interparticle distance and ε_LJ and σ_LJ represent the pairwise interaction energy and bead diameter, respectively. In the current simulations, all nonbonded interactions are identical, implying the backbone and side chains are composed of the same chemical species; thus, we have set ε_αβ = ε and σ_αβ = σ. The Lennard-Jones potential is truncated at a distance r_c = 2^1/6σ, the potential minimum, which makes interactions purely repulsive, describing an essentially athermal model (i.e., very good solvent). The constant C in the Lennard-Jones potential is a standard shift to ensure continuity of the potential at the cutoff.

Polymer connectivity is achieved via the inclusion of an additional finitely extensible nonlinear elastic (FENE) potential between adjacent beads in the backbones and side chains:

$$U_{\text{FENE}}(r)=\{\begin{array}{ll}-\frac{1}{2}k{R_0}^{2}ln\left[1-{\left(\frac{r}{R_0}\right)}^2\right]\hfill & r<R_0\hfill \\ \infty \hfill & r\ge R_0\hfill \end{array}$$

where k is the FENE force constant and R₀ is the maximum extension of the bond. The standard choice for the parameters (k = 30 ε/σ² and R₀ = 1.5σ) was used in this study.^63,64 With this set of parameters, competition between the repulsive Lennard-Jones potential and the FENE spring potential gives an equilibrium bond length of ≈ 0.97σ.

One of the factors affecting the accumulation and amplification of tension in bottle-brushes is the effect of end-tethering the backbones of the bottle-brush polymers to a substrate. As shown below, this creates a tension profile that is highest near the surface and decreases monotonically further from the surface. In our simulations, the substrate is modeled as a flat, structureless solid wall which interacts with the bottle-brushes via a Lennard-Jones 9–3 potential:

$$U_{9-3}(z)=\mathrm{\epsilon }\left[\frac{2}{15}{\left(\frac{\sigma }{z}\right)}^9-{\left(\frac{\sigma }{z}\right)}^3\right]$$

where z represents the distance normal to the wall surface. This potential models a wall located at z = 0, with the zero of the potential located at $z_0=\sqrt[6]{\frac{2}{15}}\sigma$ and the zero of the force(potential minimum) located at $z_{\mathrm{c}}=\sqrt[6]{\frac{2}{5}}\sigma$ The potential was truncated at z_c in order to provide a short-range repulsive wall that prohibits bottle-brush adsorption. Tethers were implemented by connecting the bottle-brushes to noninteracting monomers at the wall surface which are allowed to move laterally within the surface plane but not out of it. Lateral mobility in the tethering sites (“mobile” tethers) was included to allow bottle-brushes, especially in high-coverage environments, to develop their preferred packing arrangement.

Our investigation centers on three main parameters: bottle-brush backbone length in terms of the number of coarse-grained backbone beads N_bb, side chain length in terms of the number of coarse-grained side chain beads N_sc, and the density of bottle-brush polymers grafted to the surface, referred to as the coverage Σ, given in terms of the number of backbone chains per unit surface area (σ⁻²). Four different backbone lengths were chosen N_bb = 50, 100, 150, and 200 beads with one additional bead to serve as the site of attachment to the substrate. Three different side chain lengths N_sc = 50, 100, and 200 beads were studied for each of the backbone lengths, leading to a set of 12 bottle-brush molecules. The grafting density of side chains was set at one side chain per backbone unit (not counting tethering site) in order to mirror the type of bottle-brushes created through macromonomer-based approaches seen in a number of recent studies.^{18,19,22,24,25} Thus, the total number of side chains for each molecule is equal to N_bb. Throughout the rest of this article, the molecules will be referred to by their side chain and backbone lengths as N_sc:N_bb, e.g., “50:150” referring to the bottle-brush with N_sc = 50 and N_bb = 150.

Each simulation system was composed of 40 bottle-brushes in a simulation box with periodic boundary conditions in the lateral directions. The simulation box was given a square base with side length (40/Σ)^1/2 and vertical dimension larger than the length of a fully stretched bottle-brush. For each combination of N_sc and N_bb, a series of simulations were performed for bottle-brush areal densities Σ on the order of 10⁻⁵–10⁻² bottle-brushes/σ², although the specific range of Σ) for each N_sc:N_bb varies.

All simulations were performed using the LAMMPS⁶⁵ simulation package with velocity-Verlet integrator. A time step of δt = 0.005τ was used in all simulations, where τ = (mσ²/ε)^1/2 Simulations were performed at constant surface area. Temperature T = 1.0ε/k_B was maintained by coupling to a Langevin thermostat; damping constants of Γ = 0.5τ⁻¹ and Γ = 2.0τ⁻¹ were used to test performance, with no observable difference in final structures. Simulations were performed for a period of up to 1.5 × 10⁵τ, depending on the coverage and backbone/side chain degree of polymerization, with the longest runs for high coverages and N_bb, = 200. For comparison, the longest relaxation time of the backbone end-to-end distance autocorrelation function for N_bb = 200 is ≈ 4.0 × 10⁴τ.

3. RESULTS AND DISCUSSION

3.1. Bottle-Brush Structure and Characterization

In the previous work, bottle-brushes were classified as “hairy” or “crew-cut”.^52,55 “Hairy” bottle-brushes are those for which the side chain length is large enough that the diameter is much larger than the contour length of the equilibrium bottle-brush (D ≫ L). Hairy bottle-brushes have a structure and physical properties in common with tethered, densely grafted star polymers.⁵² The main difference between tethered stars and tethered hairy bottle-brushes is the distribution of side chains along the bottle-brush backbone compared to the emanation of side chains from a central group in the tethered star. Conversely, “crew-cut” bottle-brushes have a contour length much larger than the diameter of the brush (L ≫ D). While “crew-cut” bottle-brushes are most similar to linear polymer chains, they differ from linear chains in that the presence of side chains limits the maximum surface grafting density and transmits additional tension to the backbone.

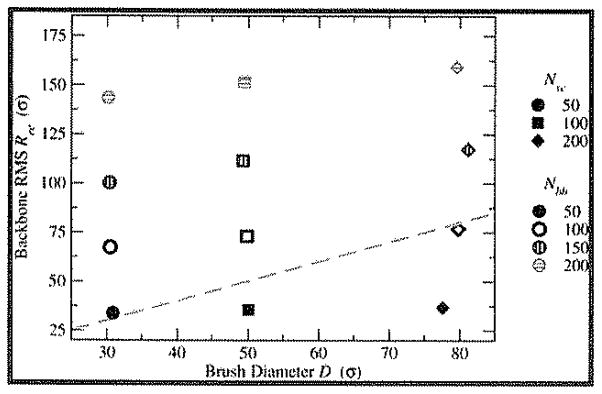
Our first consideration is the comparison of the effective brush width, D, and the effective length of the bottle-brush along the central axis in our tethered bottle-brush systems. We calculated the average brush diameter, D (defined as twice the maximum radial component of the side chain end-to-end distance), and RMS backbone end-to-end distance (R_ee = 〈R_ee,bb²〉^1/2) as an estimate of the central-axis contour length. The ratio D/R_ee is a good metric to indicate the extent to which the bottle-brush systems approach the asymptotically “hairy” or “crew-cut” regimes. Results for D and R_ee are shown in Table 1 and Figure 2.

Table 1.

Average Brush Diameter (D) and RMS End-to-End Distance (R_ee) in Units of the Reduced Length, σ (±0.1σ), and Diameter/Backbone End-to-End Distance Ratio (D/R_ee) for Mushroom-Regime Bottle-Brushes Used in Study

Nbb	Nsc	D	Ree	D/Ree
50	50	30.9	33.9	0.912
	100	50.1	35.5	1.41
	200	77.6	36.8	2.11
100	50	30.5	67.4	0.453
	100	49.9	73.1	0.683
	200	79.8	76.9	1.04
150	50	30.4	100.5	0.302
	100	49.3	111.7	0.441
	200	81.2	117.4	0.692
200	50	30.2	143.4	0.211
	100	49.5	151.4	0.327
	200	79.6	159.3	0.500

Figure 2.

Visual representation of data presented in Table 1: backbone root-mean-square end-to-end distance R_ee vs brush diameter D for lowest-coverage cases. N_bb is shown in color/filling of symbols (50: black/filled; 100: blue/open; 150: red/vertical hatching; 200: green/horizontal hatching), and N_sc is shown by symbol type (50: circle; 100: square; 200: diamond). The dashed line corresponds to 〈R_ee²〉^1/2 = D, indicating the hairy-to-crew-cut crossover.

It is clear from the data in Table 1 and Figure 2 that the bottle-brushes constructed for this investigation are outside of the asymptotic scaling regimes. Half of the bottle-brushes have D/R_ee > 0.5, but only the 200:50 bottle-brush has D/R_ee > 2, and none has D/R_ee < 0.2. In order to reach asymptotic scaling regimes, one would have to increase the length of the backbones or side chains, respectively, while leaving the lengths of the other components fixed to create more crew-cut or hairy brushes, but such an increase comes with the penalty of making the simulations increasingly intractable. Conversely, greatly decreasing N_bb or N_sc while leaving the other fixed would create more hairy or crew-cut brushes, respectively, at the cost of limiting the intrinsic flexibility of the shorter component. The systems investigated herein thus represent the wide array of available brushes in the “transition” or “crossover” regimes between asymptotic limits. By analyzing the results of these simulations in light of the predictions of the asymptotic regimes, we may be able to ascertain which factors in brush composition are most important to the widest array of real systems.

3.2. Analysis of Backbone Tension

One of the main differences between the two classes of bottle-brushes is the way backbone tension develops in a single bottle-brash, unperturbed by neighboring bottle-brushes. In both cases, tension at any point along the backbone is due to the tensile forces exerted on the backbone by side chains between that point and the free end. Thus, backbone tension amplification is greatest for bonds near the tethering surface and decreases monotonically toward the free end, where backbone tension is due solely to bond fluctuations.

The accumulation of tension in the regions near the free end saturates at distances from the free end on the order of the lateral size of the brush, D. For distances less than D from the free end, the bottle-brush behaves similarly to a tethered star polymer, in which tension is the result of the individual tensile forces from all of the side chains attached to the core. This is the focusing region of the brush described by Panyukov et al.^52,55 In the case of hairy bottle-brushes, the tension accumulates over the whole backbone from the free end to the substrate. The focusing region of tethered crew-cut bottle-brushes is within distance D of the free end of its backbone, within which tension generation is expected. At distances from the free end on the order of and greater than D, however, the side chains orient orthogonal to the brush backbone, and individual tensile forces from the side chains cancel one another. Tension generated within the focusing region is carried along the backbone, but no additional tension is generated by the side chains within this so-called transmission region beyond D from the backbone free end.

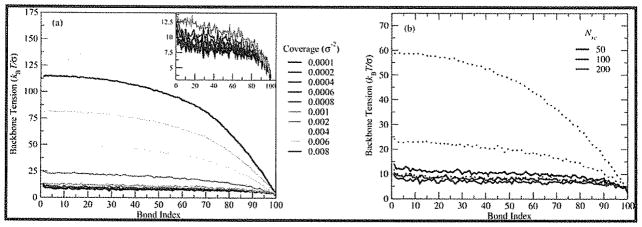
To understand how changes in side chain size and conformation affect the accumulation of backbone tension, we calculated the backbone tension as a function of the bond index, defined as the number of bonds separating a given backbone monomer from the tether, measured along the backbone. Tension is defined as the force due to the stretching of the bonds. A plot for the representative case (100:100) is shown in Figure 3a for a range of Σ. At low coverages, the tension increases most rapidly with decreasing bond index from the free end toward the surface, as in the focusing region predicted by theory (see inset in Figure 3a). At first glance, these low coverages seem to reflect a crew-cut brush, with no increase in tension outside of the focusing region at the free end apart from a slight increase near the tether site. Closer inspection (Figure 3a, inset) shows that there is a small, nearly linear increase in backbone tension for these cases, reflecting the nonasymptotic nature of these brushes.

Figure 3.

Average backbone tension vs bond index (a) for 100:100 for ten values of Σ. Inset: backbone tension vs bond index for coverages Σ ≤ 0.001 bottle-brushes/σ². (b) Average backbone tension vs bond index for N_bb = 100 at three different values of N_sc for Σ = 0.0002 bottle-brushes/σ² (solid lines) and 0.002 bottle-brushes/σ² (dotted lines).

At high coverages, the brushes become more crowded, and steric repulsion between interacting side chains on neighboring bottle-brushes increases the bond tension in their backbones. The net effect of increasing crowding is akin to an enlargement of the focusing region; the portion of the backbone in which tension is strictly increasing progresses toward the tethering surface as crowding causes more side chains on neighboring bottle-brushes to interact. There is still a region of saturation near the tethering surface, where the tension increase is not as rapid. In Figure 3b, the effect of increasing N_sc is similar to the effect of increased coverage because of the increase in lateral area of unperturbed bottle-brushes with increasing side chain length.

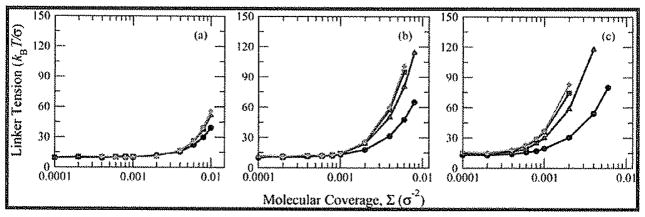
To examine the changes in tension within the brushes not only as a function of changing coverage but also as a function of side chain and backbone lengths, it is useful to define a representative segment or point that can be used for all cases. The tension in the first bond adhering the brush to the surface (the linker tension) is a reasonable choice, as theory⁵² shows this to be the point of maximum tension accumulation in both hairy and crew-cut bottle-brushes (the former by virtue of accumulation of all tension at the linker site, the latter by virtue of tension not changing outside the focusing region). The linker tension (Figure 4) can be divided into two regions as a function of coverage. At low coverages, the linker tension is nearly constant, indicative of the mushroom and loosely-grafted regimes of intramolecular tension generation. For higher coverages, however, the linker tension exhibits a strong increase with increasing Σ. This change represents the shift from tension generated primarily by intramolecular steric repulsion between side chains to intermolecular repulsion. The surface coverage dependence of the linker tension can be approximated by the expression

Figure 4.

Average linker tension as a function of coverage Σ for (a) N_sc = 50, (b) N_sc = 100, and (c) N_sc = 200 for the four values of N_bb (black/circles: N_bb = 50; red/triangles: N_bb = 100; blue/squares: N_bb = 150; green/diamonds: N_bb = 200).

$$f_{\text{link}}(\mathrm{\sum })=f_{\mathrm{d}}\left[1+{\left(\frac{\mathrm{\sum }}{\mathrm{\sum }\ast \ast }\right)}^{\beta }\right]$$ (1)

Equation 1 represents a simple empirical crossover form that connects low- and high-coverage behavior seen in Figure 4, where Σ** represents the estimated crossover coverage between the loosely-grafted and densely-grafted regimes. For Σ ≪ Σ**, the expression for the linker tension reduces to f_d, the linker tension for a mushroom-regime bottle-brush chain. The parameter β represents the scaling exponent relating tension to surface coverage for densely-grafted brushes. The values of each of these parameters for the 12 brushes are presented in Table 2 (plots of the data, with best-fit curves, are reported in the Supporting Information, Figure S1).

Table 2.

Fitting Parameters for Linker Tension Expression in Eq 1 for 12 Bottle-Brush Systems Presented, along with 1/D² Values Calculated and Estimates for σ**(D²/4)^a

Nsc	Nbb	fd(kBT/σ)	β	Σ**(1/σ2)	1/D2(1/σ2)	Σ**(D2/4)
50	50	9.38 (0.56)	1.56 (0.05)	0.0048 (0.0004)	0.0010	1.15
	100	9.86 (0.44)	1.96 (0.11)	0.0048 (0.0003)	0.0011	1.11
	150	10.08 (0.39)	2.08 (0.17)	0.0048 (0.0003)	0.0011	1.11
	200	9.75 (0.78)	2.01 (0.17)	0.0046 (0.0004)	0.0011	1.05
100	50	10.34 (0.59)	1.39 (0.08)	0.0024 (0.0002)	0.00040	1.50
	100	9.32 (1.36)	1.40 (0.09)	0.0014 (0.0003)	0.00040	0.88
	150	9.44 (1.96)	1.51 (0.16)	0.0014 (0.0004)	0.00041	0.84
	200	10.29 (1.77)	1.56 (0.16)	0.0015 (0.0004)	0.00041	0.91
200	50	11.68 (0.86)	1.20 (0.07)	0.0014 (0.0002)	0.00017	2.06
	100	11.56 (1.95)	1.26 (0.11)	0.0007 (0.0002)	0.00016	1.08
	150	13.03 (1.67)	1.51 (0.17)	0.0007 (0.0001)	0.00015	1.17
	200	14.16 (1.03)	1.63 (0.11)	0.0008 (0.0001)	0.00016	1.20

^aValues in parentheses indicate the 95% confidence interval for the parameters from the fitting procedure. Estimated error for 1/D² is on the order of ±0.0001.

The crossover coverage Σ** is independent of N_bb for N_bb > 50 (see Table 2). For crew-cut bottle-brushes, Panyukov et al.⁵⁵ predicted that tension amplification occurs in the focusing zone near the free end and remains constant throughout the transmission zone between the focusing zone and the substrate. For N_bb > 50, the brushes exhibit linker tension that places them closer to the crew-cut regime of bottle-brushes, as the linker site resides in the part of the brush where tension is not affected by N_bb. For N_bb = 50, only the 50:50 case shows similarity with the longer backbones, suggesting that this is the only case close enough to the others to show crew-cut behavior. Increasing the side chain length (N_sc ≥ 100) for N_bb = 50 results in different behavior, as D/R_ee > 1. While not necessarily indicative of hairy bottle-brushes, this places them out of the range of crew-cut brushes.

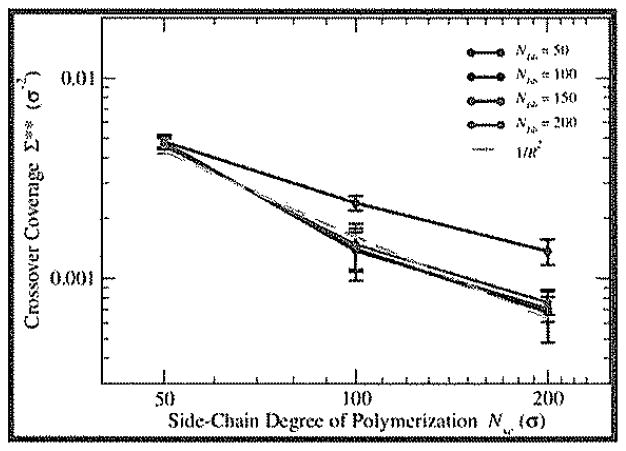
In both cases, however, we see a general trend of decreasing Σ** with increasing N_sc. This is to be expected when viewing Σ** as the boundary between loosely-grafted and densely-grafted regimes. Under the assumption that tension Amplification in the intermolecular regime occurs for Σ such that the area of the surface available for each bottle-brush (Σ⁻¹) is of the same order as the cross-sectional area D² of a single bottle-brush, we would expect to see Σ** scale as 1/D². As shown in Figure 5, there is a very nice agreement between Σ** and 1/R², the inverse square of the cross-section radius, suggesting a strong correlation between the extracted crossover coverage and the radial dimensions of the unperturbed brush.

Figure 5.

Log–log plots of Σ** vs N_sc (error bars represent 95% confidence interval from parameter extraction) with dashed orange line representing the relationships 1/R² vs N_sc for comparison.

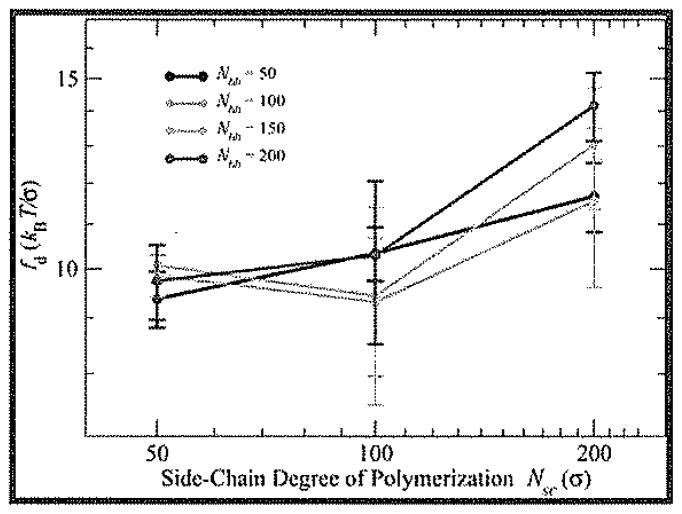
Panyukov et al.^52,55 found that the backbone tension in crew-cut bottle-brushes is dependent on the degree of polymerization of the side chains (i.e., N_sc), with tension in asymptotically crew-cut brushes increasing as N_sc^0.375. Figure 6 shows increasing linker tension f_d with increasing N_sc that would indicate crew-cut or crew-cut-like bottle-brushes; however, the exponent obtained from fitting the data in Figure 6 to the functional form expected showed all cases with exponents less than the expected 0.375. Our results indicate that apparent exponent increases from 0.13–0.16 for shorter backbones (N_bb = 50–100) to 0.21–0.3 for longer backbones (N_bb = 150–200), suggesting a possibility of reaching the theoretically predicted value of the scaling exponent (0.375) with increasing side chain length in the crew-cut regime or for very long backbones.

Figure 6.

Log–log plot of f_d as a function of N_sc for four different values of N_bb. Error bars represent 95% confidence interval from fitting procedure.

The exponent β in eq 1 describes the growth in linker tension due to the force that balances the osmotic pressure generated by the brush in the densely-grafted regime. The concentration dependence of osmotic pressure for free polymer chains in semi-dilute solutions is given by Π ∝ ϕ^{3ν/(3ν−1)}, where ν is a solvent-quality-dependent exponent (3/5 in good solvents, 1/2 in theta solvents). This gives rise to osmotic pressures proportional to the power of concentration with exponent 9/4 in good solvents and 3 in theta solvents.⁶⁷ If we extend this concept to the case of bottle-brushes, we can relate the concentration of polymer to the grafting density Σ and use that to determine the force necessary to hold the bottle-brush chains at a given osmotic pressure. With ϕ ~ Σ, Π ∝ Σ^{3ν/(3ν−1)}, and the force per chain then becomes related to Π times the surface area per bottle-brush, which is proportional to 1/Σ. Thus, the force per brush molecule scales as Π/Σ ~ Σ^1/(3ν−1), which gives exponent values ranging from 1.25 (semidilute regime/good solvent) to 2.0 (concentrated regime/theta solvent). Note that the exponent β in Table 2 covers this predicted range.

In addition to the simulations, which focus on “mobile” tethering points, simulations with two types of immobile (fixed) tethering points were also performed. One set of simulations featured fixed tethers randomly placed in the surface plane, while the other had tethering points on a hexagonal lattice. Both cases showed similar characteristics of tension accumulation, differing primarily in how much tension was generated as a function of Σ. At low Σ, where tension is generated within the brush and neighboring brushes do not interact, the tension was nearly identical for both fixed and mobile tethers, with slightly higher tension in brushes with randomly generated fixed tethers. The same effect was also seen at high Σ, where greater tension is generated by intermolecular interactions between highly crowded brushes. For intermediate Σ, however, the tension was almost identical with increasing Σ for mobile and lattice-fixed tethers, while the tension was larger for random tethering points.

3.3. Conformations of Side Chains

For Σ > Σ*, side chains on neighboring brushes produce conformational changes (see Figure 7) that result in tension transmission. To examine changes in side chain conformations with increasing Σ, we calculated the root-mean-square radius of gyration (〈R_g²〉^1/2) of the side chains in three dimensions, to take into account not only radial compression due to crowding but also extension orthogonal to the tethering surface. In Figure 8, we show 〈R_g²〉^1/2 as a function of Σ for the three different side chain lengths, for four backbone lengths.

Figure 7.

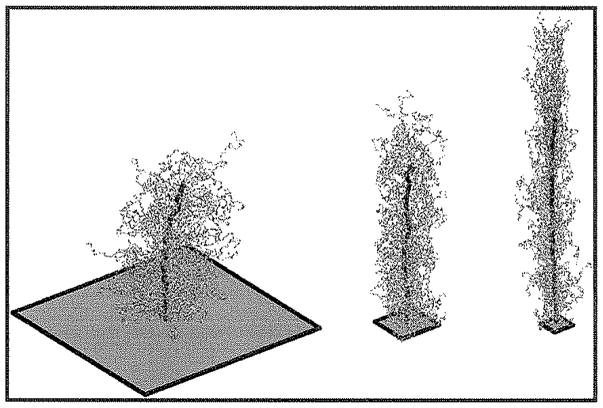
Snapshots of typical bottle-brush molecules with N_bb = 100 and N_sc = 100 from systems with Σ = 0.0001 (left), 0.002 (center) and 0.08 bottle-brushes/σ² (right). Squares at tethering site show average surface area per bottle-brush.

Figure 8.

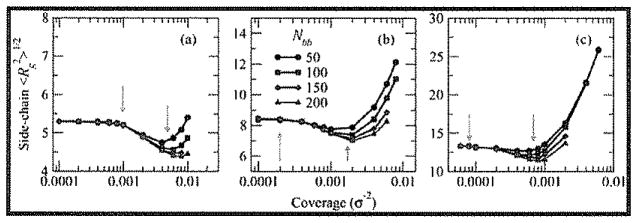
Dependence of root-mean-square radius of gyration 〈R_g²〉^1/2 of side chains on coverage for (a) N_sc = 50, (b) N_sc = 100, and (c) N_sc = 200. Arrows indicate coverages for mushroom to loosely-grafted crossover from 〈R_g²〉^1/2 (cyan) and loosely-grafted to densely-grafted crossover from Σ** (orange).

In Figure 8, we see indications of three types of behavior for the crew-cut brushes as Σ is increased. In each case, there is a regime at low Σ for which side chain 〈R_g²〉^1/2 is essentially constant, independent of Σ; this echoes the mushroom regime. Extrapolating from the intersection of the plateau region and the first decreasing region (linear in semilog form), we can obtain a rough estimate of the coverage of this first crossover Σ* between mushroom and loosely-grafted brush regimes, occurring for N_sc = 50 at Σ ≈ 1.0 × 10⁻³σ⁻² (¹/₂Σ**); for N_sc = 100 at Σ ≈ 2.0 × 10⁻⁴σ⁻² (0.1Σ**); and for N_sc = 200 at Σ ≈ 7.0 × 10⁻⁵σ⁻² (0.1Σ**). For longer side chains, this first crossover Σ* occurs at a coverage an order of magnitude lower than Σ**.

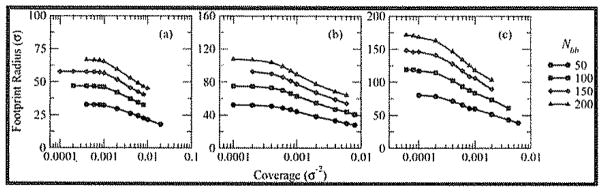
This first crossover Σ* between mushroom and loosely-grafted brush regimes may also be seen in the change in footprint radius with increasing coverage, as shown in Figure 9. The footprint radius is defined as $\langle R_{\mathrm{g},\text{bb},\text{xy}}^2+{\langle R_{\mathrm{g},\text{sc},\text{cy}}^2\rangle \rangle }^{1/2}$, where the radii of gyration refer to the projections of the backbone and side chains, respectively, onto the x–y plane. The inner average over $R_{\mathrm{g},\text{sc},xy}^2$ extends of all side chains of a given bottle-brush molecule, whereas the outer average over $R_{\mathrm{g},\text{bb},xy}^2+\langle R_{\mathrm{g},\text{sc},xy}^2\rangle$ runs over all bottle-brushes. The footprint radius, then, can be used to quantify the lateral area of the surface subsumed by the bottle-brush, taking into account any lateral bending and twisting of the backbone as well as radial extension or compression of the side chains. Especially evident for N_sc = 50 because of smaller persistence length but present for all three side chain lengths, is the transition from a plateau region at low Σ where backbones fluctuate and side chains swell in a favorable solvent environment and a region of monotonically decreasing footprint for increasing Σ in which the backbone fluctuations are suppressed and the side chains begin to compress. Estimating the crossover coverage as the point at which the plateau region ends, the crossover occurs at a coverage of ≈ 1.0 × 10⁻³σ⁻² for N_sc = 50; for N_sc = 100, it occurs at 2.0 × 10⁻⁴σ⁻²; and for N_sc = 200, the crossover takes place at a coverage of 8.0 × 10⁻⁵σ⁻². These values agree well with the estimation of the first crossover Σ* in Figure 8 and are significantly smaller than Σ**, confirming that Σ** represents a coverage of the second, loosely-grafted to densely-grafted crossover.

Figure 9.

Footprint radius of bottle-brush molecules vs coverage for (a) N_sc = 50, (b) N_sc = 100, and (c) N_sc = 200 for N_bb = 50 (black circles), 100 (blue squares), 150 (red diamonds), and 200 (green triangles). Note the logarithmic scale along the horizontal axis for all three graphs.

At coverages above the first crossover, 〈R_g²〉^1/2 exhibits a noticeable decrease from its value for low Σ (see Figure 8). This decrease in 〈R_g²〉^1/2 appears to be at least partially dependent on N_bb. Further, the decrease in 〈R_g²〉^1/2 with increasing Σ/decreasing d reaches a minimum at a higher coverage comparable to the crossover coverage Σ** estimated from the fit to the two-regime eq 1 (with d on the order of the brush radius) and is followed by an increase in side chain 〈R_g²〉^1/2 as molecular crowding increases.

To better understand the nature of the loosely-grafted to densely-grafted crossover Σ** in terms of changes in the conformations of side chains as coverage increases, we calculated the mean end-to-end distance for the side chains normal to the surface (i.e., vertical component or deflection) and parallel to the surface (i.e., radial component). In Figure 10, both the mean vertical component of end-to-end distance and mean radial extension of the side chains are plotted vs backbone monomer index of their attachment point for the representative 100:200 bottle-brush system at coverages representing the putative mushroom, loosely-grafted and densely-grafted regimes.

Figure 10.

Mean vertical component of end-to-end distance of side chains (left) and mean radial component of end-to-end distance (right) as a function of the bond index of attachment point for (100:200) brush at several different coverages.

In Figure 10a, the lowest coverage (1.0 × 10⁻⁴σ⁻²) is within the mushroom regime and shows two zones of side chain deflection: one within the region of 25 monomers closest to the backbone free end and one within the first 10–15 monomers at the substrate surface. In the former case, the deflection of side chains near the free end of the brush is to be expected as part of the focusing region of the crew-cut structure; tension is generated here by the extension of side chains in the vertical direction away from the normal to the backbone. This effect can also be seen in Figure 10b, where the radial extension is nearly constant aside from the region near the backbone free end, suggesting that side chains in this region increasingly orient themselves orthogonal to the substrate and present a smaller radial profile.

The deflection zone near the substrate is due to repulsion of side chains from the substrate surface and is not reflected in the radial extension, suggesting side chains extend out and normal to the surface. An increase in coverage in the loosely-grafted regime does not alter the vertical deflection of side chains—aside from a slight enhancement of the magnitude of deflection near the backbone free end. As Σ above the crossover into the densely-grafted regime (Σ > 0.002 bottle-brushes/σ²), the increased crowding between overlapping side chains causes the side chains to reorient toward the free surface and to stretch to a greater extent. The appearance and growth of a population of highly stretched side chains, which gives rise to the increase in average RMS R_g, can also be seen in Figures S2 and S3 of the Supporting Information. This increase in deflection carries with it the generation of tension further into the bottle-brush, as chain deflection and extension generate tension within an increasing number of side chains, transmitting increasing amounts of tension to the bonds along the backbone.

The radial extension, however, shows far less varied behavior. For all but the highest coverages simulated here, the radial component of the end-to-end distance shows minor variations from a constant value, decreasing only in the upper deflection zone previously mentioned. The radial extension in the interior of the brush decreases monotonically with increasing coverage, but when the transition from mushroom to loosely-grafted brush regime occurs, neighboring bottle-brushes cause compression almost uniformly over the majority of the brush length; as expected, side chains deswell rather than interpenetrate (until very high coverages; see Figure S4 in the Supporting Information for interpenetration data). At very high coverages, the region in which the radial extension decreases also begins to push into the main part of the brush, suggesting that at high grafting densities the chains at the free end compress radially and stretch vertically, which generates significant tension.

4. CONCLUSIONS

In this work, we have used molecular dynamics simulations of a coarse-grained model to elucidate some of the factors affecting the appearance and nature of tension amplification in layers of bottle-brush polymers tethered to a surface. We showed how increases in side chain size R correlate directly with the value of the surface coverage Σ** ≈ 1/R² at which tension in the bottle-brash backbone first begins to increase. Below this coverage, tension is almost constant, as the average distance between bottle-brush polymers remains larger than the diameter D of the bottle-brushes and side chains interact primarily with their neighbors on the same backbone. Beyond this crossover coverage, side chains of neighboring bottle-brush molecules strongly interact, and the tension generated by intramolecular interactions becomes augmented by intermolecular interactions with neighboring bottle-brushes. This data is presented primarily for bottle-brushes which were allowed to move laterally along the surface plane by virtue of “mobile” tethering points constrained to the surface plane.

We also examined correlations between the size of the footprint of tethered bottle-brush polymers and the crossover between mushroom and loosely-grafted brash regimes. As neighboring bottle-brushes begin to overlap, backbone fluctuations away from the normal to the substrate become suppressed. In addition, side chains begin to deswell, resulting in a reduction of 25–31% in 〈R_g²〉 without a concomitant increase in linker tension. Increasing the grafting density further, however, requires additional compression and reorientation of the side chains in order to minimize, as much as possible, the effects of steric hindrance, and it is this reorientation that generates the additional tension transmitted to the backbone that we see as tension amplification. This data and the proposed explanations shed some light on the basic physical properties of this interesting polymer architecture and engender new and expanded research in the future.

Figure 1.

Bottle-brush polymers (50:200) at surface grafting density Σ = 0.0008 bottle-brushes/σ². Backbones are shown in blue and side chains in red.