Diffusion Weighted MRI by Spatiotemporal Encoding: Analytical Description and In Vivo Validations

Abstract

Diffusion-Weighted (DW) MRI is a powerful modality for studying microstructure in normal and pathological tissues. DW MRI, however, is of limited use in regions suffering from large magnetic field or chemical shift heterogeneities. Spatio-temporal encoding (SPEN) is a single-scan imaging technique that can deliver its information with a remarkable insensitivity to field inhomogeneities; this study explores the use of diffusion-weighted SPEN (dSPEN) MRI as an alternative for acquiring this kind of information. Owing to SPEN’s combined use of gradients and radiofrequency-swept pulses, spatially-dependent diffusion weightings arise in these sequences that are not present in conventional k-space DW MRI. In order to account for these phenomena an analytical formalism is presented that extends Stejskal & Tanner’s and Karlicek & Lowe’s work, to derive the b-values arising upon taking into account the effects of adiabatic pulses, of imaging as well as diffusion gradients, and of cross-terms between them. Excellent agreement is found between the new features predicted by these analytical and numerical derivations, and SPEN diffusion experiments in phantoms and in anisotropic ex vivo systems. Examinations of apparent diffusion coefficients in human breast volunteers also verify the advantages of the new methods in vivo, which exhibit substantial robustness vis-à-vis comparable DW echo planar imaging.

1. Introduction

Diffusion provides an outstanding contrast mechanism for the non-invasive analysis of in vivo tissues under both normal and pathological conditions [1–3]. Single-scan “ultrafast” magnetic resonance imaging (MRI) methods play an essential role in such in vivo diffusion studies. This reflects the need to overcome spontaneous subject motions inside the magnet [4, 5], during an experiment that is trying to measure µm-sized random displacements without external interferences. Furthermore, many diffusion methodologies call for the probing of several diffusion directions and/or many gradient values, thereby prolonging significantly the scanning times. The use of restricted field of views (FOVs), parallel imaging [6] and partial Fourier reconstruction [7] can, to some extent, minimize the duration of a diffusion examination, and make it compatible with the times associated to conventional, multi-scan MRI methods –particularly if combined with animal immobilization strategies. Still in most cases, and certainly in clinical applications, Echo Planar Imaging (EPI) is the method of choice for performing in vivo diffusion studies [8, 9]. EPI is a rapid scan method sweeping the full image-reciprocal k-space in one shot [10, 11], thereby executing the entire experiments in sub-second timescales. EPI-based sequences can be modified to incorporate diffusion-weighting (DW) gradients of the kind first discussed by Stejskal and Tanner [12], resulting in a variety of alternatives [13] whose diffusion-weighting properties have been thoroughly analyzed [14, 15]. Still, it is also known that EPI’s speed is achieved at the expense of certain sacrifices in robustness; particularly with respect to chemical shift offsets and to field heterogeneities. Improvements and alternatives based on other fast imaging methods are therefore of interest [16–18]. The present study examines the potential use of one such method, based on spatiotemporal encoding (SPEN) manipulations. SPEN, like EPI, provides a single-shot imaging method. Among SPEN’s most noteworthy features counts a built-in robustness vis-à-vis field inhomogeneities [19, 20], the possibility of acquiring images under nearly T₂*-free, full-refocusing conditions [21], and an inherent insensitivity to chemical shift offsets [22]. These attributes suggest SPEN as an interesting candidate for diffusion-weighted studies –particularly in challenging cases like high-field clinical or pre-clinical analyses. Describing the new physical features arising upon modifying SPEN sequences for DW analyses and demonstrating the capabilities of the ensuing diffusion-weighted SPEN (dSPEN) method in in vitro and in vivo cases, are the main objectives of this study.

2. Theory

2.1. dSPEN MRI: Basic physical description

In a basic DW experiment, random molecular motions are monitored by exciting the spins, and subjecting them to a pair of diffusion-sensitizing magnetic field gradients G_d. Despite these gradients’ zero overall action, a net signal attenuation will arise reflecting the random motions that spins will undergo during the interval Δ separating these gradients [23]. In the absence of background or imaging gradients, this diffusion-driven signal attenuation is summarized by Stejskal-Tanner’s classical Pulsed-Gradient Spin-Echo (PGSE) formula [12]

$$S\left(b\right)=S_0{e}^{-bD}$$ (1a)

where S and S₀ are the signal intensities with and without the diffusion weighting gradients G_d, D is the free diffusion coefficient, and

$$b={\gamma }^2{G}_d^2{\delta }^2\left(\Delta -\frac{\delta }{3}\right)$$ (1b)

This b-value notation summarizes the total diffusion weighting accumulated during the PGSE sequence by incorporating the spatial winding imposed by the gradients G_d, the gyromagnetic ratio γ of the investigated nuclei, the duration of each gradient pulse δ, and the diffusion time Δ. A typical DW MRI analysis exploits the ensuing signal attenuations to calculate, for each voxel in an image, an apparent diffusion coefficient (ADC) conveying valuable insight for research and diagnosis [24–27].

Whereas the b-coefficient in Eq. (1b) fully summarizes the diffusion weighting in a PGSE experiment when the diffusion-sensitizing gradients are the only dephasing elements in a sequence, additional gradients –like those needed for recording an image– can impose further diffusion weightings of their own. Some of these will affect S and S_o identically and hence will factor out; but cross-terms between the imaging and the diffusion gradients are liable to arise, that can distort the ADC’s derived from an analysis based solely on Eq. (1b). Extracting ADC maps requires accounting for these additional terms in the final b-value expressions [13, 14]. Such analyses have been described for several mainstream MRI sequences [28–30]; one of this study’s aims is to extend these calculations to the case of ultrafast spatio-temporally encoded (SPEN) MRI.

SPEN is an imaging modality that relies on a progressive excitation and refocusing of the spins along one or more spatial sample axes. In a 1D implementation this can be achieved by applying a frequency-swept radio frequency (RF) pulse, whilst changing its frequency offset at a constant rate R while in the presence of an encoding gradient G_e. Assuming that the latter is applied along the z-axis, G = ∂B / ∂z, a 90° excitation pulse lasting for a time T_e will result in a quadratic phase profile:

$${\varphi }_e\left(z\right)=\frac{{\left(\gamma G_e\right)}^2}{2R}{z}^2-\frac{{\left(\gamma G_e\right)}^{2}FOV}{2R}z$$ (2)

where FOV defines the targeted field-of-view, R is the RF sweep rate defined by γG_eFOV/T_e, and for simplicity, constant phase terms were neglected. Eq. (2)’s quadratic spatial dependence will lead to a destructive interference among the observable signal for all points except those corresponding to the parabola’s stationary point, z= z_SP. The acquired signal S will therefore be proportional to the density of the spins emitting at this z_SP-coordinate. This focal point can be displaced throughout the FOV by applying an acquisition gradient G_a(t) acting over a time T_a, such that k_a(t=T_a) = γ ${\displaystyle \underset{0}{\overset{T_a}{\int }}{G}_a\left(t\right)dt}=-G_e{T}_e.$ k_a will shift ϕ_e’s stationary point according to z_SP(t) = -(FOV/2) + FOV(t/T_a). Signal digitized throughout this process will have a magnitude given by

$$\left|S\left(t\right)\right|\propto \Delta z\cdot \rho \left[z_{SP}\left(t\right)\right]$$ (3)

thus rasterizing the spin’s density with an intrinsic spatial resolution $\Delta z=\sqrt{\frac{FOV}{\gamma G_e{T}_e}}$[20, 31, 32]. Additional details on this imaging principle and on how it can be extended to 2D and 3D ultrafast acquisitions –as well as various ways of enhancing the method’s resolution without incurring SAR penalties– can be found in the literature [19, 33]. Most common among these recently proposed strategies are so-called “Hybrid” implementations, whereby SPEN deals with what in EPI is usually assigned to the “low-bandwidth” (phase-encoded) dimension, and a conventional k-space readout dimension monitors an orthogonal axis [19, 32]. An important feature arising in this imaging modality is its “full refocusing” capability: if in SPEN experiments a 180° refocusing pulse is inserted mid-way between encoding and acquisition processes endowed with identical durations (i.e., T_e = T_a), an echoing of all T₂*/shift effects results, for every spin-packet emitting throughout the course of the data acquisition. This opens valuable opportunities concerning the acquisition of undistorted single-scan 2D images with enhanced resilience towards shift and field heterogeneities.

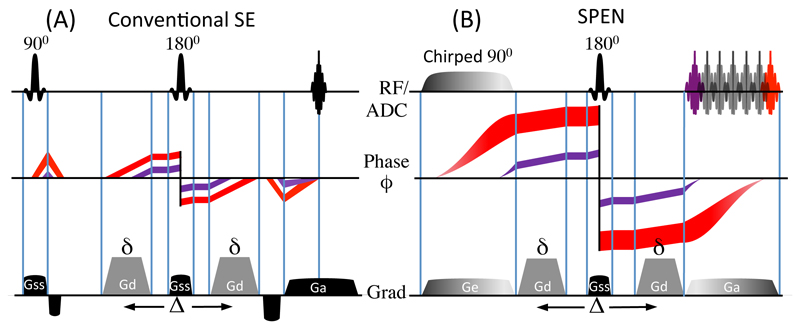
As a result of SPEN’s non-uniform temporal excitation, a number of distinct features arise upon considering its use for mapping diffusivities. Some of these are illustrated in Figure 1, which compares –for a 1D diffusion imaging case– the phases evolved by spin-packets in Spin-Echo (SE) and in SPEN experiments incorporating a PGSE diffusion-weighting module. For clarity only two spin-packets positioned towards opposite ends of the sample are depicted (in red and purple), and both the phase evolution and the phase spread undergone by each of these elements is plotted. From this cartoon one can appreciate that, whereas the amount of local dephasing arising in a conventional SE sequence will be independent of position (Fig. 1A), the fact that in SPEN spins positioned in one of the edges evolve under the action of the imaging gradient over longer periods than spins at the opposite edge can be appreciated; importantly, this implies that the diffusion-weighting effects in SPEN will be uneven throughout the sample (Fig. 1B). This will happen, despite the fact that the PGSE gradient pulses impose, in both instances, a position-independent amount of local dephasing. Further complications will arise –as happens for most MRI sequences– from the fact that even for G_d = 0 a diffusion weighting arises from the imaging gradients themselves [30], or from effects associated with background gradients [34]. Cross-terms may also arise between the diffusion and all these additional gradients [13]. Unless properly accounted for all these interactions between the imaging and the diffusion gradients can preclude an accurate quantification of the ADC maps; their description for the case of dSPEN experiments is the aim of the following Paragraph.

Figure 1.

1D Spin-Echo (A) and 1D SPEN (B) imaging experiments, depicting the phase dispersion undergone by two spin packets in each sequence. Whereas in 1D SE all spins experience the same local dephasing throughout the sample, in SPEN, the quadratic dependence (Eq. 2) induce different local ϕ-dispersion. The cartoons illustrates this for two spin-packets colored in red and purple; as b-values depend on the degree of local dephasing, a spatial weighting throughout the FOV is incurred. The RF/ADC line displays the RF and signal acquisition timings; the gradients are: G_e = encoding gradient; G_d = diffusion gradient; G_ss = slice-selective gradient; G_a = acquisition gradient; diffusion timing parameters are δ and ∆.

2.2. Diffusion SPEN MRI: b-value derivations

The Stejskal-Tanner formalism leading to (Eq. 1) considers a pair of diffusion-sensitizing gradients, applied in a step-wise manner within a spin-echo framework [12]. In a generalization of the Stejskal-Tanner formalism, Karlicek and Lowe [35] showed that in the presence of more generic, time-dependent gradient waveforms γG(t)z, the signal attenuation undergone by the spins will be given by a function A(t) = S(t)/S_o(t) that at arbitrary times is

$$A\left(t\right)=\text{exp}\left[-D\cdot {\displaystyle \underset{0}{\overset{t}{\int }}{K}^2\left(t\prime \right)dt\prime }\right]$$ (4)

where S_o is once again the signal in the absence of the diffusion-sensitizing gradients, and

$$K\left(t\prime \right)=\gamma {\displaystyle \underset{0}{\overset{t\prime }{\int }}G\left(t″\right)dt″}$$ (5)

is a wavenumber summarizing the action of all gradients up to a particular time t’ within the sequence. This description, which is fully consistent with the Stejskal-Tanner equations, is suitable as long as the local dephasing undergone by the spins –which is what DW MRI eventually relies upon to probe diffusion– is linear and independent of the spins’ absolute positions; i.e., as long as ∂B(t, z / ∂z = G(t), ∀z. Such a description is, however, insufficient in situations like those arising in SPEN, where as mentioned dephasing will be neither linear (cf. (Eq. 2)) nor independent of the spin’s absolute position. Faced with non-linear gradients, Loening et al [36] derived a more extended form for the attenuation function for the case of magnetic field distributions with arbitrary geometries. In this analysis, diffusion attenuation is still given by (Eq. 4), but with K now accommodating an “effective” wavenumber involving an arbitrary spatial dependence of the rotating frame fields

$$K^{*}\left(t\prime ,z\right)=\gamma {\displaystyle \underset{0}{\overset{t\prime }{\int }}{G}^{*}\left(t″,z\right)dt″=\gamma {\displaystyle \underset{0}{\overset{t\prime }{\int }}\left[\partial B^{*}\left(t″,z\right)/\partial z\right]dt″.}}$$ (6)

Even this extension, however, is still not general enough to describe SPEN experiments: here not only will the gradient impart a nonlinear dephasing but also the spin dynamics itself will be subject to various time- and frequency- (i.e., space-) dependent manipulations. To deal with such complexities, we employ instead the formalism described in [37], that relates diffusion effects with the spins’ rotating-frame evolution phases $\phi (t,z_o)=\gamma {\displaystyle \underset{0}{\overset{t}{\int }}B(t\prime ,z_o)dt\prime }$ that have been expanded according to:

$$\varphi \left(t,z_0+\delta z\right)=\varphi \left(t,z_0\right)+\frac{d\varphi \left(t,z_0\right)}{dz}\delta z+O\left(\delta z^2\right)\approx \varphi \left(t,z_0\right)+K_{local}\left(t,z_0\right)\delta z$$ (7)

K_local here is the phase dispersion that, in proximity to an arbitrary position z₀ within the object’s FOV, is experienced by the spins throughout the sequence. This local phase dispersion can then be incorporated into Karlicek & Lowe’s model ((Eq. 4)), to fully account for the diffusion-driven attenuation function

$$\begin{array}{l}A\left(t,z_o\right)=\exp \left[-D\cdot {\displaystyle \underset{0}{\overset{t}{\int }}{K}_{local}^2\left(t\prime ,z_o\right)dt\prime }\right]\hfill \\ =\exp \left[-D\cdot {{\displaystyle \underset{0}{\overset{t}{\int }}\left(\frac{d\phi \left(t\prime ,z_o\right)}{dz}\right)}}^{2}dt\prime \right]\hfill \end{array}$$ (8)

As expected from the Bloch-Torrey equations, this decay will be independent of the absolute value of local phases ϕ(t,z_o), and will only be given by their spatial derivatives. Such phases can be computed analytically or numerically for sequences of arbitrary complexity, as illustrated below for 2D SPEN encoding examples based on 90° chirp and 180° adiabatic sweep pulses.

2.3. Diffusion SPEN: Analytical Results for Model Experiments

Given this framework for calculating the diffusion-driven signal attenuation as a function of time and position, we focused on calculating the expected decays for a number of dSPEN imaging pulse sequences. We begin by analyzing a sequence like the one shown in Fig. 2B, taking into consideration for simplicity only the SPEN axis and its imaging gradients, and assuming for the time being that the PGSE gradients are null: i.e., G_d = 0. In the ensuing 1D imaging sequence the initial 90° chirp pulse will flip spins sequentially away from their longitudinal equilibrium state. Denoting t₉₀ as the instant at which the chirp RF’s frequency matches the spins’ resonance frequency, these nutations will occur at a position-dependent time given by

$$t_{90}\left(z\right)=\frac{\gamma G_{e}z-O_i}{R}$$ (9)

where O_i is the initial frequency of the chirp and R its constant sweep rate. At this instant spins will nutate into the x-y plane of the Bloch sphere, at a phase ϕ(z) = ϕ_RF[t₉₀(z)] + 90° depending on the instantaneous angle that the B₁(t) RF subtends with the Bloch’s x-axis at the time it becomes resonant with the spin packet: ${\varphi }_{RF}(t)=O_{i}t+\frac{R{t}^2}{2}$ [38]. For the rest of the excitation and up to a duration T_e , the excited spin will continue to evolve in the presence of a gradient G_e, accruing at the end of the overall process the phase ϕ_e(z) given in Eq. 2. Following this excitation a (slice-selective) 180° pulse flips the spins in the transverse plane, effectively reversing –within a constant value assumed as zero– the accrued phases. Then, over the course of an acquisition lasting up to a time T_a, the presence a second gradient G_a progressively shifts the parabolic phase imparted by the excitation chirp, until each spin packet reads out its contribution in a ‘first-excited / last-observed’ fashion. Throughout the course of all these processes, diffusion effects will make an imprint depending on the spins’ degree of local dephasing. On the basis of the aforementioned analysis, the overall attenuation imparted by diffusion can be calculated on the basis of the wavenumber

$$K_{local}\left(t,z\right)=\frac{d\left({\phi }_e\left(z\right)+{\phi }_a\left(t,z\right)\right)}{dz}=\frac{d}{dz}\{\begin{array}{cc}0,& 0\le t\le t_{90}\left(z\right)\\ {\phi }_{RF}\left[t_{90}\left(z\right)\right]+\gamma G_{e}z\left[t-t_{90}\left(z\right)\right],& t_{90}\left(z\right)\le t\le T_e\\ -\langle {\phi }_{RF}\left[t_{90}\left(z\right)\right]+\gamma G_{e}z\left[T_e-t_{90}\left(z\right)\right]\rangle +\gamma G_{a}zt,& T_e\le t\le T_e+T_a\end{array}$$ (10)

Based on the various definitions given earlier this equals to

$$K_{local}\left(t,z\right)=\{\begin{array}{cc}0,& 0\le t\le t_{90}\left(z\right)\\ \gamma G_e\left[t-t_{90}\left(z\right)\right],& t_{90}\left(z\right)\le t\le T_e\\ -\gamma G_e\left[T_e-t_{90}\left(z\right)\right]+\gamma G_{a}t,& T_e\le t\le T_e+T_a\end{array}$$ (11)

Substituting these expressions into Eq. (8) leads to the exponential attenuation function,

$$A\left(t,z\right)=\exp \left[-D{\gamma }^2\left(\begin{array}{l}-\frac{G_e^2{\left(t_{90}\left(z\right)-T_e\right)}^3}{3}+\\ \frac{T_a\left(3t_{90}^2\left(z\right)G_e^2+G_a^2{T}_a^2-3G_a{G}_e{T}_a{T}_e+3G_e^2{T}_e^2+3t_{90}\left(z\right)G_e\left(G_a{T}_a-2G_e{T}_e\right)\right)}{3}\end{array}\right)\right]$$ (12)

Notice that, even in the absence of diffusion-sensitizing gradients, an explicit and potentially significant z-dependence emerges for the attenuation factor imparted by diffusion on a SPEN MRI sequence, as adumbrated by the cartoons in Figure 1.

Figure 2.

2D single-scan diffusion pulse sequences assayed, with their gradients and timing definitions (delays not drawn to scale). In the 2D Spin-Echo EPI (A), single-slice 2D SPEN (B) and multi-slice 2D SPEN (C) sequences, the diffusion-sensitizing gradients are located on both sides of a central refocusing pulse. In (D) the diffusion blocks is placed in a T_a/2 delay required by SPEN’s full refocusing procedure; in (E) G_d operates as a separate diffusion block in combination with a 180° hard pulse, leading to a compensation of cross-terms and reduced spatial b-dephasing. All SPEN diffusion sequences are fully refocused. The RF/ADC line displays the RF and signal acquisition; other definitions: G_e = encoding gradient; G_d = diffusion gradient (shown in gray for all sequences); G_ss = slice-selective gradient; G_pr = purge gradient; G_a = acquisition gradient; T_a = acquisition time; N_LB = number of loops encoding the low-bandwidth (PE/SPEN) dimensions.

With this as background, it is possible to derive the full K_local and the diffusion-driven attenuation functions arising in a DW experiment that, in addition to the SPEN encoding/decoding gradients, includes diffusion gradients G_d like those shown in Figure 2B. The K_local wavenumber formalism described above then leads to

$$K_{local}\left(t,z\right)=\{\begin{array}{cc}0& 0\le t\le t_{90}\left(z\right)\\ \gamma G_e\left[t-t_{90}\left(z\right)\right],& t_{90}\left(z\right)\le t\le T_e\\ \gamma G_e\left[T_e-t_{90}\left(z\right)\right]+\gamma G_d\left(t-T_e\right),& T_e\le t\le T_e+\delta \\ \gamma G_e\left[T_e-t_{90}\left(z\right)\right]+\gamma G_d\delta ,& T_e+\delta \le t\le T_e+\Delta \\ \gamma G_e\left[T_e-t_{90}\left(z\right)\right]+\gamma G_d\delta -\gamma G_d\left(t-\left(T_e+\Delta \right)\right),& T_e+\Delta \le t\le T_e+\delta +\Delta \\ -\gamma G_e\left[T_e-t_{90}\left(z\right)\right]+\gamma G_{a}t& T_e+\delta +\Delta \le t\le T_e+\delta +\Delta +T_a\end{array}$$ (13)

where δ are the durations of pulsed gradients flanking an instantaneous 180° refocusing pulse. Substituting this equation into the exponential attenuation function in (Eq. 8), yields

$$A\left(t,z\right)=\exp \left[-D{\gamma }^2\left(\begin{array}{l}-\frac{G_e^2{\left(t_{90}\left(z\right)-T_e\right)}^3}{3}+\\ \frac{{\left(t_{90}\left(z\right)G_e-G_e{T}_e\right)}^3+\left(G_d\delta +G_e{\left(-t_{90}\left(z\right)+T_e\right)}^3\right)}{3G_d}+\left(\Delta -\delta \right){\left(G_d\delta +G_e\left(-t_{90}\left(z\right)+T_e\right)\right)}^2+\\ \frac{{\left(G_e^3\left(t_{90}\left(z\right)-T_e\right)\right)}^3+{\left(G_d\delta +G_e\left(-t_{90}\left(z\right)+T_e\right)\right)}^3}{3G_d}+\\ \frac{T_a\left(3t_{90}^2\left(z\right)G_e^2+G_a^2{T}_a^2-3G_a{G}_e{T}_a{T}_e+3G_e^2{T}_e^2+3G_e^2{T}_e^2+3t_{90}\left(z\right)G_e\left(G_a{T}_a-2G_e{T}_e\right)\right)}{3}\end{array}\right)\right]$$ (14a)

Notice that in this case, besides an explicit z-dependence of the diffusion-driven attenuation, cross-terms involving products between G_e, G_a and G_d, emerge. These terms reflect a diffusion-imposed cross-talk between the SPEN- and the G_d-gradients. For this particular case it is feasible to separate the attenuating effects imposed by the gradients employed for the encoding, for the acquisition, and for diffusion-sensitization, as well as isolating their respective cross-terms combinations. Indeed eq. (14a) can be rewritten as

$$A\left(t,z\right)=\exp \left[-Db\right]=\exp \left\{-D\left[\begin{array}{l}{\gamma }^2{G}_d^2{\delta }^2\left(\Delta -\frac{\delta }{3}\right)-\\ \frac{{\gamma }^2{G}_e^2{\left(t_{90}\left(z\right)-T_e\right)}^2\left(t_{90}\left(z\right)-3\Delta -3\delta -3T_a-T_e\right)}{3}+\\ \frac{{\gamma }^2{G}_a^2{T}_a^3}{3}+\\ {\gamma }^2{G}_a{G}_e{T}_a^2\left(t_{90}\left(z\right)-T_e\right)+\\ 2{\gamma }^2{G}_d\Delta \delta G_e\left(-t_{90}\left(z\right)+T_e\right)\end{array}\right]\right\}$$ (14b)

The first term in this expression is as the PGSE decay of (Eq. 1), the second term describes the attenuation arising during the encoding, the third term is associated solely with the acquisition gradient, and the two final terms describe the diffusion-driven cross-talk between the encoding and the acquisition gradients, and between the encoding and the diffusion-sensitizing gradients. Notice that these last two terms, which bear significance in obtaining accurate ADCs, have now become explicitly spatially dependent.

It is worth considering a different type of spatial encoding, whose diffusion effects will turn out having different spatial and cross-term dependencies than the ones just derived. The sequence in question is illustrated in Figure 2C, and it replaces the chirp 90° excitation by a hard (or eventually, a slice-selective) 90° nutation, followed by an adiabatic, linearly-swept 180° pulse implementing the SPEN encoding. In this scenario the phase accumulated by spins during the sweep will be

$${\varphi }_e(z)=-\frac{{(\gamma G_e)}^2}{R}{z}^2$$ (15)

By contrast to (Eq. 2) this encoding exhibits no linear term, implying that a purge gradient ( G_pr) will have to be introduced in order to shift the parabolic phase profile to one end of the FOV, and enable the subsequent acquisition gradient to sweep the stationary point of ϕ_e from one edge of the sample to the other. With these differences in mind one can rederive a revised version of K_local (summarized in Appendix A), and obtain therefrom an attenuation factor for this kind of dSPEN experiment:

$$A(t,z)=\exp \left[-D{\gamma }^2\left(\begin{array}{l}\frac{G_{pr}^2{T}_{pr}^3}{3}+\frac{\delta \left(G_d^2{\delta }^2-3G_d\delta G_{pr}{T}_{pr}+3G_{pr}^2{T}_{pr}^2\right)}{3}+\hfill \\ \frac{{\left(G_d\delta +t_{180}(z)G_e-G_{pr}{T}_{pr}\right)}^3+{\left(-G_d\delta +G_{pr}{T}_{pr}\right)}^3}{3G_e}+\hfill \\ \frac{{\left(t_{180}(z)G_e-\delta (G_d+G_e)+(-G_e+G_{pr})T_{pr}\right)}^3}{3G_e}+\hfill \\ \frac{{\left(G_d\delta -2t_{180}(z)G_e-G_{pr}{T}_{pr}+G_e(\text{Δ}+T_{pr})\right)}^3}{3G_e}\hfill \\ \frac{{\left(-2t_{180}(z)G_e+G_e{T}_e+G_d(-\text{Δ}+2\delta +T_e)-G_{pr}{T}_{pr}\right)}^3}{3G_d}+\hfill \\ \frac{{\left(2t_{180}(z)G_e+G_d(\text{Δ}-\delta -T_e)-G_e{T}_e+G_{pr}{T}_{pr}\right)}^3}{3G_d}\hfill \\ \frac{{\left(-2t_{180}(z)G_e+G_a{T}_a+G_e{T}_e-G_{pr}{T}_{pr}\right)}^3}{3G_a}+\hfill \\ \frac{{\left(2t_{180}(z)G_e-G_e{T}_e+G_{pr}{T}_{pr}\right)}^3}{3G_a}\hfill \end{array}\right)\right].$$ (16)

Before concluding this Paragraph, it is worth summarizing a general case whereby this 1D analysis is extended to instances involving three-dimensional gradients for diffusion and/or imaging encoding. The effective phase distribution then needs to take into account its spatial spreading in all three orthogonal directions. Free Gaussian diffusion thus ends up contributing to the overall signal attenuation as:

$$\begin{array}{l}A(t,{\overrightarrow{r}}_o)=\exp \left\{-D({\overrightarrow{r}}_o)\cdot {\displaystyle \underset{0}{\overset{t}{\int }}\left[{\left(\frac{d\phi (t\prime ,{\overrightarrow{r}}_o)}{dx}\right)}^2+{\left(\frac{d\phi (t\prime ,{\overrightarrow{r}}_o)}{dy}\right)}^2+{\left(\frac{d\phi (t\prime ,{\overrightarrow{r}}_o)}{dz}\right)}^2\right]}dt\prime \right\}\\ =\exp \left[-D({\overrightarrow{r}}_o)\cdot b({\overrightarrow{r}}_o)\right].\end{array}$$ (17)

3. Materials and Methods

3.1. Pulse Sequencing Considerations

With these theoretical and analytical tools at hand, attention was centered on exploring the utility of dSPEN in a number of scenarios. The four diffusion measurement pulse sequences tested are shown in Figs. 2B-2E; these were compared against a classical SE EPI diffusion-weighted paradigm (Fig. 2A). Two of the tested sequences, those in Figs. 2B and 2C, were alluded to in the preceding Section. These derive from the original single-scan single- and multi-slice 2D SPEN MRI sequences discussed elsewhere [19, 22] –adapted to monitor diffusion by the inclusion of G_d. An important aspect of the dSPEN sequences here assayed, centered on endowing them with a full-refocusing characteristic; i.e., making sure that the time evolved by the spins from their initial excitation until the common 180° pulse that these sequences incorporate at their center, be equal to the time elapsed from this echo until the instant at which each spin-packet emits its response in the spatial decoding process [32]. Repeated tests have demonstrated that this provides the highest quality images, allowing one to investigate regions that may be beyond EPI’s analytical abilities [39]. The incorporation of the diffusion-sensitizing gradients was in turn guided by two different aims. In the single-slice 2D SPEN sequence in Fig. 2B and in the multi-slice 2D SPEN of Fig. 2C, diffusion gradients were integrated into the original SPEN pulse sequences in the simplest way, by flanking both sides of the central 180° spin echo with identical G_d pulses (notice then the similarity between the sequence in Fig. 2B and the original diffusion-weighted SE EPI often used in DW experiments). Two additional multi-slice 2D SPEN schemes were assayed, in which the diffusion gradients were placed in different portions of the sequence. In the version shown in Figure 2D a bipolar diffusion “block” was added during the initial T_a/2 delay, that multi-slice sequences relying on 180° adiabatic passages need to incorporate for the sake of achieving full-refocusing conditions. Figure 2E presents a different encoding mode where the diffusion-sensitizing gradients possess equal signs and are separated by a hard 180° pulse. This inversion replaces the post-acquisition “rewinding” 180° pulse that these sequence otherwise need for the sake of returning all the non-transverse magnetizations (which were inverted by the sequence’s adiabatic passage) back to their equilibrium position. The varying location of the diffusion gradients in these pulse sequences result in different cross-terms between the diffusion and the imaging gradients; and hence to different DWI imaging performances. In all the diffusion studies shown below, the new dSPEN strategies were programmed and compared with similarly structured and timed EPI-based DW experiments (Fig. 2A), as well as with multi-scan gradient-echo (GE) and fast spin-echo (FSE) images taken as anatomical references.

3.2. ADC maps computations

It follows from the arguments presented in Section 2 that a quantitative calculation of the ADC maps resulting from dSPEN data requires a full b-value calculation to be performed. Although this calculation could be analytically conducted for simple 1D cases adapted from Figures 2B, 2C, it can rapidly become long and cumbersome for the remaining sequences in Figure 2. As an alternative, programming scripts accounting for all the shaped crushers, purging, G_e, G_a and G_d gradients applied along three dimensions, as well as for different kinds of RF pulses involved, were written and used to evaluate the spins phase evolution under all the events occurring in the sequences. With these phases the K_local(t)-wavenumbers (including their full 3D spatial dependency) were computed as per Eq. (8), and with them the “exact” $b\overrightarrow{(r)}$ values were calculated. Using these effective attenuation factors, $\text{ADC}\overrightarrow{(r)}$ maps could be derived from the experimental signal attenuations revealed by the SPEN images. Such scripts were programmed in MATLAB^® (The MathWorks, Inc., Natick, MA) and are available upon request.

3.3. Experiments

Ex-vivo experiments were conducted at 7T (300/89) on a Varian VNMRS vertical-bore system using a single-coil probe with overall volume of 30×30×46 mm³. Samples analyzed in this system included CuSO₄-doped water, fresh celery and formalin-fixed swine spinal cord –all at 21±1 °C. Additional in-vivo experiments were conducted on a 3T Siemens TIM TRIO clinical system using a 4-channels breast coil. In these experiments a series of scans were performed on healthy female volunteers, according to procedures approved by the Internal Review Board of the Meir Medical Center (Kfar-Saba, Israel) after obtaining informed suitable written consents. These Siemens-based experiments included scanner-supplied twice-refocused DW SE EPI tests, as well as custom-written dSPEN MRI sequences. The RF pulses and gradient waveforms needed for these experiments were calculated either using available Siemens software, or customized routines for the RF pulses and gradient shapes computed in MATLAB^® and subsequently uploaded into the instruments prior to their execution. SPEN images were reconstructed using MATLAB scripts which processed the SPEN imaging data with super-resolution (SR) along the spatiotemporal dimension, and Fourier transformation along the k-dimension [39]. Further details on the imaging and DW parameters used in these various experiments are detailed in the corresponding figure captions.

4. Results and Discussion

4.1. Diffusion SPEN: Solution Phantom Validations

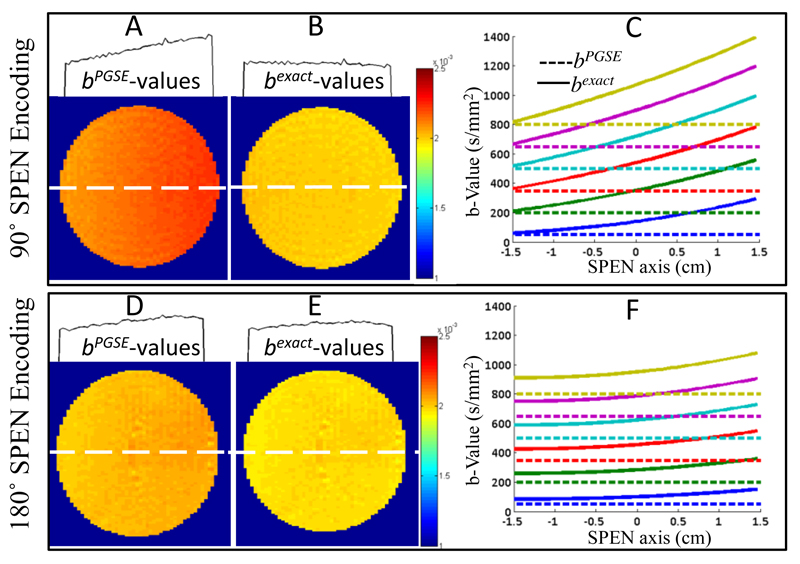
As experimental validation of the attenuation functions theoretically derived in Section 2, Figure 3 illustrates two single-shot dSPEN experiments conducted on a water sample. One of these experiments was used the single-slice sequence in Fig. 2B; the other used the 180° sweep RF SPEN in Fig. 2C, also in single-slice mode. ADC maps were derived for each of these experiments under two different assumptions: (i) that the imaging- and cross-term contributions arising from the SPEN encoding are negligible and that diffusion-driven signal attenuations arise solely due to the effects of G_d as given by the b-value in Eq. 1b (panels 3A and 3D and dashed lines in panels 3C and 3F), and (ii) by taking into account the effects that the SPEN imaging gradients will have on the effective b-values, as derived by the analytical calculations given in Section 2 (panels 3B and 3E and solid lines in panels 3C and 3F). It is interesting to notice from these figures that upon relying on a 90° encoding, there is good agreement between the PGSE-only prediction and the exact b-values at one end of the sample (the one that is last excited and first observed), but increasingly larger discrepancies arise for all remaining positions (e.g., solid lines in Fig. 3C). By contrast, discrepancies remain smaller throughout the sample for a 180°-driven SPEN encoding, but for no position is there agreement between the PGSE b-predictions and the actual b-values. The cross-sections on top of Figs. 3A and 3D present another rendition on the importance of using the exact b-values derived in Section 2 when analyzing this kind of measurements: they show the marked and clearly artificial curvatures in the ADCs of this water sample that will arise if neglecting the SPEN-derived contributions to the b-values involved. By contrast, ADC maps obtained upon employing the correct formalism (Figs. 3B and 3E) yield “flat” diffusion values, with no discrepancies vis-à-vis the literature free diffusion constant D = 1.98±0.02 x 10^-3 mm²/s [40]. Additional examples of implementing this kind of corrections are presented in Appendix B.

Figure 3.

Diffusion results for pure H₂O using 90° chirp (top panels) and 180° adiabatic sweep (lower panels) 2D SPEN sequences, upon ignoring (A, D) or accounting (B, E) for the effects of SPEN on the b-values. The A,B and D,E panels present the ADC maps together with 1D profiles illustrating cross-sections taken along the SPEN dimensions at the dashed white lines. The graphs in C, F compare the b-values expected solely on the basis of PGSE calculation (dashed lines) against the exact calculations as derived in Section 2 (solid lines). The diffusion parameters are δ = 3 ms, ∆ = 14 ms. The scanning parameters: TR=5sec, cubic FOV = 30x30 mm², resolution = 0.4×0.4 mm² on a 2 mm slice, number of averages = 4. Gradient and timing values for the 90° SPEN experiments: T₉₀ = 21ms, G_e = 1.2 G/cm, T_a = 21ms, G_a = 4.5 G/cm, total scan duration = 60 ms. Idem for the 180° SPEN parameters: T₉₀ = 2 ms, T₁₈₀ = 10.5 ms, G_e = 0.8 G/cm, T_a = 21 ms, G_a = 3 G/cm and a total scan duration = 51ms.

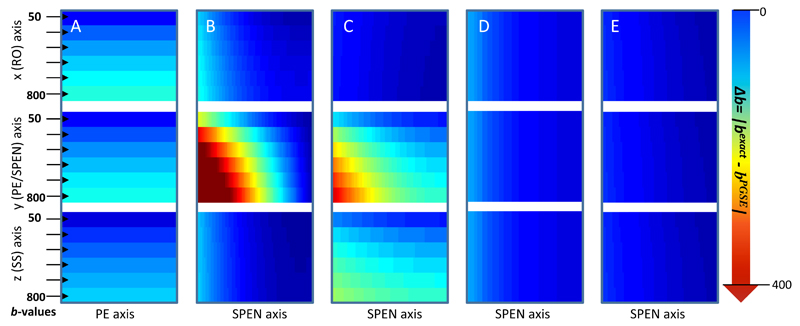
Encouraged by the lower b-curvatures arising along the SPEN axis when the encoding process involves a 180° sweep vis-à-vis what is obtained when imparting a 90° chirp excitation, the behavior for the remaining multi-slice 180°-sweep-based dSPEN sequences introduced in Figure 2 was explored. Figure 4 illustrates this comparison, showing for all the sequences in Figure 2 the residual values Δb = |b^exact (including the effects of all gradients and pulses) – b^PGSE (as calculated solely from Eq. 1b)|, arising when the diffusion-sensitizing gradients are applied along all three possible axes. The maximum flatness –i.e., minimum spatial dependence of these Δb deviations– is displayed by EPI; still this method clearly evidences the effects of cross-term Δb-values, which increase as G_d becomes higher. The variants introduced in Figs. 2B and 2C evidence both a marked spatial dependence and relatively large Δb deviations, particularly when G_d operates along the SPEN axis. By contrast the variants introduced in Figs. 2D and 2E exhibit remarkably weak spatial dependencies and a high decoupling in the cross-terms arising between the imaging and the diffusion gradients, leading to the smallest Δb-values. This behavior can be understood by examining the location chosen for these diffusion and imaging blocks within the pulse sequences. Specifically, when the diffusion block is completely separated from the imaging block –as is the case for the sequence in Fig. 2E- the image is nearly “free” of cross Δb-terms, and hence of ADC biases (Fig. 4E). In the sequence shown in Fig. 2D this is nearly the case as well; only the slice-selective adiabatic 180° may still induce very minor cross-talks between the SPEN and the diffusion blocks, and hence slightly biases the Δb-values (Figure 4D). Further experimental assessments on the effects summarized in this Figure, are presented in Appendix B based on a series of single-scan 2D MRI comparisons conducted for water samples.

Figure 4.

Residual∆b-values reflecting |b^exact(including all imaging gradients) – b^PGSE (eq.1b)|, for the five diffusion experiments described in Fig. 2. The columns correspond one-to-one to these sequences lettering, and the rows correspond to diffusion gradients applied along the indicated axes. Notice the minimal disturbance evidenced by the sequences in Fig. 2D, 2E. Parameters assumed for these diffusion calculations are δ= 3ms, ∆ = 14ms (except for Fig. 4D where ∆ = 11.4ms). The gradient and timing values taken into account for the b-value calculation are according to the experimental scanning parameters presented in Fig. 3 and Fig. B1 of Appendix B

4.2. Diffusion SPEN: Applications to Ex- and to In-Vivo Systems

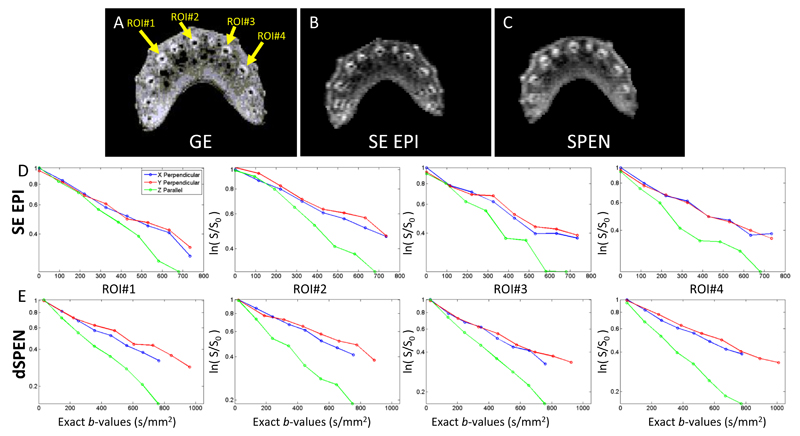
With the analytical capabilities of dSPEN derived and validated in simple phantoms, a series of measurements were done to investigate the method’s performance on more challenging systems. First among these tests we present observations made on celery, a system known to exhibit both isotropic diffusion in the outer edges of its vascular bundles (‘xylem’) as well as anisotropic water diffusion in the vascular bundles’ center (‘phloem’) [41]. Greater signal attenuation is then observed when diffusion gradients are applied parallel to the vascular bundles as opposed to applications in perpendicular directions [42]. Fresh celery positioned parallel to the magnet’s main axis was scanned using gradient-echo multi-scan MRI, SE EPI and dSPEN sequences described in Figs. 2A and 2B, leading to the results shown in Figs. 5A-C, respectively. When compared with the multi-scan results (Fig. 5A), the EPI and SPEN images display comparable qualities. Figure 5D-E shows the attenuation factors displayed by four different regions of interest, picked in the center of each vascular bundle. For these regions water diffusion was then measured upon applying G_d parallel and perpendicular to the vascular bundles’ long axes. Comparable results arise from the ensuing DW SE EPI and dSPEN scans, both in terms of the faster/slower diffusion observed parallel/perpendicular to the vascular bundles, as well as in terms of the differences between the isotropic and anisotropic water displacements. The ADC values found for these vascular bundles were 1.7 x 10^-3 mm²/s and 1.5 x 10^-3 mm²/s upon using dSPEN and SE EPI respectively. This is in good agreement with ADC values reported in the literature (1.42 and 1.47 x 10^-3 mm²/s) [41, 42].

Figure 5.

Magnitude gradient-echo (GE, A), single-scan SE EPI (B) and single-scan SPEN (C) images, displaying the different vascular bundles in fresh celery. Diffusion curves of SE EPI and dSPEN measurements at the center of the vascular bundles measured parallel (along the Z) and perpendicular (along X and Y) to it, are shown in (D) and (E) respectively. Each plot shows the average log of signal intensity vs b^exact-values for four different vascular ROI’s (see arrows in A). The diffusion parameters are δ = 10ms and ∆ = 20ms. SE EPI and SPEN scanning parameters: FOV = 28 x 22 mm², nominal resolution = 0.4×0.31 mm² on a 3 mm slice. For the multi-scan GE: FOV = 20x20 mm², resolution = 0.15×0.15 mm² on a 3 mm slice total scan duration = 4 sec. Gradient and timing values for SE EPI: T₉₀=T₁₈₀=3ms, T_a=21ms, total scan duration = 67ms. For SPEN: T₉₀ = 3 ms, G_e = 10 G/cm, T_a = 21 ms, G_a = 5.3 G/cm, total scan duration = 57 ms.

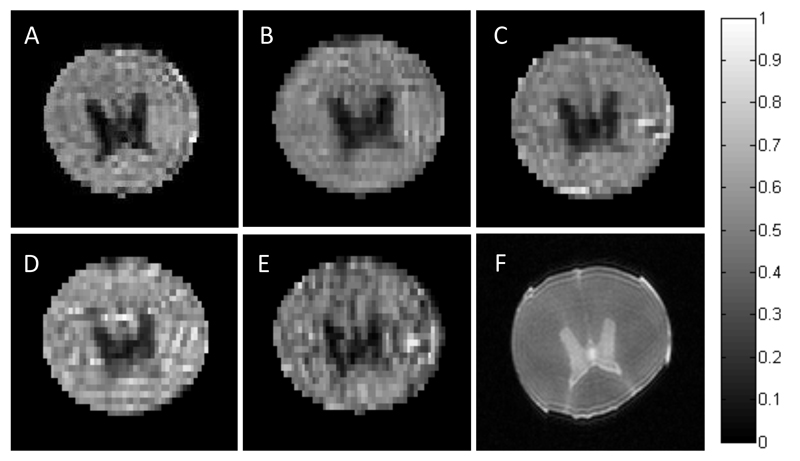
Another relevant biological system exhibiting interesting diffusion properties is the spinal cord. Spinal cords are also good models for exploring anisotropic diffusion, since they encompass white and gray matter [43] –with the white matter tissue mostly constructed from myelinated axons exhibiting preferential diffusion along their main axis, while the gray matter is constructed from neuroglia cell bodies and neuritis exhibiting apparent isotropic characteristics. Bearing in mind the challenges involved in imaging the relatively small features in this heterogeneous system, the performance of the dSPEN sequences were tested on ex-vivo spinal cord samples. To highlight the degree of anisotropy in this tissue, dSPEN diffusivity maps measured along orthogonal directions were transformed into fractional anisotropy (FA) maps [44]. Figures 6A-6E compare the anatomical FA maps obtained with the various sequences introduced in Figure 2 for this tissue, as well as a magnitude multi-scan fast spin-echo anatomical image of the targeted slice (Fig. 6F). Differences between the white and gray matter of the spine are clearly evidenced by all ultrafast experiments. Good agreement is observed between the FA values arising from the DW SE EPI sequence, and those derived from all the different dSPEN imaging modalities.

Figure 6.

(A-E) FA maps of ex-vivo swine spinal cord scanned by the pulse sequences described in Fig. 2 –panels A-E respectively. (F) Anatomical multi-scan fast spin-echo (FSE) reference image. The scale bar for the FA maps runs from 0 for isotropic to 1 for fully anisotropic diffusion. Maps were Generated considering the readout, phase-encode and slice-selection directions as λ1, λ2, λ3 respectively. Decay curves employed b^exact-values as described in Section 2. Diffusion parameters are δ= 3ms, ∆ = 14ms (except for Fig. 6D where ∆ = 11.4ms) weighted by b^PGSE-values: 50 250 450 650 850 1050. In all cases, corrected b-values were used to derive the maps. Scanning parameters of (A-E) are: TR=5sec, cubic FOV = 2 x20 mm², nominal resolution = 0.28×0.28 mm² on a 2 mm slice, number of averages = 4. (F) FOV = 20x20 mm², resolution = 0.1×0.1 mm² on a 1 mm slice, total scan duration = 2.5 sec. Other parameters were as follows: (A) T₉₀=T₁₈₀=2ms, T_a=21ms, total duration = 51.5ms. (B) T₉₀=T_a=21 ms, G_e=1.2 G/cm, G_a=4.5 G/cm, total scan duration = 60ms. (C) T₉₀=2ms, T₁₈₀=T_a/2=10.5ms, G_e=0.8 G/cm, G_a=3 G/cm, total scan duration = 51ms. (D) T₉₀=2ms, T₁₈₀=T_a/2=15.4ms, G_e=0.4 G/cm, G_a=4.4 G/cm, total scan duration = 65ms. (E) T₉₀=2ms, T₁₈₀=T_a/2=10.5ms, G_e=0.8 G/cm, G_a=3 G/cm, total scan duration = 62ms.

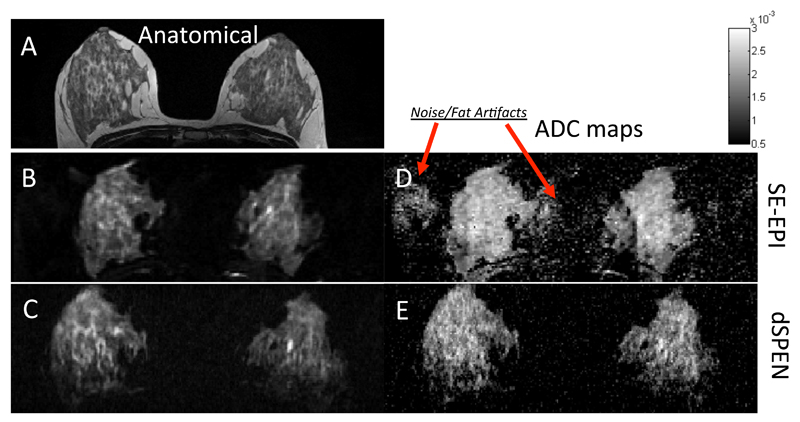
An instance where SPEN should facilitate the acquisition of quality images is upon dealing with chemically and morphologically heterogeneous environments. To explore the potential of dSPEN in such cases, the sequence in Fig. 2B was compared against a commercially-supplied, twice-refocused SE EPI DW pulse sequence [45], on a series of breast imaging scans on female volunteers. Single-scan breast MRI exemplifies well the challenges raised by in vivo heterogeneities, owing to a number of factors including the relatively high fat/water ratios that characterize breast, the off-center character of the analysis, and the unavoidability of breathing/cardiac motion influences [46, 47]. Figure 7A presents an axial T₂-weighted multi-scan anatomical image serving as reference for these studies, and contrasting condensed fibro glandular tissue and the surrounding fat tissue. Shown in Figs. 7B and 7C are, respectively, single-scan EPI and SPEN anatomical images –all recorded on the same volunteer on a clinical 3T Magnet. SPEN images clearly show superior resolution and sensitivity, mostly due to the fact that they are free from low-bandwidth artifacts, ghosting problems otherwise surrounding and overlapping the breast’s region of interest, and residual fat artifacts. These advantages are reflected as well on the ADC maps that single-shot DW SE EPI and dSPEN approaches yield for diffusivity in the connective tissue regions (Fig. 7D, 7E). Although overall a good agreement can be observed between the ADC values afforded by both imaging techniques, the focus of the SPEN data is clearly sharper. Additionally, the noise background scattering ratio was 3.5 times higher for the EPI-derived ADC maps, as compared to the dSPEN ones.

Figure 7.

Comparison between anatomical images (left-hand panels) and ADC maps (right) collected on a human breast-scan volunteer. (A) Multi-scan T₂ turbo spin echo image. (B) Axial slice, twice-refocused EPI. (C) Single-slice SPEN (sequence in Fig. 2B). The corresponding ADC maps (D, E) were originally weighted by b^PGSE-values 0 250 500 750 1000, arising from δ= 26.3 ms, ∆ = 43.4 ms. In the SPEN case, corrected b-values were used to derive the maps. Scanning parameters for the multi-scan image: cubic FOV= 360 mm on each side; resolution = 0.8×0.6 mm² on a 2.5 mm slice; total scan duration = 1080ms (without fat suppression). For EPI: square FOV = 360x360 mm², resolution = 1.9×1.9 mm², 2.5 mm slice, total scan duration (with GRAPPA parallel imaging, not used in the SPEN case) = 150 ms. SPEN parameters: FOV = 300×120 mm², resolution = 1.6×1.6 mm² on a 2.5 mm slice, T₉₀ = 47.8 ms, G_e = 0.06 G/cm, T_a = 66.1 ms and G_a = 0.043 G/cm, total scan duration = 200ms . For both EPI and SPEN, fat suppression was used.

5. Conclusions

The power to monitor random diffusion processes in a non-invasive, non-perturbing fashion regardless of a system’s opaqueness, constitutes one of NMR’s most important capabilities. Numerous manipulations and sequences have been developed over the decades to extract this information; initially from bulk samples based on Stejskal and Tanner’s seminal PGSE proposal, and eventually in combination with advanced multidimensional imaging techniques. Particularly important in the latter case is the availability of fast and robust imaging methods, to accurately characterize the signal decays introduced by the microscopic motions. The present study focused on the potential arising upon using one such technique, based on the combined use of gradients and swept pulses. While providing a robust imaging platform, the ensuing SPEN modality exhibits distinct features that cannot be ignored upon performing diffusion experiments: their progressive gradient-aided excitation/inversion processes strongly influence the outcome of the observed signal attenuations arising upon activating diffusion-sensitizing gradient blocks. To understand these effects and enable a quantitative use of dSPEN, a formalism was developed that evaluates the actual b-values characterizing the combined effects of all gradients and RF pulses. This comprehensive formalism extends Karlicek & Lowe’s work, taking it from an analysis of gradient-induced fields into one based on the local phase dispersions resulting from the joint action of gradients, of selective pulses, and of swept RF manipulations. Once diffusion effects are accounted for in this manner, the formalism allows one to compute all the relevant attenuating effects –including the diffusion-driven decays associated to the SPEN gradients, to the diffusion-sensitizing PGSE gradients, and to cross-talk terms between them. This enables accurate ADC map measurements from dSPEN characterizations; suitably computed b-values also leads to proposals like those introduced in Figures 2D and 2E, which efficiently suppress many of the complications deriving form the coupling between the SPEN manipulation and the PGSE sensitizing block. As result of all this a number of new and practical single- and multi-sliced dSPEN alternatives for retrieving accurate ADC maps, emerges. The accuracy of these schemes was verified with a number of phantom tests comparing the results arising from various dSPEN schemes against multi-scan and SE EPI diffusion experiments. SPEN’s robustness –particularly when implemented in full-refocusing mode– could then be brought to tackle challenging scenarios involving chemical and susceptibility heterogeneities, as is the case upon testing diffusion in in-vivo breast measurements. ADC maps showing less scattering and fewer distortions than their spin-echo EPI counterparts, were thus obtained. These validations of dSPEN as a reliable ultrafast diffusion measurement tool, bodes well for further uses of this method to target other challenging organs, as well as other diseases like ischemia, and for extensions to higher-field pre-clinical and clinical measurements.

Highlights.

• Analytical derivations are given to interpret diffusion SPEN MRI measurements.

• Excellent agreement is found between these analytical predictions and experiments.

• Single- and multi-slice sequence variants are presented and tested in phantoms.

• Reliable ultrafast diffusion measurements are obtained in human breast exams.

Abbreviations

SPEN

SPatio-temporal ENcoding

SE

Spin Echo

RF

Radio Frequency

EPI

Echo Planar Imaging

DW MRI

Diffusion-Weighted Imaging

PGSE

Pulsed Gradient Spin Echo

ADC

Apparent Diffusion Coefficient

FA

Fractional Anisotropy

FOV

Field of View

dSPEN

Diffusion-weighted SPEN MRI