Abstract
Two-dimensional Nuclear Magnetic Resonance (2D NMR) spectroscopy is widely used in chemical and biochemical analyses. Multidimensional NMR is also witnessing an increased use in quantitative and metabolic screening applications. Conventional 2D NMR experiments, however, are affected by inherently long acquisition durations, arising from their need to sample the frequencies involved along their indirect domains in an incremented, scan-by-scan nature. A decade ago a so-called “ultrafast” (UF) approach was proposed, capable to deliver arbitrary 2D NMR spectra involving any kind of homo- or hetero-nuclear correlations, in a single scan. During the intervening years the performance of this sub-second 2D NMR methodology has been greatly improved, and UF 2D NMR is rapidly becoming a powerful analytical tool witnessing an expanded scope of applications. The present reviews summarizes the principles and the main developments which have contributed to the success of this approach, and focuses on applications which have been recently demonstrated in various areas of analytical chemistry –from the real time monitoring of chemical and biochemical processes, to extensions in hyphenated techniques and in quantitative applications.
Keywords: NMR spectroscopy, 2D NMR, ultrafast NMR, spatiotemporal encoding, real-time NMR, quantitative analysis
1. Introduction
Nuclear Magnetic Resonance (NMR) is a highly versatile spectroscopic technique with applications in a large range of disciplines, from chemistry and physics to biology and medicine. It is widely used as an analytical tool in all chemistry laboratories and industries, where it provides a superior way to extract structural and quantitative information at site-resolved level, and hence enable the unambiguous elucidation of inorganic and organic molecular structures (1, 2). NMR is also very well recognised in biochemistry for its ability to deliver the folding and geometry of large macromolecules, alone or in complexes with drugs or with other biomacromolecules, under nearly physiological conditions (3, 4). The capabilities of NMR to shed light into dynamic chemical, biophysical and biological processes over a wide range of timescales by a range of complementary methods, are also well known (5). Enabling many –in fact most– of these applications is a revolutionary proposition by J. Jeener, dating back to 1971 and involving the concept of multi-dimensional NMR spectroscopy acquisitions. By providing a way of spreading the spectral peaks over a 2D frequency plane rather than along a 1D frequency axis, Jeener’s idea literally changed the face of magnetic resonance as it offered (i) a much better way of discriminating resonances than what could be offered by 1D traces –even at much higher fields; and (ii) a much richer and wider range of experiments for extracting structural and dynamic information maps, of a kind that could only be dreamed of by other spectroscopic methods relying on one-dimensional acquisitions (6, 7). As a result of this 2D NMR, as well as its higher-dimensional variants, has now become a routine analytical tool for the elucidation of small organic molecules, and a method of choice for the study of solution- and solid-state macromolecular structures.
The ingenuity of 2D NMR’s concept consists in reconstructing a correlation between two interconnected spin evolution frequencies, using a series of statistically independent 1D NMR acquisitions. Indeed, in conventional Fourier (pulsed) NMR, 1D spectra are obtained by exciting spins with an appropriate pulse sequence, and then monitoring their evolution in real time. As spins precess they will emit a signal that is inductively picked up; Fourier analysis of this component as a function of the acquisition time t will reveal the intervening spin evolution frequencies. 2D NMR will eventually deliver a bidimensional frequency correlation by incrementing two, rather than a single, evolution times. Although physically speaking there are no two “time variables”, 2D NMR overcomes such obstacle by performing a series of 1D experiments with one particular delay in the sequence –the so-called indirect-domain time variable– incremented in constant steps from scan to scan. When considering the acquisition of the ensuing spin signal as a function of the “physical” evolution time, also referred to as the direct-domain, one arrives at the canonical sequence of events generalized by Ernst’s landmark papers in this field (7–10):
| (Eq. 1) |
Here the “preparation” and the “mixing” events denote sequences that remain constant throughout the series of intervening scans. The repetition of this series with incremented values of t1 leads, after collecting each of the resulting data sets as a function of the conventional acquisition time t2, to a 2D S(t1,t2) depending on this two “time variables”. This complex matrix can be viewed as a 2D extension of a normal free induction decay (FID); a Fourier transform of this FID –this time in a generalized time-domain plane– gives rise to a 2D spectrum S(Ω1,Ω2). The frequencies (Ω1,Ω2) involved along the axes of these spectrum depend on the spin evolution that has taken place during the t1, t2 periods, as well as on the preparation and mixing sequences that preceded them.
In principle the scheme in eq (1) is extremely general, and a very wide variety of experiments have been designed on its basis. In biochemical applications they are usually used to correlate the chemical shifts of two identical or of two different nuclear species. This in turn gives rise to so-called homo- or hetero-nuclear families of 2D correlations counting COSY and NOESY as main members of the former, and HSQC, HMQC and HMBC as main members of the latter. The idea of 2D NMR can also be used to separate two interactions acting on the same spin; this is the case in “J-res” spectroscopy, which correlates homo- or heter-nuclear J-couplings along one axis, with chemical shift evolution along the second. Even within the context of single-spin interactions the ideas of Ernst and co-workers (7, 11–13) are very powerful, and they underly the field of 2D MRI, where the evolution of a spin (usually water 1Hs) is monitored under the action of consecutive magnetic field gradients applied along orthogonal directions, to enable the non-invasive characterization of opaque objects. The success and power of 2D spectroscopy is an essential ingredient on all uses of NMR. This popularity is reflected by their ubiquitous presence in complex molecular analyses, their use to correlate information (chemical shifts, couplings, etc.) between different nuclei, their exploitation in dynamic studies. 2D NMR provides, in sum, an incredibly helpful tool in organic (14, 15) and analytical chemistry (16, 17); as well as in biology (18, 19), pharmaceutical analyses (20), and eventually in clinical diagnosis.
In spite of its uniquely wide range of applications, 2D NMR suffers from an intrinsic drawback vis-à-vis its 1D counterpart. Due to the numerous t1 increments (typically several hundreds) needed to sample the indirect dimension with sufficient breadth and resolution, long experimental durations are a built-in feature of these experiments –regardless of sensitivity considerations. Long experimental durations have several consequences. Some of them are technical, like an overload of a spectrometer schedule that may translate into non-negligible costs. A more fundamental consequence is the impossibility to study samples in which composition evolves within the timescale of the nD experiment. This is not only the case for samples undergoing chemical reactions or dynamic processes, but also for chemical and biological samples with limited lifetimes. Another important repercussion of the experimental duration is that long experiments are more likely to be affected by spectrometer instabilities over time (21, 22). This will generate additional “t1 noise” in the indirect dimension, due to the long time interval (several seconds) between the acquisition of two successive points of the pseudo-FID, thus affecting the analytical performance of 2D NMR experiments. Another important class of experiments incompatible with conventional 2D acquisition schemes entail experiments on metastable states –foremost among them experiments relying on hyperpolarized spin states, seeking rapid decay back to thermal (Boltzmann) equilibrium.
During the last years, a number of strategies were proposed to reduce the duration of 2D NMR experiments. A first family of approaches consists of optimizing conventional pulse sequences to reduce the recovery delay separating two successive t1 increments. This can be performed by a careful optimization of pulse angles and delays (23, 24), by the addition of paramagnetic relaxation agents (25) or by implementing gradient-based fast-repetition crushing schemes (26). All of these strategies can lead to a dramatic reduction of the recovery delay in 2D NMR experiments; particularly impressive gains have resulted when implementing optimized excitations in large cross-relaxing biomolecules. Another series of complementary approaches, seek to reduce the exacting constraints of Nyquist sampling criteria; their aim is to explore the components involved in the indirect domain evolution with no compromises on the width or resolution of the resulting spectra –but without having to abide by Nyquist’s stringent demands. These efforts usually involve departing from the fast Fourier transform and relying instead on alternative forms of Fourier analysis. These involve unfolding approaches based on optimized de-aliasing procedures (27), or compressed sensing approaches that reduce the experimental duration without giving up on resolution by post-processing based on l1-norm minimization (28, 29), Linear Prediction (LP) (30, 31), Maximum Entropy (MaxEnt) reconstruction (31, 32) or numerical integration approaches (33), where algorithms are applied to reconstruct a complete FID in the F1 dimension from a limited number of points. Yet another alternative comes from covariance NMR methodologies (34), where the covariance matrix of the experimental data is calculated, thus resulting in a high resolution improvement. Many of these alternatives involve randomly sampling the (t1, t2) space in order to reduce the number of increments. Several strategies have been proposed, including exponential (35), radial (36), or random sampling (37). These approaches are often combined with one of the non-conventional processing methods described above (38). A final acquisition alternative worth highlighting is furnished by Hadamard spectroscopy, which by relying on an excitation in the frequency domain departs from the Fourier-based methodology (39) –but still demands a number of scans that may approaching those involved in Fourier methods, to deliver 2D spectra.
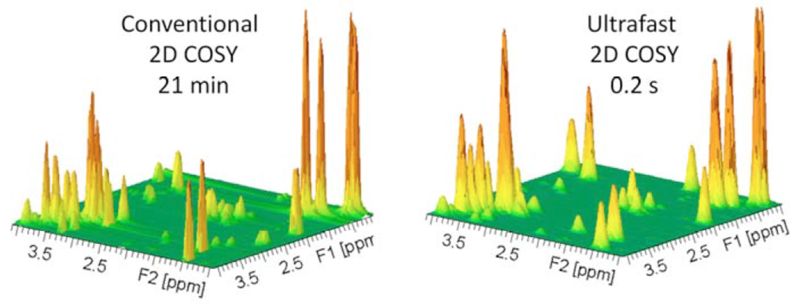
Most approaches described above aim at reducing the number of t1 increments in the indirect dimension, but are still based on the basic data sampling approach given in eq. (1). Thus, while all these strategies can accelerate the sampling of 2D NMR data, and although much faster than conventional 2D NMR acquisitions and very promising for various applications in NMR spectroscopy, all these methods will still require numerous scans associated to 10-100 second acquisition times to deliver their spectral correlations. In 2002, a different strategy inspired on imaging principles was proposed, which provides an entirely new way of acquiring multidimensional spectra. For the first time the ensuing approach could deliver arbitrary 2D NMR or MRI correlations –regardless of whether in liquids or solids, in vitro or in vivo– in a single scan. This lead to the so-called “ultrafast NMR” methodology (40, 41) which makes it possible to record any kind of 2D NMR spectra in a single scan, and therefore in a fraction of a second. During the last 10 years, the analytical performance of this methodology has been highly improved, and ultrafast (UF) NMR has moved on from the stage of method development to the one of a powerful analytical tool. The potential and performance of UF 2D NMR are shown on Figure 1, which highlights the quality of the sub-second spectra that this approach can afford. This review aims at emphasizing the analytical potential of UF 2D NMR for a variety of applications. The principles of this methodology are first summarized, as well as the developments that have increased its performance to make it a more nimble analytical tool. Applications and limitations of UF 2D NMR are then illustrated in a variety of situations where the experiment duration plays a crucial role: i) the real-time study of samples whose composition is evolving in the course of time, where the need for fast acquisition techniques is indispensable, ii) the field of quantitative analysis, where UF 2D NMR provides an original way to reach a high precision for the high-throughput, quantitative analysis of complex mixtures, and iii) the coupling of UF 2D NMR with hyphenated and hyperpolarization techniques, where the single-scan nature offers a powerful solution to the irreversibility issue of the separation/preparation processes. Finally, the perspectives and challenges opened by this new analytical tool are discussed.
Figure 1.
Conventional (left) and ultrafast (right) 2D 1H homonuclear spectra (COSY) recorded on a mixture of metabolites on a 500 MHz Bruker Avance III spectrometer equipped with a cryoprobe.
2. Principles of Ultrafast 2D NMR
2.1. Basic concepts
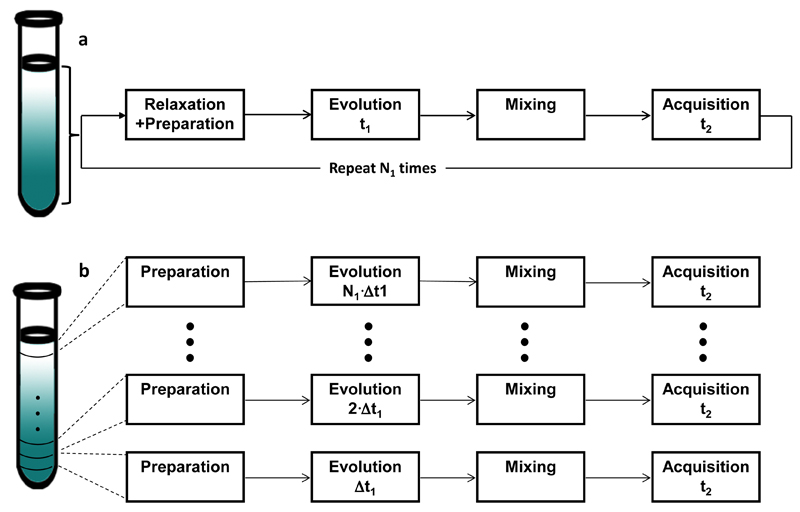
The ultrafast methodology relies on the concept of imparting a “spatiotemporal” encoding of the spin interactions to be measured (40): a time evolution of the indirect domain, that linearly incremented space as well. The basic scheme of how this is implemented and how it can be put to use for the sake of monitoring the indirect-domain evolution frequencies in a single scan, is summarized in Figure 2. This Figure bases the its description of the UF acquisition strategy on the Jeener-Ernst acquisition mode underlying conventional 2D NMR experiments and stresses how, instead of repeating N successive experiments on the sample with an array of independent time increments (Figure 2a), an analogous information could results from “dividing” the sample into N slices where the spins located at different positions undergo different evolution periods –but happening simultaneously for all slices within the course of the same scan (Figure 2b). Like in conventional 2D NMR, this spatiotemporal encoding period could be preceded by a preparation period identical for all slices and typically consisting on a relaxation delay followed by an excitation block. Also as their conventional 2D counterparts, such spatiotemporal encoding will also be followed by a mixing period charged with transferring coherences between indirect and direct domains. Finally, the signal is detected in a spatially-specific fashion that allows one to distinguish the individual t1 increments –for example using an oscillating acquisition gradient like the one characteristic of Echo-Planar Spectroscopic Imaging (42, 43). As such scheme also enables one to monitor the post-mixing chemical shift evolution, an appropriate processing procedure enables one to extract from such series of echo trains the desired 2D spectrum. Notice as well that although Figure 2 makes a comparison between multi-scan and single-scan acquisition modes based on a discrete partitioning of the spatial and temporal variables, the approach in panel 2b is also amenable to a continuous encoding of the (analog) spatiotemporal variable.
Figure 2.
Conventional (a) vs ultrafast (b) data acquisition schemes. In conventional 2D NMR (a), N1 experiments are repeated on the sample while incrementing the t1 evolution period. A relaxation delay is necessary between each t1 increment to let the magnetization return to its equilibrium position. The ultrafast 2D NMR experiment (b) can be visualized as subdividing the sample into N1 discrete slices (which may be of a nominal rather than of a real nature –equal arguments would apply if the spatial evolution would be continuously imposed) that simultaneously undergo different experiments with incremented t1 delays.
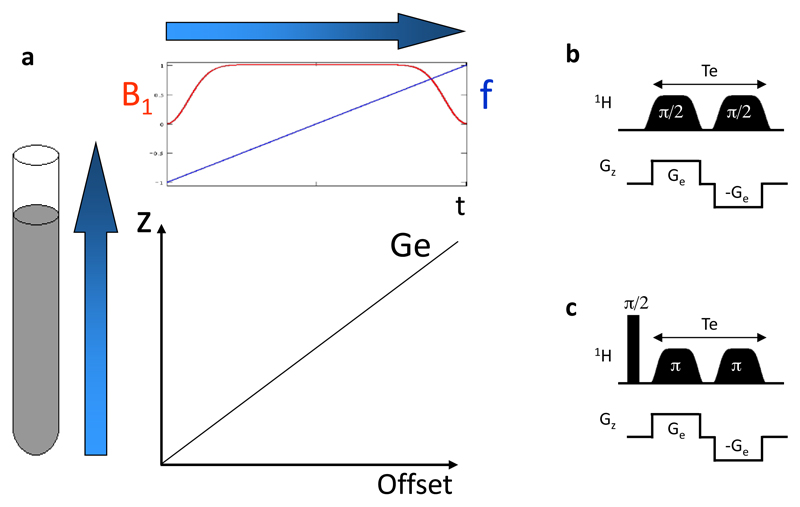
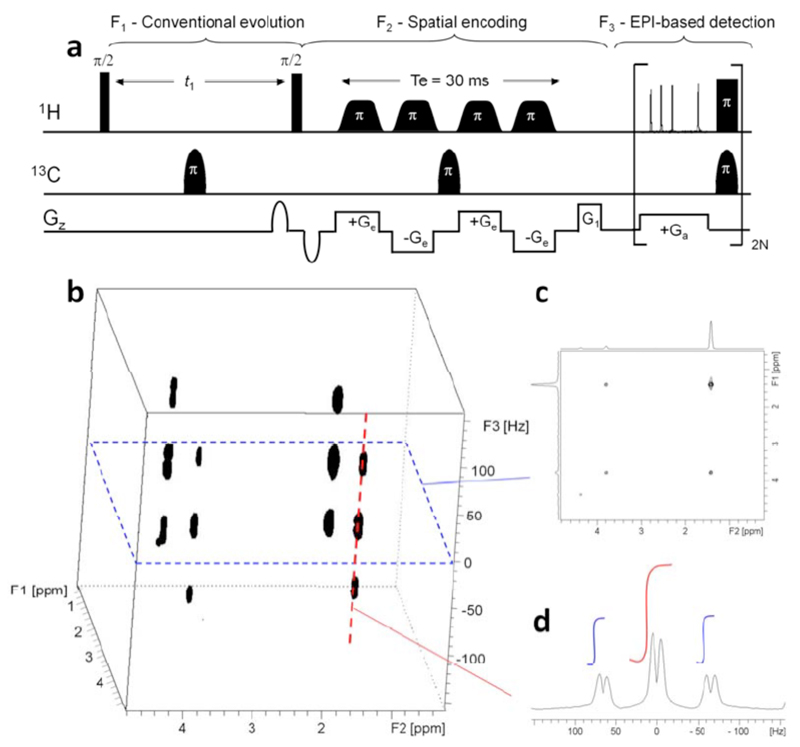
It follows that a key feature of the ultrafast methodology is its demand to create an evolution period depending on the spatial location of the spins in the sample. This can be performed in many numerous ways: in a discrete or continuous fashion; in a real- or constant-time fashion. Original demonstrations included applying a series of frequency-selective pulses played out together with pairs of bipolar gradients along the z axis (40, 41, 44); alternative modes include continuous spatiotemporal encoding schemes (45–51) where the sample can be considered as being divided into an infinite number of infinitesimal slices. All these schemes will provide, at the end of the spatiotemporal encoding period, a linear dephasing proportional to the position along the vertical z-axis. Figure 3 illustrates how this can be achieved in a real-time (46) or constant-time (45) fashion. In all cases magnetic field gradient Ge is applied along the a spatial axis, under the effect of which spins situated at different positions undergo different resonance frequencies. If a chirp pulse (52, 53) with a linear frequency sweep is applied simultaneously, spins will be excited at a different time t(z) according to their position z. The pulse/gradient combination described in Figure 3a is not sufficient to perform the spatiotemporal encoding step required by ultrafast experiments, as it creates a quadratic z2 dephasing which cannot be further refocused by linear gradients. Therefore the first pulse is generally followed by a second suitable manipulation; for instance an identical RF pulse, but applied during an opposite gradient. This scheme leads to a linear dephasing that is proportional to the position along the z axis. It is important to note that this dephasing also depends on the resonance frequency Ω1. In the real-time version proposed by Shrot and Frydman (46) this spatial encoding leads to an amplitude-modulated signal (Fig. 3b), while in the constant-time version proposed by Pelupessy (45), two 180° chirp pulses are applied following an non-selective 90° excitation, thus resulting in a phase-modulated encoding (Fig. 3c). Several alternative schemes have been proposed to reach a similar kind of linear dephasing (45–48, 50).
Figure 3.
(a) Principle of continuous spatiotemporal encoding in ultrafast 2D NMR. A chirp pulse with a linear frequency sweep is applied together with a magnetic field gradient Ge. As a result, spins located at different positions z are excited at different times t(z). Pulse sequence elements proposed to perform continuous spatiotemporal encoding in a real-time (b) or constant-time fashion (c). In both cases, two identical RF pulses are applied, sweeping between initial and final offsets ±γeGeL/2 at rates 2πR = ±2γeGeL/Te with amplitudes set so as to impart net π/2 or π rotations of the spins at all positions. The application of a first chirp pulse together with a gradient leads to a dephasing ϕ(z) containing a linear and a quadratic z-dependence. The latter is removed by the application of a second identical pulse applied with an opposite gradient, resulting in a linear dephasing ϕ(z) which also depends on the resonance frequency Ω1.
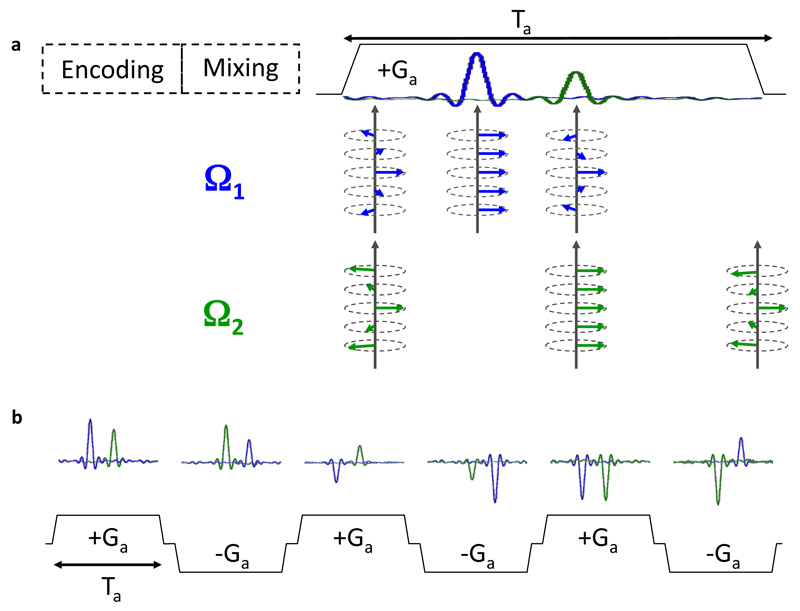
After achieving this site-specific linear dephasing, a mixing period is generally applied, allowing a transfer of information between scalar- or dipole-coupled spins, as usual in conventional 2D NMR. This period is therefore identical to its conventional counterpart, and will preserve the linear dephasing obtained after spatiotemporal encoding into the homo- or hetero-nuclear species that is going to be monitored during t2. In order to refocus this dephasing and obtain an observable signal, a gradient Ga is applied while the receiver is open, leading to a series of site-specific spin-echoes whose timing matches in a one-to-one fashion the positions that represent the various sites’ resonance frequencies (Figure 4a). By the action of this gradient a time-domain signal equivalent to the indirect-domain’s 1D spectrum, is observed during the action this gradient. Notice that no Fourier transform is needed to arrive to this signal, which forms the first dimension of the 2D spectrum being sought. Because of this, the indirect-domain is also referred to as the “ultrafast” or the “spatially-encoded” dimension, as it results from the spatiotemporal encoding process characterizing this method. Notice as well that although this read-out process can be made arbitrarily short by increasing Ga’s strength, the resolution of the various site-specific echoes still demands sufficiently long spatiotemporal encoding periods –and thereby no Nyquist-derived criterion is actually broken by this readout process.
Figure 4.
Signal detection in ultrafast 2D NMR. (a) Acquisition of the ultrafast dimension. A magnetic field gradient of amplitude Ga and duration Ta is applied while the receiver is open, which refocuses the dephasing induced by spatiotemporal encoding. It leads to a series of echoes whose positions are proportional to resonance frequencies. (b) Acquisition of the conventional dimension. A series of sub-spectra are detected during a train of bipolar gradient pulses, while the system evolves under the influence of conventional parameters (relaxation, resonance frequency, couplings, etc.). Data rearrangement and Fourier transform along the conventional dimension are necessary to obtain the final 2D spectrum.
Under typical conditions, this gradient-driven readout of the indirect-domain information only lasts a few hundreds of microseconds –much less than the natural T2 lifetimes of normal NMR signals. In order to obtain the second dimension of the 2D spectrum, a technique inspired from echo-planar-spectroscopic-imaging (EPSI) (42, 43) can thus employed. In such approach the normal free evolution is replaced by an acquisition process incorporating a series of bipolar gradient pairs (Figure 4b). These oscillating gradients lead to periodic refocusings and defocusings of the ultrafast 1D “spectra”: a train of mirror-imaged echoes reflecting the direct-domain evolution of the 1D indirect-domain spectra, thereby results. As the system continues evolving during the course of this oscillating ±Ga train under the influence of conventional parameters (T2 relaxation, direct-domain chemical shifts and J-couplings, etc), the result of this additional evolution is akin to a 2D S(F1,t2) interferogram – not unlike the one that would result from the 1D Fourier transformation of a conventional 2D NMR data set, against the indirect time-domain variable t1. It follows that an appropriate data rearrangement followed by a conventional Fourier transform that discriminates the different resonance frequencies that were active over the course of the direct time-domain t2, can lead to the full information normally contained in a 2D NMR spectrum. As this second dimension arises from a conventional evolution we refer to it as “the direct domain”. The overall procedure will therefore lead to the retrieval of a normal-looking 2D NMR spectrum –but collected within a single transient.
As a consequence of this particular data acquisition procedure, a specific processing is necessary to obtain the resulting 2D spectrum (40). This includes separating the mirror-image data acquired during positive and negative acquisition gradients in order to achieve constant Δt2 increments for every F1 coordinate, correcting for potential gradient imbalances by shearing the two resulting interferograms in the joint (F1,t2) domain, suitably weighting and Fourier transforming the resulting data along the direct domain, and adding, after inversion of one of them, the two resulting 2D spectra. The use of several home-made processing programs has been reported (40, 45, 51, 54) to perform this specific processing, whose details are described in Ref. (55).
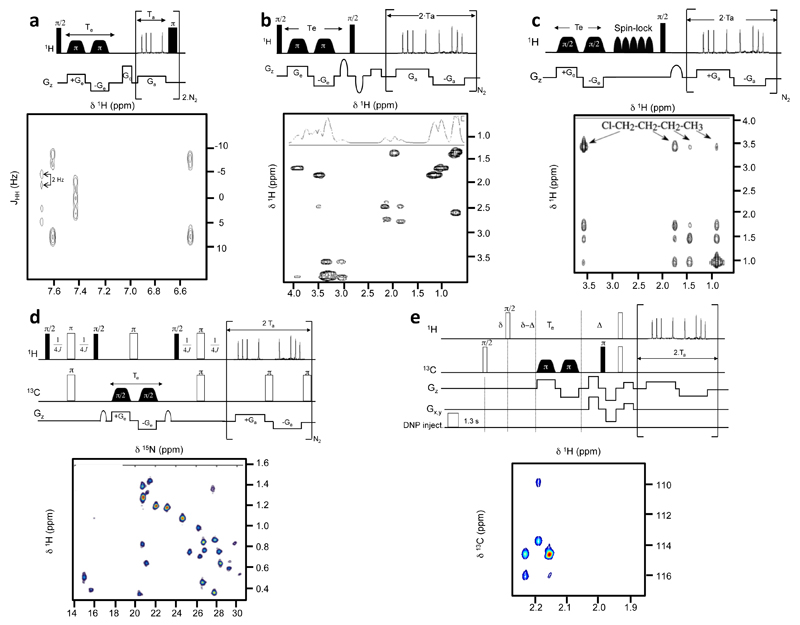
The ultrafast methodology described above makes it possible to obtain in a single scan any kind of 2D NMR correlation, provided that the sensitivity is sufficient to deliver the information being sought in that one single scan. Apart from that arbitrary ultrafast pulse sequences can be designed to encode identical correlations or separations as their conventional counterpart; most often by morphing either constant- or real-time versions of the conventional sequences into spatiotemporally encoded counterparts, and replacing their normal acquisition modules by suitably-modulated EPSI ones (incorporating homo- or heterodecoupling as per the sequence’s needs). Figure 5 presents representative examples of ultrafast spectra obtained using commercial spectrometers, together with the corresponding pulse sequences. While not comprehensive this figure is meant to illustrate the potential and versatility of this new analytical tool, and point out some of its characteristic features –such as resolution issues, or its ability to incorporate standard phase cycling or sensitivity-enhancement issues associated to multi-scan averaging (Fig. 5d).
Figure 5.
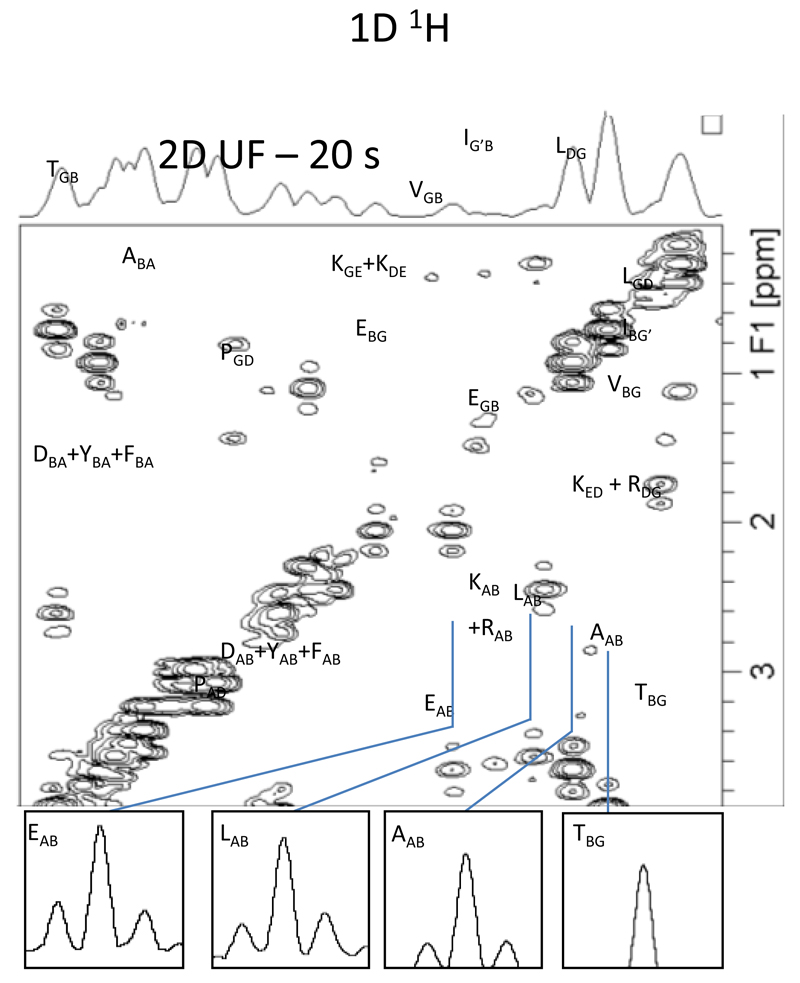
Examples of 2D spectra recorded in a single scan, shown together with the corresponding NMR pulse sequence. (a) Ultrafast constant-time J-resolved spectrum recorded in 500 ms at 500 MHz on a cinnamic acid sample in DMSO-d6 (54). (b) Ultrafast constant-time COSY spectrum recorded in 100 ms at 500 MHz with a cryoprobe on a mixture of 6 metabolites (Alanine, Threonine, Glutamic acid, Valine, Serine, Myo-Inositol) in D2O. (c) Ultrafast real-time TOCSY spectrum recorded in 150 ms at 500 MHz on a n-butylchloride sample in CDCl3 (56). (d) Ultrafast real-time 1H-15N HSQC spectrum recorded in two scans at 800 MHz with a cryoprobe on a lyophilized protein A sample in D2O (46). (e) Ultrafast constant-time 1H-13C HSQC spectrum recorded in a single scan following the injection of hyperpolarized vitamin E at a 12 mM concentration (56).
2.2. Ultrafast 2D NMR: Features and compromises
Despite its generality, ultrafast 2D NMR is characterized by a specific sampling scheme with particular acquisition parameters, which confer it a behaviour that differs from its conventional counterparts. In particular, the gradients and chirp pulses involved in the initial encoding stage, as well as the EPSI-based detection scheme, may lead to a number of compromises. This will relate in particular to sensitivity, resolution and spectral width issues (57–61), and can be summarized as follows:
(i) Spectral widths: Spectral widths SWUF and SWConv in the ultrafast and conventional dimensions, respectively, are related to the resolution in the ultrafast dimension by the following equation (62):
| (Eq. 2) |
where Δν is the peak width in the ultrafast dimension, γa the gyromagnetic ratio of the detected nuclei, L the height of the detection coil and Ga the amplitude of the acquisition gradients. This relation shows that increasing the spectral windows along any of the two dimensions without altering the targeted resolution, will condition the gradient amplitude that is required by the experiment.
(ii) Resolution and sensitivity: As in conventional 2D NMR, the resolution along the direct, FT-based dimension will be determined by its acquisition duration. In UF NMR this will in turn define the number of gradient pairs that need to be applied during the course of the acquisition. Typically 100-200 gradient pair oscillations can be achieved with conventional hardware, assuming that each cycle lasts for ≈0.5 ms and that Ga does not exceed the amplitudes targeted for long pulses (≈10-15 G/cm for spectroscopy probes; about twice these values for diffusion-specific probes). This would results in 10-20 Hz linewidths along the direct domain; this are often acceptable values, which can be further increased by processing algorithms such as linear prediction. In such instances, the resolution of homo- and hetero-nuclear J-couplings is straightforward. Further resolution limiting factors, however, may arise in the spatially-encoded dimension (cf. Fig. 5). Some of the factors impacting resolution in this dimension are conventional; e.g., the duration of spatiotemporal encoding (58). Independently of the spatial-encoding scheme and in analogy with conventional time-domain spectroscopy this duration will define the resolution of the indirect domain, which will be inversely proportional to the duration of spatiotemporal encoding (57). Consequently, resolution should be easy to increase simply by applying a lengthier spatiotemporal encoding duration. Other signal-loss / spectral-broadening mechanisms, mainly those arising from the effects of molecular diffusion in the presence of gradients (60, 63) and to a lesser extent to transverse relaxation, limit this possibility. These effects also affect line shapes, in a way that depends on the spatiotemporal encoding scheme (63). Therefore, compromises usually have to be made between resolution along the indirect domain, and sensitivity in the 2D spectrum. Finally, a most important sensitivity limitation is given by the need of the method to open up the receiver’s bandwidth, so as to succeed in capturing the evolution of two dimensions in a single scan. Indeed the scheme summarized by Figures 1-3 –like their EPI and EPSI counterparts– operate by sampling the full indirect-domain information, within the time period Δt2 that would normally be associated to the sampling of a single data point in conventional 2D NMR. The larger the direct/indirect-domain spectral widths or the indirect-domain targeted resolution, the more samples will have to be taken and/or higher amplitude of the acquisition gradients be needed and/or shorter sampling times will be required. Any of these circumstances will demand an enhanced sampling rate and thereby an increase of the ensuing spectral noise, which as in any MR spectroscopic measurement increases as the square-root of the sampling rate. On the other hand, being a single-scan technique, the amount of signal present will be limited to that available in a corresponding single scan of the conventional 2D acquisition counterpart. This is much smaller than the signal arising when a full 2D acquisition is performed, since upon subjecting the latter to a 2D Fourier transform a form of signal averaging is being done (13). Unless special precautions are taken like controlled folding, compressed sensing or other advances mentioned in the next paragraph, signal-to-noise in single-scan 2D NMR will be akin to the signal available from a single scan (using the corresponding 2D sequences with all its pulses and coherence transfer processes) scaled by the square-root of the number of spectral elements resolved along the indirect domain (62).
2.3. Ultrafast 2D NMR: Advanced acquisition considerations
In view of these limitations, research in ultrafast NMR has devoted attention to increase the analytical performance of UF NMR in terms of resolution, sensitivity and accessible spectral width. Several papers investigated the impact of molecular diffusion on resolution and sensitivity (57, 58, 60, 63), and a multi-echo spatiotemporal encoding strategy was proposed to make ultrafast experiments more immune to such effects (57). Diffusion effects can also be reduced by optimizing the sample preparation (64). Modifications of the spatial-encoding period were also proposed to increase the spectral width that can be observed in the ultrafast dimension without altering resolution, by relying on spectral/spatial pulses (62) or additional gradients (65), in order to play with the position of peaks in the k-space. Recently, the introduction of Hadamard-based strategies in the spatial-encoding schemes also helped in improving its sensitivity (66). Improvements were also brought to the detection scheme by introducing alternative sampling strategies (54, 67). Finally, the processing procedures were also optimized to obtain the best resolution and lineshape possible from a given ultrafast dataset (68, 69).
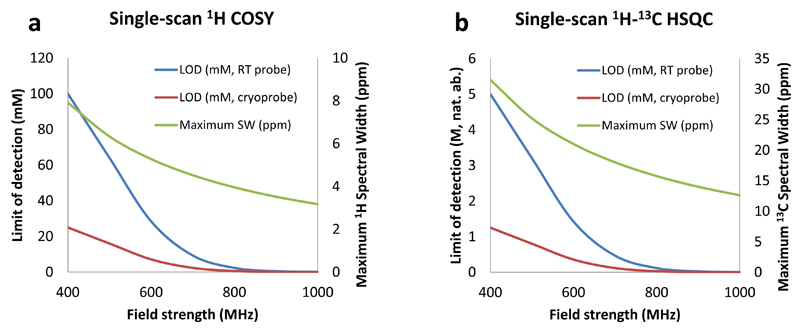
One of the key points in the success of a new analytical methodology is its capacity to be easily implemented on routine hardware, even by spectroscopists who would not be specialists of the underlying concepts. Efforts have been targeted to design protocols facilitating such an implementation in the case of UF 2D NMR (55, 70), in particular by designing pre-acquisition routines to make the setting of experimental parameters easier (71). Thanks to the numerous improvements described above, the analytical performance of ultrafast NMR has been significantly improved over the last ten years, and UF NMR has moved from the development stage on model compounds to a powerful analytical tool capable of delivering high-resolution 2D spectra in a fraction of a second. It is now possible to record single-scan spectra for which the quality is not significantly different from that obtained with their conventional counterparts. While the first ultrafast experiments were generally limited to pure model molecules, it is now possible to record, in a single scan, 2D spectra of complex diluted mixtures. Of course there is still a price to pay to the high speed gain, and potential users of UF NMR should be aware of the typical performance that can be reached with these single-scan experiments on modern hardware. While this performance is highly spectrometer and probe-dependant, Figure 6 gives typical analytical characteristics of two widely-used ultrafast experiments on modern NMR spectrometers. From these considerations, the reader might figure out how these values would translate on their own system.
Figure 6.
Typical performance of ultrafast 1H COSY and 1H-13C HSQC experiments on modern NMR hardware. Average approximate values are given, obtained from experimental data and theoretical calculations. Single-scan limits of detection are given at natural abundance for room temperature (RT) and cryogenic probes. While these values seem relatively high, the LOD can be easily decreased by signal averaging, as in conventional NMR. The performance of such a multi-scan approach is further discussed in the manuscript. Spectral widths are calculated assuming that the spatial encoding time is Te = 30 ms, which corresponds to a reasonable compromise between resolution and spectral width, and that the maximum gradient amplitude used during acquisition is 30 G.cm-1. Spectral widths are given regardless of any folding or spectral/spatial manipulation that can further increase the effective observable spectral width.
3. Application of single-scan 2D NMR to real-time studies
3.1. Interest of UF 2D NMR for monitoring unstable samples
The recent developments described above have paved the way towards the application of UF NMR to a variety of analytical situations. Not only ultrafast experiments appear promising to reduce the duration of routine 2D NMR experiments, but their main strength lie in their capacity to solve analytical problems which could not be addressed by conventional 2D acquisition strategies. This is particularly the case when the timescale of the study is not compatible with the duration of the NMR measurement, for example when samples are subject to chemical or biochemical degradation. It is very likely that samples undergo second- or minute-long chemical changes which cannot therefore be studied by conventional 2D spectroscopy where at least 10 minutes are required to record a single data point. Of course, simple samples can be studied by single-scan conventional 1D NMR, but numerous cases required the use of 2D spectroscopy, and in this case the use of fast acquisition techniques becomes indispensable.
In this context, a number of studies demonstrated the potential of UF 2D NMR for monitoring fast processes. The first experimental proof of such a real-time capability was shown by Shapira and Frydman, (72) who employed a combination of gradients to monitor, within a single acquisition, the interconversion N,N-dimethylacetamide. This was a dynamic process occurring on a ca. 1 second timescale. Besides this equilibrium demonstration, real-time monitoring of unidirectional chemical transformations by UF 2D NMR were illustrated in Ref (73) on two examples. The first one was the following of an H/D exchange process occurring upon dissolving a protonated protein in D2O, relying on a train of 2D 1H-15N HSQC spectra separated by 4 s intervals. The second one was the real-time in situ tracking of a transient Messenheimer complex that formed rapidly when mixing two reactants inside the NMR tube. By monitoring changes in a series of 2D TOCSY patterns, a competition between thermodynamic and kinetic controls could be observed within a 2 s timescale. The first studies described above prefigured what would be the two main application areas of such real-time approaches: the monitoring of fast organic reactions and the dynamic study of biomolecular processes.
3.2. Monitoring fast organic reactions by ultrafast 2D NMR
UF 2D NMR is particularly promising for the real-time study of organic processes: real-time 1D NMR is a well-known tool to identify and characterize intermediates involved in chemical reactions and therefore to understand reaction mechanisms (74, 75); 2D spectroscopy could naturally enhance such advantages. The group of A. Herrera and co-workers, for example, first applied the 1H TOCSY approach to follow the synthesis of alkylpyrimidines, by the reaction between carbonyl compounds and a strong electrophile–trifluoromethanesulfonicacid anhydride (Tf2O) – in the presence of nitriles (76). 2D spectra were recorded every 10 seconds over a 90 minutes timescale, allowing the characterization of several intermediates. The real-time monitoring of this multistep reaction revealed important data about its mechanistic and kinetic aspects, which would not have been accessible by conventional means. In order to obtain further information on the carbonyl carbon atoms involved in this kind of reaction, the same authors proposed a heteronuclear long-distance correlation approach, ultrafast HMBC, to monitor changes involving the quaternary carbon atoms. It was a applied to a model, 13C-labeled ketone and gave important structural and mechanistic information about the chemical environment and evolution of the reactive quaternary center (77).
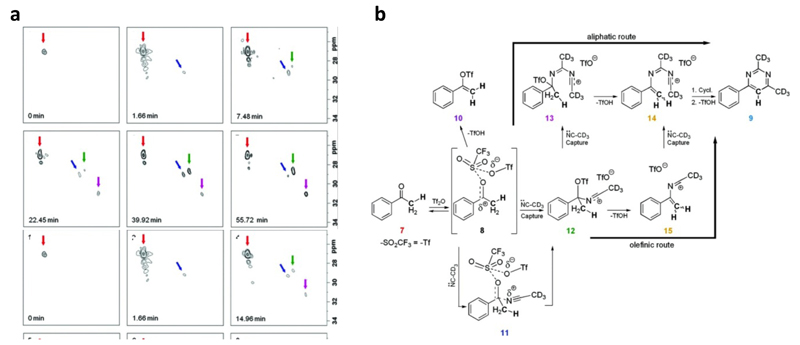
While the heteronuclear approach described above brings an efficient new tool for the study of complex organic reactions, it is still limited to labelled compounds or relatively high concentrations, thus limiting its applicability. Fortunately, the recent improvements brought to the sensitivity and robustness of ultrafast pulse sequences made it possible to extend this approach to 13C studies at natural abundance and lower concentrations. The first demonstration on the potential of the 1H-13C HSQC pulse sequence to monitor organic reactions at natural abundance was performed on a model educational example, namely the mutarotation of glucose in aqueous solution (78). A quantitative treatment of HSQC spectra recorded every 90 seconds over a 3 h timescale made it possible to determine the kinetic and equilibrium constants with a good precision. Herrera and co-workers applied this natural abundance HSQC strategy to obtain additional mechanistic details in their synthesis of alkylpyrimidines (79). The complexity of the reaction studied required the development of new ultrafast 2D methods, capable of monitoring multiple spectral regions of interest as the reaction progressed. The alternate application of these acquisitions in an interleaved, excitation-optimized fashion, allowed extracting new structural and dynamic insights (Figure 7). Up to 2500 2D NMR data sets were collected over the course of this nearly 100 min long reaction, in an approach resembling that used in functional magnetic resonance imaging. In the same year, the potentialities of UF 2D NMR to characterize reaction intermediates was illustrated by Queiroz and co-workers, who studied the real-time hydrolysis of an acetal by 1H-13C UF HSQC at natural abundance, and were able to characterize the very unstable hemiacetal intermediate with a short lifetime (80). The results of this study were confirmed and rationalized by quantum calculations of 1H and 13C NMR chemical shifts and natural bonding orbital analysis.
Figure 7.
(a) Representative selection of real-time 2D HSQC NMR spectra arising from the reaction of triflic anhydride, ketone (7) and acetonitrile-d3 shown in (b). Spectra show species (7, 11, 12 and 13) present in the aliphatic window range (1.54 - 2.87 ppm for 1H, 23.7 - 33.7 ppm for 13C) at key time points as the reaction progresses, depicted by arrows (red, blue, green and magenta respectively) (79).
3.3. Applications of Ultrafast 2D NMR to the study of biomolecular dynamic processes
NMR is also a widely employed analytical tool in the field of biochemistry, thanks to its capacity to provide structural and dynamic information on biological macromolecules in solution. The investigation of short-lived excited states is highly important to understand molecular folding, missfolding and function, but it remains a challenge for modern biomolecular NMR techniques. Off-equilibrium real-time kinetic NMR can enable the direct observation of conformational or chemical changes; to do so, however, multi-dimensional methods are often required, which are incompatible with the timescale of the targeted phenomena. UF 2D NMR provides a solution to study such fast dynamic processes. However, the latter often occur on a seconds timescale, which requires a high repetition rate of NMR experiments, thus appearing even more challenging than the organic reaction monitoring examples discussed above. Initial ultrafast experiments were not compatible with such a repetition rate, due to the interference between the heteronuclear decoupling pulses and the oscillatory magnetic field gradients applied during the acquisition. In order to circumvent this limitation, Frydman, Brutscher and co-workers proposed to combine the ultrafast 2D NMR acquisition scheme with the SOFAST technique, recently proposed to increase the repetition rate of biomolecular NMR experiments (24, 81). In combination with a fast-mixing device, the recording of 1H–15N correlation spectra with repetition rates of up to a few Hertz became feasible, enabling real-time studies of protein kinetics occurring on time scales down to a few seconds (82).
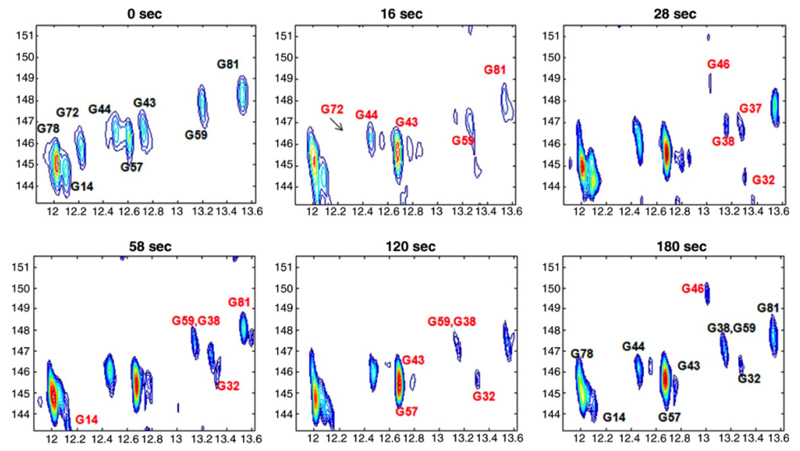
Recently, this “ultraSOFAST” approach was applied to follow, in real time, the conformational transitions and structural rearrangements of the adenine-induced folding of an adenine-sensing riboswitch (83). The latter are genetic control elements found in untranslated regions of prokaryotic mRNAs. By following changes in 2D spectra at rates of approximately 0.5 Hz, the authors were able to identify distinct steps associated with the ligand-induced folding of the riboswitch (Figure 8).
Figure 8.
Spectra from Ref. (83) illustrating the dynamic capabilities of the ultraSOFAST 2D experiment. Conformational transitions of a riboswitch are followed by recording real-time 2D 1H-15N HMQC NMR spectra. The spectra shown were recorded at pH = 6.1 and 298 K on a ∼1.7 mM 15N-G-labeled adenine riboswitch ligand-binding domain; the times indicated in each frame correspond to the time point following addition of adenine and Mg2+ to the free RNA solution.
4. Quantitative applications of Ultrafast 2D NMR
4.1. Interest and limitations of 2D NMR for quantitative analysis
While the real-time monitoring of fast occurring processes is probably the most immediate application of UF 2D NMR, a less evident but equally promising application of fast 2D techniques relates to quantitative analysis of mixtures. NMR is widely employed as a quantitative tool, with applications in fields such as pharmaceutical analysis (84, 85), metabolic studies (86–88) or the authentication of natural products (89, 90). It is of particular interest in the field of metabolomics, where it often exploits a very standardized 1D 1H NMR protocol associated with statistical analysis (91, 92), to compare samples from different sets. While this method provides an efficient discrimination between individuals, it does not allow for the quantification of metabolites responsible for this discrimination. A more targeted strategy –metabolic profiling– consists in identifying and quantifying a few tens of metabolites in unfractionated extracts (87, 92, 93). However, a true quantitative analysis of metabolic samples (i.e., a precise and accurate determination of the analytes’ concentrations), is challenged by the high degree of signal overlap characterizing complex samples. 2D NMR offers promising potential for quantitative analysis of complex mixtures. Its use for quantitative analysis, however, has expanded slowly and only over the last decade (17, 94–104). This reflects one of the main intrinsic characteristics of 2D NMR experiments: their relatively long acquisition times, particularly when seeking quantitative acquisition conditions on large batches of samples. Due to these latter demands 2D NMR experiments are inherently non-quantitative as peak volumes depend on a variety of factors, mainly relaxation times, J-couplings and pulse sequence delays –which usually are not extended to the degree that would ensure full relaxation and quantitativeness. This limitation is generally bypassed by relying on a calibration procedure, consisting of recording spectra of model mixtures at different concentrations and plotting the peak volumes versus the concentrations for each peak of interest (94, 98, 99, 105, 106). From the quantitative point of view, the main limitation comes from the experimental duration, as long experiments are more likely to be affected by spectrometer instabilities over time (21, 22). They generate additional noise in the indirect dimension, due to the long time interval (several seconds) between the acquisition of two successive points of the pseudo-FID. As a consequence of this “t1 noise”, the signal-to-noise ratio (SNR) is always lower in the indirect F1 dimension, which affects the precision and accuracy of quantitative 2D experiments. This drawback highlights the need for alternative and faster 2D acquisition strategies.
4.2. Interest and limitations of quantitative UF 2D NMR
In this context, UF 2D NMR offers promising perspectives for quantitative analysis (103). First, it potentially allows a significant reduction in the experimental duration, which is a significant bonus when considering the relatively long calibration procedures required for quantitative 2D NMR, and the frequent need to repeat these for the analysis of a large number of samples. Moreover, ultrafast experiments are potentially more immune to hardware temporal instabilities, as all the t1 increments are recorded within the same scan. In 2009, Giraudeau et al. performed an analytical evaluation of ultrafast 2D NMR on model mixtures (107). Two homonuclear ultrafast techniques, J-resolved spectroscopy and TOCSY, were evaluated on model mixtures in terms of repeatability and linearity. Repeatability better than 1% for ultrafast J-resolved spectra and better than 7% for TOCSY spectra was obtained. Moreover, both methods were characterized by an excellent linearity, thus opening promising perspectives for this new quantitative methodology called ufo-qNMR (ultrafast optimized quantitative NMR). However, when considering complex mixtures such as those involved in metabolomics studies, the question of the relative sensitivity per unit of time of ultrafast versus conventional 2D NMR needs to be discussed. As mentioned earlier (and as also fairly intuitive), a one-scan ultrafast experiment will be less sensitive than a conventional experiment where signal is accumulated during several minutes or hours. A more relevant comparison, however, begs for the consideration of the Signal-to-Noise Ratio (SNR) achieved by these two experiments along the two characterized domains, per unit of time. In other words, the question arises if for a given experimental acquisition time (e.g. 30 min), should one run a conventional 2D experiment, or rather accumulate complete sets of single-scan ultrafast 2D acquisitions in a “multi-scan single-shot” (M3S) approach. This question is of particular pertinence for metabolic samples that are generally characterized by low concentrations, where averaging several ultrafast experiments will in general be indispensable. In order to answer this question, Pathan et al. recently carried out a systematic analytical study on model mixtures of metabolites (108). Surprisingly, it turned out that for the same experimental duration, and in the case of homonuclear 2D NMR, the multi-scan single shot approach was more sensitive than conventional 2D NMR. This was attributed to the higher immunity of ultrafast experiments to hardware temporal instabilities. As a consequence, a high quantitative performance can be expected from this original approach. Indeed, Le Guennec et al. demonstrated, in the case of COSY experiments, that this multi-scan single shot acquisition strategy offers a better analytical performance (precision and linearity) than conventional 2D NMR (109).
4.3. Application to metabolic samples
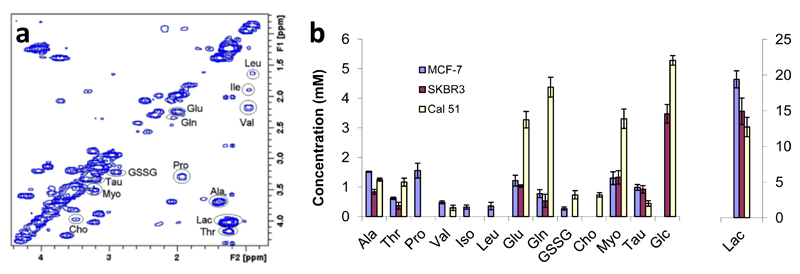
The quantitative ultrafast strategy just described can also be applied to solve metabolic issues requiring high-precision and high-accuracy 2D NMR measurements. A first demonstration of this was the determination of absolute metabolite concentrations in biological extracts; a goal of the highest relevance for determining characteristic biomarkers to fully understand metabolic complexities. Le Guennec et al. applied an optimized ultrafast COSY approach to measure the absolute metabolite concentration in three breast cancer cell line extracts, relying on a standard addition protocol (109). M3S COSY spectra of such extracts were recorded in 20 minutes and gave access to the absolute concentration of 14 major metabolites (Figure 9). The results revealed significant metabolic differences between cell lines, thus demonstrating the interest of furthering an “ultrafast 2D metabolomics” approach.
Figure 9.
Data extracted from Ref. (109), showing the potential of UF 2D NMR for quantitative analysis. (a) 2D 1H “multi-scan single shot” COSY spectrum of a breast cancer cell line extract, obtained by CHCl3/MeOH/H2O extraction of breast cancer cells. The spectrum was acquired in 20 minutes (256 transients). (b) Metabolite concentrations of intracellular extracts obtained from three cell lines: SKBR3, MCF-7 and Cal 51 by a quantitative 2D “multi-scan single shot” COSY protocol associated with a standard addition procedure. The concentrations are normalized to a 100 mg mass of lyophilized cells.
Another recent quantitative application of UF 2D NMR pertains the field of fluxomics. As demonstrated by Massou, Portais and co-workers, 2D NMR is a promising tool for studying metabolic fluxes by measuring 13C enrichments in complex mixtures of 13C-labeled metabolites (17, 101). However, the methods reported so far were hampered by long experimental durations, which limited the use of 2D NMR as a quantitative fluxomics tool. In order to take advantage of the time saving and higher precision offered by ultrafast 2D NMR, several acquisition strategies have been recently proposed to measure 13C enrichments from single-scan 2D spectra (110, 111). Two homonuclear experiments were designed, ultrafast COSY and zTOCSY, where the site-specific 13C enrichments can be measured by reading lines of the 2D spectrum (110). The two approaches were compared in terms of analytical performance, showing accuracy and precision of a few percent and an excellent linearity. They were applied to the measurement of 13C enrichments on a biomass hydrolysate (Figure 10). The experimental duration was divided by 200 compared to the conventional approach, while yielding the same information on site-specific isotopic enrichments.
Figure 10.
Ultrafast COSY spectrum of a biomass hydrolysate from E. coli cells grown on a 1:1 [U-13C]-glucose:glucose mixture (12 g/L). The sample contains mainly amino acids released from the hydrolysis of cellular proteins. The spectrum was recorded in 20 s (4 scans) on a 500 MHz spectrometer equipped with a cryoprobe. Cross-peaks are annotated according to the corresponding carbon in the amino acids, using the international one-letter code for amino-acids and using standard letters for the position of the protonated carbon in the molecular backbone, i.e., A, B, G, D, and E for α, β, γ, δ, and ε, respectively. Site-specific 13C isotopic enrichments are measured by extracting columns from the 2D spectrum and by integrating the satellites of the resulting site-specific patterns.
5. Ultrafast 2D NMR: Coupling with hyphenated techniques
Coupling NMR with other analytical techniques in order to increase its separation power -in the case of coupling with chromatography- or its sensitivity -when coupled to hyperpolarization techniques- generally involves macroscopic changes in the sample composition in the course of time. It confers these experiments an irreversible character, which is incompatible with the time-incremental procedure needed to record 2D spectra. This paragraph describes some of the recent advances that have hitherto been described to take advantage of the single-scan nature of ultrafast experiments in this context.
5.1. Ultrafast LC-NMR
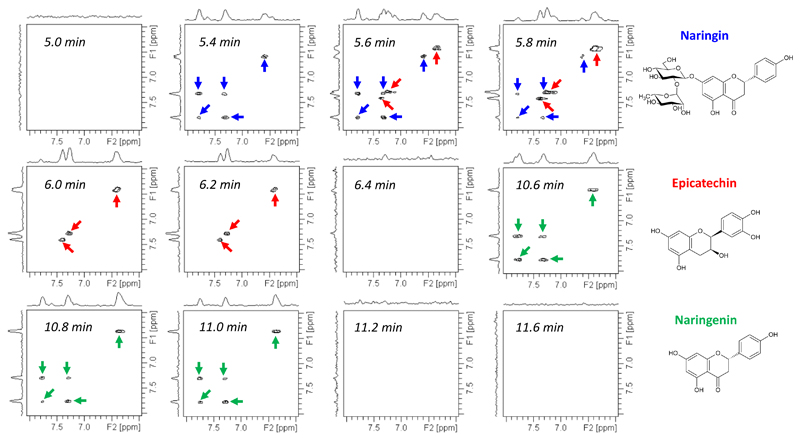
LC-NMR (consisting of coupling Liquid Chromatography with Nuclear Magnetic Resonance) combines the resolving power of chromatography with the structural insight provided by an analytical detection method (112). This efficient technology is becoming increasingly routine worldwide, particularly for pharmaceutical applications (113) or natural product analysis (114). A particularly powerful approach is the on-flow mode, where 1D NMR spectra are obtained as the analytes are eluted from the column. However, such an irreversible process is incompatible with multidimensional NMR methods that form an indispensible tool for the study of complex mixtures. As a consequence, the design and use of fast detection methods is indispensable to perform a real-time 2D NMR characterization of analytes undergoing continuous chromatographic separation. Among the fast 2D NMR methods, only two were successfully coupled with high-performance liquid chromatography (HPLC). Hadamard spectroscopy was successfully applied in a HPLC-NMR setting (115), an approach which required, however, a priori knowledge of the resonances. Alternatively, Shapira et al. showed the potentialities of coupling ultrafast NMR with a chromatographic setup to follow the real time elution of analytes (116). This study demonstrated the feasibility of such coupling on a home-made experimental setup, consisting of a classical silica-based glass column specially designed for this kind of experiments. It was applied to model organic compounds in a non-protonated solvent. More recently, this approach was extended to a commercial HPLC-NMR setup by Queiroz and co-workers (117). Ultrafast COSY spectra were acquired every 12 s in the course of a 12 min chromatographic run performed on a mixture of natural aromatic compounds (Figure 11). A noticeable feature was the use of an analytical C-18 column with regular HPLC solvents, demonstrating the applicability of the method to commonly used HPLC-NMR conditions. While this approach is still hampered by sensitivity losses due to the non-negligible flow during spatiotemporal encoding, it opens the way to a number of applications in the numerous fields in which HPLC-NMR forms a routine analytical tool.
Figure 11.
Ultrafast COSY NMR spectra (aromatic region) (117) recorded in real time in the course of a HPLC-NMR run on a mixture of naringin (blue), epicatechin (red) and naringenin (green), 10 mg/mL each, dissolved in acetonitrile/water/D2O 45:27.5:27.5. The spectra were recorded with double solvent presaturation, at 298 K on a 600 MHz Bruker Avance III spectrometer equipped with a cryogenic probe, including a cryofit accessory with an active cell volume of 60 µL.
5.2. Ultrafast DNP-NMR
Recent years have witnessed the emergence of different approaches to overcome what is probably the main limitation of NMR, i.e. sensitivity. Several alternatives have been proposed, capable of preparing nuclei in “hyperpolarized” liquid-phase states. These are metastable spin arrangements in which the bulk nuclear polarizations depart from their usual (ca. 10-5) Boltzmann distributions, and approach unity values. Once prepared and transferred into a NMR spectrometer, the “super-signals” that can be elicited from these spin arrangements can be exploited within a timescale dependent on the longitudinal relaxation time T1 of the hyperpolarized nuclei. Adequate methods proposed and demonstrated for producing and exploiting these extreme spin-polarization levels include the use of parahydrogen (118, 119), the optical pumping of noble gases (120, 121), and microwave driven dynamic nuclear polarization (DNP) from unpaired electrons (122–124). Amongst these methods, the last option has the appeal of providing high enhancements while making few requirements in terms of chemical substrate or sample preparation. Several in situ (125) or ex situ (124, 126, 127) experimental approaches have been proposed to perform DNP prior to NMR spectroscopic acquisition. Particularly promising have been the metabolic results afforded by the ex situ DNP approach proposed by Golman et al. (124), whereby the sample to be analyzed is co-mixed with a free radical, frozen in a glass at cryogenic temperatures, and hyperpolarized by irradiating the radical close to its unpaired electron’s Larmor frequency for relatively long periods of time. Rapid melting and shuttling of the nuclear spins from this cryogenic environment into a spectrometer enables an otherwise routine solution-state NMR spectroscopic observation. Yet, upon taking into account the effects of the cryogenic cooling and of the DNP process, these “routine” observations will take place on nuclei the polarization of which has been enhanced by a factor of around 104.
Despite its outstanding promise, the irreversible character of ex situ DNP NMR is best suited to collect a single or at most a small number of scans. This makes it a poor starting point for acquiring arrayed transients involving complex pulse sequences, of the kind needed to complete conventional 2D NMR acquisitions. A particularly promising solution is to record single-scan 2D NMR spectra of hyperpolarized compounds via ultrafast 2D methods. The potential of this powerful coupling was demonstrated in 2007 by Frydman and Blazina, who showed that 2D spectra of hyperpolarized liquid samples at submicromolar concentrations could be acquired within 0.1 s (128). Their results highlight the high complementarity of the two techniques: UF 2D NMR solves the irreversibility issue of ex situ DNP-NMR, while DNP offers a solution to the relatively low sensitivity of UF 2D NMR.
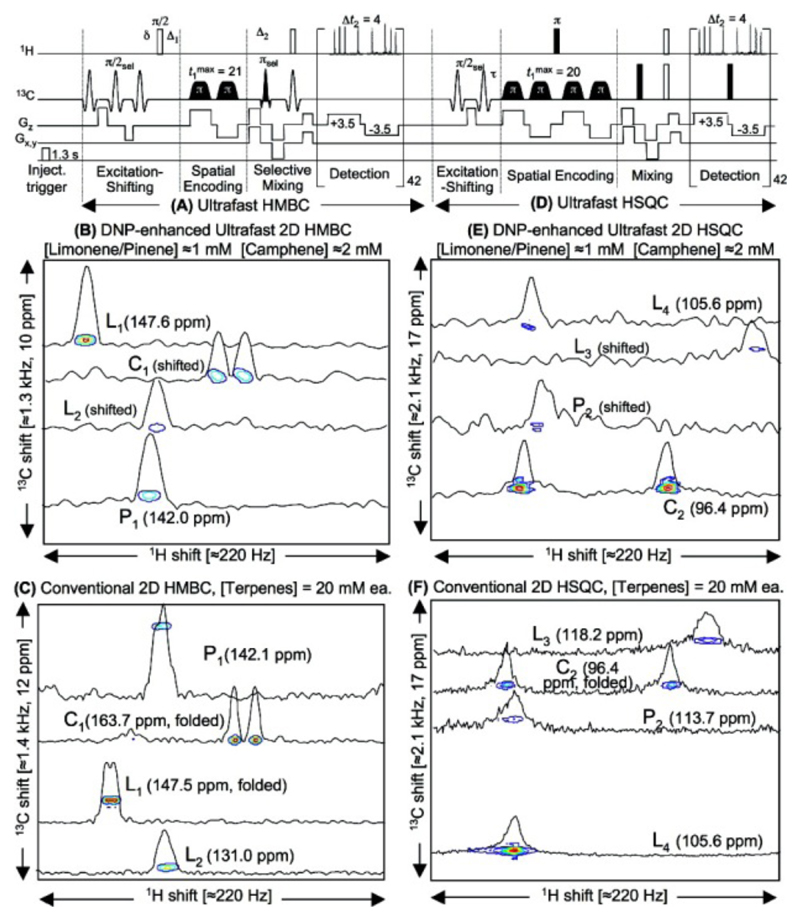
Another drawback of the ex situ DNP-NMR setting comes from the time needed to transfer the sample from the polarizer to the NMR spectrometer (c.a. 1 s). It implies that only sites with relatively long liquid state T1s will be able to retain a significant hyperpolarization. Therefore, a high performance can be expected from ultrafast 2D methods exploiting the hyperpolarization of slow relaxing, low-γ nuclei such as quaternary 13C. This suggests the interest of long-distance correlation experiments between quaternary 13C and nonbonded protons, such as the Heteronuclear Multiple-Bond Correlation (HMBC) experiment. The ultrafast version of this experiment was successfully coupled with ex situ DNP in 2008 (129), relying on hyperpolarized quaternary 13C and 15N nuclei. In 2009, band-selective approaches were proposed to simultaneously record several 2D NMR correlations in a single-scan, a strategy which was successfully applied to mixtures of hyperpolarized natural products at millimolar concentrations (130) (Figure 12).
Figure 12.
Pulse sequences and spectra from reference (130) showing the potentialities of coupling UF 2D NMR with ex situ Dynamic Nuclear Polarisation. (A,D) Successive 2D HMBC and HSQC 13C-1H ultrafast pulse sequences, including gradient and timing parameters (in G/cm and ms) and spectral/spatial manipulations bringing the relevant signals inside the targeted spectral window. (B,E) Ultrafast HMBC and HSQC 2D spectra with relevant cross sections, obtained after polarizing 4.4 µL of a 0.5 M limonene/α-pinene/camphene 1:1:2 solution in a toluene/toluene-d8 1:5 mixture with 20 mM BDPA. Sudden dissolution in methanol-d4 led to a final concentration of 1 mM for limonene and α-pinene, and 2 mM for camphene. (C,F) Conventional HMBC and HSQC 2D NMR spectra collected on a 20 mM equimolar terpene mixture in CDCl3, obtained in 90 min using 32 scans, 64 t1 increments, a 2 s recycle delay and a 0.5 s acquisition time. These conventional data were acquired with the same 13C spectral widths as the ultrafast spectra, leading to the aliasing of some of the peaks. Also shown are the unfolded positions of the 13C resonances characterized in each experiment (in ppm’s from TMS). Both HSQC and HMBC conventional pulse sequences were made spectrally selective to avoid the appearance of unwanted 13C resonances.
These recent advances highlight the interest of coupling UF 2D NMR with DNP, and open numerous application perspectives. It was also recently shown that ultrafast NMR could also be successfully coupled within a different DNP setting (131) –allowing a faster transfer of the analytes and therefore the acquisition of homonuclear ultrafast 2D experiments– but also with other hyperpolarization methods such as para-hydrogen (132).
6. Pseudo-2D Ultrafast NMR
A final group of single-scan methods worth addressing, concerns new and emerging techniques that rely on the principles of ultrafast 2D NMR but are not strictly speaking “2D NMR” acquisitions, in the sense that they do not entail the encoding of a coherent indirect domain evolution. Still these methods are of high potential usefulness in analytical studies; and the possibility to perform them in an “ultrafast” format, could enable their systematic use to study molecular dynamic properties in real time.
One such promising approach consists in the development of fast, spatially-encoded methods for the measurement of longitudinal relaxation times (T1). These determinations can provide a valuable tool to understand the dynamics of spin systems and to probe molecular motions over a wide range of timescales. The measurement of T1 generally relies on pseudo-2D experiments such as inversion-recovery (IR) (133) which are hampered by long acquisition times, and are therefore beyond the usual scope of real-time studies. Several ideas have been proposed to reduce the duration of IR experiments, such as the slice-selective approaches (134, 135) that make it possible to access small molecule T1s in a single scan. While these methods are better suited for studying long T1s (typically several seconds), sub-second relaxation times are often encountered, particularly when probing dynamic phenomena at the molecular level. Very recently, Smith et al. proposed a pulse sequence akin to ultrafast 2D NMR experiments in order to perform single-scan IR experiment adapted to short T1s (136). It can be considered as “pseudo-2D ultrafast” in the sense that it requires 2D Fourier Transform of the data, but T1 are determined from a single-scan experiment, making it possible to study real-time molecular dynamics.
In a similar vein, also worth exploring are the alternative approaches capable of separating analytes via their dynamic properties based on their diffusion coefficients (137). The diffusion-ordered spectroscopy (DOSY) methodology encodes the effect of random Brownian motion in the indirect dimension, thanks to a series of experiments recorded with incremented gradient strength. While DOSY is highly powerful for studying complex mixtures, it still suffers from an incrementation scheme akin to the one of 2D NMR which limits its applicability, particularly when dynamic or unstable systems are studied. An ultrafast version of DOSY was recently described to overcome this drawback (138), based on the intimate relationship between ultrafast spectroscopy and diffusion effects (60, 63). It opens promising perspectives for monitoring diffusion and flow phenomena in complex system.
In a final example of such pseudo-2D “ultrafast” strategies, Jerschow and co-workers (139) have recently demonstrated the use of a spatial domain to speed up the study of Chemical exchange saturation transfer (CEST) phenomena, which form a popular approach to generate MRI contrast and are particularly promising to study in vivo metabolism. In conventional CEST experiments, the polarization of water is measured as a function of incremented offsets of a saturated RF irradiation (140). In the “ultrafast” version of this experiment, signals with different irradiation offsets are recorded simultaneously in different parts of the sample, which makes it possible to record a full Z-spectrum in only two scans. While this approach, like others described above, suffers from a lower sensitivity inherent to the ultrafast approach, it is very promising when considering coupling it with hyperpolarization methods.
7. Conclusion and Perspectives
This review presents some of the progress made in the field of ultrafast 2D NMR, particularly in what relates to making this spectroscopic method a powerful complement to the NMR analytical toolkit. Thanks to recent developments this method is proving its potential for a variety of analytical applications, from the real-time monitoring of chemical and biochemical processes to the quantitative analysis of metabolic samples. While sensitivity appears as a main limitation of this methodology, signal-to-noise increase by several orders of magnitude can be expected from the coupling with hyperpolarization techniques. Such coupling could particularly benefit to the quantitative analysis of metabolic samples, where recent results obtained with UF 2D NMR have opened exciting perspectives, but where the low analyte concentration is often an issue. Research perspectives will include the design of analytical strategies to accurately measure metabolite concentrations from 2D NMR spectra following DNP. When considering complex metabolic samples, where even 2D spectra may be hampered by peak overlap, significant improvement can be expected from the development of approaches with higher dimensionality. While pure ultrafast 3D NMR approaches are feasible in practice (141), their resolution and sensitivity penalties become even more severe than those of the normal 2D UF NMR counterparts. On the other hand, high spectral qualities have been demonstrated from hybrid conventional/ultrafast 3D approaches, capable of recording a whole 3D spectrum in the time needed to record a conventional 2D spectrum. This strategy was first suggested in a biomolecular context (61), and was recently applied successfully to the measurement of site-specific 13C isotopic enrichments (142) (Figure 13).
Figure 13.
3D UFJCOSY pulse sequence (a) and corresponding 3D NMR spectrum (b) of a 13C-labeled alanine sample (142), capable of recording a 3D COSY-J-resolved spectrum in 11 minutes relying on a hybrid conventional-ultrafast acquisition strategy. A F1F2 plane read from the 3D spectrum gives rise to a COSY-type correlation (c), where the peaks are not broadened by heteronuclear couplings in spite of the 13C enrichment. The heteronuclear couplings are obtained from dimension F3, and the 13C isotopic enrichments are measured by reading a column perpendicular to the COSY plane (d).
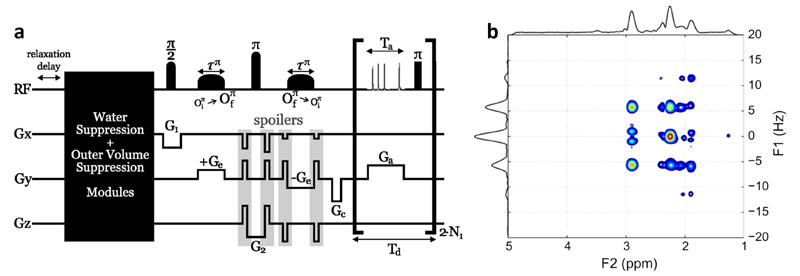
Finally, promising perspectives also arise from the extension of the ultrafast methodology to the field of in vivo spectroscopy, where considerable gains can be expected from the speed gain offered by the single-scan approach. A first step towards localized spectroscopy was recently taken by Roussel et al. (143), who proposed an approach capable of recording ultrafast 2D J-resolved localized spectra on in vitro phantoms placed in a small animal imaging system (Figure 14). The application of ultrafast spectroscopy to in vivo systems sounds particularly promising when considering the recent work of Pelupessy et al. (144) and Zhang et al. (145) who recently designed single-scan approaches capable of recording high-resolution 2D spectra in the presence of spatial inhomogeneities, which is a central issue in the field of in vivo spectroscopy.
Figure 14.
(a) Ultrafast JPRESS pulse sequence (ufJPRESS) capable of recording 3D localized 2D J-resolved ultrafast spectra on a small animal imaging system. (b) Corresponding spectrum acquired in 2 min 40 s on an n vitro phantom containing a GABA solution (10% w/w in water) placed at the center of a 50 mL tube of pure ethanol. The spectrum was recorded on a 7T Biospec Bruker imaging system (small animal).
Acknowledgements
Patrick Giraudeau thanks the French National Research Agency for a young investigator starting grant (ANR Grant 2010-JCJC-0804-01), as well as Prof. Serge Akoka for helpful discussions. Lucio Frydman acknowledges the Israel Science Foundation (Projects ISF 795/13 and iCore grant No 1775/12), ERC Advanced Grant #246754, EU’S BioNMR Grant #261863, a Helen and Kimmel Award for Innovative Investigation, and the generosity of the Perlman Family Foundation.
Acronyms and definitions list
- CEST
Chemical Exchange Saturation Transfer; Process involving the chemical exchange of a nucleus in the NMR experiment from one site to a chemically different site
- COSY
Correlation spectroscopy; a common type of homonuclear 2D experiment showing connectivities between scalarly coupled spins
- DNP
Dynamic Nuclear Polarization; method to enhance nuclear spin polarization by saturating the resonances of nearby electrons
- DOSY
Diffusion-Ordered Spectroscopy; Pseudo-2D experiment separating the analytes based on their molecular diffusion properties
- EPSI
Echo-Planar Spectroscopic Imaging; acquisition technique which maps a spatial dimension and a spectroscopic dimension in a single readout.
- FT
Fourier Transform; mathematical procedure that enables one to discern which frequency contributions compose a time-dependant signal response function
- Hadamard Spectroscopy
Alternative way of recording multi-dimensional NMR spectra in a non-Fourier fashion
- HMBC
Heteronuclear multiple-bond correlation: a common heteronuclear 2D experiment for determining long-distance coupling between heteronuclear pairs (e.g. 1H and 13C)
- HMQC
Heteronuclear multiple-quantum correlation: a common heteronuclear 2D experiment for determining connectivities between heteronuclear pairs (e.g. 1H and 13C)
- HPLC
High Performance Liquid Chromatography
- HSQC
Heteronuclear single-quantum correlation: a common heteronuclear 2D experiment for determining connectivities between heteronuclear pairs (e.g. 1H and 13C)
- J-res spectroscopy
a common type of homonuclear 2D experiment separating chemical shift and coupling interactions in two orthogonal dimensions
- LC-NMR
Hyphenated technique consisting of coupling liquid chromatography (LC) with NMR
- LP
Linear Prediction; a signal processing procedure which improves the resolution of NMR spectra by predicting the missing points in the temporal signal
- MaxEnt
Maximum Entropy Reconstruction; a signal processing procedure which improves the resolution of NMR spectra recorded with a limited number of points
- MRI
Magnetic Resonance Imaging
- NMR
Nuclear Magnetic Resonance
- NOESY
Nuclear Overhauser Effect Spectroscopy; a homonuclear 2D experiment showing connectivities between spins depending on their spatial proximity
- SOFAST
Fast 2D NMR acquisition technique based on optimized relaxation delays and pulse flip angles
- TOCSY
Total Correlation spectroscopy; a common type of homonuclear 2D experiment showing connectivities between all the spins belonging to the same spin system
References
- 1.Batta G, Kovir K, Jossuth L, Szankey C. Analytical Spectroscopy Library. London: Elsevier; 1997. Methods of Structure Elucidation by High-Resolution NMR. [Google Scholar]
- 2.Simpson JH. Organic Structure Determination Using 2-D NMR Spectroscopy: A Problem-Based Approach. Academic Press, Elsevier; 2008. [Google Scholar]
- 3.Cavanagh J, Fairbrother WJ, Palmer AG, Skelton NJ, Rance M. Protein NMR spectroscopy: Principles and Practice. Amsterdam: Elsevier; 2006. [Google Scholar]
- 4.Wüthrich K. NMR of proteins and nucleic acids. Baker Lectures Series, Wiley-Interscience; 1986. [Google Scholar]
- 5.Tycko R. Nuclear Magnetic Resonance Probes of Molecular Dynamics. Springer; 2003. [Google Scholar]
- 6.Jeener J. Lecture presented at Ampere International Summer School II, Basko Polje, Yugoslavia. 1971 [Google Scholar]
- 7.Aue WP, Bartholdi E, Ernst RR. Two-dimensional spectroscopy. Application to nuclear magnetic resonance. J Chem Phys. 1976;64:2229–46. [Google Scholar]
- 8.Aue WP, Bartholdi E, Ernst RR. Homonuclear broadband decoupling in two dimensional J-resolved NMR spectroscopy. J Chem Phys. 1976;64:2229–46. [Google Scholar]
- 9.Maudsley AA, Ernst RR. Indirect detection of magnetic resonance by heteronuclear two-dimensional spectroscopy. Chemical Physics Letters. 1977;50:368–72. [Google Scholar]
- 10.Müller L, Kumar A, Ernst RR. Two-dimensional carbon-13 spin-echo spectroscopy. J Magn Reson. 1977;25:383–90. [Google Scholar]
- 11.Aue WP, Bachmann P, Wokaun A, Ernst RR. Sensitivity of two-dimensional NMR spectroscopy. J Magn Reson. 1978;29:523–33. [Google Scholar]
- 12.Aue WP, Karhan J, Ernst RR. Homonuclear broad band decoupling and two-dimensional J-resolved NMR spectroscopy. J Chem Phys. 1976;64:4226–27. [Google Scholar]
- 13.Ernst RR, Bodenhausen G, Wokaun A. Principles of nuclear magnetic resonance in one and two dimensions. Oxford: 1987. [Google Scholar]
- 14.Topcu G, Ulubelen A. Structure elucidation of organic compounds from natural sources using 1D and 2D NMR techniques. J Mol Struct. 2007;834-836:57–73. [Google Scholar]
- 15.Li D, Owen NL, Perera P, Andersson C, Bohlin L, et al. Structure Elucidation of Three Triterpenoid Saponins from Alphitonia zizyphoides Using 2D NMR Techniques. J Nat Prod. 1994;57:218–24. doi: 10.1021/np50104a004. [DOI] [PubMed] [Google Scholar]
- 16.Koskela H. Quantitative 2D NMR studies. Annu Rep NMR Spectrosc. 2009;66:1–31. [Google Scholar]
- 17.Massou S, Nicolas C, Letisse F, Portais J-C. NMR-based fluoxomics: Quantitative 2D NMR methods for isotopomers analysis. Phytochemistry. 2007;68:2330–40. doi: 10.1016/j.phytochem.2007.03.011. [DOI] [PubMed] [Google Scholar]
- 18.Englander SW, Mayne L. Protein Folding Studied Using Hydrogen-Exchange Labeling and Two-Dimensional NMR. Annu Rev Biophys Biomol Struct. 1992;21:243–65. doi: 10.1146/annurev.bb.21.060192.001331. [DOI] [PubMed] [Google Scholar]
- 19.Machonkin TE, Westler WM, Markley JL. 13C{13C} 2D NMR: A Novel Strategy for the Study of Paramagnetic Proteins with Slow Electronic Relaxation Rates. J Am Chem Soc. 2002;124:3204–05. doi: 10.1021/ja017733j. [DOI] [PubMed] [Google Scholar]
- 20.Kriwacki RW, Pitner TP. Current Aspects of Practical Two-Dimensional (2D) Nuclear Magnetic Resonance (NMR) Spectroscopy: Applications to Structure Elucidation. Pharm Res. 1989;6:531–54. doi: 10.1023/a:1015941128608. [DOI] [PubMed] [Google Scholar]
- 21.Mehlkopf AF, Korbee D, Tiggelman TA, Freeman R. Sources of t1 noise in two-dimensional NMR. J Magn Reson. 1984;58:315–23. [Google Scholar]
- 22.Morris GA. Systematic sources of signal irreproducibility and t1 noise in high field NMR spectrometers. J Magn Reson. 1992;100:316–28. [Google Scholar]
- 23.Ross A, Salzmann M, Senn H. Fast-HMQC using Ernst angle pulses: an efficient tool for screening of ligand binding to target proteins. J-Bio NMR. 1997;10:389–96. doi: 10.1023/A:1018361214472. [DOI] [PubMed] [Google Scholar]
- 24.Schanda P, Brutscher B. Very fast two-dimensional NMR spectroscopy for real-time investigation of dynamic events in proteins on the time scale of seconds. J Am Chem Soc. 2005;127:8014–15. doi: 10.1021/ja051306e. [DOI] [PubMed] [Google Scholar]
- 25.Cai S, Seu C, Kovacs Z, Sherry AD, Chen Y. Sensitivity Enhancement of Multidimensional NMR Experiments by Paramagnetic Relaxation Effects. J Am Chem Soc. 2006;128:13474–78. doi: 10.1021/ja0634526. [DOI] [PubMed] [Google Scholar]
- 26.Vitorge B, Bodenhausen G, Pelupessy P. Speeding up nuclear magnetic resonance spectroscopy by the use of SMAll Recovery Times - SMART NMR. J Magn Reson. 2010;207:149–52. doi: 10.1016/j.jmr.2010.07.017. [DOI] [PubMed] [Google Scholar]
- 27.Jeannerat D. High resolution in heteronuclear 1H-13C NMR experiments by optimizing spectral aliasing with one-dimensional carbon data. Magn Reson Chem. 2003;41:3–17. [Google Scholar]
- 28.Donoho DL, Tsaig Y. Fast solution of l1-norm minimization problems whan the solution may be sparse. IEEE Trans Inf Theory. 2008;54:4789–812. [Google Scholar]
- 29.Stern AS, Donoho DL, Hoch JC. NMR data processing using iterative thresholding and minimum l1-norm reconstruction. J Magn Reson. 2007;188:295–300. doi: 10.1016/j.jmr.2007.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Barkhuijsen H, De Beer R, Bovée WMMJ, Van Ormondt D. Retrieval of frequencies, amplitudes, damping factors, and phases from time-domain signals using a linear least-squares procedure. J Magn Reson. 1985;61:465–81. [Google Scholar]
- 31.Stern AS, Li K-B, Hoch JC. Modern spectrum analysis in multidimensional NMR spectroscopy: comparison of linear-prediction extrapolation and maximum-entropy reconstruction. J Am Chem Soc. 2002;124:1982–93. doi: 10.1021/ja011669o. [DOI] [PubMed] [Google Scholar]
- 32.Hoch JC. Maximum entropy signal processing of two-dimensional NMR data. J Magn Reson. 1985;64:436–40. [Google Scholar]
- 33.Kazimierczuk K, Zawadzka A, Koźmiński W. Optimization of random time domain sampling in multidimensional NMR. J Magn Reson. 2008;192:123–30. doi: 10.1016/j.jmr.2008.02.003. [DOI] [PubMed] [Google Scholar]
- 34.Brüschweiler R, Zhang F. Covariance nuclear magnetic resonance spectroscopy. J Chem Phys. 2004;120:5253–60. doi: 10.1063/1.1647054. [DOI] [PubMed] [Google Scholar]
- 35.Barna JCJ, Laue ED, Mayger MR, Skilling J, Worrall SJP. Exponential sampling, an alternative method for sampling in two-dimensional NMR experiments. J Magn Reson. 1987;73:69–77. [Google Scholar]
- 36.Kupce E, Freeman R. Fast multidimensional NMR : radial sampling of evolution space. J Magn Reson. 2005;173:317–21. doi: 10.1016/j.jmr.2004.12.004. [DOI] [PubMed] [Google Scholar]
- 37.Kamzimierczuk K, Zawadzka A, Kozminski V, Zhukov I. Lineshapes and artifacts in multidimensional Fourier Transform of arbitrary sampled NMR data sets. J Magn Reson. 2007;188:344–56. doi: 10.1016/j.jmr.2007.08.005. [DOI] [PubMed] [Google Scholar]
- 38.Lafon O, Hu B, Amoureux J-P, Lesot P. Fast and High-Resolution Stereochemical Analysis by Nonuniform Sampling and Covariance Processing of Anisotropic Natural Abundance 2D 2H NMR Datasets. Chem Eur J. 2011;17:6716–24. doi: 10.1002/chem.201100461. [DOI] [PubMed] [Google Scholar]
- 39.Kupce E, Freeman R. Two-dimensional Hadamard spectroscopy. J Magn Reson. 2003;162:300–10. doi: 10.1016/s1090-7807(02)00196-9. [DOI] [PubMed] [Google Scholar]
- 40.Frydman L, Lupulescu A, Scherf T. Principles and features of single-scan two-dimensional NMR spectroscopy. J Am Chem Soc. 2003;125:9204–17. doi: 10.1021/ja030055b. [DOI] [PubMed] [Google Scholar]
- 41.Frydman L, Scherf T, Lupulescu A. The acquisition of multidimensional NMR spectra within a single scan. Prod Natl Acad Sci USA. 2002;99:15858–62. doi: 10.1073/pnas.252644399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mansfield P. Multi-planar image formation using NMR spin echoes. J Phys C: Solid State Phys. 1977;10:55–58. [Google Scholar]
- 43.Mansfield P. Spatial mapping of the chemical shift in NMR. Magn Reson Med. 1984;1:370–86. doi: 10.1002/mrm.1910010308. [DOI] [PubMed] [Google Scholar]
- 44.Shrot Y, Frydman L. Ghost-peak suppression in ultrafast two-dimensional NMR spectroscopy. J Magn Reson. 2003;164:351–57. doi: 10.1016/s1090-7807(03)00177-0. [DOI] [PubMed] [Google Scholar]
- 45.Pelupessy P. Adiabatic single scan two-dimensional NMR spectroscopy. J Am Chem Soc. 2003;125:12345–50. doi: 10.1021/ja034958g. [DOI] [PubMed] [Google Scholar]
- 46.Shrot Y, Shapira B, Frydman L. Ultrafast 2D NMR spectroscopy using a continuous spatial encoding of the spin interactions. J Magn Reson. 2004;171:163–70. doi: 10.1016/j.jmr.2004.08.001. [DOI] [PubMed] [Google Scholar]
- 47.Andersen NS, Köckenberger W. A simple approach for phase-modulated single-scan 2D NMR spectroscopy. Magn Reson Chem. 2005;43:791–94. doi: 10.1002/mrc.1624. [DOI] [PubMed] [Google Scholar]
- 48.Tal A, Shapira B, Frydman L. A continuous phase-modulated approach to spatial encoding in ultrafast 2D NMR spectroscopy. J Magn Reson. 2005;176:107–14. doi: 10.1016/j.jmr.2005.05.009. [DOI] [PubMed] [Google Scholar]
- 49.Shapira B, Shrot Y, Frydman L. Symmetric spatial encoding in ultrafast 2D NMR spectroscopy. J Magn Reson. 2006;178:33–41. doi: 10.1016/j.jmr.2005.08.015. [DOI] [PubMed] [Google Scholar]
- 50.Shrot Y, Frydman L. Spatial encoding strategies for ultrafast multidimensional nuclear magnetic resonance. J Chem Phys. 2008;128:052209. doi: 10.1063/1.2834733. [DOI] [PubMed] [Google Scholar]
- 51.Wu C, Zhao M, Cai S, Lin Y, Chen Z. Ultrafast 2D COSY with constant-time phase-modulated spatial encoding. J Magn Reson. 2010;204:82–90. doi: 10.1016/j.jmr.2010.02.005. [DOI] [PubMed] [Google Scholar]
- 52.Basus VJ, Ellis PD, Hill HDW, Waugh JS. Utilization of chirp frequency modulation for heteronuclear spin decoupling. J Magn Reson. 1979;35:19–37. [Google Scholar]
- 53.Böhlen JM, Bodenhausen G. Experimental aspects of chirp NMR spectroscopy. J Magn Reson A. 1992;102:293–301. [Google Scholar]
- 54.Giraudeau P, Akoka S. A new detection scheme for ultrafast J-resolved spectroscopy. J Magn Reson. 2007;186:352–57. doi: 10.1016/j.jmr.2007.03.007. [DOI] [PubMed] [Google Scholar]
- 55.Gal M, Frydman L. Ultrafast Multidimensional NMR Principles and Practice of Single-scan Methods. In: Morris GA, Emsley JW, editors. Encyclopedia of Magnetic Resonance. Chichester: Wiley; 2010. pp. 43–60. [Google Scholar]
- 56.Tal A, Frydman L. Single-scan multidimensional magnetic resonance. Prog Nucl Magn Reson Spectrosc. 2010;57:241–92. doi: 10.1016/j.pnmrs.2010.04.001. [DOI] [PubMed] [Google Scholar]
- 57.Giraudeau P, Akoka S. Resolution and sensitivity aspects of ultrafast J-resolved 2D NMR spectra. J Magn Reson. 2008;190:339–45. doi: 10.1016/j.jmr.2007.11.019. [DOI] [PubMed] [Google Scholar]
- 58.Giraudeau P, Akoka S. Sources of sensitivity losses in ultrafast 2D NMR. J Magn Reson. 2008;192:151–58. doi: 10.1016/j.jmr.2008.02.007. [DOI] [PubMed] [Google Scholar]
- 59.Pelupessy P, Duma L, Bodenhausen G. Improving resolution in single-scan 2D spectroscopy. J Magn Reson. 2008;194:169–74. doi: 10.1016/j.jmr.2008.06.023. [DOI] [PubMed] [Google Scholar]
- 60.Shrot Y, Frydman L. The effects of molecular diffusion in ultrafast two-dimensional nuclear magnetic resonance. J Chem Phys. 2008;128:164513. doi: 10.1063/1.2890969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Mishkovsky M, Frydman L. Principles and Progress in Ultrafast Multidimensional Nuclear Magnetic Resonance. Annu Rev Phys Chem. 2009;60:429–48. doi: 10.1146/annurev.physchem.040808.090420. [DOI] [PubMed] [Google Scholar]
- 62.Shrot Y, Frydman L. Spatial/spectral encoding of the spin interactions in ultrafast multidimensional NMR. J Chem Phys. 2009;131:224516. doi: 10.1063/1.3266422. [DOI] [PubMed] [Google Scholar]
- 63.Giraudeau P, Akoka S. Sensitivity losses and line shape modifications due to molecular diffusion in continuous encoding ultrafast 2D NMR experiments. J Magn Reson. 2008;195:9–16. doi: 10.1016/j.jmr.2008.08.001. [DOI] [PubMed] [Google Scholar]
- 64.Rouger L, Loquet D, Massou S, Akoka S, Giraudeau P. Limitation of diffusion effects in ultrafast 2D NMR by encapsulation of analytes in phospholipidic vesicles. ChemPhysChem. 2012;13:4124–27. doi: 10.1002/cphc.201200622. [DOI] [PubMed] [Google Scholar]
- 65.Giraudeau P, Akoka S. A new gradient-controlled method for improving the spectral width of ultrafast 2D NMR experiments. J Magn Reson. 2010;205:171–76. doi: 10.1016/j.jmr.2010.05.002. [DOI] [PubMed] [Google Scholar]
- 66.Tal A, Shapira B, Frydman L. Single-Scan 2D Hadamard NMR Spectroscopy. Angew Chem Int Ed. 2009;48:2732–36. doi: 10.1002/anie.200805612. [DOI] [PubMed] [Google Scholar]
- 67.Shrot Y, Frydman L. Compressed sensing and the reconstruction of ultrafast 2D NMR data: Principles and biomolecular applications. J Magn Reson. 2011;209:352–58. doi: 10.1016/j.jmr.2011.01.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mishkovsky M, Frydman L. Interlaced Fourier transformation of ultrafast 2D NMR data. J Magn Reson. 2005;173:344–50. doi: 10.1016/j.jmr.2005.01.007. [DOI] [PubMed] [Google Scholar]
- 69.Giraudeau P, Akoka S. Sensitivity and lineshape improvement in ultrafast 2D NMR by optimized apodization in the spatially encoded dimension. Magn Reson Chem. 2011;49:307–13. doi: 10.1002/mrc.2746. [DOI] [PubMed] [Google Scholar]
- 70.Queiroz Junior LHK, Ferreira AG, Giraudeau P. Optimization and practical implementation of ultrafast 2D NMR experiments. Quim Nova. 2013;26:577–81. [Google Scholar]
- 71.Pathan M, Charrier B, Tea I, Akoka S, Giraudeau P. New practical tools for the implementation and use of ultrafast 2D NMR experiments. Magn Reson Chem. 2013;51:168–75. doi: 10.1002/mrc.3927. [DOI] [PubMed] [Google Scholar]
- 72.Shapira B, Frydman L. Arrayed acquisition of 2D exchange NMR spectra within a single scan experiment. J Magn Reson. 2003;165:320–24. doi: 10.1016/j.jmr.2003.09.006. [DOI] [PubMed] [Google Scholar]
- 73.Gal M, Mishkovsky M, Frydman L. Real-time monitoring of chemical transformations by ultrafast 2D NMR spectroscopy. J Am Chem Soc. 2006;128:951–56. doi: 10.1021/ja0564158. [DOI] [PubMed] [Google Scholar]
- 74.Li W, Li J, Wu Y, Fuller N, Markus MA. Mechanistic Pathways in CF3COOH-Mediated Deacetalization Reactions. J Org Chem. 2010;75:1077–86. doi: 10.1021/jo902014z. [DOI] [PubMed] [Google Scholar]
- 75.Bussy U, Giraudeau P, Silvestre V, Jaunet-Lahary T, Ferchaud-Roucher V, et al. In situ NMR spectroelectrochemistry for the structure elucidation of unstable intermediate metabolites. Anal Bioanal Chem. 2013;405:5817–24. doi: 10.1007/s00216-013-6977-z. [DOI] [PubMed] [Google Scholar]
- 76.Herrera A, Fernández-Valle E, Martínez-Álvarez R, Molero D, Pardo ZD, et al. Real-Time Monitoring of Organic Reactions with Two-Dimensional Ultrafast TOCSY NMR Spectroscopy13. Angew Chem Int Edit. 2009;48:6274–77. doi: 10.1002/anie.200902387. [DOI] [PubMed] [Google Scholar]
- 77.Herrera A, Fernandez-Valle E, Gutiérrez EM, Martinez-Alvarez R, Molero D, et al. 2D Ultrafast HMBC: a valuable tool for monitoring organic reactions. Org Lett. 2010;12:144–47. doi: 10.1021/ol902532f. [DOI] [PubMed] [Google Scholar]
- 78.Giraudeau P, Lemeunier P, Coutand M, Doux J-M, Gilbert A, et al. Ultrafast 2D NMR applied to the kinetic study of D-glucose mutarotation in solution. J Spectrosc Dyn. 2011;1:2. [Google Scholar]
- 79.Pardo ZD, Olsen GL, Fernández-Valle ME, Frydman L, Martínez-Álvarez R, Herrera A. Monitoring Mechanistic Details in the Synthesis of Pyrimidines via Real-Time, Ultrafast Multidimensional NMR Spectroscopy. J Am Chem Soc. 2012;134:2706–15. doi: 10.1021/ja210154g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Queiroz Junior LHK, Giraudeau P, dos Santos FAB, Oliveira KT, Ferreira AG. Real-time mechanistic monitoring of an acetal hydrolysis using ultrafast 2D NMR. Magn Reson Chem. 2012;50:496–501. doi: 10.1002/mrc.3827. [DOI] [PubMed] [Google Scholar]
- 81.Corazza A, Rennella E, Schanda P, Mimmi MC, Cutuil T, et al. Native-unlike Long-lived Intermediates along the Folding Pathway of the Amyloidogenic Protein β2-Microglobulin Revealed by Real-time Two-dimensional NMR. J Biol Chem. 2010;285:5827–35. doi: 10.1074/jbc.M109.061168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Gal M, Schanda P, Brutscher B, Frydman L. UltraSOFAST HMQC NMR and the Repetitive Acquisition of 2D Protein Spectra at Hz Rates. J Am Chem Soc. 2007;129:1372–77. doi: 10.1021/ja066915g. [DOI] [PubMed] [Google Scholar]
- 83.Lee M-K, Gal M, Frydman L, Varani G. Real-time multidimensional NMR follows RNA folding with second resolution. Proc Natl Acad Sci USA. 2010;107:9192–97. doi: 10.1073/pnas.1001195107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Kwakye JK. Use of NMR for quantitative analysis of pharmaceuticals. Talanta. 1985;32:1069–71. doi: 10.1016/0039-9140(85)80126-0. [DOI] [PubMed] [Google Scholar]
- 85.Holzgrabe U. Quantitative NMR spectroscopy in pharmaceutical applications. Prog Nucl Magn Reson Spectrosc. 2010;57:229–40. doi: 10.1016/j.pnmrs.2010.05.001. [DOI] [PubMed] [Google Scholar]
- 86.Lindon JC, Nicholson JK, Holmes E, Everett JR. Metabonomics: Metabolic processes studied by NMR spectroscopy of biofluids. Concepts in Magnetic Resonance. 2000;12:289–320. [Google Scholar]
- 87.Wishart DS. Quantitative metabolomics using NMR. Trac-Trend Anal Chem. 2008;27:228–37. [Google Scholar]
- 88.Zhang S, Nagana Gowda GA, Asiago V, Shanaiah N, Barbas C, Raftery D. Correlative and quantitative 1H NMR-based metabolomics reveals specific metabolic pathway disturbances in diabetic rats. Anal Biochem. 2008;383:76–84. doi: 10.1016/j.ab.2008.07.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Tenailleau E, Lancelin P, Robins RJ, Akoka S. Authentication of the origin of vanillin using quantitative natural abundance 13C NMR. J Agric Food Chem. 2004;52:7782–87. doi: 10.1021/jf048847s. [DOI] [PubMed] [Google Scholar]
- 90.Le Grand F, George G, Akoka S. Natural abundance 2H-ERETIC-NMR authentication of the origin of methyl salicylate. J Agric Food Chem. 2005;53:5125–29. doi: 10.1021/jf050385a. [DOI] [PubMed] [Google Scholar]
- 91.Kruger NJ, Troncoso-Ponce MA, Ratcliffe RG. 1H NMR metabolite fingerprinting and metabolomic analysis of perchloric acid extracts from plant tissues. Nat Protocols. 2008;3:1001–12. doi: 10.1038/nprot.2008.64. [DOI] [PubMed] [Google Scholar]
- 92.Le Gall G, Colquhoun IJ, Davis AL, Collins GJ, Verhoeyen ME. Metabolite Profiling of Tomato (Lycopersicon esculentum) Using 1H NMR Spectroscopy as a Tool To Detect Potential Unintended Effects Following a Genetic Modification. J Agric Food Chem. 2003;51:2447–56. doi: 10.1021/jf0259967. [DOI] [PubMed] [Google Scholar]
- 93.Weljie AM, Newton J, Mercier P, Carlson E, Slupsky CM. Targeted Profiling: Quantitative Analysis of 1H NMR Metabolomics Data. Anal Chem. 2006;78:4430–42. doi: 10.1021/ac060209g. [DOI] [PubMed] [Google Scholar]
- 94.Giraudeau P, Guignard N, Hillion H, Baguet E, Akoka S. Optimization of homonuclear 2D NMR for fast quantitative analysis: Application to tropine-nortropine mixtures. J Pharmaceut Biomed Anal. 2007;43:1243–48. doi: 10.1016/j.jpba.2006.10.028. [DOI] [PubMed] [Google Scholar]
- 95.Koskela H, Kilpeläinen I, Heikkinen S. Some aspects of quantitative 2D NMR. J Magn Reson. 2005;174:237–44. doi: 10.1016/j.jmr.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 96.Koskela H, Väänänen T. Quantitative determination of aliphatic hydrocarbon compounds by 2D NMR. Magn Reson Chem. 2002;40:705–15. [Google Scholar]
- 97.Lewis IA, Karsten RH, Norton ME, Tonelli M, Westler WM, Markley JL. NMR Method for Measuring Carbon-13 Isotopic Enrichment of Metabolites in Complex Solutions. Anal Chem. 2010;82:4558–63. doi: 10.1021/ac100565b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Lewis IA, Schommer SC, Hodis B, Robb KA, Tonelli M, et al. Method for determining molar concentrations of metabolites in complex solutions from two-dimensional 1H-13C NMR spectra. Anal Chem. 2007;79:9385–90. doi: 10.1021/ac071583z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Martineau E, Giraudeau P, Tea I, Akoka S. Fast and precise quantitative analysis of metabolic mixtures by 2D 1H INADEQUATE NMR. J Pharm Biomed Anal. 2011;54:252–57. doi: 10.1016/j.jpba.2010.07.046. [DOI] [PubMed] [Google Scholar]
- 100.Martineau E, Tea I, Akoka S, Giraudeau P. Absolute quantification of metabolites in breast cancer cell extracts by quantitative 2D 1H INADEQUATE NMR. NMR Biomed. 2012;25:985–92. doi: 10.1002/nbm.1816. [DOI] [PubMed] [Google Scholar]
- 101.Massou S, Nicolas C, Letisse F, Portais J-C. Application of 2D-TOCSY NMR to the measurement of specific 13C-enrichments in complex mixtures of 13C-labeled metabolites. Metab Eng. 2007;9:252–57. doi: 10.1016/j.ymben.2007.03.001. [DOI] [PubMed] [Google Scholar]
- 102.Zhang L, Gellerstedt G. Quantitative 2D HSQC NMR determination of polymer structures by selecting suitable internal standard references. Magn Reson Chem. 2007;45:37–45. doi: 10.1002/mrc.1914. [DOI] [PubMed] [Google Scholar]
- 103.Giraudeau P, Akoka S. Fast and ultrafast quantitative 2D NMR: vital tools for efficient metabolomic approaches. Adv Bot Res. 2013;67:99–158. [Google Scholar]
- 104.Martineau E, Akoka S, Boisseau R, Delanoue B, Giraudeau P. Fast quantitative 1H-13C 2D NMR with very high precision. Anal Chem. 2013;85:4777–83. doi: 10.1021/ac4005309. [DOI] [PubMed] [Google Scholar]
- 105.Gronwald W, Klein MS, Kaspar H, Fagerer SR, Nurnberger N, et al. Urinary Metabolite Quantification Employing 2D NMR Spectroscopy. Anal Chem. 2008;80:9288–97. doi: 10.1021/ac801627c. [DOI] [PubMed] [Google Scholar]
- 106.Hu F, Furihata K, Kato Y, Tanokura M. Nondestructive quantification of organic compounds in whole milk without pretreatment by two-dimensional NMR spectroscopy. J Agric Food Chem. 2007;55:4307–11. doi: 10.1021/jf062803x. [DOI] [PubMed] [Google Scholar]
- 107.Giraudeau P, Remaud GS, Akoka S. Evaluation of Ultrafast 2D NMR for Quantitative Analysis. Anal Chem. 2009;81:479–84. doi: 10.1021/ac8021168. [DOI] [PubMed] [Google Scholar]
- 108.Pathan M, Akoka S, Tea I, Charrier B, Giraudeau P. Multi-scan single shot" quantitative 2D NMR: a valuable alternative to fast conventional quantitative 2D NMR. Analyst. 2011;136:3157–63. doi: 10.1039/c1an15278e. [DOI] [PubMed] [Google Scholar]
- 109.Le Guennec A, Tea I, Antheaume I, Martineau E, Charrier B, et al. Fast determination of absolute metabolite concentrations by spatially-encoded 2D NMRapplication to breast cancer cell extracts. Anal Chem. 2012;84:10831–37. doi: 10.1021/ac3033504. [DOI] [PubMed] [Google Scholar]
- 110.Giraudeau P, Massou S, Robin Y, Cahoreau E, Portais J-C, Akoka S. Ultrafast Quantitative 2D NMR: An Efficient Tool for the Measurement of Specific Isotopic Enrichments in Complex Biological Mixtures. Anal Chem. 2011;83:3112–19. doi: 10.1021/ac200007p. [DOI] [PubMed] [Google Scholar]
- 111.Pathan M, Akoka S, Giraudeau P. Ultrafast hetero-nuclear 2D J-resolved spectroscopy. J Magn Reson. 2012;214:335–39. doi: 10.1016/j.jmr.2011.11.008. [DOI] [PubMed] [Google Scholar]
- 112.Cardoza LA, Almeida VK, Carr A, Larive CK, Graham DW. Separations coupled with NRM detection. Trends Anal Chem. 2003;22:766–75. [Google Scholar]
- 113.Corcoran O, Spraul M. LC-NMR-MS in drug discovery. DDT. 2003;8:624–31. doi: 10.1016/s1359-6446(03)02749-1. [DOI] [PubMed] [Google Scholar]
- 114.Exarchou V, Krucker M, van Beek TA, Vervoort J, Gerothanassis IP, Albert K. LC-NMR coupling technology: recent advancements and applications in natural products analysis. Magn Reson Chem. 2005;43:681–87. doi: 10.1002/mrc.1632. [DOI] [PubMed] [Google Scholar]
- 115.Zhou Z, Lan W, Zhang W, Zhang X, Xia S, et al. Implementation of real-time two-dimensional nuclear magnetic resonance spectroscopy for on-flow high-performance liquid chromatography. J Chromatogr A. 2007;1154:464–68. doi: 10.1016/j.chroma.2007.04.018. [DOI] [PubMed] [Google Scholar]
- 116.Shapira B, Karton A, Aronzon D, Frydman L. Real-time 2D NMR identification of analytes undergoing continuous chromatographic separation. J Am Chem Soc. 2004;126:1262–65. doi: 10.1021/ja0389422. [DOI] [PubMed] [Google Scholar]
- 117.Queiroz Junior LHK, Queiroz DPK, Dhooghe L, Ferreira AG, Giraudeau P. Real-time separation of natural products by ultrafast 2D NMR coupled to on-line HPLC. Analyst. 2012;137:2357–61. doi: 10.1039/c2an16208c. [DOI] [PubMed] [Google Scholar]
- 118.Adams RW, Aguilar JA, Atkinson KD, Cowley AJ, Elliott PIP, et al. Reversible Interactions with para-Hydrogen Enhance NMR Sensitivity by Polarization Transfer. Science. 2009;323:1708–11. doi: 10.1126/science.1168877. [DOI] [PubMed] [Google Scholar]
- 119.Eisenschmid TC, Kirss RU, Deutsch PP, Hommeltoft SI, Eisenberg R, et al. Para hydrogen induced polarization in hydrogenation reactions. J Am Chem Soc. 2002;109:8089–91. [Google Scholar]
- 120.Albert MS, Cates GD, Driehuys B, Happer W, Saam B, et al. Biological magnetic resonance imaging using laser-polarized 129Xe. Nature. 1994;370:199–201. doi: 10.1038/370199a0. [DOI] [PubMed] [Google Scholar]
- 121.Navon G, Song Y-Q, Rõõm T, Appelt S, Taylor RE, Pines A. Enhancement of Solution NMR and MRI with Laser-Polarized Xenon. Science. 1996;271 [Google Scholar]
- 122.Wolber J, Ellner F, Fridlund B, Gram A, Jóhanesson H, et al. Generating highly polarized nuclear spins in solution using dynamic nuclear polarization. Nucl Instrum Methods Phys Res A. 2004;526:173–81. [Google Scholar]
- 123.Hausser KH, Stehlik D. Dynamic Nuclear Polarization in Liquids. Adv Magn Reson. 1968;3:79. [Google Scholar]
- 124.Ardenkjaer-Larsen JH, Fridlund B, Gram A, Hansson G, Hansson L, et al. Increase in signal-to-noise ratio of >10,000 times in liquid state NMR. Proc Natl Acad Sci U S A. 2003;100:10158–63. doi: 10.1073/pnas.1733835100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Joo C-G, Hu K-N, Bryant J-A, Griffin RG. In Situ Temperature Jump High-Frequency Dynamic Nuclear Polarization Experiments: Enhanced Sensitivity in Liquid-State NMR Spectroscopy. J Am Chem Soc. 2006;128:9428–32. doi: 10.1021/ja0611947. [DOI] [PubMed] [Google Scholar]
- 126.Krahn A, Lottmann P, Marquardsen T, Tavernier A, Türke A-T, et al. Shuttle DNP spectrometer with a two-center magnet. Phys Chem Chem Phys. 2010;12:5830–40. doi: 10.1039/c003381b. [DOI] [PubMed] [Google Scholar]
- 127.Leggett J, Hunter R, Granwehr J, Panek R, Perez-Linde AJ, et al. A dedicated spectrometer for dissolution DNP NMR spectroscopy. Phys Chem Chem Phys. 2010;12:5883–92. doi: 10.1039/c002566f. [DOI] [PubMed] [Google Scholar]
- 128.Frydman L, Blazina D. Ultrafast two-dimensional nuclear magnetic resonance spectroscopy of hyperpolarized solutions. Nat Phys. 2007;3:415–19. [Google Scholar]
- 129.Mishkovsky M, Frydman L. Progress in Hyperpolarized Ultrafast 2D NMR Spectroscopy. ChemPhysChem. 2008;9:2340–48. doi: 10.1002/cphc.200800461. [DOI] [PubMed] [Google Scholar]
- 130.Giraudeau P, Shrot Y, Frydman L. Multiple Ultrafast, Broadband 2D NMR Spectra of Hyperpolarized Natural Products. J Am Chem Soc. 2009;131:13902–03. doi: 10.1021/ja905096f. [DOI] [PubMed] [Google Scholar]
- 131.Panek R, Granwehr J, Leggett J, Kockenberger W. Slice-selective single scan proton COSY with dynamic nuclear polarisation. Phys Chem Chem Phys. 2010;2010:5771–78. doi: 10.1039/c002710n. [DOI] [PubMed] [Google Scholar]
- 132.Lloyd LS, Adams RW, Bernstein M, Coombes S, Duckett SB, et al. Utilization of SABRE-Derived Hyperpolarization To Detect Low-Concentration Analytes via 1D and 2D NMR Methods. J Am Chem Soc. 2012;134:12904–07. doi: 10.1021/ja3051052. [DOI] [PubMed] [Google Scholar]
- 133.Vold RL, Waugh JS, Klein MP, Phelps DE. Measurement of spin relaxation in complex systems. J Chem Phys. 1968;48:3831–32. [Google Scholar]
- 134.Bhattacharyya R, Kumar A. A fast method for the measurement of long spin-lattice relaxation times by single scan inversion recovery experiment. Chem Phys Lett. 2004;383:99–103. [Google Scholar]
- 135.Loening NM, Thrippleton MJ, Keeler J, Griffin RG. Single-scan longitudinal relaxation measurements in high-resolution NMR spectroscopy. J Magn Reson. 2003;164:321–28. doi: 10.1016/s1090-7807(03)00186-1. [DOI] [PubMed] [Google Scholar]
- 136.Smith PE, Donovan KJ, Szekely O, Baias M, Frydman L. Ultrafast NMR T1 Relaxation Measurements: Probing Molecular Properties in Real Time. ChemPhysChem. 2013;14 doi: 10.1002/cphc.201300436. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Barjat H, Morris GA, Smart S, Swanson AG, Williams SCR. High-resolution diffusion-ordered spectroscopy (HR-DOSY) - A new tool for the analysis of complex mixtures. J Magn Reson Series B. 1995;108:170–72. [Google Scholar]
- 138.Shrot Y, Frydman L. Single-scan 2D DOSY NMR spectroscopy. J Magn Reson. 2008;195:226–31. doi: 10.1016/j.jmr.2008.09.011. [DOI] [PubMed] [Google Scholar]
- 139.Xu X, Lee J-S, Jerschow A. Ultrafast scanning of exchangeable sites by NMR spectroscopy. Angew Chem Int Ed. 2013;52 doi: 10.1002/anie.201303255. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Wolff SD, Balaba RS. NMR imaging of labile proton exchange. J Magn Reson. 1990;86:164–69. [Google Scholar]
- 141.Shrot Y, Frydman L. Single-scan NMR spectroscopy at arbitrary dimensions. J Am Chem Soc. 2003;125:11385–96. doi: 10.1021/ja0350785. [DOI] [PubMed] [Google Scholar]
- 142.Giraudeau P, Cahoreau E, Massou S, Pathan M, Portais J-C, Akoka S. UFJCOSY: a Fast 3D NMR Method for Measuring Isotopic Enrichments in Complex Samples. ChemPhysChem. 2012;13:3098–101. doi: 10.1002/cphc.201200255. [DOI] [PubMed] [Google Scholar]
- 143.Roussel T, Giraudeau P, Ratiney H, Akoka S, Cavassila S. 3D localized 2D ultrafast J-resolved magnetic resonance spectroscopy: In vitro study on a 7T imaging system. J Magn Reson. 2012;215:50–65. doi: 10.1016/j.jmr.2011.12.013. [DOI] [PubMed] [Google Scholar]
- 144.Pelupessy P, Renella E, Bodenhausen G. High-Resolution NMR in Magnetic Fields with Unknown Spatiotemporal Variations. Science. 2009;324:1693–97. doi: 10.1126/science.1175102. [DOI] [PubMed] [Google Scholar]
- 145.Zhang Z, Chen H, Wu C, Wu R, Cai S, Chen Z. Spatially encoded ultrafast high-resolution 2D homonuclear correlation spectroscopy in inhomogeneous fields. J Magn Reson. 2013;227:39–45. doi: 10.1016/j.jmr.2012.11.020. [DOI] [PubMed] [Google Scholar]