Abstract
Humans share with many animals a number sense, the ability to estimate rapidly the approximate number of items in a scene. Recent work has shown that like many other perceptual attributes, numerosity is susceptible to adaptation. It is not clear, however, whether adaptation works directly on mechanisms selective to numerosity, or via related mechanisms, such as those tuned to texture density. To disentangle this issue we measured adaptation of numerosity of 10 pairs of connected dots, as connecting dots makes them appear to be less numerous than unconnected dots. Adaptation to a 20-dot pattern (same number of dots as the test) caused robust reduction in apparent numerosity of the connected-dot pattern, but not of the unconnected dot-pattern. This suggests that adaptation to numerosity, at least for relatively sparse dot-pattern, occurs at neural levels encoding perceived numerosity, rather than at lower levels responding to the number of elements in the scene.
Keywords: Vision, Number, Adaptation, Segmentation, Numerosity discrimination
1. Introduction
Even under conditions where we cannot count individual items, we can make rapid and reasonably accurate estimates of the number of items or numerosity of a scene. This capacity has been demonstrated in young infants and many animal species (Butterworth, 1999; Dehaene, Spelke, & Pica, 2008; Hauser, Carey, & Hauser, 2000; Pepperberg, 2006; Whalen, Gallistel, & Gelman, 1999; Xu & Spelke, 2000, Gallistel & Gelman, 1990). It has recently been shown that perception of numerosity is susceptible to adaptation: adapting to stimuli of high-numerosity causes a noticeable underestimation of a subsequent stimulus, while adapting to low numerosities causes overestimation (Burr & Ross, 2008). Adaptation is one of the more powerful techniques in psychophysics, usually regarded as strong proof for the existence of specialized neural mechanisms.
However, the idea that adaptation reveals specific numerosity mechanisms has been challenged (Durgin, 2008), with suggestions that the adaptation occurs via more general texture-like mechanisms. It is well known that size and texture are subject to adaptation (Anstis, 1974; Blakemore & Sutton, 1969); so adaptation to clouds of dots may be mediated via this indirect route (Durgin, 1995, 2008; Durgin & Huk, 1997; Durgin & Proffitt, 1996). One crucial distinction between numerosity and density is that numerosity perception seems to require the prior segmentation of elements in perceptual objects (Anobile, Cicchini, & Burr, 2015; Anobile, Turi, Cicchini, & Burr, 2015). One clear demonstration of this is that connecting pairs of items reduces perceived numerosity (Franconeri, Bemis, & Alvarez, 2009; He, Zhang, Zhou, & Chen, 2009: see Fig. 1a). Connecting elements with a line presumably links them perceptually, so they tend to be seen as a single object, rather than pairs of objects. Not only does this change the perceived numerosity, but also the selectivity of repetition BOLD adaptation (He, Zhou, Zhou, He, & Chen, 2015). Interestingly, underestimation also occurs when dots are arranged in a specific configuration (such as a symmetrical pattern) (Apthorp & Bell, 2015), indicating that that perceptual organization – i.e. detection of symmetry and redundancies, in this case – precedes number estimation.
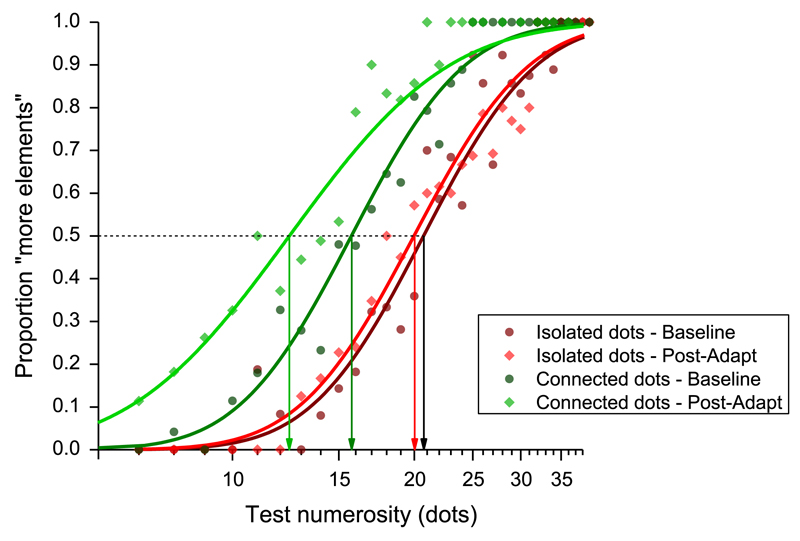
Fig. 1.
Psychometric curves for numerosity discrimination. Average psychometric functions were obtained pooling data of all the participants, plotting the proportion of trials in which the test stimulus appeared more numerous than the reference. Dark red and dark green curves refer to the baseline conditions either with isolated dots (dark red) or with dots connected by lines (dark green). Light red and light green curves refer to the post-adaptation performances, for the isolated and connected dots conditions, respectively. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Here we test whether adaptation acts upon perceived or physical number. We measure the effect of adapting to 20 dots, then testing with patches of the same numerosity, either in isolation or connected pairwise. The adapter had no effect on the numerosity of unconnected dots, but robustly reduced that of pair-wise connected dots. This shows that adaptation operates on mechanisms for numerosity, rather than more basic visual features, like the number of dots.
2. Materials and methods
2.1. Subjects
Seven subjects (two authors and five subjects naïve to the purpose of the experiment) participated in all experiments. All subjects had normal or corrected-to-normal visual acuity, and gave an informed written consent. Experimental procedures were approved by the Tuscan ethics committee and are in line with the declaration of Helsinki.
2.2. Apparatus and stimuli
The experiment was performed in a quiet and dimly illuminated room. Subjects sat in front of a 23-in. LCD monitor (mod. Acer S231HL) subtending 51 x 29 degrees of visual angle, at a viewing distance of 57 cm. Stimuli were generated with the Psychophysics Toolbox (Brainard, 1997; Kleiner et al., 2007; Pelli, 1997) for MatLab (ver. 2010b, The Mathworks, Inc.). All stimuli were patches of random-dots, presented within a circular window of 12° diameter. Each dot was 0.4° diameter, randomly black or white. Dot positions were chosen randomly from trial to trial (for adaptors and reference stimuli), respecting the conditions that two dots could not be separated by less than 0.75°. Stimuli with connected elements were calculated offline from a standard dot pattern (generated as described above) by joining iteratively dots with their closest neighbour (minimum line length 0.75°). If any line crossed another or encroached within 0.75° of another dot, the lines were discarded and regenerated iteratively until an acceptable pattern was created. If no uncrossed line combination was possible (which occurred with less than 1% of stimuli), a fresh dot-pattern was drawn and the procedure recommenced.
Adaptors comprised 20 isolated dots, and were identical to the unconnected stimuli. Probe stimuli appeared in the same position of the adapter, reference stimuli appeared on the opposite side of the screen and were varied from trial to trial, following a QUEST routine (Watson & Pelli, 1983) homing in on the point of subjective equality of the numerosity of the adapted probe patch, with an added Gaussian jitter of 0.15 log-units. The final estimate of PSE was taken as the median of the best-fitting cumulative Gaussian function to all the data of a particular condition (percentage “more elements than” against test physical numerosity). As a measure of precision we use Just Noticeable Difference (JND), the standard deviation of the underlying Gaussian function.
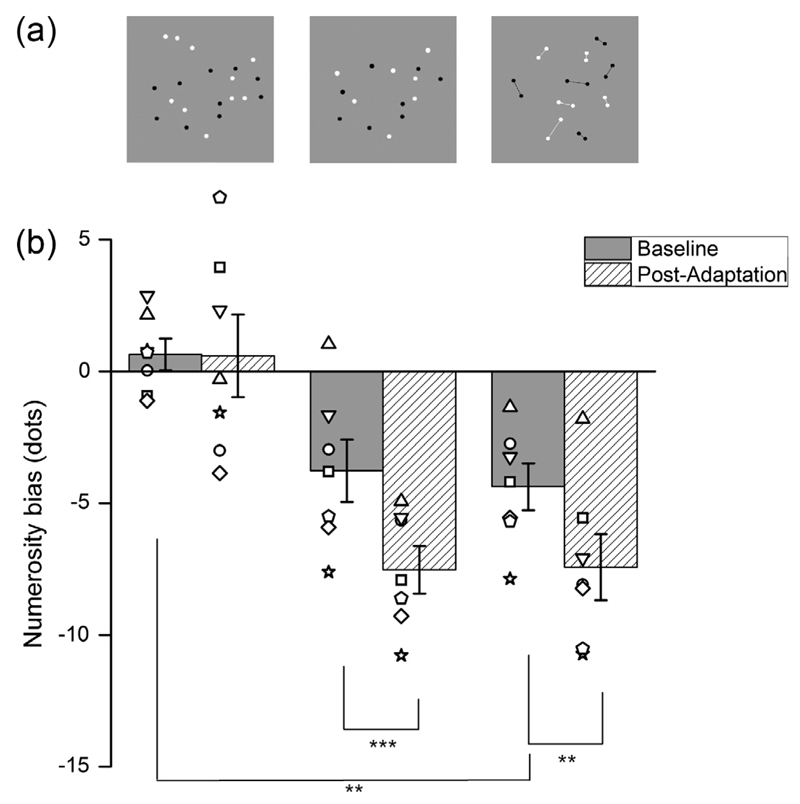
Probe stimuli were of three types (Fig. 2a), depending on condition: (left) 20 unconnected dots; (centre) 10 pairs of connected dots; (right) Unconnected dots with numerosity chosen for each subject to appear equal to the perceived numerosity of the connected patch.
Fig. 2.
Adaptation effect for the three conditions. Numerosity bias of a test patch before and after adaptation (grey and hatched bars), with individual data shown by the symbols (different shape for each subject). Three different conditions are plotted (showed in panel a): twenty unconnected dots; a reduced number of unconnected dots (matching the numerosity of the connected stimulus); and twenty dots connected by ten lines. Error bars indicate S.E.M., Stars indicate statistical significance (*p < 0.05,**p < 0.01, ***p < 0.001).
2.3. General procedure
Trials started with subjects fixating at a small red dot in screen centre. The adaptor stimulus was centred 12.7° left or right of fixation (varying randomly between session), presented for 20 s in the first trial of each experimental session, and for 6 s in subsequent trials to top-up the adaptation. Adaptors were followed by a 500 ms pause, and then probe at the same position of the adapter, together with the reference stimulus at an equal distance on the other side of fixation, were presented for 150 ms. At the end of each trial, subjects indicated which stimulus appeared to contain more elements (guessing if unsure) by pressing the appropriate key. For each subject and for each condition, we first performed a baseline measurement without adaptation. Each subject completed at least two blocks of 40 trials for each experimental condition. The different adaptation conditions were separated by breaks of at least 40–50 min.
3. Results
Fig. 1 reports average psychometric functions obtained pooling the data over the entire group of subjects, and plotting proportion of trials in which the test stimulus was judged as more numerous as function of numerosity of the test stimulus. Four conditions are shown: isolated dots baseline and adaptation, connected baseline and adaptation. The results of the isolated dot condition show that numerical estimates after 20-dot adaptation (red diamonds) do not differ from baseline (dark red circles). The psychometric functions are very similar, both estimating PSEs (points of subjective equality, the median of the curve) around 20 dots, the physical reference numerosity: adaptation does not affect a test stimulus with the same numerosity. However, adaptation does affect perceived numerosity in the connected-dots condition. In baseline, perceived numerosity of dots joined by lines is systematically underestimated, as shown by the rightward shift of the dark green curve. Importantly, adaptation caused a further shift of the curve (light green), showing that adaptation does affect numerosity under these conditions.
Fig. 2 shows pre- and post-adaptation PSEs for the three main conditions, obtained from individual data. For each subject psychometric functions like those of Fig. 1 were calculated, yielding estimates of PSE for each subject, which are plotted as points in Fig. 2. The bars show the average. While a 20-dot adaptor does not affect perceived numerosity of a 20-dot patch (left-most bars), confirming the group data of Fig. 1, it does affect perceived numerosity of probes with lower numerosities, those matched to the apparent numerosity of the connected stimuli (average numerosity 16.22 ± 1.19: centre bars). The crucial test is for the twenty connected dots (right bars), which are perceived to 15.62 ± 0.89. Adaptation also affected this stimulus, by about 20%, very similar to the effect observed in the matched condition, with stimuli with a physically smaller numerosity compared to the 20-dot adaptors (average numerosity reduction equal to 23%).
We performed a two-way repeated-measures ANOVA with factors “configuration” and ”adaptation”, with a pairwise multiple comparison analysis run according to the Holm-Sidak method. The analysis first showed that both configuration and adaptation have a significant influence on numerical estimates (df = 2, F = 28.6, p < 0.001 and df = 1, F = 21.5, p = 0.004, respectively), and that there is a significant interaction between the two factors (F = 3.9, p = 0.048). The multiple comparisons procedure showed that when dots are connected by task-irrelevant lines their perceived numerosity is underestimated significantly, compared to the unconnected dots (20.65 ± 0.60 versus 15.62 ± 0.89 dots; t(7) = 4.181, p = 0.001). Also the effect of adaptation on connected dots appear to be statistically significant (t(7) = 3.222, p = 0.005), as well as the effect of adaptation on patches with physically smaller numerosity (matched condition, t(7) = 3.968, p < 0.001).
Beside the measures of perceived numerosity, we also analyzed precision (JND) in the task, in order to control for the possibility that different patterns of underestimation could be due to a reduced sensibility to the numerical magnitude of the stimuli. However, a two-way repeated measures ANOVA showed that there is no difference in performance level, neither between baseline and post-adaptation (F = 0.0112, p = 0.919), nor among the different conditions (F = 0.456, p = 0.644).
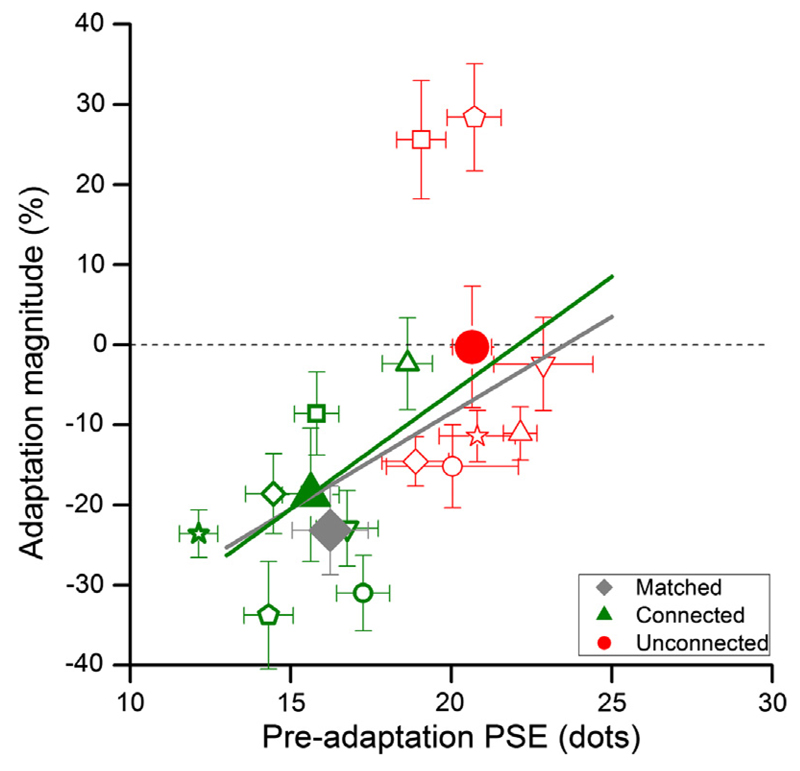
Fig. 3 shows the individual data for the two main experimental conditions, plotting adaptation effect (change in PSE normalized by baseline) in percentage against baseline PSE. While there is some scatter in the data, the trend is clear: there is little effect of adaptation, on average, on the unconnected dots (red data points), while for connected condition, adaptation had a clear effect for almost all subjects, on average about 20% adaptation.
Fig. 3.
Individual data. Individual data for the connected (green symbols) and unconnected (red symbols) conditions, plotting change in PSE normalized by baseline against baseline PSE. The large symbols show group averages, the grey diamond the average of the matched, unconnected condition. There is little effect of adaptation on the unconnected dots (average adaptation −0.087% ± 7.75), while adaptation had a clear effect for almost all subjects in the connected condition (average adaptation −20.11% ± 4.64), similar to that of the matched, unconnected condition (average adaptation −23.10% ± 1.67). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
4. Discussion
This experiment showed that adaptation a 20-dot patch, which has no effect on the perceived numerosity of a patch of 20 unconnected dots, decreases the perceived numerosity of 10 dot-pairs, to the same extent as it does to a patch whose numerosity matches the apparent numerosity of the connected dots.
Connecting dots is a simple but reliable way to dissociate perceived from physical numerosity: connecting dots not only reduces their perceived numerosity, but also affects the selectivity of the fMRI BOLD response in the number area in the Intraparietal Sulcus (He et al., 2015). These studies suggest that numerosity perception depends on segmentation of the elements in perceptual objects, following several rules such similar shape, orientation, common fate, and connectedness (Anobile, Cicchini, et al., 2015; Anobile, Turi, et al., 2015; Wagemans et al., 2012). Interestingly, there is evidence that connectedness affects only perceived numerosity, but not action. Reaching movements are biased towards the more numerous stimuli (Milne et al., 2013), but this is unaffected by connecting the elements. Perhaps the mechanism biasing action rests on a more primitive estimate of numerosity, unaffected by segmentation.
In our study, we tested the effect of adaptation on connected and unconnected dots, to probe whether adaptation acts on perceived or physical numerosity. A previous study (Abdul-Malak & Durgin, 2009) tackled the question the other way round: they tested the effect of connectedness on the adaptor, by connecting the points of a high-density 400-dot adaptor, and found that the effectiveness as an adaptor did not follow apparent numerosity. This result is interesting, but not necessarily contradictory to ours, for two reasons. One is that the density used by Abdul-Malak & Durgin was far higher. Although precise experimental details of their study are not declared in their abstract, it is likely that they presented 400 dots within a 3 or 4 deg diameter patch like in a previous study (Durgin, 2008). This leads to densities exceeding 10 items per deg2 compared to our 0.2 items per deg2. Given the evidence that density mechanisms operate at higher, non-segregable densities (Anobile, Cicchini, & Burr, 2014; Anobile, Cicchini, et al., 2015; Durgin, 1995; Durgin & Huk, 1997; Durgin & Proffitt, 1996), it is possible that the densities of that study exceeded the numerosity range. Indeed, at high densities, connecting dot-pairs does not reduce apparent numerosity (unpublished observations). Another point is that varying the adaptor and the adapted stimuli is not the same thing. Many stimuli can cause adaptation of perceived numerosity, even fast-drifting sinusoidal gratings (Fornaciai, Togoli, Burr, & Arrighi, 2015) (that also affect perceived duration: Burr, Tozzi, & Morrone, 2007; Johnston, Arnold, & Nishida, 2006), and these stimuli have no apparent numerosity. The parameters of the adaptor are no easily relatable to those of the adapted stimuli.
That the effects of adaptation are determined by perceived rather than actual numerosity, at this relatively low numerosity, is further evidence that numerosity perception relies on mechanisms distinct from those for texture, or density. Adding the lines that connect the dot-pairs increases rather than decreases the density of the stimuli. If adaptation were based on density, it should occur in the other direction, as adapting to a less dense stimulus causes the test to appear more dense. That our adaptation goes in the other direction is clear evidence that numerosity and density are distinct perceptual processes.
Recently, several researchers have suggested that numerosity and texture may be encoded by the same (or similar) neural mechanisms (Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011). While this idea is appealing for many reasons, including its economical and parsimonious use of neural resources, there has been little evidence in favour. On the contrary, the evidence points to the existence of very distinct mechanisms, obeying different psychophysical laws, operating at different densities (Anobile et al., 2014), and different dependence on eccentricity (Anobile, Turi, et al., 2015). Numerosity mechanisms are favoured by conditions where the individual items can be segregated to allow enumeration: densities cannot be too high, and the limit depends on eccentricity (2.27 dots per square deg for central viewing, 0.8 for 15° eccentricity). When these conditions are met thresholds obey Weber’s law. For higher densities, texture-like mechanisms cut in, obeying a square-root law (see Anobile, Cicchini, et al., 2015, for review). We predict that if this experiment were repeated at high densities, it would fail.
The current study provides further evidence for this distinction, and shows that adaptation acts directly on perceptual mechanisms sensitive to numerosity, rather than via surrogate mechanisms such as density. At the moderate densities used here, the effects of adaptation depended not on the density of the stimuli, but on their apparent numerosity (which was less for the physically denser stimulus). This is further evidence for the existence of numerosity mechanisms, quite separate from those encoding density, and evidence that adaptation of numerosity works directly on mechanisms encoding number, not via some other route. Likely candidates for the site of the adaptation are LIP, which has a gradient response to number or, perhaps more likely, IPS, which has been shown to be influenced by the connectedness illusion (Harvey, Klein, Petridou, & Dumoulin, 2013; He et al., 2015).
Appendix A. Supplementary material
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.cognition.2016.03.006.
Acknowledgements
This study has been supported by the Italian Ministry of University and Research (FIRB 2013 – RBFR1332DJ) and by European Community Projects “STANIB” and “ECSPLAIN” (FP7 ERC Advanced Grant No. 338866).
Footnotes
Author contribution
M.F., G.M.C. and D.C.B. conceived and developed the experiment. M.F. and G.M.C. collected and analyzed the data. M.F., G.M.C. and D.C.B. wrote the article.
References
- Abdul-Malak D, Durgin FH. Dividing the legs of sheep: Does Burr’s Australian stockman strategy work? Journal of Vision. 2009;9(8):980. [Google Scholar]
- Anobile G, Cicchini GM, Burr DC. Number as a primary perceptual attribute: A review. Perception. 2015 doi: 10.1177/0301006615602599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anobile G, Cicchini GM, Burr DC. Separate mechanisms for perception of numerosity and density. Psychological Science. 2014;25:265–270. doi: 10.1177/0956797613501520. [DOI] [PubMed] [Google Scholar]
- Anobile G, Turi M, Cicchini GM, Burr DC. Mechanisms for perception of numerosity or texture-density are governed by crowding-like effects. Journal of Vision. 2015;15(5):4. doi: 10.1167/15.5.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anstis SM. Size adaptation to visual texture and print: Evidence for spatial-frequency analysis. The American Journal of Psychology. 1974;87(1–2):261–267. [PubMed] [Google Scholar]
- Apthorp D, Bell J. Symmetry is less than meets the eye. Current Biology. 2015;25(7):R267–R268. doi: 10.1016/j.cub.2015.02.017. [DOI] [PubMed] [Google Scholar]
- Blakemore C, Sutton P. Size adaptation: A new aftereffect. Science (New York, N.Y.) 1969;166(902):245–247. doi: 10.1126/science.166.3902.245. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The psychophysics toolbox. Spatial Vision. 1997;10:433–436. doi: 10.1163/156856897X00357. [DOI] [PubMed] [Google Scholar]
- Burr D, Tozzi A, Morrone MC. Neural mechanisms for timing visual events are spatially selective in real-world coordinates. Nature Neuroscience. 2007;10(4):423–425. doi: 10.1038/nn1874. [DOI] [PubMed] [Google Scholar]
- Burr D, Ross J. A visual sense of number. Current Biology. 2008;18(6):425–428. doi: 10.1016/j.cub.2008.02.052. [DOI] [PubMed] [Google Scholar]
- Butterworth B. The mathematical brain. London: Macmillan; 1999. [Google Scholar]
- Dakin S, Tibber M, Greenwood J, Kingdom F, Morgan M. A common visual metric for approximate number and density. Proceedings of the National Academy of Sciences. 2011 doi: 10.1073/pnas.1113195108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S, Spelke E, Pica P. Log or linear ? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science. 2008 (May):1217–1220. doi: 10.1126/science.1156540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durgin FH, Proffitt DR. Visual learning in the perception of texture: Simple and contingent aftereffects of texture density. Spatial Vision. 1996;9(4):423–474. doi: 10.1163/156856896X00204. [DOI] [PubMed] [Google Scholar]
- Durgin FH. Texture density adaptation and the perceived numerosity and distribution of texture. Journal of Experimental Psychology: Human Perception and Performance. 1995 doi: 10.1037/0096-1523.21.1.149. [DOI] [Google Scholar]
- Durgin FH. Texture density adaptation and visual number revisited. Current Biology. 2008 doi: 10.1016/j.cub.2008.07.053. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Huk AC. Texture density aftereffects in the perception of artificial and natural textures. Vision Research. 1997;37(23):3273–3282. doi: 10.1016/S0042-6989(97)00126-0. [DOI] [PubMed] [Google Scholar]
- Fornaciai M, Togoli I, Burr DC, Arrighi R. Motion-induced compression of perceived numerosity. Perception ECVP 2015 Abstract Supplement. 2015;44(S1):277. doi: 10.1177/0301006615598674. [DOI] [Google Scholar]
- Franconeri SL, Bemis DK, Alvarez GA. Number estimation relies on a set of segmented objects. Cognition. 2009;113:1–13. doi: 10.1016/j.cognition.2009.07.002. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Gelman R. The what and how of counting. Cognition. 1990;34(2):197–199. doi: 10.1016/0010-0277(90)90043-j. [DOI] [PubMed] [Google Scholar]
- Harvey BM, Klein BP, Petridou N, Dumoulin SO. Topographic representation of numerosity in the human parietal cortex. Science. 2013;341(6150):1123–1126. doi: 10.1126/science.1239052. [DOI] [PubMed] [Google Scholar]
- Hauser MD, Carey S, Hauser LB. Spontaneous number representation in semi-free-ranging rhesus monkeys. Proceedings of the Royal Society of London B: Biological Sciences. 2000;267(1445):829–833. doi: 10.1098/rspb.2000.1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He L, Zhang J, Zhou T, Chen L. Connectedness affects dot numerosity judgment: Implications for configural processing. Psychonomic Bulletin & Review. 2009;16(3):509–517. doi: 10.3758/PBR.16.3.509. [DOI] [PubMed] [Google Scholar]
- He L, Zhou K, Zhou T, He S, Chen L. Topology-defined units in numerosity perception. Proceedings of the National Academy of Sciences. 2015;112(41):E5647–E5655. doi: 10.1073/pnas.1512408112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston A, Arnold DH, Nishida S. Spatially localized distortions of event time. Current Biology: CB. 2006;16(5):472–479. doi: 10.1016/j.cub.2006.01.032. [DOI] [PubMed] [Google Scholar]
- Kleiner M, Brainard D, Pelli D, Ingling A, Murray R, Broussard C. What’s new in psychtoolbox-3? Perception 36 ECVP Abstract Supplement. 2007;14 doi: 10.1068/v070821. [DOI] [Google Scholar]
- Milne JL, Chapman CS, Gallivan JP, Wood DK, Culham JC, Goodale Ma. Connecting the dots: Object connectedness deceives perception but not movement planning. Psychological Science. 2013;24(8):1456–1465. doi: 10.1177/0956797612473485. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision. 1997;10:437–442. doi: 10.1163/156856897X00366. [DOI] [PubMed] [Google Scholar]
- Pepperberg IM. Cognitive and communicative abilities of Grey parrots. Applied Animal Behaviour Science. 2006;100(1–2):77–86. doi: 10.1016/j.applanim.2006.04.005. [DOI] [Google Scholar]
- Wagemans J, Elder JH, Kubovy M, Palmer SE, Peterson MA, Singh M, von der Heydt R. A century of Gestalt psychology in visual perception: I. Perceptual grouping and figure–ground organization. Psychological Bulletin. 2012 doi: 10.1037/a0029333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watson AB, Pelli DG. QUEST: A Bayesian adaptive psychometric method. Perception & Psychophysics. 1983;33(2):113–120. doi: 10.3758/BF03202828. [DOI] [PubMed] [Google Scholar]
- Whalen J, Gallistel CR, Gelman R. Nonverbal counting in humans: The psychophysics of number representation. Psychological Science. 1999 doi: 10.1111/1467-9280.00120. [DOI] [Google Scholar]
- Xu F, Spelke ES. Large number discrimination in 6-month-old infants. Cognition. 2000;74(1) doi: 10.1016/S0010-0277(99)00066-9. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.