Number As a Primary Perceptual Attribute: A Review

Abstract

Although humans are the only species to possess language-driven abstract mathematical capacities, we share with many other animals a nonverbal capacity for estimating quantities or numerosity. For some time, researchers have clearly differentiated between small numbers of items—less than about four—referred to as the subitizing range, and larger numbers, where counting or estimation is required. In this review, we examine more recent evidence suggesting a further division, between sets of items greater than the subitizing range, but sparse enough to be individuated as single items; and densely packed stimuli, where they crowd each other into what is better considered as a texture. These two different regimes are psychophysically discriminable in that they follow distinct psychophysical laws and show different dependencies on eccentricity and on luminance levels. But provided the elements are not too crowded (less than about two items per square degree in central vision, less in the periphery), there is little evidence that estimation of numerosity depends on mechanisms responsive to texture. The distinction is important, as the ability to discriminate numerosity, but not texture, correlates with formal maths skills.

Introduction

It is well established that the human visual system is able to reliably generate summary statistics of the visual environment. One clear example is “Approximate Numerosity Estimation”, our ability to produce a raw estimate of the quantity of a collection of objects or events, without serial counting. Although humans may be the only species with a linguistically mediated code for numbers, we share an approximate, nonverbal representation of number with many animal species (Dehaene, 2011). The evolutionary advantage of this capacity is obvious, allowing people and animals to choose zones with more food, and quickly determine which group of competitors is more numerous. Numerosity is a growing field of research, crossing many disciplines, including vision research, human and animal cognition, anthropology, developmental psychology, clinical and basic psychology, and computational neuroscience. However, the mechanisms of numerosity perception are still poorly understood and highly debated. One reason why this topic is particularly compelling is that numerosity is intrinsically correlated with many other physical features. For example, when you continuously put more red apples on a table, you change not only the numerosity of apples but also decrease the distance between them, increase the total red-covered area and also the density (numbers of items/area). It is thus plausible that numerosity is not sensed as such, but indirectly via other congruent cues. Does this mean that numerosity does not exist as a direct and immediate perceptual “qualia?”

We are both fast and accurate when reporting the number of items within a small set, up to about four objects, the so-called subitizing range; but slower and more error prone for larger numbers (Jevons, 1871; Kaufman & Lord, 1949). Nevertheless, we can estimate the number of items in, say, a cloud of dots, with reasonable accuracy and precision. This capacity is thought to be mediated by the “approximate number system” (ANS). But what happens when the number of items increases to the point that they blur into a texture or when the stimuli are presented at an eccentricity where they become “crowded?” Are they still encoded by the approximate number system or do they stimulate separate mechanisms? This review will present evidence for the existence of three separate systems, covering three ranges of numerosity and density: subitizing, for very small numerosities, less than about four; number estimation, for items above four but not packed so densely that they crowd each other; and texture mechanisms, for densely packed items that cannot be individuated as separate items.

Adaptation and Number

One clear signature of the existence of a dedicated perceptual mechanism is its susceptibility to adaptation (Clifford & Rhodes, 2005; Mollon, 1974; Thompson & Burr, 2009): Several seconds of exposure to a given stimulus (say a leftward moving pattern) change the appearance of stimuli viewed in the same position, causing a negative aftereffect (in this case, illusory rightward motion of stationary stimuli). Adaptation, ubiquitous throughout sensory systems, represents a form of experience-dependent plasticity in which our current sensory experience is intimately affected by how we viewed the world only moments before (Barlow & Foldiak, 1989; Boynton, 2004; Kohn, 2007; Solomon & Kohn, 2014). It is widely held to pose numerous functional advantages, including serving to autocalibrate perceptual systems to their environment by dynamically tuning its responses to match the distribution of stimuli to make maximal use out of the limited working range of the system. Burr and Ross (2008) recently showed that numerosity is strongly susceptible to visual adaptation. The effect is illustrated in the online animation¹¹ (Movie 1): After a period of adaptation to dense or sparse dot clouds (say about 30 seconds), subsequently viewed dot clouds appear to differ considerably in their numerosity, showing a strong negative aftereffect. Based largely on the fact that numerosity shows adaptation, combined with other known facts such as the approximation to Weber’s law (threshold varies proportionally with number of items), led them to suggest that number was a “primary-visual-attribute.” In other words, under a wide range of conditions, ensembles of objects are subjectively experienced as a specific quantity of items, irrespective of other correlated perceptual features. In this review, we examine further this concept, detailing how, and under what conditions, numerosity perception differs from texture or density perception. We also extend the notion of a “primary visual attribute” to encompass other senses and other formats of numerosity.

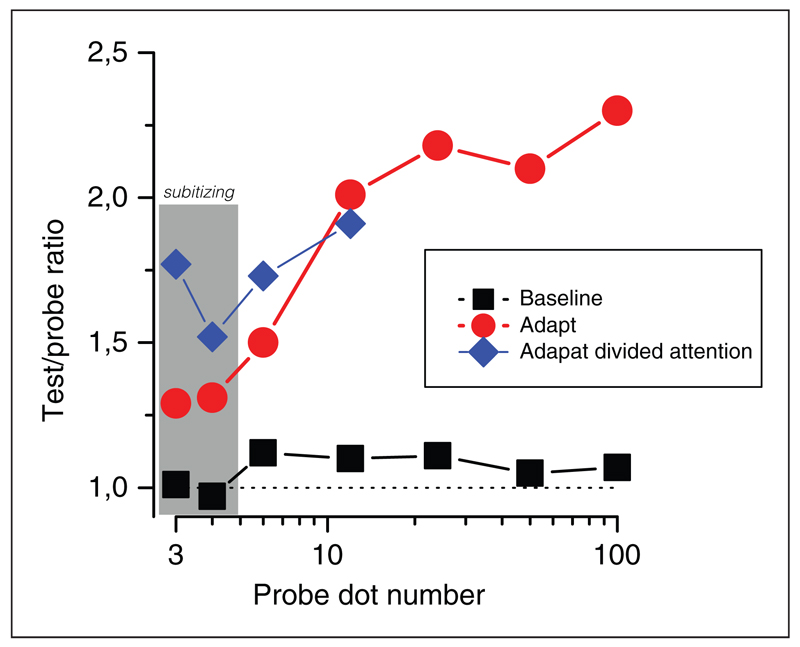
Figure 1 shows the results of the initial experiment, measuring the perceived numerosity after adaptation to a 400-dot pattern (red circles). The results are plotted as a function of the standard (comparator) numerosity. For all numerosities except the lowest (within the subitizing range, which we will return to later), the effect of adaption was very strong, a factor of about two. With several control studies, Burr and Ross demonstrated that the illusion is largely independent of dot size, contrast, spatial frequency, density, and shape.

Figure I. Numerosity adaptation.

Magnitude of adaptation (expressed as a ratio of number of dots in the test patch to that in the probe) as a function of number of dots in the probe. Red circles show standard results with a single task, blue diamonds results when attention was deprived with a demanding conjunction task. Black squares show baseline performance with no adaptation or attentional load. Values above the unity line (dashed) indicate underestimation after adaptation to a high numerosity (400). The gray shading indicates probes in the subitizing range (discussed later). Reproduced with permission from Burr and Ross (2008) and Burr, Anobile, and Turi (2011).

However, the claim that number is a primary visual attribute was soon to be challenged. Durgin (2008) was the first to protest that the adaptation occurred via texture mechanisms, rather than numerosity mechanisms. Several studies show that adapting to coarse texture, such a low-frequency grating, causes subsequent patterns to appear finer, and vice versa (Blakemore & Campbell, 1969; Durgin, 1995). This also works with “sandpaper” textures (Anstis, 1974) and random-dot patterns (Anstis, 1974; Durgin, 1995). Durgin (2008) claimed was that it was adaptation to texture causing the apparent adaptation to number, rather than being a direct effect. His primary argument for this claim was a demonstration showing that when area is varied (thus dissociating number from density), it is the numerosity within a given area that determines adaptation, not total numerosity in the field. While this is important to emphasize, it is not surprising. The demonstration of Movie 1 itself relies on the spatial selectivity of the adaptation, otherwise the highly numerous adapting field on the left would average with that on the right, with no net effect. It has been suggested that the adaptation may be mediated by a homologue of neurons found in monkey lateral intraparietal cortex (LIP; Roitman, Brannon, & Platt, 2007; discussed in Neural Mechanisms for Encoding Numerosity section). As LIP cells have reasonably circumscribed receptive fields, they will respond to the numerosity within that receptive field, not across the entire visual field. And this, of course, this selectivity is functional: Animals need an estimate of number of apples (or fish or lions) in a given part of the scene in order to take appropriate action. So although Durgin’s demonstration does confirm that numerosity adaptation is spatially specific, it tells us little about whether estimates of numerosity (within an area) show adaptation or whether all is a by-product of texture density.

Durgin’s challenge was soon followed by others (Dakin, Tibber, Greenwood, Kingdom, & Morgan, 2011; Durgin, 2008; Morgan, Raphael, Tibber, & Dakin, 2014; Tibber, Greenwood, & Dakin, 2012), all with the similar goal of equating numerosity estimation with texture density or claiming that the two tap very similar mechanisms. This review aims to address this specific issue, examining whether there exists evidence for numerosity mechanisms distinct from those involved with texture discrimination.

Cross-modal and Cross-format Adaption to Sequences of Events

In his critique questioning the idea that that number is directly adaptable, Durgin (2008) threw down the gauntlet with a clear challenge of what he would consider definitive proof for direct adaption of number: “it may yet turn out that perceived number itself is indeed adaptable, but cross-modal studies seem a more promising avenue for distinguishing aftereffects of perceived number from retinotopic aftereffects in the early visual analysis of texture density.” This challenge has been met head on by Arrighi, Togoli, and Burr (2014).

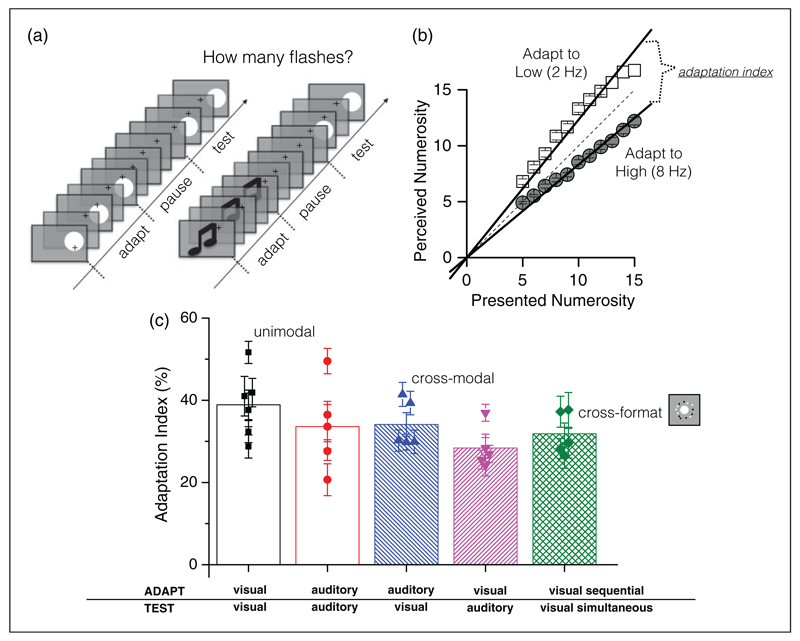
Arrighi et al. devised a simple technique to demonstrate adaptation of serially presented items (see Figure 2 and Movie 2). In principle, the method was like that of Burr and Ross (2008), except they manipulated time instead of space. They presented sequences of briefly displayed disks of light and asked subjects to estimate their number. Adapting to several seconds of a slow presentation rate (2 flashes/sec) caused a subsequently displayed sequence appeared more numerous; adapting to a fast sequence (8 flashes/sec) caused stimuli to appear less numerous (Figure 2(b)). Both sets of adaptation data were well fit by linear regression. The magnitude of the aftereffect was taken as the difference between the slopes of the regression lines: For the data of Figure 2(b), it was about 0.4, a very large effect. Importantly, the aftereffect was spatially selective, suggesting that it has a perceptual rather than cognitive nature and probably occurs at a reasonably high level of information processing (the selectivity was in external, not retinal coordinates). Certainly, these effects have little to do with texture density.

Figure 2. Cross-modal, cross-format numerosity adaptation.

(a) Examples of stimuli for the serial number adaptation, visual unimodal (at left), and auditory-visual cross-modal (at right). (b) Sample results in the visual unimodal adaptation task. Adapting to low numbers (2 Hz, open squares) produces an overestimation of numerosity, and adaption to high numbers (8 Hz, gray circles) and underestimation. Data were well-fitted with linear regressions (lines on the data) constrained to pass throughout zero, and the strength of the adaptation effect (adaptation index) given by the difference in slope of the regression lines. (c) Mean adaptation indexes for the various experimental conditions: uni-modal visual and auditory adaptation; cross-modal auditory-visual and visual-auditory adaptation; and “cross-format” adaptation (adapt to serial presentation, test with simultaneous). Bars show average data, symbols single subject data). Adapted with permission from Arrighi et al. (2014).

Arrighi et al. went on to demonstrate cross-modal adaptation to numerical sequences: Adapting to a series of tones changed the apparent numerosity of visual flashes, and vice versa, to the same extent as within-modal adaptation (Figure 2(c) and Movies 3 and 4). But for the purposes of dissociating number from texture, the clinching experiment was “cross-format” adaptation: They adapted with a series of centrally displayed flashes, then measured the apparent numerosity of a spatial array of dots: Apparent numerosity changed, in both directions, again by about 30% (Figure 2(c) and Movie 5). These results provide a clear response to Durgin’s challenge, showing that perception of numerosity can be completely unrelated to texture perception.

Neural Mechanisms for Encoding Numerosity

There is now a wealth of physiological evidence, from both human and nonhuman primates, for the existence of neural mechanisms dedicated to processing number. As the ability to discriminate between numerical quantities is not specific to humans, it can be studied in animals, particularly primates. By training monkeys to extract, memorize and compare the numerosity of a sample stimulus (delayed match-to-sample paradigm), Nieder et al. have demonstrated the existence of “number-neurons” in intraparietal sulcus (IPS) and lateral prefrontal cortex (IPFC; Nieder, Diester, & Tudusciuc, 2006; Nieder, Freedman, & Miller, 2002). These cells fire most vigorously when a preferred number is displayed, and firing rate decreases with the numerical distance of the stimulus from the preferred numerosities, producing a clear tuning function for numerosity. Cells in the parietal cortex have onset responses about 30 ms shorter than those in the prefrontal cortex, suggesting a hierarchical processing chain.

All studies of numerosity in animals take great care to control for number-correlated features such as density, shape, covered area, spatial arrangements, and circumference. Even when these factors are controlled or randomized, cells remain tuned for the number of items presented, not the density, luminance, or quantity of ink. Some have suggested that the tuning of neurons to number may not be innate, but a result of training (given that parietal neurons are particularly susceptible to learning: Roitman, Brannon, & Platt (2012)). However, number selectivity has been reported in monkeys which have never made a numerosity discrimination (Viswanathan & Nieder, 2013). In that set of experiments, monkeys were trained to discriminate the color (and not the numerosity) of the items composing the sample and match stimuli, then switched to number: The switch required no training.

Besides the number-selective neurons in the IPS and prefrontal cortex, which exhibit a clear tuning for numerosity (cardinality), there exists another class of number neurons in the LIP of monkeys which show a gradient response to number (Roitman et al., 2007). These cells are of two kinds: Those preferring low numerosities and those preferring high. Both encode monotonically the number of visual items with a response gradient, increasing or decreasing their activity as a function of number of items. Again, the modulation in firing rate was not due to differences in other stimulus attributes, such as total covered area, element size, or density. These cells could act as “integrators,” and provide input to the cells encoding cardinality in the IPS and frontal cortex.

These cells may mediate adaptation to numerosity (Dehaene, 2009). They have receptive fields that are reasonably well-defined in space, accounted for the specificity of the adaptation; and the gradient response is consistent with the monotonic dependency on numerosity of the adaptor (Figure 2 of Burr & Ross, 2008). Interestingly two neural models of numerosity perception have suggested a crucial step for numerosity perception is the ability to integrate the number of items across visual space (see Models of Numerosity Computation section). The output of these integrations can be then passed on to a second stage of processing where cardinal values are extracted by looking up at the activity of the integrator units. The properties of neurons in LIP and lPFC make them ideal candidates for the two stages in these models.

Nieder’s group has recently reported “number-neurons” in monkey IPS that encode the number of items presented over time (Nieder, 2012; Nieder et al., 2006). These cells are a likely neural substrate for the temporal adaptation effects reported Arrighi, Togoli, and Burr (2014), described in the previous section. Some of the cells were number-selective in both space and time, a likely substrate for the cross-format adaption shown in Figure 2.

Interestingly number selectivity might emerge in networks dedicated to plan and track goal-directed actions. Sawamura, Shima, and Tanji (2002) trained monkeys to monitor the number of self-produced actions in order to successfully perform a task and obtain reward. A significant portion of cells in a portion of parietal cortex (superior parietal lobule) showed selective activation for the number of actions performed. These cells seem to keep track of the number of self-produced actions.

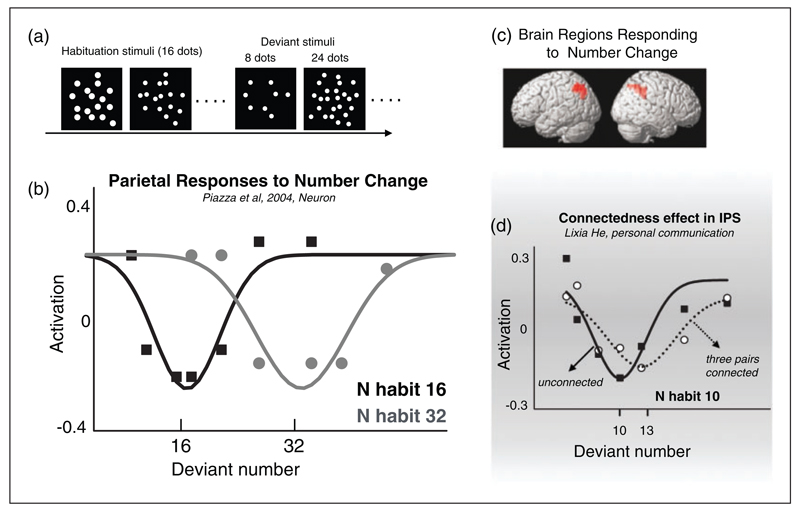
Functional magnetic resonance imaging (fMRI) studies have also revealed neural mechanisms selective for number in humans. Piazza, Izard, Pinel, Le Bihan, and Dehaene (2004) used an fMRI adaptation paradigm to reveal tuning curves for approximate numerosity in the human intraparietal sulcus (hIPS). The paradigm consists of the repeated presentation of a specific numerosity (to habituate neurons tuned to that number), then displaying an occasional “deviant” number, which elicits an activation that increases with the numerical distance between adaptor and deviant. This way they were able to show clear selectivity curves for number in the intraparietal sulcus (hIPS), like those of Figure 3, but no selective activation in areas such as V1. Like the animal studies, the stimuli were designed to control for all the low-level parameters (size, contrast, etc.), so the only relevant feature was the number of items. Using a similar fMRI adaptation paradigm, they also found evidence for notation-independent coding of numerical quantity in IPS and also frontal cortex showing cross-format habituation for numerosity and number symbols (Piazza, Pinel, Le Bihan, & Dehaene, 2007).

Figure 3. Selectivity to numerosity in human parietal cortex.

(a) Example of the stimuli used by Piazza et al. (2004) in the habituation paradigm (habituation stimulus 16 dots and deviants 8 and 24 dots). (b) Activation curves expressed as change in BOLD elicited by deviant stimuli compared with activation induced by habituation stream. (c) Brain regions responding to number change. (d)Habituation paradigm, adapting with 10 dots then testing with standard dot stimuli and with three pairs connected (like Figure 5(a)). When three pairs of dots are connected, the peak in the function is at 13 rather than 10 dots, showing that connectivity reduces effective numerosity in IPS. Adapted with permission from Piazza et al. (2004) and Piazza, Fumarola, Chinello, and Melcher (2011). IPS: intraparietal sulcus.

Interestingly, the neural tuning for number in human cortex revealed by BOLD activation is tuned to perceived rather than physical numerosity. As described in more detail in the next section, perceived numerosity of a cloud of dots is reduced when pairs of dots are connected (see Figure 5). When stimuli with three dot pairs connected are used as adaptors, the minimum in IPS activity adaptation occurs not only when the adaptor and deviant are most similar but also when their perceived numerosity is most similar: at 13 rather than 10 dots. This study further shows that IPS codes the perceived numerosity, rather than low-level attributes of the stimuli (Figure 3(d)).

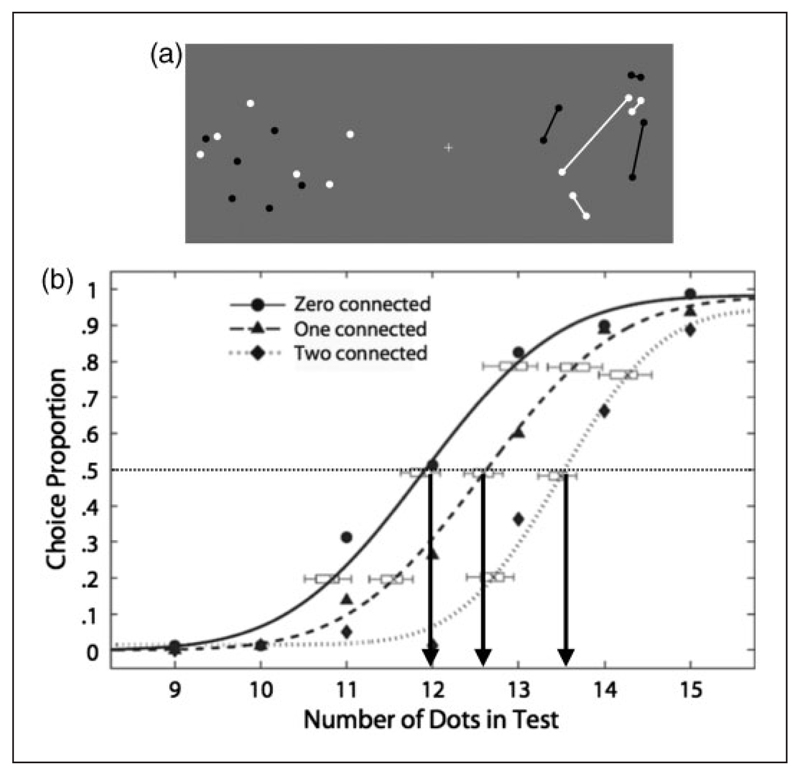
Figure 5. Connectedness effect on numerosity perception.

(a) Example of stimuli configuration illustrating the effect of connectedness: The pattern on the right appears less numerous. (b) Sample psychometric functions of one subject from He, Zhang, Zhou, and Chen (2009) showing proportion of choice test stimulus as more numerous then the reference (containing 12 unconnected dots). Test stimuli could contain zero, one, or two pairs of connected dots. The rightward shift of psychometric functions compared with the zero-connected indicates underestimation of the test when dots were connected. Adapted with permission from He, Zhang, Zhou, and Chen (2009).

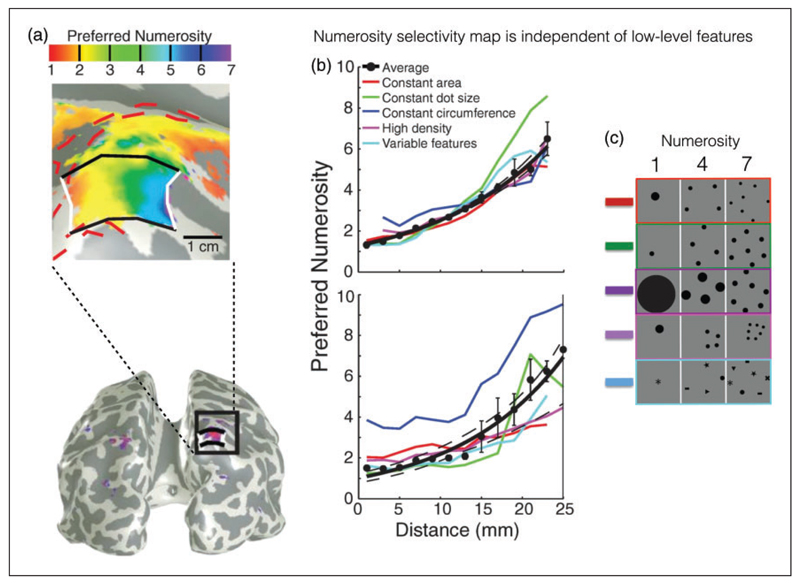
More recently, Harvey, Klein, Petridou, and Dumoulin (2013) used high-field 7T fMRI to isolate in the human parietal cortex topographically organized neural populations tuned to number (Figure 4). Just as area V1 has a columnar organization for orientation tuning, so does the human intraparietal sulcus have a columnar organization for number. Again, this study took great care to vary all other possible confounds, such as size, contour length, contrast, and so forth, and found that the selectivity was clearly to the number of items, rather than any of the other variables. This work clearly demonstrates that early visual cortex (V1) does not drive the number-response selectivity found in the parietal cortex, showing that number is not derived from low-level visual features. Number-selective neurons fire when the preferred stimulus, not the highest, is presented; V1 responded most strongly to the highest numerosity. In other words, numerosity-selective neuronal activity does not follow the amount of contrast energy in the stimulus, while V1 does.

Figure 4. Topographic representation of numerosity in human parietal cortex.

(a) Spatially organized numerosity map for small numbers of elements (from 1 to 7) in the parietal cortex. Color code reflects brain regions preferentially activated by given numerosities. (b) Progression of numerosity selectivity (dots) as a function of distances from white lines in Figure 4(a). Different line colors refer to separate conditions where low-level features of stimuli were controlled for Figure 4(c). Adapted with permission from Harvey et al. (2013).

In our laboratory, we have studied the effect of adaptation, like that used in the psychophysical experiments, on neural representations of number. Applying pattern recognition analysis, Castaldi, Aagten-Murphy, Tosetti, Burr, and Morrone (2014) used the BOLD response from IPS and V1 to train a classifier to discriminate the numerosity of dot clouds before and after adaptation. Classification worked well in IPS (but not V1). Importantly, however, IPS classifiers trained with preadaptation presentations could accurately decode numbers only when tested with other preadaptation trials, but not when tested with postadaptation presentations, and vice versa. This suggests that adaptation changes the cortical maps underling the representation of numerosity in IPS, while classification was not possible at all in V1.

The neurophysiological evidence from both monkey and human all points to the existence of specialized circuitry for encoding numerosity. These seem to reside in intraparietal cortex and frontal cortex. There is no neuro-physiological evidence that adaptation to number is mediated by texture mechanisms in V1 or anywhere else. However, it remains possible that numerosity perception is not restricted to IPS, but other regions participate in the distributed analysis (Anderson & Penner-Wilger, 2013).

The Relationship Between Numerosity and Texture-Density

Since psychophysicists have become interested in numerosity estimation, a good deal of evidence has accrued to suggest that it is a perceptual attribute quite distinct from texture density. One of the earliest and perhaps most unequivocal demonstrations, alluded to in the above section, was discovered independently by He et al. (2009) and Franconeri, Bemis, and Alvarez (2009). Figure 5 shows the effect. Both figures comprise 12 randomly distributed dots, but at right pairs have been joined. The impression, especially for brief presentations (see also Movie 6), is that the numerosity of the connected pattern is considerably lower than that of the unconnected dots. Figure 5 shows psychophysical curves for comparing the numerosity of a 12-dot standard with dot patterns with zero, one, or two dot-pairs connected. Each connection had the same effect on perceived numerosity as removing a dot. And as mentioned in the previous section, joining the dots also affects the fMRI BOLD response, suggesting that linking dots changes the neural coding of number in human intraparietal sulcus (Figure 3(d)).

Why should the connected or partially connected pattern appear less numerous? If numerosity was based—even partially—on texture density, adding lines to the pattern should increase numerosity (as it clearly increases the amount of “stuff” in the pattern). Presumably linking the dots with a line perceptually converts two dots into a single unit. The estimate of numerosity is clearly based on the number of separable items, rather than how much stuff is in the field. This to our minds is the clearest demonstration that numerosity is quite different from texture density.

Interestingly, Milne et al. (2013) have asked whether the effect of connecting the dots takes affects any judgement, whether purely perceptual or also motor. To this aim, they displayed four dots either connected or not and asked subjects either to judge them or to reach toward them. They found that whilst numerical estimation underwent the illusory decrement of dots, motor action was determined solely by physical numerosity. It is hard to reconcile this finding with the idea that the connectedness illusion possibly along with the whole of numerical estimation takes place early in the visual system.

Recently Apthorp and Bell (2015) reported finding closely related to connectedness, that symmetric dot patterns appear less numerous than asymmetric patterns. It is not quite clear why this should be so, but possibly because symmetric patterns appear more “connected” than random patterns, with symmetrically opposing dots tending to be perceptually joined.

There is a good deal of other evidence that number and texture are dissociable. For example, Ross and Burr (2010) showed that numerosity depended on luminance, with apparent numerosity increasing with decreasing luminance, by 6% per log-unit. However, dense-textured patterns were entirely unaffected by luminance. It remains unclear why numerosity is affected by luminance. Nor for that matter is it clear why other attributes such as apparent speed are luminance-dependent (Hammett, Champion, Thompson, & Morland, 2007; Vaziri-Pashkam & Cavanagh, 2008). But that numerosity is affected by mean-luminance, and texture density is not, clearly shows that the two are distinct.

Interestingly, Kramer, Di Bono, and Zorzi (2011) have demonstrated that low-level visual attributes actually play little role in estimating the number of items in a visual scene. In their experiment, they asked subjects to enumerate a set of moving items on the screen. In one condition, the items could be resolved monitoring luminance (black bars), in one condition, the items were defined by second order motion (i.e., polarity reversal of the background). Interestingly subjects performed similarly in both conditions under several parameters, including the coefficient of variation which was 0.33 in both cases. The only difference was a slight underestimation for the second-order stimuli (about 8%), which is surprisingly small considering that second-order stimuli are harder to detect.

Although there exists good evidence that numerosity is perceived independently of texture, common sense suggests that the two must be related in some way. If we continue to increase the number of items within a given area, we will reach a point where we can no longer resolve the items, and they will merge into what is commonly termed texture. When does this occur? What determines whether an array of items turns into an amorphous texture?

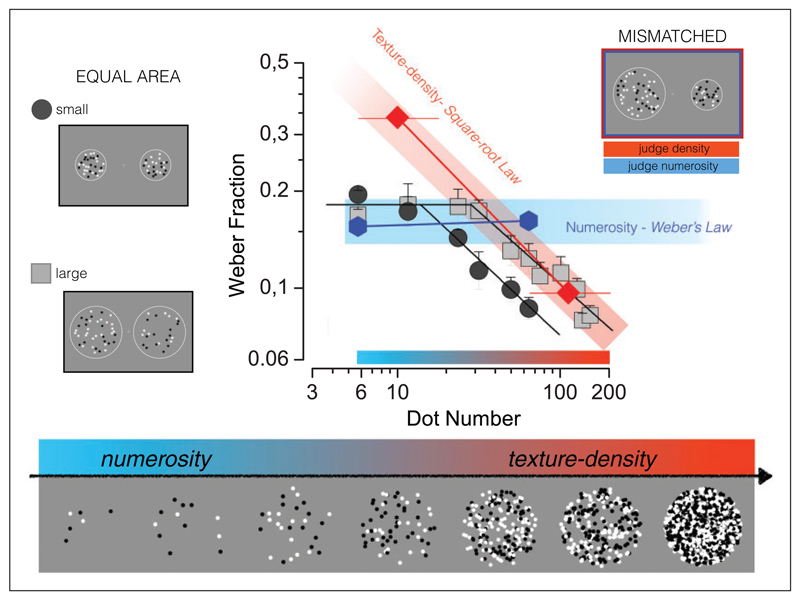
We used a simple technique to investigate the transition from number to texture (Anobile, Cicchini, & Burr, 2014). We measured Weber fractions—the minimal detectable change in numerosity, normalized by PSE—over a large range of numerosities and densities. Although, it is commonly assumed that Weber fractions for numerosity are constant (Dehaene, 2011; Ross, 2003; Whalen, Gallistel, & Gelman, 1999), when carefully measured over a wide range it is clear that this is not strictly true. Figure 6 shows the results for measurements made with a large stimulus patch (150 deg²) and a smaller patch (54 deg²), over a very wide range of numerosities. In both cases, Weber fractions were constant for the lower range of numbers, but after a critical point, decreased at a rate proportional to the square root of numerosity. The critical numerosity was lower for the smaller than for the larger patch, in both cases corresponding to a critical density of about 0.3 dots/deg². The results suggest the existence of two psychophysical regimes, one for number obeying Weber’s law and another for density or texture, following a square root law.

Figure 6. Different sensory thresholds for numerosity and texture density discrimination.

Weber Fractions as a function of dot number, for two different stimulus areas of test and probe. Dark gray circles refer to test and probe stimuli confined in small circular areas (8° diameter), light gray squares to large areas (14° diameter), for numerosity discriminations. Weber fractions in both areas conditions remain constant up to a critical numerosity, then start to decrease, with a slope of −0.5, consistent with a square-root relationship. The blue hexagons show thresholds for discriminating numerosity in the unequal-area condition, red diamonds density discriminations for unequal areas. Adapted with permission from Anobile et al. (2014).

To test this idea further, we measured Weber fractions for both numerosity and density of stimuli of different areas. Here, both the Weber fractions for numerosity (blue symbols) and for density (red symbols) follow the predictions of constant Weber and square root law. With mismatched area, density cannot be used as a proxy for number and vice versa. So at low numerosities, the density thresholds are higher than when both cues are available, and at high numerosities, the numerosity thresholds are higher. When the areas of the stimuli were matched, both cues could be used and the most sensitive presumably dominated.

What determines the transition from numerosity to density? We believe that texture mechanisms come into play when the individual items are not longer discernable as separate items, but blend into an amorphous mosaic. In some ways, this transition is similar to the well-known visual phenomenon of “crowding,” where clearly detectable stimuli are difficult to identify when flanked with others, within a critical range. The crowding concept suggests that when the packing is too dense, the individual items cannot be segregated and therefore are not countable: At this point, texture mechanisms come in to play.

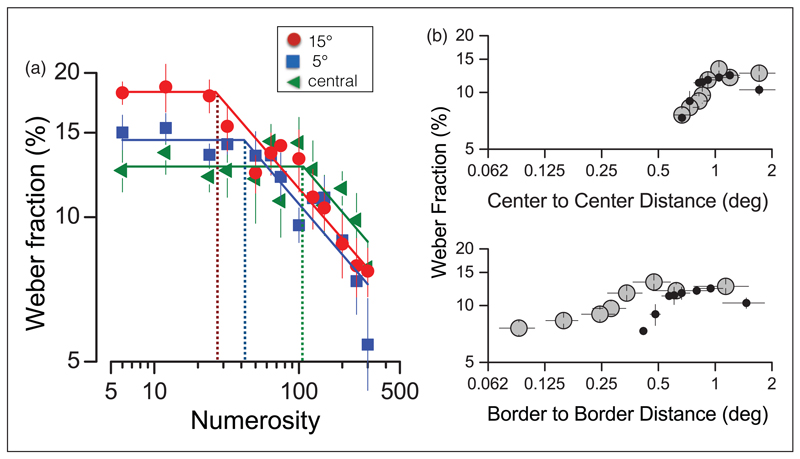
The crowding hypothesis makes two strong predictions: The transition between numerosity should depend on eccentricity, occurring at lower densities in the periphery; and it should depend on center-to-center spacing rather than edge-to-edge separation, or total coverage of dots. Both these predictions are clearly born out by our recent data (Anobile, Turi, Cicchini, & Burr, 2015). Figure 7(a) shows Weber fractions as a function of numerosity for three different eccentricities. The break point in the curve shifts steadily to lower densities as eccentricity increases. Figure 7(b) shows measurements made with two dot diameters, 0.58° and 0.25°, plotted as a function of average center-to-center or edge-to-edge separation. When plotted as separation of dot centers, all data for both large and small dots clearly line up in a simple two-limbed function, with a clear break for separations of around 1°. When plotted as edge distance, the two dot-sizes form clearly distinct curves with different and nonconstant slope.

Figure 7. Transition point between numerosity and texture density.

(a) Weber Fractions for numerosity discrimination of dots patches centered at three different eccentricities (15° red circles, 5° blue squares, central presentation, green triangles). Transition points between numerosity (Weber’s Law, flat zone) and texture-density regime (square-root law, descending zone) depend on eccentricity (dotted lines). (b) Weber fractions for numerosity plotted as a function of average center-to-center inter-dot distance (upper panel) or average border-to-border distance (bottom panel). Large gray-circles refer to stimuli patches comprising large dots (diameter 0.58°), small-black filled symbols to small dots (diameter 0.25°). Adapted with permission from Anobile et al. (2015).

Both the experiments of Figure 7 support the similarity between crowding and limits of numerosity perception. However, we emphasize that we are not claiming that the phenomena are identical. For example, in classic crowding studies, subjects must identify the form of a crowded object (typically an alphanumeric letter); whereas to estimate numerosity, it is not necessary to identify the object be enumerated. Indeed, while the principles governing the processes are similar, the absolute distances defining the limits of numerosity are of a far finer spatial scale than those for classic crowding: For example, at 5° eccentricity, the thresholds are at about 1° rather than 2.5°. It is not clear at what stage of analysis this fine-scale crowding interferes with segregation for numerosity estimates. Certainly, the distances seem too small to be limited by the receptive field sizes of numerosity areas like IPS; so presumably the limit occurs at earlier levels in the hierarchy.

Two other studies reinforce the idea of different regimes for number and density. Zimmermann and Fink (personal communication, 01/04/2015 investigated the effect of size adaptation on numerosity. Adapting for a few seconds, a large homogeneous disk causes a subsequently viewed disk to appear smaller that it physical is and vice versa (Pooresmaeili, Arrighi, Biagi, & Morrone, 2013). Zimmermann and Fink adapted observers to large and small stimuli left and right of fixation, then asked them to compare the numerosity of a stimulus presented to the adapted regions. Adaptation changed the apparent size of the stimuli, as expected, but also the apparent numerosity. However, the change in apparent numerosity occurred principally at higher numerosities, where texture mechanisms may be expected to operate at lower numerosities, there was little effect. It may be argued that changing the apparent size of the stimuli, without changing the number of items within the region, affected the apparent density and in the texture—but not numerosity—regime, this affected perceived numerosity.

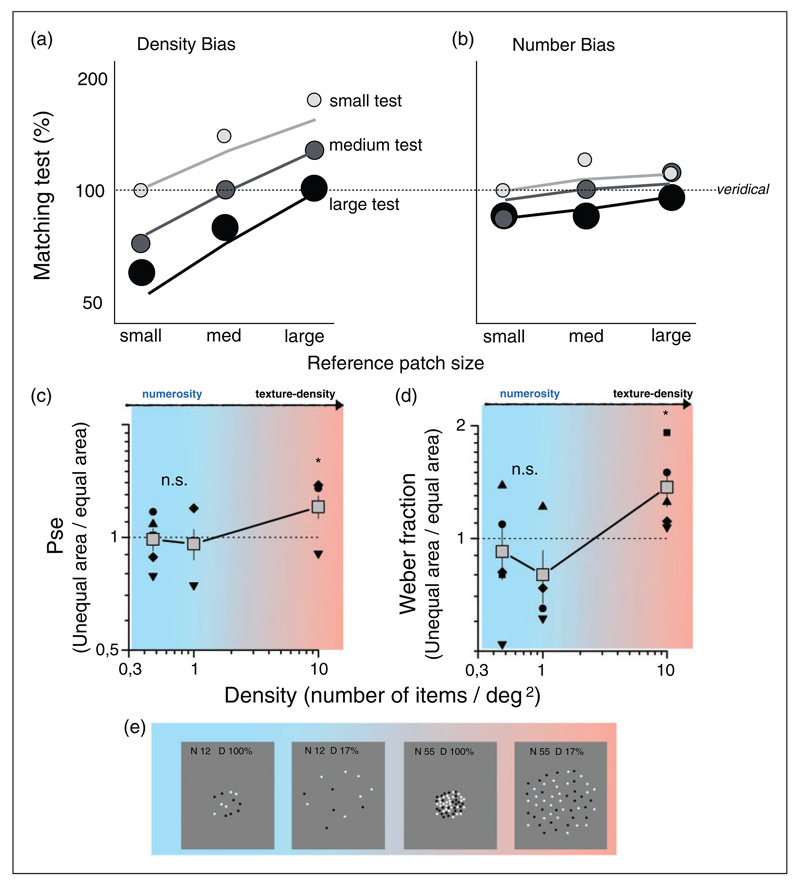
We report in this review further new evidence from our laboratory for a clear separation between texture and number, based on the study of Dakin et al. (2011). They asked subjects to make numerosity and density judgements between stimuli of different area (therefore dissociating density from number). They reported cross-leakage between the two qualities, although the bias was quite asymmetrical: Numerosity strongly biased density estimates, with a doubling in numerosity causing a 28% increase in density (Figure 8(a)); but density biased numerosity only weakly, with a 9% increase in numerosity for every doubling in density (Figure 8(b)). They also reported that observers found it more difficult to spot differences in either density or numerosity when patches were mismatched in overall size. Dakin et al. interpreted these results to support the idea that numerosity and density share the same visual metric. On the other hand, Ross and Burr (2010) had reported that varying area from trial to trial had no effect on density of numerosity judgements compared with the blocked condition. One possible reason for the discrepancy is the difference in dot density of the two studies: Densities were 1 dots/deg² for Ross and Burr and 5 dots/deg² for Dakin et al. (2011).

Figure 8. Effect of area mismatching on numerosity discrimination.

(a and b) Biases in the PSE reported by Dakin, Tibber, Greenwood, Kingdom, and Morgan (2011), as a function of reference patch size for three levels of the test sizes (light-gray small, mid-gray medium, and black large) for density (a) and number (b) discrimination. Horizontal dashed lines indicate no bias. The data show clear size-dependent biases in estimation of density and smaller dependence for numerosity. (c and d) Testing the bias at different stimulus densities. (e) Examples of stimuli of different density. Stimuli were presented centered at 13° left and right of central fixation point. The probe numerosity was kept fixed, in separate sessions at N = 6 (0.47 dots/deg²), 12 (0.95 dots/deg²), or 128 (10.18 dots/deg²) dots. Test stimuli varied according subjects’ responses following the QUEST algorithm. In the equal-area condition, probe and test areas were both 113 deg². In the unequal area, condition probe area was reduced to 12.56 deg². (c) Accuracy biases expressed as the ratio of PSE measured in the unequal- to the equal-area condition, as a function of density. Values above one indicate overestimation of the larger stimulus. (d) Precision biases measured as the ratio of Weber Fraction measured in the unequal- and equal-area conditions. Values above one indicate worse precision in the area-mismatched conditions. T test reveals statistically significant effect (t₍₄₎ = 2.37, p < .05) of mismatch area on both PSE and Weber Fraction only for highest tested density (N = 128, 10.18 dots/deg²). Adapted with permission from Dakin et al. (2011).

To test this idea, we repeated Dakin et al.’s experiment with mismatched area at three densities, asking subjects to compare the numerosity of two clouds of dots of either equal or unequal areas. Figure 8(c) and (d) plots the ratio of PSEs and Weber fractions measured with unequal stimulus areas compared with equal stimulus areas, as a function of stimulus density. At high densities, we confirm Dakin et al.’s results, for both PSE and Weber fraction. However, at the two lower densities, within the range of numerosity judgments, there was no significant dependency in either quantity. These results provide further proof that the interaction between numerosity and density occurs only at medium to high densities, where texture mechanisms come into play. Within the number regime, there is no cost in sensitivity for unequal area (hence unequal density), and no systematic bias, or “leakage” between the two systems.

In brief, we are proposing that when object segmentation is prevented (e.g., by crowding), stimuli will be treated as comprise a texture, rather than being treated as individual objects. An elegant fMRI study shows how the response of IPS depends on stimulus segmentation. They measured the BOLD response of human IPS to colored (blue and green) stimuli that can change either abruptly (discrete and numerous stimuli) or smoothly (analogue and nonnumerous stimuli) in space or in time. Subjects were asked to decide whether they saw more green or more blue. IPS responded more for discrete stimuli than for smooth variations. This study strongly suggests that IPS treats stimuli as a number of objects or events, until item segmentation is prevented.

Subitizing

So far we have talked of two mechanisms, numerosity and texture, neglecting completely the other very well known number range termed subitizing (Kaufman & Lord, 1949): the rapid, accurate, and confident judgments of number for small numbers of items, usually less than four (derived, like the common Italian word subito, from the Latin adjective subitus, meaning “sudden”). How does this fit with the dichotomy being proposed here?

A good deal of evidence suggests that subitizing reflects a fundamentally different mechanism from estimation. Revkin, Piazza, Izard, Cohen, and Dehaene (2008) tested whether small and medium numbers tap the same system by comparing naming times and accuracy over the range of 1 to 8 (grain of 1) and 10 to 80 (grain of 10): Precision was much better in the range 1 to 4 then 10 to 40. Choo and Franconeri (2014) showed that comparing 2 versus 3 elements was much faster and more accurate then comparing 20 versus 30, demonstrating that the advantage previously found was not due to more experience in verbal labeling of small numbers. Another line of research that has clearly confirmed that subitizing taps a different system from estimation examines the effect of attention on number estimation. Although subitizing is often thought to be preattentive (or at least relying on preattentive mechanisms (Trick & Pylyshyn, 1994)), many studies have shown that it is greatly compromised when attention is deprived, both during dual tasks (Vetter, Butterworth, & Bahrami, 2008), inattentional blindness (Railo, Koivisto, Revonsuo, & Hannula, 2008), and with the attentional blink paradigm (Egeth, Leonard, & Palomares, 2008; Olivers & Watson, 2008; Xu & Liu, 2008).

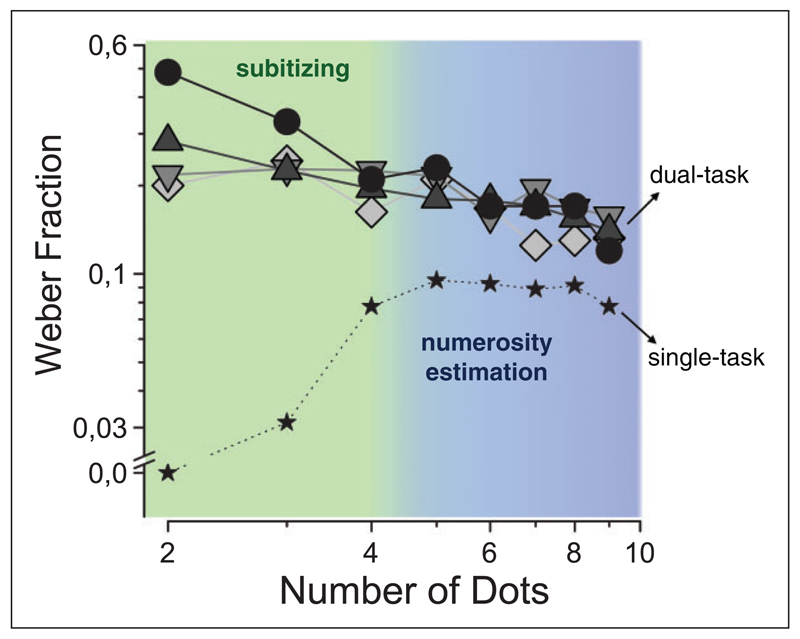
We have confirmed that subitizing is highly dependent on attentive mechanisms, and shown that under the same conditions, estimation mechanisms (within the numerosity range) are relatively immune to availability of attentive resources (Anobile, Turi, Cicchini, & Burr, 2012; Burr, Turi, & Anobile, 2010). We asked participants to estimate the number of items (dots) briefly presented around a central fixation point. We manipulated the availability of attentional resources by dual-task paradigms or by attentional blink. In separate conditions, we used visual distractors, of the same sensory modality as the stimuli to be enumerated, or stimuli from different modalities, such as audition and touch. Figure 9 shows the main results: Firstly, attention has a very large effect in the subitizing range (N ≤ 4), but very little in the estimation range (4 < N ≤ 9), despite the fact that subitizing is often held to be “preattentive.” Secondly, attentional manipulations in all domains (visual, auditory, or haptic) had similar effects, showing complete cross-modal transfer (unlike what is observed for discrimination of textures, where attentional resources seem to be quite distinct: Alais, Morrone, & Burr, 2006; Arrighi, Lunardi, & Burr, 2011). Indeed, the strongest effect for attentional load in the subitizing range was from haptic stimuli, possibly reflecting an interesting functional connection between visual and finger counting strategies (Chinello, Cattani, Bonfiglioli, Dehaene, & Piazza, 2013).

Figure 9. Effect of multisensory attention in subitizing and estimation range.

Weber fractions in number estimation (standard deviation divided by physical numerosity) in the single-task (dotted line, small stars) and as a secondary task in divided attention condition. The primary tasks were haptic time bisection (circles), auditory time bisection (diamonds), auditory pitch discrimination (downward triangles), and visual conjunction (upward triangles). Attentional load strongly impairs precision in the subitizing range (4 and below), irrespective of the modality or type of distractor task. Adapted with permission from Anobile et al. (2012).

These results suggest that subitizing could reflect a more general sensory process than has been previously suspected: an amodal prioritization of small numbers of objects. This idea finds support from studies showing that subitizing is not only restricted to vision but also operates in audition (Camos & Tillmann, 2008; Repp, 2007) and with haptic stimuli (Plaisier, Tiest, & Kappers, 2009; Riggs, Ferrand, Lancelin, Fryziel, Dumur, & Simpson, 2006). Recently, visual subitizing has been shown to be strongly related to visual working memory capacity (Piazza et al., 2011). Interestingly, loading working memory impairs estimation precision in the subitizing range but not in the numerosity estimation range (N > 4).

We examined the effect of attention over a fairly restricted range, covering subitizing and estimation, but not encroaching the texture range (remaining under 0.1 dots/deg²). However, there is evidence that attention strongly affects texture discrimination, possibly more strongly than numerosity discrimination. Tibber et al. (2012) measured “numerosity” judgments under dual-task conditions and found very strong effects of attention (factor of 1.7), stronger than we report (factor of 1.32). However, as their densities ranged from 3 to 7 dots/deg², and their eccentricity 6°, their stimuli were well into the texture range (cutoff around 1 element/deg²). If this result is confirmed, it may reflect another difference between numerosity and texture mechanisms, the relative immunity of numerosity estimates to attention deprivation. This seems likely as Tibber et al. (2012) also found strong attentional effects for relative density judgments. It is also consistent with the strong attentional effects reported for other judgments of pattern, such as contrast discrimination (Lee, Itti, Koch, & Braun, 1999; Morrone, Denti, & Spinelli, 2002). It would be interesting to measure the effects of attention across the entire range of numerosity and densities, to see how the various regimes are affected. It would also be interesting to look at the effects of cross-modal dual tasks, as previous work suggests that sensitivity is limited by attentional resources within, but not between modalities (Alais, Morrone, & Burr, 2006; Arrighi, Lunardi, & Burr, 2011). Another possible variation in future research would be to use similar dual-task techniques to study counting, rather than estimation, given the suggestion that counting relies on focused attention and estimation of distributed attention (Chong & Evans, 2011).

We have suggested that subitizing reflects the operation of attentive mechanisms, which have a very limited capacity of about four items (Burr, Turi, & Anobile, 2010). This system may sit on top of the numerosity-estimation system, supporting rather than replacing estimation for low numbers. To test this idea, we measured numerosity adaptation in the subitizing range. As Figure 1 (red circles) shows, there is normally very little adaptation in this range, presumably because the attentive-based subitizing mechanisms do not allow errors to occur. However, when adaptation was measured in this range in the dual-task condition (Figure 1, blue diamonds), strong adaptation effects were observed (Burr et al., 2011). This suggests that adaptable numerosity-estimation mechanisms operate over the whole low range of numbers, up to the transition point to texture; but under normal conditions, when attention is not deprived, the subitizing mechanisms prevail.

Models of Numerosity Computation

The previous sections show very clearly that numerosity is not the same as texture and probably taps quite distinct mechanisms. What is the nature of these mechanisms? In this section, we briefly describe and compare some models of numerosity.

To be credible, a model of numerosity must accounts for the key aspects of number perception. It should discount irrelevant low-level features, such as element size, shape, and contrast. It should also account for the more compelling illusions, such as the effect of connecting dot-pairs into “dumbbells,” decreasing both perceived numerosity (Figure 5(b)) and BOLD selectivity (Figure 3(d)). But perhaps the most basic property to explain is Weber’s law, the scaling in discriminability with average number, over a broad range. Weber’s law is not easy to explain. Indeed, in the field of time perception, it is considered one of the major hurdles (Staddon & Higa, 1999). Simple models involving noisy interval generators predict a square root relationship between discriminability and duration, as the variance will increase directly with duration, and root-variance determines the limiting noise. Complex models have been devised specifically to account for Weber’s law, including cascades of clocks with different time constants (Matell & Meck, 2004). A similar argument can be applied to number discrimination: The signal-to-noise ratio decreases with the square root of number, easily explaining the square root relationship of discriminability in the texture range, but not in the number range, where it varies directly with number. Like time perception, specific mechanisms are needed to account for Weber law behavior in the perception of number.

One of the earliest models of numerosity was proposed by Dehaene and Changeux (1993). It is a four-stage connectionist-style model with two major computational blocks: The first discounts nonrelevant spatial features of the items (“normalization” stage); the second classifies the normalized activity and gives it a numerical label (“classification” stage). The strength of the model is that it attains important computational steps with fairly simple mechanisms. The normalization stage is implemented by first buffering the visual input, then accessing a series of object detectors tuned for position and size of the object. The nodes (clusters) of this second stage have reciprocal inhibition, so that if an object of given size activates two detectors, they inhibit each other and eventually only the closest match wins. This part of the model effectively creates spatial segregation, by a simple inhibitory surround mechanism. Having detectors for the various sizes permit a representation that transcends size, effectively activating one node regardless of the space covered by each object. Dehaene and Changeaux specifically refer to normalization across size, but it is easy to envisage implementing similar mechanisms to obtain normalization for other features, such as shape or color. The last two layers of the model associate the pattern of activities in the second layer with a precise numerical label. The third layer pools over the entire second layer and has units which fire beyond a certain input level, thus implementing a battery of integrators. The fourth, final layer has nodes with excitatory connections with nodes with a given threshold and inhibitory connections with nodes with a slightly higher threshold. In this way, a node of the fourth layer is active only if some nodes of the third layer reach a certain threshold, but not a higher threshold, effectively making up a number-selective detector.

Dehaene and Changeaux’s model exhibits Weber’s law behavior over a limited range. The main reason for this is that the width of the tuning functions increases with numerosity. However, the simulations were with a rather simple network with only 50 input nodes: It is not certain that Weber-like behavior would emerge in more powerful networks. Interestingly, Dehaene and Changeaux were the first to propose a possible implementation for the problem of normalization across stimulus features. Although, the mechanism they propose requires a distinct boundary between objects, it is easy to imagine how a dumbbell stimulus could lead the system into underestimating the number of items, thus modeling this compelling illusion.

Interestingly, a recent neural model of numerosity investigates which neural architectures subserve the mapping of visual numerosities into numerical categories (numbers). Verguts and Fias (2004) have developed a standard three-layer neural network (input + hidden + output) which learned the mapping between input patterns and numerical categories using error back-propagation (Zipser & Andersen, 1988). Interestingly, the network developed two types of units: In the hidden layer, the perceptrons evolved to work as “integrating units,” in the output layer, they responded selectively for number using a mixture of excitatory and inhibitory connections with the nodes of the previous layer. Both features are remarkably similar to what Dehaene and Changeaux have proposed in this model and reinforce the idea that numerosity perception can be within realistic and simple neural networks.

Allik and Tuulmets (1991) proposed a model in which numerosity comparisons are achieved by comparing the amount of covered area including both the items themselves and a small neighborhood surrounding each (“Occupancy Model”). As the estimation takes into account the neighbourhood of the dots, the model predicts that when two dots are close together they are slightly underestimated in agreement to experimental data (Allik & Tuulmets, 1991; Dakin et al. (2011); See also Figure 8). Although the original formulation of the occupancy model did not encompass possible a neural implementation, their model is formally similar to a system that performs a broad low pass filter and then passes the activity map though a hard threshold (or a nonlinearity). Alternatively, a similar computation can be performed by “mexican hat” or difference-of-gaussian operators.

Unfortunately, the authors do not investigate sensitivity of the model as a function of number to see if it predicts Weber’s Law. However, at a glance it does not: The relationship between covered area and numerosity is a family of curves of the type 1 − e^−N which asymptote to unity (Schachter & Ahuja, 1979). The just-noticeable-difference of a system of this type follows an exponential function, and therefore does not predict Weber’s Law, without major modifications. In their current implementation, Allik and Tuulmets did not investigate the effect on item size on numerosity estimation: However, it is easy to imagine that their framework predicts some size independence as long as the size of the dots is small compared with the size of the extended region which comprises the dot as well as its neighborhood.

Stoianov and Zorzi (2012) took a quite different approach to modeling numerosity: They developed an unsupervised learning neural network and observed what nodes developed spontaneously. They implemented a three-stage model, with an input-buffer first stage and two hidden layers implementing a deep neural network (Hinton & Salakhutdinov, 2006; Stoianov & Zorzi, 2012). They trained the network only for efficient coding of sensory data, yet numerosity selectivity emerged as a statistical property of the deepest layer of the model. The network was able to classify numerosity well, exhibiting several features of human numerical perception: They obey Weber’s law (with a Weber fraction of 0.15, similar to humans), and they are completely invariant to stimulus area, density, and object features. Interestingly, the nodes have center-surround selectivity profiles. This is important, as previous models had assumed surround inhibition and showed by simulations that this computational solution is indeed the simplest and easiest to implement (Dakin et al. (2011); Dehaene & Changeux, 1993).

Sengupta, Surampudi, and Melcher (2014) have built on Zorzi’s and Stoianov idea and explored the properties of networks with various degrees of reciprocal inhibition. Their work shows that networks with high levels of inhibition reliably encode small numerosities, but saturate at higher numerosities. On the other hand, networks with mild levels of inhibition can encode well numerosities up to tens of items. The authors stress the idea that networks with high levels of inhibition perform rather well the task of object segregation, while those with mild levels of inhibition are less capable at this. An interesting conclusion from their work is that it is not necessary to have two distinct neural mechanisms for subitizing and numerosity as the same network can code either of the ranges: The one mechanism can handle both, simply by changing the strength of the surround inhibition. As mentioned in Subitizing section, we have also suggested that subitizing phenomena do not require a separate “number mechanism”: A single preattentive mechanism could operate over both subitizing and larger numbers but, in normal condition, small numbers take advantage from additional attentional resources. Sengupta et al. (2014) proposed the alternative explanation in which it is the task-dependent top-down modulation of the recurrent inhibition that separates the subitizing and estimation ranges. While the exact nature of the mechanisms regulating the inhibition strength is not clear, attention could be needed to change to higher inhibition and make the system suitable to perceive low numbers. It is interesting to note that top-down control modulation on attentional selection forms the basis of the classic-biased competition theory of selective attention (Desimone & Duncan, 1995).

Recently Dakin et al. (2011) and Morgan et al. (2014) have developed models aimed at simulating both texture and numerosity discrimination simultaneously, using spatial filtering to build summary statistics of the stimulus. It normalizes the amount of high spatial frequency content in a stimulus (an estimate obtained via filtering with a small Laplacian of Gaussians), with the low spatial frequency content (an estimate obtained via a larger Laplacian of Gaussians). With suitable choice of filter size (with the low frequency filter similar to dot size and the high frequency filter four times smaller), the high frequency response grows proportionally with element number. On the other hand, the low frequency estimator shows hybrid behavior, growing only moderately with number and area. Whilst being suitable as an “area” estimator, it does so imperfectly by underestimating the area covered by larger patches (Figure 8(a) and (b)). In this way, density judgements reveal a bias with the large patches looking denser, in agreement with psychophysical data.

Ironically this model, which emphasizes the fact that there is a processing stage which calculates a hybrid measure of number, density, and area, disposes altogether with the normalization stage when it comes to number judgements: Number judgements are made simply by looking at the high frequency content, essentially implementing a very basic principle by which, with fixed element size, number of items will correlate with the amount of borders. They do not specifically address the issue of sensitivity, but as the major noise limitation of the model seems to be stimulus based, one would expect square root rather than weber-law behavior.

More crucially, the model will not—without major modifications—explain the dumbbell effect shown in Figure 5. Their model basically looks at the ratio of high to low spatial frequency information, so the image with the connected dots (at right of Figure 5(a)), which has more signal in the high spatial frequencies, will be encoded as being more—not less—numerous. Interesting, they did look at a specific example of connected dots, the one used in some experiments, where one field had joined dots and the other had the same amount of lines, but these did not join dots (He, Zhang, Zhou, & Chen, 2009). With these two images, they found a small effect in favor of the illusion. But this condition was designed only to control for various issues in the experiment; it does not represent the generic case of comparing a set of isolated dots with one with joined pairs. It is obvious that the joined dots have more energy at high spatial frequencies, and should therefore be seen as more numerous, the opposite of the compelling illusion: Informal simulations in our lab verify that this is the case. Admittedly, their model was not designed to deal with this specific issue, but as it is such a compelling effect, it really does deserve more serious consideration in future refinements of the model.

Conclusions

Research over the last few decades has firmly established that number is a perceptual attribute: Humans are able to make rough but rapid and effortless appraisals of the quantities of a cloud of items, estimating numerosity efficiently over an extremely wide range, from unity up to hundreds or even thousands of items.

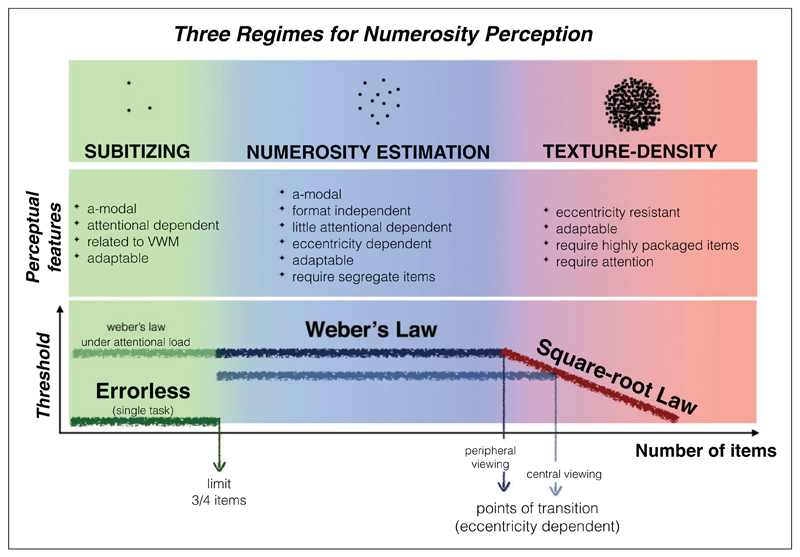
In this review, we propose three distinct processes, working over distinct ranges (see Figure 10). In the low subitizing range, up to about four, estimation is both rapid and errorless. This system is highly attention-demanding, and linked to working memory. There is also evidence that the system spans several sensory modalities, rather than being limited to vision. For higher numbers, numerosity is estimated with a rapid but error-prone process, where error increases linearly with numerosity, following Weber’s law. Weber fractions vary considerably between individuals, but also with eccentricity, being lower for centrally viewed than peripherally viewed stimuli. At high densities, texture-like mechanisms kick in, which seem to be equally sensitive at all eccentricities. In this regime, Weber fraction is not constant but decreases with the square root of density (or number, if area is held constant). Put another way, just-noticeable-differences increase not linearly with numerosity but with the square root of numerosity, as may be expected if discrimination is limited by the variance of the stimuli. Importantly, the transition from numerosity to texture is determined by density, defined as average center-to-center spacing of the elements.

Figure 10. Summary of psychophysical characteristics of numerosity judgments in the three numerosity regimes/ranges.

Main characteristics or properties of numerosity judgments are listed in middle row: Weber fractions as a function of numerosity are sketched in the bottom row.

There are unlikely to be strict demarcations between the regimes. For example, the numerosity range probably extends well into the subitizing range; but when measuring thresholds, the most sensitive mechanism (subitizing) prevails, and we are errorless. However, when subitizing is compromised by depriving attention, estimation remains possible and yields similar Weber fractions as the rest of the estimation range (Figure 9) and adaptation also occurs when attention is deprived (Figure 1). Similarly, when asked to make numerosity or density judgements between stimuli of equal area, one can act as a proxy to the other, and the most sensitive will prevail. However, if the areas to be compared are unequal (so the two properties are not the same), then thresholds consistent with constant Weber fraction or square-root law can be seen extending well beyond the normal range (Figure 7). Again, the system will always use the more sensitive signal when more than one is available, but if the systems can be isolated they seem to cover a very wide range, suggesting that they are very general purpose.

The evidence for multiple systems may account for some seemingly conflicting results reported by different groups, all using nonstandardized stimuli. Table 1 reports the densities used by some example studies over the past few years. Clearly different studies have used different stimulus densities, presumably stimulating different mechanisms. For example, most of the test stimuli used by Burr and Ross (2008), Ross and Burr (2010), and Burr et al. (2011) fell well within the confines that favor numerosity over texture. On the other hand, Dakin et al. (2011) used stimuli that clearly stimulate the texture region, five times the switching density. The stimuli of Morgan et al. (2014) were also well into the texture limit. Given this variability, it is unsurprising that the results are not always identical between groups.

Table I.

Comparison of Eccentricities and Densities of Stimuli Used in Some Recent Experiments.

References	Eccentricity (deg)	dots/deg2	switching point (dots/deg2)	Regime
Burr and Ross, Current Biology (2008)	7	0.38 (N = 30) 0.63 (N = 50)	Around 0.6	Numerosity
Ross and Burr, Journal of Vision (2010)	Central	1 (N = 50)	Around 2	Numerosity
Burr et al. Seeing Perceiving (2011)	6	0.5 (N = max 24)	Around 1	Numerosity
Morgan et al. Proceedings of Biological Sciences (2014)	Central	2.7 (N = 64)	Around 2	Texture (near limit)
Dakin et al. Proceedings of the National Academy of Sciences of the United States of America (2011)	6	5.2 (N = 128)	Around 1	Clearly texture
Halberda, Mazzocco, and Feigenson Nature (2008)a	Central	0.37(N = max 30)	Around 2	Numerosity
Tibber et al. Vision Research (2013)a	Uncertain	64	Around 1	Near the limit

^aInferred.

Prediction of Mathematical Performance

A good deal of evidence suggests that numerosity perception may act as a form of “start-up tool” for the acquisition of formal math skills (Piazza, 2010). Several studies have demonstrated that numerosity discrimination thresholds (Weber Fractions) are a reliable predictor of both current and future formal math achievements in school-age children (Anobile, Stievano, & Burr, 2013; Dehaene, 2011; Halberda et al., 2008); and children affected by dyscalculia have very large Weber Fractions (Piazza, 2010). This is important, as it suggests that understanding the mechanisms behind numerosity may have important practical implications. For example, if the perception of numerosity was indeed independent of texture, we may expect to find a clear dissociation between thresholds for texture and numerosity in predicting math performance.

Indeed, this dissociation has been reported. Tibber et al. (2013) tested a large sample of 300 participants, ranging in age from 6 to 73 years, with several psychophysical and cognitive tasks, including a math test (series of problems) and four perceptual tasks in which two grating patches had to be adjusted to match one another with respect to many features, including numerosity or density. The results were clear after chronological age was regressed out, numerosity but not density thresholds predict math scores. This is perfectly consistent with notion that density and numerosity are encoded by largely independent mechanisms. Strangely, however, the authors failed to appreciate the importance of the dissociation they had discovered. Rather they found this important result puzzling:

Particularly puzzling is the lack of an association between mathematical performance and density thresholds since we have previously demonstrated an intimate link between numerosity and density judgments (Tibber et al., 2012) and provided a relatively simple model of their completion based on a common filtering stage. Dakin et al. (2011)

This result is less puzzling once you accept the accumulated evidence showing that density and numerosity are distinct perceptual processes.

Concluding Remarks

Perhaps the most important conclusion to be drawn from the series of recent results is that there exists a system seemingly dedicated to the perception of numerosity, of knowing how many objects are within a particular field of view. This system seems to be quite independent of others, which may be more connected with texture perception. On the other hand, the spatial number system seems to be closely connected with systems for estimating serially presented number streams, pointing to an abstract number system.

It would seem obvious that the capacity to estimate the number of items—be they fruits, potential mates or lions—is of ecological advantage. It therefore seems reasonable that some human computation capacity is dedicated to this important function. Many works over the past decade or so have defined the limits and in general characterized this system. The next major challenge is to understand how the estimate is done: What are the computational principles and neural substrates?