Identifying gene regulatory network rewiring using latent differential graphical models

Abstract

Gene regulatory networks (GRNs) are highly dynamic among different tissue types. Identifying tissue-specific gene regulation is critically important to understand gene function in a particular cellular context. Graphical models have been used to estimate GRN from gene expression data to distinguish direct interactions from indirect associations. However, most existing methods estimate GRN for a specific cell/tissue type or in a tissue-naive way, or do not specifically focus on network rewiring between different tissues. Here, we describe a new method called Latent Differential Graphical Model (LDGM). The motivation of our method is to estimate the differential network between two tissue types directly without inferring the network for individual tissues, which has the advantage of utilizing much smaller sample size to achieve reliable differential network estimation. Our simulation results demonstrated that LDGM consistently outperforms other Gaussian graphical model based methods. We further evaluated LDGM by applying to the brain and blood gene expression data from the GTEx consortium. We also applied LDGM to identify network rewiring between cancer subtypes using the TCGA breast cancer samples. Our results suggest that LDGM is an effective method to infer differential network using high-throughput gene expression data to identify GRN dynamics among different cellular conditions.

INTRODUCTION

At the level of transcription, gene expression is controlled via transcription factor (TF) proteins that selectively bind to cis-regulatory elements to regulate target genes. There are less than 2000 TFs in the human genome and they work cooperatively to regulate target genes to perform complex cellular functions in specific context (1–3). Such regulatory interactions among TFs and their target genes can be modeled as a gene regulatory network (GRN), where nodes are TFs and their target genes, and edges represent the regulatory relationships. It is acknowledged that gene expression and GRNs are highly dynamic among different tissues (4–6). In other words, some gene regulatory interactions may be very conserved and ubiquitous in different tissue types and many may only occur in certain tissues. Therefore, identifying tissue-specific gene regulation is critically important to understand gene function in a particular cellular context, providing key insights into complex biological systems (7–9). Such knowledge can also help us unravel gene-disease association in a tissue-specific manner (10). In recent years, numerous gene expression data sets across various cell/tissue types and conditions have been collected. For example, the Genotype-Tissue Expression (GTEx) consortium profiled the transcriptomes using RNA-seq over large number of different tissue types in human (5,11) with the advantage of having many biological replicates for each tissue type. Such data provide a great opportunity to more robustly infer tissue-specific GRNs.

To reconstruct GRNs from gene expression data, Gaussian graphical models have been widely used (12–16) (see Materials and Methods section for an introduction). Gaussian graphical models have the advantage of inferring direct dependencies between genes that correspond to edges in the estimated network, while missing edges in the estimated network indicate conditional independence. However, most existing methods estimate a GRN for a specific cell/tissue type or in a tissue-naive way, or do not specifically focus on the network rewiring between different tissues. Therefore, methods for estimating differential networks between two tissue types remain under-explored.

One challenge of using Gaussian graphical model to estimate GRNs in the high dimensional setting (where the number of genes is much greater than the number of samples (p > n)) is that the sample covariance matrix is singular and the estimation of the GRN is impossible unless we make some assumptions on the GRN, e.g. the estimated GRN is sparse and approaches such as (14) have been developed. To estimate the differential network, one straightforward method is to estimate the network of each tissue type separately and then find the difference between the two estimated networks. However, this straightforward procedure does not take full advantage of the similarity shared between GRNs. In addition, in existing Gaussian graphical models, normal distribution is an important assumption for the gene expression values. However, the gene expression values from high-throughput method such as RNA-seq, even after being normalized, do not follow a normal distribution (17,18) (see our own analysis later). As a result, in Gaussian graphical models, the computed sample covariance matrix from gene expression data cannot precisely capture the associations among genes. The motivation of our new method in this work is to estimate the differential network between two tissue types directly without inferring the network for individual tissues, which has the clear advantage of utilizing much smaller sample size to achieve reliable differential network estimation. Importantly, our new method also does not have the normal distribution assumption for gene expression values.

In this paper, we develop a new method to address the following problem of inferring differential networks using graphical models. Instead of assuming that the GRN is sparse, we only assume that the differential network between two tissue types is sparse. This assumption is reasonable and much milder because for many tissue types, the corresponding GRNs are very similar to each other. For example, on average 72.4% of regulatory interactions are shared between any pair of networks from the 41 transcriptional regulatory networks in (4). In particular, we propose to directly estimate the differential network from high-throughput gene expression data. Our new method is called Latent Differential Graphical Model (LDGM). In LDGM, we have two random vectors 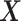and 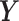that represent gene expression profiles in two networks and follow two different nonparanormal distributions (19,20). More specifically, a random vector 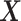is said to follow a nonparanormal distribution, if there exists a set of univariate monotonic functions 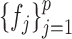such that 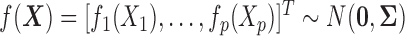with 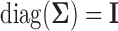. It is denoted by 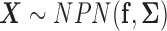, where 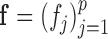. 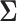is called the latent correlation matrix for 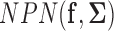. In other words, we assume 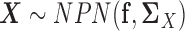and 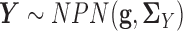, where 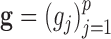. The corresponding latent precision matrices are denoted by 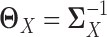and . 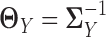Different from other high-dimensional Gaussian graphical model based methods, where we need to assume that 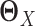and 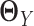are sparse, here we only assume their difference 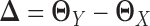is sparse. The key novelty of LDGM is that it directly estimates 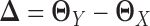from sample latent correlation matrices 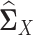and 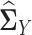by quasi log likelihood function maximization with ℓ₁ norm penalty. Based on our simulation evaluation and real data application, we found that LDGM is a very effective model that can be applied to a wide range of differential network inference scenarios.

Our new method is conceptually different from existing approaches. As mentioned above, our model only assumes that the differential network between two tissue types is sparse, while it needs to be assumed that the GRN itself is sparse in Gaussian graphical model based approaches such as graphical lasso (Glasso) (14), joint graphical lasso (JGL) (16) and co-hub node joint graphical lasso (CNJGL) (15) that we will directly compare performance with in the Results section. Our method is also different from recently developed approaches for constructing tissue-specific networks. In (21), the authors used 987 publicly available genome-scale expression data sets in ∼38 000 conditions to identify tissue-specific networks. However, the method relies on a compiled list of known interactions from databases such as BioGRID and Gene Ontology annotations, while the goal of our method is to estimate the tissue-specific network rewiring only from the gene expression data with the potential to identify novel interactions that have not been annotated. In (22), the authors developed an algorithm called GNAT to derive shared and tissue-specific gene co-expression networks utilizing hierarchy of multiple related tissues. It uses multiple graphical lasso to estimate the precision matrices of Gaussian graphical models on different tissues, and constrains the precision matrices of tissues that were nearby in the hierarchy to have similar entries. When applying the method to two tissues (which is the goal in our work also), the method in GNAT is very similar to JGL with fused lasso penalty (GNAT uses ℓ₂ penalty). Even though the methods developed in (21) and (22) consider related tissues simultaneously to enhance its ability of estimating networks, both of them need to specify reliable tissue relationships or hierarchies. A more relevant work to our method is (23), which was proposed to directly estimate the difference of the precision matrices from two multivariate normal distributions. In contrast, we consider estimating the difference of the latent precision matrices from two nonparanormal distributions. Since nonparanormal distribution is a strictly larger family of distributions including multivariate normal distribution as a special case, our proposed LDGM is more powerful in modeling without the limit of Gaussian data. Moreover, the estimator proposed by (23) is based on estimating equation and solved by linear programming, which is very time consuming in practice (note that we did not compare with (23) in this work because the code from (23) is too slow to be evaluated comprehensively). Our estimator is based on pseudo likelihood and can be solved by accelerated proximal gradient descent efficiently (24). Therefore, our LDGM method not only has unique methodology contribution but also has much broader application potential.

The rest of this paper is organized as follows. We first introduce the details of our LDGM algorithm and the principles of other graphical lasso models in the Materials and Methods section. In the Results section, we first demonstrate the performance of LDGM as compared to other methods on simulated data sets, including JGL and CNJGL. We then evaluate LDGM by applying to the GTEx dataset to identify network rewiring between brain and blood. Finally, we apply LDGM to the TCGA breast cancer samples to study network differences between cancer subtypes.

MATERIALS AND METHODS

Brief introduction on gaussian graphical models

Before we introduce our new method, we first briefly review Gaussian graphical models. In Gaussian graphical model, a p-dimensional random vector 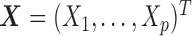follows a multivariate normal distribution 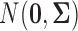. The conditional independence structure of a pair of marginal random variables X_j and X_k is exactly encoded by the precision matrix 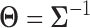(25). More specifically, X_j and X_k are independent conditioned on the other marginal random variables iff Θ_jk = 0. Gaussian graphical models can be used for GRN estimation, where each marginal random variable X_j, 1 ≤ j ≤ p, corresponds to the expression level of a gene, and the edge weight between X_j and X_k is Θ_jk. Therefore, the estimation of GRN can be reduced to the estimation of the precision matrix in Gaussian graphical model. The remaining question is how to estimate based on the covariance matrix 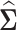. In the high-dimensional setting, the number of genes is much larger than the number of samples, thus the sample covariance matrix 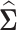is singular and not invertible. In order to overcome this problem, one has to make some assumptions on . For example, we can assume that is sparse. Under the sparsity assumption, graphical lasso (14) was proposed to estimate the sparse precision matrix as follows:

(1)

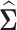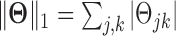where is the sample covariance matrix, λ is a non-negative regularization parameter, Θ_jk is the (j, k)-th element in and is the element-wise ℓ₁ norm of the matrix . The graphical lasso estimator guarantees that the solution is positive definite. Generally, increasing λ will decrease the number of non-zero elements in that makes sparse. In terms of the network, there is only a small number of edges in the corresponding network, i.e. the estimated GRN is sparse. Based on the estimated sparse precision matrix , we can immediately obtain an estimated GRN as follows: if 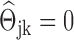, there is no edge between the j-th gene and the k-th gene; if 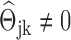, there is an edge between the j-th gene and the k-th gene, and the edge weight is .

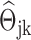Latent differential graphical models (LDGM)

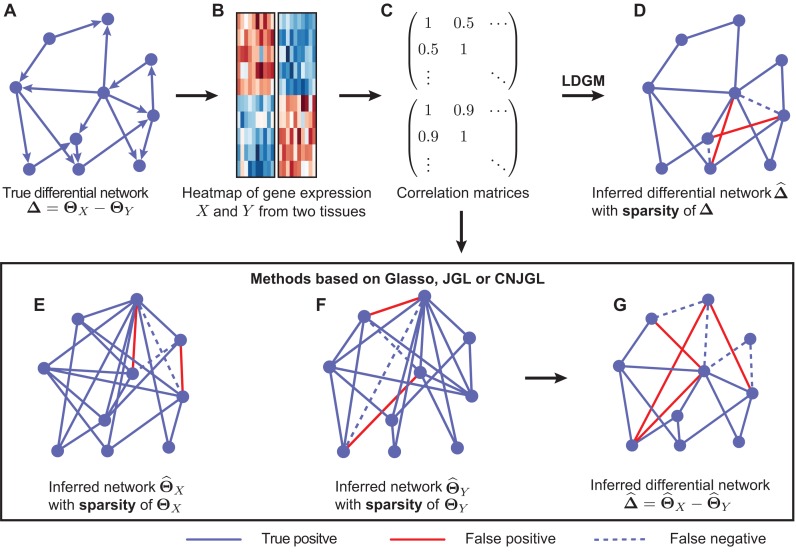
In this paper, we only consider the problem in the context of high-dimensional gene expression data from two different tissue types. In Figure 1, we illustrate the workflow of LDGM and also the key differences between LDGM and other Gaussian graphical model based methods. Let 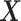and 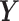be the expression of the p genes in two tissue types. We assume that the gene expression data are sampled from two different nonparanormal distributions (19,20), i.e. 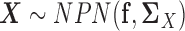and 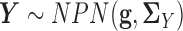. In other words, we consider two nonparanormal graphical models together. As we explained before, GRNs for the two tissue types can be characterized by the latent precision matrix 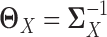and 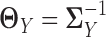, respectively. Some gene regulations are rewired while the other regulatory relationships remain unchanged. These rewired interactions form the differential GRN between the two tissue types. In particular, the differential network can be defined as 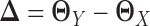(Figure 1A). There is an estimated edge between the j-th gene and the k-th gene in the differential network iff the corresponding element in 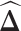, i.e. 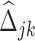, is non-zero. Given the high-dimensional gene expression samples 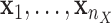of 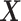, and samples 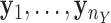of 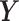(Figure 1B), our goal is to estimate the differential network 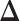. 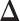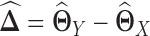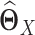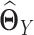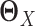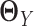A straightforward procedure is to estimate by (Figure 1 G), where and are estimators of and respectively, using (20) introduced before (Figure 1E and F). 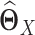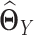However, in order to obtain and , we have to assume that 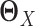and 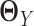are sparse and we need sufficient sample size for both tissue types. The goal of our new method is to significantly relax this assumption. We observe that the differential network between two tissue types is typically more sparse and we only need about half the sample size (as compared to estimating the GRN for individual tissues separately) if we focus on estimating the differential network directly. Based on this key rationale, we propose a novel graphical model named LDGM, for differential network inference. 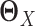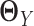In LDGM, instead of assuming that and are sparse, we only assume 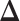is sparse (Figure 1D).

Figure 1.

Illustration of Latent Differential Graphical Model (LDGM) as compared to other graphical model based methods. (A) A toy example of a differential network between two tissues. (B) Gene expression levels of genes X and Y involved in the differential network in two tissues. (C) Sample correlation matrices of gene expression levels in the two tissues. (D) LDGM directly infers the differential network from the two correlation matrices. In contrast, other graphical model based methods (Glasso, JGL or CNJGL) first infer individual gene regulatory networks of tissues (E) X and (F) Y from correlation matrices separately, then infer the differential network by the difference between the (G) two reconstructed networks. Red solid lines represent false positive interactions while blue dashed lines represent false negative interactions in the reconstructed networks.

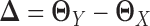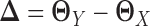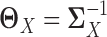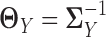LDGM directly models the differential network between two tissue types based on high-throughput gene expression data. To achieve this, we directly estimate based on quasi log likelihood maximization with ℓ₁ norm penalization. Recall that , and , we have:

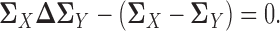(2)

Therefore, a reasonable procedure to estimate 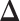is to solve the following estimating equation:

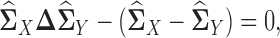(3)

where we replace the population latent correlation matrices 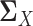and 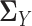in Equation (2) with the sample latent correlation matrices 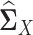and 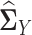, respectively. Note that Equation (3) is a Z-estimator (26). The Z-estimator can be translated into an M-estimator (26) by noticing that 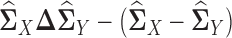can be seen as the score function of the following negative quasi log likelihood function:

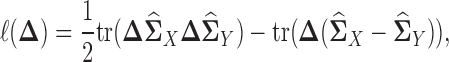(4)

where tr( · ) denotes trace operator of a matrix. Since Equation (4) is the negative quasi log likelihood, we can estimate 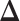by using maximum likelihood principle. Moreover, since we assume 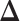is sparse, we can use ℓ₁ norm penalty in addition to the maximum likelihood estimator. This leads to the following ℓ₁ norm penalized M-estimator:

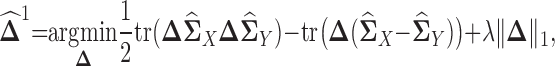(5)

where λ > 0 is a regularization parameter and 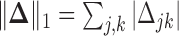is the element-wise ℓ₁ norm of 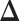that encourages 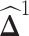to be sparse. Since 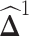is not guaranteed to be symmetric, we symmetrize 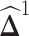by the following procedure (27):

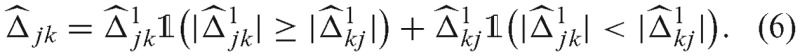
In other words, we take eithe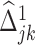r or 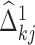depending on whose magnitude is larger. Note that we can also add a constraint such as 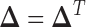in Equation (6) to make 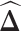symmetric. However, this additional constraint would make the resulting optimization problem more complex and inefficient to solve. The remaining question is how to estimate the latent correlation matrices 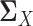and 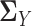, respectively. 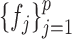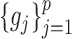Due to the existence of the marginal monotonic transformations and , the estimation of 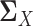and 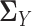depends on the estimation of 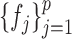and 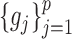. In order to address this challenge, following the idea in (20), instead of estimating 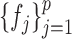, , 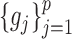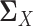and 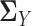simultaneously, we avoid the estimation of 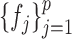, 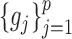by exploiting the relation between the latent correlation matrix and the Kendall tau correlation matrix. In detail, it is shown in (28) that the Kendall tau statistics between X_j and X_k, i.e. denoted by τ_jk, and the Pearson correlation coefficient between X_j and X_k, i.e. Σ_jk, satisfy the following:

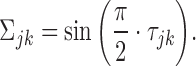To this end, for 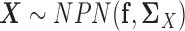, we use the following estimator for the latent correlation matrix :

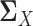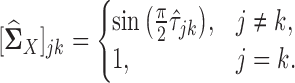(7)

where 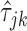is the estimator for the Kendall tau statistic

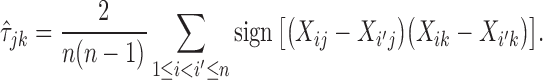Similarly, we can estimate 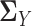in the same way. By plugging the above estimators 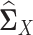and 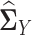into Equation (5), we can estimate 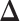directly.

In order to solve Equation (5) efficiently, by some linear algebra identities, we have 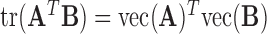and 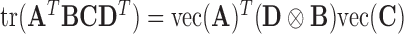for any matrices 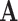, , 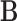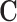and 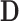with appropriate size. Note that 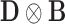is the Kronecker product (29) of matrices 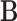and 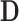. Using these identities, we can rewrite the negative quasi log likelihood in Equation (4) as:

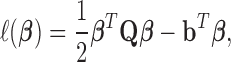(8)

where 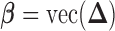, , 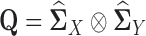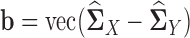. Therefore, the estimator in Equation (5) can be rewritten as:

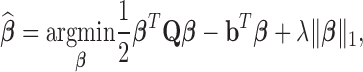(9)

where λ is a non-negative regularization parameter. Increasing λ will make 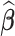sparse. It is worth noting that Equation (9) can be solved by accelerated proximal gradient descent efficiently (24). Given 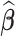, we can obtain 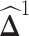immediately by converting 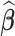back into a matrix. The estimated differential network can be sparse when we properly choose λ. 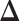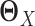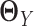Note that when we estimate the differential network directly by Equation (9), we only assume the unknown differential network is sparse and we do not assume individual networks and are sparse. In addition, LDGM only has one regularization parameter to tune. In contrast, if we apply Gaussian graphical models or non-paranormal graphical models to estimate 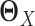and 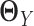separately, we need to tune two regularization parameters, which is less convenient in practice.

Other related works

There are existing methods that estimate the precision matrices of two Gaussian graphical models simultaneously. These methods can be directly applied to gene expression data from two tissue types to estimate the corresponding GRNs. To facilitate the method comparison in the Results section, here we briefly introduce two methods developed by others very recently: JGL with fused lasso penalty function (16) and CNJGL (15). Both methods are able to estimate the precision matrices 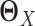and 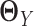of two Gaussian graphical models simultaneously. The key idea of these methods is to borrow information across different cell types when estimating each network that would lead to more accurate estimation than simply estimating each network individually.

JGL encourages network estimates to share similar edges. It estimates the precision matrices of two Gaussian graphical models simultaneously based on penalized joint log likelihood maximization as follows:

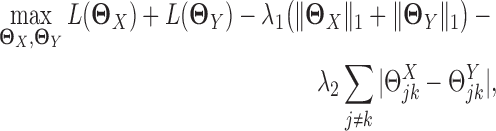(10)

where 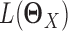is the log likelihood for the Gaussian graphical model on 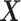, i.e. 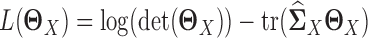, and similarly, 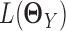is the log likelihood for the Gaussian graphical model on 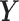. λ₁ and λ₂ are non-negative regularization parameters. Note that the fused lasso penalty 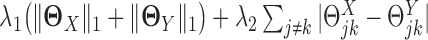has been incorporated to encourage the two networks to share similar edges.

CNJGL estimates the precision matrices of two Gaussian graphical models in a similar way to JGL. The only difference is that instead of using fused lasso penalty, CNJGL uses a penalty that encourages the two precision matrices to have a common set of hub nodes in the networks. In particular, CNJGL estimates the precision matrices based on penalized joint log likelihood maximization as follows:

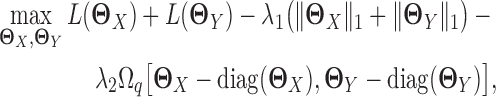(11)

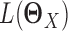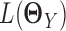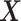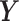where and are the log likelihood for the Gaussian graphical models on and , respectively, and Ω_q is the row-column overlap norm proposed in (15) that encourages network estimates to have a common set of hub nodes.

Note that in this study, when we compare the performance from different methods, we always ran JGL and CNJGL with different λ₂ and reported the best result without explicitly mentioning the corresponding λ₂. For JGL, λ₂ = 1e-04, 1e-03, …, 10. For CNJGL, λ₂ = c × n, where c = 1e-04, 1e-03, …, 10, following (15). The approaches for selecting λ for LDGM and Glasso and λ₁ for JGL and CNJGL are described in Supplementary Text.

Additionally, (23) proposed to directly estimate the difference of two precision matrices from two multivariate normal distributions that is given by the following estimator:

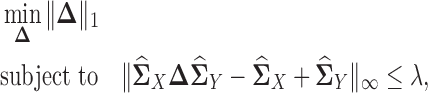(12)

where 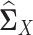and 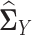are sample covariance matrices for the two multivariate normal distributions, λ > 0 is a tuning parameter.

Methodological comparisons

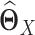Both JGL and CNJGL suffer from the problem that they estimate indirectly. In other words, JGL and CNJGL both first estimate and 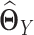separately, and then estimate 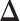by 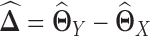(Figure 1E–G). This requires JGL and CNJGL to access twice the number of observations (i.e. sample size) than LDGM, because estimating 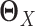and estimating 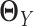individually is as difficult as estimating 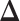. In addition, the assumptions in JGL and CNJGL on network topology similarity between two tissues may not hold in reality for many application settings. For example, the hub nodes in the GRNs in two different tissues may not be the same, which is what CNJGL assumes, because key TF proteins in two tissues could be quite different. The above aspects suggest clear conceptual advantages of LDGM over JGL and CNJGL. On the other hand, the idea of our method is similar to (23). Nevertheless, the method in (23) is limited to multivariate normal distributions, while our method is applicable to the non-paranormal family of distributions that admits multivariate normal distribution as a special case. Furthermore, our estimator in Equation (9) can be solved by accelerated proximal gradient descent efficiently, while the estimator in Equation (12) is a constrained optimization problem, which is computationally very time consuming.

RESULTS

Performance evaluation using simulation

We assessed the performance of LDGM by comparing to Glasso, JGL and CNJGL on simulated data sets. We used huge function with ‘method=glasso’ from the R package huge (30) for Glasso (14). For JGL, we used the JGL function with ‘penalty=fused’ from the R package JGL. We used the CNJGL source code from (15). Note that we did not include the method from (23) in the comparison because their code is too time consuming, making the comprehensive evaluation infeasible.

We first briefly describe our method that generated the sythetic data. In the simulated networks, we set number of nodes p = 50, 100. Network density ρ is defined as the number of edges divided by p × (p − 1)/2. ρ = 0 if no edge is in the graph, ρ = 1 if every pair of nodes are connected by an edge. We chose ρ as individual network sparsity parameter and set ρ = 0.05, 0.1, 0.2, 0.3 in our evaluation. Let ρ₁ be the proportion of edges only found in network G_X when it is compared to network G_Y or only found in G_Y when compared to G_X. When ρ is fixed, the higher ρ₁ is, the more different the networks G_X and G_Y are; so the differential network is denser. We used a combination of ρ and ρ₁ as differential network sparsity parameters. We set ρ₁ = 0.025, 0.05, 0.1. We set sample size n = 100, 200, 300 for p = 50 and n = 200, 300, 400 for p = 100. In order to assess the performance of LDGM and the other graphical models under various individual network sparsity levels, ρ starts from 0.05 to approximately match the average density (0.045) of GRNs reported in (4). Then ρ gradually increases to 0.3 to cover more general network sparsity levels. Sample size n is selected to guarantee that the true differential network structure can be recovered by graphical models under different combinations of p, ρ, ρ₁. To make a fair comparison with the other methods which have a Gaussian assumption, we simulated gene expression samples from multivariate normal distributions. Then we computed sample Pearson correlation matrices as the input for all the methods.

For every combination of p, ρ, ρ₁ and n, we repeated the following steps 30 times:

1. We first generated an undirected scale-free (SF) network G_X (since SF networks and biological networks share many topological properties (31)). We generated another network G_Y in the following way. First we made a copy of G_X, denoted as G_Y. Then we randomly rewired a proportion (ρ₁) of edges in G_Y. At each rewiring step, two edges A–B, C–D were randomly chosen from G_Y and substituted with A–D, C–B if they do not already exist in G_Y.

2. We constructed the precision matrices 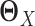and 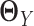separately from adjacency matrices of G_X and G_Y following the method used in (30). We constructed 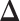by .

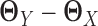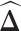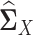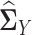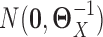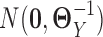3. We applied each of the graphical models to compute from and , which were sample correlation matrices computed from n independent samples drawn from and , respectively.

4. We computed true positive rate (TPR) and recall by TP/(TP + FN), false positive rate (FPR) by FP/(TN + FP), precision by TP/(TP + FP). Here, TP, FP, TN and FN stand for true positives, false positives, true negatives and false negatives, respectively:

   

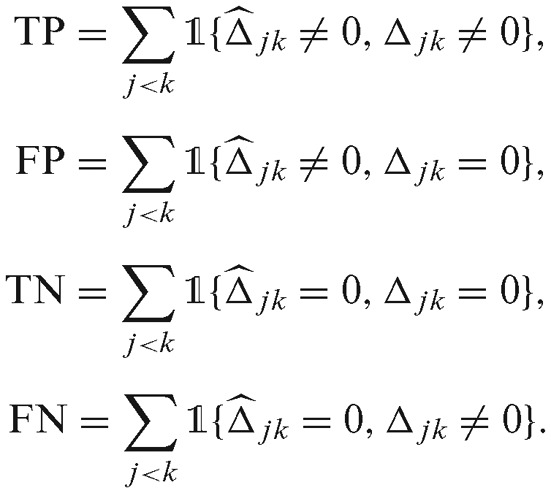
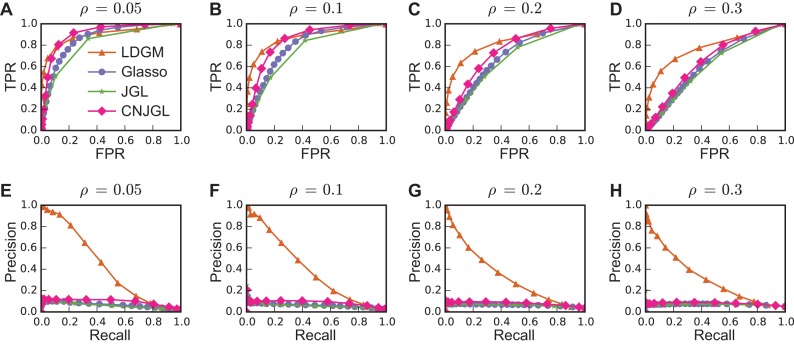
To assess the performance of differential network estimation, we first compared the ROC curves (Figure 2A–D) and precision-recall curves (Figure 2E–F) when ρ is varied with p = 100, n = 300 and ρ₁ = 0.1. Our results suggest that LDGM has clear advantage over other methods in two aspects. First, generally LDGM has better performance based on ROC as compared to other models, and the advantage becomes much clearer when we gradually increase density ρ of G₁ and G₂ (Figure 2A–D). Second, LDGM consistently identifies a remarkably higher proportion of true edges when the estimated differential networks are more sparse, as demonstrated by much larger area under precision-recall curves from LDGM than those from the other models (Figure 2E–H). One main reason for LDGM's better performance is that, as expected, LDGM does not assume individual networks to be sparse while the other graphical models need the sparsity assumption for individual networks.

Figure 2.

Performance of different methods on simulated data with varied individual network density ρ. (A–D) are ROC curves. (E–H) are precision-recall curves. LDGM consistently achieves better performance than other models. Here the proportion of network-specific edges ρ₁ = 0.1, the number of nodes p = 100 and the sample size n = 300. Each curve is the average over 30 runs.

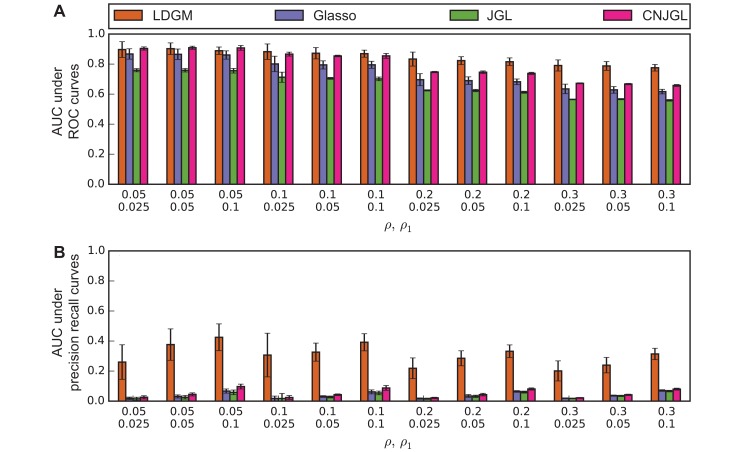
In addition, the advantages of LDGM on differential network estimation were observed over different combinations of parameters. Area-under-the-curve (AUC) under ROC curves (Figure 3A) and under precision-recall curves (Figure 3B) is computed to numerically summarize the performance of a model under a combination of parameters ρ and ρ₁, when p = 100 and n = 300. LDGM has comparable AUC under ROC curves with the other graphical models when ρ = 0.05, 0.1. But when ρ gradually increases from 0.05 to 0.3, LDGM has a larger AUC under ROC curve as compared to other methods and the difference becomes more significant (Figure 3A). Besides, LDGM always has a much larger AUC under precision-recall curves than the other methods, regardless of the values of ρ, ρ₁ (Figure 3B). Furthermore, these advantages of LDGM are robustly held when we vary p, n (Supplementary Figure 1 and Supplementary Figure S2).

Figure 3.

Performance of different methods on simulated data with different ρ and ρ₁ when p = 100, n = 300. (A) AUC under ROC curves. Advantage of LDGM on ROC becomes more visible when differential networks are more dense with an increased network density ρ. (B) AUC under precision-recall curves. LDGM consistently has a much larger AUC under a precision-recall curve than Glasso, JGL and CNJGL. Bar height represents an AUC under an averaged curve over 30 runs. Error bar represents one standard deviation of AUC under 30 replicated curves.

Taken together, our simulation results suggest that LDGM outperforms Glasso, JGL and CNJGL in estimating differential networks. When individual graph density is ρ = 0.05, which is close to the density of regulatory networks in (4), the estimated sparse differential network by LDGM has a significantly higher proportion of true edges than other methods. When individual graph density increases from 0.05 to 0.3 to represent a more general network sparsity level, the quality of inferred differential networks by LDGM is mildly affected. In contrast, the quality by Glasso, JGL and CNJGL are greatly affected. Overall, our simulation results strongly suggest that LDGM can be robustly applied to a wide range of differential network inference scenarios.

Performance evaluation using the GTEx data sets

We further assessed the performance of estimating differential networks by LDGM and the other graphical models on real data. The GTEx project generated RNA-seq expression data for a large number of human tissues (as of October 2015, there are 8020 samples in more than 60 tissues) (11). However, these samples are not evenly distributed across tissues. Some tissues have a large sample size while others have very limited sample size. Generally, a larger sample size improves performance of graphical lasso models. In this analysis, we estimated differential networks between brain and blood using the expression data from GTEx and we utilized the network from (4) as a comparison benchmark.

We downloaded the RPKM expression values from 357 samples across 13 human brain tissues and 191 samples for whole blood (dbGaP Accession phs000424.v4.p1). Since human brain tissues are more closely related when compared to other tissues (22), we treated these 357 samples from brain tissues as samples from the human brain. As a common challenge in evaluating the reconstructed GRNs comprehensively, a gold standard differential network is not available for assessing the accuracy of the inferred differential networks, and high-confidence large-scale GRNs are not available to directly construct a benchmark differential network. However, GRNs constructed from high-throughput experimental TF ChIP-seq or DNase-seq open chromatin data for specific tissue types can be used as reasonable benchmark. We therefore constructed our benchmark network based on GRNs from (4).

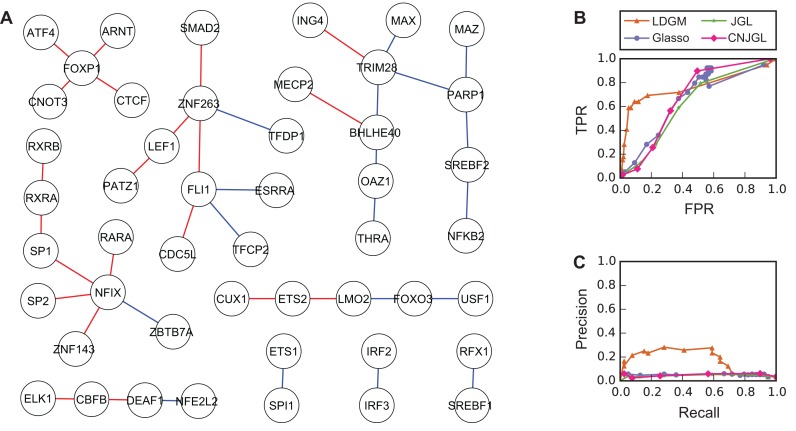
Neph et al. (4) reported the TF regulatory networks of 41 human cell types based on the DNase-seq profiles. There are 7 networks from cell types related to whole blood: B-lymphocyte, B-lymphoblastoid (GM06990 and GM12865), erythroid, haematopoietic stem cell, acute promyelocytic leukemia cell and T-lymphocyte. We constructed the GRN for whole blood from interactions found in at least 6 out of these 7 networks in (4). We also downloaded the brain network. Among the TFs with RPKM >1 in over 80% of the samples in both tissues, 137 TFs are found in both GRNs. These TFs are connected by 2139 interactions that are common in both tissue types, 412 interactions specific to brain and 356 interactions specific to whole blood. To be more conservative, we used the following rule to keep specific interactions in the benchmark network. Given an interaction A–B, we first compute the correlation coefficient of gene expression levels of A and B in brain and whole blood. A–B is kept if the difference between the two correlation coefficients is greater than a threshold (r_b for brain and r_w for blood). The rationale is that a differential interaction A–B indicates that the expression of B is enhanced or inhibited by A only in one tissue. This regulatory relationship changes the expression of B in that tissue, which in turn would change the correlation coefficient between the expression levels of A and B. We set r_b = 0.8 and r_w = 0.7. Eventually in our benchmark network, brain and whole blood have 20 and 19 tissue specific interactions, respectively. A total of 48 TFs are involved in these 39 specific interactions (Figure 4A). We then generated the correlation matrices of expression levels of these TFs based on RPKM values in brain and whole blood, respectively (see Supplementary Text). Methods with varied tuning parameters were applied to the correlation matrices to estimate a series of differential networks. The inferred differential networks were compared to the benchmark network to evaluate the performance of the models.

Figure 4.

Performance of different methods on the GTEx data (brain and whole blood data). (A) The benchmark network with 48 TFs and 39 tissue-specific interactions. Red edges are interactions specific to brain while blue edges are specific to whole blood. (B) ROC curves and (C) Precision-recall curves of different models to recover the benchmark network. Overall, LDGM outperforms the other models. LDGM, Glasso, JGL and CNJGL have AUC under ROC curves of 0.762, 0.593, 0.617, 0.637 and AUC under precision-recall curves of 0.178, 0.044, 0.048, 0.049, respectively.

Overall, LDGM outperforms the other methods, which is consistent with our simulation results. LDGM has a much higher AUC under ROC curve (Figure 4B). The AUC is 0.762, 0.593, 0.617, 0.637 for LDGM, Glasso, JGL and CNGJL, respectively. Besides, LDGM identifies a significantly higher proportion of true edges when the estimated differential networks are sparse, as indicated by a much higher precision than the other models when recall is relatively small (Figure 4C). The AUC under precision-recall curves is 0.178, 0.048, 0.044, 0.049 for LDGM, Glasso, JGL and CNGJL, respectively. Moreover, the advantage of LDGM is always observed when r_b and r_w are varied by setting different benchmark data set with different numbers of TFs and tissue-specific interactions (Supplementary Figure S3 and Supplementary Figure S4).

Applying LDGM to TCGA breast cancer data sets

Breast cancer has been classified into five major subtypes based on gene expression: Luminal A, Luminal B, HER2-enriched, Basal-like and normal-like (32). Luminal A subtype is characterized by high expression of estrogen receptor (ER) pathway genes and low expression of proliferation genes, and is associated with a better prognosis (33). Basal-like subtype mostly consists of triple-negative breast cancer that is characterized by low expression levels of ER, progesterone receptor (PR) and HER2, and high expression of genes associated with cell proliferation, and is associated with a poor prognosis (34). As a proof of principle, we applied LDGM using TCGA data to identify differential network between Luminal A and Basal-like subtypes. LDGM, Glasso, JGL and CNGJL with different tuning parameters were performed to identify a series of differential networks with different sparsity levels. Detailed description of the data used here is in Supplementary Text. Note that from these expression values of the genes, we further confirmed that they typically do not completely follow normal distributions (Supplementary Figure S5 and Supplementary Figure S6).

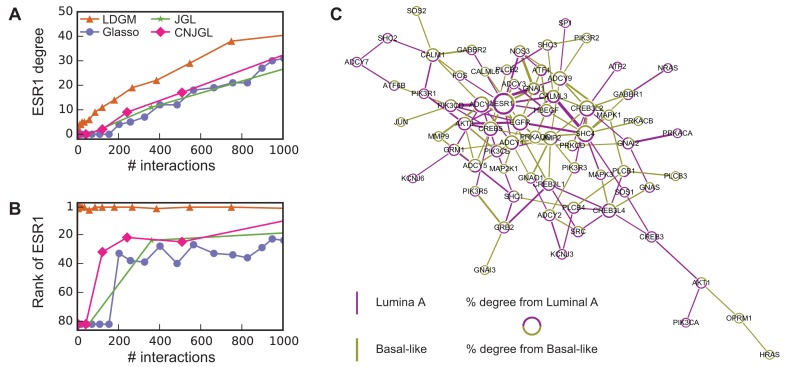
In contrast to the other methods, LDGM consistently identifies ESR1, encoding ER, as one of the genes whose regulatory relationships are rewired greatly between the two subtypes. ER can function as a TF and bind to chromatin directly through estrogen response elements or indirectly by interacting with other TFs, e.g. JUN, SP1, NFKB1. ER can also recruit co-regulators to regulate transcription of target gene expression (35). As demonstrated in Figure 5A and B, ESR1 is consistently among the top genes with highest degrees in differential networks constructed by LDGM. However, it is not among the top 20 genes with highest degrees in differential networks by the other methods. The difference is much greater when the reconstructed networks are more sparse (<150 interactions).

Figure 5.

Differential networks on estrogen signaling pathway reconstructed based on gene expression data from breast cancer Luminal A and Basal-like subtypes. (A) The degree of ESR1 in estimated differential networks with increased number of interactions. (B) The rank of ESR1 by its degree in differential networks. The number of interactions is up to 1000 in (A) and (B). (C) A differential network estimated by LDGM with λ = 0.362. Node size is proportional to the node's degree. Width of an interaction i − j is proportional to the score 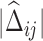. The origin of interactions in the differential network is inferred by a principle of majority approach based on Glasso (see Supplementary Text).

The majority of interactions involved by ESR1 in differential networks by LDGM are from Luminal A subtype, inferred by a principle of majority method based on Glasso (see Supplementary Text). For example, 9 out of 11 interactions involved in ESR1 are from Luminal A subtype in a differential network produced by LDGM with λ = 0.362 (Figure 5C). This observation is consistent with the high expression of ESR1 in Luminal A subtype and low expression of ESR1 in Basal-like subtype.

To further explore the functions of the reconstructed differential interactions, we performed pathway enrichment analysis by DAVID (36,37) on two exclusive sets of genes in the reconstructed differential network by LDGM (shown in Figure 5C). One set of genes contains 31 genes where the majority (>50%) of differential interactions are from Basal-like subtype. These genes are significantly enriched in a pathway cadmium-induced DNA synthesis and proliferation in macrophages (FDR = 1.44E-03), including MAPK1, HRAS, MAP2K1, JUN, PLCB. Another set of genes contains 25 genes where the majority of differential interactions (>50%) are from Luminal A subtype. These genes are enriched with a pathway PTEN-dependent cell cycle arrest and apoptosis (FDR=1.40E-02), including AKT1, SOS1, PIK3CA, SHC1 and PIK3R1. Also, AKT1, PIK3CB and SOS1 are involved in a pathway of inhibition of cellular proliferation. Our results are consistent with the characteristics of Luminal A and Basal-like breast cancer subtypes. For example, proliferation related genes are known to have high expressions in Basal-like subtype and low expressions in Luminal A subtype, and PTEN loss frequently occurs in Basal-like subtype (38). All enriched pathways (FDR < 0.05) are reported in Supplementary Table S1.

In addition, we performed analysis to evaluate the differential network related to ESR1 using ChIP-seq data sets generated in MCF-7 breast cancer cell line which has the luminal phenotype. A total of 54 ChIP-seq experiments on ESR1 from MCF-7 cell line were downloaded from CistromeDB (39,40). A putative target gene of ESR1 in MCF-7 cell lines is defined as a gene where there is at least one ESR1 ChIP-seq peak within 5 kbp of the gene in at least 10 out of 54 ChIP-seq experiments. We found that when ESR1 has at least 10 neighbors, over 50% of the neighboring genes in the differential networks are putative target genes of ESR1 in at least 10 ChIP-seq experiments on MCF-7 (Supplementary Figure S7).

These analyses suggest that LDGM has great potential to identify specific differential networks between different cancer subtypes to help better understand molecular mechanisms of tumor heterogeneity.

DISCUSSION

In this paper, we introduced a new method LDGM to infer differential network among different tissues. The novelty of our method is that we now can estimate the differential network between two tissue types directly, without inferring the network for individual tissues and without assuming normal distribution of the gene expression values. This approach also has a clear advantage of utilizing much smaller sample size to achieve reliable differential network estimation. Unlike other Gaussian graphical model based methods that need to assume the GRN is sparse, our method only assumes that the differential network between two tissue types is sparse. In addition, we do not have the assumption on certain topological similarity of the GRNs between two tissues. For example, some previous graphical model based methods assume that the two GRNs have similar hub nodes (e.g. CNJGL), which do not hold for tissues with very different key regulatory proteins that regulate many downstream genes. Our comprehensive simulation results demonstrated that LDGM consistently outperforms other Gaussian graphical model-based methods. This is further confirmed by the evaluation using GTEx data. Finally, we applied our method to the TCGA breast cancer samples to study network rewiring between cancer subtypes. We demonstrated the potential of LDGM to identify subtype specific network interactions that could provide insight into the molecular mechanisms of inter-tumor heterogeneity.

One limitation of LDGM is that it cannot directly tell which tissue type a differential interaction comes from. However, once LDGM identifies the differential network, we can use other method as a subsequent step to distinguish that. For example, in our analysis of the TCGA breast cancer data, we used a principle of majority method based on Glasso to help infer the origin of a differential interactions. It would be an interesting future work to reconstruct differential interactions and their origin simultaneously.

A common challenge in evaluating GRN inference comprehensively using real data is the lack of gold standard. In this work, we made effort to construct a benchmark differential network when comparing LDGM with graphical model based methods using GTEx data. The benchmark network was from (4) where the authors built the network interactions based on the presence of TF binding site motif within DNaseI hypersensitive sites close to the genes. However, this type of network for the entire transcriptome is reasonable but still not perfect. As a matter of fact, it is not always true that TF A regulates gene B whenever there are binding motifs of A within the promoter regions of gene B. This could also be the reason why the average AUC for LDGM and Glasso in the GTEx evaluation are both not very high, aside from the possibility of tissue variation and difference between the two studies. Nevertheless, with more data from large-scale projects such as the ENCODE project (41) and the Roadmap Epigenomics project (42), we now have access to comprehensive functional genomic profiles to characterize regulatory regions in the human genome across various cell lines and tissues. The data from such high-throughput assays in a given cellular context is very informative to study gene regulation across cell/tissue types even though the sample size for each tissue type is typically very limited. The LDGM method developed in this work may provide a unique way of integrating network inference from large gene expression data sets such as GTEx and regulatory genomics data sets from ENCODE and Roadmap Epigenomics projects to better ascertain the GRN dynamics globally across different tissue types and cell types.

AVAILABILITY OF DATA AND MATERIAL

The source code of our LDGM method can be found at https://github.com/ma-compbio/LDGM.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institutes of Health [HG007352, CA182360 and DK107965 to J.M., in part]; National Science Foundation [1054309 and 1262575 to J.M., in part]. Funding for open access charge: National Science Foundation [1262575].

Conflict of interest statement. None declared.