A Tensegrity Model of Cell Reorientation on Cyclically Stretched Substrates

Abstract

Deciphering the mechanisms underlying the high sensitivity of cells to mechanical microenvironments is crucial for understanding many physiological and pathological processes, e.g., stem cell differentiation and cancer cell metastasis. Here, a cytoskeletal tensegrity model is proposed to study the reorientation of polarized cells on a substrate under biaxial cyclic deformation. The model consists of four bars, representing the longitudinal stress fibers and lateral actin network, and eight strings, denoting the microfilaments. It is found that the lateral bars in the tensegrity, which have been neglected in most of the existing models, can play a vital role in regulating the cellular orientation. The steady orientation of cells can be quantitatively determined by the geometric dimensions and elastic properties of the tensegrity elements, as well as the frequency and biaxial ratio of the cyclic stretches. It is shown that this tensegrity model can reproduce all available experimental observations. For example, the dynamics of cell reorientation is captured by an exponential scaling law with a characteristic time that is independent of the loading frequency at high frequencies and scales inversely with the square of the strain amplitude. This study suggests that tensegrity type models may be further developed to understand cellular responses to mechanical microenvironments and provide guidance for engineering delicate cellular mechanosensing systems.

Introduction

Studies of the active responses of biological cells to external mechanical stimuli are crucial for understanding stem cell differentiation, angiogenesis, invasion, and metastasis of cancer cells (1, 2, 3, 4). For example, experiments have shown that cells align parallel to the stretching direction when the underpinning substrate is subjected to a static stretch (5, 6). In the case of cyclic loads, cells undergo changes in both shapes and orientations, depending on the loading conditions (7, 8, 9, 10, 11, 12). Under uniaxial cyclic stretches, cells align perpendicular to the loading direction at frequencies at ∼1 Hz (7, 8, 9). A few theoretical models based on cytoskeletal stresses (13) and strains (9, 10, 14) have been developed to explain the different orientations of cells in response to static and dynamic loadings. These models suggest that polarized cells tend to align in an orientation that allows them to maintain an optimal stress or strain state. In addition, the dynamical behavior of focal adhesions (FAs) can significantly affect cell reorientation. Kong et al. (15) found that an adhesion cluster is prone to losing its stability under high-frequency loading, because the receptors and ligands do not have enough contact time to form stable bonds due to the high-speed deformation of the substrate. Chen et al. (16, 17) showed that cyclic loadings induce oscillating forces on catch bonds in the FAs and destabilize the latter, thereby reorienting cells toward an orientation with minimal force oscillations.

In many physiological processes (e.g., heart beating, pulsating blood vessels, and breathing), cells and their extracellular matrix are exposed to biaxial cyclic deformations. Jungbauer et al. (11) revealed that the dynamical process of cell reorientation under cyclic stretches follows an exponential law with a characteristic time that decreases with increasing stretch frequency and saturates above a threshold frequency of ∼1 Hz. Recently, Livne et al. (12) demonstrated that cell reorientation under biaxial cyclic stretches can be quantitatively characterized by two parameters: the biaxial ratio of cyclic stretches and the elastic anisotropic index of the cell. The authors showed that their findings are incompatible with existing stress- (13) or strain-based (9, 10, 14) models, and then developed a model based on the passively stored elastic energy in the cell (12). Chen et al. (16, 17) proposed an alternative theoretical model based on the stability of FAs to interpret the experimental data of Livne et al. (12). To date, however, how cellular alignment is precisely regulated, and what mechanistic principles govern the cell’s mechanosensing system, remain elusive.

Here we propose a cytoskeletal tensegrity model of cell reorientation on cyclically stretched substrates. Ingber (18, 19) was the first to model the cytoskeleton as a tensegrity structure. In his theory, cell’s cytoskeletal structure is modeled as a continuous series of strings, bearing only tensile forces, and a discontinuous series of bars that can support both compressive and tensile forces. Using this methodology, Stamenović and Ingber (20) and Ingber (21) illustrated how living cells can utilize a tensegrity structure to respond to mechanical forces at different length scales. In this article, a planar tensegrity model is proposed to study the dynamics of cell reorientation on a substrate under biaxial cyclic stretches. We discuss the common physical mechanisms underlying the similarity of various cell types responding to external mechanical stimuli. It is shown that besides the longitudinal stress fibers (SFs), the lateral actin network also plays a crucial role in cell orientation. Our model is capable of reproducing all existing experimental observations related to cellular orientation dynamics.

Materials and Methods

Free energy difference of the cellular system under biaxial stretches

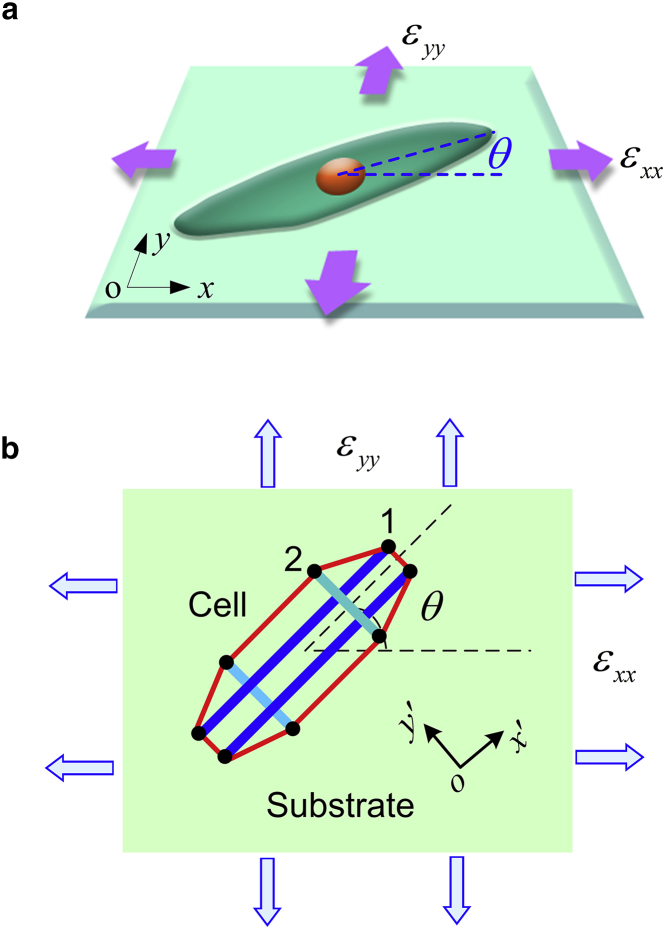
Consider a cell adhering on a substrate subjected to biaxial stretches, as illustrated in Fig. 1 a. Following the convention adopted in experiments (11, 12), the cell orientation, in the range of 0–90°, is defined as the orientation of cell’s long axis with respect to the horizontal stretching direction. We model the cell structure as a planar tensegrity structure consisting of four bars and eight strings (see Fig. 1 b). The direction of cell’s long axis corresponds to the orientation of SFs (10, 12) that are modeled as long bars in the tensegrity. Experiments have shown that the SFs often align parallel to each other within a polarized cell adhering on a substrate (12), and there exists an actin filament network that spans these separated SFs and interconnects them (22). The actin network, acting as the lateral support of the cytoskeletal structure, is modeled as short bars perpendicular to the SF orientation. The strings denote the microfilaments, ensuring the integrity of the whole cellular structure. At the ends of the bars, FAs form as a result of integrin assembly at the cell-substrate interface, providing traction forces for cell mobility. Due to the relatively large deformation in the SFs, the long bars in the tensegrity are assumed to have either linear or nonlinear elastic properties in this study.

Figure 1.

(a) Schematics of a polarized cell adhered on a substrate subjected to biaxial strains ${\epsilon }_{xx}$ and ${\epsilon }_{yy}$. The polarized cell is oriented at angle θ measured from the x direction. (b) The tensegrity model consists of four bars, representing the longitudinal SFs and lateral actin network, and eight strings, denoting the microfilaments. At two ends of bars, the FAs form and provide traction forces for cell mobility. The polarized direction of cells is defined as the orientation of SFs that are modeled as long bars. To see this figure in color, go online.

In this tensegrity model of a cell, the total potential energy $U_e$ includes the elastic energies of the bars, strings, and FAs. It has been demonstrated that a pulling force can strengthen the integrin-mediated FAs of cells (23). Here, we use a thermodynamic model to describe the mechanosensitivity of FAs. The work term $U_f=-f_{\text{pull}}\Delta l$ represents the loss in free energy of FAs under loading, where $\Delta l$ is the stretch of FAs and $f_{\text{pull}}$ is the pulling force induced by the substrate deformation, and this term is identified as an important constituent of the thermodynamic state of FAs (24). Thus, when the substrate is stretched, the variation in the free energy of the cellular system, $\Delta U$, consists of those values associated with the elastic energies of tensegrity elements and FAs, as well as the work done by the applied force, which can be written as

$$\Delta U=\sum _{i=1}^{2}2w_i{L}_i+\sum _{j=1}^8{W}_j^{\left(\text{st}\right)}+2\sum _{i=1}^2{k}_{\text{fa}}\Delta l_i^2-2\Delta f_1\Delta L_{x^{\prime }}-2\Delta f_2\Delta L_{y^{\prime }},$$ (1)

where $w_i$ and $L_i$ are the strain energy density per unit initial length and the initial length of the ith bar, with the subscripts 1 and 2 standing for the $x^{\prime }$ and $y^{\prime }$ directions, respectively; $W_j^{\left(\text{st}\right)}$ is the elastic energy of the jth string; $k_{\text{fa}}=EA/l$ is the spring constant of FAs, with E, A, and l being the Young’s modulus, cross-sectional area, and characteristic size of each FA, respectively; $\Delta l_i$ and $\Delta f_i=k_{\text{fa}}\Delta l_i$ are the changes in lengths and traction forces of FAs, respectively; and $\Delta L_{x^{\prime }}$ and $\Delta L_{y^{\prime }}$ are the length changes of the tensegrity structures along the corresponding directions. The stiffness of microfilaments, modeled as strings, is much smaller than that of SFs, because both microfilaments and SFs are composed of actin filaments and the former has a much smaller cross-sectional area. Thus, we will neglect the contribution of strings, $W_j^{\left(\text{st}\right)}$, to the free energy in this study. The strain energy density $w_i$ of the ith bar depends on its constitutive relation and strain. The lateral support of the cytoskeleton, modeled as short bars, is assumed to be linear elastic, and the strain energy density of the short bar is given as $w_2=C_2{\epsilon }_2^2/2=E_{2}A{\epsilon }_2^2/2$, where $C_2=E_{2}A$, $E_2$ is the Young’s modulus, and ${\epsilon }_2$ is the strain. The strain energy density $w_1$ of the linear or nonlinear long bars (i.e., SFs) will be formulated below.

In the existing stress- and strain-based models (9, 10, 13, 14), the SFs have been assumed to obey a linear elastic constitutive relation. These models can qualitatively predict different cellular orientations under static and cyclic stretches. Besser and Schwarz (25) investigated cellular behaviors under different substrate stiffnesses by using a linear Kelvin-Voigt model of SFs, consisting of a dashpot and a harmonic spring connected in parallel. Besides these linear models, Lazopoulos and Parentis (26) and Lazopoulos and Stamenović (27) developed a nonlinear elastic model of SFs to study cell reorientation under uniaxial stretch. Using this model, they explained the experimental observation (28) that for uniaxial cyclic stretches, the SFs in normal cells were perpendicular to the stretching direction but aligned along the tensile direction when the cells were treated with Rho inhibition. They also discussed the experimental phenomenon (29) that two distinct directions of SFs coexisted in the cells under uniaxial cyclic stretches.

These previous studies suggested that both linear and nonlinear models of SFs can capture some features of cellular response to external loadings. Linear SF models usually make it easier to derive analytical solutions (9, 10, 13, 14, 16, 17). To reveal the general mechanisms underlying cell reorientation, we will first consider linear elastic SFs with the Young’s modulus $E_1$. In this case, the elastic energy of a long bar is expressed as $W_1=w_1{L}_1=K_1\Delta L_1^2/2$, where the spring constant $K_1=E_{1}A/L_1$ and $\Delta L_1=L_1{\epsilon }_1$ with ${\epsilon }_1$ being the strain. Noting that $\Delta L_{x^{\prime }}=\Delta L_1+2\Delta l_1$ and $\Delta L_{y^{\prime }}=\Delta L_2+2\Delta l_2$, Eq. 1 becomes

$$\Delta U=\frac{1}{2}\sum _{i=1}^2\left(2K_i+k_{\text{fa}}\right)\Delta L_i^2-\frac{1}{2}{k}_{\text{fa}}\left[{\left(L_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}^2+{\left(L_{y^{\prime }}{\epsilon }_{y^{\prime }{y}^{\prime }}\right)}^2\right],$$ (2)

where $L_{x^{\prime }}=L_1+2l_1$ and $L_{y^{\prime }}=L_2+2l_2$ are the initial lengths of the tensegrity along the $x^{\prime }$ and $y^{\prime }$ directions, and ${\epsilon }_{x^{\prime }{x}^{\prime }}$ and ${\epsilon }_{y^{\prime }{y}^{\prime }}$ are the corresponding strains. The effects of material nonlinearity of SFs will be discussed in the sequel.

Dynamics of stress fibers

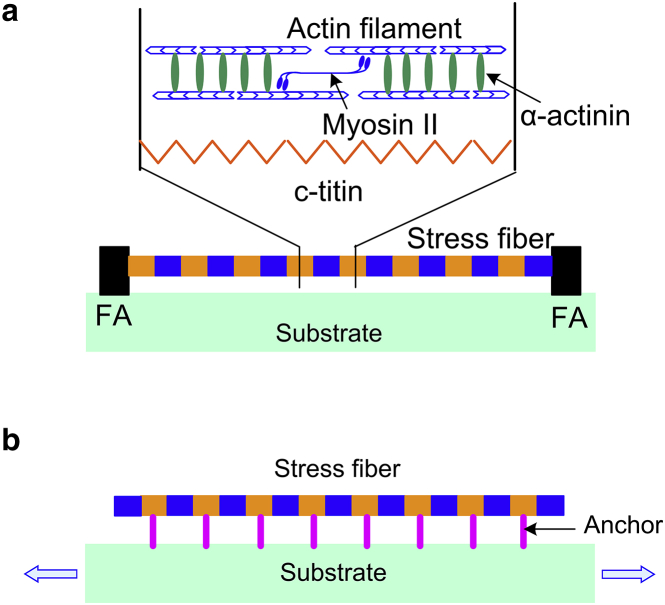
An SF is comprised of a bundle of actin filaments connected by binding proteins (α-actinin), c-titin proteins, and motors (myosin II), as illustrated in Fig. 2 a. The length change of SFs results from both the passive movement of actin filaments and the action of myosin II motors.

Figure 2.

Schematics of a single SF links to the substrate: (a) only via two FAs and (b) via multiple distributed anchors along the actin bundles. As shown in (a), an SF is composed of sarcomeric units in series, including actin filaments, myosin II motors, c-titin, and cross-linker (α-actinin) proteins. The myosin II motors provide the contractive force, and the c-titin proteins connect the adjacent units. To see this figure in color, go online.

First, consider the dynamics of an SF without an active contribution from myosin II motors. The SF consists of repeated sarcomere-like units, whose growth and contraction are driven by actin polymerization and depolymerization, respectively. The actin polymerization rate depends on the resistance force $f_0$ acting on the filament. Following the elastic Brownian ratcheting model (30, 31), one has the relation

$$\frac{\text{d}\Delta L_{\text{u}}}{\text{d}t}=V_{+}\text{exp}\left(-\frac{f_0\delta }{k_{\text{B}}T}\right)-V_{-},$$ (3)

where $\Delta L_{\text{u}}$ is the length change of a sarcomere unit; $V_{+}$ and $V_{-}$ are the free polymerization and depolymerization velocities of actins, respectively; $\delta$ is the size of a single actin; $k_{\text{B}}$ is the Boltzmann constant; and T is the temperature. Before stretching, one has $\text{d}\Delta L_{\text{u}}/\text{d}t=0$ in equilibrium, with $f_0=\left(k_{\text{B}}T/\delta \right)\text{ln}\left(V_{+}/V_{-}\right)$.

When the sarcomere is subjected to an external force $f_{\text{pull}}$, its length change is expressed as

$$\frac{\text{d}\Delta L_{\text{u}}}{\text{d}t}=V_{+}\text{exp}\left(\frac{f_{\text{pull}}-f_0-K_{\text{u}}\Delta L_{\text{u}}}{k_{\text{B}}T}\delta \right)-V_{-}=V_{-}\left[\text{exp}\left(\frac{f_{\text{pull}}-K_{\text{u}}\Delta L_{\text{u}}}{k_{\text{B}}T}\delta \right)-1\right],$$ (4)

where $K_{\text{u}}$ is the spring constant of a sarcomere arising from the elasticity of c-titin proteins that connect the adjacent units. Here the sarcomere is first assumed to be linear elastic, and the effects of nonlinearity will be addressed shortly. The analytical solution of Eq. 4 is

$$\Delta L_{\text{u}}\left(t\right)=\frac{f_{\text{pull}}}{K_{\text{u}}}+\frac{k_{\text{B}}T}{K_{\text{u}}\delta }\text{log}\left\{1-\left[1-\text{exp}\left(-\frac{f_{\text{pull}}\delta }{k_{\text{B}}T}\right)\right]\text{exp}\left(-\frac{t}{{\tau }_{\text{act}}}\right)\right\},$$ (5)

where ${\tau }_{\text{act}}={\left(K_{\text{u}}\delta V_{-}/k_{\text{B}}T\right)}^{-1}$ is a characteristic time for actin binding/unbinding. The Young’s modulus $E_1$ of SFs in endothelial cells is experimentally measured from 5 to 15 kPa (32), and that of SFs in fibroblasts is estimated as 5 kPa (33). The sarcomere length $L_{\text{u}}$ is ∼1 μm (16, 34), and its elastic constant $K_{\text{u}}=E_{1}A/L_{\text{u}}$ is estimated in the range of 0.1–1 $\text{pN}/\text{nm}$ with cross-sectional area $A=0.1\mu {\text{m}}^2$. Using $\delta =2.7\text{nm}$ and $V_{-}=2.2\text{nm}/\text{s}$ (31), the relaxation time ${\tau }_{\text{act}}$ is estimated to be 1–10 s. If $t>>{\tau }_{\text{act}}$, Eq. 5 becomes

$$\Delta L_{\text{u}}\left(t\right)=\frac{f_{\text{pull}}}{K_{\text{u}}}-\frac{k_{\text{B}}T}{K_{\text{u}}\delta }\left[1-\text{exp}\left(-\frac{f_{\text{pull}}\delta }{k_{\text{B}}T}\right)\right]\text{exp}\left(-\frac{t}{{\tau }_{\text{act}}}\right).$$ (6)

This equation indicates that the SF behaves like a viscoelastic material. Its viscous property stems from actin binding and unbinding, and the associated viscosity ${\eta }_{\text{act}}=K_{\text{u}}{\tau }_{\text{act}}=k_{\text{B}}T/\left(\delta V_{-}\right)$ is estimated to be in the order of 1.0 $\text{pN}\cdot \text{s}/\text{nm}$.

Next, consider the active contractility of a sarcomere arising from the activity of myosin II motor proteins. Let $f_{\text{myo}}$ denote the force applied on the actin filament by molecular motors with contracting velocity $V_{\text{myo}}$. Following Hill’s law (35), one has

$$f_{\text{myo}}=f_{\text{s}}\left(1-\frac{V_{\text{myo}}}{V_{\text{s}}}\right)=f_{\text{s}}-{\eta }_{\text{myo}}{V}_{\text{myo}},$$ (7)

where $V_{\text{s}}$ is the zero-load velocity of the motor, which is ∼0.3 $\mu \text{m/s}$ (36); $f_{\text{s}}$ is the stall force estimated to be hundreds of piconewtons, which is provided by tens of myosin motors with a few pN per myosin head (37); and ${\eta }_{\text{myo}}=f_{\text{s}}/V_{\text{s}}$ represents the viscosity of motor movements (∼$1\text{pN}\cdot \text{s}/\text{nm}$), which is comparable to the viscosity ${\eta }_{\text{act}}$ due to actin binding/unbinding.

Noting the contracting velocity $V_{\text{myo}}=-\text{d}\Delta L_{\text{u}}/\text{d}t$, the length change of a sarcomere can be described by differential equation

$$\left({\eta }_{\text{act}}+{\eta }_{\text{myo}}\right)\frac{\text{d}\Delta L_{\text{u}}}{\text{d}t}+K_{\text{u}}\Delta L_{\text{u}}=f_{\text{pull}}-f_{\text{s}},$$ (8)

with the initial condition ${\Delta L_{\text{u}}|}_{t=0}=0$. The solution to Eq. 8 is

$$\Delta L_{\text{u}}\left(t\right)=\frac{f_{\text{pull}}-f_{\text{s}}}{K_{\text{u}}}\left[1-\text{exp}\left(-\frac{t}{{\tau }_{\text{u}}}\right)\right],$$ (9)

where ${\tau }_{\text{u}}={\eta }_{\text{u}}/K_{\text{u}}$ denotes the characteristic time of a sarcomere relaxation with ${\eta }_{\text{u}}={\eta }_{\text{act}}+{\eta }_{\text{myo}}$ being the viscosity coefficient. Because an SF is composed of sarcomeric units in series, its elasticity and viscosity coefficients are $K_1=K_{\text{u}}/N_{\text{u}}$ and ${\eta }_1={\eta }_{\text{u}}/N_{\text{u}}$, respectively, where $N_{\text{u}}$ is the number of sarcomeres in the SF. Therefore, as observed in the experiment of Kumar et al. (38), the SFs can be described by a viscoelastic model, consisting of a spring of stiffness $K_1$, a dashpot of effective viscosity ${\eta }_1$, and a contractive stall force $f_{\text{s}}$. Based on the above analysis, the characteristic relaxation time ${\tau }_1={\eta }_1/K_1$ of an SF is estimated to be in the range of 1–10 s.

Effects of distributed anchors of stress fibers

It is worth mentioning that in cells, an SF may link to the substrate via multiple distributed anchors along the actin bundles (39), as illustrated in Fig. 2 b. Here, we compare the expression for the free energy of an SF anchored by multiple distributed anchors with that for an SF anchored only by two focal adhesions, as in our tensegrity model.

Suppose that the deformation of each sarcomere-like unit in an SF is homogeneous. Analogous to the derivation of the free energy difference of a whole SF, the free energy difference of each sarcomere-like unit after the stretch can be described by

$$\Delta U_{\text{u}}=\frac{1}{2}\left(2K_{\text{u}}+k_{\text{anchor}}\right)\Delta L_{\text{u}}^2-\frac{1}{2}{k}_{\text{anchor}}{\left(L_0{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}^2,$$ (10)

where $k_{\text{anchor}}$ is the spring constant of a linked anchor, and $L_0$ is the initial distance between two neighboring anchors on the substrate. The free energy difference of an SF is the summation of all sarcomere units

$$\Delta U_1=N_{\text{u}}\Delta U_{\text{u}}=\frac{1}{2}\left(2K_{\text{u}}+k_{\text{anchor}}\right)N_{\text{u}}\Delta L_{\text{u}}^2-\frac{1}{2}{k}_{\text{anchor}}{N}_{\text{u}}{\left(L_0{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}^2.$$ (11)

Note that the initial length between two anchors at the SF ends is $L_{x^{\prime }}=N_{\text{u}}{L}_0$. Using the relation $K_1=K_{\text{u}}/N_{\text{u}}$, Eq. 11 is reexpressed as

$$\Delta U_1=\frac{1}{2}\left(2K_1+\frac{k_{\text{anchor}}}{N_{\text{u}}}\right)\Delta L_1^2-\frac{k_{\text{anchor}}}{2N_{\text{u}}}{\left(L_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}^2.$$ (12)

In our tensegrity model, the SF is linked to the substrate via two FAs. As described in the previous section, the free energy change of the SF due to stretch can be written as

$$\Delta U_1=\frac{1}{2}\left(2K_1+k_{\text{fa}}\right)\Delta L_1^2-\frac{1}{2}{k}_{\text{fa}}{\left(L_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }}\right)}^2.$$ (13)

It can be seen that Eqs. 12 and 13 have the same form when $k_{\text{anchor}}=N_{\text{u}}{k}_{\text{fa}}$. If the Young’s moduli of the anchors and FAs are the same, the relation $k_{\text{anchor}}=N_{\text{u}}{k}_{\text{fa}}$ holds for $l_{\text{anchor}}=l_{\text{fa}}/N_{\text{u}}$. Because the sizes of the anchors $\left(l_{\text{anchor}}\right)$ and FAs $\left(l_{\text{fa}}\right)$ are ∼0.1 μm (40) and a few micrometers (41), respectively, and $N_{\text{u}}$ = 50 (16), one might expect that $l_{\text{anchor}}\propto l_{\text{fa}}/N_{\text{u}}$ and in turn, $k_{\text{anchor}}\propto N_{\text{u}}{k}_{\text{fa}}$. In this case, the free energy change of an SF with multiple distributed anchors would be comparable to that of an SF supported by two FAs. Therefore, our conclusions from the tensegrity model should hold approximately even when the SFs are supported by multiple distributed anchors.

Results and Discussion

Steady cellular orientations under biaxial static stretches

We first examine the case when the substrate is subjected to a biaxial static stretch. As shown in Fig. 1 b, the strains in the x and y directions are denoted as ${\epsilon }_{xx}={\epsilon }_0$ and ${\epsilon }_{yy}=-\nu {\epsilon }_{xx}$, respectively, where ${\epsilon }_0$ is the strain amplitude and ν is the biaxial ratio. The strains in the $x^{\prime }$ and $y^{\prime }$ directions are ${\epsilon }_{x^{\prime }{x}^{\prime }}={\epsilon }_{xx}\left({\text{cos}}^2\theta -\nu {\text{sin}}^2\theta \right)$ and ${\epsilon }_{y^{\prime }{y}^{\prime }}={\epsilon }_{xx}\left({\text{sin}}^2\theta -\nu {\text{cos}}^2\theta \right)$, respectively. Using the force balance and displacement constraint conditions, the length changes of bars in the longitudinal and lateral directions are $\Delta L_1=k_{\text{fa}}{L}_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }}/\left(k_{\text{fa}}+2K_1\right)$ and $\Delta L_2=k_{\text{fa}}{L}_{y^{\prime }}{\epsilon }_{y^{\prime }{y}^{\prime }}/\left(k_{\text{fa}}+2K_2\right)$, respectively. The free energy change $\Delta U$ in Eq. 2 is

$$\Delta U=-\frac{k_{\text{fa}}{K}_1}{k_{\text{fa}}+2K_1}{L}_{x^{\prime }}^2{\epsilon }_{x^{\prime }{x}^{\prime }}^2-\frac{k_{\text{fa}}{K}_2}{k_{\text{fa}}+2K_2}{L}_{y^{\prime }}^2{\epsilon }_{y^{\prime }{y}^{\prime }}^2.$$ (14)

Experiments have shown that the Young’s modulus of FAs is ∼5.5 kPa (41), and that of SFs is in the range 5–15 kPa (32). For convenience, we assume FAs, long and short bars in the tensegrity, have the same Young’s modulus E. Similar analysis can be made when their Young’s moduli are different without changing the main conclusions. The characteristic size of FAs falls in the range of a few micrometers (12, 41), and the bars in the tensegrity are approximately tens of micrometers in length (10, 12). Hence, it is known from the relation $K=EA/L$ that $k_{\text{fa}}>>K_1$ and $k_{\text{fa}}>>K_2$. Thus, Eq. 14 can be simplified as

$$\Delta U=-K_1{L}_{x^{\prime }}^2{\epsilon }_0^2{\left({\text{cos}}^2\theta -\nu {\text{sin}}^2\theta \right)}^2-K_2{L}_{y^{\prime }}^2{\epsilon }_0^2{\left({\text{sin}}^2\theta -\nu {\text{cos}}^2\theta \right)}^2.$$ (15)

From $\partial \Delta U/\partial \theta =0$, we obtain three possible steady-state orientations: two limiting values $\overline{\theta }=0$ and $\pi /2$, and one intermediate value ${\text{cos}}^{-1}\sqrt{\left(\left({\xi }_2+\nu {\xi }_1\right)/\left(\left(1+\nu \right)\left({\xi }_1+{\xi }_2\right)\right)\right)}$, where ${\xi }_1=K_1{L}_{x^{\prime }}^2$ and ${\xi }_2=K_2{L}_{y^{\prime }}^2$. Among the three solutions, there is only one stable state with minimum free energy. The steady cell orientation is determined to be $\overline{\theta }=0$ when ${\xi }_1>{\xi }_2$ and $\overline{\theta }=\pi /2$ otherwise. Because the bar in the polarized direction is longer than that in the lateral direction, we have ${\xi }_1>{\xi }_2$, and thus, the cell will align with the stretching direction (i.e., $\overline{\theta }=0$), in agreement with experimental results (5, 6).

Steady cellular orientations under biaxial cyclic stretches

In the following subsections, we investigate the response of cells to biaxial cyclic strains with ${\epsilon }_{xx}=0.5{\epsilon }_0\left(1-\text{cos}\omega t\right)$ and ${\epsilon }_{yy}=-\nu {\epsilon }_{xx}$, where ${\epsilon }_0$ and ω are the strain amplitude and frequency, respectively. In the longitudinal direction, the force balance and displacement constraint conditions are ${\eta }_1\text{d}\Delta L_1/\text{d}t+K_1\Delta L_1=k_{\text{fa}}\Delta l_1$ and $\Delta L_1+2\Delta l_1=L_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }}$, respectively. Then the dynamics of SFs can be described by

$$2{\eta }_1\frac{\text{d}\Delta L_1}{\text{d}t}+\left(2K_1+k_{\text{fa}}\right)\Delta L_1=k_{\text{fa}}{L}_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }}.$$ (16)

The solution to above is

$$\Delta L_1=\left[\frac{k_{\text{fa}}}{k_{\text{fa}}+2K_1}-\frac{k_{\text{fa}}\left(\text{cos}\omega t+\omega /{\omega }_1\text{sin}\omega t+e^{-{\omega }_{1}t}{\omega }^2/{\omega }_1^2\right)}{\left(k_{\text{fa}}+2K_1\right)\left(1+{\omega }^2/{\omega }_1^2\right)}\right]L_{x^{\prime }}{\epsilon }_{x^{\prime }{x}^{\prime }},$$ (17)

where ${\omega }_1=\left(k_{\text{fa}}+2K_1\right)/2{\eta }_1$ is the characteristic frequency of the system in the $x^{\prime }$ direction. Note that $\Delta L_2$ can be easily calculated by using the force balance and displacement constraint conditions in the $y^{\prime }$ direction. Because the term $\text{exp}\left(-{\omega }_{1}t\right)$ approaches zero when $t\to \infty$, the free energy change $\Delta U$ per period T is

$$\Delta U=\frac{1}{T}{\int }_0^T\Delta U\left(t\right)\text{d}t={\xi }_{x^{\prime }{x}^{\prime }}{\epsilon }_0^2{\left({\text{cos}}^2\theta -\nu {\text{sin}}^2\theta \right)}^2-{\xi }_{y^{\prime }{y}^{\prime }}{\epsilon }_0^2{\left({\text{sin}}^2\theta -\nu {\text{cos}}^2\theta \right)}^2,$$ (18)

where

$$\begin{array}{c}{\xi }_{x^{\prime }{x}^{\prime }}=\frac{1}{16}{k}_{\text{fa}}{L}_{x^{\prime }}^2\left[\frac{4k_{\text{fa}}}{k_{\text{fa}}+2K_1}-3-\frac{k_{\text{fa}}/\left(k_{\text{fa}}+2K_1\right)}{1+{\left(\omega /{\omega }_1\right)}^2}\right]\\ =\frac{1}{16}{k}_{\text{fa}}{L}_{x^{\prime }}^2\left[1-\frac{1}{1+{\left(\omega /{\omega }_1\right)}^2}\right],\end{array},$$ (19)

$${\xi }_{y^{\prime }{y}^{\prime }}=\frac{3}{8}{K}_2{L}_{y^{\prime }}^2.$$ (20)

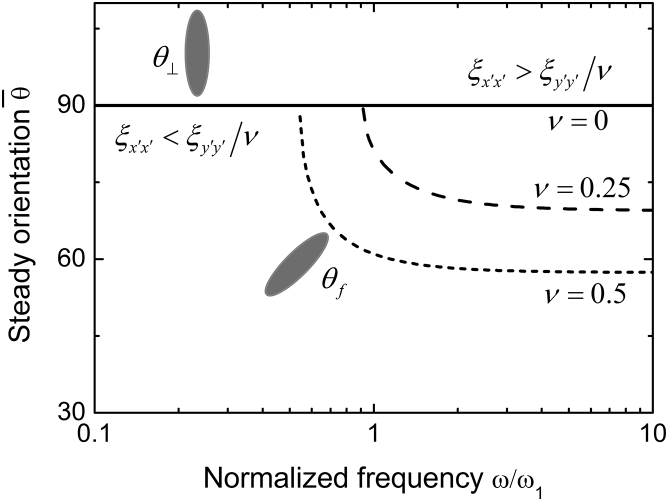
In Eq. 19, we have assumed $k_{\text{fa}}>>K_1$ because the SF length $L_1$ is much larger than the FA size $l_1$. From $\partial \Delta U/\partial \theta =0$, one finds three possible steady-state orientations: $\overline{\theta }=0$, $\pi /2$, and ${\theta }_f={\text{cos}}^{-1}\sqrt{\left({\xi }_{x^{\prime }{x}^{\prime }}\nu -{\xi }_{y^{\prime }{y}^{\prime }}\right)/\left(\left(1+\nu \right)\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right)\right)}$. Minimizing $\Delta U$ among the three possible states leads to the stable orientation $\overline{\theta }$ in a wide range of normalized frequency $\omega /{\omega }_1$, as shown in Fig. 3. When the frequency is low, we find $\overline{\theta }=\pi /2$, meaning that the cell is perpendicular to the stretching direction. As the frequency increases, the stable orientation becomes ${\theta }_f$, which depends on the biaxial ratio ν, the elastic constants, and geometric sizes of the cellular elements.

Figure 3.

Steady cell orientation $\overline{\theta }$ as a function of the normalized frequency $\omega /{\omega }_1$ at three values of ν under biaxial cyclic loads. The curve can be divided into two regimes, corresponding to ${\theta }_{\perp }={90}^{\circ }$ (solid line) and ${\theta }_f={\text{cos}}^{-1}\sqrt{\left(\left({\xi }_{x^{\prime }{x}^{\prime }}\nu -{\xi }_{y^{\prime }{y}^{\prime }}\right)/\left(\left(1+\nu \right)\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right)\right)\right)}$ (dashed line), respectively.

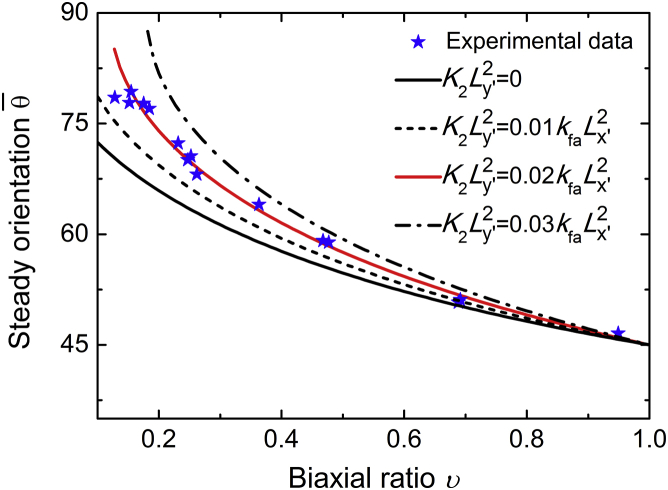
When $\omega >{\omega }_1$, the SFs cannot follow the rapidly changing strain, because the rate of their length change is limited by the rates of actin binding/unbinding and the viscosity of molecular motors. If ω is much higher than ${\omega }_1$, one has ${\xi }_{x^{\prime }{x}^{\prime }}=k_{\text{fa}}{L}_{x^{\prime }}^2/16$ and ${\theta }_f$ approaches a constant at a given biaxial ratio (see Fig. 3). Letting $b={\xi }_{x^{\prime }{x}^{\prime }}/\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right)$ leads to the relation ${\text{cos}}^2{\theta }_f=\left[\left(\nu -1\right)b+1\right]/\left(1+\nu \right)$, which is identical to the expression used by Livne et al. (12) to fit their experimental data. Their experimental results suggested b = 1.13, corresponding to $K_2{L}_{y^{\prime }}^2=0.02k_{\text{fa}}{L}_{x^{\prime }}^2$ in this tensegrity model. Because $k_{\text{fa}}>>K_2$ and $L_{x^{\prime }}>L_{y^{\prime }}$, it seems reasonable that the effective longitudinal stiffness $k_{\text{fa}}{L}_{x^{\prime }}^2$ is much larger than the effective lateral stiffness $K_2{L}_{y^{\prime }}^2$. If the effect of the lateral stiffness is omitted, one obtains b = 1 and ${\text{cos}}^2{\theta }_f=\nu /\left(1+\nu \right)$, which is identical to the predictions from the minimal strain model (9, 10, 14). Fig. 3 also shows that if ν = 0, the cell will always align perpendicular to the stretching direction, in consistency with experimental observations of cell orientations on a substrate under pure uniaxial stretch (9). Fig. 4 plots the steady cell orientation as a function of biaxial ratio $\nu$ under different values of $K_2{L}_{y^{\prime }}^2$. It can be seen that a little change in $K_2{L}_{y^{\prime }}^2$ can significantly affect the final cellular orientation. Therefore, $K_2{L}_{y^{\prime }}^2$, which is much smaller than $k_{\text{fa}}{L}_{x^{\prime }}^2$ and has been neglected in most of the existing models (9, 10, 13, 14, 15, 16), can play a significant role in determining cell orientation.

Figure 4.

Steady cell orientation $\overline{\theta }$ as a function of the biaxial ratio ν at four values of effective stiffness $K_2{L}_{y^{\prime }}^2$ under cyclic loads. The theoretical results fit well with the experimental data of Livne et al. (12) at $K_2{L}_{y^{\prime }}^2=0.02k_{\text{fa}}{L}_{x^{\prime }}^2$. To see this figure in color, go online.

Effect of substrate stiffness on steady cellular orientations

To account for the effect of substrate stiffness, we use an effective elastic constant ${\left(k_{\text{fa}}^{\text{eff}}\right)}^{-1}=k_{\text{fa}}^{-1}+k_{\text{sub}}^{-1}$ of FAs to describe the elasticity of FA-substrate system, where $k_{\text{sub}}$ denotes the elastic stiffness of the substrate. The parameter $k_{\text{fa}}$ in the expression of ${\xi }_{x^{\prime }{x}^{\prime }}$ is replaced by $k_{\text{fa}}^{\text{eff}}$. For a very soft substrate, the term $k_{\text{fa}}^{\text{eff}}/\left(k_{\text{fa}}^{\text{eff}}+2K_1\right)$ in Eq. 19 is very small, and ${\xi }_{x^{\prime }{x}^{\prime }}$ and $\Delta U$ are negative. In this case, the cell prefers $\overline{\theta }=0$, as in the case of a static stretch. When the substrate is stiff, $k_{\text{fa}}^{\text{eff}}$ is dominated by the elasticity of FAs, and the cell prefers the orientation ${\theta }_f$ under biaxial cyclic stretches and $\overline{\theta }=\pi /2$ under uniaxial cyclic stretches at high frequencies, as discussed above. This result is in accord with recent experiments of Tondon and Kaunas (42), who observed that cells align perpendicular to the stretch direction on a stiff substrate but parallel to the stretch direction on a very soft substrate. It is worth noting that if the substrate is very soft, the characteristic frequency ${\omega }_1=\left(k_{\text{fa}}^{\text{eff}}+2K_1\right)/2{\eta }_1$ of the cell-substrate system will be small, indicating that the system becomes obtuse to dynamic loads.

Rotational dynamics of cell reorientation

From a phenomenological point of view, the rotational dynamics of cell orientations can be described as $\text{d}\theta /\text{d}t=-\text{d}\Delta U/{\eta }_R\text{d}\theta$ (12, 13), where ${\eta }_R$ denotes the viscous coefficient. Using the expression of $\Delta U$ in Eq. 18, one obtains

$$\frac{\text{d}\theta }{\text{d}t}=\frac{2\left(1+\nu \right){\epsilon }_0^2}{{\eta }_R}\text{sin}\left(2\theta \right)\left[{\xi }_{x^{\prime }{x}^{\prime }}\left({\text{cos}}^2\theta -\nu {\text{sin}}^2\theta \right)+{\xi }_{y^{\prime }{y}^{\prime }}\left({\text{sin}}^2\theta -\nu {\text{cos}}^2\theta \right)\right],$$ (21)

which can be rewritten as

$$\frac{\text{d}\theta }{\text{d}t}=\frac{2\left(1+\nu \right){\epsilon }_0^2}{{\eta }_R}\text{sin}\left(2\theta \right)\left[\left(1+\nu \right)\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right){\text{cos}}^2\theta +{\xi }_{y^{\prime }{y}^{\prime }}-\nu {\xi }_{x^{\prime }{x}^{\prime }}\right].$$ (22)

With the notation $b={\xi }_{x^{\prime }{x}^{\prime }}/\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right)$, the above equation becomes

$$\frac{\text{d}\theta }{\text{d}t}=\frac{2\left(1+\nu \right){\xi }_{x^{\prime }{x}^{\prime }}{\epsilon }_0^2}{{\eta }_R}\text{sin}\left(2\theta \right)\left[\frac{\left(1+\nu \right){\text{cos}}^2\theta -1}{b}+1-\nu \right].$$ (23)

Under high loading frequencies, ${\xi }_{x^{\prime }{x}^{\prime }}$ approaches a constant. If we let ${\xi }_{x^{\prime }{x}^{\prime }}=3K/8b$, Eq. 23 is exactly the same as the equation used by Livne et al. (12) to fit their experimental data. It is interesting to note that Livne et al. (12) modeled the cell as a two-dimensional anisotropic continuum, with parameters K and b depending on cell’s anisotropic elastic constants, while we treat it here as a discretized tensegrity structure, yet the two models predict the same results of cell reorientation at high frequencies. Moreover, our model can also predict the dynamics of cell reorientation in the cases of lower frequencies and static stretches, which have not been addressed in the model of Livne et al. (12).

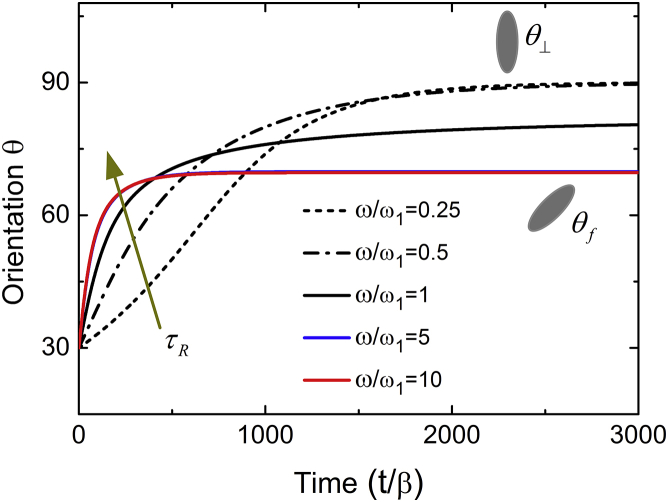
For five representative frequencies, Fig. 5 plots the cell orientation as a function of time. When the frequency is low (e.g., $\omega /{\omega }_1=0.25$ or 0.5), the orientation angle first increases and then approaches ${\theta }_{\perp }={90}^0$. As the frequency increases, the cell rotates toward the orientation angle ${\theta }_f$. For higher frequencies (e.g., $\omega /{\omega }_1=5$ and 10), ${\theta }_f$ becomes a constant and the rotational process is almost independent of $\omega /{\omega }_1$. It can be seen from Fig. 5 that the characteristic time of cell rotation decreases with increasing frequency and saturates beyond a threshold frequency, in agreement with experimental observations (11).

Figure 5.

Rotational dynamics of cell reorientation at different frequencies under cyclic loads. The two curves under high frequencies of $\omega /{\omega }_1=5$ and 10 are identical. The arrow means the characteristic time τ_R of cell rotation decreases with increasing the frequency and saturates at a high frequency. The time is scaled by the parameter $\beta =8{\eta }_R/K_{\text{fa}}{L}_{x^{\prime }}^2$. Here, we take ν = 0.25 and ε₀ = 10%. To see this figure in color, go online.

Multiplying Eq. 22 by $\text{sin}\left(2\theta \right)$ on both sides leads to

$$\frac{\text{dcos}2\theta }{\text{d}t}=-\frac{2\left(1+\nu \right){\epsilon }_0^2}{{\eta }_R}\left[\left(1-\nu \right)\left({\xi }_{x^{\prime }{x}^{\prime }}+{\xi }_{y^{\prime }{y}^{\prime }}\right)+\left(1+\nu \right)\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right)\text{cos}2\theta \right]+o\left({\text{cos}}^{2}2\theta \right).$$ (24)

Neglecting the quadratic and higher-order terms of $\text{cos}2\theta$, we obtain an analytical solution

$$\text{cos}2\theta =\text{cos}2\overline{\theta }+\left(\text{cos}2{\theta }_0-\text{cos}2\overline{\theta }\right)\text{exp}\left(-t/{\tau }_R\right),$$ (25)

where ${\theta }_0$ is the cell orientation at the onset of stretching, $\overline{\theta }$ is the stable orientation, and ${\tau }_R$ is the characteristic time of rotational dynamics

$${\tau }_R=\frac{{\eta }_R}{2{\left(1+\nu \right)}^2\left({\xi }_{x^{\prime }{x}^{\prime }}-{\xi }_{y^{\prime }{y}^{\prime }}\right){\epsilon }_0^2}.$$ (26)

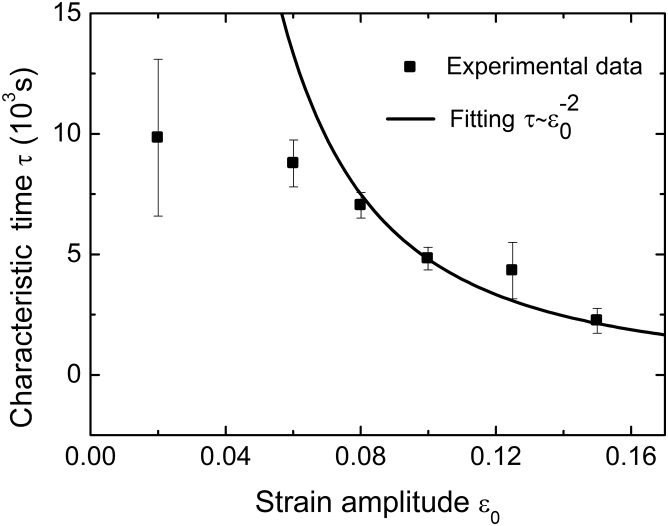
Equation 25 provides a concise description of the dynamics of cell reorientation on a stretched substrate, which has been used previously to fit the dynamics of cell orientation in experiments (11). As mentioned in Materials and Methods, the characteristic frequency ${\omega }_1=\left(K_{\text{fa}}+2K_1\right)/2{\eta }_1$ falls in the range of 0.1–1 Hz. At a relatively high frequency (e.g., 1 Hz), the parameter ${\xi }_{x^{\prime }{x}^{\prime }}$ is essentially a constant and hence the characteristic time ${\tau }_R$ does not change with frequency, in agreement with Fig. 5. It can be seen from Eq. 26 that the characteristic time ${\tau }_R$ is inversely proportional to ${\epsilon }_0^2$. By comparing this prediction with the experimental data in Jungbauer et al. (11), it is found that Eq. 26 works well when the applied strain is relatively large (e.g., ${\epsilon }_0>6\%$) but not for very small strains (see Fig. 6). This is because in the latter case, there exist a number of molecular noises (e.g., experimental fluctuations) that could drown out the external signal. Equation 26 also suggests that ${\tau }_R$ decreases with the biaxial ratio $\nu$ and scales with the term ${\left(1+\nu \right)}^{-2}$. This finding suggests a novel, to our knowledge, route to quantitatively regulate the dynamics of cellular mechanosensing system through simple physical factors, such as the frequency, amplitude, or biaxial ratio of applied dynamic loads.

Figure 6.

Characteristic time τ_R as a function of the strain amplitude ε₀ under cyclic loads. The theoretical model (solid line) fits with the experimental data (dots) in Jungbauer et al. (11) when the strain amplitude is relatively large.

Effects of SF nonlinearity

We next discuss the effects of constitutive nonlinearity of SFs. We use a nonlinear constitutive model, in which the strain energy density function $w_1$ is expressed as

$$w_1=\frac{1}{2}{C}_{11}{\epsilon }_1^2+\frac{1}{2}{C}_{12}{\epsilon }_1^4,$$ (27)

where $C_{11}$ and $C_{12}$ are two elastic coefficients. It follows that the force in an SF under strain ${\epsilon }_1$ is $F_1=\partial w/\partial {\epsilon }_1=C_{11}{\epsilon }_1+2C_{12}{\epsilon }_1^3$.

In the case of biaxial static stretches, the force balance and displacement constraint conditions give the relation

$$4{\overline{C}}_{12}{\epsilon }_1^3+\left(2{\overline{C}}_{11}+{\beta }_1\right){\epsilon }_1-\left(2+{\beta }_1\right){\epsilon }_{x^{\prime }{x}^{\prime }}=0,$$ (28)

where ${\beta }_1=L_1/l_1$, ${\overline{C}}_{11}=C_{11}/EA$, and ${\overline{C}}_{12}=C_{12}/EA$. The solution of ${\epsilon }_1$ can be solved from Eq. 28, and thereby we derive the total energy difference $\Delta U$ in Eq. 1 with the effects of nonlinearity. As discussed above, the ratio ${\beta }_1$ between the sizes of SFs and FAs is in the range of 10–100. Here, we take ${\beta }_1=100$, $\nu =0.25$, ${\epsilon }_0=0.1$, $L_{x^{\prime }}=100\mu \text{m}$, and $L_{y^{\prime }}=20\mu \text{m}$. Fig. 7 plots the steady-state orientation with respect to the elastic constant ${\overline{C}}_{12}$ under several representative values of ${\overline{C}}_{11}$. It can be seen that if ${\overline{C}}_{11}=1$, the cells will align along the stretching direction, in agreement with relevant experiments (5, 6) and the predictions of our linear model. When ${\overline{C}}_{11}$ is much smaller than unity (e.g., ${\overline{C}}_{11}=0.01$ or 0.1), the steady-state orientation will be perpendicular to the stretching direction for small ${\overline{C}}_{12}$ and parallel to the stretching direction for large ${\overline{C}}_{12}$. This is because for a smaller value of ${\overline{C}}_{11}$, the nonlinearity of SFs will become stronger with the increase in ${\overline{C}}_{12}$. Therefore, the strong nonlinearity in the constitutive relation of SFs may affect the final cellular orientation.

Figure 7.

Steady-state orientation $\overline{\theta }$ with respect to the normalized coefficient ${\overline{C}}_{12}$ under biaxial static stretches. Here, we take β₁ = 100, ν = 0.25, ε₀ = 0.1, L_x′ = 100 μm, and L_y′ = 20 μm.

In the case of biaxial cyclic stretches, one can numerically solve the force balance and displacement constraint conditions accounting for the effects of SF nonlinearity. The obtained steady-state orientation depends on the elastic and viscous parameters and the sizes of SFs, as well as the loading frequency. For example, we can consider the situation with a high loading frequency $\omega$. In this case, as demonstrated by De et al. (13), the cells cannot follow the time-dependent strain and only respond to the time average of the sinusoidally varying strain. Assuming $L_1>>l_1$ and $L_2>>l_2$, the normalized free energy change $\Delta \overline{U}=\Delta U/EA$ per period is estimated as

$$\Delta \overline{U}=\frac{3}{8}{\epsilon }_0^2{L}_1\left({\overline{C}}_{11}-2\right){\left({\text{cos}}^2\theta -\nu {\text{sin}}^2\theta \right)}^2+\frac{105}{384}{\overline{C}}_{12}{L}_1{\epsilon }_0^4{\left({\text{cos}}^2\theta -\nu {\text{sin}}^2\theta \right)}^4+\frac{3}{8}{\epsilon }_0^2{L}_2\left({\overline{C}}_2-2\right){\left({\text{sin}}^2\theta -\nu {\text{cos}}^2\theta \right)}^2.$$ (29)

From $\partial \overline{U}/\partial \theta =0$, one can obtain three possible cellular orientations, $\overline{\theta }=0$, $\pi /2$, and ${\theta }_f$, among which the last one satisfies

$$35{\overline{C}}_{12}{L}_1{\epsilon }_0^2{f}^3\left({\theta }_f\right)+24\left({\overline{C}}_{11}{L}_1-2L_1+{\overline{C}}_2{L}_2-2L_2\right)f\left({\theta }_f\right)-24\left({\overline{C}}_2-2\right)\left(\nu -1\right)L_2=0$$ (30)

with $f\left(\theta \right)=\nu -\left(1+\nu \right){\text{cos}}^2\theta$. If the cellular longitudinal size is much larger than its lateral size $\left(L_1>>L_2\right)$, Eq. 30 reduces to $35{\overline{C}}_{12}{\epsilon }_0^2{f}^3\left({\theta }_f\right)+24\left({\overline{C}}_{11}-2\right)f\left({\theta }_f\right)=0$, leading to solutions ${\text{cos}}^2{\theta }_f^{\left(1\right)}=\nu /\left(1+\nu \right)$ and ${\text{cos}}^2{\theta }_f^{\left(2\right)}=\left(\nu -\gamma \right)/\left(1+\nu \right)$ with $\gamma =\sqrt{24\left(2-{\overline{C}}_{11}\right)/35{\overline{C}}_{12}}/{\epsilon }_0$. The value of ${\theta }_f^{\left(1\right)}$ is identical to the orientation predicted by the minimal strain model (9, 10, 14). Because ${\theta }_f^{\left(2\right)}$ > ${\theta }_f^{\left(1\right)}$, the steady-state orientation may be larger than that predicted by the minimal strain model. This conclusion is in agreement with the results of the experiments of Livne et al. (12).

Conclusions

A cytoskeletal tensegrity model has been proposed to describe the rotational dynamics of polarized cells on a substrate subjected to either static or cyclic stretches. The dynamic response of SFs to cyclic stretches is limited by the actin binding/unbinding rates and the intrinsic viscosity of molecular motors. Due to this mechanism, the mechanical response of cells is sensitive to the frequency of cyclic loads. Interestingly, the lateral constituent of cytoskeleton is shown to play a vital role in determining the final cell orientation. The steady cellular orientations are quantitatively determined by not only the geometrical dimensions and elastic properties of cellular elements but also the frequency and biaxial ratio of cyclic stretches. Then, we demonstrate that the dynamic process of cell reorientation follows an exponential law with a characteristic time that scales inversely with the square of the strain amplitude, decreases with the cyclic frequency, and saturates beyond a threshold frequency. Furthermore, we showed that the nonlinearity in the constitutive relation of SFs may affect the final cellular orientation in some extreme situations. The predictions of our tensegrity model are in broad agreement with many different types of experimental phenomena.

Recently, it is found that within a confluent cell layer where the cell geometry is affected by neighboring cells, cells align and migrate along the direction of maximal principal stress (43, 44). It may be possible to describe such confluent cell layer as a large-scale assembly of tensegrity structures. In this sense, this model could be extended to study the collective alignment and movement of cells within a confluent monolayer. Our study thus suggests a strong potential of using tensegrity type models to capture the essential mechanisms of cellular mechanosensing in various mechanical environments.

Author Contributions

G.-K.X. and X.-Q.F. designed the research; G.-K.X. and B.L. performed the research; and G.-K.X., B.L., X.-Q.F., and H.G. analyzed the data and wrote the article.

Editor: Michael Dustin.