Integration of Known Transcription Factor Binding Site Information and Gene Expression Data to Advance from Co-Expression to Co-Regulation

Abstract

The common approach to find co-regulated genes is to cluster genes based on gene expression. However, due to the limited information present in any dataset, genes in the same cluster might be co-expressed but not necessarily co-regulated. In this paper, we propose to integrate known transcription factor binding site information and gene expression data into a single clustering scheme. This scheme will find clusters of co-regulated genes that are not only expressed similarly under the measured conditions, but also share a regulatory structure that may explain their common regulation. We demonstrate the utility of this approach on a microarray dataset of yeast grown under different nutrient and oxygen limitations. Our integrated clustering method not only unravels many regulatory modules that are consistent with current biological knowledge, but also provides a more profound understanding of the underlying process. The added value of our approach, compared with the clustering solely based on gene expression, is its ability to uncover clusters of genes that are involved in more specific biological processes and are evidently regulated by a set of transcription factors.

Introduction

Current technologies have enabled scientists access to complete sequence information as well as to genome-wide gene activity measurements for an ever-growing number of organisms. However, unraveling gene regulation by means of promotor analysis and/or cluster analysis remains a challenging task. In the last few years, many new computational methods have been developed to automatically detect regulatory motifs. These tools can be divided into two main categories: scanning methods and de novo methods. The scanning methods use a motif representation resulting from experimentally determined binding sites to scan the genome sequence to find additional matches (1). The de novo methods attempt to find novel motifs that are enriched in a set of upstream sequences 2., 3., 4., 5., 6.. In order to identify regulatory programs, those de novo motif detection methods can be applied to the promotor regions of gene clusters to detect frequently occurring sequence patterns, which may be related to certain transcription factors (TFs) 7., 8.. However, in these methods, the identified regulation program of a gene cluster is considered as the final result; whether the regulatory program sufficiently explains the observed expression of all members of the gene cluster is not evaluated.

Segal et al. (9) used a more advanced method that attempts to construct complex regulatory mechanisms from the expression profiles of known TFs. They assume that the expression level of the TFs is directly related to the expression of the genes that are regulated by them. There exists, however, clear biological evidence that this simple model is not always valid (10). Beer et al. (11) circumvented the need to use the TF profiles as input by using sequence data instead. Utilizing AND, OR, and NOT logic and placing severe constraints on motif strength, orientation, and relative position, a large number of complex rules can be derived. However, these hypotheses need to be biologically validated before they would be useful to be incorporated in a clustering scheme.

We propose to incorporate TF binding potential data into the clustering scheme, such that for each newly discovered cluster, a single common regulatory structure sufficiently explains the behavior of all the genes in the cluster. Recently, different methods have been proposed that also let the regulation program adapt the grouping of genes. Segal et al. (12) employed the expectation maximization algorithm that iteratively partitions the gene set and applied this gene partition to detect new motif candidates. In this way transcriptional modules are built that are both coherent in expression profiles and have common binding sites. Middendorf et al. (13) used both gene regulators and putative binding sites to build a decision tree that tries to explain the gene expression profiles in terms of regulators and motifs. A similar method from Ruan et al. (14) applies a multivariate regression tree to discover a model for gene expression patterns.

The above methods generally aim to find new motifs that are assumed to be involved in the regulation of the uncovered clusters of genes. In other words, both the clusters and the motifs are free parameters that have to be optimized. However, the rather poor performance of de novo motif discovery methods (15), combined with the uncertainty that remains in gene clustering (16), make it often difficult to link the regulatory programs with existing biological knowledge. As both the motifs and the gene clusters can be unknown, the biological interpretation of such results is, therefore, severely limited.

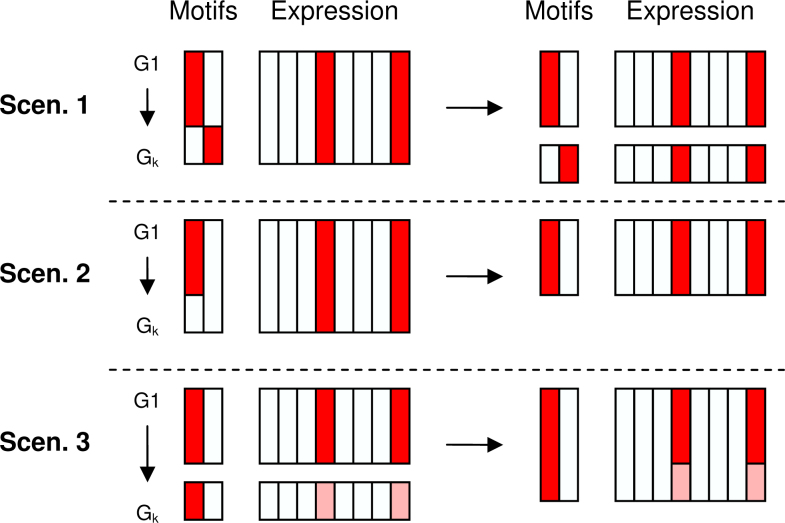
In this work, we propose to integrate the occurrence of known regulating elements in the upstream region of genes together with their expression levels as a combined input to the clustering system. The fact that our method only inputs validated TF motifs allows for an easier biological interpretation of the clusters and their discovered regulation structure. This increases the usefulness of the results and facilitates biologists in their studies to decipher the function of the genes regulated under given experimental conditions. More specifically, we identify three different scenarios where the integration of known TF binding site information and gene expression data leads to clusters of co-regulated genes that are not only expressed similarly under the measured conditions, but also share a regulatory structure that may explain their common regulation (Figure 1).

Fig. 1.

The goal of the proposed method is to find co-regulated gene clusters that have similar expression profiles and share a similar set of motifs. The reason why the integration of motif enrichment results in a more functionally related module is threefold. Scenario 1: A cluster that is actually regulated by two different motifs is split up into separate clusters. Scenario 2: A cluster showing homogeneous expression is shrunk to a smaller cluster in which all genes contain the same motif. Scenario 3: Genes that show weak co-expression are integrated in one cluster because they share the same motif.

Results

Combining gene expression and gene regulation

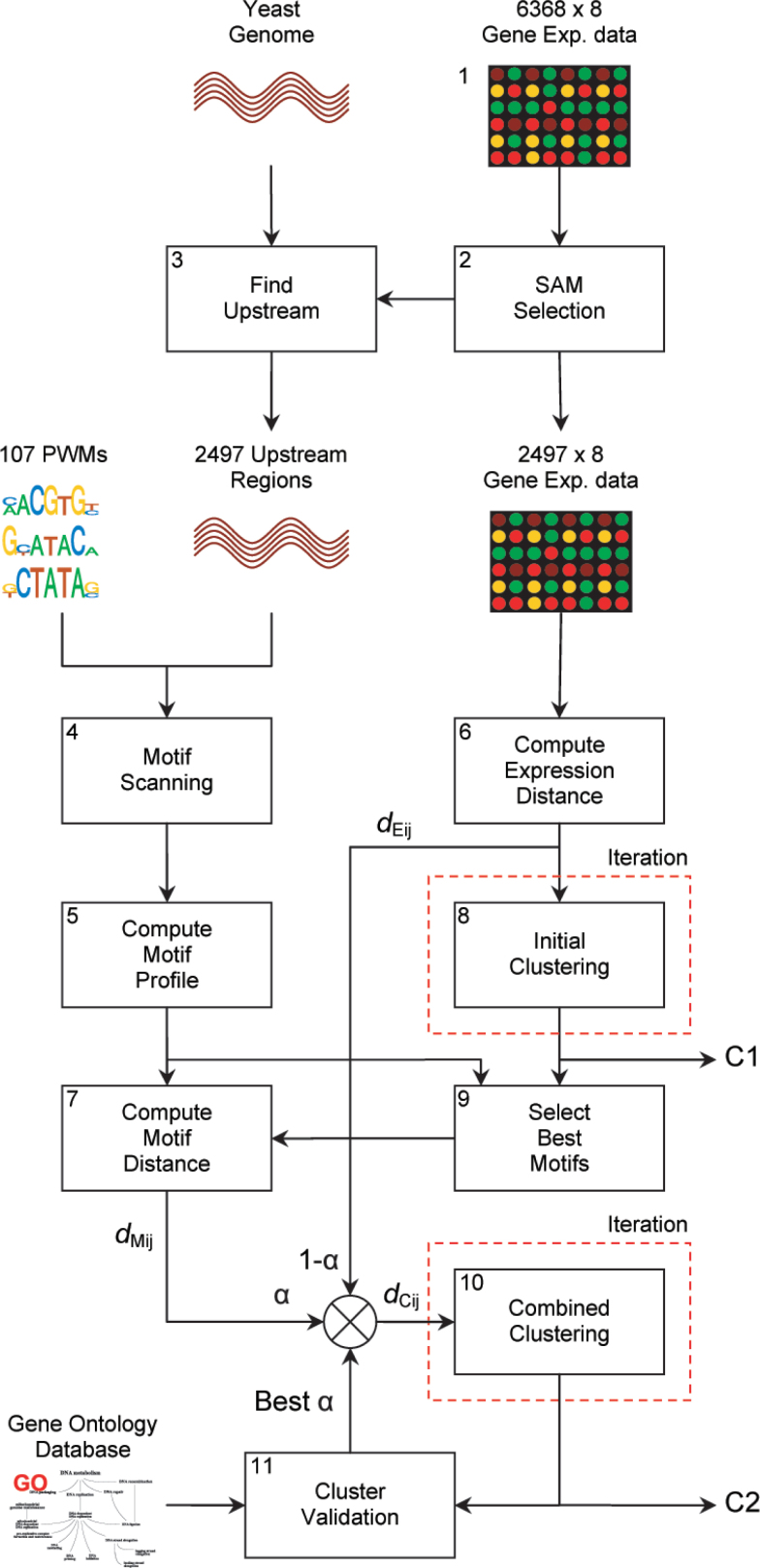
Our proposed methodology is depicted in Figure 2. Complete details can be found in Materials and Methods. Here we give a short description of each step.

Fig. 2.

The integration of enriched TF binding sites into the clustering process of gene expression data. After gene selection, gene distances are computed on both expression and motif profiles. The motif distance is computed on a subset of the motifs, selected by the initial clustering. The second clustering step combines both information sources with the weighting parameter α, which is optimized by finding the clustering with the highest GO enrichment. Finally, C1 and C2 represent the initial and combined consensus clustering that are compared to show that our method generates more biologically relevant clusters.

To evaluate our method, we have employed a dataset from Tai et al. (17) that is comprised of 6,383 Saccharomyces cerevisiae genes with expression values measured over 8 well-defined conditions (Step 1). After selection of the most differentially expressed genes in these conditions by using the significance analysis of microarrays (SAM) algorithm (18), we retained 2,497 genes for our analysis (Step 2). From these genes we extracted the 1,000 bp upstream region of each gene by using gene location data from the Saccharomyces Genome Database (19) and the S288C S. cerevisiae strain from Ensembl V35 (20) (Step 3).

Using a compendium of 107 position weight matrices (PWMs), we scanned the upstream regions of the genes for potential binding sites of known TFs (Step 4). To obtain a single value for the binding potential for each gene-motif pair, we have adopted the score function from Segal et al. (12), which combines all scores from the upstream region into a single value. We set a threshold for these continuous values to obtain a true-false relationship for each gene-motif combination. For each gene, the set of 107 thresholded motif scores represents the binary motif profile of that gene (Step 5).

We used the Pearson correlation coefficient to compute the distance between genes based on their expression profiles (Step 6). The Pearson correlation is generally accepted to provide a useful distance measure for grouping co-regulated genes because it is insensitive to differences in offset and scaling of the profiles 21., 22..

However, it is not trivial to define a distance measure between genes based on their motif profiles. The main difficulty is that the combinatorial effect of two factors may differ from the individual effect of one factor 11., 23.. After comparison of several measures (see Supporting Online Material), we selected the normalized Hamming distance on the binary motif profiles to compute this distance, since this measure has a large selective ability for profiles with different motif combinations (Step 7).

To be able to tune the relative influence of the motif information, the weighted combination of both expression distance and motif distance is taken as a new distance measure, d_Cij, that is, the distance between genes i and j is given as:

$$d_{C_{ij}}=(1-\alpha )d_{E_{ij}}+\alpha d_{M_{ij}}$$ (1)

where α (0 ≤ α ≤ 1) is the weighting parameter that sets the balance between the expression distance d_Eij and the motif distance d_Mij. Using this combined distance measure d_Cij, we employed hierarchical clustering with complete linkage to divide the genes into 50 distinct groups. We expect that this number is slightly above the true number of clusters in the dataset, so that there is enough possibility to obtain compact clusters without over-segmenting the data. In order to improve the robustness of the clusters, we iteratively clustered 500 times on samplings of 80% of the data and combined the resulting clusterings using consensus clustering, which has proven to provide more reliable data groupings 24., 25..

Obviously, not all motifs in our database are functionally active in the conditions under investigation. Therefore, we initially clustered the data purely on the expression distance (Step 8) and determined which motifs are significantly enriched in one or more clusters (Step 9). To avoid the introduction of irrelevant information, only the significant motifs were employed to compute the motif distance between genes (Step 10).

We then combined both expression and motif information using Equation 1, with α varying between 0 and 1. We optimized α by finding the clustering that obtains the highest enrichment of functional categories using the Gene Ontology (GO) annotation database (26) (Step 11).

Finally, we compared the consensus clustering of the initial clustering (α = 0) (C1) with the consensus clustering at the selected ideal value of α (C2). The differences between these two clusterings are illustrated by relating to the scenarios in Figure 1. Furthermore, we show that the improved clusters have an increased biological relevance.

Initial clustering and motif selection

From the initial consensus clustering, which is purely based upon expression data, we computed p-values of the motif enrichment for each cluster. All motifs were ranked according to the lowest p-value that they attain in any of the clusters. We considered a motif to be significantly enriched if it attains a p-value < 0.005, using a Bonferroni correction for 50 clusters and 100 motifs, which results in a threshold of 10⁻⁶. Figure 3 shows the logos and p-values of the motifs that pass this threshold. The nine motifs displayed in this figure are selected as features for the combined clustering. Consistent with the biological context of the data, we found that all of these nine TFs are known to be functionally related to a relevant form of nutrient limitation. Other feature selection methods have been evaluated and are discussed in Supporting Online Material.

Fig. 3.

Motifs that are enriched in the initial clustering. We show only the motifs that attained a p-value smaller than 10⁻⁶ in any of the 50 clusters. For each motif we show its common name, its enrichment p-value, and a logo that indicates the information content for each base in the motif. See Supporting Online Material for the complete list.

Combined clustering and α estimation

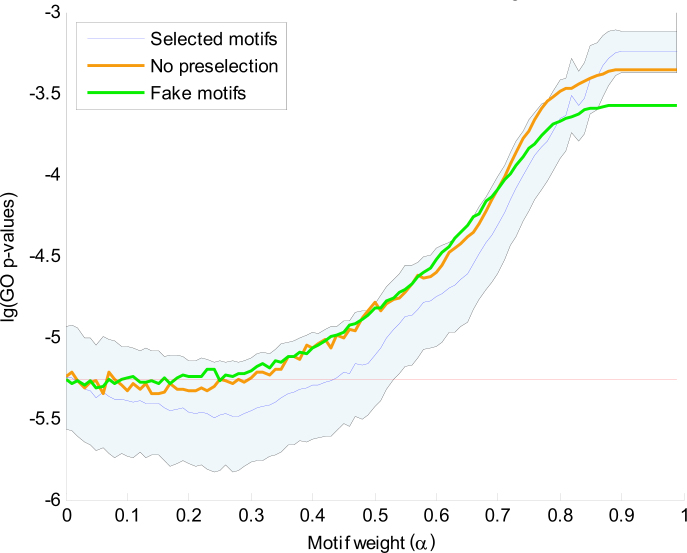
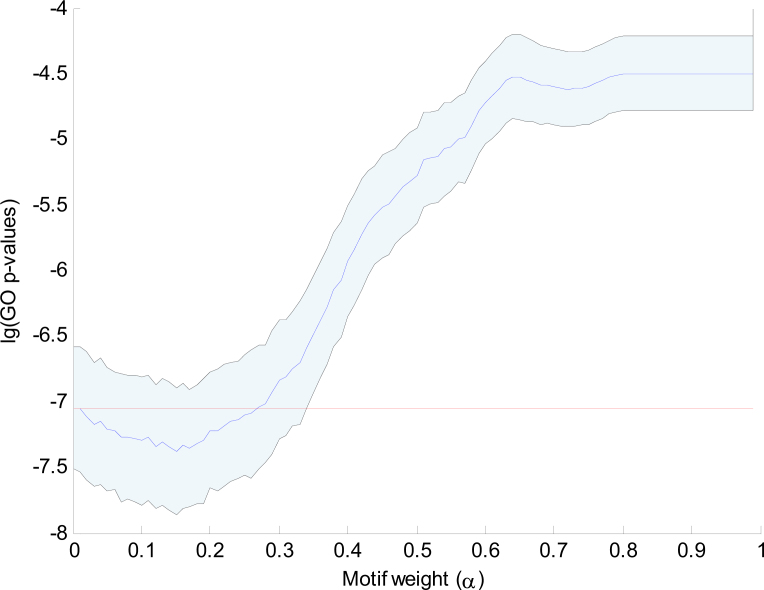
The combined clustering uses the binary profile with the nine selected motifs as well as the complete gene expression profile to compute a combined distance between genes. To show that the integration of gene expression data with motif data leads to more functionally related clusters, we have computed the GO enrichment for clusterings with different settings of the combining weight α. For each clustering, we computed the GO clustering enrichment score as the average GO enrichment of the x most enriched clusters (see Materials and Methods). Figure 4 shows the distribution of GO clustering enrichment scores as a function of 0 ≤ α < 1. The distribution was obtained by taking 500 samplings of 80% of the genes for each different α setting. These results show that the GO enrichment of the purely gene expression based clustering (α = 0) is much better than that of the purely motif based clustering (α = 1). However, the GO enrichment of the expression based clustering can be further improved by integration with the motif information as long as α < 0.45.

Fig. 4.

The mean and standard deviation of the 500 GO clustering enrichment scores of the sampled clusterings (selected motifs). GO clustering enrichment scores are averages of the x most enriched clusters, with here x = 25. The logarithm of the GO enrichment p-values is plotted against 100 values of α. We use the consensus clustering at α = 0.25 as the final combined clustering. To show the biological relevance of the selected motifs, the mean p-values achieved over 500 clustering iterations with randomly selected motifs (no preselection) and with random base strings (fake motifs) are also shown.

To demonstrate the biological relevance of the motifs that were selected in the initial clustering, Figure 4 also shows the scores obtained when, in each iteration, 9 motifs are randomly selected from the database of 107 motifs. We observed only a very limited improvement around α = 0.2. If fake motifs (random ACGT patterns) are used, no significant improvement is visible for α > 0.

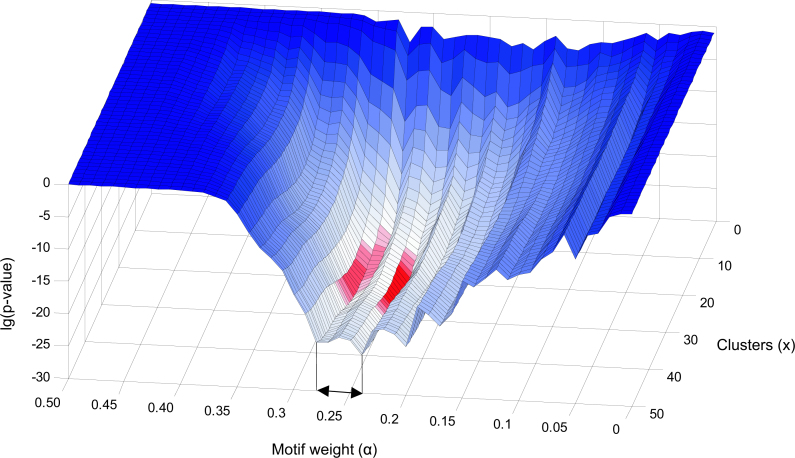
In order to determine the best value of α and to study if this value is sensitive to the choice of x, we have computed the gain in GO enrichment for each combination of x and α. The gain in GO enrichment is defined as the significance of the difference between the initial clustering and a combined clustering as measured with a one-tailed two-sample t-test (see Materials and Methods). Figure 5 shows that the optimal value of α does not strongly depend on x. For any x > 5, the optimal value for α lies within the region 0.24 ≤ α ≤ 0.28. We have taken the consensus clustering at α = 0.25 as the final combined clustering.

Fig. 5.

This graph shows the lg(p-value) of the t-statistic on the vertical axis, indicating the difference of the combined clustering with respect to the initial clustering for each x ϵ N (1 ≤ x ≤ 50) and each 0 ≤ α < 1 (100 steps). The minimal values of the plot are shown in red. We conclude that the optimal improvement is obtained in the region 0.24 ≤ α ≤ 0.28. The part where α > 0.5 is omitted since the one-tailed t-test causes all p-values to be 1 in this area.

Figure 5 also shows that the strongest improvement in GO enrichment is found for the top 25 clusters (x = 25). However, we found it better to preserve the additional amount of clusters to allow the relevant clusters to shrink as depicted in Scenario 2 in Figure 1.

To demonstrate the general applicability, we have also applied our method on the Hughes’s microarray compendium (27). This dataset consists of the gene expression measurements of 300 diverse mutations and chemical perturbations applied to S. cerevisiae. Figure 6 shows the mean and standard deviation of 500 clustering iterations for α values between 0 and 1 on Hughes’s dataset, again using 50 clusters. From the figure we also found a minimum at α > 0, indicating that the inclusion of motif information improves the clustering result in terms of GO enrichment. In comparison with the results on the data from Tai et al. (17), we found that the shape of the curve is very similar, but the value of α where the optimal score is reached (α ≈ 0.17) is significantly smaller. We contribute this to the well-defined growth conditions in Tai’s dataset, as compared with Hughes’s dataset. In Tai’s dataset, the yeast was grown in chemostat cultures, in which all parameters, except the limited nutrient or oxygen regime, were kept constant. Expression differences between the conditions can therefore be attributed to a single cultivation parameter, and thus lead to changes in a limited number of biological processes. Consequently, there exists a more clear-cut relation between the relevant biological processes and sets of TFs involved in these processes, which may allow for a larger contribution of the motif enrichment. It is also for these reasons that we employed Tai’s dataset to analyze and interpret the uncovered results in order to validate our approach. Conclusively, the optimal value of α is dependent on the experimental setup and needs to be determined for every selection of experimental conditions or binding motifs.

Fig. 6.

The mean and standard deviation of the 500 GO clustering enrichment scores of the sampled clusterings on Hughes’s dataset.

Cluster comparison

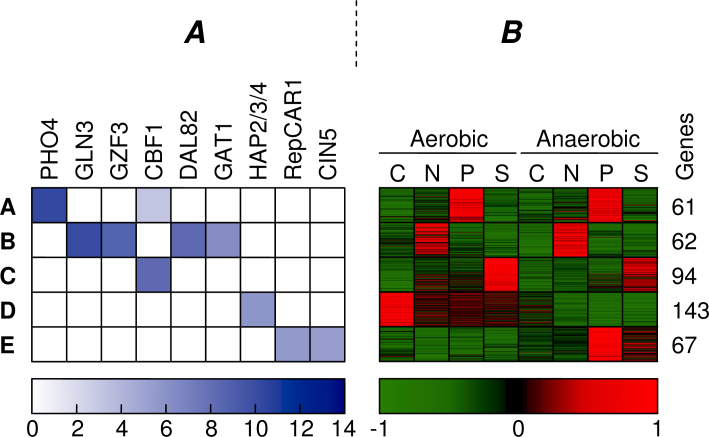
We used Tai’s dataset to extensively discuss the effects of the integrated clustering within the individual clusters. In order to compare the initial and combined clustering, we studied the differences between the consensus clustering for α = 0 and for α = 0.25. For the discussion, we restrict our analysis to the clusters that show the strongest motif enrichment. Figure 7 shows the clusters of the initial clustering for which at least one of the motifs was enriched with a p-value smaller than 10⁻⁶. For these five clusters (A–E), we show both motif enrichment and expression profiles.

Fig. 7.

Appearance of the most enriched motifs found in the initial clustering, ranked from left to right in the order of significance (A). Only the clusters in which at least one motif showed significant enrichment (p-value < 10⁻⁶) are shown. The color of the squares indicates the −lg(p-value) of the enrichment for each motif and cluster. For each of these clusters, we show the normalized expression profiles of all genes and the total number of genes in the cluster (B). All values that exceed a standard deviation of −1/1 are truncated to −1/1. The carbon, nitrogen, phosphor, and sulfur limitations are depicted as C, N, P, and S.

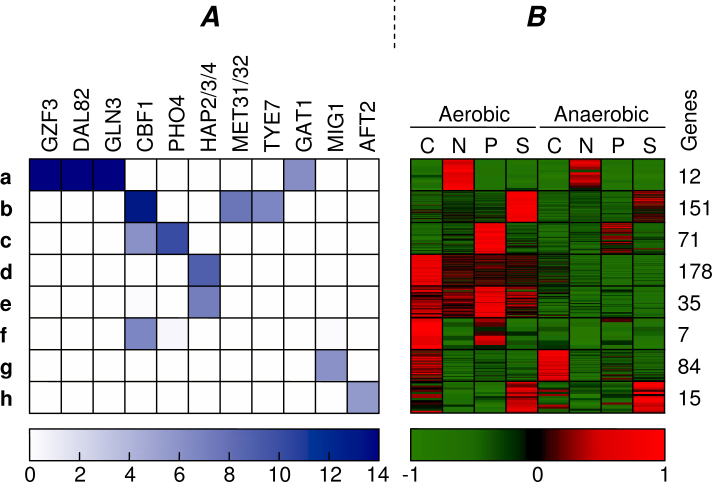
For the combined clustering with α = 0.25, we obtained the results shown in Figure 8. As may be expected, we can see that the combined clustering results in more clusters (a–h) with highly enriched motifs (p < 10⁻⁶). The specific changes with regard to the initial clustering are summarized for each cluster separately.

Fig. 8.

Appearance of the most enriched motifs (p-value < 10⁻⁶) found in the combined clustering. Similar visualization as in Fig. 7.

Nitrogen cluster

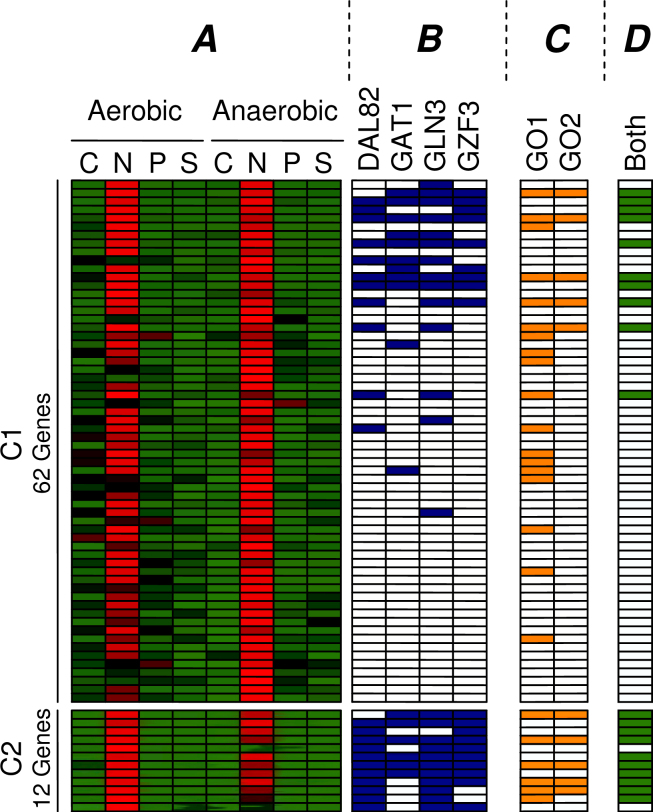
The cluster that shows differential expression under nitrogen limitation in the initial clustering (Figure 7, Cluster B) has now become the cluster with the highest motif enrichment in the combined clustering (Figure 8, Cluster a), increasing its motif enrichment from p = 10⁻¹¹ to p = 10⁻¹⁴. The reason for this is that this cluster has been shrunk to about one fifth (62 → 12 genes) of the original cluster size. Only the genes that are not only similarly expressed (upregulated under nitrogen limitation) but also share a regulatory structure that may explain their common regulation (binding sites for DAL82, GAT1, GLN3, GZF3) have been conserved in this cluster. Figure 9 shows the genes that were found in the initial clustering and in the combined clustering. This figure depicts the expression profiles of the genes and indicates whether we have found binding sites for the enriched motifs (DAL82, GAT1, GLN3, GZF3). All of these four detected motifs have been previously implicated with nitrogen limitation by Tai et al. (17). It is clear that many genes in the initial clustering display the expected expression profile, but lack the presence of known regulating motifs. The newly discovered cluster only contains genes that demonstrate an expression profile in combination with the regulation program. Moreover, we noticed that the genes containing the related motifs show higher expression in the aerobic condition, while the initial cluster is overall more strongly expressed in the anaerobic environment. This indicates that the activity of the TFs that bind to these motifs might be influenced by oxygen concentration.

Fig. 9.

The initial (C1) and combined (C2) clusters that demonstrate higher expression under nitrogen limitation (A). The normalized expression profiles are shown in red (high) and green (low). For each gene it is indicated if either of the four known nitrogen related motifs (DAL82, GAT1, GLN3, GZF3) is present in its upstream region (B). The GO categories that show the highest enrichment in C1 and C2 are Catabolism (GO1) and Allantoin Catabolism (GO2), and the genes annotated with the two categories are denoted (C). The column “Both” indicates the genes that are found in both C1 and C2 (D). In the second cluster, only the genes with a clear regulation remain. In this way, we have gained more confidence in the co-regulation of this cluster.

Furthermore, we observed that the combined cluster obtains a p-value of 5.9 × 10⁻¹² on the GO category Allantion Catabolism. In a nitrogen limited environment, the allantoin degradation pathway, which converts allantoin (C₄H₆N₄O₃) to ammonia and carbon dioxide, allows S. cerevisiae to use allantoin as a sole nitrogen source. We found that all genes that are part of this pathway according to the Saccharomyces Genome Database (19) are included in our cluster.

For the initial cluster, the best matching GO term was less enriched and more general (Catabolism with p-value 9.6 × 10⁻¹⁰). Thus, in this example the addition of motif information led to a cluster that can be related to a more specific condition and in this way has a higher biological relevance. Since all genes that lack the regulating motif have been removed, this type of change is a clear example of Scenario 2 in Figure 1.

Sulfur cluster

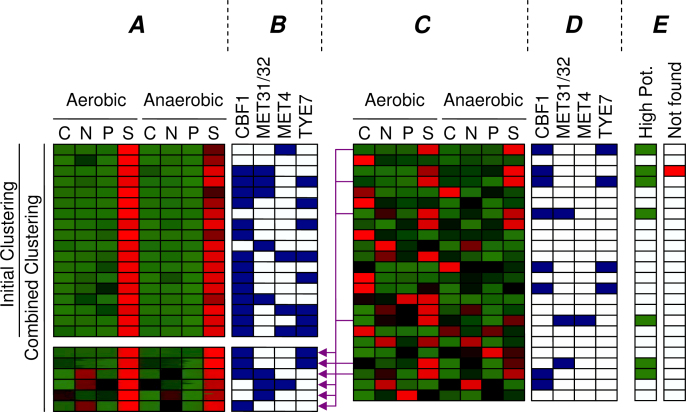
The cluster expressed under sulfur limitation in the combined clustering (Figure 8, Cluster b) clearly shows highly enriched motifs (CBF1, MET31/32, and TYE7), whereas the initial cluster (Figure 7, Cluster C) could only be matched to CBF1. Indeed, in Tai et al. (17), both CBF1 and MET31/32 were found to be related to this condition, together with MET4. Although Tai et al. did not find the TYE7 motif, others have also related this TF to sulfur limitation (28). The sulfur cluster from the combined clustering has become larger than the initial cluster (94 → 151 genes), while maintaining a similar expression profile and improving motif enrichment. Apparently, the initial cluster missed some sulfur related genes, because the p-value of the GO category Sulfur Metabolism has improved from 7.5 × 10⁻¹⁶ to 1.3 × 10⁻¹⁹ as six more genes with this annotation were included in the combined cluster. Figure 10 depicts which genes of this category were found by the initial and combined clustering. To illustrate the intended behavior of our method, we have indicated which genes we expected to be clustered differently in the combined clustering. This cluster is an example of Scenario 3 in Figure 1, because the cluster has been increased to include more genes with the same motifs.

Fig. 10.

All of the genes that are annotated with Sulfur Metabolism in GO. The normalized expression profiles are shown in red (high) and green (low), and for each gene it is indicated if either of the four known sulfur related motifs are present in its upstream region. The two groups of genes on the left (A) show the sulfur genes found by the initial clustering and the genes additionally included in the combined clustering (purple arrows). The block on the right (C) shows the sulfur metabolism genes that were initially not found. The bar indicated by “High Pot.” (E) shows the genes that are considered to have a high potential to be found by the combined clustering, because they contain at least one of the known motifs and do not deviate greatly from the desired expression profile [a minimal correlation between the expression profile and the perfect profile (00010001) of 0.5]. The “Not found” bar shows that only one of these genes was eventually not included in the combined cluster.

Second aerobic cluster

In the initial clustering, one cluster was found to be controlled by HAP motifs and typically expressed under aerobic conditions as well as showing a higher expression under carbon limitation (Figure 7, Cluster D). The combined clustering, however, is able to distinguish two HAP-controlled aerobic clusters, that is, a similar aerobic cluster (Figure 8, Cluster d) as well as a new aerobic cluster that shows a higher expression under phosphorus limitation (Figure 8, Cluster e). We know that the HAP2/3/4 motif has been related to both carbon limitation and aerobic conditions 17., 29.. Our finding suggests that the HAP motif also plays a role in phosphorus metabolism.

Anaerobic phosphor cluster

The last cluster from Figure 7, Cluster E, is not present in Figure 8. This cluster, however, has remained almost unaltered, except that the motif p-values just exceed 10⁻⁶ in the combined clustering.

Carbon cluster

Apart from increasing specificity in the initial clusters, the combined clustering also discovered a few additional clusters with significant motif enrichment. We have found a carbon cluster with clearly enriched motif MIG1 (Figure 8, Cluster g). This motif has been related to carbon limitation by Tai et al. (17) but our initial clustering did not clearly show this relation. Our combined clustering indicates that the genes regulated by MIG1 are more strongly expressed in an anaerobic environment.

Second sulfur cluster

An additional sulfur cluster was discovered that lacks the well known sulfur related motifs but does contain the AFT2 motif (Figure 8, Cluster h). The set of genes activated by AFT1 and AFT2 is designated as the iron regulon, and its activation was suggested to depend on a product of the mitochondrial iron-sulfur cluster biogenesis pathway (30). These genes are thus part of a different pathway than the genes in the Sulfur Metabolism cluster (Figure 8, Cluster b) and may indicate a novel mechanism working under sulfur limitation.

Discussion

In this study, we have presented an approach that integrates known TF binding potential and gene expression data into a single clustering scheme, which is further augmented with GO enrichment analysis. Our integrated clustering approach discovers modules of functionally related genes that are not only expressed similarly but also share a regulatory structure that may explain their common regulation. As a result, our approach allows to associate these specific shared regulation programs with the functional annotation of the module. More detailed analysis of the modules discovered for nutrient and oxygen limited yeast cultures shows that they are not only consistent with current biological knowledge, but also present more detailed information that may provide a deeper understanding of the underlying process.

One of the principal differences between our method and comparable work is the fact that our method does not attempt to find new motifs. Because our method only employs validated TF motifs, it allows for an easier biological interpretation of the found modules and their discovered regulation structure.

We have compared our approach with the clustering purely based on gene expression data (α = 0) followed by TF enrichment analysis. We have shown that our approach results in clusters with a stronger TF enrichment as well as a stronger (and more specific) functional enrichment. Because our results were optimized on the GO enrichment scores, the obtained p-values cannot be reported as qualitative improvement. Therefore, the Results section mainly puts the focus on the increased understanding of the clusters, derived with our algorithm, in terms of regulation and genomic function. However, it should be taken into account that the optimal parameters of the clustering scheme should be optimized for each set of expression data.

The fact that we used a fixed number of clusters and employed a crisp clustering method forces every gene to belong to a distinct group. To allow Scenario 2 from Figure 1 to occur, we deliberately chose a rather high number of clusters, such that genes are able to be assigned to one of the other (non-relevant) clusters. Further investigation needs to be done to see if alternative clustering schemes that circumvent this problem, such as fuzzy clustering schemes, are able to improve upon current results.

The motif distance was computed on a selection of significantly enriched motifs. To determine the stability of this selected set, we iteratively re-determined the set of significantly enriched motifs for the newly obtained clustering and re-computed the clustering (see Supporting Online Material). We found that the set of motifs always contained the same core of six motifs and that enrichment did not deviate strongly. Additional research may determine if the results may benefit from a motif selection procedure that is adaptive to each cluster separately instead of on the whole clustering.

As is already visible in Figure 3, our database contains some motifs that strongly resemble each other (like GLN3-GZF3-DAL82-GAT1 or CBF1-PHO4). However, similar motifs do not necessarily mean that the TFs play a similar role. For instance, the motifs CBF1 and PHO4 show great resemblance although the TFs are known to play a role under different conditions (sulfur and phosphorus limitation respectively). In fact, other studies have shown that the base T just before the core sequence CACGTG in CBF1 inhibits the binding of PHO4p but not CBF1p 31., 32.. One might argue that our approach may have a tendency to produce clusters in which similar motifs are always combined. However, because we integrate gene expression with motif information instead of sequentially applying them, our method is able to distinguish “similar and functionally related” motifs from “similar, but functionally different” motifs. In fact, we see that GLN3-GZF3-DAL82-GAT1 are only found together in a single cluster, which unambiguously relates them to an expression profile (Figure 8, Cluster a), while the presence of CBF1 can lead to different expression profiles dependending on the other motifs it occurs with (Figure 8, Clusters b, c, and f). This is a clear example of the fact that the specific combination of TFs will result in different expression pattern and function. It is exactly this relation that our approach attempts to unravel.

Materials and Methods

Expression dataset

The proposed combined clustering method was developed and applied on the expression data of S. cerevisiae chemostat cultures from Tai et al. (17). This dataset is comprised of 6,383 genes and 24 arrays. The 24 arrays are made up of 3 replicated measurements of 8 conditions. In these eight conditions, the response of aerobic as well as anaerobic chemostat cultures of S. cerevisiae is compared with the growth limitation by four different macronutrients (carbon, nitrogen, phosphorus, and sulfur) (17).

Additionally, we applied our method on the Hughes’s microarray compendium (27). This dataset consists of the gene expression measurements of 300 diverse mutations and chemical perturbations applied to S. cerevisiae.

Gene preselection

The SAM method (18) was used to select the genes that demonstrate the most significant response under one or more nutrition limited growth conditions. Using SAM, the significance of change in at least one of the conditions was computed and all genes were ranked according to this score. Then the top 2,500 genes were selected according to this rank for further analysis (obtaining a false discovery rate of 0.01%).

Three of the selected genes have an upstream region shorter than 1,000 bp. These genes were disregarded, so 2,497 genes were retained for further evaluation.

Motif scanning

PWM is the matrix that is most frequently used to score a test sequence with a given motif consensus. It is computed by 3., 5.:

$$W_{b,j}=\ln \frac{(n_{b,j}+p_b)/N+1}{p_b}\approx \ln \frac{f_{b,j}}{p_b}$$ (2)

where N is the number of known motif sites, p_b is the background frequency of base b in the entire genome, and f_b,j is the frequency matrix computed by n_b,j/N. The alignment matrix (n_b,j) contains the occurrences of base b at position j of all the previously known sites for this motif.

A test sequence may be aligned along the weight matrix, and its score is the sum of the weights for the letters aligned at each position:

$$S{c}_i=\sum _{j=1}^p{W}_j[S_{i+j-1}]$$ (3)

where S_i is the base at position i in the upstream region to be scanned, p is the size of the motif, and W is the PWM.

To scan the upstream regions of the genes for instances of known TF binding motifs, a compendium of 107 PWMs was built, collected from three different online databases [18 from Transfac (33), 13 from SCPD (34), and 76 from Harbison et al. (35)].

Computation of gene-motif agreement score

Because regulatory motifs can occur on both strands of the DNA, a scan over a region of 1,000 bp will result in 2(1000 − p + 1) ≈ 2000 scores per gene for a PWM of length p. To obtain a single score for each gene-motif combination, several methods were compared (see Supporting Online Material) and the method used by Segal et al. (12) has been adopted, which computes:

$$P(g.M=\mathit{true}|S_1,\dots ,S_n)=\varsigma \left(\log \left(\frac{1}{n-p+1}{\displaystyle \sum _{i=1}^{n-p+1}}\exp \left\{S{c}_i\right\}\right)\right)$$ (4)

where ς, is the function [ς(p) = 1/(1 + e^−p)] and n is the length of the upstream region. This function takes the mean of the exponent of all alignment scores Sc_i along the upstream region and in this way gives a higher weight to large scores and neglects very low scores. The sigmoid function scales the resulting score values between 0 and 1.

Threshold on the gene-motif agreement score

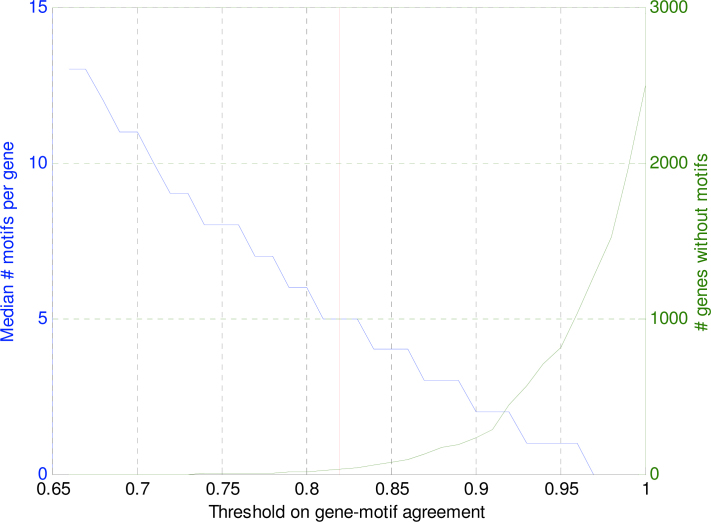
Equation 4 returns a continuous value that can be seen as a probability that a certain motif is present in an upstream region of a gene. For both computational simplicity and comprehensibility, it is desirable to set threshold to these gene-motif agreement scores and obtain a true-false relationship between gene upstream region and motif. Figure 11 shows the resulting median number of motifs per gene for thresholds ranging between 0.65 and 1. In addition, the total number of genes without any motif is depicted.

Fig. 11.

Median number of motifs per gene (blue line, left y-axis) and the number of genes without motif (green line, right y-axis) as a function of the threshold on the scoring function (Equation 4). The chosen threshold of 0.82 (red line) results in a median of 5 motifs per gene and a total of 31 genes without motifs.

To be able to distinguish between gene regulation programs, a reasonable number of motifs per gene is needed and the number of genes without a motif needs to be reduced as much as possible. Therefore, the threshold on the score value is set, such that the median number of motifs for an upstream region equals to 5 (threshold = 0.82). This number was also observed by Zhang et al. (36), who used a database of known and experimentally verified motifs to scan the upstream regions of yeast genes. For vertebrates, Prakash and Tompa found a similar amount of 6 (37), based on over-representation in an orthologous human, chimp, mouse, and rat dataset. Note that if a more stringent threshold would have been chosen, the number of genes without any motif annotation would have increased dramatically as is visible in Figure 11. The set of 107 thresholded motif scores will be called the binary motif profile of a gene.

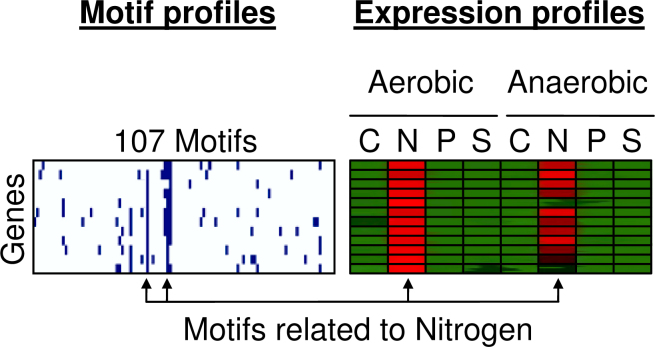
Figure 12 shows the binary motif profiles of twelve genes that show higher expression levels in a nitrogen limited environment, independent of the oxygen supply. The vertical lines in this figure indicate that all genes in this group have this binding site in their upstream regions. If a group of genes shows similar expression profile and their upstream regions contain one or more similar motifs, we can say that the gene cluster is co-regulated.

Fig. 12.

The binary motif profiles of twelve genes that show higher expression levels in a nitrogen limited environment. The right block shows the normalized expression profiles over eight experimental conditions. The left block shows the binary motif profiles that indicate if any of the 107 motifs is present in the upstream region of a gene.

Motif profile distance

To obtain a motif distance between each gene pair, the normalized Hamming distance between the binary motif profiles is computed as follows:

$$d_H=\frac{{\sum }_{i=1}^N|P_1(i)-P_2(i)|}{N}$$ (5)

where N is the total length of the motif profiles and the numerator is the number of differences between profiles P₁ and P₂.

The drawback of this method is the fact that it takes all the motifs in the motif profile into account, which causes a lot of noise, because not all motifs are active in our experimental setup. To compensate for this, a feature selection method is used so that only motifs that play a significant role under the tested conditions will contribute to the distance measure. This feature selection constitutes the selection of highly enriched motifs in the initial clustering that is solely based on expression data. Other selection methods have been assessed, but did not give improvements (see Supporting Online Material).

Data clustering

In both clustering steps we use hierarchical clustering to divide the data into 50 distinct groups. Complete linkage is used, which has shown to provide the most reliable clusters on genetic data (38) (see Supporting Online Material). Because we chose to compute more clusters than we expected in the dataset, we assume that not all resulting clusters will be relevant. Therefore, only a selected number of clusters will be regarded in order to assess the value of our method in cluster comparison.

To improve the robustness of the putative clusters to variations in data sampling, we clustered 500 times on 80% of the data and employed consensus clustering 24., 25.. This methodology first computes a consensus matrix that contains, for each pair of items, the proportion of clusterings in which the two items are clustered together:

$$M(i,j)=\frac{{\sum }_h{M}^{(h)}(i,j)}{{\sum }_h{I}^{(h)}(i,j)}$$ (6)

where I^(h) indicates if items i and j are both selected by the data sampling, and M^(h) is the co-occurrence matrix that stores the number of times that items i and j are clustered together in clustering h:

$$M^{(h)}(i,j)=\{\begin{array}{ll}1\hfill & \mathrm{if}i\mathrm{and}j\text{belong}\text{to}\text{the}\text{same}\text{cluster},\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}$$

From the consensus matrix we compute a new distance matrix D = 1 − M, which is used to derive a new clustering, using again hierarchical clustering with complete linkage.

Enrichment computation

For both the computation motif and GO enrichment, the hypergeometric distribution is employed to compute the probability of detecting the observed number of motifs/annotations or more in a random selection of genes with the same size as the given cluster. As a measure of enrichment we compute the p-value as follows:

$$p=P(i\ge b)={\displaystyle \sum _{i=b}^{\mathit{min}(B,g)}}\frac{\left(\begin{array}{c}B\\ i\end{array}\right)\left(\begin{array}{c}G-B\\ g-i\end{array}\right)}{\left(\begin{array}{c}G\\ g\end{array}\right)}$$ (7)

where G is the total number of genes, B is the number of genes within this cluster, g is the total number of genes that have this motif/annotation, and b is the number of genes from the cluster that have this motif/annotation.

Cluster evaluation

In order to evaluate the different clusterings, the GO database (26) is used to find the enrichment of functional categories in the individual clusters. First, all GO categories with less than 5 annotations are removed, resulting in 576 categories. Then, p-values of the detected number of annotations for each cluster category combination are computed using the hypergeometric distribution, and the lowest p-value over all categories is assigned as a score for a cluster.

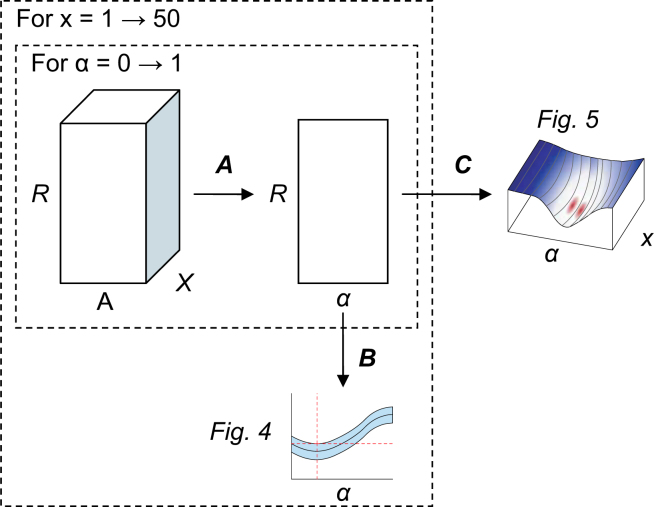
The combined clustering step iterates 500 times over 80% of the data and varies α between 0 and 1 in 100 steps. Figure 13 shows that this results in R × A × X cluster scores. In Step A, the score for a clustering is computed by taking the average over the x best clusters, varying x between 1 and X. Step B computes the mean and standard deviation over the 500 iterations. The mean and standard deviation of the individual scores is plotted in Figure 4. Finally, in Step C the gain of the combined clustering with respect to the initial clustering is computed, using a two-sample t-test with respect to the clustering on expression data (α = 0) as follows:

$$T=\frac{{\overline{X}}_{\mathit{init}}-{\overline{X}}_{\mathit{comb}}}{\sqrt{\frac{S_{\mathit{init}}^2+S_{\mathit{comb}}^2}{R}}}$$ (8)

where ${\overline{X}}_{\mathit{init}}$ and ${\overline{X}}_{\mathit{comb}}$ are the sample means of the initial and combined clustering, R is the number of cluster iterations, $S_{\mathit{init}}^2$ and $S_{\mathit{comb}}^2$ are the sample variances. Since we were only interested in clusterings that have a mean score lower than the initial clustering, we computed a one-tailed t-test. The p-values of the t-statistic for each α and x are shown in Figure 5.

Fig. 13.

The steps we take to estimate the optimal value for α. Here, R is the number of cluster iterations (500), x is the number of clusters we use to compute a single score for a clustering (between 1 and X), and α is the motif weight that we vary between 0 and 1 in A steps. The total number of clusters X is set to 50 and A is set to 100.

Authors’ contributions

MC carried out the clustering experiments and created the first draft of the manuscript. EPS contributed in the design of the study and took part in writing the final document. TAK supported the analysis of the dataset and the biological results of the method. MJTR coordinated this study and participated in the design and finalization of the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.

Supporting Online Material

http://ict.ewi.tudelft.nl/pub/maarten/supplement.pdf