Quality Assessment of Transcriptome Data Using Intrinsic Statistical Properties

Abstract

In view of potential application to biomedical diagnosis, tight transcriptome data quality control is compulsory. Usually, quality control is achieved using labeling and hybridization controls added at different stages throughout the processing of the biologic RNA samples. These control measures, however, only reflect the performance of the individual technical manipulations during the entire process and have no bearing as to the continued integrity of the RNA sample itself. Here we demonstrate that intrinsic statistical properties of the resulting transcriptome data signal and signal-variance distributions and their invariance can be identified independently of the animal species studied and the labeling protocol used. From these invariant properties we have developed a data model, the parameters of which can be estimated from individual experiments and used to compute relative quality measures based on similarity with large reference datasets. These quality measures add supplementary, non-redundant information to standard quality control estimates based on spike-in and hybridization controls, and are exploitable in data analysis. A software application for analyzing datasets as well as a reference dataset for AB1700 arrays are provided. They should allow AB1700 users to easily integrate this method into their analysis pipeline, and might instigate similar developments for other transcriptome platforms.

Introduction

Transcriptome studies using microarrays have become a commonplace assay in biological research. A major limitation of the technology challenges data analysis. The absence of a correct theoretical model for the hybridization process combined with the impossibility to generate gold-standard samples make it unachievable to normalize signals either between different probes or absolutely, and hence, the quantification of RNA molecule abundance in the sample is only relative. In view of potential utilization of microarrays in biomedical applications, this limitation is a severe draw-back. For instance, inter-assay, inter-method, and inter-platform comparisons become extremely challenging without absolute quantification of the molecular species under study. Comparative studies of inter- and intra-platform variations clearly support this view ^{1, 2, 3, 4}. The absence of positive controls for the ensemble of the scored RNA species thus significantly augments the need for tight quality control of the experiments in order to achieve reliable measurements. The importance of developing quality control approaches and standards is well illustrated by the existence of the MicroArray Quality Control (MAQC) Project ^{4, 5}, where scientists from academia and the main commercial technology providers work together on the definition of assay and data standards and practices to follow.

Today, quality control (QC) of transcriptome measurements is typically assured through the combination of four different elements: First, the to-be-analyzed RNA samples, as well as the labeled products of the reverse transcriptase reactions, are assayed for the quantity, purity and integrity. These measurements rely entirely on the determination of average parameters that only reflect the overall quality of the sample and not the quality of the preparation of individual species within the complex mixture. Ironically, the only individual species that – for reasons of their abundance – receive particular attention during this assessment are the major ribosomal rRNAs that have subsequently to be removed from the mixture. Furthermore, these measurements can only be performed prior to hybridization on the arrays. Since the hybridization process itself takes typically longer than ten hours at heightened temperatures, nothing can be said about the integrity of the sample on the array ^{6, 7}.

Second, the so-called spike-in controls are added at various steps of sample preparation, labeling and hybridization in order to control the efficacy of the different enzymatic reactions or enrichment steps. The spike-in molecules are often RNA, cDNA, or cRNA sequences derived from distant species, or synthetic sequences that are then captured by dedicated probes on the microarray in order to testimony efficiency and homogeneity of the different experimental steps. These controls are of defined quantity and tested for minimal cross-hybridization to the reminder of the probes. Likewise, synthetic sequence probes are spotted to the arrays for background appreciation through cross-hybridization ^{1, 8, 9}.

Third, the spot integrity of the array is often also assayed through the use of uniform, pre-labeled sequence species that hybridize to co-deposited control oligonucleotides at each spot on the array. These controls are thought to testimony the presence of the main probes following essentially a guilt-by-association reasoning. More importantly, they quantify the uniformity of the array spotting and array surface, and thus can be used for normalization of heterogeneities at this level ^{10, 11}.

Finally, different computational methods based on the above measurements and sometimes mean signal intensities are used to estimate probe by probe and global reliability measures. These are then used to eliminate individual measurements or the entire array from down-stream analysis ^{12, 13}.

To offer another view of the quality control issue and complete the existing solutions, we propose a method to estimate quality through intrinsic statistical properties of the signal and the signal-variance distributions of all probes on an array.

By analyzing large numbers of transcriptome experiments from our Applied Biosystems AB1700 platform, we have previously reported a particular data-structure of the microarray signal and signal-variance distributions, which is quite distinct from Affymetrix platform generated data (14). The main characteristic of AB1700 system data is the presence of a mixture of two lognormal distributions for the signals, rather than a single one (15). The signal-variance distribution of the data also reflects this bimodal separation of probes and thus reinforces the observation (14). The dual distribution character of the data is suggested to be independent of the animal species analyzed or the amplification protocol chosen. While the origin of this distinct feature of AB1700 transcriptome data is today not fully understood [for a discussion of different hypotheses please refer to Noth et al. (14)], it is of no importance to the fact that it can be exploited in characterizing this particular type of microarray experiments. In fact, we have shown that a model created to capture the main characteristics of this invariant property of the AB1700 data can be used to estimate a parameter set from individual experiments, which in turn can serve to generate synthetic, random pseudo-data with indistinguishable statistical properties (16).

Here, we first demonstrate that the above distribution properties indeed need to be considered as invariant with respect to the origin of the RNA samples and the protocol used for hybridization, by using 1,050 AB1700 experiments generated in part (65%) in our group and in part (35%) from published experiments from other research groups. Furthermore, the intrinsic statistical properties of the data are well captured by a slightly modified version of the previously developed data model. Finally, by estimating the parameters for the refined model from a given experiment and comparing them to a large reference dataset containing the averages and variances of the corresponding parameters from either a curated set of 500 or an un-curated set of 300 experiments drawn from the total 1,050 ones as reference, a similarity measure can be computed. We show that this similarity measure is characteristic of the distinctness of the analyzed experiment with respect to the reference set, and hence can be used to analyze the homogeneity of individual assays within a group. Since the similarity measure is calculated from the sample generated signals and coefficients of variance only, it is totally independent of the above discussed quality control estimators, and thus adds non-redundant information to the QC process. As demonstrated using two publicly available datasets, which meet all of the standard QC measures, outliers can be identified and their removal can lead to significant changes in the interpretation of the data.

Results and Discussion

Invariance of mixture signal distribution in AB1700 data

The AB1700 microarray technology commercialized by Applied Biosystems is characterized through the use of long (60 mer) oligonucleotides as probes, a chemiluminescence-based detection chemistry, and optimized array surface chemistry (14). We have previously shown that the AB1700 platform is more sensitive than the Affymetrix setup by comparing 50 unrelated and heterogeneous AB1700 experimental datasets to an identically sized group of publicly available similarly heterogeneous Affymetrix datasets (14). A similar study has compared AB1700 to current Agilent technology (17). In our study we have furthermore made the unexpected observation that AB1700 generated data represent a mixture distribution of yet unidentified significance (14) (Figure S1). Theoretical studies had suggested that transcriptome signal distributions are always lognormal distributed (15), while the signal distribution of AB1700 data clearly is composed of two independent lognormal distributions as evidenced by expectation maximization and likelihood analysis (14). Based on the characterization of the signal and signal-variance distribution of this initial set of 50 experiments, we had developed a mathematical model that can be efficiently used to describe the statistical properties of AB1700 data by estimating the model parameters on individual datasets ^{14, 16} (Figure S1).

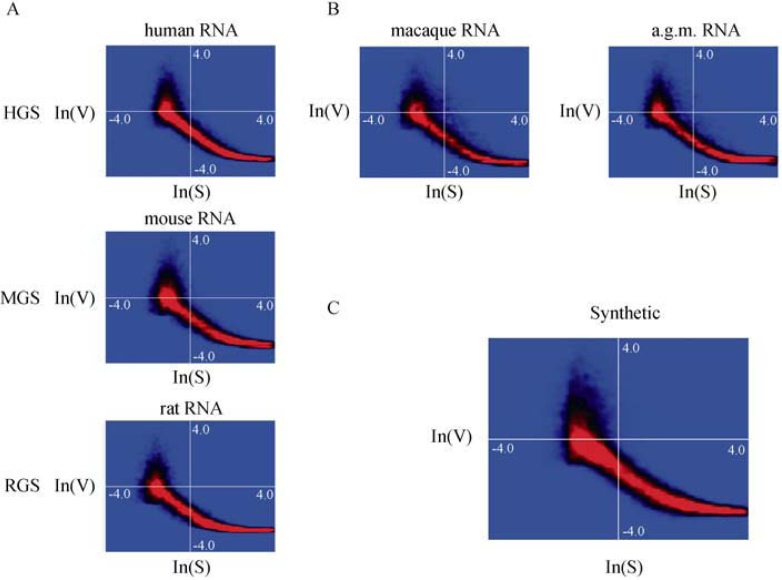
The analysis of a total of 1,050 publicly available and new experiments generated in our group permits to validate the mathematical description of the statistical properties of AB1700 data. Lists of 500 and 300 arrays used to generate reference compendia can be found in Tables S1 and S2 for details on the array technology, species, and labeling methodology. We thereby included data for the three different species for which dedicated microarrays are available (human, mouse, rat). Furthermore, we also used experiments where primate mRNAs were hybridized to human arrays, as we have shown before that the human array versions are suitable to determine transcriptome profiles both from Asian Macaques and African Green Monkeys ^{18, 19}. An initial dataset of 750 arrays encompassing data generated using either of the two alternate labeling protocols, first and second generation arrays, as well as the human arrays hybridized with RNA isolated from the two different monkey species, was assembled in order to be representative for all of these different conditions (Data File S1). The resemblance of data from different species as well as from different tissues of a single species is striking, as shown in Figure 1A, which displays heatmaps with natural logarithm transformed signal-variance over signal data. It is independent of cross-hybridizing monkey RNA to human arrays (Figure 1B). Importantly, synthetic, random pseudo-data generated using our mathematical model display the same distribution properties (16) (Figure 1C). When analyzing more carefully the parameter value distributions of the entire set of 750 arrays (Figure S1 and Data File S1), these initial findings are confirmed. For instance, the relative weight of the two signal distributions, and therefore the fraction of probes returns signal values that belong to the second lognormal distribution averaging at 0.649 with standard deviation 0.06 (consult Figure S2 for a histogram). Therefore, on average, a third of all probes returns signal values belonging to the first signal distribution (14) (Figure S1). If the same signal distribution model is applied to Affymetrix data, the average over 50 individual experiments is 0.400 with standard deviation 0.07 (Figure S2), confirming the distinct (the means differ by >3.5× standard deviations) distribution properties between the two technologies (14). Similar observations can be made for the other parameters of our model. In conclusion, we confirm that the overall mixture distribution structure of AB1700 data, independent of biological origin and labeling protocol, is an invariant.

Figure 1.

A. Heatmaps of signal-normalized logarithmic coefficient of variance (V) against logarithmic signal (S) for one actual dataset example from each of the three species for which AB1700 arrays are available. The color gradient from blue to black to red indicates the density of the data points. The distribution is characteristic of the AB1700 data. B. Similar heatmaps showing the distribution of ln(V) vs. ln(S) for two monkey species hybridized to the human AB1700 arrays. C. A heatmap of the same distribution for random data generated from our AB1700 signal and signal-variance model. Note that the distribution closely resembles those from actual data.

A modified signal and signal-variance distribution model for AB1700 data

We have already shown previously how this invariance of the data structure of AB1700 experiments can be efficiently used to draw random pseudo-data from the parameterized model we had previously presented (16). In order to even better capture the statistical properties of individual experiments, and after having observed a certain variability in the signal and signal-variance ranges that is only poorly captured by the parameters of the two lognormal distributions, we have decided to add the natural logarithm of the signal range and the signal-variance range, as estimated on the 99% quantile in both dimensions, as independent characteristic parameters to our model. The estimation of both parameters, alongside the previously defined parameters for the entire set of 750 assays, their averages and standard deviations, can be found in Data File S1.

Similarity measures for QC

Having obtained 750 independent parameter estimates for the signal and signal-variance distributions, we can calculate now their averages and standard deviations. For any new experiment, after having estimated its parameter values as well, the question of how similar or distinct they are when compared to the averages of the 750 previous experiments can be assessed. Given the fact that the main statistical properties of the data distributions are invariant for all the experiments, we have so far analyzed and constituted a representative sample for all the species studied, such a similarity measure will capture significant deviations from the average. While in such, a significant deviation from the average of analyzed data does not necessarily indicate technical problems with the array analyzed, but may indeed reflect a very particular biological setting. This information gained by analyzing similarity can provide an important indicator as to verify the given experimental result through bioinformatics analysis or experimental repetition in form of technical or biological replicates.

Calculation of the similarity measure, or index, is simply achieved by calculating a normalized sum of the deviations from the variance-weighted averages of the entire set of parameter estimates between the reference file and the array being analyzed (see Materials and Methods). In this way, the Similarity Index (S.I.) takes form of a likelihood measure that can take non-zero values only in the interval [0, 1]. Furthermore, the S.I. is more sensitive to outliers. Obviously, the S.I. does not have any absolute bearing and depends on the reference dataset used for its calculation. Therefore, reporting S.I. values requires concomitant reporting of the reference data.

A robust reference set

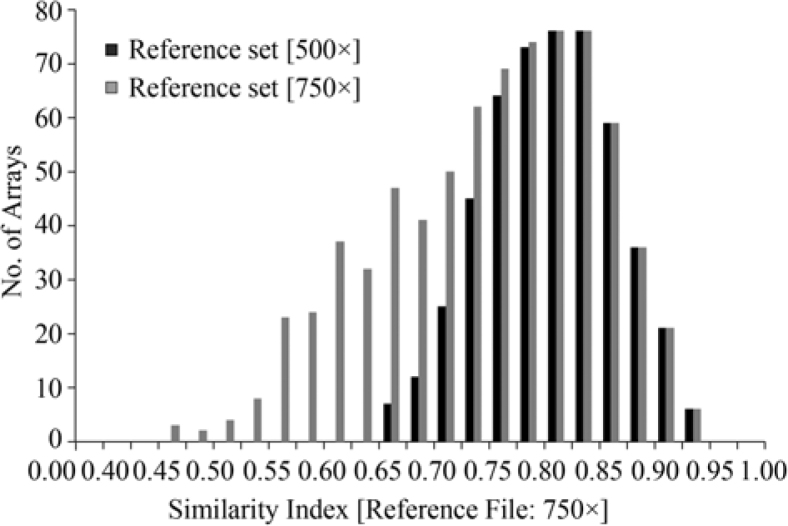
In absence of an absolute standard we next asked how representative and robust our reference dataset is. To this end, we calculated the S.I. measures for all of the 750 experiments in the reference dataset using this very same reference file. While every array is analyzed against a standard it contributes to, this auto-referencing is of negligible (1/750) extent. A histogram of the repartition of the S.I. values for the entire dataset is shown in Figure 2 (gray histogram). The distribution of S.I. values is smooth and skewed towards lower S.I. values. As the only criterion that was available in order to select an experiment for the reference dataset was whether or not the array had met the standard QC criteria defined by the AB1700 system (which in some cases we only could assume to be true for the published experiments we analyzed), we expect that the reference dataset contains arrays of different technical quality. On the other hand, to some small extent, statistically not appreciable given the sample size, we cannot rule out the possibility that differences in S.I. values also reflect some biological reality. Hence a compromise between robustness and representation had to be established. We therefore used a simple bootstrapping procedure to remove in total a third of the experiments from the 750× reference dataset. This was achieved by removing in successive rounds of 100, 100, and then 50 of those experiments with the smallest S.I. values, while at each round recreating a reference dataset of size 650, 550, and finally 500, respectively, and recalculating the S.I. values (see Materials and Methods). When testing the resulting 500× dataset (Data File S2) on the original 750× reference set, we accordingly obtained a more symmetric distribution, which is no longer significantly skewed to lower S.I. values (black histogram in Figure 2).

Figure 2.

Superposition of the two S.I. value histograms for the 750× and 500× reference files. Note that the first (empty) bin is of different size than the others.

We next tested the robustness of our 500× reference dataset. To this end, we first compared again arrays from different species (HGS, MGS, RGS) in order to insure that the distribution of the S.I. values still is homogeneous and comparable between the different array versions. From all three organisms (human, mouse, rat), we selected 50 independent experiments at random and calculated their S.I. values with respect to the 500× reference set (Figure S3). No significant differences can be observed, hence, the 500× reference dataset faithfully reflects the species invariance of the signal and signal-variance distributions. Note also that the 500× reference set is similarly composed of about 30% of publicly available data and 70% of our own, yet unpublished, datasets. Therefore, the bootstrapping strategy has not detected any significant differences in the overall quality of the data from both origins.

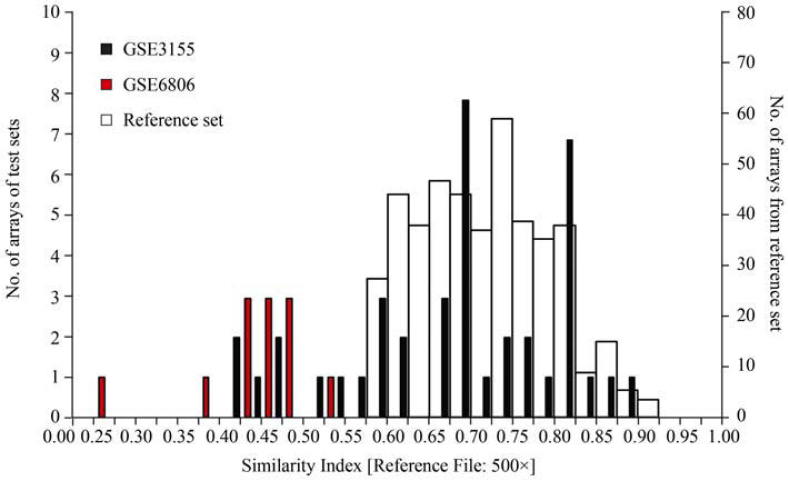
Second, we compared the S.I. values calculated using either the 750× or the 500× reference dataset for one given experimental series (GEO dataset GSE3155) (20) containing 40 individual arrays (Table S3). The S.I. values based on the 500× dataset are always higher than those calculated based on the 750× dataset. This is expected, as we had removed the low ranking experiments when creating the 500× set, thereby obviously increasing the average and median values. Furthermore, the ranking of the arrays based on the 750× dataset is different from the one when using the 500× set. This can also be expected since small changes in the average values will translate into a non-homogenous effect on very closely related S.I. values. The idea of restricting the reference dataset to the 500 high-ranking experiments was precisely to enhance the resolution of the S.I. values for homogeneous series such as the one analyzed here (Figure 3). It is, however, also clear from this analysis that those experiments that can be considered significantly different from the reminder of the experiments (Figure 3, black histogram, 0.40<S.I.<0.50) are the lowest ranking arrays in both analyses using either the 750× or the 500× reference dataset (Table S3, labeled in red). Both reference files therefore generate similar distributions and permit reproducibly the detection of inhomogeneities within an experimental series. The 500× reference dataset thereby permits higher resolution given its higher average and median values.

Figure 3.

Superposition of the S.I. value histograms for the two data series GSE3155 (black) and GSE6806 (red) as calculated using the 500× reference dataset. Note that the first (empty) bin is of different size than the others. The auto-referenced set of 500 arrays making up the 500× is shown as backdrop (white bars).

As a last test of robustness, we selected 100 experiments from both the 750× and the 500× reference datasets at random. From these subsets new reference files were calculated. The procedure was repeated a total of 10 times for both original reference datasets. The data from the experimental series GSE3155 (20) were then analyzed based on these 20 reference files created from the random subsets. For comparison, we then analyzed their mean S.I. variance, the variance over the mean S.I., and the rank of every single experiment across the entire set of 20 classifications (Table S4). Furthermore, we determined the mean of S.I. variances and the variance of the S.I. means. Again, while significant numbers of experiments change rank when comparing the different reference datasets, these rank changes are basically only local random permutations of closely related experiments as indicated by the low values of the mean of S.I. variances and the low variance of the S.I. means. Therefore, even reference datasets created of 1/5 and 1/7.5 of the initially collected experiments can faithfully reproduce the overall distribution of data (Figure S4), yet another indicator of the robustness of the strategy.

In conclusion, the 500× reference dataset generated here is sufficiently representative and robust to analyze the homogeneity of experimental results within an experimental dataset. Obviously, no absolute indicator of quality can be derived based on such a strategy; however, the relative distance of a single experiment to the average of a large and representative data collection, as well as intra series inhomogeneity is easily appreciable. The S.I. values calculated here thereby have no bearing as to either absolute technical quality or biological variability, but serve as a sensitive indicator of rare events. This information is unique, as standard QC protocols do not take into consideration the intrinsic statistical properties of the data signal and signal-variance distributions. The S.I. values can then be utilized for downstream analysis as demonstrated below. As a final proof of robustness of the approach developed here, we then generated another reference file from 300 new experiments taken again from the public database GEO and our ongoing experimentation (Table S2 and Data File S3). These data are completely unrelated to the ones we had used above, and were not curated as the 500× reference set. Both this new 300× and the curated 500× reference sets were then compared to each other (Figure S5) by recalculating the S.I. values for the 500 experiments used for the 500× reference file using the 300× reference file (Figure S5A), and vice versa (Figure S5B). The bell-shaped distribution of the 500 experiments from the curated 500× reference file is preserved when using the 300× file, similarly the distribution of the 300 non-curated experiments is preserved when using the 500× reference file. This cross-over analysis demonstrates that the overall properties of the S.I. value distributions are independent of the experiments that were used to generate the reference files. It also demonstrates that the bootstrapping approach we used to generate the 500× reference set out of the initial 750 experiments is an appropriate method to sharpen the distribution, and consequently increase the resolution achieved with the curated reference file. Both the curated 500× and the un-curated 300× reference sets were then used in parallel to demonstrate their effectiveness as QC measures for biological analysis.

Using S.I. measurements in transcriptome data analysis

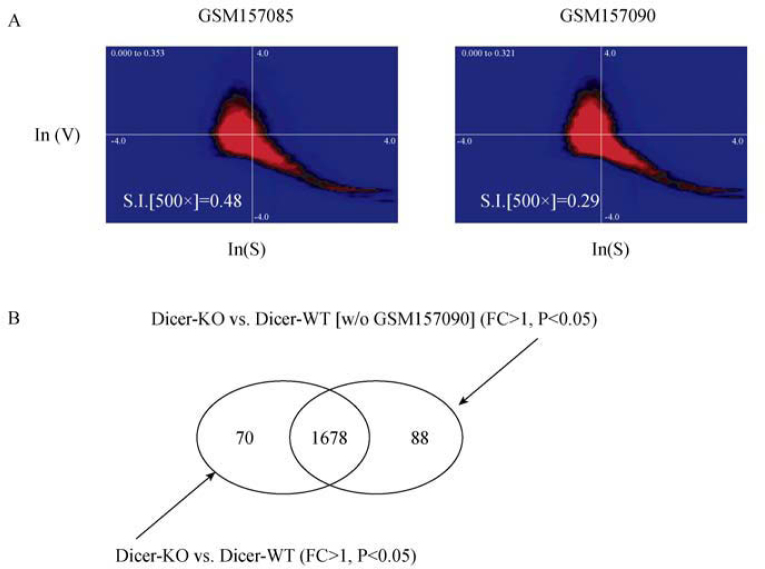
In order to demonstrate the interest of our method of estimating experimental homogeneity based solely on invariant properties of the intrinsic statistical signal and signal-variance distributions, we chose to analyze another public experimental dataset (GEO No. GSE6806) (21). As can be appreciated in Figure 3 (red histogram), this small experimental series of 12 independent experiments displays both a relatively strong deviation from the mean of the 500× reference dataset (white histogram in background) and one outlier. The deviation from the mean of the 500× set can be explained by the nature of the data. In fact, the microarrays from the GSE6806 study were generated using RNA from single mouse oocytes, thus from very small quantities of total RNA by using an amplification strategy (21). Both the small amount of starting material and the amplification lead to slightly modified signal and signal-variance distributions as one can expect. Figure S6 shows that a similar distribution of the data from GSE6806 is obtained when comparing the curated 500× and the new 300× reference file in the calculation of S.I. values. Most importantly, independently of which reference file is used, the array/experiment GSM157090 is isolated as an outlier. In Figure 4A we show a ln(variance) over ln(signal) plot for two different datasets from this series. The overall shape of the signal and signal-variance distributions closely resembles the examples shown in Figure 1; however, the parameter estimation reveals differences sufficient in amplitude and consistent over several parameters as to clearly set this dataset apart from the mean of datasets analyzed (Figure 3, red versus white histogram). Therefore, our procedure is capable of detecting faithfully such differences, whether they stem from particular experimental conditions as in this case or from technical difficulties.

Figure 4.

A. Ln(V) versus ln(S) heatmaps for two experiments from the GSE6806 series. The S.I. values based on the 500× reference set are indicated. B. A Venn diagram depicting the number of probes considered statistically significantly (P<0.05) upregulated when comparing the Dicer knockdown (Dicer-KO) versus the wild-type (Dicer-WT) case either with or without the GSM157090 experiment.

We next decided to reanalyze the data from the GSE6806 series once with and once without the assay GSM157090, for which we calculated the S.I. of 0.29 and which even when compared to the mean of the experiments in the GSE6806 study should be considered an outlier. Note that from the distributions of the data, by eye no significant difference between the sample GSM157090 (outlier) and other samples of the same series such as GSM157085 can be made (Figure 4A). As detailed in the Materials and Methods section, we utilized an analysis strategy closely resembling the initial analysis performed by the authors of the original study (21). We thereby simply determined the number of statistically significant probe signal differences between the two experimental conditions (Dicer knock-down, and control) (21) once including all datasets and once without the dataset GSM157090 (Figure 4B and Data File S4). As can be appreciated from the Venn diagram shown in Figure 4B, slight differences (<5%) in the number of probes reporting statistically significant (P<0.05) induction (FC>1) of genes can be observed.

We next performed a downstream pathway analysis of the retained probe sets for the two conditions using the Panther database annotations and the same conditions as those of the initial study (21) and a multiple testing correction by the Bonferoni method. The authors of the GSE6806 study reported on 10 biological processes that were enriched in after their data analysis (21). We see seven of these pathways also enriched with a statistical significance of P<0.05 taking into account the Bonferoni correction for multiple testing (from the published data, it is not clear whether the authors of the initial study also used a correction and what the nature of the procedure was, which might explain the differences observed). In any case, analyzing both datasets (with and without sample GSM157090), we observe an enrichment of probes corresponding to the same biological processes (Table 1). When removing the sample GSM157090, however, we do isolate an additional eleven genes that map to the two highest ranking biological processes (Table 1), and thereby augmenting the significance of the observation (please compare the P values). In this second analysis guided by our QC procedure, no genes belonging to any of the other biological process ontologies are “lost”. Note that the corresponding P values increase slightly as the relative distribution of genes to ontological categories changes due to the fact that the additional eleven genes map only to the first two categories. Hence, the removal of the GSM157090 dataset from the downstream analysis enhances the quality of the observation made by sharpening for instance the differences between the statistically significant biological process categories. It can be expected that not only the additional eleven genes mapping to the two most significant biological process categories are of relevance, but also others of the 88 additional probes detect significant changes in gene expression relevant to the biological phenomenon studied.

Table 1.

Comparison of the biological processes detected as significantly (P<0.05) enriched in the analysis of statistically significantly upregulated probes either including or not the GSM157090 experiment

Biological process	Dicer KO vs. Dicer WT			Dicer KO vs. Dicer WT [w/o GSM157090]
	Count	Expect	P value	Count	Expect	P value
Protein biosynthesis	157	32.68	8.31E-55	167	33.02	1.78E-61
Chrom. Segreg.	25	6.15	1.72E-6	26	6.22	4.94E-7
Translational Reg.	20	4.97	5.90E-5	20	5.02	6.89E-5
Chrom. Pack & Remod.	31	12.36	8.69E-4	31	12.48	1.05E-3
DNA replication	19	6.60	1.03E-2	19	6.66	1.17E-2
Oxidat. Phos.	14	4.23	2.49E-2	14	4.28	2.75E-2
Nuclear transport	15	5.02	4.13E-2	15	5.07	4.58E-2

Note: “Count” indicates the number of probes annotated to the corresponding ontology term and present in the list of statistically significantly regulated probes of the corresponding condition. “Expect” is the number of probes corresponding to the ontology term that would be expected based on a random zero-hypothesis. P values were determined using a Bonferoni correction for multiple testing.

In conclusion, the QC procedure introduced here is capable of detecting inhomogeneities (of whichever origin) between transcriptome experiments within an experimental series or between different experimental series. This information can be used to better guide downstream analysis, for instance, by removing outliers that otherwise went undetected using standard quality assessment techniques.

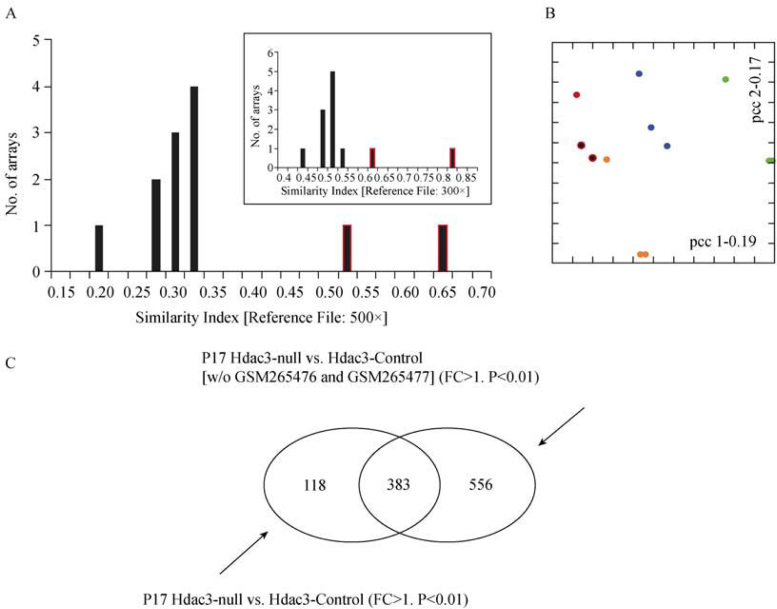
In order to demonstrate generality of our QC methodology, we next analyzed another published dataset (GEO No. GSE10503) (22). This dataset is again composed of twelve independent experiments in four different biological conditions, where mouse Hdac3-null versus control cells are compared at two different developmental stages (P17, P28) (22). Using the 500× reference file, we determined the S.I. values for the entire series of experiments (Figure 5A). We also calculated the S.I. values for all 12 experiments using the 300× reference file (inlet, Figure 5A). In both cases two outliers can be identified (indicated by red-borders in the histograms). Interestingly, the outliers in this dataset have higher S.I. values than the majority of experiments. As the S.I. values have no absolute meaning (see also Conclusion section), this does not imply that the two outlier experiments are of better quality than the others. Simply, there is a significant heterogeneity in this experimental series that can be picked up using our approach. It is also interesting that this heterogeneity is not appreciable when using other methodology such as principal component analysis (PCA). Figure 5B shows a PCA in correspondence space for the same set of data. The two outliers we identified independently using the two reference datasets (Figure 5A) are again marked with red borders. Similarly, as for the data shown in Figure 4, we then re-analyzed this experimental series in two different ways: (1) as described originally (22), and (2) by removing the two outlier experiments. The relative numbers of genes identified as statistically significantly (P<0.01) regulated between the Hdac3 knock-out and control cells at P17 are illustrated in the Venn diagram of Figure 5C. Through subsequent ontology enrichment analysis of the QC curated data, we identify the same biological process as the authors of the original study as being the most significantly enriched (Table 2) (22). However, and similarly to the results shown in Figure 4, we detect more genes belonging to this biological process as being regulated, and therefore, increase statistical significance of the result by three orders of magnitude (Table 2). Table 3 lists those genes belonging to the “Lipid, fatty acid and steroid metabolism” biological process that we identify in addition to those found by the authors of the original study (22), which are statistically significantly regulated at both P17 and P28. Note that our QC procedure only affected the P17 condition.

Figure 5.

A. S.I. histogram of the individual experiments of series GSE10503 using the 500× reference file. The inlet shows the same series analyzed using the 300× reference file. The two outlier experiments are displayed with a red border. B. A principal component analysis in correspondence space of the GSE10503 series. The two outlier experiments as identified in (A) are indicated using the same color code as in (A). Every biological condition is displayed using its own coloring. C. A Venn diagram depicting the number of probes considered statistically significantly (P<0.01) regulated when comparing the Hdac3-null versus the Hdac3-control experiments either with or without the two outliers identified in (A).

Table 2.

Comparison of the biological process detected as most significantly enriched in the analysis of statistically significantly regulated probes either including or not the outlier experiments

Biological process	P17∩P28 Hdac3-null vs. Hdac3-Control			P17∩P28 Hdac3-null vs. Hdac3-Control [w/o GSM265476 and GSM 265477]
	Count	Expect	P value	Count	Expect	P value
Lipid, fatty acid and steroid metabolism	26	4.29	7.12E-12	33	5.37	3.14E-15

Table 3.

Additional genes identified as being statistically significantly regulated in both the P17 and P28 biological conditions after removal of the two outliers in the P17 condition

Probe ID	Gene name	Gene symbol	Average fold change
			P17 [w/o replicates]	P28
381504	monoacylglycerol O-acyltransferase 2	Mogat2	2.9058	5.9897
400599	ATP-binding cassette, sub-family A (ABC1), member 8a	Abca8a	-1.1872	-3.1906
437440	hydroxysteroid (17-beta) dehydrogenase 9	Hsd17b9	-1.2689	-4.2387
441362	sulfotransferase family, cytosolic, 1C, member 2	Sult1c2	-1.0925	-1.9719
501043	ethanolamine kinase 2	Etnk2	-1.2624	-1.8293
772131	cytochrome P450, family 2, subfamily d, polypeptide 13	Cyp2d13	-1.0796	-5.3676
829262	acyl-CoA thioesterase 10|acyl-CoA thioesterase 9	Acot10|Acot9	1.2657	2.2433
916709	hexosaminidase A	Hexa	1.2189	1.0132
920047	cytochrome b5 reductase 3	Cyb5r3	1.0222	1.4030

Note: The average fold changes are expressed as log2.

In conclusion, we have shown by using two previously published datasets that our QC methodology is capable of identifying outlier experiments that went undetected using standard QC approaches. The re-analysis of both experimental series after removing the outliers can be shown to lead to results of higher statistical significance and the identification of additional genes that are important to the biological function under study. Finally, we have demonstrated the robustness of our empirical method, as we have demonstrated that both the 500× reference file and the totally unrelated and un-curated 300× reference file in both cases lead to the identification of the same outliers.

The ace.map QC 1.0 application

Having shown that our procedure indeed adds valuable information to the quality control process of transcriptome data, we decided to generate a software application for this purpose and make it available to any researcher interested in using this QC procedure when working with AB1700 data. The application that we sought to create is specifically tailored to the process detailed in the works presented here, and comes with the 500× reference dataset discussed. In order to assure computational platform independence, and given the heterogeneity of exploiting systems used, we have decided to develop a JAVA program that can be executed on any standard operating system (Solaris, Linux, Windows, Macintosh) equipped with the freely available SUN Microsystems JRE package. The ace.map QC program was conceived to be as user friendly as possible and comes with a detailed user’s guide, which should be consulted for information on the operation of the software. The algorithms implemented allow automatic processing individual AB1700 data files as well as entire datasets composed of several input files. The model parameter for the signal and signal-variance distributions are automatically calculated and displayed through a graphics interface. Furthermore, the S.I. values are calculated based on a user-specified reference file. While we provide the 500× reference file discussed here together with the application, the functionality for creating such reference files is included in the application, and any user can generate her/his own reference file. Details on the algorithm and the software can be found in the user’s guide (Data File S5). The software can be downloaded for non-commercial, public research from the website (http://seg.ihes.fr) in the “web sources”, “software” section (Data File S6). Figure S7 shows an exemplary screen-shot of the running application.

Conclusion

Using invariant statistical properties of AB1700 transcriptome profiles, we describe here a simple procedure to estimate microarray quality using reference datasets. Interestingly, the similarity estimation is based solely on the intrinsic signal and signal-variance distributions, and hence independent of spike-in and control probes on the microarrays. Our procedure is thus complementary to those standard procedures as it provides non-redundant a posteriori information on the overall integrity of the RNA sample analyzed. While our method is based on empirical observations, the interpretation of the S.I. values that we can determine from the statistical properties of the signal and signal-variance distributions is not straight-forward. However, it does not affect the robustness of the approach that has been developed using a total of 1,050 experiments from very different sources, as we demonstrated using two independent reference datasets. We believe that the bias in the purification, enrichment and labeling of mRNAs of different length and structure will result in skewed distributions of the signals obtained during microarray analysis. Our method faithfully picks up these skews and translates them into a single quantity that can be used to compare experiments from within a series or across series. We have also shown by using two independent, public, and previously published datasets to illustrate how our novel methodology can be used to identify outliers in experimental series and how the elimination of outliers enhances the statistical significance of the analysis results. In this way we have provided compelling evidence for the statistically significant regulation of additional genes that had gone undetected in the analysis schemes originally employed ^{21, 22}. Most importantly, our method is thereby complementary but non-redundant to existing QC approaches, hence provides additional and new insights into the quality of the microarray experimentation. The provided software application as well as the reference files should allow AB1700 users to easily integrate this method into their analysis pipeline, and might instigate similar developments for other transcriptome platforms.

Materials and Methods

AB1700 microarray technology

All experimental data referred to in this manuscript were either generated on our Applied Biosystems AB1700 transcriptome platform (Product No. 4338036), or downloaded from the NCBI Gene Expression Omnibus (http://ncbi.nlm.nih.gov/geo). Tables listing the size and origin of the different datasets used to generate the 500× and the 300× reference files are found as Tables S1 and S2.

RNA labeling, hybridization and detection

RNA amplification, RNA labeling, hybridization and detection were done following the protocols supplied by Applied Biosystems together with the corresponding kits. 15-20 μg of total RNA sample was subjected to Chemiluminescence RT labeling (Applied Biosystems, Product No. 4339628), alternatively 1-2 μg of total RNA was subjected to RT-IVT amplification and labeling (Applied Biosystems, Product No. 4339628). Labeled cDNAs were then hybridized and detected according to the supplied protocols (Applied Biosystems, Product No. 4346875).

Data preprocessing and primary analysis

Applied Biosystems Expression Array System Software v1.1.1 (Product No. 4364137) has been used to acquire the chemiluminescence and fluorescence images and primary data analysis. Briefly, the primary analysis consists of the following individual operations: (1) Image correction. Calibration images are used to subtract any device-dependent bias from the raw images and to correct for spectral bleed-through from the chemiluminescence (CL) into the fluorescence (FL) channel. Pixels that are saturated in the long exposure (25 s) CL image are replaced by appropriately scaled values of the short exposure (5 s) CL image. (2) Global and local background correction. Correct globally for non-specific signals and unwanted hybridization, using specific random-oligo-sequence control spots and locally for bleeding between adjacent probes with high intensity differences. A single bias is calculated over the entire array and subtracted from all probes, and a background estimate is calculated using pixels inside an annulus around the feature aperture. (3) Feature normalization. Compensation of spotting variations (comparable to print tip normalization) and optical trends. Normalization of CL intensities by FL-CL ratios. In this step, the variance estimate is calculated, too. (4) Spatial normalization. Spatial trend correction on the feature level using specific (SPN) control spots evenly placed over the array (~1 SPN control in 300 spots). Spatial normalization mainly captures non-uniform illumination of the array. (5) Global normalization. Division of all signals by the median. Note that we renormalize the resulting data according to the median once more after having removed probes for which the Applied Biosystems software has set flags equal to or greater than 2¹², indicating compromised or failed measurements (as recommended by Applied Biosystems) as well as the control probes. This second normalization is not part of the standard AB1700 protocol, and thus was done for both our and the publicly available datasets.

Secondary data analysis

Calculation of subtraction profiles was performed according to standard procedures with the following modifications: data for technical replicates were averaged with weights anti-proportional to their coefficient of variance estimates. Biological replicates from different biologic conditions were compared in an “everyone-against-everyone” scheme and log2 fold-change estimates (“logQ”, “L”) were then determined as averages of weighted individual logQ values. The weights were anti-proportional to the variance over the individual logQ values. For these inter-assay comparisons, the NeONORM method was used for normalization (23) with k=0.20. P values were determined based on a normal distribution hypothesis of signal intensities using standard ANOVA methods. Multiple probes for a single gene, cross-reactivity of a single probe to several genes, as well as the resolution of probe-ID annotations were done according to the standards defined previously (24). Combining GO, KEGG and PANTHER annotations, we assigned all probes present on the arrays to the biological processes from the PANTHER Database (25). We then calculated the relative representation of those probes detected as significantly regulated as compared to a random set of probes drawn from the ensemble of probes. P values for over- and under-representation of pathways were calculated using a binominal distribution and a Bonferoni correction for multiple testing.

Parameter estimation for the 21+2p model

The estimation of parameters for our signal and signal-variance model is described in detail in previous studies ^{14, 16}. Briefly, the ensemble of parameters is estimated for every data file individually using a combination of techniques in the following (also compare Figure S1):

The estimation process is embedded into individual Expectation Maximization (EM) steps. Every EM step thereby re-estimates all parameters over the weighted sample data (logarithmic signal and logarithmic variance) in the previous step. In our case, for every data point i [ln(Signal_i) | ln(Variance0.0_i)] and [ln(Signal_i) | ln(Variance0.34_i)] (from here on: [S_i | V_i]), the weights w_1,i and w_2,i are calculated, which correspond to the combined probabilities:

$$p\left({\theta }_n\left|\right[S_i\left|V_i\right]\right)/\left(p\left({\theta }_1\left|\right[S_i\left|V_i\right]\right)+p\left({\theta }_2\left|\right[S_i\left|V_i\right]\right)\right).$$

These combined probabilities p(θ_1,2 | [S_i | V_i]) are the product of the a priori probability p(θ_n | S_i), and hence the mixture function, and the probability that is determined over the lognormal probability density function at position Vi with the parameters for the corresponding S_i. The weights are being used for the calculation of weighted mean and weighted variance for the first lognormal distribution [m₁(S_i) and s₁(S_i)]. They are also being used by the Gradient Method (below) based parameter estimation as factors for calculating the cumulative error, which is being minimized for the second lognormal distribution. After each EM estimation step, the mixture function is re-estimated using the new weights w_1,i. The EM algorithm terminates either after a preset number of steps is reached (negative abortion), or if the likelihood increase between two EM steps falls below a preset convergence threshold (positive abortion).

A gradient method forming an orthonormal basis via the Gram-Schmidt orthogonalization method is used in succeeding EM steps to ensure improvement of all parameter estimates and in order to avoid oscillations. The iterative search is thus subdivided into n orthogonalization steps, n being the number of parameters of the function to find the minimum for. Each scan consists either of a stepwise movement from the current parameter vector $\stackrel{\mathrm{r}}{x}$, which carries the actual parameter estimates for the distribution at the actual position, into direction $\stackrel{\mathrm{r}}{d}$, with $\stackrel{\mathrm{r}}{d}$ being the orthonormal basis (Gram-Schmidt), using a predefined step-width until the error stops to decrease, or, if the first step already lead to a greater error, the step-width is divided by two until either the error decreases or a maximum number of divisions has been reached. In both cases, the errors of the last three sampled parameter points are used for quadratic interpolation to further improve the estimate. Depending on ε and/or c, a new $\stackrel{\mathrm{r}}{x}$ is calculated. If the corresponding error should be higher than for the best scan estimate, it is replaced by the latter.

Finally, the signal range and signal-variance range are directly calculated over the 99% quantile in logarithmic base 2 space and added to the parameter list.

Generating reference files

For the generation of reference files we used the ace.map QC 1.0 application that is being published here. The algorithm thereby runs the parameter estimation on the specified input data files individually, and once all parameters have been estimated for the entire set of experiments, a table containing the individual parameter estimates, their mean values, their variance, and their standard deviation is generated. Furthermore, a weight for each parameter is determined based on the variance of the corresponding mean parameter estimate. The weights thereby are anti-proportional to the variance, and add up to unity. These weights thus reflect the variability of any given parameter over the datasets used for generating the reference file, and thus define the relative contribution of each parameter to the Similarity Index calculation (see below). Three examples of reference files are found as Data Files S1-S3.

Similarity Index (S.I.) estimation

To be able to estimate the similarity of a new experimental dataset, a reference file has to be created first (see above). The Similarity Index (S.I.) is then calculated by comparing the values of the 23 parameters of the model estimated for the experimental dataset with those from the reference file. The Similarity Index is the variance-weighted sum of the difference between the experimental dataset analyzed and the reference dataset-mean for individual parameters and is defined as:

$$S.I.=\sum _{i=0}^{22}(w_i{e}^{-\frac{{(p_i-m_i)}^2}{2{{\sigma }_i}^2}})$$

with:

$$w_i=\frac{1}{{\sigma }_i.{\displaystyle \sum _{i=0}^{22}}\frac{1}{{\sigma }_i}}$$

and thus can take values between 0 (no similarity) to 1 (perfect match).

Authors’ contributions

FXP, SN and AB conceived the initial idea. GB and SN performed programming. FXP, GB and AB conducted reference file assembly, testing, data analysis and illustrations. AB wrote the manuscript. All authors read and approved the final manuscript.

Competing interests

The authors have declared that no competing interests exist.

Supplementary Material

Figures S1-S7, Tables S1-S4 and Data Files S1-S6

DOI: 10.1016/S1672-0229(10)60006-X