Abstract
The ratio of nonsynonymous substitution rate (Ka) to synonymous substitution rate (Ks) is widely used as an indicator of selective pressure at sequence level among different species, and diverse mutation models have been incorporated into several computing methods. We have previously developed a new γ-MYN method by capturing a key dynamic evolution trait of DNA nucleotide sequences, in consideration of varying mutation rates across sites. We now report a further improvement of NG, LWL, MLWL, LPB, MLPB, and YN methods based on an introduction of gamma distribution to illustrate the variation of raw mutation rate over sites. The novelty comes in two ways: (1) we incorporate an optimal gamma distribution shape parameter a into γ-NG, γ-LWL, γ-MLWL, γ-LPB, γ-MLPB, and γ-YN methods; (2) we investigate how variable substitution rates affect the methods that adopt different models as well as the interplay among four evolutional features with respect to Ka/Ks computations. Our results suggest that variable substitution rates over sites under negative selection exhibit an opposite effect on ω estimates compared with those under positive selection. We believe that the sensitivity of our new methods has been improved than that of their original methods under diverse conditions and it is advantageous to introduce novel parameters for Ka/Ks computation.
Key words: substitution rate, approximate method, gamma distribution, Ka, Ks
Introduction
One of the important parameters for molecular evolutionary analyses is the estimation of the synonymous (Ks) and nonsynonymous (Ka) nucleotide substitution rates, which are respectively defined as the number of synonymous substitutions per synonymous site and the number of nonsynonymous substitutions per nonsynonymous site per year or per generation. It is commonly accepted that Ka>Ks, Ka=Ks, and Ka<Ks generally indicate positive selection, neutral mutation, and negative selection, respectively 1., 2.. There are multifarious methods for estimating Ka and Ks on the basis of various substitution models, which are categorized into two essential types: approximate methods and maximum likelihood ones. In practice, these methods should be applied cautiously and simple conclusions are not easily drawn when only one method is adopted (3). Therefore, it is necessary for us to continue developing diversified models to accurately calculate Ka and Ks.
Since both approximate and maximum likelihood methods usually yield similar estimates based on the same hypothesis 2., 4. and the latter are often time-consuming (5), we only focus on the approximate methods for our analyses. Most existing methods, such as NG (Nei-Gojobori) (6), LWL (Li-Wu-Luo) (7), MLWL (a modified LWL method) (8), LPB (Li-Pamilo-Bianchi) 9., 10., MLPB (a modified LPB method) (8), YN (Yang-Neilsen) (5), and MYN (a modified YN method) (11), consider three significant dynamic features of evolving DNA sequences: transition/transversion rate bias, nucleotide frequency bias, and unequal transitional substitution, but omit another substantial character—unequal substitution rates across sites. In fact, rate variation among nucleotide sites is commonly observed, due to the functional restraint of amino acids at the active centers of proteins 1., 2.. In particular, this is true for protein-coding genes where the three codon positions have different functional constraints for nucleotide substitutions 1., 12.. Since γ-distribution has been widely used to illustrate the characteristics of nucleotide mutation rate 13., 14., 15., 16., especially in the field of estimating sequence divergence 6., 14., 17., 18., 19., 20., 21., we have developed a γ-MYN method (22) by introducing γ-distribution into MYN method (11), and observed that the performance of the new method is better than that of the original one under certain conditions. In this paper, we bring this assumption into other existing methods so that the series of new γ-methods are denoted as γ-NG, γ-LWL, γ-MLWL, γ-LPB, γ-MLPB, and γ-YN. We focus on the performance evaluation of these new methods in combination with properties of various parameters and dynamic features of evolving DNA sequences as well as their influences on Ka and Ks calculations. The descriptions of symbols used in this paper are shown in Table 1.
Table 1.
Symbols used in this paper
| Symbol | Description |
|---|---|
| S | Number of synonymous sites |
| N | Number of nonsynonymous sites |
| Ks | Synonymous substitution rate |
| Ka | Nonsynonymous substitution rate |
| ω | Estimator of selective pressure, ω=Ka/Ks |
| Sd | Number of synonymous substitutions |
| Nd | Number of nonsynonymous substitutions |
| t | Divergence time between two sequences |
| a | The shape parameter of gamma distribution |
| α | Transitional rate |
| α1 | Transitional rate between purines |
| α2 | Transitional rate between pyrimidines |
| β | Transversional rate |
| κ | Ratio of transitional rate/transversional rate |
| κR | Ratio of transitional rate between purines to transversional rate, κR=α1/β |
| κY | Ratio of transitional rate between pyrimidines to transversional rate, κY=α2/β |
| gN | Frequency of nucleotide N, N∈[T, C, A, G] |
| gR | gR = gA + gG |
| gY | gY = gT + gC |
Results and Discussion
Effect of γ-distribution on various methods
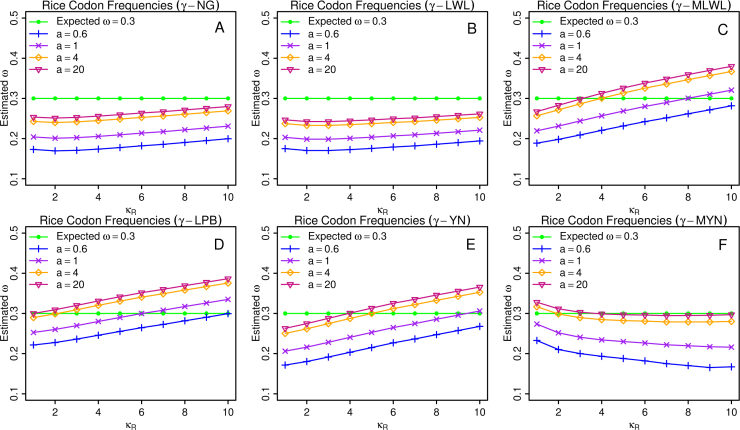
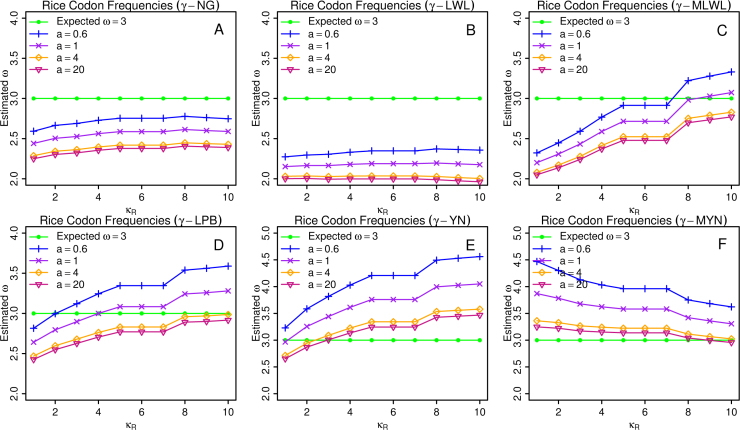
On the assumption that the rate of nucleotide substitution approximately follows the gamma distribution, we have supplemented seven methods: γ-NG, γ-LWL, γ-MLWL, γ-LPB, γ-MLPB, γ-YN, and γ-MYN (22). Since γ-MLPB performs the same as γ-LPB does (Tables 2 and S1; data not shown), we chose γ-LPB for our analyses. We plotted the percentage errors for Ka and Ks, and estimated ω against κR for different expected values, using rice codon frequencies in three conditions of expected ω=0.3, 1, and 3, respectively (Figure 1, Figure 2, Figure 3 and S1–S6).
Table 2.
The optimal values of gamma distribution shape parameter a based on a combination of nine terms and seven methods
| Condition | Term |
a values |
||||||
|---|---|---|---|---|---|---|---|---|
| γ-NG | γ-LWL | γ-MLWL | γ-LPB | γ-MLPB | γ-YN | γ-MYN | ||
| ω=0.3 | Ka | 0.6 | 0.6 | ∞ | ∞ | ∞ | ∞ | 20 |
| Ks | ∞ | ∞ | 4 | 4 | 4 | 20 | ∞ | |
| ω | ∞ | ∞ | 4 | 1 | 1 | 4 | 20 | |
| ω=1 | Ka | 1 | 1 | 4 | 20 | 20 | 20 | 4 |
| Ks | ∞ | ∞ | ∞ | 4 | 4 | 4 | 20 | |
| ω | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | |
| ω=3 | Ka | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Ks | ∞ | ∞ | ∞ | ∞ | ∞ | 4 | 4 | |
| ω | 0.6 | 0.2 | 0.6 | 1 | 1 | ∞ | ∞ | |
Figure 1.
Average ω estimates under the condition of expected ω=0.3. We plotted average ω estimates over 2,000 pairs of sequences based on γ-NG, γ-LWL, γ-MLWL, γ-LPB, γ-YN, and γ-MYN, when κY=3.75 and κR varies from 1 to 10, under the condition of expected ω=0.3.
Figure 2.
Average ω estimates under the condition of expected ω=1.
Figure 3.
Average ω estimates under the condition of expected ω=3.
Let us examine the characteristics of these plots in general. Among them, the curves yielded from γ-NG and γ-LWL remain nearly horizontal regardless the variables Ka, Ks, or ω (Figure 1, Figure 2, Figure 3 and S1–S6). When we examined Ka and Ks, the trends from γ-MLWL, γ-LPB, and γ-YN showed the opposite directions, increasing for Ka and decreasing for Ks (Figures S1–S6). The trend from γ-MYN seems distinct from all the other methods (Figure 1, Figure 2, Figure 3 and S1–S6). From above observations, we categorized these six methods into three categories: (1) γ-NG and γ-LWL; (2) γ-MLWL, γ-LPB, and γ-YN; and (3) γ-MYN, according to their similar tendencies as key parameter varies. We believe that the reason for such tendencies is related to their underlying models; as we know, γ-MLWL, γ-LPB, and γ-YN consider transition/transversion rate bias, γ-MYN takes unequal transitional substitution (between the two purines, or the two pyrimidines), while both γ-NG and γ-LWL leave out the major dynamic features of evolving DNA sequences utilized by other methods.
We now investigate how the diversified values of shape parameter a affect the performances of various methods. Mathematically, when a→∞, γ-series methods are reduced to their corresponding conventional methods. For example, as a→∞ as a=∞ γ-LWL→LWL. Naturally, we denoted a→∞ as a=∞ for simplicity and chose six values (0.2, 0.6, 1, 4, 20, and ∞) as typical a values. Here we did not show the results related to conditions of a=0.2 and a=∞ for two reasons. First, the curves of a=0.2 always extend out of the normal range in comparison with the expected outlines (data not shown) as these cases may not be meaningful for arithmetic applications. Second, the curves of a=20 and a=∞ perform so similar that we are unable to distinguish them (data not shown), therefore we used one of them, a=20, not a=0.2 and a=∞. In Figure 1, Figure 2, Figure 3 and S1–S6, we noticed that most of the curves remain parallel as a varies with minor exceptions in Figure 2. We have a few interesting observations. First, each curve rises in parallel as a decreases when Ka and Ks are examined, regardless whether ω=0.3, 1, or 3. Even though our findings on expected ω=3 are consistent with above observations when ω is examined, the results when expected ω=0.3 are opposite under most of the other conditions. We believe that it is attributable to the distributions of the curves under two other assumptions: expected ω=0.3 and ω=3 (Figure 1, Figure 3). Interestingly, when expected ω=1, each curve seems to rotate around the center in each panel (Figure 2) when ω is examined. Next, when expected ω=0.3, ω changes lie on those of Ks, due to the fact that Ks is more sensitive to the changes of a than Ka. When expected ω=3, ω changes depend on Ka as Ka is more sensitive to a changes. When expected ω=1, a changes have less impact on ω, due to the fact that Ka and Ks have similar sensitivity to a changes. Combining above observations, we conclude that larger values of Ka and Ks are more sensitive to the changes of a.
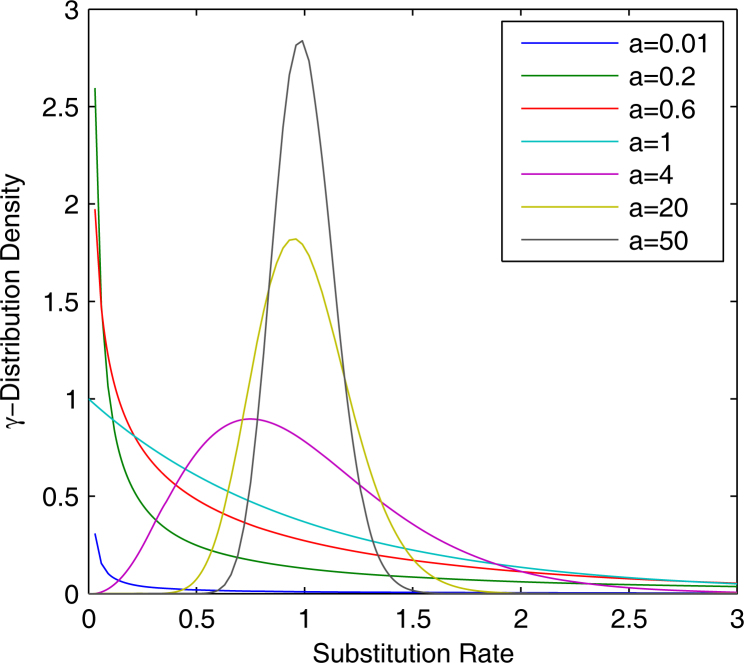
The optimal values of gamma distribution shape parameter a
We computed the optimal indexes (see Materials and Methods) for optimal values of a under various conditions (Table S1) and found the minimal values in each column, whose corresponding a values are considered as optimal (Table 2). To study the implication, we divided a into three categories 1., 2. according to the shapes of γ-distribution (Figure 4): (1) when a<1, the distribution indicates that most of the sites have very low substitution rates despite the existence of a few sites with higher substitution rates; (2) when a>1, the distribution shows that the majority of the sites have intermediate rates around 1, except the fact that some sites may exhibit extreme rates (very low or high); (3) when a goes to the infinity, the distribution becomes a simpler type that all sites have the same rate. Now we only discuss the term ω in combination with Table 2. When the positive and negative selection forces balance each other (neutral mutation), all sites evolve in the same rate regardless what methods were actually used. When γ-NG, γ-LWL, and γ-MLWL are examined, a value decreases with the increasing selective pressure varying from 0.3 to 3. This indicates that significant increase in selective pressure makes more sites evolve in very low rate. However, we found slightly opposite effects in γ-YN and γ-MYN, perhaps due to their shared consideration in nucleotide frequency bias (codon frequency bias) and the complex interplay between nucleotide frequency and variable substitution rates across sites. Another interesting observation is that the pattern of rate variation at sites holds the line under the conditions of both ω=0.3 and ω=3, when γ-LPB is examined.
Figure 4.
γ-distribution densities as a function of substitution rates at various a values of 0.01, 0.2, 0.6, 1, 4, 20, and 50.
Effect of codon frequencies
To examine the influence of codon frequencies on the capability of our new methods, we simulated hypothetical common ancestral sequences on the basis of three datasets: equal, human, and rice codon frequencies. We estimated the performance of our new methods at their optimal values of a under three conditions of ω=0.3, ω=1, and ω=3, using three sets of codon frequencies (Figure 5A–I). As a whole, different codon frequencies have little influence on the performance of our new methods. We also found that their performances under human codon frequencies are similar to those under rice codon frequencies but not under equal codon frequencies.
Figure 5.
Average ω estimates based on the six methods under three different codon frequencies, when κY=3.75 and κR varies from 1 to 10. The codon frequencies used are: equal (A, B, C), human (D, E, F), and rice (G, H, I). ω=0.3 (A, D, G), ω=1 (B, E, H), and ω=3 (C, F, I) stand for purifying selection, neutral mutation, and positive selection, respectively. The values of a used in the six methods are listed in Table 2.
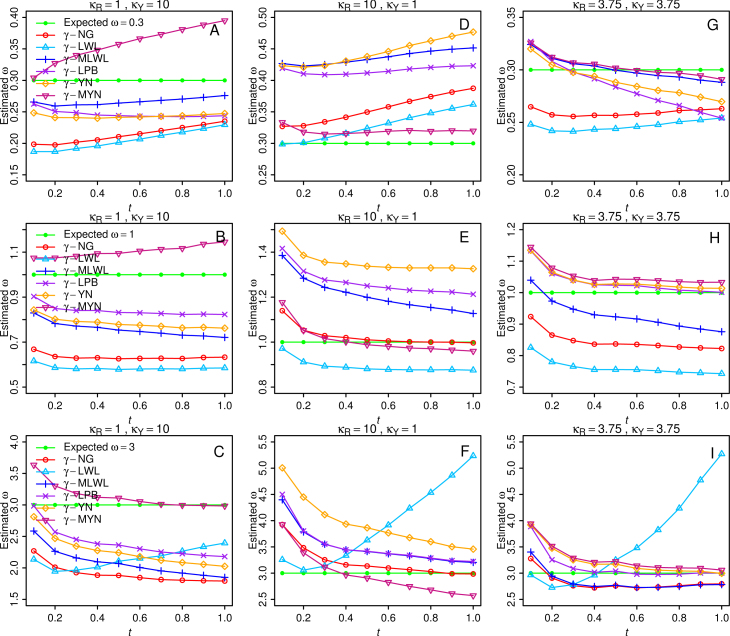
Effect of t
To examine the effect of divergence time based on our new methods, we plotted estimated ω against t (from 0.1 to 1), using rice codon frequencies (Figure 6). To measure the robustness of the methods, we focused on three extreme cases: (1) κR=1, κY=10; (2) κR=10, κY=1; and (3) κR=κY=3.75. In general, most of them do not change much as t increases; it is a sign for robustness. One exception is γ-LWL when the expected ω is 3 and when κR=10, κY=1, and κR=κY=3.75. The fact suggests that γ-LWL is less robust when t approaches the extreme. We thought that the divergence time t is the major factor. However, γ-LWL performs well when κR=1, κY=10, and the expected ω=3.
Figure 6.
Average ω estimates based on the six methods with the consideration of divergence time (t) that varies from 0.1 to 1. We considered the typical values for purifying selection, neutral mutation, and positive selection as ω=0.3 (A, D, G), ω=1 (B, E, H), and ω=3 (C, F, I), respectively. Three different combinations of κR and κY were examined: κR=1, κY=10 (A, B, C); κR=10, κY=1 (D, E, F); κR=κY=3.75 (G, H, I). The values of a used for the six methods are listed in Table 2.
Effects of other parameters
We are aware of other parameters used for arithmetical estimation 5., 11. but paid less attention to them. For S% (the percentage of synonymous sites in a sequence), we found that γ-NG, γ-LWL, and γ-MLWL do not change the estimation of S% much but γ-LPB, γ-YN, and γ-MYN always overestimate S% to different extent (data not shown). In terms of sequence length, an increase often induces biases (11). Since we chose an average sequence length of 400 codons for the analyses, we believe that our new methods should maintain their advantages when sequence length changes.
Testing real data
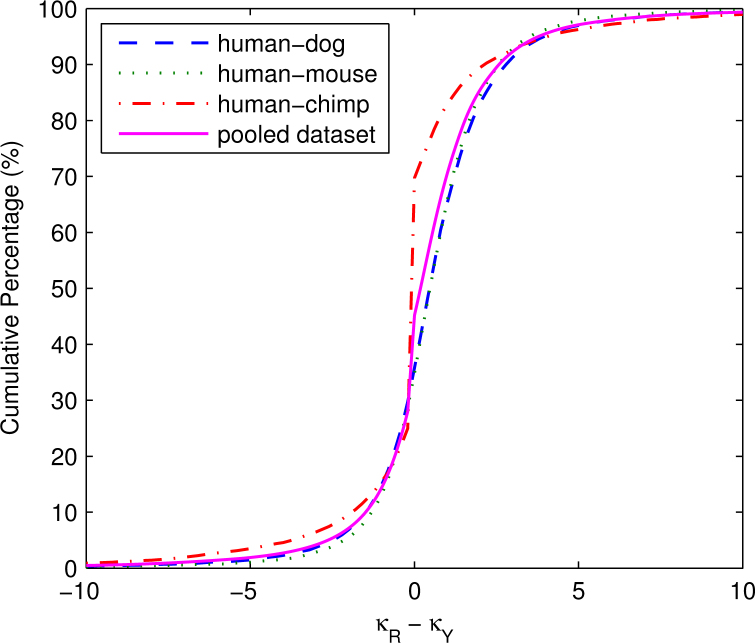
We utilized three mammalian homologous gene sets to verify the efficiency of these new methods. Plotting the distributions of κR−κY in three individual datasets and one pooled dataset (Figure 7), we found that the pooled dataset represents reasonably the three raw orthologous datasets and has sufficient gene pairs falling in each interval of κR−κY. Subsequently, we only dealt with the pooled data and analyzed S%, Ka, Ks, and ω in four intervals of κR−κY (Table 3). We also carefully selected three values (−0.5, 0.5, and 1.5) as segmentation boundaries to obtain the four subintervals, when κR=3.75: (1) κR=1, 2 and 3; (2) κR=4; (3) κR=5; and (4) κR=6, 7, 8, 9 and 10. As the majority of genes are driven by negative selection, we set a values according to the optimal values when ω=0.3 (Table 2) for the convenience of comparing the results from the real data with those from computer simulations (Figure 5).
Figure 7.
Cumulative percentage of κR−κY for human-dog, human-mouse, and human-chimp orthologs and a pooled dataset at a bin size of 0.2.
Table 3.
Estimates of S%, Ka, Ks, and ω based on an aggregate of three datasets and twelve methods
| Method |
κR − κY < −0.5 |
−0.5 ≤ κR−κY < 0.5 |
||||||
| S% | Ka | Ks | ω | S% | Ka | Ks | ω | |
| NG/γ-NG | 23.63% | 0.0624 | 0.3705 | 0.2521 | 23.73% | 0.0637 | 0.3128 | 0.2672 |
| LWL/γ-LWL | 22.36% | 0.0625 | 0.3717 | 0.2376 | 22.46% | 0.0620 | 0.3133 | 0.2508 |
| MLWL | 27.59% | 0.0641 | 0.3114 | 0.2888 | 26.33% | 0.0628 | 0.2738 | 0.2824 |
| LPB | 27.81% | 0.0664 | 0.3033 | 0.3171 | 28.52% | 0.0650 | 0.2602 | 0.3385 |
| YN | 25.45% | 0.0635 | 0.4271 | 0.2731 | 24.38% | 0.0634 | 0.3811 | 0.2617 |
| MYN | 26.86% | 0.0646 | 0.3993 | 0.2960 | 24.29% | 0.0636 | 0.3954 | 0.2593 |
| γ-MLWL | 27.59% | 0.0660 | 0.3401 | 0.2813 | 26.33% | 0.0649 | 0.3010 | 0.2755 |
| γ-LPB | 28.36% | 0.0759 | 0.4393 | 0.2900 | 28.95% | 0.0754 | 0.3796 | 0.3124 |
| γ-YN | 25.51% | 0.0653 | 0.4935 | 0.2653 | 24.43% | 0.0659 | 0.4447 | 0.2545 |
| γ-MYN | 26.88% | 0.0651 | 0.4098 | 0.2944 | 24.30% | 0.0641 | 0.4083 | 0.2577 |
| Method |
0.5 ≤ κR−κY < 1.5 |
κR−κY ≥ 1.5 |
||||||
| S% | Ka | Ks | ω | S% | Ka | Ks | ω | |
| NG/γ-NG | 23.95% | 0.0840 | 0.4701 | 0.2107 | 24.02% | 0.0515 | 0.4027 | 0.1817 |
| LWL/γ-LWL | 22.69% | 0.0842 | 0.4702 | 0.2040 | 22.74% | 0.0521 | 0.4035 | 0.1729 |
| MLWL | 27.21% | 0.0857 | 0.4050 | 0.2343 | 28.61% | 0.0537 | 0.3315 | 0.2198 |
| LPB | 27.64% | 0.0887 | 0.3884 | 0.2607 | 28.32% | 0.0557 | 0.3282 | 0.2343 |
| YN | 25.22% | 0.0835 | 0.5622 | 0.2047 | 26.14% | 0.0515 | 0.4566 | 0.1991 |
| MYN | 24.38% | 0.0825 | 0.6360 | 0.1874 | 24.33% | 0.0502 | 0.5768 | 0.1703 |
| γ-MLWL | 27.21% | 0.0884 | 0.4456 | 0.2241 | 28.61% | 0.0548 | 0.3608 | 0.2127 |
| γ-LPB | 28.33% | 0.1025 | 0.5770 | 0.2235 | 28.94% | 0.0610 | 0.4570 | 0.2088 |
| γ-YN | 25.29% | 0.0863 | 0.6573 | 0.1941 | 26.19% | 0.0526 | 0.5291 | 0.1918 |
| γ-MYN | 24.40% | 0.0830 | 0.6578 | 0.1849 | 24.34% | 0.0504 | 0.6002 | 0.1684 |
We have the following observations. First, the new γ-methods seem not overestimate ω, as compared to their original methods, in accordance with our simulation results and theoretical analyses. Second, we observed some variations of the new methods in ω estimates; for instance, γ-MYN produces consistent results with our simulations (Figure 5A, D, G). In the case of κR−κY<−0.5, when κR=1, 2, and 3, γ-MYN overestimates ω compared with other γ-methods and the values are 0.2521, 0.2376, 0.2813, 0.2900, 0.2653, and 0.2944 for γ-NG, γ-LWL, γ-MLWL, γ-LPB, γ-YN, and γ-MYN, respectively. When confined κR−κY ≥ 1.5 (κR= 6, 7, 8, 9 and 10), γ-MLWL, γ-YN and γ-LPB overestimate ω evidently but γ-MYN, γ-NG and γ-LWL do not, as the values are 0.2127, 0.1918, 0.2088, 0.1684, 0.1817, and 0.1729 for γ-MLWL,γ-YN, γ-LPB, γ-MYN, γ-NG, and γ-LWL, respectively. However, when −0.5 ≤ κR−κY < 1.5, simulation results showed that the performance of each method becomes similar. Finally, Ka estimates among all γ-methods are very similar except γ-LPB. The major distinction in ω estimation with various γ-methods lies in Ks estimates—the changes of ω are mostly attributable to those of Ks as Ks is more sensitive than Ka to the changes of a under negative selection. In conclusion, our findings largely agree with the simulation studies.
How does the consideration of variable substitution rates improve Ka/Ks calculation?
Let us first examine how parameter a in the γ-series of methods improves the original methods. As we know, overlooking the fact of rate variation among sites often results in underestimation of both the sequence distance and the transition/transversion rate ratio κ (both κR and κY) (2). The ratio κ plays a key role in two necessary processes of both (1) estimating S and N and (2) generating a transition probability matrix for computing Sd and Nd, and therefore ω=Ka/Ks ≈ (Nd/N)/(Sd/S), where the “≈” is a result of the absence of correcting for multiple hits.
We next discuss three special cases. The case of purifying selection has been discussed previously (22), and the underestimated κ is used in the original methods that lead to underestimation of Sd/S and overestimation of ω in contrast to our γ-series methods. In the case of positive selection, we would like to only discuss Ka (Nd/N) since nonsynonymous substitutions are more likely to occur than synonymous ones. As κ is positively related to substitution number between two codons, underestimation of κ gives rise to underestimation of Nd. Since it is more likely that transitions between two codons are synonymous, primarily at the third codon positions, the underestimation of κ often leads to the underestimation of S and the overestimation of N. Therefore, underestimations of Nd/N or ω can be attributable to an underestimated κ. In the case of neutral mutation where synonymous substitutions occur in the same probability as nonsynonymous ones, a decrease in κ leads to dithering of the curves, and the power of parameter a is related to κR (or κY), so we recommend to use the less complex conventional methods. Our analyses are consistent with the results from both simulation (Figure 1, Figure 2, Figure 3) and real data (Table 2, Table 3).
Usage, performance, and program availability
We evaluate the performance of the new methods using the parameters representing various selection pressures, especially negative selection, and often consider all conditions and integrate various parameter settings into the algorithm (Table 2) by identifying the scope of ω using a traditional method (ω>1 or ω< 1) and computing final ω using γ-method with a combination of selected parameters. In our previous study (22), we showed that the GY method (a popular maximum likelihood method) consumes more time than approximate methods do. We therefore recommend our new methods to be used in the cases when large amounts of data are to be analyzed. C++ programs implementing γ-series methods such as γ-NG, γ-LWL, γ-MLWL, γ-LPB, and γ-YN are included in KaKs_Calculator version 2.0, which is a software package updated from KaKs_Calculator version 1.0 (23).
Prospective
As methods for calculating the two kinds of distances, nonsynonymous substitution rate as Ka and synonymous substitution rate as Ks between protein-coding sequences have been developed and widely used in the field of molecular evolution, and different models have been introduced into emerging new methods. However, it is still surprising that results from real data tend to produce similar results despite the fact that various methods are applied in parallel (2). Although it was shown that different correlations between selective pressure and Ks can be drawn from different methods (24), the major conclusions when detecting positive selection are not usually changed. Is it true that the Ka/Ks argument is too weak to have the ability in detecting positive selection? We believe that it is not, especially not due to the methodology for Ka/Ks calculations. By using these methods, we are able to obtain average selection pressures in a way where individual genes are used as an object. If one needs to determine whether any individual genes are subjected to positive selection, the LRT (likelihood ratio test)-like methods (25) should be used and they tend to be more qualitative. In conclusion, the two methods (LRT-like methods and Ka/Ks methods) should be applied to the study of different outcomes, and they are neither the same nor mutually exclusive. Therefore, our attempts in improving Ka/Ks methods are not only meaningful but also will increase the sensitivity to detect positive selection, especially when new strategies [e.g. sliding window 26., 27., 28., 29., 30., 31.] are sought out for better resolutions.
Conclusion
We compared γ-methods with their conventional counterparts by carrying out computer simulations and examining real data. As neglecting the variation of substitution rates across sites may reflect on biased estimates of Ka and Ks in these examined methods, our new γ-methods have minimal deviations under various conditions. We show that incorporating variable substitution rates into the calculation of Ka and Ks and their ratio ω often exhibits merits over their conventional counterparts when applied appropriately.
Materials and Methods
Overview of general steps
Our γ-series of modified methods assumed that the rate of nucleotide substitutions approximately follows the gamma distribution, and introduced the shape parameter a into conventional methods of calculating Ka and Ks. Therefore, these new methods can be regarded as the generalization of conventional approximate methods. An approximate method usually involves three steps 1., 2.:
-
1.
Count synonymous and nonsynonymous sites;
-
2.
Count synonymous and nonsynonymous differences;
-
3.
Calculate the proportions of differences and correct for multiple hits.
We describe the modified methods step by step focusing on the modifications.
γ-NG method
γ-NG performs in the same mode as NG does in the procedures of counting sites and counting differences (6). Now we have
| (1) |
| (2) |
However, it uses a modified JC69 model to correct for multiple hits as follows (see more details in Supporting Online Material) (32):
| (3) |
As a result, we have
| (4) |
| (5) |
γ-LWL method
In comparison with LWL method (7), we pay more attention to the estimation for the number of transitional and transversional substitutions. We denote Pi and Qi as the number of observed transitional and transversional differences at i-fold degenerate sites according to Li (i=0, 2 or 4), which means the number of sites in the three corresponding degeneracy categories averaging over paired sequences. To compute the number of transitional (Ai) and transversional (Bi) substitutions per site (i=0, 2 or 4), we apply a modified K80 model based on Pi and Qi as follows (see more details in Supporting Online Material) (33):
| (6) |
| (7) |
And the subsequent procedures are the same as those in LWL method (7):
| (8) |
| (9) |
where di = Ai + Bi (i = 0, 2, or 4).
γ-LPB method
γ-LWL leaves out the transition/transversion rate difference in the procedure of counting two-fold site as 1/3 synonymous and 2/3 nonsynonymous, giving rise to underestimation of S and overestimation of Ks (and underestimation of Ka) and thus underestimation of ω (Ka/Ks). To overcome this drawback, we follow the same strategy as that in LPB method 9., 10.:
| (10) |
| (11) |
γ-MLWL method and γ-MLPB method
γ-MLWL follows another strategy to solve the problem that γ-LWL may perform poorly for large κ, as below (8):
When κ ≥ 2,
| (12) |
| (13) |
When κ < 2,
| (14) |
| (15) |
where di = Ai+ Bi (i = 0, 2, or 4).
We also correct for arginines as described in the literature for complex conditions based on LWL method and LPB method (8) and denoted the modified versions as γ-MLWL and γ-MLPB.
γ-YN method
Our γ-YN method introduces gamma distribution into YN method (5), categorized with modified HKY85 (34) and F84 (20). Compared with YN method, the changed components are as follows:
The modified HKY85-F84 model is adopted to estimate κ on the basis of the nondegenerate and fourfold-degenerate sites (for more details see Supporting Online Material).
| (16) |
where
| (17) |
and
| (18) |
| (19) |
where and stand for the proportions of transitional and transversional differences for each synonymous and nonsynonymous site groups, respectively.
The modified F84 model is used to correct for multiple substitutions in terms of the divergent distance.
| (20) |
where gR=gA + gG and gY=gT + gC.
Optimal index
To determine the optimal parameter a, we established an optimal index:
| (21) |
In this expression, the values of i from 1 to 10 stand for the κR values increasing from 1 to 10, fixing κY=3.75, as used in the analyses. denotes the estimated values of ω, Ka or Ks, and denotes the expected values of ω, Ka or Ks, when κR=i. This function measures the deviation from expected values, regardless if the deviation is positive or negative. We calculate the f value that corresponds to six different a values and choose the minimal f value as the optimal.
Comparative analysis based on computer simulation and real data testing
We employed the “evolver” Monte Carlo program, implemented in the PAML (Phylogenetic Analysis by Maximum Likelihood) package (35), to generate evolving protein-coding sequences based on specified substitution models. To reduce the influence of stochastic errors, we generate 2,000 pairs of sequences with 400 codons in each simulation. We choose appropriate ranges of related parameters for computer simulations, including codon frequencies, gamma distribution shape parameter (a), divergence time (t), two ratios of transitional rate between purines (κR) and between pyrimidines (κY) to transversional rate, and selective pressure ω. In principle, we focus on the performance of various γ-methods at the optimal values of a. Moreover, we usually use rice codon frequencies as the defaults. And ω=0.3, 1, and 3 are used to represent negative selection, neutral mutation, and positive selection, respectively, and parameter t=0.6 is considered as a constant value except special occasions 5., 36., 37.. In view of the unequal transitional substitutions, we often fix κY to 3.75 and allow κR to vary from 1 to 10. To weigh the accuracies of Ka and Ks estimations, we computed the expected Ka and Ks values using the following equations (8):
| (22) |
| (23) |
We formulate the error rate with a common definition:
To examine the performance of our new methods in real data, 14,725 human-dog, 16,368 human-mouse, and 15,646 human-chimp orthologous gene pairs were collected from NCBI’s HomoloGene database (build 61) (ftp://ftp.ncbi.nih.gov/pub/HomoloGene/). After eliminating ambiguous data (extremes in sequence homology), 14,309 human-dog, 16,046 human-mouse, and 12,278 human-chimp gene pairs were used for further analysis. In consideration of decreasing the random errors, we pooled the three datasets into one dataset, which was used for comparing the methods evaluated in this study.
Authors’ contributions
DW conducted mathematical calculation, performed computational simulation, collected and analyzed the data, and drafted the manuscript. DW and SZ conceived and designed this study. FH, JZ, and SH contributed to data analysis. JY supervised the study and revised the manuscript. All authors read and approved the final manuscript.
Competing interests
The authors have declared that no competing interests exist.
Acknowledgements
We thank Dr. Zhang Zhang (Department of Ecology and Evolutionary Biology, Yale University) and Miss Yanyang Zhi (Institute of Genetics and Developmental Biology, Chinese Academy of Sciences) for their sincere help on this manuscript. This work was supported by the National Basic Research Program of China (Grant No. 2006CB910404) awarded to JY.
Supporting Online Material
Figures S1-S6, Tables S1 and S2, and other materials
References
- 1.Nei M., Kumar S. Oxford University Press; New York, USA: 2000. Molecular Evolution and Phylogenetics. [Google Scholar]
- 2.Yang Z. Oxford University Press; New York, USA: 2006. Computational Molecular Evolution. [Google Scholar]
- 3.Zhang Z., Yu J. Evaluation of six methods for estimating synonymous and nonsynonymous substitution rates. Genomics Proteomics Bioinformatics. 2006;4:173–181. doi: 10.1016/S1672-0229(06)60030-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Muse S.V. Estimating synonymous and nonsynonymous substitution rates. Mol. Biol. Evol. 1996;13:105–114. doi: 10.1093/oxfordjournals.molbev.a025549. [DOI] [PubMed] [Google Scholar]
- 5.Yang Z., Nielsen R. Estimating synonymous and nonsynonymous substitution rates under realistic evolutionary models. Mol. Biol. Evol. 2000;17:32–43. doi: 10.1093/oxfordjournals.molbev.a026236. [DOI] [PubMed] [Google Scholar]
- 6.Nei M., Gojobori T. Simple methods for estimating the numbers of synonymous and nonsynonymous nucleotide substitutions. Mol. Biol. Evol. 1986;3:418–426. doi: 10.1093/oxfordjournals.molbev.a040410. [DOI] [PubMed] [Google Scholar]
- 7.Li W.H. A new method for estimating synonymous and nonsynonymous rates of nucleotide substitution considering the relative likelihood of nucleotide and codon changes. Mol. Biol. Evol. 1985;2:150–174. doi: 10.1093/oxfordjournals.molbev.a040343. [DOI] [PubMed] [Google Scholar]
- 8.Tzeng Y.H. Comparison of three methods for estimating rates of synonymous and nonsynonymous nucleotide substitutions. Mol. Biol. Evol. 2004;21:2290–2298. doi: 10.1093/molbev/msh242. [DOI] [PubMed] [Google Scholar]
- 9.Li W.H. Unbiased estimation of the rates of synonymous and nonsynonymous substitution. J. Mol. Evol. 1993;36:96–99. doi: 10.1007/BF02407308. [DOI] [PubMed] [Google Scholar]
- 10.Pamilo P., Bianchi N.O. Evolution of the Zfx and Zfy genes: rates and interdependence between the genes. Mol. Biol. Evol. 1993;10:271–281. doi: 10.1093/oxfordjournals.molbev.a040003. [DOI] [PubMed] [Google Scholar]
- 11.Zhang Z. Computing Ka and Ks with a consideration of unequal transitional substitutions. BMC Evol. Biol. 2006;6:44. doi: 10.1186/1471-2148-6-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bofkin L., Goldman N. Variation in evolutionary processes at different codon positions. Mol. Biol. Evol. 2007;24:513–521. doi: 10.1093/molbev/msl178. [DOI] [PubMed] [Google Scholar]
- 13.Kocher T.D., Wilson A.C. Sequence evolution of mitochondrial DNA in humans and chimpanzees: control region and a protein-coding region. In: Osawa S., Honjo T., editors. Evolution of Life: Fossils, Molecules, and Culture. Springer; Tokyo, Japan: 1991. pp. 391–413. [Google Scholar]
- 14.Tamura K., Nei M. Estimation of the number of nucleotide substitutions in the control region of mitochondrial DNA in humans and chimpanzees. Mol. Biol. Evol. 1993;10:512–526. doi: 10.1093/oxfordjournals.molbev.a040023. [DOI] [PubMed] [Google Scholar]
- 15.Wakeley J. Substitution rate variation among sites in hypervariable region 1 of human mitochondrial DNA. J. Mol. Evol. 1993;37:613–623. doi: 10.1007/BF00182747. [DOI] [PubMed] [Google Scholar]
- 16.Wakeley J. Substitution-rate variation among sites and the estimation of transition bias. Mol. Biol. Evol. 1994;11:436–442. doi: 10.1093/oxfordjournals.molbev.a040124. [DOI] [PubMed] [Google Scholar]
- 17.Jin L., Nei M. Limitations of the evolutionary parsimony method of phylogenetic analysis. Mol. Biol. Evol. 1990;7:82–102. doi: 10.1093/oxfordjournals.molbev.a040588. [DOI] [PubMed] [Google Scholar]
- 18.Li W.H. Molecular phylogeny of Rodentia, Lagomorpha, Primates, Artiodactyla, and Carnivora and molecular clocks. Proc. Natl. Acad. Sci. USA. 1990;87:6703–6707. doi: 10.1073/pnas.87.17.6703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yang Z. Maximum-likelihood estimation of phylogeny from DNA sequences when substitution rates differ over sites. Mol. Biol. Evol. 1993;10:1396–1401. doi: 10.1093/oxfordjournals.molbev.a040082. [DOI] [PubMed] [Google Scholar]
- 20.Yang Z. Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 1994;39:306–314. doi: 10.1007/BF00160154. [DOI] [PubMed] [Google Scholar]
- 21.Yang Z. Comparison of models for nucleotide substitution used in maximum-likelihood phylogenetic estimation. Mol. Biol. Evol. 1994;11:316–324. doi: 10.1093/oxfordjournals.molbev.a040112. [DOI] [PubMed] [Google Scholar]
- 22.Wang D.P. Gamma-MYN: a new algorithm for estimating Ka and Ks with consideration of variable substitution rates. Biol. Direct. 2009;4:20. doi: 10.1186/1745-6150-4-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang Z. KaKs_Calculator: calculating Ka and Ks through model selection and model averaging. Genomics Proteomics Bioinformatics. 2006;4:259–263. doi: 10.1016/S1672-0229(07)60007-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li J. Correlation between Ka/Ks and Ks is related to substitution model and evolutionary lineage. J. Mol. Evol. 2009;68:414–423. doi: 10.1007/s00239-009-9222-9. [DOI] [PubMed] [Google Scholar]
- 25.Yang Z. Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics. 2000;155:431–449. doi: 10.1093/genetics/155.1.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Berglund A.C. Tertiary windowing to detect positive diversifying selection. J. Mol. Evol. 2005;60:499–504. doi: 10.1007/s00239-004-0223-4. [DOI] [PubMed] [Google Scholar]
- 27.Fares M.A. SWAPSC: sliding window analysis procedure to detect selective constraints. Bioinformatics. 2004;20:2867–2868. doi: 10.1093/bioinformatics/bth303. [DOI] [PubMed] [Google Scholar]
- 28.Fares M.A. A sliding window-based method to detect selective constraints in protein-coding genes and its application to RNA viruses. J. Mol. Evol. 2002;55:509–521. doi: 10.1007/s00239-002-2346-9. [DOI] [PubMed] [Google Scholar]
- 29.Liang H. SWAKK: a web server for detecting positive selection in proteins using a sliding window substitution rate analysis. Nucleic Acids Res. 2006;34:W382–W384. doi: 10.1093/nar/gkl272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Siltberg J., Liberles D.A. A simple covarion-based approach to analyse nucleotide substitution rates. J. Evol. Biol. 2002;15:588–594. [Google Scholar]
- 31.Suzuki Y. Three-dimensional window analysis for detecting positive selection at structural regions of proteins. Mol. Biol. Evol. 2004;21:2352–2359. doi: 10.1093/molbev/msh249. [DOI] [PubMed] [Google Scholar]
- 32.Jukes T.H., Cantor C.R. Evolution of protein molecules. In: Munro H.N., editor. vol.III. Academic Press; New York, USA: 1969. pp. 21–132. (Mammalian Protein Metabolism). [Google Scholar]
- 33.Kimura M. A simple method for estimating evolutionary rates of base substitutions through comparative studies of nucleotide sequences. J. Mol. Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- 34.Hasegawa M. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- 35.Yang Z. PAML 4: phylogenetic analysis by maximum likelihood. Mol. Biol. Evol. 2007;24:1586–1591. doi: 10.1093/molbev/msm088. [DOI] [PubMed] [Google Scholar]
- 36.Li W.H. Sinauer Associates, Inc.; Sunderland, USA: 1997. Molecular Evolution. [Google Scholar]
- 37.Messier W., Stewart C.B. Episodic adaptive evolution of primate lysozymes. Nature. 1997;385:151–154. doi: 10.1038/385151a0. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figures S1-S6, Tables S1 and S2, and other materials