B-cell Ligand Processing Pathways Detected by Large-scale Comparative Analysis

Abstract

The initiation of B-cell ligand recognition is a critical step for the generation of an immune response against foreign bodies. We sought to identify the biochemical pathways involved in the B-cell ligand recognition cascade and sets of ligands that trigger similar immunological responses. We utilized several comparative approaches to analyze the gene coexpression networks generated from a set of microarray experiments spanning 33 different ligands. First, we compared the degree distributions of the generated networks. Second, we utilized a pairwise network alignment algorithm, BiNA, to align the networks based on the hubs in the networks. Third, we aligned the networks based on a set of KEGG pathways. We summarized our results by constructing a consensus hierarchy of pathways that are involved in B cell ligand recognition. The resulting pathways were further validated through literature for their common physiological responses. Collectively, the results based on our comparative analyses of degree distributions, alignment of hubs, and alignment based on KEGG pathways provide a basis for molecular characterization of the immune response states of B-cells and demonstrate the power of comparative approaches (e.g., gene coexpression network alignment algorithms) in elucidating biochemical pathways involved in complex signaling events in cells.

Introduction

B-cell ligand recognition plays a large role in various immune responses ranging from the recognition of foreign invaders such as viruses and bacteria to the recognition of cancerous cells. B-cells act as the body’s most effective line of defense to invaders [1]. Several types of responses may be induced in naïve mature B-cells through the activation of different receptors (e.g., cytokine and chemokine receptors) [2], [3]. Recognition of ligands by the B-cell Ag receptor (BCR) begins with the activation of an array of intracellular effector molecules and ends with phenotypic modifications that define the cell’s response to the stimulus [3]. As more and more players in this process are uncovered, the current schematic of BCR signal transduction has become a “labyrinth” of interconnecting pathways [4]. Despite the complicated events that occur during this process, the resultant reaction is very ordered and precise. The activation of various signal transduction pathways in mature B cells is influenced by the combination of ligands presented to the B-cells. The presence of different ligands may trigger cell-proliferation, activation, differentiation, migration, isotype switching and apoptosis [1], [5], [6]. Of particular interest in this area is the elucidation of the regulatory mechanisms that are involved in B-cell recognition of various ligands. These data provide a detailed look at the finite states that B-cells can enter upon exposure to ligands. Understanding the genetic interactions that are required for this process allows the design of drugs that are capable of triggering a specific immune response at a given time point, identifying the mechanisms that underly different auto-immune diseases, and allowing for the detection of key molecules involved in the regulation of B-cell function.

Several studies [7], [8], [9] have examined the changes in expression patterns of B-cells in response to exposure to different ligands. These studies used differential gene expression analysis of microarray data, such as Significance Analysis of Microarrays (SAM) [10] and Gene Ontology (GO) [11] terms, to detect genes that were significantly differentially expressed and whose pathway annotations shared significant GO terms. This approach, although well developed and widely used, suffers from an important limitation: it focuses on differences in expression patterns of individual genes across the different treatments or time points rather than differences between specific pathways/modules based on prior information of pathway relationships. It is of note that although software such as Gene Set Enrichment Analysis (GSEA) [12] conducts analysis based on pathways or selected groups of genes of interest, such methods do not account for the topology of networks or connectivity/relationships within the genes of interest.

Gene coexpression networks in which the nodes represent genes and the weighted links between pairs of nodes encode the correlations in expression patterns of the corresponding genes offer a useful way to represent cellular responses to each of the different treatments (e.g., exposure to different ligands). Network alignment methods are available to overcome the limitation of differentially expressed gene analysis and GO enrichment analysis [13], [14], [15], [16], [17], [18], [19], [20]. The advantage of using these methods is that they account for the connectivity of genes rather than focusing on single gene regulation. Hence, we utilized a pairwise network alignment algorithm, BiNA [21], to align 33 gene coexpression networks generated from a set of microarray experiments spanning 33 different ligands (see Table 1 for a complete list of the ligands) [8]. A network alignment (analogous to a sequence alignment) compares two input networks and returns a set of common pathways across the networks with a score denoting the similarity between the networks being compared. By constructing a symmetric 33 × 33 distance matrix using the alignment scores across the 33 networks, a hierarchical cluster was constructed based on the distance matrix to visualize relationships across the networks representing the gene expression changes due to exposure to different ligands. The common pathways detected across the most similar networks were examined and the pathways were annotated according to KEGG [22]. Using this approach, we examined the regulation mechanisms specific to certain groups of ligands. Based on this method, we identified a set of specific genes and pathways that appear to be involved in BCR-mediated ligand capture, vesicle function and vesicle trafficking during B-cell antigen processing and presentation for the set of 33 ligands we examined.

Table 1.

Full list of the ligands and their abbreviations examined in the current study

Ligand abbreviation	Ligand name
2MA	2-Methyl-thio-ATP
AIG	Antigen (Anti-Ig)
BAF	BAFF (B-cell activating factor)
BLC	BLC (B-lymphocyte chemoattractant)
BOM	Bombesin
40L	CD40 ligand
70L	CD70/CD27 ligand
CGS	CGS-21680 hydrochloride (2-p-[2-Carboxyethyl]phenethylamino-5′-N-ethylcarboxamidoadenosine)
CPG	CpG-containing oligonucleotide
DIM	Dimaprit
ELC	ELC (Epstein Barr Virus-induced molecule-1 ligand chemokine)
FML	fMLP (formyl-Met-Leu-Phe)
GRH	Growth hormone-releasing hormone
IGF	Insulin-like growth factor 1
IFB	Interferon-beta
IFG	Interferon-gamma
I10	Interleukin 10
IL4	Interleukin 4
LPS	Lipopolysaccharide
LB4	Leukotriene B4 (LTB4)
LPA	Lysophosphatidic acid
M3A	MIP3-alpha (Macrophage inflammatory protein-3)
NEB	Neurokinin B
NPY	Neuropeptide Y
NGF	Nerve growth factor
PAF	Platelet activating factor
PGE	Prostaglandin E2
SDF	SDF1 alpha (Stromal cell derived factor-1)
SLC	Secondary lymphoid-organ chemokine
S1P	Sphingosine-1-phosphate
TER	Terbutaline
TNF	Tumor necrosis factor-alpha
TGF	Transforming growth factor-beta 1

Note: This list was adapted from Lee et al. [7].

Results and discussion

Cells respond to stimuli through a myriad of pathways. However, they deploy similar modules in their response to distinct ligands. The major objective of this study was to explore the space of signaling responses of B-cells to naturally occurring stimuli and identify the commonality and differences in the ligand response. Such analysis will provide an insight into the space of responses of B-cells in native physiology and provide pathway motifs that can be explored through further experimentation.

We utilized several different approaches for comparing and aligning gene coexpression networks constructed from microarray data obtained from B-cells treated with different ligands. These include comparison of degree distributions of networks using Kolmogorov-Smirnoff statistic, and alignment of the networks based on the top 2000 highly connected nodes and based on KEGG pathways that were enriched with high intensity probes.

Clustering based on degree distribution

In order to determine the relationships of the ligand networks based on the network topology, we computed the degree distribution (Figure S1) for each of the 33 ligand networks. The degree distribution plots show the relationship between the degree of a node and the frequency of nodes with that degree (P(Degree)). We show that it is possible to get a reasonable estimate of the relationships between networks by utilizing only the degree distributions of the networks.

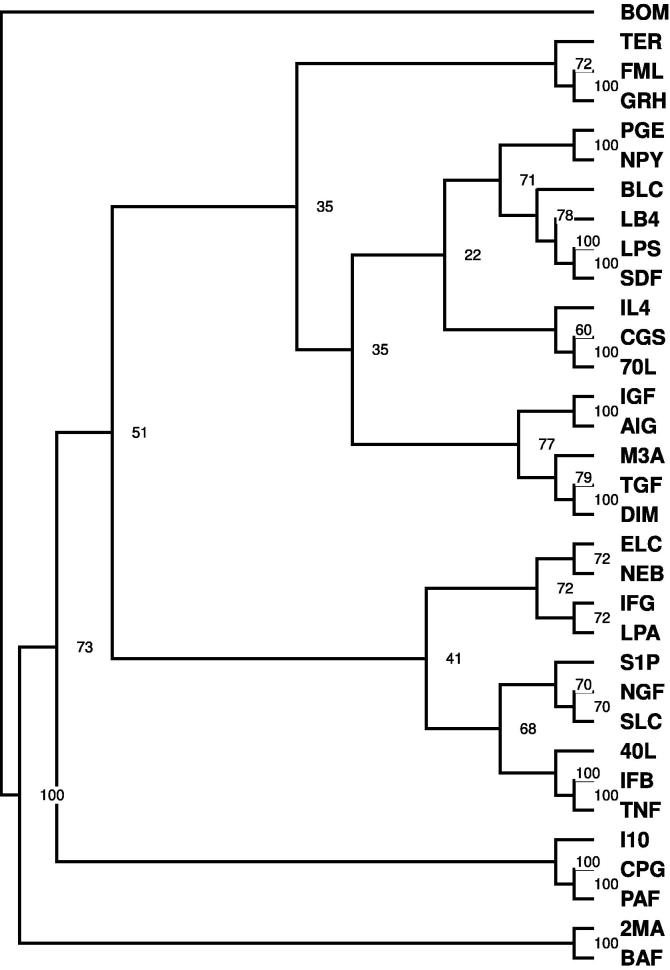
We compared the resulting 33 distributions using the two-sample Kolmogorov–Smirnov statistic [23]. Specifically, we used the Kolmogorov–Smirnov statistic to compute the 33 × 33 pairwise distances from the 33 degree distributions. Thus, we constructed a 33 × 33 matrix D^toplogical where the entry in the i-th row and j-th column in the matrix corresponds to the distance between the degree distributions of the i-th and j-th networks as determined by the Kolmogorov–Smirnov statistic. The D^toplogical matrix was then fed into a hierarchical neighbor-joining algorithm to construct the hierarchical cluster. Figure 1 shows the relationships between the ligand networks obtained by the topological comparison of the networks based on their degree distributions. Ligand networks with high number of (at least 100) differentially expressed genes at the 4 h time point relative to untreated samples, based on the classification of Lee et al. [7] using the SAM [10] tool, have been highlighted in the figure. As shown in Figure 1, ligand networks with a high number of differentially expressed genes relative to untreated samples share the same subtree/clade in the hierarchical network (P = 0.032, see “Hierarchical clustering” section in Methods). This result indicates that the network structure that was measured by the degree distribution and compared by the Kolmogorov–Smirnov statistic (similarly utilized in [24], [25], [26]) can be used to detect ligands that elicit similar responses upon exposure to B-cells.

Figure 1.

Network clustering based on degree distribution The figure shows the result of hierarchically clustering of the networks based on Kolmogorov–Smirnov test statisitic between degree distributions of the networks as distance measure of network similarity. Ligand networks with a high number of differentially expressed genes relative to untreated samples (as indicated in [7] have been highlighted in the figure (LPS, I04, BOM, 2MA, AIG, GRH, IFB, CGS, 40L, CPG). The clade with an asterisk (*) is highly enriched (P = 0.032 in ligand-response networks that induced a high number of differentially expressed genes).

Although topological comparison of gene coexpression networks based on their degree distributions is simple, intuitive, and computationally inexpensive, it fails to take into account the node labels or the biological annotation for the nodes in the networks. In order to compare the networks based on both the network topology and the node labels/biological annotation (e.g., signaling pathways, metabolic pathways…etc.) for the nodes, we utilized a network alignment algorithm implemented in the Biomolecular Network Alignment (BiNA) toolkit [21], [27].

Clustering based on alignment of high degree nodes in ligand networks

The network alignment algorithm implemented in BiNA allows the comparison of gene coexpression networks based on not only the extent to which they share similar topologies, but also the weights on the links (e.g., similarities in gene coexpression patterns) and the similarities of node and/or edge labels (biological annotations). We used the BiNA toolkit to run all-vs-all comparisons between all 33 ligand networks and construct a 33 × 33 distance matrix D^hubs whose entries signify the similarity score between ligands. Initially, we reduced the comparison to an alignment of the neighborhood around the top 2000 highly connected nodes (hubs) between all 33 ligand networks. Although we started aligning all nodes in the network, we quickly noticed that the total alignment score between two networks saturated after 2000 hubs (Figure S4). Specifically, to construct D^hubs, the output of a pairwise alignment between two networks (e.g., between ligand network 1, L¹(V¹, E¹) and ligand network 2, L²(V², E²)) is considered as a set of matched nodes S¹ (for ligand network 1, where $S^1\subset V^1$) and S² (for ligand network 2, where $S^2\subset V^2$) with a corresponding score set M. The corresponding entries $S_i^1$, $S_i^2$ and M_i signify matching k-hop neighborhoods around the nodes $S_i^1$ and $S_i^2$ with a similarity score M_i (where 1 ⩽ i ⩽ 2000 since we are considering 2000 hubs). The overall pairwise similarity score between the two ligand networks is calculated by summing the scores across all matched neighborhoods ${\sum }_{m\in M}m$ (see Alignment subsection in Methods for more information on how neighborhood scores are calculated). The overall similarity scores between all 33 ligand networks were assembled into a similarity matrix D^hubs with each entry in the matrix signifying the similarity score between the ligand networks (e.g., entry $d_{1\text{,}2}^{\mathit{hubs}}$ in D^hubs contains the similarity score between ligand network 1 and ligand network 2 as determined by BiNA). The D^hubs matrix was then fed into a hierarchical neighbor-joining algorithm to construct the hierarchical cluster representing the similarity between the ligand networks.

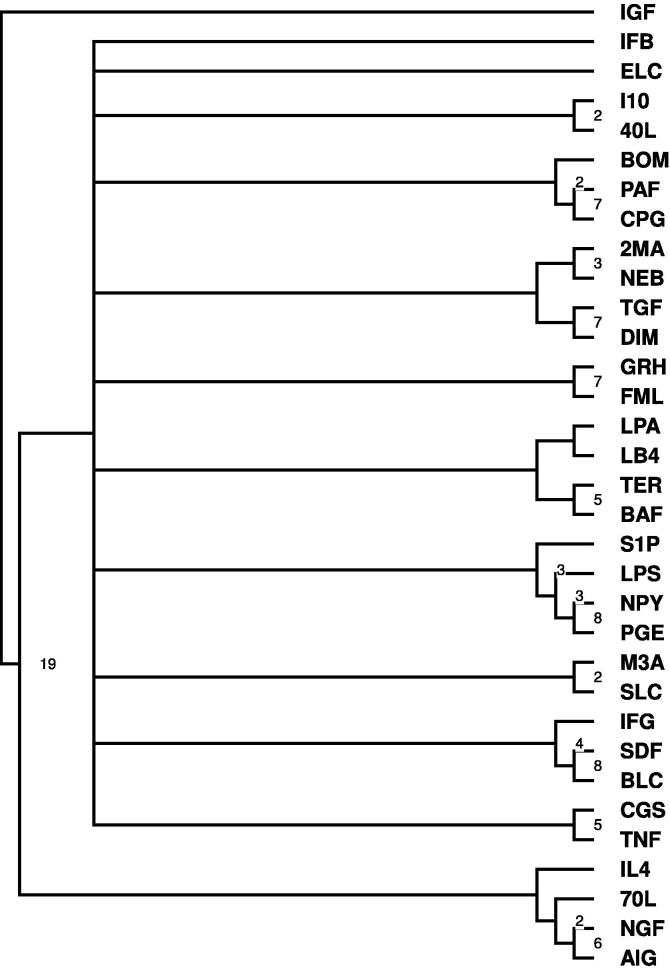
Finally, in order to calculate confidence measures on the branches of the hierarchical clusters produced by the alignment, the tree produced by hierarchical clustering was bootstrapped [28], [29] by sampling randomly (with replacement) from the top 2000 hubs 100 times. This random resampling on the M set, followed by summing the scores of the resampled set for each cell in D^hubs results in 100 distance matrices ${\text{D}}_{1\dots 100}^{\mathit{bootstrappedhubs}}$ which are fed into the same hierarchical neighbor-joining algorithm to construct 100 hierarchical similarity trees. The consensus tree of the hierarchical clusters based on the bootstrapped trees is produced using the Phylip [30] “consense” tool. Figure 2 shows the bootstrapped tree resulting from this method.

Figure 2.

Bootstrapped tree showing the relationship between all 33 ligand networks The tree was constructed using the network alignment score to measure the distance between networks. This tree shows that ligands with similar induced reaction (e.g., LPS and SDF, both affect pathways involved in cell migration) are clustered together.

Figure 2 shows that ligands with a similar induced reaction (e.g., LPS and SDF, both affect pathways involved in cell migration) are clustered together. It is important to note that the pathways necessary for migration would still be activated regardless of whether migration was the end point phenotypic response of B-cells to migratory ligands such as LPS and SDF, thus clustered together in our analysis. Such an analysis yields not only general similarity relationships between the ligand networks, but also provides specific gene and pathway information as seen from clustering based on signaling pathways (see below). The cluster shown in Figure 2 describes the similarity of expression based on node labels as well as correlation between the genes in the ligand networks. However, the hierarchical cluster from Figure 2 does not provide specific information as to which sets of pathways are shared/similarly regulated across ligand networks that fall under the same clade/subtree in the hierarchical cluster. KEGG [22] annotation of pathways was used to link the node labels in the networks to biological pathways (such as metabolism or signal processing). The additional pathway annotation can be used to determine the specific biological pathways that are involved in B-cell ligand recognition, and how those pathways are regulated based on exposure to each ligand. This procedure is described in detail in the next section.

Clustering based on ligand similarity across signaling pathways

We wanted to choose pathways based on the highly regulated genes in the microarray dataset rather than relying on a priori knowledge from the literature. The reasons for this choice are: (i) a choice of pathways that is unbiased by what is currently known in the literature can help identify novel pathways involved in B-cell ligand recognition (ii) if the list of pathways determined to be highly regulated based on the microarray data happens to share a high degree of overlap with the list generated based on literature surveys, it helps establish the utility of the approach in settings where prior knowledge available in the literature is quite sparse.

We choose pathways according to the following procedure. Firstly (step 1), in the fully normalized dataset (all 422 microarray samples), we search for genes that meet the following criteria (referred to as “high intensity” genes in what follows). Briefly, we wanted to maximize the sensitivity of detection of genes that are differentially regulated upon exposure of B-cells to ligands compared to untreated B-cells. This procedure maximizes sensitivity at the cost of specificity. The list of genes generated by this approach will be further reduced by comparing the neighborhoods in the ligand networks using network alignments. To do this, we (a) calculate the fold difference between the average probe expression level and the expression level for all probes in each sample (see Methods section); (b) select probes whose fold-difference is higher than 1 in at least one of the 422 samples and (c) of the probes selected in step (b), find probes that are expressed at least 1-fold higher compared to the same probes from the untreated samples. Secondly (step 2), once the high intensity probes are selected from (c), the probe IDs are mapped back to their respective gene IDs. Lastly (step 3), among all the pathways in KEGG, we count the number of genes from step 2 that show up in each KEGG pathway.

The results of the preceding steps are summarized in Table 2. As shown in Table 2, many of the pathways enriched in high-intensity genes are known to be implicated in the development of the immune system and processing of ligands. It should be noted that although KEGG considers the immune system pathways (KEGG category 5.1) to be a part of organismal system (KEGG category 5), we considered the immune system pathways separately (Table 2) since we wanted to specifically examine the immune system pathways.

Table 2.

List of pathways detected based on high-intensity probes from the microarray data

KEGG pathway category	No. of subpathways	KEGG subpathway ID
Cellular processes	10	mmu04142, mmu04144, mmu04145, mmu04520, mmu04540, mmu04810, mmu04110, mmu04114, mmu04115, mmu04140
Environmental information processing	2	mmu04150, mmu04310
Organismal system	6	mmu04962, mmu04964, mmu04966, mmu04260, mmu04722, mmu04910
Genetic information processing	15	mmu03020, mmu03022, mmu03030, mmu03040, mmu03050, mmu03060, mmu03410, mmu03420, mmu03430, mmu03440, mmu04120, mmu04130, mmu00970, mmu03010, mmu03018
Human diseases	12	mmu05100, mmu05210, mmu05212, mmu05214, mmu05215, mmu05216, mmu05219, mmu05222, mmu05010, mmu05012, mmu05014, mmu05016
Immune system	4	mmu04623, mmu04662, mmu04666, mmu04622
Metabolism	19	mmu00020, mmu00030, mmu00051, mmu00072, mmu00100, mmu00130, mmu00190, mmu00230, mmu00240, mmu00260, mmu00290, mmu00460, mmu00510, mmu00511, mmu00563, mmu00630, mmu00670, mmu00740, mmu00900

Note: This table with pathway names and relative number of genes enriched in the pathway based on the data. Please see Table S1 for more detail.

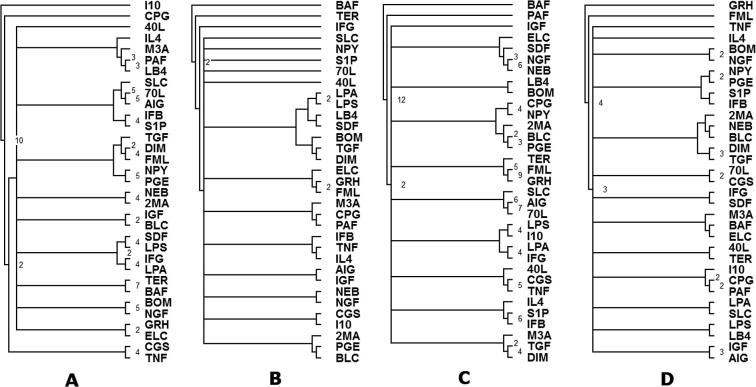
After considering all pathways of each of the seven general KEGG categories summarized in Table 2, we constructed a clustering tree for each pathway across each of the subcategories, a consensus network across each of the subcategories (Figure 3, Figure 4, Figure 6 and S3) and a consensus network based on all the networks in Table 2 (shown in Figure 5).

Figure 3.

Consensus tree constructed based on all metabolism pathways inTable 2 The tree was constructed using the network alignment score to measure the distance between networks. The values on the branches indicate the total number of times that the branch appeared across all networks (total of 19). If no value is indicated, the branch appeared only once.

Figure 4.

Consensus tree constructed based on all Genetic Information Processing Pathways inTable 2 The tree was constructed using the network alignment score to measure the distance between networks. The values on the branches indicate the total number of times that the branch appeared across all networks (total of 15). If no value is indicated, the branch appeared only once.

Figure 6.

Consensus trees constructed based on other pathways inTable 2 Consensus tree was constructed based on other pathways in Table 2 including all cellular processes pathways (A), all environmental information processing pathways (B), all human diseases pathways (C) and all immune system pathways (D), respectively. The values on the branches indicate the total number of times that the branch appeared across all networks (totals of 10, 2, 12, and 4 for A, B, C, and D, respectively). If no value is indicated, the branch appeared only once.

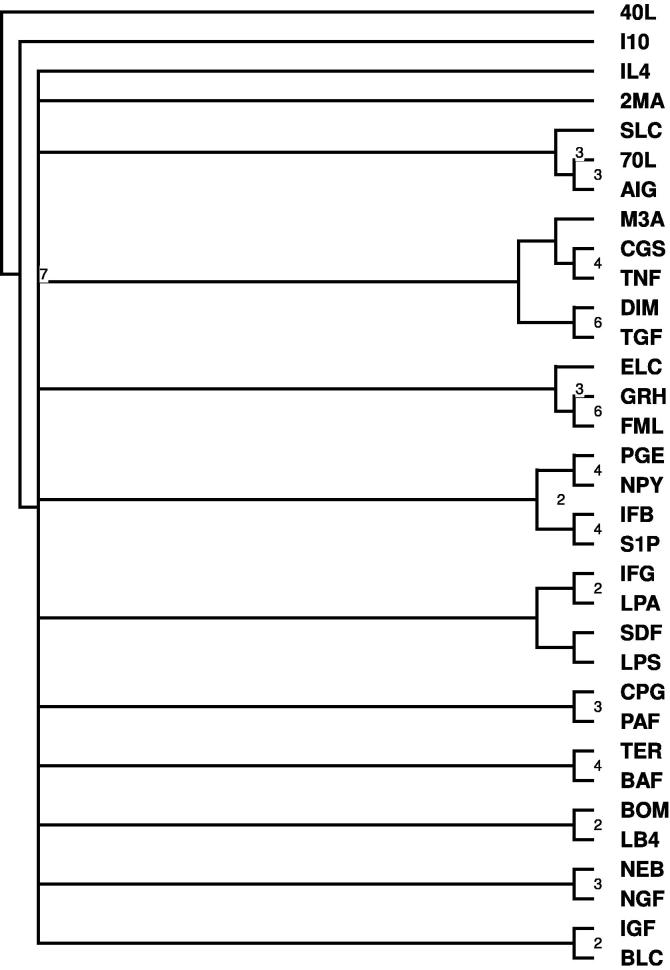
Figure 5.

Consensus of all pathway categories inTable 2 The values on the branches indicate the total number of times that the branch appeared across all networks (total of 7). If no value is indicated, the branch appeared only once.

Figure 3, Figure 4 present examples of the alignment based on the KEGG metabolism and Genetic Information Processing pathways. The numbers on the branches signify the number of similarly regulated subpathways between any two ligands. It was shown that some ligand networks (e.g., TER/BAF and FML/GRH) fall under the same clade/subtree in the two pathways, signifying general similarity in the regulation/signaling of pathways by such ligands. Differences between the trees show that the ligands may have different effects depending on the pathway being observed.

Figure 5 shows a consensus tree based on all seven general pathway categories highlighted in Table 2. GRH and FML, for example, fall under the same clade/subtree in the consensus tree in Figure 2 and the consensus tree constructed based on differentially expressed pathways (Table 2) shown in Figure 5. Overall, this shows that the results of the alignment is consistent across the different pathways chosen to ascertain the similarity hierarchy between the overall networks. The numbers on the branches can also serve as confidence measures for grouping certain leaves/networks with each other.

We also utilized specific signaling pathways highlighted in the literature [7], [8] (Table S1) to align the networks and constructed a cladogram (Figure S2) describing the relationship between the ligands. The results from the alignments showed that some ligands tend to have similar expression patterns based on the KEGG pathways used to anchor the pairwise all-vs-all alignments for the 33 ligand networks. Table 3 presents a detailed list of ligands that induce similar expression cascades in the KEGG pathways highlighted in Table 2. Several of the matched ligands (Figure 5) are actually known to induce similar reactions in B-cells based on a literature search we conducted. It is important to point out that the algorithm is detecting expression patterns that are similar in B-cells across different ligands, though not all such patterns may necessarily be important for cell function.

Table 3.

Top matched ligands based on expression patterns in the consensus tree shown in Figure 5

Matched ligands	Conserved KEGG pathway categories	Conserved KEGG subpathways
70L/AIG/SLC	Cellular processes, human diseases, organismal system	Cell cycle, p53 signaling pathway, phagosome, Parkinson’s disease, Huntington’s disease
LPA/IFG	Cellular processes, human diseases	p53 signaling pathway, bacterial invasion of epithelial cells
GRH/FML	Cellular processes, environmental information processing, genetic information processing, Human diseases, metabolism, organismal system	Cell cycle, regulation of autophagy, Aminoacyl-tRNA biosynthesis, ribosome, RNA degradation, RNA polymerase, DNA replication, ubiquitin mediated proteolysis, Parkinson’s disease, Huntington’s disease, thyroid cancer, TCA cycle, oxidative phosphorylation, pyrimidine metabolism, glyoxylate and dicarboxylate metabolism
PGE/NPY	Cellular processes, immune system, metabolism, organismal system	Oocyte meiosis, cytosolic DNA-sensing pathway, Fc gamma R-mediated phagocytosis, TCA cycle, ubiquinone and other terpenoid-quinone biosynthesis, oxidative phosphorylation, pyrimidine metabolism, riboflavin metabolism, terpenoid backbone biosynthesis
IFB/S1P	Cellular processes, human diseases, immune system, organismal system	Cell cycle, oocyte meiosis, p53 signaling pathway, Parkinson’s disease, Huntington’s disease, bacterial invasion of epithelial cells, Fc gamma R-mediated phagocytosis
BOM/LB4	Human diseases, organismal system	Colorectal cancer, Glioma, Cardiac muscle contraction
NEB/NGF	Environmental information processing, human diseases, organismal system	mTOR signaling pathway, Parkinson’s disease, Amyotrophic lateral sclerosis, Colorectal cancer, Glioma, Neurotrophin signaling pathway
TNF/CGS	Cellular processes, genetic information processing, human diseases, metabolism	Cell cycle, p53 signaling pathway, ribosome, DNA replication, mismatch repair, SNARE interactions in vesicular transport, Parkinson’s disease, bacterial invasion of epithelial cells, steroid biosynthesis, oxidative phosphorylation, glyoxylate and dicarboxylate metabolism
PAF/CPG	Environmental information processing, immune system, metabolism	RIG-I-like receptor signaling pathway, cytosolic DNA-sensing pathway, pyrimidine metabolism, cyanoamino acid metabolism, one carbon pool by folate, riboflavin metabolism
TER/BAF	Cellular processes, environmental information processing, genetic information processing, metabolism	Cell cycle, oocyte meiosis, p53 signaling pathway, endocytosis, aminoacyl-tRNA biosynthesis, RNA degradation, spliceosome, ubiquitin mediated proteolysis, TCA cycle, pentose phosphate pathway, cyanoamino acid metabolism
DIM/TGF	Environmental information processing, genetic information processing, human diseases, immune system, metabolism, organismal system	Aminoacyl-tRNA biosynthesis, ribosome, RNA polymerase, basal transcription factors, spliceosome, protein export, mismatch repair, bacterial invasion of epithelial cells, colorectal cancer, RIG-I-like receptor signaling pathway, cytosolic DNA-sensing pathway, B-cell receptor signaling pathway, TCA cycle, pentose phosphate pathway, steroid biosynthesis, oxidative phosphorylation

Note: The KEGG pathway categories correspond to the pathway categories highlighted in Table 2. Please see Table S3 for an expanded version.

For example, lipopolysaccharide (LPS) and stromal cell derived factor-1 (SDF) are known to affect cellular migration, interferon-gamma (IFG) and lysophosphatidic acid (LPA) are known to trigger changes in isotype switching [7], [8]. Macrophage inflammatory protein-3 (M3A)/dimaprit (DIM)/transforming growth factor-beta 1 (TGF) have several effects: M3A is strongly chemotactic for lymphocytes, DIM, an analog to histamine, activates immune response, while TGF provides a chemotactic gradient for leukocytes and down-regulates the activity of immune cells [31]. Neurokinin B (NEB) and nerve growth factor (NGF) have both been shown to be involved in the growth and development of neurons [32], [33]. Furthermore, tumor necrosis factor-alpha (TNF) has been shown to be highly involved in mediating inflammatory and immune responses [34], similar to what has been recently observed using CGS (CGS-21680 hydrochloride) [35].

In addition, the relationship between each of the above ligands as to exactly which ligands trigger similar expression patterns in the selected KEGG subpathways is also shown (Tables 3 and S3, the expanded version of Table 3). We can see that several major pathways are regulated in B-cells in response to the exposure to the 33 ligands shown in Table 1. First, human disease pathways (e.g., cancer and asthma) are the most prevalent pathways triggered by over half the ligands: 70L, AIG, SLC, LPA, IFG, GRH, FML, IFB, S1P, BOM, LB4, NEB, NGF, TNF, CGS, DIM and TGF. Those ligands constitute a set of molecules that trigger a wide variety of responses in B-cells and can be used to further ascertain the conditions under which B-cells activate under certain situations in human diseases. Second, cellular process pathways (e.g., endocytosis and apoptosis) seem to be also over-represented among the pathways that significantly change in expression across upon exposure to ligands. Some of the ligands (70L, AIG, SLC, LPA, IFG, GRH, FML, IFB, S1P, TNF and CGS) seem to trigger both human disease and cellular process pathways, while other ligands (PGE, NPY, TER and BAF) only trigger cellular pathways. Such ligands constitute a set of molecules that trigger changes in B-cells that may affect their growth and proliferation. The third major pathway commonly regulated in B-cells upon ligand exposure is metabolism with a sizable number of ligands (GRH, FML, PGE, NPY, TNF, CGS, PAF, CPG, TER, BAF, DIM and TGF) triggering pathways in that category. Ligands that only triggered pathways in B-cells related to metabolism but not “human diseases” or “cellular processes” are PGE, NPY, PAF, CPG. Since those ligands are known to affect inflammation and antibody production, the metabolic pathways expressed as a result of B-cell exposure to those ligands may be important indicators of B-cell immune response.

Conclusion

Identifying sets of ligands that trigger similar B-cell responses provides a basis for elucidating the specific genetic interactions that play a role in the recognition of ligands by B-cells. To achieve this goal, we constructed 33 gene coexpression networks that represented the genetic interactions in B-cells after exposure to each of the 33 ligands. Each network represents the response of normal splenic B-cells to a specific ligand across four different time points with three replicates per time point. We then utilized several comparative approaches to identify shared subnetworks/pathways among the 33 networks. Based on those pathways (Table 2), we were able to identify ligands that trigger similar expression changes in each of the pathways (Table 3, Figure 5, Figure 6, and Supplementary materials).

Aligning the 33 ligand networks allowed the detection of the specific relationships between the ligands in terms of the pathways that they regulate in B-cells. Additionally, the alignment pointed out specific pathways that share expression patterns across ligands and are involved in BCR activation. We have been able to validate some of the relationships we uncovered based on the immune responses described in the literature in the case of some of the ligands in our dataset. The computation tools and methods we utilized for constructing the alignments and analyzing the results are available online as part of the BiNA (Biomolecular Network Alignment) toolkit http://www.cs.iastate.edu/~ftowfic. An analysis pipeline based on network alignment such as the one used in this study may also serve as a general template for identifying pathways with conserved expression patterns across different conditions in other types of experiments. Some promising directions for further work include integrating additional types of information (e.g., protein–protein interaction networks) in our analyses and overlaying our pathways with already known protein–protein interactions to detect specific proteins that are responsible for triggering the signaling cascades for each ligand. Such information can aid in narrowing down the list of pathways to their core protein interactions.

Materials and methods

Microarray data

The microarray data [7], [8] were collected from the Alliance for Cell Signaling (AfCS) site (http://www.signaling-gateway.org/) [36]. Briefly, the experiments were designed to examine gene expression changes induced by the 33 single ligands.

Mouse splenic B-cells were cultured with ligands in serum-free medium for 0.5, 1, 2, and 4 h. cDNA synthesized from the RNA of B-cells was labeled with Cy5 and hybridized onto custom-made two-color Agilent cDNA arrays (Containing 16273 probes) with a Cy3-labeled cDNA prepared from the RNA of total splenocytes. There were a total of 424 Agilent chips hybridized in this study [7], [8].

The data was processed using MatLab® Bioinformatics toolbox. The background corrected intensity values were used for each chip. Some of the background corrected intensities were negative and made it difficult to take the logarithm of the data. To circumvent this problem, a very low positive value (10, a value that was 500 times below the mean intensity of all chips) was assigned to these probes. Each chip was also normalized to its mean intensity. Chip-to-chip normalization was performed via the LOWESS normalization method to allow for adequate analysis between chips [37]. After the normalization, the replicate chips were averaged. To remove the outliers each replicated probe was subjected to an outlier test. The outlier test was as follows: First, we calculate the mean and standard deviation (SD) for all replicates of each probe. Second, select the probes in the range of mean ± 1.2 SD for the calculation of a new mean and SD. Third, we discard the probes out of the range of the new mean ± 2 new SD. Finally, we calculate the fold change as ligand treated divided by control (untreated) samples for each probe on the chip. The log fold-change was calculated using R’s [38] BioConductor [39] package.

Construction of gene coexpression networks

After obtaining the expression matrices for each of the 33 ligands (33 expression matrices total), we merged expression levels from probesets that mapped onto the same gene. This was done by averaging the log(FC) values across the probesets that mapped to the same gene as indicated by the microarray chip annotation information provided by Agilent. After obtaining a single expression matrix per ligand (where rows in the matrix are genes and columns are the replicates/timepoints for that particular ligand), Pearson correlation was used to obtain the gene coexpression matrices. We obtained 33 gene coexpression matrices (E^1…33), one for each ligand, then applied a correlation cutoff of ⩾0.8 to sparsify the matrices. Entries $e_{i\text{,}j}^k$ in the matrix E^k were set to 0 whenever $|e_{i\text{,}j}^k|<0.8$ for 1 ⩽ k ⩽ 33 and 1 ⩽ i,j ⩽ n where n is the number of genes/rows in the matrix E^k. Remaining entries $|e_{i\text{,}j}^k|>0$ signified edges in the networks that connected genes whose expression patterns were correlated above our chosen cutoff. It is important to note that when a gene does not change in treatment samples (distribution of expression follows a normal distribution) relative to control (also a normal distribution due to normalization), the correlation is 0. As such, the edge does not exist in the graph. Additionally, we did not disregard any nodes in the networks explicitly based on a strict cutoff of differential expression since we did not want to bias the network analysis based on network size. As a result, all genes were considered in our analysis. The resulting networks were treated as undirected, weighted graphs with an average of 10,000 nodes (genes) and 1 million edges ($\left(\begin{array}{c}\hfill 10\text{,}000\hfill \\ \hfill 2\hfill \end{array}\right)\approx 50$ million possible edges in a fully connected graph). We varied the threshold cutoff around our chosen value (0.8) from [0.78, 0.82] in 0.01 increments and the distances between the degree distributions (see Figure S1 for example) of the ligand networks did not significantly (P < 0.01) differ as measured by the Friedman test. We also removed edges whose P value (calculated using Student’s t-distribution for a transformation of the correlation as implemented in Matlab) did not pass a significance threshold of P < 0.05. The percentage of edges removed using the correlation significance procedure is indicated in Table S4. Removing such edges did not influence the results as measured by comparing the degree distributions of the networks with and without such edges using the Friedman test.

Gene coexpression network alignment

Given two gene coexpression networks (graphs 1 and 2), the graphs are treated as weighted (where the weights on the edges denote the pairwise correlation in the expression of the corresponding genes). A k-hop neighborhood-based approach to alignment is used [21], [27]. The k-hop neighborhood of a vertex $v_x^1\in V_1$ of the graph G₁(V₁, E₁) is simply a subgraph of G₁ that connects $v_x^1$ with the vertices in V₁ that are reachable in k-hops from $v_x^1$ using the edges in E₁. Given two graphs G₁(V₁, E₁) and G₂(V₂, E₂), a mapping matrix P that associates each vertex in V₁ with zero or more vertices in V₂ (the matrix P can be constructed based on BLAST matches or gene IDs. In our analysis, using a 1-to-1 mapping between expression networks based on gene IDs and a user-specified parameter k, we construct for each vertex $v_x^1\in V_1$ its corresponding k-hop neighborhood C_x in G₁. We then use the mapping matrix P to obtain the set of matches for vertex $v_x^1$ among the vertices in V₂ and construct the k-hop neighborhood Z_y for each matching vertex $v_y^2$ in G₂ and $P_{v_x^1{v}_y^2}=1$. Let $S(v_x^1\text{,}{G}_2)$ be the resulting collection of k-hop neighborhoods in G₂ associated with the vertex $v_x^1$ in G₁. We compare each k-hop subgraph C_x in G₁ with each member of the corresponding collection $S(v_x^1\text{,}{G}_2)$ to identify the k-hop subgraph of G₂ that is the best match for C_x (based on a chosen similarity measure). We utilized a k-hop value of 1 for the analysis we discussed in this paper. The analysis was conducted on eight nodes from the San Diego Supercomputer Center’s Triton cluster with eight cores and 24 GB of memory per node.

Shortest path graph kernel score

The shortest path graph kernel was first described by Borgwardt and Kriegel [40]. The kernel acts as a scoring function that compares the length of the shortest paths between any two nodes in a graph based on a pre-computed shortest-path distance. The shortest path distances for each graph may be computed using the Floyd–Warshall algorithm. We modified the Shortest-Path Graph Kernel to take into account the labels of the nodes being compared as computed by BLAST [41] or as a mapping in the mapping matrix P. The shortest path graph kernel for subgraphs $Z_{G_1}$ and $Z_{G_2}$ (e.g., k-hop subgraphs) is given by:

$$S={\displaystyle \sum _{v_i^1\text{,}{v}_j^1\in Z_{G_1}}}{\displaystyle \sum _{v_k^2\text{,}{v}_p^2\in Z_{G_2}}}{P}_{v_i^1{v}_k^2}\times P_{v_j^1{v}_p^2}\times d(v_i^1\text{,}{v}_j^1)\times d(v_k^2\text{,}{v}_p^2)$$

$$K(Z_{G_1}\text{,}{Z}_{G_2})=\left\{\begin{array}{cc}0\hfill & S=0\hfill \\ \mathit{Log}[S]\hfill & \mathit{otherwise}\hfill \end{array}\right)$$

where $d(v_i^1\text{,}{v}_j^1)$ and $d(v_k^2\text{,}{v}_p^2)$ are the lengths of the shortest paths between $v_i^1\text{,}{v}_j^1$ and $v_k^2\text{,}{v}_p^2$ computed by the Floyd–Warshall algorithm. For gene coexpression networks, the Floyd–Warshall algorithm takes into account the weight of the edges (correlations) in the graphs. The runtime of the Floyd–Warshall Algorithm is O(n³). The shortest path graph kernel has a runtime of O(n⁴) (where n is the maximum number of nodes in the larger of the two graphs being compared).

Hierarchical clustering

A set of symmetric 33 × 33 distance matrices using the alignment scores across the 33 networks was constructed. Each matrix was constructed based on a specific subset of genes on the microarray chip (e.g., all genes involved in Calcium Signaling Pathway, all genes involved in Notch Signaling Pathway…etc. Please see Table 2, S1 and S2 for a full list of pathways utilized for comparing the networks). For each matrix, the diagonals contained the sum of the rows in the matrix and the off diagonals contained the alignment score comparing the network from row i with the network in column j where 1 ⩽ i,j ⩽ 33. The hierarchical cluster was constructed using a neighbor-joining method based on the distance matrix in Matlab. The hierarchical cluster can be used to visualize the relationship across the networks representing the gene expression changes due to exposure to different ligands. TreeView [42] was used to visualize the hierarchical clusters and the “consense” program of Phylip [30] was used to merge hierarchical clusters and to compute majority-rule consensus trees. The majority rule consensus approach has been shown to minimize the number of false groupings and provides a good summary of the posterior distribution over the trees that were used to construct the consensus tree [43]. Significance of clusters was computed using a hypergeometric distribution using the simple scheme:

$$P(X=r)=\frac{\left(\begin{array}{c}d\hfill \\ r\hfill \end{array}\right)\left(\begin{array}{c}l-d\hfill \\ c-r\hfill \end{array}\right)}{\left(\begin{array}{c}l\hfill \\ c\hfill \end{array}\right)}$$

where d is the number of ligands that had a high number of differentially expressed genes (10, as highlighted in Figure 1). c is the number of ligands in the cluster (17, which includes TFR, SLC, IGF, TGF, IFG, CPG, M3A, S1P, 40L, CGS, IFB, 70L, GRH, AIG, 2MA, ELC, BOM). l is the number of ligands in the experiment (namely 33), and r is the number of ligands that had a high number of differentially expressed genes in the cluster (eight from Figure 1, namely: CPG, 40L, CGS, IFB, GRH, AIG, 2MA, and BOM).

Authors’ contributions

FT and SG assembled and verified the datasets for the analysis. FT wrote the algorithms, FT and SG ran the experiments and drafted the manuscript. SS and VH supervised the analysis, the algorithm design and manuscript revisions. All authors read and approved the final manuscript.

Competing interests

The authors declared that they have no competing interests.

Supplementary material

Supplementary Figure 1.

Number of clusters/k-hop neighborhoods needed for the network alignment This plot shows that we need around 638 nodes with the highest degree to accurately approximate the total alignment score if we had used up to 5,000 k-hops. In other words, one can reach within 0.9 or 90th percentile of the total score (that results from utilizing 5000 k-hop neighborhoods) by utilizing only the k-hop neighborhoods around the top 638 highly connected nodes. In summary, this plot shows that we only need to compute the alignment of the top 638 nodes if we are simply interested in the distance between two networks. The full alignment may later be computed after determining which networks are closest.

Supplementary data 1

Example of degree distributions used for Kolmogorov-Smirnov test for initial clustering of the ligands based on network topology As seen from the figure, the expression networks exhibit scale-free like behavior as described by Barabsi and Oltavai [1].

Supplementary data 2

Consensus tree constructed based on all KEGG pathways in Table S1 The values on the branches indicate the total number of times that the branch appeared across all networks (total of 11). If no value is indicated, the branch appeared only once.

Supplementary data 3

Consensus tree constructed based on all organismal system pathways in Table S2 The values on the branches indicate the total number of times that the branch appeared across all networks (total of 6). If no value is indicated, the branch appeared only once.

Supplementary data 4

Schematic of the experiments utilized to construct the gene coexpression networks for the 33 Ligands B cells were stimulated with 33 possible ligands (listed in Table 1) and harvested at 0.5,1, 2 and 4 hours (hr) post stimulation. Gene expression was assayed using Agilent cDNA arrays. Gene coexpression networks were then constructed by assembling the time point expression data from each stimulation and the correlation between all probes was then measured across all 4 time points (and 3 replicates per time point). A correlation magnitude cutoff of 0.8 was utilized to finally yield the networks used for this study (positive correlations are indicated by solid edges, while negative correlations are indicated by dashed edges in the figure). The networks were compared using a network alignment approach that took into account the weight on the edges around each respective node. Networks with similar topologies and weights around respective genes had higher score than those with a good toplogical match, but poor weight matches around matching genes.

Supplementary data 5

Supplementary Tables