Different combinations of atomic interactions predict protein‐small molecule and protein‐DNA/RNA affinities with similar accuracy

ABSTRACT

Interactions between proteins and other molecules play essential roles in all biological processes. Although it is widely held that a protein's ligand specificity is determined primarily by its three‐dimensional structure, the general principles by which structure determines ligand binding remain poorly understood. Here we use statistical analyses of a large number of protein−ligand complexes with associated binding‐affinity measurements to quantitatively characterize how combinations of atomic interactions contribute to ligand affinity. We find that there are significant differences in how atomic interactions determine ligand affinity for proteins that bind small chemical ligands, those that bind DNA/RNA and those that interact with other proteins. Although protein‐small molecule and protein‐DNA/RNA binding affinities can be accurately predicted from structural data, models predicting one type of interaction perform poorly on the others. Additionally, the particular combinations of atomic interactions required to predict binding affinity differed between small‐molecule and DNA/RNA data sets, consistent with the conclusion that the structural bases determining ligand affinity differ among interaction types. In contrast to what we observed for small‐molecule and DNA/RNA interactions, no statistical models were capable of predicting protein−protein affinity with >60% correlation. We demonstrate the potential usefulness of protein‐DNA/RNA binding prediction as a possible tool for high‐throughput virtual screening to guide laboratory investigations, suggesting that quantitative characterization of diverse molecular interactions may have practical applications as well as fundamentally advancing our understanding of how molecular structure translates into function. Proteins 2015; 83:2100–2114. © 2015 The Authors. Proteins: Structure, Function, and Bioinformatics Published by Wiley Periodicals, Inc.

INTRODUCTION

Proteins and other biological macromolecules function largely through their three‐dimensional structure, which determines the spatial distributions of physical‐chemical properties as well as their dynamics.1, 2, 3 However, understanding how structural characteristics quantitatively affect molecular function has proven one of the most challenging objectives in structural biology.4 Particular examples have been elucidated in detail,5, 6, 7, 8 but we know very little about the general principles by which molecular structure determines function.

Although a drastic simplification of a protein's functional repertoire, binding affinity is typically used to characterize protein−ligand interactions. Affinity is commonly measured using the dissociation constant [Kd or pKd = −log(Kd)], which is the ligand concentration at which half the protein in solution is bound to ligand at equilibrium.9, 10, 11, 12, 13 Predicting molecular binding affinity from structural complexes has been investigated for decades, due to its fundamental importance in biochemistry and applications to structure‐based drug development.14, 15, 16, 17, 18 Most approaches attempt to produce a quantitative mapping to binding affinity from features that can be derived from a protein−ligand structure.9, 18, 19 Mapping atomic interactions to binding affinity is not trivial, and a variety of methods have been developed. These methods can be broadly classified into approaches that attempt to directly model the physical forces contributing to molecular binding and those that rely on statistical associations between combinations of atom−atom interactions and ligand affinity.14, 18, 20, 21, 22, 23, 24, 25 Robust physics‐based methods such as molecular dynamics are able to infer information about changes in system energy and other factors and can produce highly accurate affinity prediction, albeit at the cost of increased computation time.26 Statistical prediction methods are typically much faster than physics‐based approaches and can generally predict protein‐small molecule affinity with accuracy suitable for high‐throughput drug screening and similar applications.24, 26, 27, 28, 29, 30, 31, 32, 33 It has also been suggested that linear combinations of atomic interaction features suitable for statistical prediction methods correlate strongly with more complex physics‐based energy calculations.33, 34

Protein‐small molecule interactions have received the most extensive research attention—primarily due to applications in structure‐based drug design—and great progress has been made toward understanding how protein structure impacts small‐molecule binding.17, 35, 36, 37, 38, 39 However, predicting protein‐DNA/RNA and protein−protein binding from structural data has remained challenging, suggesting that these types of interactions may not follow the same rules governing protein‐small molecule binding.4, 21, 24, 27, 34, 40, 41, 42, 43, 44, 45, 46

Here we use statistical machine learning to examine the general patterns of atomic interactions determining protein‐small molecule, protein‐DNA/RNA, and protein−protein binding affinities. We find that atomic interaction data present in the X‐ray structure of the protein−ligand complex is generally sufficient to predict protein‐small molecule and protein‐DNA/RNA affinities with similar accuracy, but protein−protein affinity prediction was much less accurate. Although protein‐small molecule and protein‐DNA/RNA affinities were similarly predictable, the specific combinations of atomic interactions required for accurate prediction differed between the two types of ligands, suggesting that the way patterns of atom‐atom interactions translate into macromolecular interaction strength differ between proteins that bind small chemical ligands and those that bind DNA/RNA. Developing a more thorough understanding of how different sets of atomic interactions determine a protein's affinity for different types of ligands is expected to deepen our understanding of the structural basis of molecular function while providing new avenues for predicting—and ultimately modulating—protein function.

METHODS

Structural data sets and feature extraction

The X‐ray structures of protein‐ligand complexes and their associated experimental binding affinity measurements (‐log₁₀‐transformed dissociation constants, pKds) were obtained from PDBbind,47 BindingDB48 and a recent large‐scale study of protein−protein interactions.49 Complexes with ambiguous ligand information were excluded, as were complexes with multiple ligands or mulitimeric proteins. For proteins bound to DNA or RNA, we removed any complexes with DNA/RNA strands >1000 nucleotides. Enzyme commission (EC) numbers were extracted from PDB‐to‐EC mapping databases,50, 51 and transmembrane proteins were identified using the Protein Data Bank of Transmembrane Proteins (PDBTM).52 From each protein−ligand complex, we extracted a suite of non‐redundant atom‐atom interactions thought to potentially correlate with ligand binding affinity9 (see Fig. 1). We included only those atomic interactions that could be determined entirely from atomic coordinates and atom types in a standard PDB file.

Figure 1.

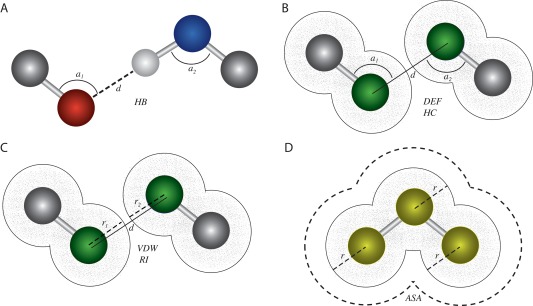
Atomic interactions potentially underlying protein−ligand binding can be extracted from three‐dimensional atomic coordinates. We modified existing approaches to extract a wide variety of atomic interactions from crystalized protein−ligand complexes (see Methods). A: Hydrogen bonding (HB) can be calculated by examining the distance, d, between a hydrogen atom (white sphere) covalently bound to a hydrogen donor (blue) and a potential hydrogen acceptor (red), as well as the angles formed across the hydrogen donor (a₂) or acceptor (a₁) and its respective root atoms (gray). B: Deformation effect (DEF) and hydrophobic contacts (HC) are calculated by examining the distance, d, between two hydrophobic atoms (green) and the relative angles formed across them and their root atoms (gray). C: van der Waals (VDW) and repulsive interactions (RIs) are calculated by examining the distance, d, between two hydrophobic atoms (green), relative to the van der Waals radii of the two interacting atoms (r ₁ and r ₂, respectively). D: The accessible to solvent area (ASA) is estimated as the area surrounding a group of covalently bound atoms (yellow spheres) that is not occluded by any other atoms in the group, taking into account the van der Waals radii of each atom (r).

Hydrogen bonds (HBs)

A hydrogen bond is a noncovalent interaction between two negatively charged atoms, in which hydrogen is covalently bound to one atom (the donor, D) and interacts with the other negatively charged atom (the acceptor, A) through electrostatic attraction. To extract the hydrogen bonding parameter (HB), we used a function that relates the distance between potential hydrogen donors and acceptors as well as the angles among them and their root atoms, to the presence or absence of a hydrogen bond [see Fig. 1(A)]. Potential hydrogen donors (D) and acceptors (A) were determined from negatively charged nitrogen, sulfur, and oxygen atoms. The acceptor root (AR) and donor root (DR) atoms were determined from the atoms covalently bound to acceptors and donors, respectively. We related these atomic types and coordinates to hydrogen bonding via the function:

$$\mathrm{H}\mathrm{B}=\sum _{i,j=1}^{n}f(d_{i,j}, {a1}_{i,j},{a2}_{i,j})$$

where i and j are potential hydrogen donors and acceptors in the protein and ligand, respectively; a1 is the angle among AR, A, and D, and a2 is the angle among A, D, and DR [see Fig. 1(A)]. The distance and angle functions were adapted from Ref. 24, and acceptable bond angle parameters were obtained from Ref. 53. The summation was performed over all potential hydrogen donor‐acceptor pairs bridging the protein and its ligand.

Hydrophobic contacts (HCs)

Hydrophobic contacts are noncovalent interactions between two nonpolar atoms from different molecules. For extracting this parameter from the 3D coordinates of a structural complex, we use the following equation:

$$\mathrm{H}\mathrm{C}=\sum _{i,j}^{n}f\left({HC}_{i,j}\right); \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}$$

$${\mathrm{H}\mathrm{C}}_{i,j}=\left[\left(1/1.5\right)*{\left(r_i+r_j+2.0\right)}^2‐{d_{i,j}}^2\right]$$

$$f\left({\mathrm{H}\mathrm{C}}_{i,j}\right)={\mathrm{H}\mathrm{C}}_{i,j} if\left[\left(r_i+r_j+0.5\right)<d_{i,j}\le \left(r_i+r_j+2.0\right)\right]$$

$$=1 if\left[d_{i,j}\le \left(r_i+r_j+0.5\right)\right]$$

$$=0 if\left[d_{i,j}>\left(r_i+r_j+2.0\right)\right]$$

where r is the van der Waals radius of a given hydrophobic atom (i or j), and d_i,j is the distance between hydrophobic atoms i and j [see Fig. 1(B)]. Again, we sum over all pairs of potential hydrophobic contacts between the protein receptor (i) and its ligand (j).

van der Waals interactions (VDWs)

The van der Waals interaction parameter (VDW) is obtained by summing the attractive and repulsive forces between protein and ligand atoms, excluding those due to covalent bonds and hydrogen bonds. These attractive or repulsive forces are estimated from a function that uses the van der Waals radii of two interacting atoms and the distance between them (equation adapted from Ref. 31, van der Waals radii obtained from Ref. 54):

$$VDW=\sum _{i,j}^{n}f\left[{\left(\frac{r_i‐r_j}{d_{i,j}}\right)}^8‐2x{\left(\frac{r_i‐r_j}{d_{i,j}}\right)}^4\right]$$

where i and j are atoms in the protein and ligand, respectively; r is the van der Waals radius of a specified atom, and d_i,j is the distance between atoms i and j [see Fig. 1(C)]. To minimize the over‐estimation of strong attractive forces, we set f(i,j)=100 if the calculated value was >100.

Deformation effect (DE)

The deformation effect (DE) represents the number and extent of distortions in the root atoms (of hydrogen bond donor and acceptor or hydrophobic atoms) that occur in order to form intermolecular interactions. DE was calculated using the equation (adapted from Ref. 53):

$$\mathrm{D}\mathrm{E}=\sum _{i,j}^{n}f({a1}_{i‐1,i,j},{a2}_{i,j,j‐1}); \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}:$$

$$f\left({a1}_{i‐1,i,j},{a2}_{i,j,j‐1}\right)=1\hspace{1em}if\left[\left({a1}_{i‐1,i,j}\ge 60°\right) and \left({a2}_{i,j,j‐1}\ge 60°\right)\right]$$

$$f\left({a1}_{i‐1,i,j},{a2}_{i,j,j‐1}\right) = 0\hspace{1em}if\left[\left({a1}_{i‐1,i,j}<60°\right) or \left({a2}_{i,j,j‐1}<60°\right)\right]$$

where i − 1 is the root atom of the interacting atom i; j − 1 is the root atom of the interacting atom j; a1 is the angle among the atoms i − 1,i,j; and a2 is the angle among the atoms i,j,j − 1 [see Fig. 1(B)]. If there were more than one root atom for a given interacting atom, the root was considered as the geometric center of the coordinates of all root atoms.

Repulsive interactions (RIs)

The repulsive interaction (RI) parameter is the sum of all repulsive atomic contacts between two molecules, excluding contacts due to hydrogen bonds or hydrophobic interactions [see Fig. 1(C)]. This parameter was calculated as:

$$\mathrm{R}\mathrm{I}=\sum _{i,j}^{n}f\left({\mathrm{R}\mathrm{I}}_{i,j}\right); \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}:$$

$$f\left({\mathrm{R}\mathrm{I}}_{i,j}\right)=1 if[d_{i,j}\le {(r}_i+r_j)]$$

$$f\left({\mathrm{R}\mathrm{I}}_{i,j}\right)=0 if[d_{i,j}>{(r}_i+r_j)]$$

where d_i,j is the distance between atoms i and j in the protein receptor and its ligand, respectively; r_i is the van der Waals radius of atom i, and r_j is the radius of atom j. The sum is over all potential interacting atom pairs: i,j.

Accessible to solvent area (ASA)

The accessible to solvent area (ASA) is the area of a molecule's surface that is exposed to solvent and therefore available for interacting directly with other molecules. We calculated the accessible to solvent area of the protein and its ligand using the algorithm of Shrake and Rupley,55 which generates a spherical mesh of equidistant points around every atom in a given molecule and counts the number of points that are not occluded by other atoms in the molecule and therefore available to interact with solvent [see Fig. 1(D)]. The algorithm was adapted from code available at (https://github.com/boscoh/pdbremix/blob/master/pdbremix/asa.py) . The van der Walls radii were altered to the values provided by Ref. 54, and the number of sphere points was increased to 960.

We determined the extent to which each type of atomic interaction was correlated with experimental binding affinity by calculating the Spearman correlation between the atomic interaction term measured in this section and the experimental binding affinity in pKd units [pKd = −log(Kd)], obtained from binding affinity databases.47, 48, 49

Statistical modeling, model selection and Cross‐validation

We used three types of regression methods to identify sets of atom−atom interactions—and their statistical interaction terms—correlating with experimentally determined binding affinity (pKd).56, 57, 58 We used generalized linear models (GLMs, implemented in the GLMULTI package in R),56 assuming a Gaussian error distribution with logarithmic link function, which provided the best fit to our data. We also used single‐layer and double‐layer support vector regression (SLSVR and DLSVR, respectively), implemented using the approach developed by Li et al.57 For each type of statistical regression, we used the GLMULTI genetic algorithm to generate 500 candidate models (default parameters, except population size = 500, level = 2, and marginality enabled) and selected the top 100 best‐fit models using either Akaike or Bayesian information criteria (AIC or BIC, respectively).

We used replicate cross‐validation to evaluate the potential accuracy with which generated models can predict binding affinity of unseen data sets (see Fig. 2). For each replicate analysis, we randomly partitioned the structural data into a testing data set of size n = 1, 10, 30, 50, or 100 complexes, with the remaining complexes being used to train the regression model. On each testing data set, we calculated the Pearson correlation (r ²) and root mean squared deviation (RMSD) between predicted and experimentally determined binding affinity (pKd). We repeated each cross‐validation analysis 100 times and report the average r ² and RMSD. Differences in accuracy between models were assessed using the parametric two‐sample t test, assuming unequal variances, and the nonparametric Mann‐Whitney U test.

Figure 2.

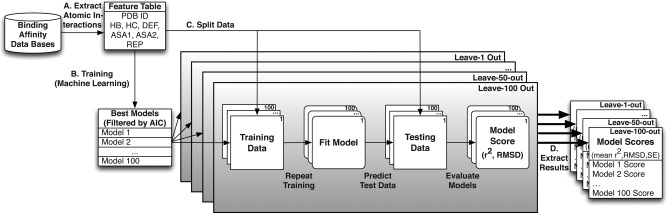
Replicated cross‐validation evaluates expected model accuracy. We used multiple different hierarchical, replicated cross‐validation analyses to evaluate the accuracy with which statistical models could predict molecular binding affinities from structural information (see Methods). A: Atomic interactions (see Fig. 1) were extracted from the atomic coordinates of each protein−ligand complex. B: Statistical models were fit to different portions of these data, with the best‐fit models selected by AIC (see Methods). C: Each data set was randomly partitioned into training and testing data, using 5 different leave‐out strategies (see Methods). Each model was fit to the training data, and accuracy was evaluated on the set‐aside testing data by calculating Pearson's correlation (r ²) and the root mean squared deviation (RMSD) between predicted and experimentally determined binding affinities (see Methods). D. The entire cross‐validation procedure was repeated 100 times, and we report the mean and standard error in r² and RMSD across the 100 cross‐validation replicates.

We performed the same cross‐validation analyses using other binding affinity estimation tools: X‐Score v1.2,31 Drugscore v0.88,22 and Fastcontact,59 assuming default parameters. We restricted our comparative analyses to freely available tools that use only atomic interactions that can be extracted from the 3D coordinates of bound complexes.

We performed mixed model analysis using the Lme4 v1.1.7 package for fitting linear and generalized linear mixed‐effects models.58, 60 One mixed model was generated for each data set by adding random effects to the best‐fit GLM obtained from cross‐validation analysis (see above). Mixed models were fit and validated using the same input data and cross‐validation method applied to simple GLMs.

Empirical analysis examples

We performed docking simulations between SelB and its native mRNA ligand using Haddock v2.1⁶¹ and Patchdock v1.0,62 generating a total of 100 predicted complexes. We obtained the original protein−ligand structure of SelB from the Protein Data Bank (PDB ID: 1WSU)63 and calculated the RMSD (in angstroms) between the X‐ray crystal structure and predicted complexes generated by molecular docking. We considered docking poses with RMSD < 3.5 Å as near‐native, while poses having RMSD ≥ 3.5 Å were considered decoy complexes. We used the best‐fit GLM (see above) to predict the SelB‐mRNA pKd of each generated complex.

CsrA/RsmE‐RNA binding affinities were estimated from NMR strcutures available from the Protein Data Bank64: RsmE‐SL1 (PDB ID: 2MFC), RsmE‐SL2 (2MFE), RsmE‐SL3 (2MFF), RsmE‐SL4 (2MFG) and RsmE‐RsmZ(36–44) RNA (2MFH). Alanine‐screening mutagenesis for CsrA‐RNA was simulated by molecular modeling using Phyre v2.065 and molecular docking simulations using Haddock v2.1.61

HYL1(HR1)‐dsRNA binding affinity was estimated from the crystal structure of the bound complex (PDB ID: 3ADI). TRBP2(TR2)‐dsRNA and HYL1(HR2)‐dsRNA complexes were inferred by molecular docking using Haddock v2.1.61 Receptor models of TRBP(TR2) and HYL1(HR2) were obtained from available crystal structures (PDB IDs: 3ADL and 3ADJ, respectively), and the dsRNA ligand model was obtained from the HYL1(HR1)‐dsRNA complex (3ADI).

RESULTS AND DISCUSSION

Protein‐DNA/RNA affinity can be predicted with accuracy similar to protein‐small molecule affinity

To characterize how patterns of atomic interactions govern protein‐small molecule, protein‐DNA/RNA and protein−protein binding affinities, we examined a large database of > 4700 protein−ligand complexes having both X‐ray crystal structures and empirically determined binding affinities.47, 48, 49 After removing complexes with ambiguous binding‐affinity measurements or multiple ligands, large multimeric complexes and DNA‐packaging proteins such as histones, our filtered database contained 2342 complexes with a protein bound to a small molecule such as a chemical signal or drug, 300 protein‐DNA/RNA complexes, and 784 protein−protein dimers (see SI Text S1 for statistical descriptions of the data sets and the effects of filtering).

From each complex, we extracted a set of nonredundant atomic interactions expected to correlate with ligand‐binding affinity (see Methods, Fig. 1). We fit a large number of statistical models to these data—representing different linear combinations of atomic interactions and statistical interaction terms capturing ratios of simple atom−atom interactions—and selected the best 100 models fitting each type of protein−ligand data set by Akaike information criterion (AIC). For each statistical model, we used generalized linear modeling (GLM) and two types of support vector frameworks to predict pKd from atomic interactions (see Methods). After training each model on set‐aside training data of different sizes, we measured the average Pearson correlation (r ²) and root mean squared deviation (RMSD) between predicted and experimentally determined binding affinities on multiple replicates of unseen testing data (see Methods). This approach provides a strong cross‐validation evaluation of each model's expected accuracy for predicting pKd from novel structural data (Fig. 2).

Protein‐small molecule binding affinity could be predicted with average accuracy similar to current state‐of‐the‐art statistical prediction tools. The best‐fit GLM predicted protein‐small molecule pKds on unseen testing data with r ² = 0.79 (RMSD = 0.94; Fig. 3). These results were generally robust to different statistical modeling frameworks and cross‐validation strategies. RMSD results were equivalent to GLM using either single‐layer or double‐layer support vector regression as the statistical modeling framework (t test P > 0.78, U test P > 0.75). Results were also similar across a wide variety of cross‐validation strategies, with average r ² differing by at most 3% when comparing different testing data set sizes [Fig. 3(B) and SI Fig. S5, t test P > 0.06 and U test P > 0.001]. That predictive accuracy does not depend strongly on a particular statistical modeling framework or cross‐validation scheme suggests that these results are generally robust, given our structural data, and that the accuracy we observed may reflect a reasonable estimate of the extent to which the atomic interactions we extracted can predict binding affinity. In our tests, the GLM performed significantly better than existing tools designed to predict small‐molecule affinity from structural data (XSCORE31 and Drugscore,66 r ² = 0.73 and 0.68, respectively, t test P < 1.5 × 10⁻²⁵, U test P < 4.7 × 10⁻²²), but differences in accuracy were relatively small.

Figure 3.

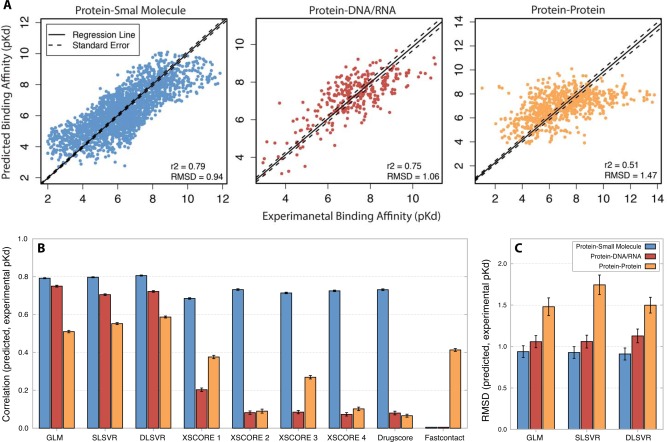
Statistical models predict protein‐small molecule and protein‐DNA/RNA binding affinities with high accuracy. We trained and cross‐validated statistical models to predict experimental binding affinity (pKd) from atomic interactions (see Methods, Figs. 1 and 2). A. For each type of molecular interaction, we plot the experimentally determined (x axis) vs. predicted (y axis) pKd of each complex. Dark line indicates best‐fit linear regression; dotted lines indicate standard error of regression line. Results are shown for the best‐fit generalized linear model (GLM). B: We plot the mean and standard error in Pearson's correlation (r²) between each model's predicted pKd and experimental pKd [mt]100 replicates of leave‐100‐out cross‐validation (see Methods). Results are shown for the GLM, single‐layer and double‐layer support vector regression (SLSVR and DLSVR, respectively) and a number of existing binding‐prediction algorithms (see also SI Fig. S4). C: We plot the mean and standard error in root mean square deviation (RMSD) between each model's predicted pKd and experimental pKd [mt]100 replicates of leave‐100‐out cross‐validation.

Protein‐DNA/RNA binding affinity could be predicted with accuracy similar to that achievable for small‐molecule affinity [Fig. 3(B), SI Fig. S5]. The GLM trained on protein‐DNA/RNA data had mean r ² between predicted and experimental pKd of 0.75 on unseen testing data, marginally less than what we observed for protein‐small molecule interactions (r ² = 0.79, t test P = 9.0 × 10⁻¹², U test P = 8.5 × 10⁻¹¹). The DNA/RNA and small‐molecule predictors had equivalent RMSDs on their respective data sets (1.04 for DNA/RNA vs. 0.94 for small‐molecule, t test P = 0.24, U test P = 0.23).

As with the small‐molecule data set, results for DNA/RNA binding prediction were generally robust to different statistical modeling frameworks (Fig. 3, SI Fig. S5, t test P > 0.53 U test P > 0.66) and different cross‐validation approaches (SI Fig. S5, t test P > 0.04 and U test P > 0.006), suggesting that these results likely reflect the extent to which extracted atomic interactions predict pKd and are not strongly dependent on a particular statistical framework or cross‐validation strategy. The accuracy of our new models was much higher than that of existing tools on the protein‐DNA/RNA data set [r ² = 0.75 vs. 0.20 for XSCORE and 0.08 for Drugscore, t test P = 6.6 × 10⁻⁹⁴, U test P = 2.6 × 10⁻³⁴, Fig. 3(B)], which is not unexpected, given that existing tools were designed to predict small‐molecule binding affinity, not DNA/RNA affinity.

Protein−protein binding affinity predictions were much less accurate (Fig. 3). Overall, r ² was <0.6 on the protein−protein data, ∼1.2 five‐fold less than that of the small‐molecule and DNA/RNA data sets (t test P < 7.3 × 10⁻³⁵, U test P < 2.3 × 10⁻²⁹). Similarly, RMSD was ∼1.5‐fold greater for the protein−protein data (t test P < 1.4 × 10⁻³, U test P < 9.6 × 10⁻³). Even though protein−protein affinity was predicted with reduced accuracy, predictive accuracy was still fairly robust to different statistical frameworks (t test p > 0.10, U test p > 0.12) and cross‐validation strategies (SI Fig. S5, t test P > 0.09, U test P > 3.9 × 10⁻³). Our new statistical models were significantly more accurate than Fastcontact, an existing tool developed for predicting protein−protein binding affinity using similar atomic interaction data59 (Fig. 3, t test P = 7.2 × 10⁻¹⁹, U test P = 1.5 × 10⁻¹⁶). However, the difference in accuracy was relatively small (r² = 0.51 for our model vs. 0.41 for Fastcontact).

Analysis of the residuals from each data set suggests that the potential for fitting bias is low, with no discernible linear trend (SI Fig. S6A, P = 0.99) and a generally good fit to a normal distribution (SI Fig. S6B). Quantile‐quantile plots did exhibit a slight skewing at extreme values, but this curved trend represented <10% of the validation data set size (SI Fig. S6C). We did not observe a major change in accuracy when we removed potential outlier complexes with pKd ≤3 or ≥10 from either the training data (t test P = 0.59, U test P = 0.30 for small molecule; t test P = 0.75, U test P = 0.45 for DNA/RNA; t test P = 2.0 × 10⁻⁹, U test P = 1.6 × 10⁻¹¹ for protein data set), or the testing data (t test P > 0.10, U test P > 0.16). In all cases, the change in mean accuracy was <3% (SI Fig. S7).

Although the results of examining residuals and outliers argue against model over fitting, concerns have been raised that AIC can be biased toward selecting overly complex models in some cases.67, 68 Bayesian model selection strategies—such as the Bayesian Information Criterion (BIC)—provide a more conservative approach, although they can be biased in favor of too‐simple models.69 As expected, we observed a general decrease in the complexity of best‐fit models when we used BIC for model selection instead of AIC (t test P < 2.3 × 10⁻⁴², U test P < 1.2 × 10⁻³⁰, SI Fig. S8A). However, no differences were observed in the predictive accuracy of models selected by BIC vs. AIC (t test P > 0.30, U test P > 0.60, SI Fig. S8B,C). Overall, these results suggest that the accuracy of inferred models is unlikely to be affected by over fitting bias and that our results are generally robust to different modeling frameworks, cross‐validation strategies and model‐selection procedures.

Although average predictive accuracy across a data set is an important component of assessing model performance, we wanted to examine whether affinity prediction accuracy was strongly affected by features that might differ across complexes in each data set, such as specific metabolic pathways, receptor or ligand flexibility, or structural similarity. Clustering structural complexes by metabolic pathway (using KEGG KOBAS v2.0³⁰) revealed no increase in accuracy for over‐represented pathways (SI Fig. S9A; Spearman correlation between the number of representatives in a pathway and RMSD = 0.32, P = 0.01 for small molecule; 0.71, P = 2.69 × 10⁻⁵ for DNA/RNA; −0.08, P = 0.58 for the protein data set). Similarly, there was no strong correlation between affinity prediction accuracy and receptor or ligand flexibility in any of the data sets examined (SI Fig. S9B,C; Spearman correlation between receptor flexibility and prediction error = −0.01, P = 0.60 for small molecule; −0.04, P = 0.46 for DNA/RNA; and 0.10, P = 0.01 for the protein data set. Spearman correlation between ligand flexibility and prediction error = 0.05, P = 0.02 for small molecule; 0.06, P = 0.28 for DNA/RNA; and 0.08, P = 0.03 for the protein data set). Finally, we observed only minimal changes in predictive accuracy when receptors in each data set were clustered by 90% sequence similarity (SI Fig. S9D). Together, these results suggest that affinity prediction accuracy is not confined to particular metabolic pathways, is not strongly affected by receptor or ligand flexibility, and is not particular to specific types of similar molecular structures.

Using a mixed modeling strategy to statistically characterize heterogeneity within each data set identified a number of atomic interaction types exhibiting significant heterogeneity in all three data sets (SI Fig. S10A). However, incorporating this heterogeneity in the statistical model did not improve predictive accuracy, compared to simpler homogeneous models (SI Fig. S10B), although we did observe a ∼twofold decrease in the variance of predictive accuracy in the protein−protein data set (var = 0.03 for the mixed‐model GLMM vs. 0.06 for GLM, 0.07 for SLSVR and 0.06 for DLSVR, f‐test p < 0.02). Overall, mixed model analyses suggest that heterogeneity is unlikely to strongly affect our results.

Statistical models trained on one type of ligand do not predict affinity for other ligand types

To evaluate the extent to which the atomic interactions predicting ligand‐binding affinity are different among protein‐small molecule, protein‐DNA/RNA and protein−protein data sets, we determined the accuracy with which statistical models trained on each data set predicted pKds on the other data sets [Fig. 4(A)]. In all cases, we observed that models trained on one data set exhibited dramatically reduced accuracy when predicting pKds of different data sets. The model trained using protein‐small molecule complexes showed the greatest specificity, decreasing in accuracy ∼1fivefold when tested on protein‐DNA/RNA data (r² = 0.79 on small‐molecule vs. 0.05 on DNA/RNA, t test P = 8.2⁻¹¹³, U test P = 2.6 × 10⁻³⁴) and ∼4‐fold when tested on protein−protein data (r² = 0.18, t test P = 2.2 × 10⁻¹³¹, U test P = 2.6 × 10⁻³⁴). Models trained using protein−protein data showed the highest generalizability to other data sets, but accuracy was still significantly reduced in cross‐prediction tests (r² = 0.51 for protein−protein data vs. 0.36 for small‐molecule and −0.17 for DNA/RNA, t test P < 5.8 × 10⁻⁶⁷, U test P < 2.6 × 10⁻³⁴). These results suggest that how particular atomic interactions correlate with binding affinity is generally different for different types of macromolecular interactions.

Figure 4.

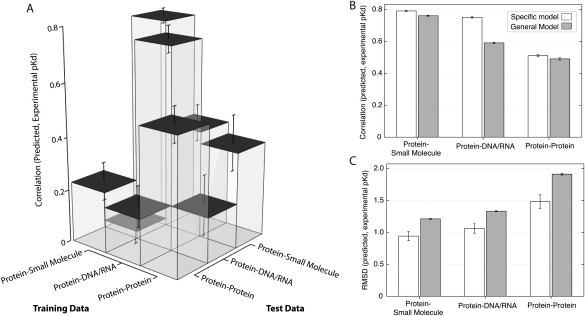
Binding affinity prediction is specific to each interaction type. For each type of molecular interaction (protein‐small molecule, protein‐DNA/RNA, and protein−protein), we fit a statistical model using cross‐validation (see Methods, Fig. 2) and evaluated each model's accuracy on set‐aside testing data of either the same interaction type or a different interaction type. A: We plot the mean and standard error in Pearson's correlation (r ²) between predicted and experimental pKd, showing how the statistical models trained using each type of training data predicted pKds on testing data of either the same or different type. B: We plot the mean and standard error in r ² between predicted and experimental pKd, comparing a general statistical model trained on all data sets (gray) to specific models (white) trained on each data set, respectively. C: We show the mean and standard error in root mean square deviation (RMSD) between predicted and experimental pKd, comparing a general statistical model (gray) trained on all data sets to specific models (white) trained on each data set.

Further supporting this conclusion, we observed that a “general” model trained on the combined small‐molecule+DNA/RNA+ protein−protein data exhibited reduced accuracy when used to analyze each particular data set [Fig. 4(B), t test P < 0.02, U test P < 0.03]. The largest reduction in accuracy occurred for the protein‐DNA/RNA data, for which the use of the general model decreased accuracy 1.27‐fold (r² = 0.59), compared to the model trained on the DNA/RNA data (r² = 0.75, t test P = 1.8 × 10⁻⁵⁸, U test P = 1.9 × 10⁻³²). Additionally, RMSD increased substantially when the general model was applied to each specific data set [Fig. 4(C), t test P < 2.9 × 10⁻⁴, U test P < 2.7 × 10⁻⁴]. This was particularly noticeable for the protein−protein data set, for which RMSD increased ∼1.2‐fold, from 1.47 to 1.91 (t test P = 1.1 × 10⁻⁴, U test P = 7.8 × 10⁻⁵). Together, these results suggest that the combinations of atomic interactions governing ligand‐binding affinity differ markedly among proteins that bind small‐molecules, those that bind DNA/RNA and those that interact with other proteins.

Different combinations of atomic interactions predict affinities for different ligands

Predicting molecular binding affinity is important for applications such as structure‐based drug development, but statistical analyses of protein−ligand complexes can also be used to directly investigate the general principles governing ligand binding. Statistical model selection is an objective, systematic way of examining how combinations of different atom‐atom interactions—as well as statistical “interaction terms” combining ratios of atomic interactions—correlate with ligand affinity.70 As such, the specific models selected as best fitting observed data provide some information about how patterns of atomic interactions might impact ligand affinity.

Across the three different ligand types, we observed strong differences in (1) which specific atomic interactions correlated with ligand affinity and (2) the extent to which single atomic interactions correlated with binding affinity (see SI Text S2 for details). In general, single atomic interaction terms were more correlated with binding affinity in the protein‐small molecule data set (43% average correlation) than in the protein‐DNA/RNA (25% average correlation) or protein−protein (21% correlation) data sets [Fig. 5(A)]. We also observed differences in the size and sign of coefficients applied to each atomic interaction term in the models that best fit each data set,71 further suggesting that there are marked differences in how atom‐atom interactions translate into macromolecular affinity among proteins that bind small molecules, DNA/RNA and other proteins [see Fig. 5(B) and SI Text S2 for details].

Figure 5.

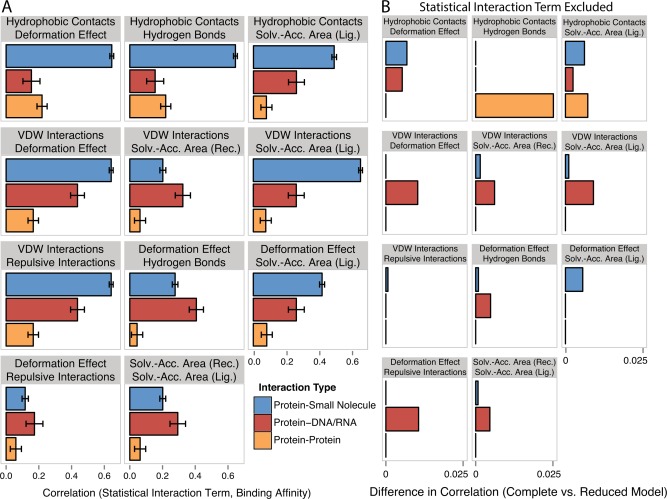
Combinations among atomic interactions contribute differentially to binding affinity prediction in different data sets. We determined the 100 best‐fit statistical models for each data set and identified the statistical interaction terms present in at least 95 of the models in any data set (see Methods, SI Fig. S12). A: We plot the Spearman correlation between each statistical interaction term and experimental binding affinity (pKd). Bars indicate standard error. B: We generated reduced models by excluding one statistical interaction term from each data set's best‐fit complete statistical model including all atomic interactions and statistical interaction terms. The plot shows the difference in the Pearson correlation (r ²) between predicted and experimental binding affinities, comparing each complete model to the best‐fit reduced model obtained by removing the indicated interaction term.

We directly assessed the importance of each atomic interaction term for predictive accuracy by comparing the accuracy of the best‐fit model including that term to the accuracy of the best‐fit model without the term (SI Fig. S11C). As expected, excluding hydrogen bonding information from the protein‐DNA/RNA models substantially reduced mean predictive accuracy (by 12%, William's test P = 2.5 × 10⁻⁹). In contrast, eliminating hydrogen bonding information had only modest effects on the accuracy of small‐molecule and protein−protein binding affinity prediction (difference in r² = 0.81% and 5.60%, William's test P = 6.0 × 10⁻⁶ and 0.01, respectively).

Eliminating hydrophobic contact information had the largest effect on predictive accuracy for the protein−protein data set, changing the accuracy of the best‐fit model from r² = 0.52 to 0.40 (William's test P = 3.1 × 10⁻⁴). Eliminating hydrophobic contact information also had a modest effect on the accuracy of protein‐small molecule prediction (3.1%, William's test P = 1.7 × 10⁻¹⁸) but had little effect on the accuracy of protein‐DNA/RNA affinity prediction (1.5%, William's test P = 0.03).

Overall, the effect of removing single statistical interaction terms on predictive accuracy was small (< 2.5% change in r², Fig. 5). However, we did observe a 2.29‐fold larger effect on protein‐DNA/RNA accuracy than on that of the small‐molecule data set. On average, removing a single statistical interaction term reduced the accuracy of protein‐DNA/RNA affinity prediction by 0.48%, whereas the effect on protein‐small molecule affinity prediction was only 0.21% (t test P = 3.0 × 10⁻³, U test p = 1.0 × 10⁻³).

Our results support the conclusion that different combinations of atomic interactions are important for determining macromolecular binding affinity in protein‐small molecule, protein‐DNA/RNA, and protein−protein interactions. However, the generally low accuracy of protein−protein predictions limits our conclusions regarding the atomic interactions important for predicting protein−protein affinity. In general, we would expect protein‐small molecule interactions to have simpler structural bases than protein‐DNA/RNA and protein−protein complexes, to be more highly determined by a small number of atomic interactions, and to be easier to predict; our results support this general conclusion.

Protein‐DNA/RNA affinity prediction can differentiate near‐native from decoy SelB‐mRNA complexes

That DNA/RNA binding affinity can be rapidly predicted with average accuracy approaching that of small‐molecule binding prediction suggests that these models could be useful for “virtual screening” of DNA‐ and RNA‐binding proteins to predict the affinity with which two molecules interact as well as the structure of the interacting complex.72, 73 Virtual screening is widely used in drug discovery to predict binding affinities between a protein ‘target’ and a (possibly very large) number of candidate compounds.24, 28, 74 Although virtual screening is widely used to predict protein‐small molecule affinity, to date there are no approaches that are both fast and accurate enough to enable virtual screening of protein‐DNA/RNA complexes.

To determine the potential suitability of our protein‐DNA/RNA affinity prediction models for virtual‐screening applications, we evaluated the ability of our model to predict the native SelB‐mRNA complex, given a large set of near‐native and “decoy” structural complexes33 (see Methods). In the native conformation, the α5‐α6 winged‐helix domain of SelB binds a characteristic mRNA hairpin to regulate gene expression72, 75, 76 [see Fig. 6(A)]. We used structural docking algorithms to generate 50 SelB‐mRNA complexes similar to the native complex (RMSD<3.5 Å) and 50 complexes with >3.5 Å RMSD to the native SelB‐mRNA complex. Our protein‐DNA/RNA affinity prediction model was used to screen each complex, and we measured the correlation between predicted binding affinity and how different the predicted complex was from the native complex.

Figure 6.

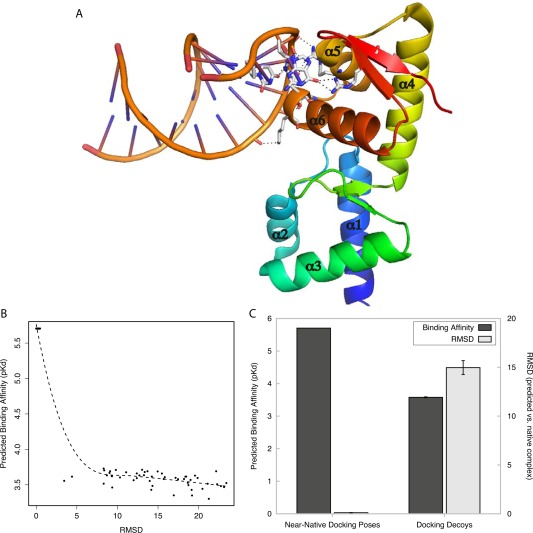
Protein‐DNA/RNA affinity prediction differentiates near‐native complexes from docking decoys. Using molecular docking simulations, near‐native poses and docking decoys were generated for a case study of a protein‐DNA/RNA complex (SelB‐mRNA complex, PDB ID: 1WSU). A: Crystal Structure of SelB‐mRNA complex. Hydrogen bonds between SelB and its mRNA ligand are indicated by dashed lines, and alpha helices are numbered. B: Predicted binding affinity (y axis) is plotted against the root mean square deviation (RMSD, in angstroms, x axis) between each generated complex and the SelB‐mRNA crystal structure. Dotted line indicates the best‐fit polynomial regression. C: We separated generated SelB‐mRNA docking complexes into near‐native poses (RMSD ≤ 3.4 Å) and docking decoys (RMSD ≥ 3.4 Å). The plot shows the mean predicted binding affinity of complexes in each group (dark gray, left y axis) and mean RMSD between generated complexes and the experimentally determined SelB‐mRNA structure (light gray, right y axis). Bars indicate standard error.

We found that our scoring function was able to confidently identify the complexes that were most similar to the experimentally determined structure [Fig. 6(B)]. There was a strong inverse correlation between RMSD and predicted pKd (r ² = −0.91, Spearman correlation = −0.81, P = 2.9 × 10⁻⁴⁰). Complexes very similar to the native complex (RMSD < 3.4 Å) tended to have high predicted binding affinities (mean pKd = 5.7), while decoy complexes (mean RMSD = 14.97 Å) had significantly lower affinity estimates [mean pKd = 3.57, t test P = 9.6 × 10⁻⁶⁷, U test P = 7.1 × 10⁻¹⁸, Fig. 6(C)]. These results suggest that our protein‐DNA/RNA affinity model has the potential to differentiate near‐native from decoy complexes, which is suggestive of possible suitability for virtual screening protocols.

It is important to note that the SelB‐mRNA complex was not in the original data set used to train our predictive model, and although the majority of training complexes had DNA ligands (80%), this result reinforces that the model may also accurately predict binding affinity for RNA ligands. However, this result suggests the possible suitability of our model for virtual screening and does not represent a large‐scale validation supporting its use in this application.

Protein‐DNA/RNA affinity prediction can identify the native ligand and mutations that knock down binding affinity in a CsrA‐RNA complex

The identification of native ligands and mutations that strongly affect ligand‐binding affinity are major goals in molecular biology. The carbon storage regulator protein (CsrA) is an RNA‐binding protein that regulates a large number of metabolic processes in many bacteria.13, 38, 77 A recent study measured binding affinities and generated NMR structures of the Pseudomonas fluorescens CsrA ortholog (RsmE) complexed with 5 different stem‐loop structures of the RsmZ regulatory RNA, with the goal of identifying the precise CsrA ligand.38 The authors concluded that the SL2 region of RsmZ exhibited the highest affinity for CsrA and was most likely the primary native ligand [see Fig. 7(A)]. A related study using alanine‐scanning mutagenesis of CsrA identified R44 as a primary contributor to CsrA‐RNA binding affinity [see Fig. 7(B)].39

Figure 7.

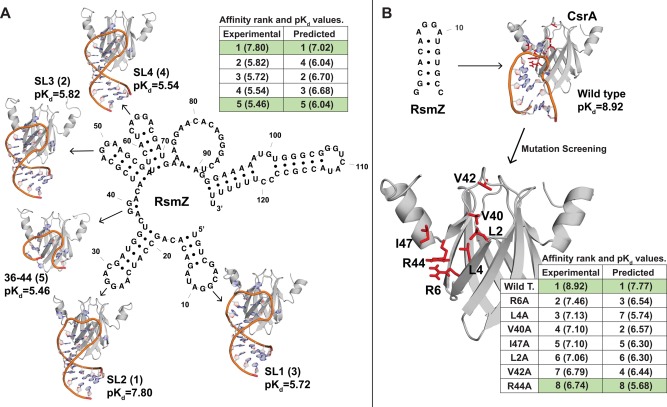
Protein‐DNA/RNA affinity prediction can identify native ligands and mutations of large effect on RNA binding. A: We used the our protein‐DNA/RNA model to predict binding affinities between Pseudomonas RmsE (a CsrA ortholog) and a set of 5 potential RNA ligands derived from the RmsZ regulatory RNA from experimentally determined NMR structures.38 Next to each structure, we identify the experimentally determined pKd and the rank order in RNA affinity (in parentheses). Table compares experimentally determined and predicted pKd values (in parentheses), with integers indicating rank order of RNA affinity inferred from each analysis. B: We use molecular modeling and docking to simulate the CsrA alanine‐screening mutagenesis performed by Mercadante et al.39 Mutations examined are indicated in red on the CsrA structure. Table compares experimentally determined and predicted pKd values (in parentheses) of wild‐type CsrA and each mutant protein, with integers indicating inferred rank order of RNA affinity.

We found that our protein‐DNA/RNA affinity prediction model was able to correctly identify the highest‐ and lowest‐affinity RsmZ ligand from available structural data [Fig. 7(A)]. Similarly, when we performed in silico site‐directed mutagenesis of CsrA by structural modeling (see Methods), our statistical model correctly identified wild‐type CsrA as having the highest RNA affinity and the R44A mutant as having the strongest impact on RNA affinity [Fig. 7(B)]. Although in both cases, intermediate‐effect differences in affinity were not always correctly ordered by our prediction model, compared to experimental results, these results suggest that the protein‐DNA/RNA prediction model may be a useful tool for guiding experimental investigations of protein‐DNA/RNA interactions.

Protein‐DNA/RNA affinity prediction can differentiate high‐affinity from low‐affinity dsRNA binding domains in A. thaliana HYL1

Arabidopsis thaliana hyponastic leaves 1 (HYL1) is a double‐stranded RNA (dsRNA) binding protein involved in microRNA processing.35, 36, 37 The HYL1 protein consists of two homologous functional domains, HR1 and HR2, which have recently been shown to differ in their capacity to bind dsRNA.40 Both HR1 and the homologous TR2 domain of human TRBP2 exhibit high affinity for dsRNA, whereas the HR2 domain does not (see Fig. 8).

Figure 8.

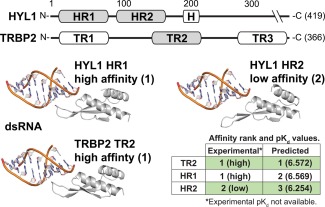
Protein‐DNA/RNA affinity prediction can differentiate high‐affinity double‐stranded RNA (dsRNA) binding domains from low‐affinity homologs. We used our protein‐DNA/RNA model to predict the binding affinity between homologous dsRNA binding domains of A. thaliana HYL1 and human TRBP2 (see Methods). Results are compared to the qualitative analysis of Yang et al.,40 which found that the first dsRNA binding domain of HYL1, HYL1(HR1), and the second dsRNA binding domain of TRBP2, TRBP2(TR2), bound dsRNA with high affinity, whereas HYL1(HR2) did not. Predicted pKd values are indicated in parentheses.

Although quantitative affinity measurements of HYL1‐RNA and TRBP2‐RNA are not available, we found that our protein‐DNA/RNA prediction model assigned high affinity for dsRNA to human TRBP2(TR2) and A. thaliana HYL1(HR1) domains, but much lower affinity to HYL1(HR2), consistent with experimental and structural results (∼two‐fold difference in affinity between HR1/TR2 and HR2; Fig. 8). This result suggests that our model may be useful for examining functional differences among homologous protein domains involved in protein‐DNA/RNA interactions.

SOFTWARE AVAILABILITY

Best‐fit prediction models obtained for each data set were implemented in ANSI C++. Source code, tutorials and data sets are available at https://github.com/Klab-Bioinfo-Tools/GLM-Score. Prediction models were generated using R's GLMULTI package; source code implementing our machine learning protocols is available at https://github.com/Klab-Bioinfo-Tools/GLM-Score/R.

CONCLUSIONS

Understanding the general principles by which molecular structure determines ligand‐binding affinity is an important and long‐standing goal of structural biochemistry. Although considerable progress has been made toward the fast and accurate prediction of protein‐small molecule affinity, few attempts have been made to extend these approaches to prediction of other types of molecular interactions, and—to our knowledge—no studies have explicitly set out to quantify how patterns of atom‐atom interactions impact macromolecular binding across the range of interactions likely to be of biological importance.

Here we collected and curated available X‐ray crystal structures capturing the atomic interactions of interacting protein‐small molecule, protein‐DNA/RNA and protein−protein pairs and combined this information with experimentally determined binding affinity measurements of each complex. Using cross‐validated statistical machine learning, we quantified how atomic interactions inferred by the structural complex contributed to binding affinity. We found that there were significant and consistent differences across ligand types in the particular combinations of atomic interaction features that were most important for determining binding affinity. The specific features we identified will likely form a basis for further understanding the general principles through which molecular structure impacts function.

We found that protein‐DNA/RNA interactions—which had a more complex structural basis that was more strongly influenced by statistical interactions among and combinations of simple atom‐atom interactions—could be predicted with accuracy similar to that currently obtained for simpler protein‐small molecule interactions, even though the amount of available structural data was much more limited in the case of protein‐DNA/RNA complexes. That protein‐DNA/RNA binding affinity can be predicted quickly and accurately suggests that high‐throughput “virtual screening” techniques might be viable for examining protein‐DNA/RNA interactions and guiding laboratory experiments.

However, given the available structural data, protein−protein binding affinity could not be accurately predicted. Protein−protein binding may involve secondary structure segmentation, conformational changes and changes in system free energy during complex formation and cooperative folding, none of which are likely to be captured in a static image of the bound complex.24, 43, 46 Considering how structures change during complex formation may be important for accurately predicting protein−protein affinity.31 Leveraging existing sequence and structural data to predict binding affinities based on similarity to experimentally characterized systems is an alternative approach that could prove both fast and accurate.32

Supporting information

Supporting Information