Single-index Varying Coefficient Model for Functional Responses

Summary

Recently, massive functional data have been widely collected over space across a set of grid points in various imaging studies. It is interesting to correlate functional data with various clinical variables, such as age and gender, in order to address scientific questions of interest. The aim of this paper is to develop a single-index varying coefficient (SIVC) model for establishing a varying association between functional responses (e.g., image) and a set of covariates. It enjoys several unique features of both varying-coefficient and single-index models. An estimation procedure is developed to estimate varying coefficient functions, the index function, and the covariance function of individual functions. The optimal integration of information across different grid points are systematically delineated and the asymptotic properties (e.g., consistency and convergence rate) of all estimators are examined. Simulation studies are conducted to assess the finite-sample performance of the proposed estimation procedure. Furthermore, our real data analysis of a white matter tract dataset obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) study confirms the advantage and accuracy of SIVC model over the popular varying coefficient model.

1. Introduction

As a semiparametric regression modelling strategy, single-index modelling has attracted much attention in the literature due to its balance between exibility and fidelity. A classical single-index model is often written as

$$Y=g(X^T\beta )+\epsilon ,$$ (1)

where Y is a response variable, g(·) is an unknown index function, X is a covariate vector, and ε is an error term such that E(ε|X) = 0. See Horowitz (2009) for a comprehensive review of various estimation methods for single-index models and references therein (Li, 1991; Cook and Weisberg, 1991; Zhu et al., 2010; Xia et al., 2002; Xia, 2007; Ma and Zhu, 2012, 2013). For instance, dimension reduction approaches, such as likelihood-based methods (Cook and Forzani, 2009), are also commonly used for estimation. However, the existing literature primarily considers univariate response observed from cross-sectional studies.

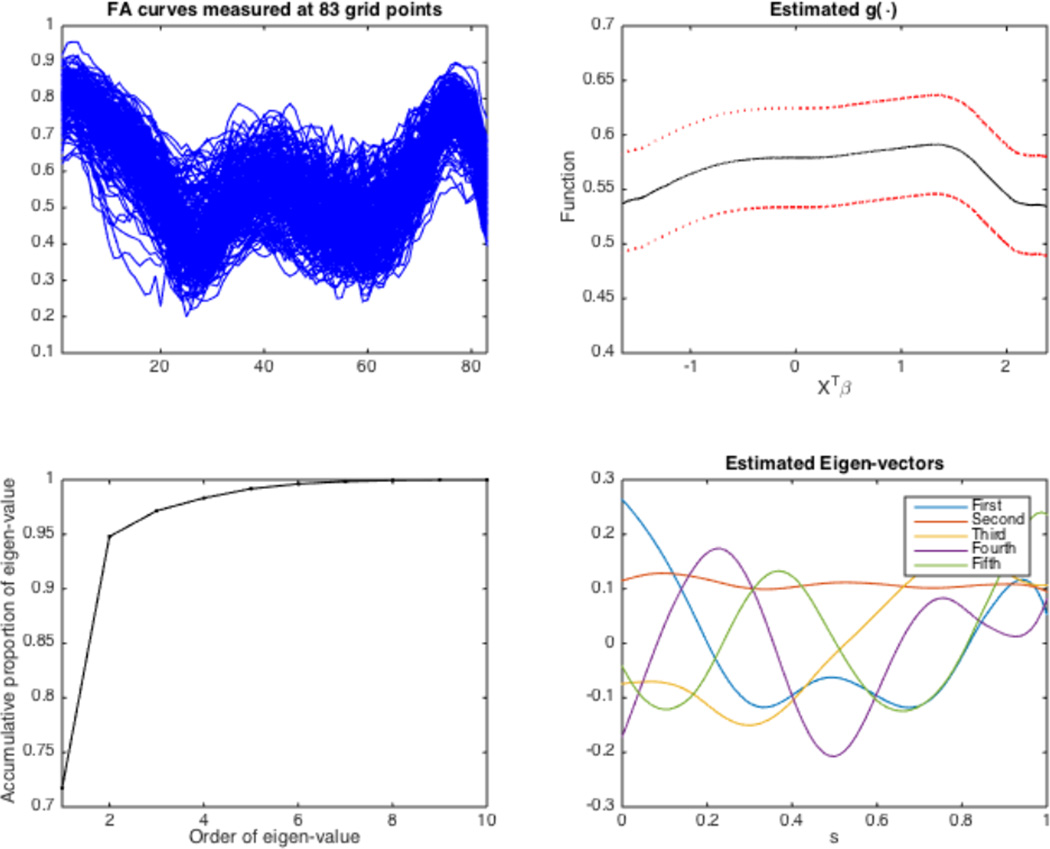
This paper is motivated by the analysis of a real diffusion weighted imaging (DWI) data set with n = 213 subjects collected from NIH Alzheimer’s Disease Neuroimaging Initiative (ADNI) study. For each subject, we calculated a Fractional Anisotropy (FA) curve at all the 83 grid points along the skeleton of the midsagittal corpus callosum as shown in Figure 1. We are interested in establishing an association between FA curves and several covariates of interest, such as age and gender. To establish such association, standard grid-wise methods are to fit a linear model to functional observations at each grid point as responses and clinical variables, such as age and gender, as covariates, and to generate a statistical map of test statistics or p-values across all grid points (Lazar, 2008;Worsley et al., 2004). These grid-wise methods have several major limitations. First, compared with model (1), the classical linear model used in the neuroimaging literature is often restrictive, since it assumes that the index function g(·) is an identity function. When g(·) is truly nonlinear, directly fitting a classical linear model can cause substantial efficiency loss and reduce prediction accuracy. Second, since the grid-wise methods treat all grid points as independent units, they ignore two key functional features of functional data including spatial smoothness and spatial correlation.

Figure 1.

ADNI data analysis: raw FA curves measured at 83 grid points (upper-left panel), the estimated index function with the broken red lines representing 95% simultaneous Confidence bands (upper-right panel), the estimated accumulative proportion of estimated eigenvalues (lower-left panel) and estimated eigenfunctions (lower-right panel) corresponding to the five largest eigenvalues.

Some advanced methods have been developed to specifically incorporate these features by using function-on-scalar regression under the functional data analysis (FDA) framework (Zhu et al., 2012; Ramsay and Silverman, 2005; Staicu et al., 2010; Zhang and Chen, 2007; Reiss et al., 2010). Some important estimation methods for FDA include adaptive smoothing methods (Polzehl and Spokoiny, 2006; Li et al., 2011), the integration of FDA and adaptive smoothing methods (Zhu et al., 2014), and spatial priors within the Bayesian framework (Gossl et al., 2001; Penny et al., 2005; Bowman et al., 2008; Smith and Fahrmeir, 2007; Yue et al., 2010; Miranda et al., 2013), among others. See Morris (2015) and Wang et al. (2015) for a comprehensive review of various FDA models for functional responses. However, to the best of our knowledge, none of the references cited above address the two functional features and estimate the nonparametric index function simultaneously.

The aim of this paper is to develop a single-index varying coefficient (SIVC) model to establish a varying association between functional responses and a set of covariates. Specifically, we extend the single-index model (1) to SIVC for functional responses as follows:

$$Y(s)=g(X^T\beta (s))+\epsilon (s),$$ (2)

where {Y (s) : s ∈ 𝒮} is an observed stochastic process on a compact set 𝒮 and ε(s) is a random function characterizing the within-subject correlations and measurement errors at different grid points such that E{ε(s)|X} = 0 for all s ∈ 𝒮. The β(s) allows us to characterize the dynamic association between covariate X and functional response, whereas g(·) is a nonparametric function, while being fixed across all s ∈ 𝒮. Model (2) differs from the functional single index model in Jiang and Wang (2011), in which g(·) varies across s, but β(s) is assumed to be stationary. When g(x) = x, model (2) reduces to standard voxel-wise methods based on linear model and the most popular FDA model considered in (Zhang and Chen, 2007; Ramsay and Silverman, 2005; Zhu et al., 2014). For notational simplicity, we set 𝒮 = [0, 1]. The results can be readily extended to more general cases with compact subset 𝒮 of the Euclidean space.

Compared with the existing literature, we make several unique contributions. (i) We develop a new estimation procedure to estimate various parametric and non-parametric components of SIVC. (ii) Theoretically, we delineate the integration of information across all grid points by using an optimal weight function and then establish the asymptotic properties of various estimates for SIVC. (iii) Our analysis of the ADNI data confirms the advantage and accuracy of SIVC model over the popular varying coefficient model (Zhang and Chen, 2007; Ramsay and Silverman, 2005; Zhu et al., 2014).

The rest of this paper is organized as follows. Section 2 introduces the estimation procedure to estimate varying coefficient functions, index function, and the covariance function of individual functions. Section 3 systematically investigates the asymptotic properties of all estimators. A simulation study and a real data analysis of Alzheimer’s Disease Neuroimaging Initiative (ADNI) study are presented in Section 4 to demonstrate the finite sample performance of SIVC. Section 5 concludes with some discussions.

2. Methods

2.1 Single-index Varying Coefficient Model

We formally introduce the single-index varying coefficient model as follows. Consider {({Y_i(s) : s ∈ 𝒮}, X_i) : i = 1, …, n} from n independent subjects, where 𝒮 is a compact set that characterizes the range of all possible grid points. Our single-index varying coefficient (SIVC) model is written as

$$Y_i(s)=g(X_i^T\beta (s))+{\eta }_i(s)+{\epsilon }_i(s)\text{ for all }s\in 𝒮\text{ and }i=1,\dots ,n,$$ (3)

where X_i is a p × 1 covariate vector, β(s) = (β₁(s), ⋯, β_p(s))^T is a p × 1 vector of varying coefficient functions, g(·) is an unknown index function, η_i(s) characterizes individual curve variations, and ε_i(s) is a random function of measurement errors. The process {η_i(s) : s ∈ 𝒮} is assumed to be a Gaussian process with zero mean and a covariance function Σ_η(s, t) = Cov{η(s), η(t)}. The error terms ε_i(s) follow a Gaussian process with zero mean and a diagonal covariance function Cov{ε(s), ε(t)}. That is, ε_i(s) and ε_i(t) are assumed to be independent for s ≠ t, and Cov{ε(s), ε(t)} takes the form of ${\sigma }_{\epsilon }^2(s)\mathbf{1}(s=t)$, where 1(·) is an indicator function. Moreover, Y_i(s) are usually measured at the same set of locations for all subjects and exhibit both the within-curve and between-curve dependence structures. Thus, without loss of generality, it is assumed that Y_i(s) are observed on M grid points 𝒮_M = {s_m : 0 = s₁ ≤ ⋯ ≤ s_M = 1} for all subjects.

For single index model, β(s) is not identifiable since g(X^T β(s)) and g(β₀(s) + δX^T β(s)) are not distinguishable, where δ is any nonzero scalar. A simple solution in the literature (Zhu et al., 2010; Xia et al., 2002) is to impose some constraints on β₀(s) and β(s), such as β₀(s) = 0 and β(s)^T β(s) = 1. Therefore, throughout the paper, it is assumed that X does not contain the intercept, β(s)^T β(s) = 1 holds for all s ∈ 𝒮 and the first entry of β(s) is positive at each s.

2.2 Estimation Procedure

Our estimation procedure consists of three steps for estimating the varying coefficient functions β(·), the index function g(·), and the covariance function Σ_η(s, s′).

Step I. Estimating varying coefficient β(s)

We first consider the estimation of β(s_m) at each given grid point s_m. Model (3) reduces to a classical single-index model given by

$$Y_i(s_m)=g(X_i^T\beta (s_m))+{\epsilon }_i^{*}(s_m),$$ (4)

where ${\epsilon }_i^{*}(s_m)={\eta }_i(s_m)+{\epsilon }_i(s_m)$ such that $E\{{\epsilon }_i^{*}(s_m)|X_i\}=0$ and $\text{Var}\{{\epsilon }^{*}(s_m)|X_i\}={\sigma }_{\epsilon *}^2(s_m)={\mathrm{\Sigma }}_{\eta }(s_m,s_m)+{\sigma }_{\epsilon }^2(s_m)$. The likelihood function of a random observation (X, Y (s_m)) in model (4) is given by

$$f_1(X)\times f_2(Y(s_m)-g(X^T\beta (s_m));X),$$

where f₁ is the probability density function of X, and f₂ is the conditional probability density function of ε*(s_m) = Y (s_m) − g(X^T β(s_m)) given X.

Based on the Gaussian assumption of ${\epsilon }_i^{*}(s)$, f₂(·) is the normal density with mean zero and variance ${\sigma }_{\epsilon *}^2(s_m)$. Thus, the score function for β(s_m), denoted as S(β(s_m)), is given by

$$S(\beta (s_m))=-X{\epsilon }^{*}(s_m)ġ(X^T\beta (s_m))/{\sigma }_{\epsilon *}^2(s_m)=(\mathrm{I})+(\mathrm{I}\mathrm{I})=-E\{X|X^T\beta (s_m)\}{\epsilon }^{*}(s_m)ġ(X^T\beta (s_m))/{\sigma }_{\epsilon *}^2(s_m)-[X-E\{X|X^T\beta (s_m)\}]{\epsilon }^{*}(s_m)ġ(X^T\beta (s_m))/{\sigma }_{\epsilon *}^2(s_m),$$ (5)

where ġ(t) = dg(t)/dt. Following the reasoning in Ma and Zhu (2014), (I) and (II) belong to the tangent space of model (4) with respect to β(s_m), denoted by Λ_g(s_m), and its orthogonal component, denoted by Λ_g(s_m)^⊥, respectively. For any s ∈ 𝒮, Λ_g(s) and Λ_g(s)^⊥ are, respectively, given by

$${\mathrm{\Lambda }}_g(s)=\{-{\epsilon }^{*}(s)h(X^T\beta (s))/{\sigma }_{\epsilon *}^2(s):\forall h(\cdot )\},$$

$${\mathrm{\Lambda }}_g{(s)}^{\perp }=\{-{\epsilon }^{*}(s)[\alpha (X)-E\{\alpha (X)|X^T\beta (s)\}]:\forall \alpha (·)\}.$$

Therefore, the efficient score function for β(s_m) is given by

$$S_{\text{eff}}(\beta (s_m);X,Y(s_m))={\epsilon }^{*}(s_m)[X-E\{X|X^T\beta (s_m)\}]ġ(X^T\beta (s_m)).$$ (6)

To calculate an efficient estimator of β(s_m), denoted as β̃(s_m), we can solve

$$\sum _{i=1}^n{S}_{\text{eff}}(\tilde{\beta }(s_m);X_i,Y_i(s_m))=\mathbf{0}.$$ (7)

Since S_eff depends on three unknown quantities E{X|X^T β(s_m)}, g(X^T β(s_m)) and ġ(X^T β (s_m)), we construct their nonparametric estimators as follows (Ma and Zhu, 2013). The Nadaraya-Watson kernel estimator of E{X|X^T β(s_m)} is given by

$$Ê\{X|X^T\beta (s_m)\}=\frac{{\sum }_{i=1}^n{X}_i{K}_{h_x}(X_i^T\beta (s_m)-X^T\beta (s_m))}{{\sum }_{i=1}^n{K}_{h_x}(X_i^T\beta (s_m)-X^T\beta (s_m))},$$ (8)

where K_h(·) = K(·/h)/h is a kernel function and h_x is a given bandwidth. We can calculate the estimates of g(X^T β(s_m)) and ġ(X^T β(s_m)) at X^T β(s_m) = X^T β₀(s_m), denoted by ĝ(X^T β₀(s_m)) and ġ̂(X^T β₀(s_m)), by minimizing

$$\sum _{i=1}^n{[Y_i(s_m)-g(X^T{\beta }_0(s_m))-ġ(X^T{\beta }_0(s_m))(X_i^T-X^T){\beta }_0(s_m)]}^2{K}_{h_y}((X_i^T-X^T){\beta }_0(s_m)).$$ (9)

As suggested by Ma and Zhu (2014), we set h_x = cn^−1/3 and h_y = cn^−1/5, where c is the average standard deviation of X. By plugging Ê{X|X^T β(s_m)}, ĝ(X^T β₀(s_m)) and ġ̂(X^T β₀(s_m)) into (7), we get an estimate of S_eff(β(s_m); X_i, Y_i(s_m)), denoted by Ŝ_eff(β(s_m); X_i, Y_i(s_m)) and then calculate β̃(s_m) by solving

$$\sum _{i=1}^n{Ŝ}_{\text{eff}}(\tilde{\beta }(s_m);X_i,Y_i(s_m))=\mathbf{0}.$$ (10)

To estimate β(s) at any s ∈ 𝒮, we need to construct a weighted estimating equation to borrow information across all grid points by using the functional features of imaging data (Wang et al., 2004; Zhu et al., 2012; Polzehl and Spokoiny, 2006; Li et al., 2011). Specifically, the weighted estimating equation is given by

$${Ŝ}_{nM}(\beta (s);w)=\sum _{i=1}^n\sum _{m=1}^{M}w(s_m,s){Ŝ}_{\text{eff}}(\beta (s);X_i,Y_i(s_m)),$$ (11)

where w(s_m, s) is a weight function of (s_m, s) and may depend a few parameters, such as bandwidth. Then, we calculate an estimate of β(s), denoted by β̂(s), by solving the following equation:

$${Ŝ}_{nM}(\hat{\beta }(s);w)=\mathbf{0}.$$ (12)

A critical issue in (12) is how to select an optimal weight function w(s_m, s). Theoretically, one may choose w(s_m, s) by minimizing the mean integrated squares error (MISE) of β̂(·) for all s ∈ 𝒮, but it can be challenging due to the lack of precise information about β(s). Without such information, a simple solution is to set w(s_m, s) = K((s_m − s)/h)/h and then select the bandwidth h by using some criteria, such as cross-validation method, based on MISE. Furthermore, when β(s) is a piecewise constant function, we will show how to optimally select w(s_m, s) in Section 3.

Step II. Estimating the unknown index function g(·)

We use the local linear technique to estimate g(X^T β(s)). We define $Z_{i,m}(s)={(1,\{X_i^T\beta (s_m)-X^T\beta (s)\}/h_1)}^T$ and

$$\mathrm{\Sigma }(X^T\beta (s),h_1)=\sum _{i=1}^n\sum _{m=1}^M{K}_{h_1}(X_i^T\beta (s_m)-X^T\beta (s))Z_{i,m}{(s)}^{\otimes 2},$$

where Z^⊗2 = ZZ^T for any vector Z. By replacing β(s_m) by β̂(s_m), we get Ẑ_i,m(s) and Σ̂(X^T β(s), h₁). Denote G(X^T β (s)) = (g(X^T β (s)), h₁ġ(X^T β (s)))^T, we directly minimize a weighted least square function given by

$$\sum _{i=1}^n\sum _{m=1}^M{\{Y_i(s_m)-{Ẑ}_{i,m}{(s)}^{T}G(X^T\beta (s))\}}^2{K}_{h_1}(X_i^T\hat{\beta }(s_m)-X^T\beta (s)).$$ (13)

Thus, we have ĝ(X^T β(s)) = [1 0]Ĝ (X^T β (s)), where Ĝ (X^T β(s)) is given by

$$\hat{\mathrm{\Sigma }}{(X^T\beta (s),h_1)}^{-1}\sum _{i=1}^n\sum _{m=1}^M{K}_{h_1}(X_i^T\hat{\beta }(s_m)-X^T\beta (s)){Ẑ}_{i,m}(s)Y_i(s_m).$$

The bandwidth h₁ is chosen by using the cross-validation method.

Step III. Estimating the covariance function Σ_η(s, t)

Let d_i(s) = (η_i(s), h₂η̇_i(s))^T, W_m,s = (1, (s_m−s)/h₂)^T, and $Y_i^{*}(s_m)=Y_i(s_m)-ĝ(X_i^T\hat{\beta }(s_m))$. We minimize the following function

$$\sum _{m=1}^M{\{Y_i^{*}(s_m)-W_{m,s}^T{d}_i(s)\}}^2{K}_{h_2}(s_m-s)$$ (14)

to obtain

$${\hat{d}}_i(s)={(\sum _{m=1}^M{K}_{h_2}(s_m-s)W_{m,s}^{\otimes 2})}^{-1}\sum _{m=1}^M{K}_{h_2}(s_m-s)W_{m,s}{Y}_i^{*}(s_m).$$

Then, η(s) can be estimated by

$${\hat{\eta }}_i(s)=[10]{\hat{d}}_i(s)=\sum _{m=1}^M{\tilde{K}}_{h_2}(s_m-s)Y_i^{*}(s_m),$$ (15)

where ${\tilde{K}}_{h_2}(s_m-s)=[10]{({\sum }_{m=1}^M{K}_{h_2}(s_m-s)W_{m,s}^{\otimes 2})}^{-1}{K}_{h_2}(s_m-s)W_{m,s}$, which is the empirical equivalent kernel. The bandwidth h₂ is also chosen by using the cross-validation method.

We consider the spectral decomposition of Σ_η(s, t) and its approximation. Suppose Σ_η(s, t) is continuous on 𝒮², then according to Mercer’s theorem, it can be decomposed as

$${\mathrm{\Sigma }}_{\eta }(s,t)=\sum _{k=1}^{\infty }{\lambda }_k{\psi }_k(s){\psi }_k(t),$$

where λ₁ ≥ λ₂ ≥ ⋯ ≥ 0 are ordered eigenvalues and ψ_k(s) are the corresponding orthonormal eigenfunctions. Furthermore, the eigenfunctions form an orthonormal system on the space of square-intergrable function on 𝒮, and η_i(s) admits the Karhunen-Loeve expansion as ${\eta }_i(s)={\sum }_{k=1}^{\infty }{\xi }_{ik}{\psi }_k(s)$, where ${\xi }_{ik}={\int }_0^1{\eta }_i(s){\psi }_k(s)ds$ is the k-th functional principal component scores of the i-th subject. For a fixed i, ξ_ik are uncorrelated random variables with mean zero and variance λ_k.

By following Rice and Silverman (1991), the covariance matrix Σ_η(s, t) and its spectral decomposition can be estimated by

$${\hat{\mathrm{\Sigma }}}_{\eta }(s,t)={(n-p)}^{-1}\sum _{i=1}^n{\hat{\eta }}_i(s){\hat{\eta }}_i(t)=\sum _{k=1}^{\infty }{\hat{\lambda }}_k{\hat{\psi }}_k(s){\hat{\psi }}_k(t),$$ (16)

where λ̂₁ ≥ λ̂₂ ≥ ⋯ ≥ 0 are estimated eigenvalues and ψ̂_k(s) are the corresponding estimated eigenfunctions. Moreover, the k-th functional principal component scores can be computed by ${\hat{\xi }}_{ik}={\sum }_{m=1}^M{\hat{\eta }}_i(s_m){\hat{\psi }}_k(s_m)(s_m-s_{m-1})$ for i = 1, …, n.

2.3 Simultaneous Confidence Bands

Given a Confidence level α, we construct a simultaneous Confidence band for each β_l(s) such that $P({\hat{\beta }}_l^{L,\alpha }(s)<{\beta }_l(s)<{\hat{\beta }}_l^{U,\alpha }(s)\text{ for all }s\in 𝒮)=1-\alpha$ where ${\hat{\beta }}_l^{L,\alpha }(s)$ and ${\hat{\beta }}_l^{U,\alpha }(s)$ are the lower and upper limits of simultaneous Confidence band, respectively. Specifically, we set

$${\hat{\beta }}_l^{L,\alpha }(s)={\hat{\beta }}_l(s)-\text{bias}({\hat{\beta }}_l(s))-C_{{\beta }_l}(\alpha )\text{ and }{\hat{\beta }}_l^{U,\alpha }(s)={\hat{\beta }}_l(s)-\text{bias}({\hat{\beta }}_l(s))+C_{{\beta }_l}(\alpha ),$$ (17)

where bias(β̂_l(s)) is the bias of β̂_l(s) at s ∈ 𝒮 and C_βl(α) is a scalar. By following the arguments in Zhu et al. (2012), we use the local polynomial technique to estimate bias(β̂_l(s)) for each l and then approximate C_βl(α) by using the wild bootstrap as follows:

• Step 1: We calculate ${\hat{r}}_i(s_m)=Y_i(s_m)-ĝ(X_i^T\hat{\beta }(s_m))$ for all i and m.

• Step 2: For q = 1, …, Q, we independently generate {${\tau }_i^{(q)}$ : i = 1, ⋯, n} from N(0, 1) and construct ${Ŷ}_i{(s_m)}^{(q)}=ĝ(X_i^T\hat{\beta }(s_m))+{\tau }_i^{(q)}{\hat{r}}_i(s_m)$. Then, based on {Y_i(s_m)^(q)}, we recalculate β̂(s)^(q), and obtain a stochastic process G_βl(s)^(q) = | β̂_l(s)(q) − β̂_l(s)^(q)| for each l.

• Step 3: For all q, we calculate the 1 − α empirical percentile of G_βl(s)^(q), denoted by C_βl(s, α), at each s ∈ 𝒮. Finally, an estimate of C_βl(α) is sup_s |C_βl(s, α)|.

Similarly, for a given α, we construct a simultaneous Confidence band for g(·) as follows:

$$P({ĝ}^{L,\alpha }(u)<g(u)<{ĝ}^{U,\alpha }(u)\text{ for all }u\in 𝒰)=1-\alpha ,$$

where 𝒰 is a compact set in R and ĝ^L,α(u) and ĝ^U,α(u) are the lower and upper limits of simultaneous Confidence band, respectively. Specifically, we set

$${ĝ}^{L,\alpha }(u)=ĝ(u)-\text{bias}(ĝ(u))-C_g(\alpha )\text{ and }{ĝ}^{U,\alpha }(u)=ĝ(u)-\text{bias}(ĝ(u))+C_g(\alpha ).$$ (18)

Subsequently, we use the local polynomial technique to estimate bias(ĝ(u)) and then use the wild bootstrap to approximate C_g(α) as follows:

• Step 1: We calculate ${\hat{r}}_i(s_m)=Y_i(s_m)-ĝ(X_i^T\hat{\beta }(s_m))$ for all i and m.

• Step 2: For q = 1, …, Q, we independently generate {${\tau }_i^{(q)}$ : i = 1, ⋯, n} from N(0, 1) and construct ${Ŷ}_i{(s_m)}^{(q)}=ĝ(X_i^T\hat{\beta }(s_m))+{\tau }_i^{(q)}{\hat{r}}_i(s_m)$. Then, based on {Y_i(s_m)^(q)}, we recalculate ĝ(·)^(q), and obtain a stochastic process G_g(u)^(q) = |ĝ(u) − ĝ(u)^(q)|.

• Step 3: For all ℓ, we calculate the 1 − α empirical percentile of G_g(u)^(q) denoted by C_g(u, α) at every u ∈ 𝒰 and then approximate C_g(α) by using sup_u∈𝒰 |C_g(u, α)|.

3. Theoretical Results

3.1 Optimal weight Functions

We consider a challenging issue of optimally selecting the weight function w(s_m, s) in order to gain efficiency, since Ŝ_nM (β(s);w) for a given weight function w(·, ·) may not be an efficient estimating equation. Specifically, Λ_g(s) and Λ_g(s′) may interact with each other for s ≠ s′ by noting that

$$E[{\epsilon }^{*}(s)h(X^T\beta (s)){\epsilon }^{*}(s\prime )h\prime (X^T\beta (s\prime ))/\{{\sigma }_{\epsilon *}^2(s){\sigma }_{\epsilon *}^2(s\prime )\}]={\mathrm{\Sigma }}_{\eta }(s,s\prime )E\{h(X^T\beta (s))h\prime (X^T\beta (s\prime ))\}/\{{\sigma }_{\epsilon *}^2(s){\sigma }_{\epsilon *}^2(s\prime )\}.$$ (19)

Therefore, Λ_g(s) and Λ_g(s′) are orthogonal with each other for s ≠ s′ if and only if Σ_η(s, s′) = 0 for s ≠ s′. It also holds for {Λ_g(s)^⊥ : s ∈ 𝒮} due to Λ_g(s) ⊥ Λ_g(s)^⊥.

First, we consider how to choose the weight function when β(s) = β₀ does not vary across s ∈ 𝒮. With some calculations, we can show that the covariance matrix of $\sqrt{n}\hat{\beta }(s)$ can be approximated by

$${\mathrm{\Sigma }}_1(\mathbf{w}(s))=D(\mathbf{w}(s))E{\{{[X-E\{X|X^T{\beta }_0\}]}^{\otimes 2}ġ{(X^T{\beta }_0)}^2\}}^{-1},$$ (20)

where w(s) = (w(s₁, s), ⋯, w(s_M, s))^T and D(w(s)) is given by

$$\frac{{\sum }_{m,m\prime =1}^{M}w(s_m,s)w(s_{m\prime },s)\{{\mathrm{\Sigma }}_{\eta }(s_m,s_{m\prime })+{\sigma }_{\epsilon }^2(s_m)\mathbf{1}(s_m=s_{m\prime })\}}{{\{{\sum }_{m=1}^{M}w(s_m,s)\}}^2}.$$ (21)

We can obtain an optimal weight vector, denoted by w_*, by minimizing Σ₁(w(s)) such that w_* = argmin_w(s)Σ₁(w(s)). As shown in Theorem 1 (i) below, w_* is associated with the eigenvalue-eigenvector pairs of ${\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}{\mathrm{\Sigma }}_{\eta *,M}{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}$, denoted by {(λ_m*,M, ψ_m*,M) : m = 1, …, M}, where Σ_η*,M = (Σ_η(s_m, s_m′)) and ${\mathrm{\Lambda }}_{\epsilon *,M}=({\sigma }_{\epsilon }^2(s_m)\mathbf{1}(s_m=s_{m\prime }))$ are two M × M matrices.

Second, we set ω(s_m, s) as K_h(s_m − s), which is a kernel function of (s_m − s)/h, when β(s) may vary across s ∈ 𝒮. If h → 0, then it can be shown that the covariance matrix of $\sqrt{n}\hat{\beta }(s)$ can be approximated by Σ₁(w(s)) in (20). We will show in Theorem 1 (ii) that the use of the kernel function can lead to substantial efficiency gain even under this general scenario.

Theorem 1

We have the following results.

1. Suppose that β(s) = β₀ does not vary across s ∈ 𝒮. The optimal w_* is given by

   $${\mathbf{w}}_{*}={\sum }_{\epsilon *,M}^{-1}{\mathbf{1}}_M/{\Vert {\sum }_{\epsilon *,M}^{-1}{\mathbf{1}}_M\Vert }_2,$$ (22)

   where ‖·‖₂ is the Euclidean norm of a vector, Σ_ε*,M = Σ_η*,M+Λ_ε*,M is an M×M matrix, and 1_M is an M × 1 vector of ones. Thus, the optimal D(w) is given by $D({\mathbf{w}}_{*})={({\mathbf{1}}_M^T{\sum }_{\epsilon *,M}^{-1}{\mathbf{1}}_M)}^{-1}$ and is independent of s. The ${\mathrm{\Sigma }}_{\epsilon *,M}^{-1}{\mathbf{1}}_M$ can be written as

   $$\{{\mathbf{I}}_M-{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}\sum _{m=1}^M\frac{{\lambda }_{m*,M}}{1+{\lambda }_{m*,M}}{\psi }_{m*,M}{\psi }_{m*,M}^T{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}\}{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}{\mathbf{1}}_M.$$ (23)

2. Suppose that β(s) may vary across s ∈ 𝒮. Under Assumptions (C6) and (C7), if w(s_m, s) = K_h(s_m − s), h → 0, and Mh → ∞, then D(w(s)) can be approximated by Σ_η(s, s).

Theorem 1 has several interesting implications. If Σ_η(s, s′) = 0 for any s ≠ s′, then w_* is proportional to ${\mathrm{\Lambda }}_{\epsilon *,M}^{-1}{\mathbf{1}}_M={({\sigma }_{\epsilon }^{-2}(s_1),\cdots ,{\sigma }_{\epsilon }^{-2}(s_M))}^T$. In this case, we can set $w(s_m,s)={\sigma }_{\epsilon }^{-2}(s_m)$ for all m, and then the optimal weighted estimating equation is given by

$${Ŝ}_{nM}(\beta (s);{\mathbf{w}}_{*})=\sum _{m=1}^M\sum _{i=1}^n{\epsilon }_i^{*}(s_m)[X_i-E\{X_i|X_i^T\beta (s_m)\}]ġ(X_i^T\beta (s_m))/{\sigma }_{\epsilon *}^2(s_m).$$

Theorem 1 (i) also implies that in general cases, w(s_m, s) is given by

$${\sigma }_{\epsilon }^{-2}(s_m)-{\sigma }_{\epsilon }{(s_m)}^{-1}\sum _{m\prime =1}^M\frac{{\lambda }_{m\prime *,M}}{1+{\lambda }_{m\prime *,M}}{\mathbf{e}}_m^T{\psi }_{m\prime *,M}{\psi }_{m\prime *,M}^T{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}{\mathbf{1}}_M,$$

where e_m is an M × 1 vector with the m-th element one and zero otherwise. For functional data, it is common to assume that λ_m*,M = 0 for all m > K, where K is a positive integer. Under some additional conditions, it can be shown that λ_m*,M and ψ_m*,M converge to the m–th eigenvalue and its corresponding eigenfunction of the covariance function Σ_η(s, s′)/{σ_ε(s)σ_ε(s′)}, respectively.

Another implication of Theorem 1 (i) is the lower bound of D(w_*). Specifically, D(w_*) is given by

$${({\mathbf{1}}_M^T{\mathrm{\Lambda }}_{\epsilon *,M}^{-1}{\mathbf{1}}_M-{\mathbf{1}}_M^T{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}\sum _{m=1}^M\frac{{\lambda }_{m*,M}}{1+{\lambda }_{m*,M}}{\psi }_{m*,M}{\psi }_{m*,M}^T{\mathrm{\Lambda }}_{\epsilon *,M}^{-1/2}{\mathbf{1}}_M)}^{-1},$$ (24)

which is greater than ${({\mathbf{1}}_M^T{\mathrm{\Lambda }}_{\epsilon *,M}^{-1}{\mathbf{1}}_M)}^{-1}=1/\{{\sum }_{m=1}^M{\sigma }_{\epsilon }^{-2}(s_m)\}$. In general, the presence of spatial correlation increases the covariance matrix of β̂(s). Such lower bound is achievable only when Σ_η(s, s′) = 0 holds for any s ≠ s′. Furthermore, such lower bound is asymptotically achievable when λ_1*,M = o_p(1), since x/(1 + x) is a monotone function of x.

Theorem 1 (ii) implies that the use of w(s_m, s) = K_h(s_m − s) can lead to substantial efficiency gain if there are substantial measurement errors. Specifically, if w(s_m) = e_m, then we consider information at the m–th grid point. In this case, we have $D(\mathbf{e}(s_m))={\mathrm{\Sigma }}_{\eta }(s_m,s_m)+{\sigma }_{\epsilon }^2(s_m)$, which can be much larger than Σ_η(s_m, s_m) when ${\sigma }_{\epsilon }^2(m)$ is much larger than Σ_η(s_m, s_m). The ratio of Σ₁(e(s_m)) over Σ₁((K_h(s_m−s))) is equal to $1+{\sigma }_{\epsilon }^2(s_m)/{\mathrm{\Sigma }}_{\eta }(s_m,s_m)$. Therefore, the efficiency gain of using w(s_m, s) = K_h(s_m − s) can be substantial if the value of ${\sigma }_{\epsilon }^2(s_m)/{\mathrm{\Sigma }}_{\eta }(s_m,s_m)$ is large.

3.2 Asymptotic Properties

Second, we investigate the asymptotic properties of β̂(·), ĝ(X^T β̂(s)) and Σ̂_η(s, t) when we set w(s_m, s) = K_h(s_m − s). For any smooth function f(s) and g(s, t), define ḟ(s) = df(s)/ds, f̈(s) = d² f(s)/ds² and g^(a,b)(s, t) = ∂^a+bg(s, t)/∂s^a∂t^b, where a and b are any nonnegative integers. We state the following theorems regarding the weak convergence of {β̂(s) : s ∈ 𝒮} and ĝ(X^T β̂(s)), whose detailed assumptions and proofs can be found in Web Appendix. Moreover, we also include additional asymptotic properties and their proofs in the same Web Appendix.

Theorem 2

Under Assumptions (C1)–(C11), as n, M → ∞, we have the following results.

1. $\sqrt{n}(\hat{\beta }(s)-{\beta }_0(s)-0.5h^2{A}_n{(s)}^{-1}\{\frac{1}{n}{\sum }_{i=1}^n{B}_i(s)[\ddot{g}(X_i^T\beta (s))+2Ġ(X_i^T\beta (s))\dot{\pi }(s)/\pi (s)]{\mu }_2(K)\})$ converges weakly to a Gaussian process with mean zero and covariance function, which is the limiting function of $A_n{(s)}^{-1}[n^{-1}{\sum }_{i=1}^n{B}_i(s){\mathrm{\Sigma }}_{\eta }(s,t)B_i{(t)}^T]A_n{(t)}^{-1}$, where A_n(·) and B_i(·) are defined in Web Appendix.

2. $\sqrt{n}[ĝ(X^T\hat{\beta }(s))-g(X^T\beta (s))-0.5h_1^2{\mu }_2(K)\ddot{g}(K^T\beta (s))]$ converges weakly to a Gaussian process with mean zero and covariance function Σ_η(s, t).

Theorem 2 ensures that we can make formal statistical inference on β(·) and g(·). Based on Theorem 2 (i) and (ii), we develop a wild bootstrap method to construct the Confidence bands of β̂(·) and ĝ(·) and include it in Section B of Web Appendix.

4. Numerical Studies

4.1 Simulation Results

We generated Y (s_m) according to model (3) with ε(s_m) ~ N(0, σ² = 0.3²) and X_i ~ N(0_p, Σ), where Σ is a 4 × 4 matrix with elements ρ^|j′−j| for j, j′ = 1, …, 4. Moreover, the varying coefficients β_j(s) are, respectively, given by

$${\beta }_1(s)=1+s^2,\hspace{1em}\hspace{1em}{\beta }_2(s)={(1-s)}^2,$$

$${\beta }_3(s)=4s(1-s),\hspace{1em}\hspace{1em}{\beta }_4(s)=-1+4{(s-0.5)}^2,$$

and then they were scaled as β(s)/‖β(s)‖₂. We set s_m as M = 50 equidistant grid points in [0,1] with s₁ = 0 and s_M = 1. We set ${\eta }_i(s)={\sum }_{k=1}^2{\xi }_{ik}{\psi }_k(s)$ with ${\xi }_{i1}~N(0,{\lambda }_1^2=1),{\xi }_{i2}~N(0,{\lambda }_2^2={0.5}^2),{\psi }_1(s)=\sqrt{2}\text{ sin}(2\pi s)$, and ${\psi }_2(s)=\sqrt{2}\text{ cos}(2\pi s)$. We consider two index functions including $g_1(X_i^T\beta (s_m))=\text{sin}(2X_i^T\beta (s_m))+2\text{ cos}(2+X_i^T\beta (s_m))$ and $g_2(X_i^T\beta (s_m))=X_i^T\beta (s_m)$.

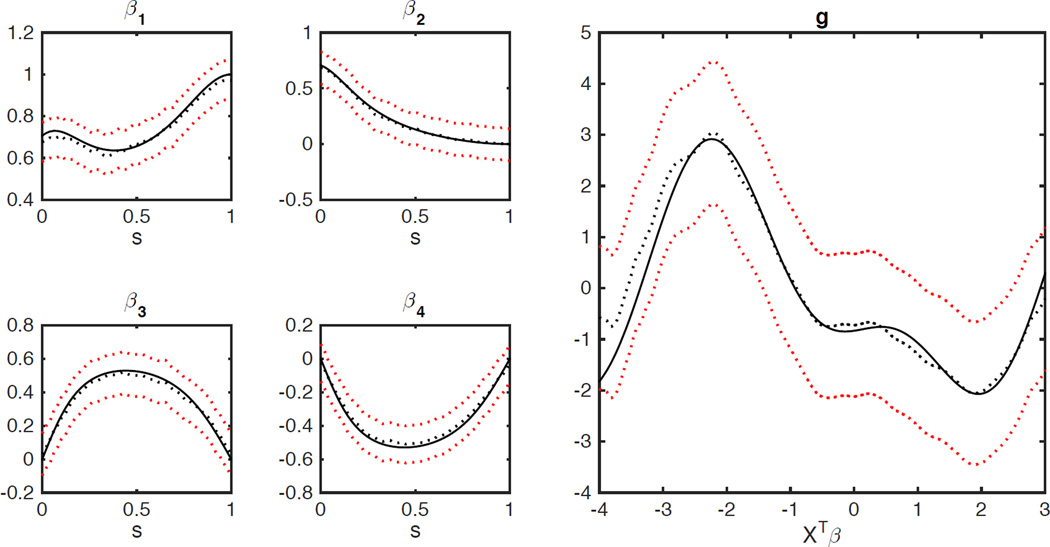
We conducted extensive simulation studies under different settings, but we only report some representative results for the sake of space. First, we set n = 40 and 200 and simulated data sets from model (3) for the first index function $g_1(X_i^T\beta (s_m))$ as described above. We fitted SIVC to each simulated data set and calculated all unknown quantities. Table 1 summarizes the mean absolute error (MAE) and root mean square error (RMSE) of all parameter estimates and the mean integrated absolute error (MIAE) and mean integrated squared error (MISE) of all estimated functions based on 200 simulations. The results in Table 1 indicate satisfactory performance of our estimators since all MAE, MSE, MIAE and MISE values are quite small. Typical estimated functions with mean performance are displayed in Figure 2 and Figure 1 in Web Appendix. The estimated curves (broken lines) closely resemble the corresponding true functions (solid lines) in these figures. As expected, all the errors increase as sample size decreases. Moreover, Table 2 includes the coverage probabilities of the simultaneous Confidence bands of β_l(s)s and g₁(u) for n = 40 and 200 based on 500 simulations. These coverage probabilities get close to the specified Confidence level 95% as sample size increases, while the results for g(·) are slightly worse than those of β_l(s).

Table 1.

Estimation results from 200 simulated data sets corresponding to the index function g₁(X^T β(s)) with n = 200 and 40. MAE is mean absolute error, RMSE is root mean square error, MIAE is mean integrated absolute error, and MISE is mean integrated square error

	n = 200				n = 40
Parameters	λ1	λ2	σ2		λ1	λ2	σ2
MAE	0.1551	0.0621	0.0202		0.1773	0.1026	0.0594
RMSE	0.1724	0.0726	0.0267		0.2108	0.1212	0.0667
n = 200
Functions	β1(s)	β2(s)	β3(s)	β4(s)	ψ1(s)	ψ2(s)	g(·)
MIAE	0.0288	0.0440	0.0403	0.0119	0.0137	0.0138	0.1063
MISE	0.0042	0.0077	0.0093	0.0039	0.0033	0.0034	0.0412
n = 40
Functions	β1(s)	β2(s)	β3(s)	β4(s)	ψ1(s)	ψ2(s)	g(·)
MIAE	0.0488	0.0751	0.0686	0.0597	0.0291	0.0299	0.2536
MISE	0.0121	0.0249	0.0251	0.0241	0.0061	0.0060	0.1530

Figure 2.

Simulation results for model (3) with the first index function and n = 200: the true and estimated varying coefficient functions and the true and estimated index functions. In each panel, the solid line represents the true function, the broken line represents the estimated function, and the red broken lines are the corresponding 95% simultaneous Confidence bands.

Table 2.

Coverage probabilities of simultaneous confidence bands for n = 40 and 200 based on 500 simulated data sets. The confidence level is 95%.

n	β1(s)	β2(s)	β3(s)	β4(s)	g(·)
40	0.936	0.932	0.944	0.934	0.924
200	0.946	0.954	0.948	0.946	0.942

Second, we illustrate the superiority of SIVC over multivariate varying coefficient model (MVCM) in Zhu et al. (2012) in terms of prediction accuracy. We set n = 200 and then simulated data sets from model (3) for both $g_1(X_i^T\beta (s_m))$ and $g_2(X_i^T\beta (s_m))$. For each simulated dataset, we randomly split it into a training set and a test set according to proportions π and 1 − π, respectively. We used the training set to estimate all unknown parameters, and then predicted the responses in the test set. Finally, we calculated the prediction error for each simulated dataset. We consider three values of π including 0.3, 0.5, and 0.7. For each case, we repeated 200 times. Table 3 reports the MAE and RMSE of prediction errors for SIVC and MVCM. For the index function $g_1(X_i^T\beta (s_m))$, SIVC significantly outperforms MVCM with smaller MAE and RMSE. Even for $g_2(X_i^T\beta (s_m))$, SIVC is slightly better than MVCM. It may indicate that SIVC is a useful tool for modeling functional data.

Table 3.

Prediction results corresponding to both index functions g₁(X^T β(s)) and g₂(X^T β(s)) with n = 200. MAE is mean absolute error and RMSE is root mean square error.

	g1(XT β(s))		g2(XT β(s))
	MAE	RMSE	MAE	RMSE
	π = 0.3
SIVC	1.013 (0.040)	1.282 (0.052)	0.987 (0.042)	1.248 (0.053)
MVCM	1.215 (0.040)	1.530 (0.053)	1.031 (0.045)	1.299 (0.060)
	π = 0.5
SIVC	1.002 (0.049)	1.267 (0.063)	0.978 (0.048)	1.236 (0.060)
MVCM	1.207 (0.048)	1.520 (0.065)	1.014 (0.050)	1.278 (0.062)
	π = 0.7
SIVC	0.977 (0.068)	1.236 (0.081)	0.966 (0.065)	1.222 (0.082)
MVCM	1.188 (0.063)	1.494 (0.082)	1.006 (0.068)	1.268 (0.084)

4.2 Real Data Analysis

We applied model (3) to the DWI data set described in Section 1. One goal of NIH ADNI is to test whether genetic, structural and functional neuroimaging, and clinical data can be integrated to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). We downloaded the structural brain MRI data and corresponding clinical and genetic data from baseline and follow-up from the ADNI publicly available database (http://adni.loni.usc.edu/).

The DWI data were processed by using a FSL TBSS pipeline (Smith et al., 2006) to register DTIs from multiple subjects to create a mean image and a mean skeleton. We used FMRIB software library to compute maps of fractional anisotropy (FA) for all subjects from the DTI after eddy current correction and automatic brain extraction. Then, we fed FA maps into the TBSS tool, which is also part of FSL. In the TBSS analysis, we aligned the FA data of all the subjects into a common space by using non-linear registration and created and thinned the mean FA image to obtain a mean FA skeleton, which represents the centers of all white matter tracts common to the group. Subsequently, we projected each subject’s aligned FA data onto this skeleton. Finally, we obtained the FA template curve measured at all the 83 grid points along the skeleton of the midsagittal corpus callosum as shown in Figure 2 in Appendix for all the subjects.

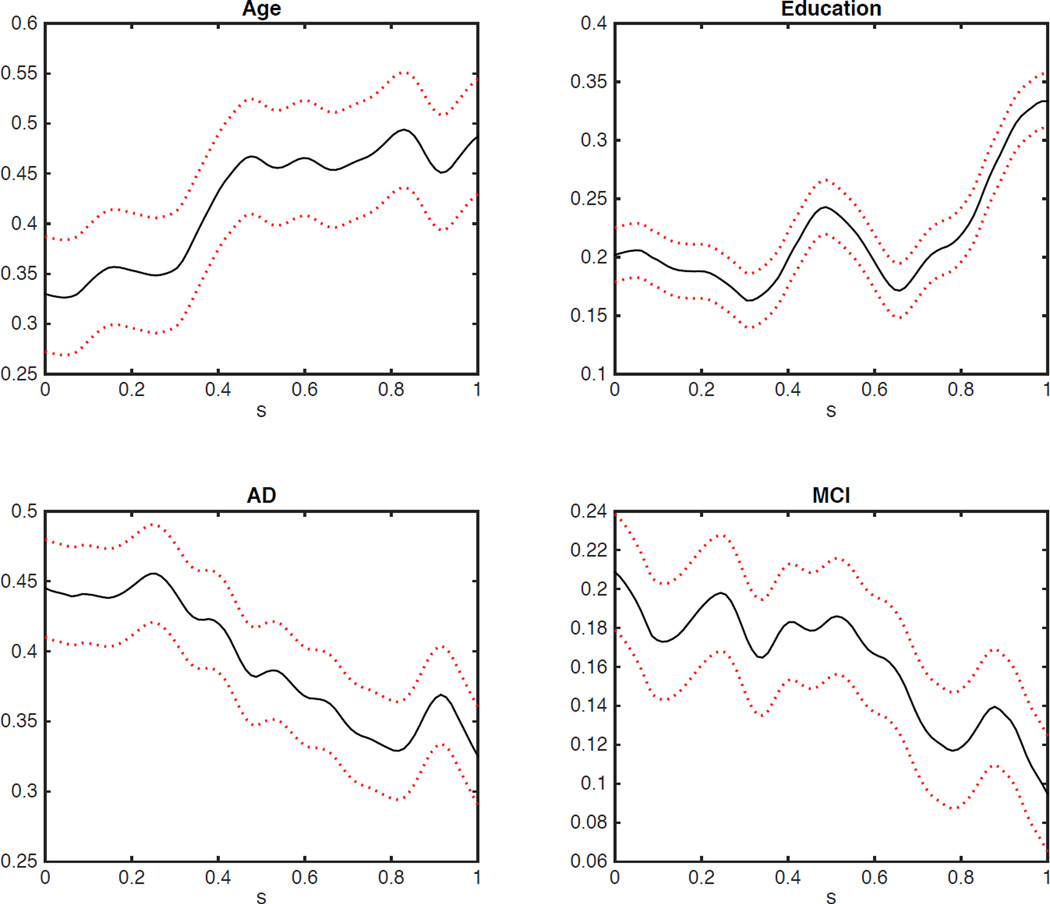
We are interested in establishing an association between FA and seven covariates including the gender variable (123 male and 91 female, coded by a dummy variable indicating for male), the age of the subject (years, ranges from 48.4 (years) to 90.4, mean 73.20), an indicator for handiness (193 right-hand and 20 left-hand, coded by a dummy variable indicating for left-hand), the education level (years, ranges from 9 to 20 (years), mean 15.91), an indicator for Alzheimer’s disease (AD) status (19.6%), an indicator for mild cognitive impairment (MCI) status (55.1%) and Mini-Mental State Exam (MMSE) of ADNI. We standardized all variables to have mean zero and variance one. We fitted model (3) and applied the estimation procedure in Section 2 to the data set. Figure 3 presents the estimated varying coefficients corresponding to age, education, AD status, and MCI status. The results reveal that MMSE, age, education, MCI, and AD are the most important factors. Moreover, gender and handiness have little effects on FA.

Figure 3.

ADNI data analysis: the four estimated varying coefficients for Age, Education, AD, and MCI. The black solid lines are estimated coefficients and the red broken lines are their corresponding 95% simultaneous Confidence bands.

We estimated the single index function g(·) and the covariance function Σ_η(s, s′) and its associated eigenvalues and eigenfunctions. See Figure 1 for details. The single index function shows a pattern with small values at the left and right ending points of the range $X_i^T\beta (s)$ and two modes in the middle of the range. The top five non-zero eigenvalues of Σ̂_η(s, s′) are 0.8628, 0.2771, 0.0284, 0.0142, and 0.0102, respectively. The first two eigenvalues account for 94.8% of the total variability, while the remaining eigenvalues rapidly drop to zero. The first eigenfunction, with a dominant eigenvalue accounting for 71.8% of the total variation, is simple in structure and resembles a single cycle of a sine wave. The remaining eigenfunctions are also quite simple and roughly sinusoidal representing additional functional structure that cannot be captured by the mean structure of model (3).

Finally, we compared the prediction accuracy of SIVC with that of MVCM in Zhu et al. (2012). We randomly split the 213 subjects into a training set and a test set with corresponding proportions π and 1 − π, respectively. We used the training set to estimate all the parameters, and then predicted the responses of the testing set. The 100 replications were used to calculate the prediction errors corresponding π = 0.3, 0.5 and 0.7. Table 4 reports the MAE and RMSE of the prediction errors and indicates that SIVC significantly outperforms MVCM in terms of both MAE and RMSE.

Table 4.

Prediction results for the ADNI data analysis. EST is estimate, SE is standard error, MAE is mean absolute error, and RMSE is root mean square error.

		MAE	RMSE	MAE	RMSE	MAE	RMSE
		π = 0.3		π = 0.5		π = 0.7
SIVC	EST	0.114	0.1374	0.113	0.136	0.112	0.135
	SE	0.001	0.001	0.002	0.002	0.002	0.002
MVCM	EST	0.599	0.650	0.599	0.627	0.600	0.628
	SE	0.012	0.028	0.014	0.022	0.013	0.016

5. Conclusion

In this paper we have developed a single-index varying coefficient model for establishing a varying association between functional responses (e.g., image) and a set of covariates. We have developed an estimation procedure to estimate varying coefficient functions, link function, and the covariance function of individual functions. We have investigated a strategy to integrate the information across all grid points. We have used simulations and real data analysis to demonstrate that SIVC is a useful tool for modeling functional data.

Many important issues need to be addressed in future research. First, the computational burden associated with SIVC can be quite heavy making it infeasible for large-scale imaging data at this moment. We will develop more computationally efficient algorithms to address such challenge. Second, we need to develop an effective procedure to carry out statistical inference, such as hypothesis test. Third, it is scientifically interesting to extend SIVC to carry out regression analysis of longitudinal functional data.