Integrating biogeochemistry with multiomic sequence information in a model oxygen minimum zone

Significance

Modern molecular sequencing is beginning to provide great insight into microbial community structure and function at ecosystem scales. However, the quantitative integration of multiomic sequence information (DNA, mRNA, and protein) and geochemical processes has so far been elusive. Here, we develop a biogeochemical model that integrates geochemistry and multiomic sequence information to explain key metabolic processes in the oxygen-starved waters of Saanich Inlet, a model ecosystem for studying microbial community responses to oxygen minimum zone expansion. Our model largely explains DNA, mRNA, and protein distributions and sheds light on the metabolic networks coupling carbon, sulfur, and nitrogen transformations across a redox gradient. Our approach is extensible to other biogeochemical models incorporating feedbacks of global change on ecosystem functions.

Abstract

Microorganisms are the most abundant lifeform on Earth, mediating global fluxes of matter and energy. Over the past decade, high-throughput molecular techniques generating multiomic sequence information (DNA, mRNA, and protein) have transformed our perception of this microcosmos, conceptually linking microorganisms at the individual, population, and community levels to a wide range of ecosystem functions and services. Here, we develop a biogeochemical model that describes metabolic coupling along the redox gradient in Saanich Inlet—a seasonally anoxic fjord with biogeochemistry analogous to oxygen minimum zones (OMZs). The model reproduces measured biogeochemical process rates as well as DNA, mRNA, and protein concentration profiles across the redox gradient. Simulations make predictions about the role of ubiquitous OMZ microorganisms in mediating carbon, nitrogen, and sulfur cycling. For example, nitrite “leakage” during incomplete sulfide-driven denitrification by SUP05 Gammaproteobacteria is predicted to support inorganic carbon fixation and intense nitrogen loss via anaerobic ammonium oxidation. This coupling creates a metabolic niche for nitrous oxide reduction that completes denitrification by currently unidentified community members. These results quantitatively improve previous conceptual models describing microbial metabolic networks in OMZs. Beyond OMZ-specific predictions, model results indicate that geochemical fluxes are robust indicators of microbial community structure and reciprocally, that gene abundances and geochemical conditions largely determine gene expression patterns. The integration of real observational data, including geochemical profiles and process rate measurements as well as metagenomic, metatranscriptomic and metaproteomic sequence data, into a biogeochemical model, as shown here, enables holistic insight into the microbial metabolic network driving nutrient and energy flow at ecosystem scales.

Microbial communities catalyze Earth’s biogeochemical cycles through metabolic pathways that couple fluxes of matter and energy to biological growth (1). These pathways are encoded in evolving genes that, over time, spread across microbial lineages and today shape the conditions for life on Earth. High-throughput sequencing and mass-spectrometry platforms are generating multiomic sequence information (DNA, mRNA, and protein) that is transforming our perception of this microcosmos, but the vast majority of environmental sequencing studies lack a mechanistic link to geochemical processes. At the same time, mathematical models are increasingly used to describe local- and global-scale biogeochemical processes or predict future changes in global elemental cycling and climate (2, 3). Although these models typically incorporate the catalytic properties of cells, they fail to integrate the information flow from DNA to mRNA, proteins, and process rates as described by the central dogma of molecular biology (4). Hence, a mechanistic framework integrating multiomic data with geochemical information has remained elusive.

Recent work based on metagenomics and quantitative PCR (qPCR) suggests that biogeochemical processes may be described by models focusing on the population dynamics of individual genes (5, 6). In such gene-centric models, genes are used as proxies for particular metabolic pathways, with gene production rates being determined solely by the Gibbs free energy released by the catalyzed reactions. Although compelling, these models stop short of incorporating the entire central dogma of molecular biology, and therefore do not achieve a truly quantitative integration of multiomic information and geochemical processes. For example, although such models allowed for a qualitative comparison between modeled gene production rates and selected transcript profiles, they do not provide any explicit mechanistic links (5). The absence of a quantitative validation against process rate measurements or other proxies for activity (e.g., proteins) leaves the adequacy of gene-centric models as a description for microbial activity unsubstantiated.

Here, we construct a gene-centric model for Saanich Inlet, a seasonally anoxic fjord on the coast of Vancouver Island, Canada (7) and a tractable analog for the biogeochemistry of oxygen minimum zones (OMZs). OMZs are widespread and expanding regions of the ocean, in which microbial community metabolism drives coupled carbon, nitrogen, and sulfur cycling (8, 9). These processes exert a disproportionately large influence on global N budgets, with resulting feedbacks on marine primary productivity and climate (10, 11). Extensive time-series data collection in Saanich Inlet provides an opportunity to interrogate biogeochemical processes across defined redox gradients extensible to coastal and open ocean OMZs (12, 13). Our model explicitly describes DNA, mRNA, and protein dynamics as well as biogeochemical reaction rates at ecosystem scales. To calibrate and validate our model, we use geochemical depth profiles; rate measurements for N cycling processes; and metagenomic, metatranscriptomic, and metaproteomic sequence data as well as qPCR-based abundance estimates for SUP05 Gammaproteobacteria—the dominant denitrifiers in Saanich Inlet (14), all obtained from a single location in Saanich Inlet in early or mid-2010.

Construction and Calibration of a Gene-centric Model

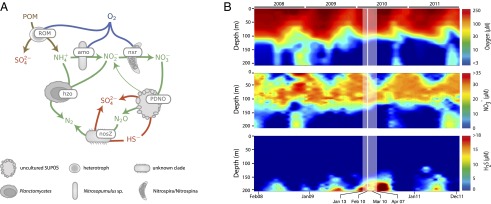
A recurring cycle of deep water renewal and stratification in Saanich Inlet results in an annual formation of an oxygen-depleted (${\text{O}}_2$) zone in deep basin waters (Fig. 1B). As this OMZ slowly expands upward during spring, anaerobic carbon remineralization in the underlying sediments leads to an accumulation of ammonium (${\text{NH}}_4^{+}$) and hydrogen sulfide (${\text{H}}_2\text{S}$) at depth (15). The oxidation of sulfide using nitrate produced through nitrification in the upper water column fuels chemoautotrophic activity and promotes the formation of a narrow sulfide–nitrate transition zone (SNTZ) at intermediate depths (12, 16, 17).

Fig. 1.

Metabolic network and selected time-series data. (A) Coupled carbon, nitrogen, and sulfur redox pathways considered in the model: Aerobic remineralization of organic matter (ROM), aerobic ammonia oxidation (amo), aerobic nitrite oxidation (nxr), and anaerobic ammonia oxidation (hzo), as well as sulfide-driven partial denitrification to nitrous oxide (PDNO) and reduction of nitrous oxide (nosZ) coupled to hydrogen sulfide oxidation. Depth profiles of all shown substrates, except for particulate organic matter (POM), were explicitly modeled; POM concentrations were fixed (more details are in Materials and Methods). Major taxonomic groups encoding specific pathways are indicated. (B) Water column oxygen (${\text{O}}_2$), nitrate (${\text{NO}}_3^{-}$), and hydrogen sulfide (${\text{H}}_2\text{S}$) concentrations measured at Saanich Inlet station SI03 from January 2008 to December 2011. The shaded interval and the dates at the bottom indicate the chemical measurements that were used for model calibration. The vertical white line marks the time of molecular sampling. The model considers depths between 100 and 200 m.

Our model describes the dynamics of several genes involved in carbon, nitrogen, and sulfur cycling across the Saanich Inlet redox gradient. Each gene is a proxy for a particular redox pathway that couples the oxidation of an external electron donor to the reduction of an external electron acceptor. The model builds on a large reservoir of previous work that provides conceptual insight into the microbial metabolic network in Saanich Inlet (12–14, 16–18) and includes aerobic remineralization of organic matter (ROM), nitrification, anaerobic ammonium oxidation (anammox), and denitrification coupled to sulfide oxidation (Fig. 1A). Certain pathways found in other OMZs, such as aerobic sulfide oxidation (19), dissimilatory nitrate reduction to ammonium (DNRA), (20) and sulfate reduction (5), were excluded from our model based on information from previous studies (12–14, 16–18) as well as preliminary tests with model variants (as explained below). Reaction rates (per gene) depend on the concentrations of utilized metabolites according to first- or second-order (Michaelis–Menten) kinetics (21). In turn, the production or depletion of metabolites at any depth is determined by the reaction rates at that depth. The production of genes is driven by the release of energy from their catalyzed reactions and proportional to the Gibbs free energy multiplied by the reaction rate (22).

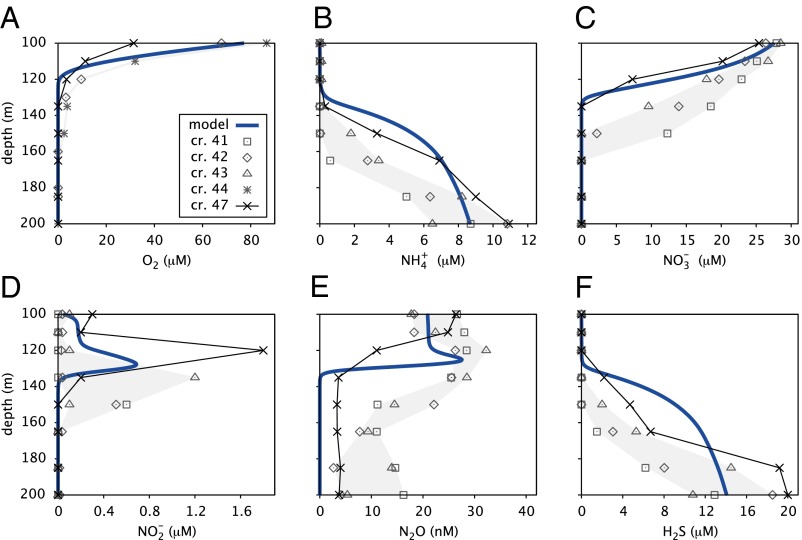
The model was evaluated at steady state between 100- and 200-m depth. Accordingly, free parameters were calibrated using geochemical profiles obtained in early 2010 during a period of intense water column stratification, which resulted in an extensive anoxic zone that approached a steady state (Fig. 2 and SI Appendix, Section S2.7). After calibration, most residuals to the data are associated with an upward offset of the predicted SNTZ (Fig. 2 B, C, and F) and an underestimation of nitrous oxide (${\text{N}}_2\text{O}$) concentrations in deep basin waters (Fig. 2E). These residuals can be explained by subtle deviations from a steady state. Such deviations were revealed in subsequent time-series measurements, during which the SNTZ continued to migrate upward in the water column (Fig. 2).

Fig. 2.

Measured and predicted geochemical profiles. (A) Oxygen, (B) ammonium, (C) nitrate, (D) nitrite, (E) nitrous oxide, and (F) hydrogen sulfide concentrations, as predicted by the calibrated model at steady state (thick blue curves). Dots indicate data used for the calibration measured during cruise 41 (cr. 41) on January 13, 2010 (SI041_01/13/10; □), cr. 42 (SI042_02/10/10; ♢), and cr. 43 (SI043_03/10/10; △). Oxygen profiles were not available for cr. 41 and cr. 43; hence, data from cr. 44 (SI044_04/07/10; *) were used instead. Thin black curves indicate data measured during cr. 47 (SI047_07/07/10), shortly before deep water renewal. Details on data acquisition are in SI Appendix, Section S1.

DNA Profiles and Process Rates

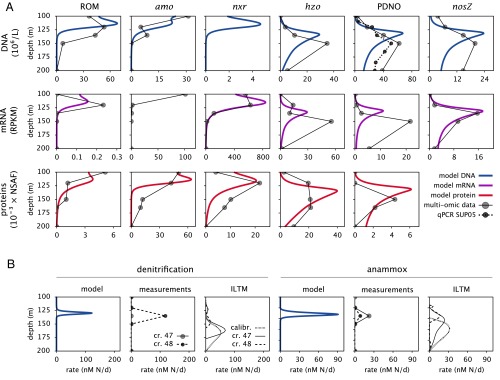
The calibrated model makes predictions about gene abundance and process rates, which can be validated using metagenomic sequence data and N process rate measurements from the same location and period as the geochemical calibration data (Fig. 3). Consistent with metagenomic depth profiles, the model predicts a redox-driven partitioning of pathways across the water column. Genes associated with ROM (ABC transporters mapped to dominant aerobic heterotrophs), aerobic ammonium oxidation to nitrite [ammonia monooxygenase (amo)], and aerobic nitrite oxidation to nitrate [nitrite oxidoreductase (nxr)] decline precipitously in deep basin waters, whereas genes associated with partial denitrification to nitrous oxide [PDNO; represented by nitric oxide reductase (norBC)], nitrous oxide reduction [nitrous oxide reductase (nosZ)], and anammox [hydrazine oxidoreductase (hzo)] are most abundant in the SNTZ (Fig. 3).

Fig. 3.

Molecular and rate profiles. (A) Predicted DNA, mRNA, and protein concentrations for ROM, amo, nxr, norBC, hzo, and nosZ genes (thick curves) compared with corresponding metagenomic, metatranscriptomic, and metaproteomic data (circles; February 10, 2010). The dashed curve under PDNO genes (row 1, column 4) shows concurrent qPCR-based abundance estimates for SUP05, the dominant denitrifier in Saanich Inlet. (B) Denitrification and anammox rates predicted by the model (thick blue curves) compared with rate measurements (circles) during cruise (cr.) 47 (SI047_07/07/10) and cr. 48 (SI048_08/11/10) as well as rates estimated from geochemical concentration profiles using ILTM (SI Appendix, Section S5). The ILTM estimates calibration (calibr.) in columns 3 and 6 is based on the same geochemical data as used for model calibration (Fig. 2).

The similarity of the PDNO, nosZ, and hzo gene profiles is indicative of their strong metabolic interaction (Fig. 3A). In particular, the co-occurring peaks of PDNO and nosZ gene abundances in the absence of ${\text{N}}_2\text{O}$ accumulation (Fig. 2E) reflect a quantitative coupling between the two denitrification steps and imply that both steps support extensive microbial growth at the SNTZ. This coupling is intriguing, because genomic reconstructions from both uncultivated and cultivated SUP05, the dominant denitrifier in Saanich Inlet, have not identified the nosZ gene (14, 17, 23). The absence of nosZ from SUP05 suggests that incomplete nitrate reduction by SUP05 and reduction of nitrous oxide by unidentified community members constitute separate and complementary metabolic niches in Saanich Inlet under low-oxygen and anoxic conditions (24).

The superposition of electron donor–acceptor pairs in redox transition zones supports chemical energy transfer in stratified water columns (25, 26), and previous studies have revealed relatively high cell abundances and chemoautotrophic activity in such zones (12, 27, 28). At the SNTZ in Saanich Inlet, the simultaneous availability of ${\text{NO}}_3^{-}$ and ${\text{H}}_2\text{S}$ fuels chemoautotrophic nitrate reduction coupled to sulfide oxidation, in turn supplying anammox with ${\text{NO}}_2^{-}$ via “leaky” denitrification (up to $88\mathrm{\%}$ of ${\text{NO}}_2^{-}$ supplied by PDNO) (SI Appendix, Section S2.11). Most of the ${\text{NH}}_4^{+}$ used by anammox ($0.3\hspace{0.17em}\text{mmol}\cdot {\text{m}}^{-2}\cdot {\text{d}}^{-1}$), however, is predicted to originate from the underlying sediments and reach the SNTZ via eddy diffusion. Accordingly, both anammox and denitrification rates are predicted to peak around the SNTZ and lead to production of ${\text{N}}_2$. This prediction is consistent with process rate measurements from discrete depth intervals during subsequent cruises in 2010 (Fig. 3B) as well as elevated SUP05 abundances at the SNTZ (Fig. 3A) (estimated via qPCR). In fact, the good agreement between predicted PDNO gene counts and observed SUP05 abundances suggests that energy fluxes associated with denitrification can be accurately translated to denitrifier growth rates. Predicted peak sulfide-driven denitrification rates are somewhat higher than peak anammox rates, although depth-integrated nitrogen loss rates are comparable for both pathways ($\sim 0.3\hspace{0.17em}\text{mmol}-{\text{N}}_2\cdot {\text{m}}^{-2}\cdot {\text{d}}^{-1}$). These predictions are partly consistent with rate estimates derived directly from the geochemical profiles using inverse linear transport modeling (ILTM) (details in Materials and Methods and Fig. 3B). Hence, near steady-state conditions, coupled sulfide-driven denitrification and anammox can concurrently drive significant nitrogen loss in the water column.

The fraction of ${\text{NO}}_2^{-}$ leaked during denitrification, compared with the total ${\text{NO}}_3^{-}$ consumed ($L_{\text{PDNO}}=0.352$) (SI Appendix, Section S2.3), was calibrated as a free model parameter based on the observed geochemical profiles. Such a high ${\text{NO}}_2^{-}$ leakage may result from an optimization of energy yield under electron donor limitation. Additional experimental work is needed to determine the mechanisms controlling this leakage by SUP05. Heterotrophic denitrification and nitrification are conventionally thought of as the primary sources of both nitrite and ammonium for anammox in OMZs (20, 29), and so far evidence for a direct coupling between sulfide-driven denitrification and anammox has been scarce (28). Our results indicate that incomplete sulfide-driven denitrification can be an important precursor for anammox, particularly under conditions of organic carbon limitation (30). This coupling and the benthic supply of ammonium lead to a substantial departure of the fraction of total nitrogen loss via anammox in Saanich Inlet ($\sim 50\hspace{0.17em}\mathrm{\%}$; predicted at steady state) from previous predictions based on labile organic matter stoichiometry ($\sim 28\hspace{0.17em}\mathrm{\%}$) (31).

Steady-state gene production rates for chemoautotrophic pathways are predicted to peak around the SNTZ, reaching $\sim 3.2\times {10}^6\hspace{0.17em}\text{genes}\cdot {\text{L}}^{-1}\cdot {\text{d}}^{-1}$. This gene production rate corresponds to a dark carbon assimilation (DCA) rate of $\sim 60\hspace{0.17em}\text{nmol}-\text{C}\cdot {\text{L}}^{-1}\cdot {\text{d}}^{-1}$, assuming a carbon:dry weight ratio of 0.45 (32) and a dry cell mass of $m=5\times {10}^{-13}\hspace{0.17em}\text{g}$ (22). Previously measured peak DCA rates in the Saanich Inlet OMZ reached $2\hspace{0.17em}\text{μmol}-\text{C}\cdot {\text{L}}^{-1}\cdot {\text{d}}^{-1}$ (16), which is significantly higher than the values predicted here. The potential activity of pathways not considered here, such as heterotrophic or mixotrophic inorganic carbon assimilation (33), may explain some of these differences. Moreover, the model assumes steady-state conditions, whereas redox conditions were far from steady state during previous DCA measurements (16). Transient dynamics in Saanich Inlet can exhibit significantly higher nitrogen fluxes and chemoautotrophic activity (34), which might further explain discrepancies between the model and measured DCA rates. Accounting for chemoautotrophic productivity based on oxidant and reductant supply in redox transition zones is generally difficult because of limited knowledge on active pathways, the possibility of cryptic nutrient cycling, and potential lateral substrate intrusions, and discrepancies similar to our study are frequently reported for other OMZs (35–38). Hence, fully accounting for measured DCA rates remains an unresolved problem with important implications for carbon cycling in OMZs.

Previously detected amino acid motifs similar to those found in proteins catalyzing DNRA suggested that SUP05 may also be providing ${\text{NH}}_4^{+}$ to anammox through DNRA (14). DNRA, not included in the model, is known to fuel anammox in anoxic sediments and water columns (20, 39). So far, incubation experiments have not revealed any DNRA activity in Saanich Inlet, and measured ammonium profiles do not indicate a significant ammonium source at or below the SNTZ (Fig. 2B). Nevertheless, DNRA could be active in Saanich Inlet and remain undetected because of rapid ammonium consumption by anammox (39). An extension of the model that included DNRA as an additional pathway, which we calibrated to the same geochemical data (January to March 2010), predicted negligible DNRA rates compared with denitrification and anammox and consistently converged to the same predictions as the simpler model. These results suggest that DNRA may be absent from the Saanich Inlet water column—at least near steady-state conditions in late spring—and that the hydroxylamine-oxidoreductase homolog encoded by SUP05 plays an alternative role in energy metabolism (17, 24).

DNA concentration profiles of anammox and denitrification genes appear more diffuse and are skewed toward deep basin waters compared with their corresponding rate profiles and the SNTZ (Fig. 3). The model explains this apparent discrepancy based on turbulent diffusion and sinking, which transport genes away from their replication origin. Hence, community composition at any depth is the combined result of local as well as nonlocal population dynamics. Metabolic flexibility encoded in the genomes of microorganisms mediating these processes may also contribute to broader distributions of individual genes than their predicted activity range (30). This disconnect between local metabolic potential and activity needs to be considered when interpreting metagenomic profiles in a functional context, especially in environments with strong redox gradients, such as OMZs (9) or hydrothermal vents (6).

The concentration maxima of anammox and denitrification genes are predicted at shallower depths than measured (Fig. 3A). This observation is consistent with the upward offset of the predicted SNTZ and highlights an important limitation of steady-state models applied to dynamic ecosystems. Indeed, process rate maxima predicted via ILTM at multiple time points continue to move upward beyond the time interval used for model calibration (Fig. 3B). In reality, an electron donor/electron acceptor interface as narrow as predicted by the model would only develop after sufficient time for transport processes and microbial activity to reach a true steady state. Such narrow interfaces do appear in permanently stratified meromictic lakes (40) or the Baltic Sea, where stagnation periods can persist for many years (30).

mRNA and Protein Profiles

Metatranscriptomics and metaproteomics present powerful means to assess community metabolic activity—rather than just metabolic potential—and each method comes with its own set of advantages (14, 41). For example, although transcripts represent immediate proxies for gene up-regulation (e.g., in response to changing redox conditions), proteins reflect the immediate catalytic potential of a community, and in vitro characterization of enzyme kinetics can facilitate the projection of protein abundances to in situ process kinetics (42). Transcript abundances need not always correlate strongly with protein abundances (for example, in cases of translational control or protein instability) (42, 43), and hence, metatranscriptomics and metaproteomics provide different perspectives on community activity. Hence, a systematic evaluation of the consistency between these alternative layers of information in real ecosystems is warranted. In fact, a unifying mechanistic model describing the processes that control environmental mRNA and protein distributions is crucial for the correct interpretation of multiomic data in relation to biogeochemical processes (41).

Although DNA replication and process rates are predicted by our gene-centric model merely based on environmental redox conditions, it is uncertain to what extent intermediate stages of gene expression (transcription and translation) can be explained based on such a paradigm. For example, environmental mRNA concentrations measured via qPCR have previously been directly compared with predicted reaction rates (5), but such a heuristic comparison ignores other mechanisms controlling environmental biomolecule distributions, such as physical transport processes. Here, in an attempt to mechanistically describe mRNA and protein dynamics at ecosystem scales, we hypothesized that both mRNA and protein production rates at a particular depth are proportional to the total reaction rate at that depth (calculated using the calibrated model). This premise is motivated by observations of elevated transcription and translation rates during high metabolic activity or growth (44–46). Furthermore, we assumed that mRNA and protein molecules are subject to the same hydrodynamic dispersal processes as DNA, while decaying exponentially with time postsynthesis. The decay time of each molecule as well as the proportionality factor between the reaction rate and synthesis were estimated statistically using metatranscriptomic and metaproteomic data (SI Appendix, Section S2.10).

The general agreement between this model and the molecular data (Fig. 3A) suggests that the production–degradation dynamics of several of these molecules is, at the ecosystem level, dominated by the mechanisms described above. The best fit (in terms of the coefficient of determination) (SI Appendix, Table S5) is achieved for nosZ and nxr mRNA as well as amo, norBC, ROM, and nxr proteins. The greater number of protein over mRNA profiles that can be explained by the model suggests that the proteins considered here are, indeed, simply produced on demand and slowly degrade over time, whereas mRNA dynamics are subject to more complex regulatory mechanisms (41, 47). In particular, the decay times of some transcripts and proteins were estimated to be as high as several weeks (SI Appendix, Table S5). For proteins, these estimates fall within known ranges (47); however, for transcripts, these estimates are much higher than decay times determined experimentally in cells (48). One reason for this discrepancy seems to be the underestimation of the SNTZ depth range by the model, which in turn leads to longer estimates for mRNA decay times needed to explain the detection of these molecules outside of the SNTZ. Alternatively, transcripts and proteins might persist in the cells in inactive states for a significant period, even after dispersal into areas with low substrate concentrations. For example, stable but silent transcripts have been found in bacteria after several days of starvation (49, 50). Furthermore, gene expression may not change immediately in response to external stimulus (14). For example, for some prokaryotic transcription cascades, the basic time unit may be the cell doubling time (which can reach several weeks in anoxic environments) (51) because of regulation by long-lived transcription factors (52). Hence, the decay times estimated here may reflect a hysteresis in gene down-regulation after nutrient depletion, perhaps in anticipation of potential future opportunities for growth (53, 54). Overall, these observations suggest that future metatranscriptomic sequencing efforts and models for environmental mRNA dynamics would benefit from a consideration of additional control mechanisms (for example, derived from cell-centric transcription models) (55, 56).

Consequences for Geobiology

Gene-centric models have the potential to integrate biogeochemical processes with microbial population dynamics (5, 6). According to the central dogma of molecular biology (4), gene transcription and translation are intermediate steps that regulate metabolic processes in individual cells, but the appropriate projection of the central dogma to ecosystem scales remained unresolved, because transcription and translation were not explicitly considered in previous models (5, 6). We have developed a biogeochemical model that explicitly incorporates multiomic sequence information and predicts pathway expression and growth in relation to geochemical conditions. In particular, when mRNA and protein dynamics are omitted, the gene-centric model only includes four calibrated parameters and yet is able to largely reproduce geochemical profiles (Fig. 2), relative metagenomic profiles (Fig. 3A), and SUP05 cell abundances, indicating that the good agreement between the model and the data is unlikely caused by overfitting. In fact, as we refined and calibrated our model to the geochemical profiles, we observed that the metagenomic profiles were well-reproduced as soon as the model’s geochemical predictions roughly aligned with the data, even if the parameters being calibrated had not converged yet. This observation reinforces the interpretation that fluxes of matter and energy are robust predictors of microbial productivity and functional community structure.

Our model successfully explains a large fraction of environmental mRNA and protein distributions based on DNA concentration profiles and biochemical reaction rates in the OMZ. These results are consistent with the idea that DNA is a robust descriptor of an ecosystem’s biotic component (57, 58), which in conjunction with the geochemical background, determines pathway expression and process rates (59). This idea implies that the co-occurrence of a metabolic niche with cells able to exploit it is sufficient to predict microbial activity. Under this paradigm, DNA may be regarded as directly interacting with the geochemical background, whereas the production of mRNA and proteins is an inevitable consequence of the biologically catalyzed flow of matter and energy. This interpretation is supported by the overall consistency between the metatranscriptomic and metaproteomic profiles for N and S cycling genes (Fig. 3A). Hence, mRNA and proteins may each be adequate proxies for pathway activity in Saanich Inlet, although as discussed above, questions regarding the relevant time scales remain. Additional work is needed to test this paradigm in other ecosystems, especially under non–steady-state conditions. Nevertheless, many aquatic ecosystems are permanently or almost permanently anoxic (8, 40, 60), and hence, our approach and conclusions are expected to be particularly applicable to these systems.

In addition to providing a systematic calibration and validation of the model, we identified processes that need to be considered when interpreting multiomic data. Conventional proxies for activity, such as mRNA and proteins, are themselves subject to complex population dynamics that include production and active or passive degradation as well as physical transport processes. Consequently, the close association between process rates and biomolecule production suggested above does not imply that biomolecule distributions, per se, are equivalent to local microbial activity rates. In Saanich Inlet, for example, the wide distribution of DNA, mRNA, and proteins across the OMZ, in contrast to a relatively narrow metabolic “hot zone” at the SNTZ, is predicated on a balance between spatially confined production and dispersal across the water column. This “mass effect” (61) means that geochemical or biochemical information is needed to assign actual activity to genes or pathways identified in multiomic data, especially for components mediating energy metabolism. This conclusion is generalizable and should be applied to other ecosystems exhibiting dispersal across strong environmental gradients, such as estuaries (62) or hydrothermal vents (6). Moreover, in dynamic ecosystems with rapidly changing geochemical conditions, past population growth rates can influence future community structure and biomolecular patterns, and hence cross-sectional community profiles may not reflect current dynamics (63). In such systems, an incorporation of multiple layers of geochemical and biological information into a mechanistic model—as shown here—will be crucial for disentangling the multitude of processes underlying experimental observations.

The gene-centric model constructed here, although evaluated at steady state, is in fact a spatiotemporal model that could, in principle, predict gene population dynamics and process rates over time. A spatiotemporal analysis of the model would require multiomic time series coverage and knowledge of nonstationary physical processes, such as seasonal patterns in surface productivity and hydrodynamics during deep water renewal events. Multiomic time series would be especially useful for improving the mRNA and protein models introduced here because of the high number of currently unknown parameters. For example, integrating metatranscriptomic, metaproteomic, and geochemical time series during rapid environmental changes into our model would allow for a more direct determination of in situ transcriptional and translational responses and biomolecule decay times.

The multiomic profiles that we used to validate our model are only given in terms of relative—rather than absolute—biomolecule concentrations. Hence, the observed abundance of each biomolecule may be influenced by the abundances of other biomolecules, which could explain some of the discrepancies between the model and the multiomic data. Unfortunately, this limitation is currently pervasive across environmental shotgun sequencing studies, largely because of technical challenges in estimating in situ DNA, mRNA, and protein concentrations (64). These challenges will likely be overcome in the future (65, 66). Given this current caveat, the general agreement of the model with the shape of the multiomic profiles (Fig. 3A) is remarkable and suggests that the spatial structuring of the metabolic network is well-captured by the model. In fact, our qPCR-based estimates for absolute SUP05 abundances are consistent with absolute PDNO gene concentrations predicted by the model as well as the shape of the PDNO abundance profiles in the metagenomes (Fig. 3A). This double agreement suggests that—at least for PDNO—both our model and our metagenomic datasets (Datasets S1 and S2) reflect the actual gene distributions.

Conclusions

Most major metabolic pathways driving global biogeochemical cycles are encoded by a core set of genes, many of which are distributed across distant microbial clades (1). These genes are expressed and proliferate in response to specific redox conditions and in turn, shape Earth’s surface chemistry. Here, we have shown that the population dynamics of genes representative of specific metabolic pathways, their expression, and their catalytic activity at ecosystem scales can all be integrated into a mechanistic framework for understanding coupled carbon, nitrogen, and sulfur cycling in OMZs. This framework largely explained DNA, mRNA, and protein concentration profiles and resolved several previous uncertainties in metabolic network structure in Saanich Inlet, including a direct coupling of sulfide-driven denitrification and anammox through leaky nitrite production by SUP05 as well as the presence of a metabolic niche for nitrous oxide reduction contributing to nitrogen loss. Beyond OMZ-specific predictions, model results indicate that geochemical fluxes are robust indicators of microbial community structure and reciprocally, that gene abundances and geochemical conditions largely determine gene expression patterns. Such integrated modeling approaches offer insight into microbial community metabolic networks and allow prediction of elemental cycling in a changing world.

Materials and Methods

Model Overview.

The core model is a set of differential equations for the concentrations of eight metabolites and six proxy genes (DNA) across depth (100–200 m) and time. Each gene is a proxy for a particular energy-yielding pathway, which couples the oxidation of an external electron donor to the reduction of an external electron acceptor. Each gene is considered as a replicating unit that is independent of other genes. This simplifying assumption corresponds to the case where each cell occupies a single metabolic niche associated with one of the modeled pathways (14, 67). Gene-specific reaction rates depend on the concentrations of metabolites according to first- or second-order (Michaelis–Menten) kinetics (5, 21) (SI Appendix, Section S2.4). In turn, the production or depletion of metabolites at any depth is determined by the reaction rates at that depth, taking into account reaction stoichiometry (SI Appendix, Section S2.3) and diffusive transport across the water column. The production of genes at any depth is driven by the release of energy from their catalyzed reactions and is proportional to the Gibbs free energy multiplied by the reaction rate (22) (SI Appendix, Section S2.5). In addition, gene populations are subject to exponential decay rates, diffusive transport, and sinking.

Mathematical Model Structure.

The DNA concentration for gene r (${\mathrm{\Gamma }}_r$; copies per volume) exhibits the dynamics

$$\frac{\partial {\mathrm{\Gamma }}_r}{\partial t}=-q_r{\mathrm{\Gamma }}_r+\frac{1}{c}{Z}_r{H}_r{\mathrm{\Gamma }}_r-\text{v}\frac{\partial {\mathrm{\Gamma }}_r}{\partial z}+\frac{\partial }{\partial z}\left(K\frac{\partial {\mathrm{\Gamma }}_r}{\partial z}\right)\mathrm{,}$$ [1]

whereas the concentration of the mth metabolite ($C_m$; mole per volume) follows

$$\frac{\partial C_m}{\partial t}={\displaystyle \sum _r{S}_{mr}{H}_r{\mathrm{\Gamma }}_r}+\frac{\partial }{\partial z}\left(K\frac{\partial C_m}{\partial z}\right).$$ [2]

Both the gene concentrations ${\mathrm{\Gamma }}_r$ and metabolite concentrations $C_m$ depend on time t and depth z. The first term on the right-hand side of Eq. 1 corresponds to cell death, with $q_r$ being the exponential death rate in the absence of any metabolic activity for pathway r. The second term corresponds to gene production, with $H_r$ being the per-gene reaction rate as a function of metabolite concentrations (SI Appendix, Section S2.4). The biomass production coefficient $Z_r$ is a linear function of the Gibbs free energy of reaction r (SI Appendix, Section S2.5); c is the average dry cell mass, which is used to convert biomass production into cell production. The third term corresponds to cell sinking at speed $\text{v}$. The last term in Eqs. 1. and 2 corresponds to diffusive transport, with K being the vertical eddy diffusion coefficient. In Eq. 2, $S_{mr}$ is the stoichiometric coefficient of metabolite m in reaction r (SI Appendix, Section S2.3). The sum on the right-hand side of Eq. 2 iterates through all reactions and accounts for microbial metabolic fluxes. Eqs. 1. and 2 specify the rates of change for the DNA and chemical concentration profiles. Steady-state profiles were obtained after long simulations when all profiles had eventually stabilized.

Considered Pathways.

Redox pathways occurring in a single cell require at least two enzymes: one involved in the oxidation of the initial electron donor and one involved in the reduction of the final electron acceptor. In the model, such pathways are represented by single proxy genes, chosen such that ambiguities in their functional role are minimized. For example, nitrous oxide reduction using nosZ coupled to sulfide oxidation is identified with nosZ, because many sulfur oxidizing enzymes are reversible. Other pathways considered in the model are partial denitrification of nitrate to nitrous oxide coupled to sulfide oxidation (PDNO), aerobic ammonium oxidation using amo, aerobic nitrite oxidation to nitrate using nxr, and anammox (i.e., the anammox involving hzo) as well as aerobic remineralization of (dissolved) organic matter (ROM). PDNO comprises three denitrification steps that are thought to be predominantly performed by the same microorganisms in the SUP05 clade (14, 17): dissimilatory nitrate reduction to nitrite by membrane-bound respiratory nitrate reductases (narGHIJ) or periplasmic dissimilatory nitrate reductases (napAB), nitrite reduction to nitric oxide using nitrite reductases (nirKS), and nitric oxide reduction to nitrous oxide using norBC. The first denitrification step was assumed to be leaky, so that a small fraction of nitrite is released into the extracellular environment (20). We used norBC as a proxy for PDNO when interpreting molecular data (Fig. 3A shows coverage of the dissimilatory sulfide oxidation pathway, and SI Appendix, Fig. S4 D–F shows narGHIJ, napAB, and nirKS multimolecular data). ROM is associated with the release of ammonium and sulfate (${\text{SO}}_4^{2-}$) at ratios corresponding to marine bacterial biomass stoichiometry (32). The choice of redox pathways in the model follows the hypotheses put forward by Hawley et al. (14) based on molecular depth profiles as well as reports of nitrous oxide reduction coupled to hydrogen sulfide oxidation in Saanich Inlet (68).

Hydrogen sulfide is assumed to originate via diffusion from the sediments, where intense sulfate reduction occurs (15) (SI Appendix, Section S3.1). Sulfate reduction was omitted from our model, because both our molecular as well as chemical data suggest that sulfate reduction in the water column is negligible compared with the oxidation of sulfur compounds (a detailed discussion is in SI Appendix, Section S3.1). In fact, when we included sulfate reduction in preliminary tests of our model, the agreement between the model and the ${\text{H}}_2\text{S}$ profiles decreased dramatically, providing additional evidence that ${\text{H}}_2\text{S}$ is largely supplied from the bottom rather than produced in the water column.

Aerobic ${\text{H}}_2\text{S}$ oxidation was omitted from the model based on extensive previous work that points toward ${\text{NO}}_3^{-}$ and other nitrogen compounds as dominant electron acceptors for ${\text{H}}_2\text{S}$ oxidation during periods of strong stratification (18, 16, 12–14). For example, as shown in Fig. 2B, the upper boundary of ${\text{H}}_2\text{S}$ concentrations closely follows the lower boundary of ${\text{NO}}_3^{-}$—rather than ${\text{O}}_2$—over time, especially during the period considered here (early 2010). We mention that, during renewal events in the fall, ${\text{O}}_2$ can become an important electron acceptor for ${\text{H}}_2\text{S}$ oxidation (12); however, this possibility does not affect this study, which focuses on a period of intense stratification near steady-state conditions. A more detailed discussion on the role of aerobic sulfide oxidation is provided in SI Appendix, Section S3.3.

Pathways for hydrogen (${\text{H}}_2$) and methane (${\text{CH}}_4$) metabolism are not included on grounds of parsimony, because these pathways are not directly linked to the other considered pathways (12) and because low hydrogen and methane fluxes into the OMZ suggest that hydrogen and methane pathways are of secondary importance (12, 69).

Model Calibration and Data.

Unknown parameters of the basic gene-centric model (Eqs. 1. and 2) (ignoring mRNA and protein dynamics) were calibrated by comparing steady-state predictions with measured depth profiles of oxygen, ammonium, nitrate, nitrite, hydrogen sulfide, and nitrous oxide. Chemical calibration data were acquired on January 13, February 10, and March 10, 2010 (or February 10 and April 7 for oxygen) from a single location in Saanich Inlet ($123\mathrm{°}\hspace{0.17em}30.3\mathrm{0}\prime$ W, $48\mathrm{°}\hspace{0.17em}35.5\mathrm{0}\prime$ N) (SI Appendix, Section S1.2). The calibrated parameters were the maximum cell-specific reaction rate $V_{\text{PDNO}}$ and the first-order rate constants $A_{\text{ROM}}$ and $A_{\text{nosZ}}$ as well as the PDNO leakage fraction $L_{\text{PDNO}}$ (SI Appendix, Table S3). Calibration was performed by maximizing the likelihood of a statistical model, in which the deterministic part (i.e., expectation) is given by the predictions of the gene-centric model and the stochastic part (i.e., error) is normally distributed (SI Appendix, Section S2.8). This calibration method is known as maximum likelihood estimation and is widespread in statistical regression and physics (70). Maximization of the likelihood was performed using the MATLAB function fmincon, which uses repeated simulations and gradual exploration of parameter space (71). The sensitivity of the model to parameter variation was assessed via local sensitivity analysis (72) as described in SI Appendix, Section S2.12. An overview of our workflow is shown in SI Appendix, Fig. S2.

Samples for molecular sequencing were collected on February 10, 2010 from the same geographical location as the geochemical data (SI Appendix, Sections S1.3 and S1.4). Because metaproteomes were missing at depth 100 m (the upper bound of our simulation domain) and to increase statistical power when evaluating our protein models, we used linear interpolation between depths 97 and 120 m (where metaproteomes were available) to estimate protein normalized spectral abundance factor (NSAF) values at 100-m depth (“unit imputation”). Metagenomic profiles (a priori in relative units) were rescaled to match the model scales using maximum likelihood estimated factors (SI Appendix, Section S2.9). SUP05 abundances for February 10, 2010 were estimated via qPCR using SUP05-specific primers targeting the 519–1,048 region of the SUP05 16S rRNA gene following the protocol in ref. 73; 16S gene counts were corrected for the number of 16S rRNA gene copies per cell estimated using the Tax4Fun pipeline (74) (SI Appendix, Section S1.6). Denitrification and anammox rates were measured on cruises 47 (SI047_07/07/10) and 48 (SI048_08/11/10) via ex situ incubation experiments and subsequently corrected for differences between in situ and incubated substrate concentrations (SI Appendix, Section S1.5).

mRNA and Protein Models.

As mentioned previously, following calibration of the gene-centric model to the geochemical profiles, we extended the model to describe mRNA (and similarly, protein) dynamics in the water column. Specifically, the production rate of an mRNA (transcripts produced per time and volume of seawater) at a particular depth was assumed to be proportional to the total reaction rate (moles per time and volume of seawater) at that depth. A linear relation, although only an approximation, can be justified by the fact that increased enzyme dilution rates at elevated cell division rates must be balanced (at the population level) by correspondingly increased translation—and hence, transcription—rates (55). We also assumed that mRNA molecules disperse via diffusion and sinking similar to genes (because they are hosted by the same cells) and decay exponentially with time. Thus, environmental mRNA concentrations satisfy the partial differential equation

$$\frac{\partial T_r}{\partial t}=-\frac{T_r}{{\tau }_r}+\frac{R_r}{{\alpha }_r}-\text{v}\frac{\partial T_r}{\partial z}+\frac{\partial }{\partial z}\left(K\frac{\partial T_r}{\partial z}\right)\text{,}$$ [3]

where $T_r$ is the mRNA concentration corresponding to the rth reaction, ${\tau }_r$ is the decay time of the mRNA molecule, $R_r=H_r{\mathrm{\Gamma }}_r$ is the total reaction rate, and ${\alpha }_r$ is an unknown proportionality constant. We considered $T_r$ in the same units as the multiomic data, i.e., reads per kilobase per million mapped reads (RPKM) for metatranscriptomes and NSAF for metaproteomes. Consequently, ${\alpha }_r$ is the ratio between the rth reaction rate ($\text{moles}\cdot {\text{day}}^{-1}\cdot {\text{liter}}^{-1}$) and the corresponding RPKM (or NSAF) “production rate” ($\text{RPKM}\cdot {\text{day}}^{-1}$), and thus it depends on not only the particular reaction but also on our sampling protocol and sequencing pipeline. The above model was evaluated at steady state, when mRNA production, dispersal, and decay are balanced at each depth ($\partial T_r/\partial t=0$). The parameters of the mRNA and protein models (proportionality factors and decay times) were calibrated by fitting to the metatranscriptomic and metaproteomic data, respectively (SI Appendix, Section S2.10). Calibration to metatranscriptomic data failed for amo mRNA. Metagenomic and metaproteomic data were not available for nxr and nosZ, respectively (SI Appendix, Section S1.3). For all other mRNAs and proteins, the iterative calibration converged rapidly to an optimum, and this optimum was robust against various starting values for the parameters.

ILTM.

In addition to the model predictions and rate measurements, denitrification and anammox rates were also estimated directly from chemical concentration profiles via ILTM (SI Appendix, Section S5). ILTM provides an estimate for the metabolic fluxes in the OMZ based on the observed chemical concentration profiles. The exact shape of estimated rate profiles depends sensitively on measurement errors and the noise reduction method applied to the concentration profiles. Hence, ILTM only serves as a rough verification of the order of magnitude of rates predicted by the model or measured experimentally. ILTM fitting was applied separately to concentration profiles from cruises 47 and 48 as well as the chemical profiles used for model calibration (cruises 41–44) (Fig. 2) after averaging across replicates at each depth.