Biophysical comparison of ATP synthesis mechanisms shows a kinetic advantage for the rotary process

Significance

All living organisms—archaea, bacteria, and eukarya—use an intricate rotary molecular machine to synthesize ATP, the energy currency of the cell. Why did evolution select such an elaborate machine when a simpler alternating-access mechanism, already present in cells, could be used for ATP synthesis? Our analysis shows that the rotary mechanism is faster than other possible mechanisms, particularly under challenging conditions, suggesting a possible evolutionary advantage.

Abstract

The ATP synthase (F-ATPase) is a highly complex rotary machine that synthesizes ATP, powered by a proton electrochemical gradient. Why did evolution select such an elaborate mechanism over arguably simpler alternating-access processes that can be reversed to perform ATP synthesis? We studied a systematic enumeration of alternative mechanisms, using numerical and theoretical means. When the alternative models are optimized subject to fundamental thermodynamic constraints, they fail to match the kinetic ability of the rotary mechanism over a wide range of conditions, particularly under low-energy conditions. We used a physically interpretable, closed-form solution for the steady-state rate for an arbitrary chemical cycle, which clarifies kinetic effects of complex free-energy landscapes. Our analysis also yields insights into the debated “kinetic equivalence” of ATP synthesis driven by transmembrane pH and potential difference. Overall, our study suggests that the complexity of the F-ATPase may have resulted from positive selection for its kinetic advantage.

The F-ATPase performs molecular-level free-energy (FE) transduction to phosphorylate ADP and yield ATP, the primary energy carrier that drives a vast range of cellular processes. It spurred Mitchell’s chemiosmotic hypothesis (1) and Boyer’s now-validated proposal for the binding-change mechanism (2) in which a proton electrochemical gradient is transduced to rotation-based mechanical energy and then back to chemical FE as ADP is phosphorylated. The F-ATPase’s two-domain uniaxial rotary structure is conserved across all three domains of life (3–6), and details of its function have been the subject of a multitude of studies (e.g., refs. 7–30).

Here, we address a relatively narrow question with potentially significant evolutionary implications: Why is ATP synthesized by a rotary mechanism instead of a potentially much simpler alternating-access mechanism (Fig. 1)? Using thermodynamic and kinetic constraints, we address the question of whether evolution tends to arrive at optimal molecular processes (31), building on established concepts of optimality-derived evolutionary convergence (32, 33). Presumably, performance advantages in the central task of ATP synthesis would be under significant evolutionary pressure. Previous modeling studies of the F-ATPase have addressed structural and mechanistic questions about the rotary mechanism (e.g., refs. 11–20), but not the metaissue of the mechanism itself compared with alternatives.

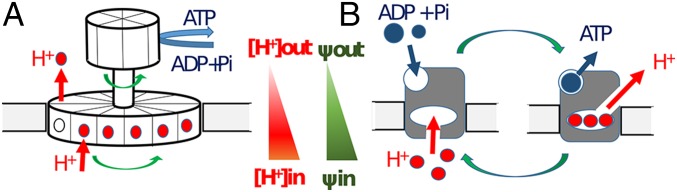
Fig. 1.

ATP synthesis by rotary and alternating-access mechanisms. H⁺ transport across the membrane is driven by transmembrane differences in pH and electric potential ψ. (A) In the rotary mechanism, H⁺ transport drives the rotation of the transmembrane ring, which induces conformational changes that catalyze phosphorylation of ADP. (B) In the alternating-access mechanism, H⁺ binding allosterically produces the conformational changes necessary to catalyze phosphorylation of ADP.

To assess whether the rotary mechanism possesses any intrinsic performance advantage, we constructed a series of kinetic models abstracted from known mechanisms (Fig. 1). Beyond the rotary-based model, we considered a series of alternating-access analogs (Fig. 2), building on the demonstrated capacity for ATP-hydrolyzing transporters to be driven in reverse to synthesize ATP (34, 35). The discrete-state models do not include structural details, but implicitly incorporate conformational transitions; the models embody the basic mechanisms that have been appreciated over decades of biochemical and structural studies (25–30, 36), as well as thermodynamic constraints (36). In our approach, there is no parameter fitting. Instead, the minimax approach, which optimizes parameters for the worst case (37), was adapted to ensure robust performance over a wide range of potential cellular conditions (38) for each mechanism.

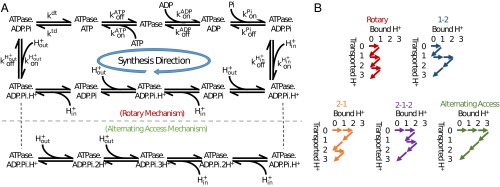
Fig. 2.

Minimalist kinetic modeling of rotary and alternative mechanisms for ATP synthesis. (A) Synthesis cycles for the rotary and basic alternating-access mechanisms, which are (kinetically) distinguished by their orders of proton transport. (B) Other possible mechanisms based on proton transport order for a 3:1 H⁺:ATP stoichiometry. Note that conformational processes, such as rotation, are implicitly included in the binding and chemical processes shown, in a thermodynamically consistent way. Alternative stoichiometries as well as event orders (binding and reaction sequences) were also considered as described in the text and SI Appendix.

When kinetic models of different possible ATP synthesis mechanisms were compared, the data paint a surprisingly clear picture: the rotary mechanism exhibits superior performance over a broad range of potentially physiological and pathological conditions, particularly in low-energy conditions. Although the complexity of the rotary mechanism may appear unnecessary, our findings suggest that the elaborate mechanism may have resulted from positive selection for significant kinetic advantage, especially under adverse conditions.

We used an exact closed-form nonequilibrium steady-state (NESS) solution for an arbitrary chemical cycle, to understand why the rotary mechanism is faster than other possible alternatives. The exact NESS solution makes transparent the dependence of rate on the numerous FE difference terms between pairs of states.

Additional analysis sheds light on contradictory reports on the “kinetic equivalence” of different components of the driving proton-motive force (pmf) (39–46): should the synthesis rate be sensitive to whether the pmf is generated by a pH difference or transmembrane potential difference? We show that kinetic behavior is approximately equivalent under most physiological conditions, but that variant conditions can clearly exhibit nonequivalence.

Models and Thermodynamics of ATP Synthesis

A key differentiating characteristic of the rotary mechanism compared with the basic alternating-access mechanism, for ATP synthesis, is the order of proton binding and transport. See Figs. 1 and 2A. In the rotary mechanism, protons bind to the membrane-spanning subunit of the ATP synthase facing the lower pH/higher proton concentration side (“in”-side) of the membrane, and are transported across the membrane (to the “out”-side) one at a time (8). In contrast, in the basic alternating-access mechanism (Figs. 1 and 2A), multiple protons bind to the low pH side of the ATPase and are transported across the membrane simultaneously (47). For the analysis below, we also consider the remaining possible event orderings comprising other putative alternating-access mechanisms for a 3:1 H⁺:ATP stoichiometry (Fig. 2B), building on the demonstrated capacity for ATP-hydrolyzing transporters to be driven in reverse to synthesize ATP (34, 35). In SI Appendix, analysis of 4:1 stoichiometry is given, yielding similar results. Based on the vast diversity of known passive and driven alternating-access transporters (47), it appears likely that at least some of the mechanisms we study could have evolved. Indeed, before the evolution of the rotary mechanism, some alternative must have been used for ATP synthesis.

The kinetics of the rotary and other possible mechanisms coupling proton transport to ATP synthesis can be analyzed via the kinetic cycles shown in Fig. 2 and the standard master equation as described in SI Appendix. We use standard thermodynamic definitions used in bioenergetic descriptions of ATP synthase (35): the proton motive force,

$$\text{pmf}=-F\mathrm{\Delta }\psi +2.3RT\mathrm{\Delta }\text{pH},$$ [1]

where $\mathrm{\Delta }\psi ={\psi }_{\text{out}}-{\psi }_{\text{in}}$ is the electrostatic potential across the membrane, $\mathrm{\Delta }$ pH = pH_out − pH_in is the pH difference across the membrane, F is the Faraday constant, R is the gas constant, and T is the temperature. Note that both terms in Eq. 1 are positive under typical synthesis conditions: both components of pmf tend to drive proton transport. The driving potential is as follows:

$$\mathrm{\Delta }{G}_{\text{driv}}=n\cdot \text{pmf}-\mathrm{\Delta }{G}_{\text{ATP}},$$ [2]

where n is the number of protons transported per ATP synthesized, and $\mathrm{\Delta }{G}_{\text{ATP}}$ is the energy required for ATP synthesis. The $n=3$ choice is approximately representative of Escherichia coli and animal mitochondria ATP synthase (48). Results are qualitatively similar for other stoichiometries and event orders (reaction sequences), as described in the text and SI Appendix.

Results

Rotary Mechanism Is Faster Across a Diverse Range of Conditions: A Potential Evolutionary Advantage.

The rotary mechanism was found to be faster than the other possible alternative ATP synthesis mechanisms (Fig. 2) over a wide range of operating conditions, which specify the driving potential $\mathrm{\Delta }{G}_{\text{driv}}$. These conditions consist of substrate concentrations [ATP], [ADP], [Pi], [${\text{H}}_{\text{in}}^{+}$], and [${\text{H}}_{\text{out}}^{+}$], and membrane potential $\mathrm{\Delta }\psi$. The values for these conditions span the range of values reported in the literature (48); see SI Appendix for details.

We systematically and extensively tested the sensitivity of our results to model assumptions as shown in Fig. 3A. A brief description of the sensitivity analysis follows, with a more detailed description in SI Appendix. The model assumptions include event order (sequence of binding and reaction events), optimization protocol for kinetic parameters, parameter values, and ranges of pH values. In addition to the event order shown in Fig. 2, we tested six other event orders for each mechanism. Our implementation of the minimax approach separately optimizes the parameters for each mechanism, without fitting, to maximize the rate of ATP synthesis under challenging conditions (37, 38). See Methods. Four variations of this protocol based on different characterizations of “challenging conditions” were tested. In addition to the set of parameters determined by the optimization protocol, we tested six different randomly generated sets of parameters, sampled from a uniform distribution in log space, in the vicinity of literature values. We also tested three ranges of values for pH_out. Each set of model assumptions was tested for the full range of operating conditions, and the results were qualitatively similar (Fig. 3A).

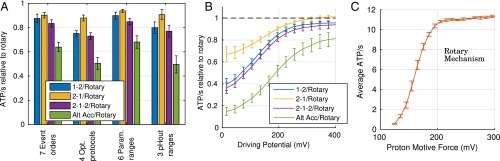
Fig. 3.

Performance of ATP synthesis mechanisms. (A and B) Performance relative to rotary calculated as the geometric average ratio for each mechanism relative to the rotary process, for a wide range of conditions. (A) Varying model assumptions—event order, optimization protocol, parameter values, and pH_out range—show that relative performance is qualitatively insensitive to these assumptions. (B) The advantage of the rotary mechanism is the greatest under challenging conditions (low driving potential $\mathrm{\Delta }{G}_{\text{driv}}$). (C) The average rate of ATP synthesis is quantitatively and qualitatively similar to experimentally reported values when pmf is varied (39, 43), providing further support for these results. Error bars show the standard error of the mean when sampling over a range of conditions. Data for B and C are from the default set of models described in SI Appendix.

The data show the average and condition-dependent advantage of the rotary mechanism. The average advantage is relatively small in some cases, for example, 5–10% compared with the 2–1 mechanism (Fig. 3A). However, as Fig. 3B shows, the rotary model has the greatest advantage under challenging conditions (poor driving potential). The kinetic advantage under challenging conditions may be particularly important for survival, possibly providing the rotary mechanism with a critical evolutionary advantage. It is unknown, moreover, whether the 2–1 mechanism ever evolved.

Even though our procedure does not involve any parameter fitting, the quantitative rate of ATP synthesis calculated by our models (0–12 ATP per s) for the pmf range 100–300 mV Fig. 3C, and the sigmoidal relationship, is surprisingly similar to experimentally reported values: 0–15 ATP per s for E. coli (43) and 0–19 ATP per s for Bacillus PS3 (39). The reasonable quantitative agreement provides support for our use of simplified kinetic models.

A Physically Interpretable Closed-Form NESS Solution.

For an arbitrary single-cycle chemical process, the NESS flow J can be calculated exactly from its kinetic parameters as follows:

$$J=\text{ATP}/\text{s}=\left(1-e^{-\beta \mathrm{\Delta }{G}_{\text{driv}}}\right){\left[{\displaystyle \sum _{i=1}^s{\displaystyle \sum _{j=1}^s\frac{e^{-\beta \left(G_{i-j}-G_i\right)}}{{\alpha }_{i,i+1}}}}\right]}^{-1},$$ [3]

where i and j are state indices, s is the number of steps in the cycle, and $\beta =1/k_{\mathrm{B}}T$, where $k_{\mathrm{B}}$ is the Boltzmann constant. $G_i$ is the “basic” FE for state i, defined in terms of the effective first-order rate constants by $G_{i+1}-G_i=-\left(1/\beta \right)\ln \left({\alpha }_{i,i+1}/{\alpha }_{i+1,i}\right)$ with $G_1\equiv 0$ by convention (49). Here, ${\alpha }_{i,j}=c_i{k}_{ij}$ is the effective first-order rate constant for i-to-j transitions: $c_i=1$ for first-order processes, $c_i=$ [X] when species X binds in the transition, and $k_{ij}$ is the corresponding rate constant. For $i-j<1,\hspace{0.17em}{G}_{i-j}=G_{s-\left(i-j\right)}+\mathrm{\Delta }{G}_{\text{driv}}$, which represents the FE of the state corresponding to $s-\left(i-j\right)$ in the previous cycle. For the ATP synthesis cycle, the flux J is the rate of ATP synthesis, ATP per second, and the number of steps $s=10$ as shown in Fig. 2. Fig. 4 shows an example of the FE landscape for the rotary and basic alternating-access mechanisms for ATP synthesis. Eq. 3, which is equivalent to a previously derived expression (50), provides a precise analytic relationship between kinetics and the FE landscape, in contrast to some prior work (51, 52). See SI Appendix for details.

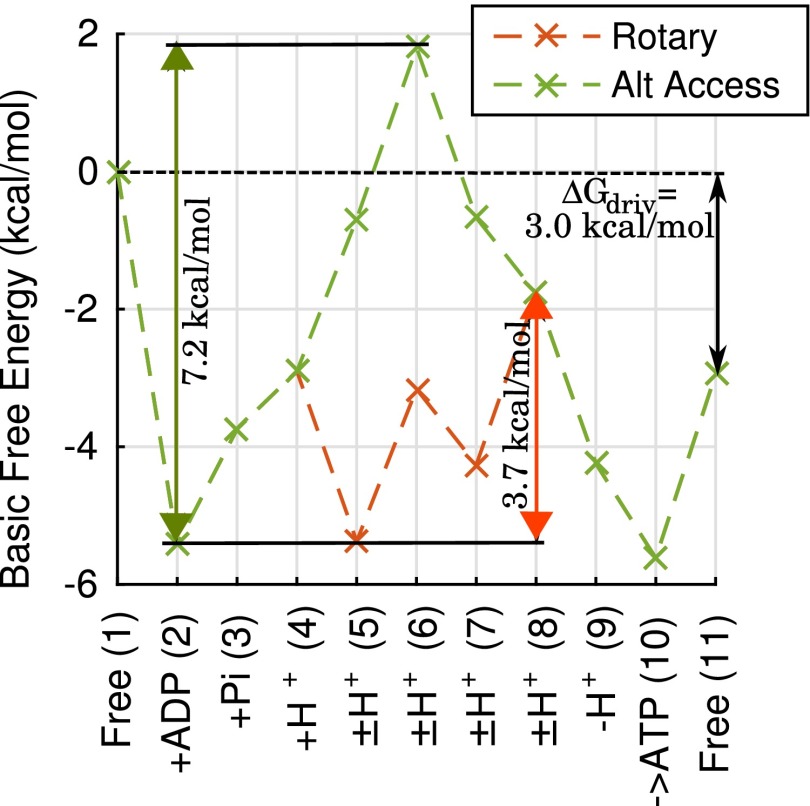
Fig. 4.

Free-energy (FE) landscape effects on ATP synthesis rate: the maximum FE climb. FE landscapes are shown for the rotary and basic alternating-access mechanisms represented in Fig. 2A, with a representative set of kinetic parameters determined by the parameter optimization protocol, and typical physiological conditions, as described in Methods. The specific parameter and condition values are listed in SI Appendix. For the example shown here, the maximum FE climbs are 3.7 and 7.2 kcal/mol for the rotary and alternating-access mechanisms, respectively, with corresponding rates of 9.5 and 2.5 ATP per s.

The form of Eq. 3 permits direct physical interpretation. Because $i\ge i-j$ in the summation, $G_i-G_{i-j}$ is the FE change required to reach state i from $i-j$, and the summation is the cumulative effect of all such FE “climbs.” The exponential term $e^{-\beta \left(G_{i-j}-G_i\right)}$ in the NESS solution, Eq. 3, suggests that the maximum FE climb is likely to be a key determinant of overall cycle flow J assuming variation among α rates is modest (e.g., Fig. 4). However, it is important to note that, under some conditions, the maximum FE climb can be the same for different mechanisms, in which case the contributions of smaller FE climbs must also be considered.

Kinetic Equivalence of pmf Components May Depend on Experimental Conditions.

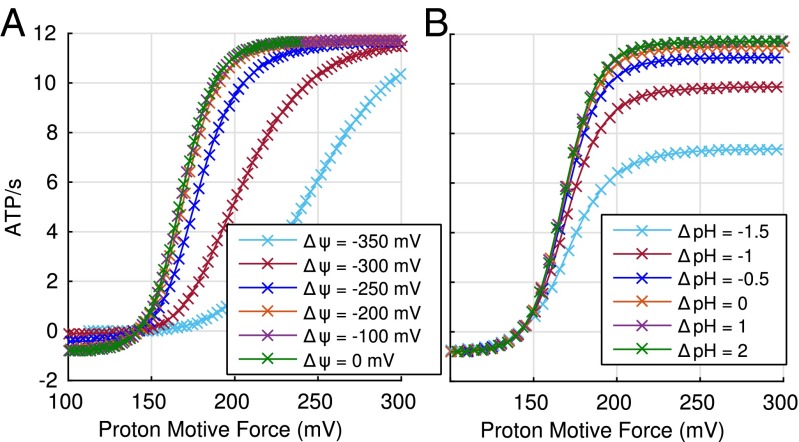
Our analysis suggests that variant experimental conditions likely underlie conflicting evidence regarding kinetic equivalence of pmf components $\mathrm{\Delta }$ pH and $\mathrm{\Delta }\psi$. Some in vitro studies have found that the effect of the two components of pmf are equivalent (39–42), whereas others have concluded that they are not (43–45). There is no inherent reason to expect kinetic equivalence (53) because $\mathrm{\Delta }$ pH and $\mathrm{\Delta }\psi$ affect kinetics through different mechanisms: $\mathrm{\Delta }$ pH through H⁺ concentration, and $\mathrm{\Delta }\psi$ most likely through binding affinity dictated by the thermodynamic cycle constraint, as described in SI Appendix. From Fig. 5, it is evident that the two components of the pmf are not always equivalent in our rotary model. However, for typical physiological conditions, $\mathrm{\Delta }$ pH $>0$ and $\mathrm{\Delta }\psi$ greater than −200 mV, the two components are approximately equivalent (Fig. 5).

Fig. 5.

Sensitivity of apparent kinetic equivalence of pmf components to driving conditions. (A) Synthesis rate as a function of $\mathrm{\Delta }$ pH for different fixed values of membrane potential $\mathrm{\Delta }\psi$. (B) Synthesis rate as a function of $\mathrm{\Delta }\psi$ for different fixed values of $\mathrm{\Delta }$ pH. Condition values, other than those for $\mathrm{\Delta }\psi$ and $\mathrm{\Delta }$ pH, represent typical physiological conditions (48). Parameter values are from the parameter optimization protocol for the rotary mechanism. See Methods. Atypical ranges for $\mathrm{\Delta }$ pH (−4 to 4) and $\mathrm{\Delta }\psi$ (−500 to 500 mV) were used to extend the performance curves sufficiently.

Some studies have suggested that kinetic nonequivalence is due to a minimal transmembrane electrostatic potential required for enzymatic activation (43–46). We do not discount that this may very well be the case, but our analysis (Fig. 5) suggests that differences in in vitro conditions may also contribute to these differing experimental results. Differences in in vitro conditions are evident in the rates of ATP synthesis reported. For example, we found that the reported range of rates for chloroplast varied widely [190–230 ATP per s (45), 0–160 ATP per s (46), and 0–400 ATP per s (40)], strongly suggesting differences in experimental conditions beyond substrate concentration. A clear understanding of kinetic equivalence should lead to a better understanding of the ATP synthase mechanism.

Discussion

Biomolecular Complexity and Maximum FE Climb.

To generalize the relationship between complexity and the FE landscape described above, consider that the alternating-access mechanism may be viewed as a two-step conformational process where the ATPase flips between two possible conformations (47). The rotary mechanism, on the other hand, may be viewed as a multistep process where the conformation changes incrementally with the transport of each proton. In F-ATPases, the number of protons transported varies from 8 to 15 per 360$°$ rotation (yielding three ATPs) depending on cell and organelle type (21–23, 48). The FE change that is possible in each step is limited by conformational and chemical constraints (31, 54). In the case of ATP synthase, it appears that “breaking up” the two-step process into multiple conformational steps reduces the maximum FE climb and thus increases the rate of ATP synthesis.

Nature is replete with similar examples of seemingly excessive biomolecular complexity. The electron transport chain, for example, consists of a four-step process involving four different membrane-embedded protein complexes, where three of the four complexes transport protons across the membrane to generate the electrochemical potential required for ATP synthesis (55). Are all four steps of the process necessary or do they serve to break up the FE landscape so as to reduce the maximum FE climb and accelerate proton transport? The analytic approach presented here could be used to help provide important insights into the evolution of such seemingly unnecessarily complex systems.

Stoichiometry of an ATPase May Reflect a Balance Between Speed and Efficiency.

The varying ATPase stoichiometries found in nature may reflect an evolution-driven balance between speed and efficiency as previously suggested for the chloroplast ATP synthase (56). Increasing n, the H⁺:ATP stoichiometry, can also increase the rate of ATP synthesis, but at the cost of reduced efficiency, that is, more spilled energy ($\mathrm{\Delta }{G}_{\text{driv}}$; Eq. 2). Efficiency is calculated as $\mathrm{\Delta }{G}_{\text{ATP}}/\left(n\cdot \text{pmf}\right)$ for ATP synthases (48), and as $n\cdot \text{pmf}/\mathrm{\Delta }{G}_{\text{ATP}}$ for proton pumps. Here, n is the structural stoichiometry based on the number of proton-binding and catalytic sites. The experimentally measured stoichiometry may be lower due to slippage, that is, ATP hydrolysis without the transport of a full complement of H⁺, and/or leakage of ions across the membrane.

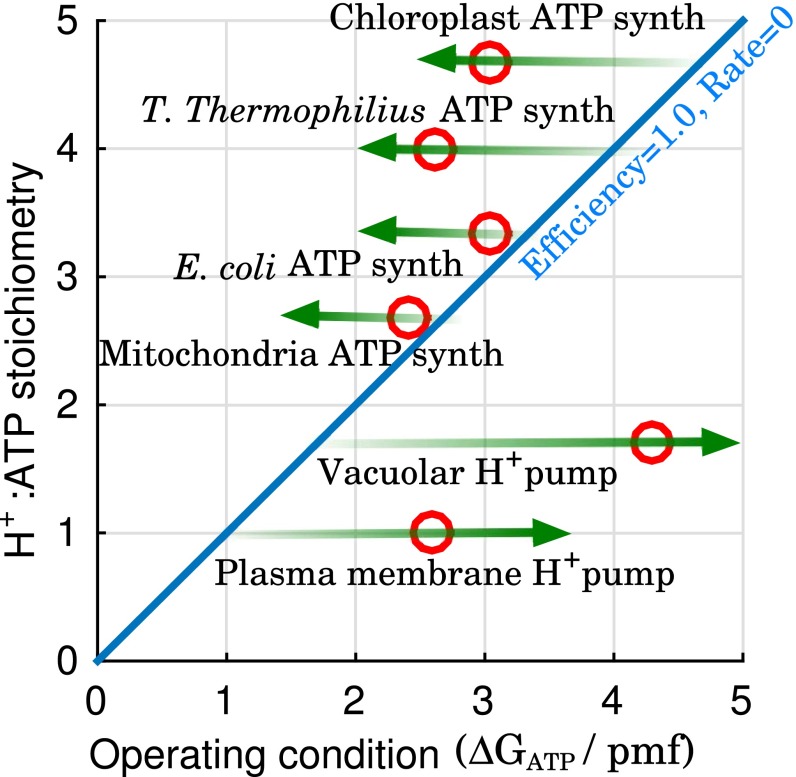
We examined the speed–efficiency trade-off more broadly by considering the range of possible operating conditions for several ATPases based on their stoichiometry (Fig. 6), where the operating condition is characterized by the ratio $\mathrm{\Delta }{G}_{\text{ATP}}$/pmf. Fig. 6 suggests that the stoichiometry for these ATPases are constrained by the range of conditions under which they must be able to operate to ensure survival, that is, $n\ge \min \left(\mathrm{\Delta }{G}_{\text{ATP}}/\text{pmf}\right)$ for ATP synthases and $n\le \max \left(\mathrm{\Delta }{G}_{\text{ATP}}/\text{pmf}\right)$ for H⁺ pumps, as previously suggested for chloroplast (57) and mitochondrial (48) ATP synthase. Beyond that, the actual stoichiometry may be determined by the energy available to drive synthesis or pumping versus the importance of rapidly synthesizing ATP or pumping protons.

Fig. 6.

Stoichiometry effect on ranges of productive operating conditions. Green arrows represent range of productive operating condition for each of the ATPases shown. Red circles represent examples of reported stoichiometry and physiological conditions (42, 48, 60, 61, 63–67). The diagonal represents equilibrium behavior where the efficiency, as defined in the text, is maximum but the rate of synthesis or pumping would vanish. “Mitochondria” refers to animal mitochondria.

Stoichiometry May Explain Why Both Rotary and Alternating-Access Mechanisms Are Used for ATP-Driven Ion Transport.

Plant cell V-ATPases use a rotary mechanism similar to ATP synthase, except operating in reverse (58), whereas the plasma membrane proton pump uses an alternating-access mechanism (59). Why? The answer may lie in the stoichiometry (n) required to generate the necessary driving potential −$\mathrm{\Delta }{G}_{\text{driv}}$, for the physiological conditions under which the pump typically operates. When $n=1$, that is, one proton is transported per ATP hydrolyzed, there is no intrinsic difference in the FE landscape between the two mechanisms, and therefore no theoretical difference in the possible rate of proton pumping. In such a situation, we speculate that evolution is likely to select the simpler alternating-access mechanism with its lower cost of gene replication, translation, and transcription: for example, the plant plasma membrane H⁺-ATPase with $n=1$ (59, 60). On the other hand, when $n>1$, there will be clear differences in the FE landscape (e.g., Fig. 4), and evolution is likely to select the rotary mechanism for its kinetic advantage, for example, the vacuolar H⁺ V-ATPase ($n=2$) (61), and the lemon fruit tonoplast H⁺ V-ATPase ($n>2.7$) (62). A more detailed examination of the ion-pumping mechanisms will be quantitatively explored in a forthcoming work.

Limitations of This Study.

Generally speaking, we prioritized the ability to comprehensively search model space over the inclusion of model details. We subsumed mechanism details into overall kinetic steps: most notably, binding and mechanical activation were combined. In a rotary mechanism, mechanical activation implies rotation, whereas it might imply an inward–outward conformational transition in an alternating-access mechanism. We note that, under fixed conditions, a reduced kinetic model is guaranteed to yield the same maximal flux as a more complicated single cycle, but the performance over multiple conditions generally may differ.

We also approximated each ATP synthesis mechanism with a single cycle as shown in Fig. 2. Although we explored seven different event orders and found the results to be qualitatively insensitive to event order (SI Appendix), it is possible that a single-cycle approximation is not a realistic representation of the ATP synthase process. It excludes, for example, possible slippage subcycles (36). In future work, we will investigate the error introduced by approximating a process consisting of multiple pathways by a single cycle.

Conclusions

The rotary ATP synthase is universally used by living organisms as the primary mechanism for synthesizing ATP. Here, we have tried to address the narrow but apparently novel question of why evolution selected such an elaborate mechanism despite the availability of much simpler alternating-access mechanisms.

After analyzing all possible mechanisms of ATP synthesis, based on a coarse-grained event-ordering picture and a systematic exploration of parameter space, a clear picture emerges: synthesis of ATP by a rotary mechanism—in which protons pass one at a time through the synthase—is more efficient than other mechanisms, particularly under challenging low-energy conditions. It is possible, even likely, that evolution selected the more elaborate rotary mechanism for its kinetic advantage under the same thermodynamic driving potential, compared with simpler alternating-access mechanisms.

To understand why the rotary mechanism is faster, we used a closed-form nonequilibrium steady-state solution for an arbitrary chemical cycle. The physically interpretable solution suggests that the maximum FE climb, which typically involves multiple steps, may be a key determinant of the rate of ATP synthesis. Additional analysis of the rotary mechanism suggests an experimentally pertinent hypothesis—namely, kinetic equivalence of pmf components will depend on experimental conditions.

Methods

Kinetic Models.

The kinetics of the mechanisms shown in Fig. 2 are modeled using the standard master equation. See SI Appendix.

Parameter Optimization.

For a given mechanism, the objective of our parameter optimization protocol is to find a set of rate constants (parameters), without parameter fitting, that perform the best under relatively challenging conditions. Such a model (parameter set) is presumed to optimize survival under the diverse range of conditions almost certainly encountered in physiological and pathological states. It is also important to avoid any parameter fitting, because any such fitting would, by necessity, be to experimental data from the rotary ATP synthase and could therefore bias the results.

The minimax approach was developed with a similar goal in mind (38, 50). Our implementation of minimax consists of two steps. First, for each mechanism, we separately calculate optimal sets of parameters, that is, parameters that maximize synthesis rate, for a large number (>1,000) of randomly generated conditions spanning a range of physiological and pathological states. Within these parameter sets, a relatively lower maximal rate implies that the corresponding conditions are more challenging. Accordingly, we next select 10 parameter sets at the lowest 10th percentile of rates, representative of models that perform the best under relatively challenging conditions. Thus, the models optimized for the more challenging conditions are considered evolutionarily optimized and used to generate the data shown. Fig. 3 also shows, and SI Appendix details, results obtained based on percentiles besides the 10th. The range of values for the conditions and kinetic parameters used for the optimization protocol are described in SI Appendix.