Abstract
Continuous time-series data are frequently distilled into single values and analyzed using discrete statistical methods, underutilizing large datasets. Statistical parametric mapping (SPM) allows hypotheses over the entire spectrum, but consistency with discrete analyses of kinematic data is unclear. We applied SPM to evaluate effect of load and postural demands during reaching on thoracohumeral kinematics in older and young adults, and examined consistency between one-dimensional SPM and discrete analyses of the same dataset. We hypothesized that older adults would choose postures that bring the humerus anterior to the frontal plane (towards flexion) even for low demand tasks, and that SPM would reveal differences persisting over larger temporal portions of the reach. Ten healthy older (72.4±3.1yrs) and 16 young (22.9±2.5yrs) adults reached upward and forward with high and low loads. SPM and discrete t-tests were used to analyze group effects for elevation plane, elevation, and axial rotation joint angles and velocity. Older adults used more positive (anterior) elevation plane and less elevated postures to initiate and terminate reaching (p<0.008), with long duration differences during termination. When reaching upward, differences in elevation persisted over longer temporal periods at midreach for high loads (32–58% of reach) compared to low load (41–45%). SPM and discrete analyses were consistent, but SPM permitted clear identification of temporal periods over which differences persisted, while discrete methods allowed analysis of extracted values, like ROM. This work highlights the utility of SPM to analyze kinematics time series data, and emphasizes importance of task selection when assessing age-related changes in movement.
Keywords: aging, older adults, kinematics, upper limb, statistical parametric mapping, reaching
Introduction
Analysis of continuous time-series data describing movement trajectories during functional tasks is challenging. Frequently continuous data are distilled into single metrics (e.g. peak, mean values) (Ketcham et al., 2002; Hortobágyi et al., 2003; Darling et al., 1989) and analyzed using discrete statistical methods (e.g. t-test, ANOVA), ultimately underutilizing large datasets and introducing bias (Pataky et al., 2013). Statistical parametric mapping (SPM) (Pataky, 2010; 2012; Pataky et al., 2013) was originally developed for neuroimaging to study continuous and bounded data while 1) eliminating regional focus bias (i.e. due to a priori selection of timepoint or extracted value), allowing hypotheses to be proposed over the entire spectrum (Friston et al., 1991; 2007; Worsley et al. 1992; Frackowiak, 2004), and 2) eliminating covariance bias from multiple comparisons by using a family-wise approach for inference of significance. SPM permits statistical results to be presented in their original spatiotemporal data spectra, resulting in a more intuitive context for understanding of temporal or spatial regions where significant differences are detected. SPM has been applied to analyze ground reaction forces (Pataky, 2010), kinematics (Pataky et al., 2013), and muscle forces (Pataky et al., 2013). However, the extent to which one-dimensional SPM and traditional discrete analyses provide consistent information has not been explicitly examined, and SPM has not been applied to interpret upper limb movement, for which multiple kinematics strategies can be used to position the hand when performing tasks throughout the workspace (Buckley et al., 1996; Murray and Johnson, 2004).
Aging is commonly associated with altered movement patterns when performing upper limb tasks (Kozak et al., 2003; Morgan et al., 1994; Tsai and Lin, 2015), but specific influence of task selection on these observations is unclear. Most prior work in the upper limb has evaluated tasks that emphasize precision (e.g. finger pointing) and are unloaded. In these types of tasks, older adults use longer movement times with lower peak velocities and increased secondary (i.e. corrective) movements when reaching to a target (Ketcham et al., 2002; Hortobágyi et al., 2003; Darling et al., 1989; Morgan et al., 1994). These movement strategies have been attributed to loss of certainty (e.g. movement jerk) (Morgan et al., 1994), difficulty modulating forces (Ketcham et al., 2002), and altered muscle activation patterns (Hortobágyi et al., 2003; Darling et al., 1989). However, many daily tasks require load management while reaching, with less emphasis on precision. Tasks representing daily activities are critical for understanding meaningful functional declines associated with aging and are understudied (Landers et al., 2001; Narici and Maffulli, 2010). Evidence suggests that adequate upper limb strength and modulation of arm stiffness is needed to maintain hand stability when managing load (Trumbower et al., 2009; Perreault et al., 2001; Krutky et al., 2009) and that young adults choose limb postures with the humerus anterior to the thorax to accommodate anticipated loading (Trumbower et al., 2009; Chen et al., 2010). Whether older adults adopt this strategy during functional tasks requiring load management is unknown.
Our goal was to apply SPM to evaluate the effect of load and postural demand on thoracohumeral kinematic trajectories in older adults compared to young adults, and examine consistency between one-dimensional SPM and discrete analyses of these upper limb kinematic data. We hypothesized that older adults would choose postures that bring the humerus anterior to the thorax (toward flexion plane) even for low demand task requirements, and that SPM would reveal differences persisting over larger temporal portions of the reach.
Methods
Participants and Procedures
Ten older adults (6 female/4 male, mean age 72.4±3.1 yrs) and sixteen young adults (9 female/7 male, mean age 22.9±2.5 yrs) participated (Table 1). Participants met inclusion criteria: 1) free of medical condition exacerbated by physical testing; 2) no history of neuromuscular disorder or upper limb injury; and 3) able to stand without assistive devices. The study was approved by Wake Forest Health Sciences Institutional Review Board and all participants provided written informed consent. Participants performed forward and upward seated reaching tasks (table height=0.68 m) with their dominant arm (Figure 1). The load conditions were 0.63 kg (low) and 3.84 kg (high); loads were selected to replicate typical household items, including a canister of sugar (low load) and a 1 gallon jug (high load). The low target was a forward reach on the table surface. For the high target, a line from the shoulder to the target formed a 20° angle to the horizontal level of the shoulder. Participants were initially positioned with the arm adducted and elbow flexed 90° to set the hand position. After hand placement, movement was unconstrained. Participants reached to the target (defined as 50% of movement) at a distance 80% of forearm length, then returned to the starting hand position. Tasks were randomized to avoid possible ordering effects; all trials for a single task condition were completed before beginning the next condition. Participants were asked to complete tasks at a self-selected comfortable speed. The torso was firmly restrained with a chest strap to a chair reclined 10° from vertical, and wrist movement was restricted with a brace. Three trials were recorded for each task with 60 s of rest between trials and 2 min rest between tasks. The second trial of each task was chosen for analysis.
Table 1.
Participant demographic information.
| Age (yrs) | Height (cm) | Weight (kg) | Total arm length (cm) | Forearm length (cm) | ||
|---|---|---|---|---|---|---|
| Young adults | Female | 21.8 ± 2.1 | 167.3 ± 5.2 | 62.1 ± 8.7 | 53.8 ± 2.3 | 25.3 ± 1.3 |
| Male | 24.0 ± 2.7 | 181.1 ± 8.8 | 84.2 ± 11.4 | 59.0 ± 3.8 | 28.1 ± 1.5 | |
| All | 22.9 ± 2.5 | 173.0 ± 9.9 | 72.0 ± 14.9 | 56.2 ± 3.9 | 26.5 ± 2.0 | |
|
| ||||||
| Older adults | Female | 72.0 ± 4.0 | 161.7 ± 4.4 | 72.0 ± 13.6 | 52.7 ± 2.6 | 24.2 ± 1.5 |
| Male | 73.0 ± 0.8 | 176.8 ± 6.3 | 82.4 ± 5.7 | 57.0 ± 3.6 | 27.3 ± 1.7 | |
| All | 72.4 ± 3.1 | 167.8 ± 9.2 | 76.2 ± 11.9 | 54.4 ± 3.6 | 25.4 ± 2.2 | |
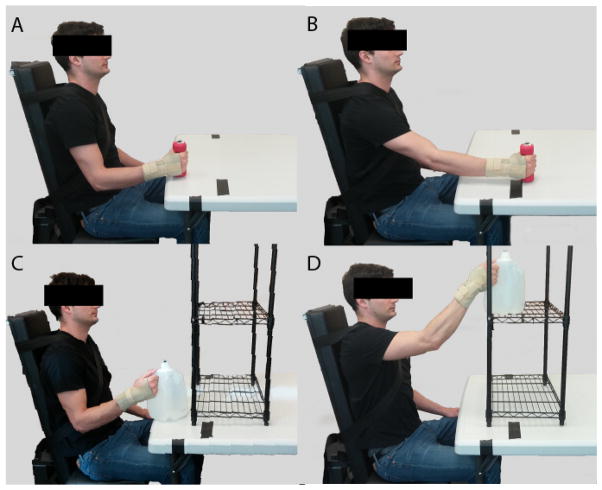
Figure 1.
Experimental setup for forward (A, B) and upward (C, D) reach tasks.
Forward reach (low load (0.63kg) shown) began with the arm adducted and elbow flexed 90° (0% of movement) (A), reached forward to 80% forearm length (50% of movement) (B), then returned to the starting position (100% of movement). Upward reach (high load (3.84kg) shown) began in the same starting posture (0% movement) (C), reached to a target 20° above the shoulder (50% movement) (D), then returned to the starting posture (100% movement).
Instrumentation
Kinematics were recorded at 200 Hz using 7 Hawk cameras (Motion Analysis Corporation, Santa Rosa, CA) tracking 1 cm retroreflective markers placed on 13 anatomical landmarks (Table 2). Data were post-processed and smoothed with a 6 Hz filter (Cortex, Motion Analysis Corporation, Santa Rosa, CA). Prior to performing tasks, a static recording was obtained for use in marker definition and model scaling.
Table 2.
Locations of retroreflective markers.
| Marker | Location |
|---|---|
| 1 | 7th cervical vertebra |
| 2 | Suprasternal notch |
| 3 | Xiphoid process |
| 4 | Acromion |
| 5 | Mid upper arm |
| 6 | Medial humeral epicondyle |
| 7 | Lateral humeral epicondyle |
| 8 | Mid forearm |
| 9 | Radial styloid |
| 10 | Ulnar styloid |
| 11 | 2nd metacarpal phalangeal joint |
| 12 | 5th metacarpal phalangeal joint |
| 13 | Load held in the hand |
Joint postures were extracted from marker locations using an upper limb musculoskeletal model (Holzbaur et al., 2005; Saul et al., 2015a) implemented in OpenSim (Delp et al., 2007; v3.1). Shoulder posture was defined using three degrees of freedom (DOF) (elevation plane, thoracohumeral elevation, axial rotation). To ensure consistency and clarity, thoracohumeral kinematics were calculated according to International Society of Biomechanics (ISB) standards for axis definition and order of rotation (Wu et al., 2005) (Figure 2). Briefly, positive elevation in the +90° elevation plane corresponds with forward flexion, while positive elevation in the 0° elevation plane corresponds with abduction; positive axial rotation corresponds with internal rotation (Wu et al., 2005). Scaling was conducted such that distances between the model’s virtual markers matched distances between experimental markers for each participant (Delp et al., 2007). Inverse kinematic analyses were used to obtain joint angle trajectories corresponding to recorded marker positions. Joint angle trajectories for each task were filtered using a zero-phase digital moving window filter with a custom Matlab program using the filtfilt function (The MathWorks, Inc., Natick, MA).
Figure 2.
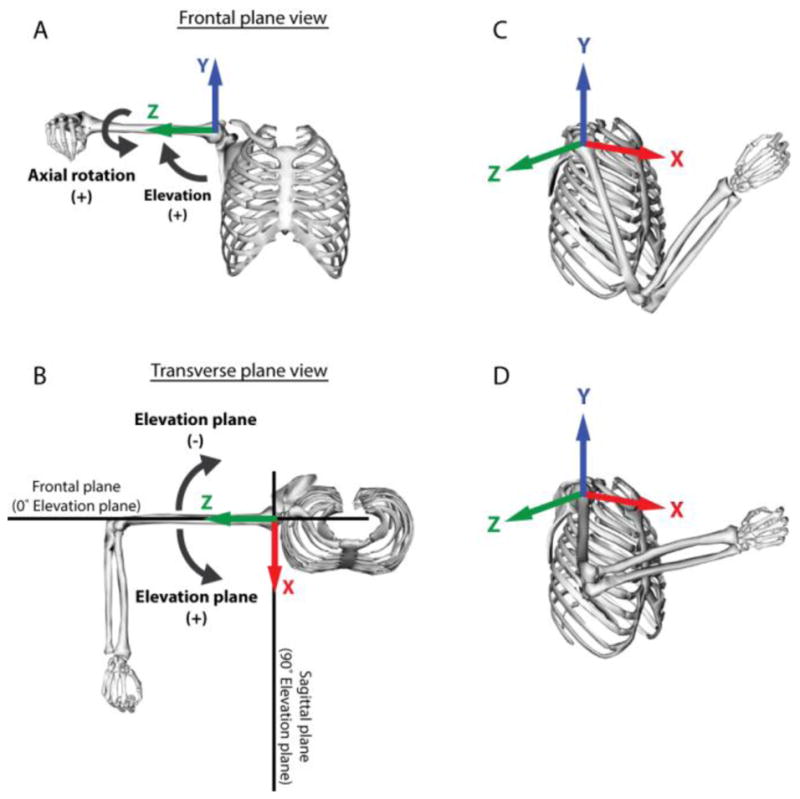
Degrees of freedom and rotation axes are defined according to the ISB standards (Wu et al., 2005). Shoulder degrees of freedom are for thoracohumeral motion, including thoracohumeral elevation (A), elevation plane (B), and axial rotation (A). 0° of thoracohumeral elevation is defined when the long axis of the humerus is aligned with Y axis (A), and 90° is when long axis of the humerus is aligned with Z axis (shown)., 0° elevation plane is defined when the humerus is aligned with frontal plane (B). Positive thoracohumeral elevation moves the humerus away from the thorax, positive elevation plane moves the humerus anterior (towards flexion (saggital) plane at 90°), and positive axial rotation is internal rotation. Because of the kinematic redundancy of the upper limb, it is possible to place the hand at a reach target using multiple kinematic strategies, including using an anterior strategy bringing the humerus towards the flexion plane (C) or with the humerus elevated more laterally (D).
Joint velocity was computed from joint angle trajectories using a three-point finite difference method. Minimum and maximum values for posture and velocity were identified for each DOF. Range of motion (ROM) for each DOF was calculated by subtracting minimum joint angle from maximum joint angle. To account for potential differences in self-selected speed across participants, joint angle trajectories were normalized by total movement time for SPM analysis and are represented as percentage of total time to task completion; 50% represents hand at the target.
Statistical Methods
A custom Matlab program was used to conduct one-dimensional SPM analyses incorporating SPM1D functions described by Pataky (2014). To conduct SPM t-tests on continuous joint angle trajectories, the experimental outcomes matrix Y in the general linear model formulation (i.e. Y = Xβ + ε) was defined as an N × K matrix where N and K are the number of subjects and number of time points per subject, respectively. Since we normalized the temporal axis to percentage of movement, 100 temporal data points were extracted for each subject, resulting in a 26 × 100 matrix. With 16 young (n1=16) and 10 older subjects (n2=10), the design matrix X was composed of 1 elements and 0 elements with the number of entries of each corresponding to the number of subjects per group: .β are parameters corresponding to each of the terms in X. The error term (ε) was N × 1 in dimension, representing precision of floating point numbers. To solve the general linear model equations, a set of estimated parameters β̂ that best fit the data were used; this was required because the number of experimental outcomes is typically higher than the number of parameters, resulting in a set of unsolvable simultaneous equations (Kiebel and Holmes, 2004). The least square method was used to estimate β̂. To calculate the least square estimates β̂, SPM1D used Matlab’s Moore-Penrose pseudo-inverse function. For formulation of the two-sample t-test, we tested the null hypothesis cT β = 0 where c =[1, −1]T, β = [μ1, μ2]T represented equal means between groups. The t-statistic was calculated by the student’s t-distribution where σ̂2 is calculated from the residual sum-of-squares divided by the degrees of freedom (DOF) (Kiebel and Holmes, 2004). With the null hypothesis cT β = 0, the t-statistic can be further simplified to . SPM1D employs the single inference procedure to evaluate significance of temporal clusters, or regions of contiguous values for which the test statistic exceeds the significance threshold. In this method, as smoothness of a random field increases, so does the breadth of temporal clusters, and very broad/high clusters are less expected to emerge. A single p-value is reported for each observed cluster above the threshold, interpreted as probability that the observed cluster resulted from a smooth random process (Pataky, 2012). The critical threshold for significance was computed using the Bonferroni correction (1), with family-wise significance level of PFWE=0.05:
| (1) |
Since wrist motion was restrained, the number of correlated DOF available for limb movement, γ, equaled 5 (elevation plane, elevation, axial rotation, elbow flexion, forearm rotation), resulting in a critical threshold of p≤0.0102.
Discrete t-tests with unequal variances were conducted between groups for minimum, maximum, and ROM of thoracohumeral joint angles during each task by load combination to compare against analogous SPM t-test analyses. To evaluate whether each group modified joint postures when load demand was increased, t-tests with equal variances were conducted for minimum, maximum, and ROM of thoracohumeral joint angles, comparing load conditions for each group by task combination.
Results
Effects of Age
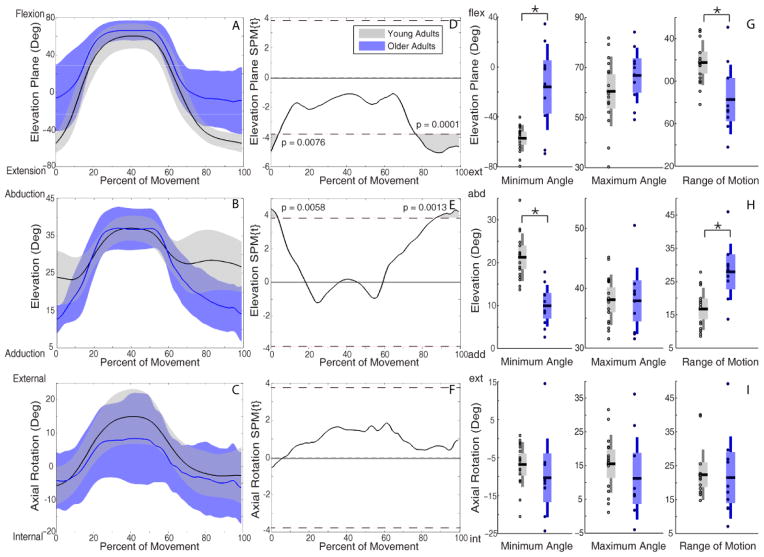
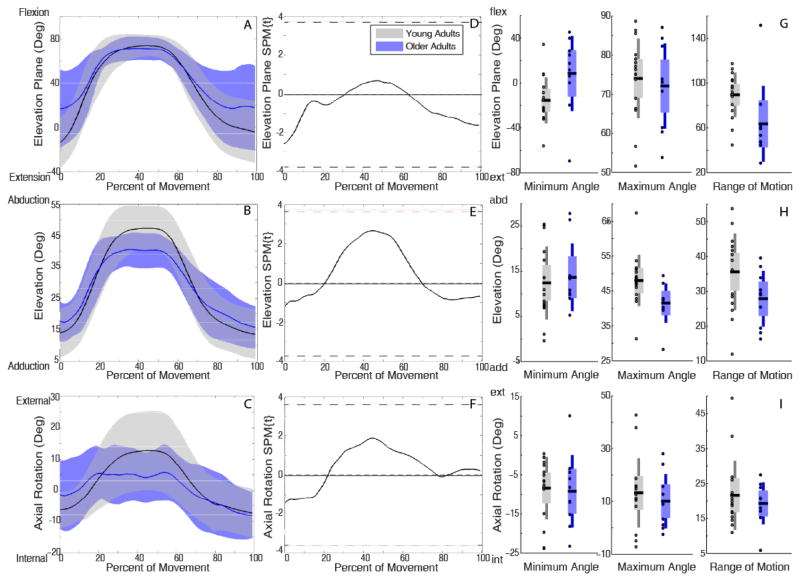
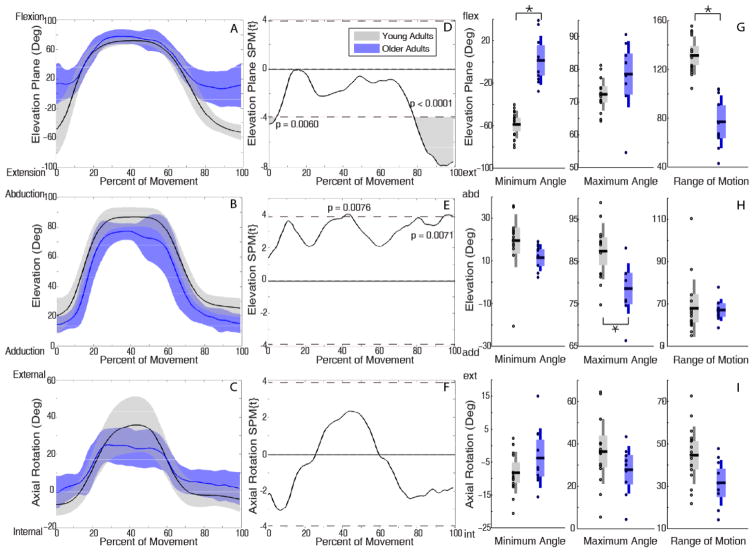
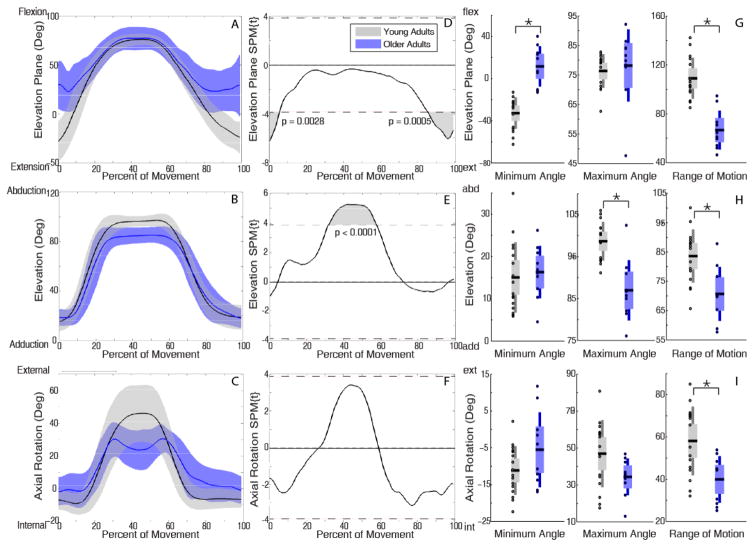
Older adults performed tasks with more positive elevation plane (e.g. toward flexion) and less elevated posture (humerus closer to thorax) than young adults briefly at the beginning and more extensively at the end of reaching. For forward reach with low load, older adults had significantly more positive elevation plane during 0–4% (p=0.008) and 76%–100% (p=0.0001) of movement (Figure 3D), and lower elevation during 0–4% (p=0.006) and 87%–100% (p=0.001) of movement (Figure 3E). During forward reach with high load, SPM did not detect any significant differences (Figure 4). During upward reaches, SPM analyses showed older adults used more positive elevation plane at the beginning and, more extensively, at the end of the movement, but were less elevated when the hand was near the target (~50%) (Figure 4E, 5E). Specifically, for upward reach with low load, older adults had more positive elevation plane during 0–4% (p=0.006) and 78%–100% (p<0.0001) of movement (Figure 5D) and lower elevation at 41%–45% (p=0.008) and 94%–100% (p=0.007) of movement (Figure 5E). The marked difference in elevation was more temporally pronounced for upward reach with high load, where older adults were less elevated during 32%–58% of movement as the load approached the target (p<0.0001) (Figure 6E). Under this reach condition, they also exhibited more positive elevation plane during 0–6% (p=0.003) and 85%–100% (p=0.0005) of movement (Figure 6D).
Figure 3.
Kinematic trajectories of forward reach with low load. Mean (solid line) ± SD (shaded band) for elevation plane (A), elevation (B), and axial rotation (C), with young adults in black and older adults in blue. SPM calculated t-value trajectories for elevation plane (D), elevation (E), and axial rotation (F) comparing age groups. Shaded grey areas indicate significant differences, with dotted line indicating the significance threshold (pFWE =0.05). SPM two sample t-tests indicate that older adults used significantly greater positive (more anterior) elevation plane and less elevated postures during the initiation and completion of the movements. Discrete two sample t-tests (G, H, I) showed consistent results. Older adults had smaller elevation plane ROM (G) and higher elevation ROM (H).
Figure 4.
Kinematic trajectories of forward reach with high load. Mean (solid line) ± SD (shaded band) for elevation plane (A), elevation (B), and axial rotation (C) with young adults in black and older adults in blue. SPM calculated t-value trajectories for elevation plane (D), elevation (E), and axial rotation (F) comparing age groups. Shaded grey areas indicate significant differences, with dotted line indicating the significance threshold (pFWE =0.05). No significant kinematic differences were identified between young and older adults in either SPM or discrete two sample t-tests (G,H,I).
Figure 5.
Kinematic trajectories of upward reach with low load. Mean (solid line) ± SD (shaded band) for elevation plane (A), elevation (B), and axial rotation (C) with young adults in black and older adults in blue. SPM calculated t-value trajectories for elevation plane (D), elevation (E), and axial rotation (F) comparing age groups. Shaded grey areas indicate significant differences, with dotted line indicating the significance threshold (pFWE =0.05). SPM two sample t-tests indicated older adults used significantly more anterior elevation plane (A) and less elevated (B) postures during movement initiation and completion, and reduced elevation during 41%–45% of the movement. Discrete two sample t-tests showed consistent results (G, H, I). Older adults used smaller elevation plane ROM (G).
Figure 6.
Kinematic trajectories of upward reach with high load. Mean (solid line) ± SD (shaded band) for elevation plane (A), elevation (B), and axial rotation (C) with young adults in black and older adults in blue. SPM calculated t-value trajectories for elevation plane (D), elevation (E), and axial rotation (F) comparing age groups. Shaded grey areas indicated significant differences, with dotted line indicating the significance threshold (pFWE =0.05). Older adults used significantly more anterior elevation plane postures during movement initiation and completion (A), and significantly less elevated postures during 32%–58% of the movement (B). Discrete two sample t-tests showed consistent results (G, H, I). Older adults used smaller elevation plane ROM (G), smaller elevation ROM (H), and smaller axial rotation ROM (I).
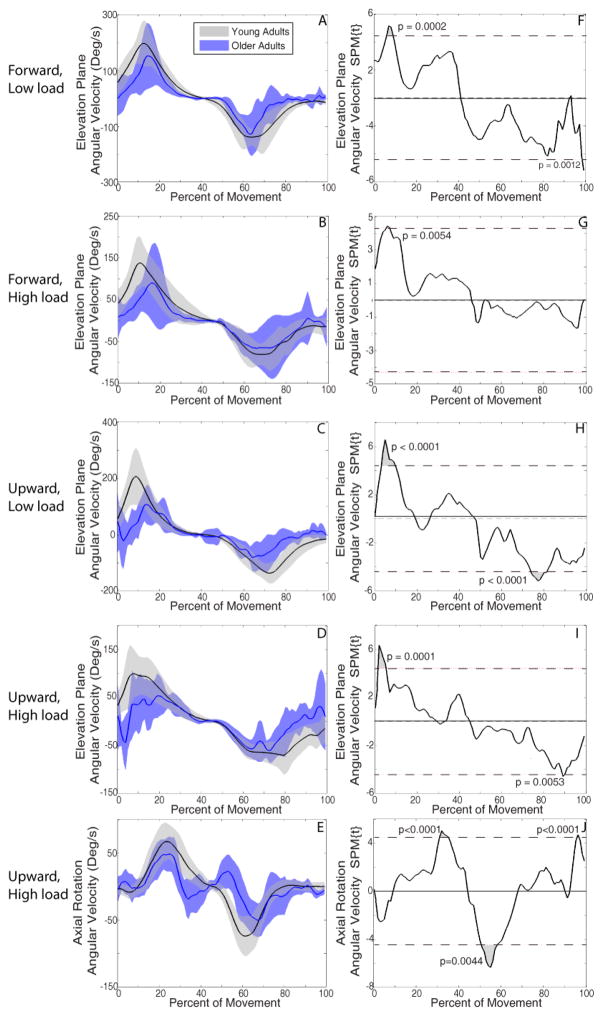
SPM analyses demonstrated lower joint velocities for older adults compared to young adults during the periods of peak velocity (Figure 7). For forward reaches with low load, angular velocity was significantly lower for older adults with regard to elevation plane during 6%–9% (p=0.0002) and 99%–100% (p=0.001) of movement compared to young adults (Figure 7F). Similarly, during forward reaches with high load, angular velocity for elevation plane was lower for older adults during 6%–7% of movement (p=0.005) (Figure 7G).
Figure 7.
Elevation plane and axial rotation angular velocity. Mean (solid line) ± SD (shaded band) of elevation plane angular velocity during forward/low load (A), forward/high load (B), upward/low load (C), upward/high load (D) and axial rotation upward/high load (E) reaches. SPM calculated t-value trajectories of elevation plane angular velocity during forward/low load (F), forward/high load (G), upward/low load (H), upward/high load (I) reaches, and axial rotation angular velocity during upward/high load (J) reach after SPM1D two sample t-tests. Shaded grey areas indicate significant differences, with dotted line indicating the significance threshold (pFWE =0.05). Older adults had more flattened velocity profiles, lower peak angular velocities, and less smooth movements as task demands increased compared to young adults across all task combinations (A–E).
For upward reaches with low load, older adults used lower angular velocity for elevation plane during 3%–10% (p<0.0001) and 74% –81% (p<0.0001) of movement (Figure 7H). For upward reaches with high load, older adults used lower angular velocity for elevation plane during 2%–5% (p=0.0001) and 89% (p=0.005) of movement (Figure 7I), lower axial rotation angular velocity during 31%–35% (p<0.0001) and 56% –58% (p=0.004) of the movement, and higher axial rotation angular velocity at 96%–97% (p<0.0001) of the movement (Figure 7J).
Effects of Load
Older adults did not significantly alter their posture when load was increased for either forward or upward reaches. However, young adults modified their postures to a more positive (i.e. toward flexion) elevation plane when load demand was increased. Specifically, for young adults during forward reaches, high load resulted in reduced elevation plane ROM (p=0.0006) with greater positive minimum (p<0.0001) and maximum (p=0.004) angles which position the humerus in front of the thorax. However, young adults had increased elevation ROM (p<0.0001) during high load demand tasks, exhibiting more positive maximum elevation angle (p<0.0001) and less positive minimum elevation angle with high load (p=0.001). Similarly, for upward reaches with high load, young adults adopted a posture with the humerus more anterior to the thorax, including more positive minimum elevation plane (p<0.0001) and smaller elevation plane ROM (p=0.0005), and a more positive maximum elevation (p<0.0001) with larger elevation ROM (p=0.0006) (Table 3).
Table 3.
Discrete analysis of effect of load for young adult group. Values included for those parameters that reached statistical significance.
| Parameter (°) | Forward reach low load | Forward reach high load | p-value |
|---|---|---|---|
| Min Elevation Plane | −57.1±10.6 | −15.5±20.4 | <0.0001 |
| Max Elevation Plane | 60.4±13.9 | 74.0±10.2 | 0.004 |
| ROM Elevation Pane | 117.5±21.2 | 89.6±19.9 | 0.0006 |
| Min Shoulder Elevation | 21.3±5.6 | 12.4±8.1 | 0.001 |
| Max Shoulder Elevation | 38.1±4.2 | 48.0±7.3 | <0.0001 |
| ROM Shoulder Elevation | 16.8±6.3 | 35.6±11.0 | <0.0001 |
| Parameter (°) | Upward reach low load | Upward reach high load | p-value |
|---|---|---|---|
| Min Elevation Plane | −59.0±13.0 | −32.7±14.9 | <0.0001 |
| ROM Elevation Plane | 131.3±15.7 | 109.1±16.8 | 0.0005 |
| Max Shoulder Elevation | 87.5±6.7 | 98.7±4.6 | <0.0001 |
| ROM Shoulder Elevation | 68.0±13.6 | 83.6±9.1 | 0.0006 |
SPM and Discrete Analyses
Overall SPM and discrete analyses (Table 4) revealed consistent results, although discrete analyses provided information about ROM. SPM is unable to explicitly test for extracted values like ROM. Specifically, discrete analyses found older adults had more positive minimum elevation plane (p=0.004), smaller ROM for elevation plane (p=0.010) (Figure 3G), more positive minimum elevation angle (p<0.0001), and larger elevation ROM (p=0.003) (Figure 3H) during forward reach with low load. SPM revealed movement intervals near movement initiation and termination where significant age effects were observed for both DOFs. Notably, these movement intervals captured minimum shoulder angles, consistent with discrete analyses. During forward reach with high load, neither test detected any significant age effect (Figure 4G,H,I).
Table 4.
Discrete analysis of effect of age for young and older adult groups. Values included for those parameters that reached statistical significance.
| Task | Parameter (°) | Young adults | Old adults | p-value |
|---|---|---|---|---|
| Forward Reach with Low Load | Min elevation plane | −57.06±10.63 | 15.91±34.45 | 0.004 |
| ROM elevation plane | 117.50±21.15 | 82.69±32.70 | 0.010 | |
| Min elevation | 21.30±5.55 | 9.97±4.84 | <0.0001 | |
| ROM elevation | 16.78±6.33 | 27.93±8.45 | 0.003 | |
|
| ||||
| Upward Reach with High Load | Min elevation plane | 58.96±13.00 | 1.36±22.97 | <0.0001 |
| ROM elevation plane | 131.3±15.72 | 77.15±21.62 | <0.0001 | |
| Max elevation | 87.47±6.65 | 78.64±5.95 | 0.002 | |
|
| ||||
| Upward Reach with Low Load | Min elevation angle | 32.73±14.93 | 11.54±19.09 | <0.0001 |
| ROM elevation angle | 109.1±16.81 | 66.66±15.89 | <0.0001 | |
| Max shoulder elevation | 98.65±4.62 | 86.97±7.17 | 0.0004 | |
| ROM shoulder elevation | 83.62±9.07 | 70.68±9.21 | 0.002 | |
| ROM shoulder rotation | 58.12±16.23 | 39.92±11.02 | 0.002 | |
During upward reach with low load, discrete analyses detected that older adults used more positive minimum elevation plane (p<0.0001), smaller elevation plane ROM (p<0.0001) (Figure 5G), and a more positive maximum elevation angle (p=0.002) (Figure 4H). SPM analyses detected significant age effects for elevation plane during movement intervals near initiation and termination of reaching, which also included the smaller minimum angle as detected with discrete analyses. During upward reach with high load, discrete analyses indicated that older adults used greater positive minimum elevation plane (p<0.0001), smaller elevation plane ROM (p<0.0001) (Figure 5G), greater maximum elevation angle (p=0.0004), smaller elevation ROM (p=0.002) (Figure 5H), and smaller axial rotation ROM (p=0.002) (Figure 5I).
Discussion
The current study explicitly compares one-dimensional SPM results to discrete analyses of upper limb reaching under different load and postural demands. The SPM results indicate that older adults use arm postures with more positive elevation plane and less elevation when performing reaches under both low and high postural and load demands. These differences were particularly prevalent during the return portion of reaching for most tasks and when the hand was at the target during upward reaches. During high load conditions, young adults employed a similar strategy to older adults, adopting postures with greater positive elevation plane. During upward reaching, the temporal portion over which kinematic differences between ages were observed was increased. This work highlights importance of task selection when assessing age-related changes in movement, emphasizing that both postural and load demand can amplify movement changes. Notably, this research leverages temporal and spatial information of the full movement recording to elucidate portions of a reaching movement during which kinematic differences may exist by using SPM analysis.
Overall, analyses using discrete t-tests of minimum and maximum angles were consistent with the SPM analysis for regions of movement containing kinematic extrema. However, discrete analysis only addressed differences in peak values, while SPM identified timing and duration of temporal regions where differences occurred. For example, during upward reaches, discrete analyses simply detected lower elevation for older adults for both load conditions, while SPM identified markedly different temporal scopes, indicating that higher load induced a larger temporal change in thoracohumeral elevation. Kinematic differences in small windows may play a less important role in movement than differences over larger windows. However, discrete tests will only identify differences in minimum or maximum extracted values, regardless of the time span over which differences exist. The temporal regions identified by SPM where differences persist represent new targets for future analyses.
SPM has some limitations as a method for kinematic analysis. Extracted ROM values were not possible to test using SPM, although ROM differences were sometimes detected by discrete analyses. ROM is obtained by subtraction of two scalars extracted from the original dataset without regard to time of occurrence. If ROM is a measure of interest, as in clinical evaluation, separate discrete analyses should be performed. Other demonstrations of SPM have revealed inconsistent results between discrete and SPM methods (Pataky et al., 2013), attributed to post-hoc regional focus bias and inter-component covariance bias present in discrete methods. Additionally, data sets with temporal shifts in kinematics between groups may confound interpretation of SPM and could lead to additional differences between SPM and discrete analyses, which deserves additional exploration in future work. In the current study, both groups performed tasks with similar timing of minimum/maximum joint angles during the task.
The more positive (anterior) elevation plane used by older adults is consistent with previous findings that anterior humerus postures provided participants with increased dexterity and greater limb stiffness during unloaded tasks in young adults (Trumbower et al., 2009; Perreault et al., 2001; Chen et al., 2010). Although limb stiffness and stability were not directly measured here, the choice of anterior postures, even under low loads, may reflect older adults’ desire to position the limb beneath the load to provide support and stability regardless of load demand. While declined force production ability and altered muscle activation patterns may contribute to this strategy, it is also possible that older adults preserve the ability to respond to load requirement by increasing co-contraction and limb stiffness without the need to alter posture (Hogan, 1985; Perreault et al., 2001; Krutky et al., 2009). In contrast, young adults were able to compensate for increased task demand as needed, and did not use a posture with greater elevation plane at lower loads, but did adopt this stabilizing posture when load was increased. This is consistent with reports that young adults exhibit better postural control by integrating somatosensory, vestibular, and visual information (Johansson and Magusson; 1991; Rankin, 2000). Although outside the scope of the current study, interactions between the three independent variables (group, task, load) should be explored in future studies.
The altered kinematics we observed may be a result of shoulder weakness often reported in older adults. Numerous studies provide evidence of reduced shoulder strength (e.g. Hughes et al., 1999b) and muscle volume (e.g. Holzbaur et al., 2007a,b; Saul et al., 2015b; Vidt et al. 2012) with age. Age-related losses at the shoulder are more profound than at other upper limb joints (Vidt et al. 2012), and shoulder muscle volume and strength are better predictors of functional arm strength than that of other upper limb joints (Daly et al., 2013). Hughes et al. (1999a) found declines in isometric strength ratio (agonist/antagonist) for flexion and abduction at 90° elevation with increasing decade of age beginning at age 20. They concluded that aging has a profound effect on the shoulder when subjects are in an elevated posture. This is consistent with our findings that older adults were more challenged at higher postural demands during the time period that the arm was maximally elevated (~50%). In this study older adults also exhibited lower magnitude joint velocities at movement intervals near peak velocities, suggesting older adults’ inability to propel their limbs as quickly as young adults under the same absolute task demands.
SPM analyses revealed kinematic differences near the termination of the movement (~80–100% of the task) which may indicate an age-associated change in movement control strategy. Ketcham et al. (2002) and Morgan et al. (1994) observed that older adults’ movement patterns are characterized by shortened acceleration phase and prolonged deceleration phase moving to the target for precision tasks, suggesting that terminating some tasks may be challenging. Reaching is a shoulder-centered movement (Dutta et al., 2013), whereby the muscle torque generated by the shoulder is primarily responsible for execution of the movement while the elbow and wrist torques are secondarily responsible for hand placement (Dounskaia, 2005; Galloway and Koshland, 2002). However, age has been shown to alter the shoulder-centered strategy, leading to Dutta et al.’s (2013) observation of increased variability in hand placement at the initiation and termination of a reaching task. In the current study, differences were marked during the termination of the task as the load was lowered; distinguishing the strategies employed during lowering of a load from height deserves attention in future work.
There are limitations to this study. Small groups were evaluated, limiting generalization to a larger group or other ages. Muscle activation patterns were not evaluated. Alterations to activation have been associated with force production variability, movement slowing, and stability changes (Hortobágyi et al., 2003; Darling et al., 1989; Hogan, 1985; Perreault et al., 2001; Krutky et al., 2009). Future work to evaluate muscle coordination would illuminate whether co-contraction or other altered activation is observed under these conditions. Tasks studied here do not span the upper limb workspace and represented a subset of functional tasks. Future studies are warranted on multi-plane movements under various postural and load conditions. Older adults may be able to accomplish tasks under loads greater than those examined here. For example, older adults in one study completed one repetition maximum exercises with load up to 60.4 kg during a compound row prior to resistance training (Daly et al., 2013). Using maximum loads during reaching tasks may provide insight into older adults’ movement strategies for very high loads. In this work, we used Bonferroni correction to control family-wise error rate. However, Bonferroni correction is the most conservative method for determining a significance threshold, which may increase likelihood of type II error. One-dimensional SPM is susceptible to underestimation of temporal correlation (Pataky et al., 2013). A multivariate SPM analysis method that retains correlations among DOFs would analyze joint angle values simultaneously in the form of vectors, but would require post-hoc analysis analogous to the one-dimensional analyses performed here to interpret the source of differences (e.g. which joint angle). Hotelling’s T2 test is the multivariate analog of the t-test in univariate statistics and is useful for comparing multivariate means of two groups (Hotelling, 1931; Pataky et al., 2013). Other methods exist for analysis of continuous data, including functional data analyses (FDA) (Ramsay and Silverman, 2002; 2005), and these methods should also be explored for application to biomechanical data.
We conclude that application of one-dimensional SPM to upper limb reaching tasks revealed results consistent with discrete analyses while minimizing the required number of statistical tests. Further, we demonstrate that SPM holds the advantage of presenting results in the original time spectrum, allowing for more intuitive interpretation of movement kinematics to efficiently distinguish between groups and tasks. We conclude that kinematic differences between young and older adults are influenced by loading conditions and target positions; the return portion of reaching is affected for a substantial temporal period, even under low load and target, while mid-reach is affected when reaching upward. Older adults consistently maintained more positive elevation plane and lower thoracohumeral elevation, placing their arms underneath the load to obtain more support, suggesting muscle strength may be a factor. Older adults used similar postural choices regardless of load, while increased postural demand led to more marked differences between age groups, especially with the hand at the target. This work highlights the utility of SPM and suggests that experimental designs should carefully consider influence of load or postural demand when choosing tasks.
Acknowledgments
We acknowledge support from National Science Foundation CBET 1405246, Wake Forest University Science Research and Cross-Campus Collaboration Funds, WFU Claude Pepper Older Americans Independence Center, National Institutes for Aging P30 AG021332; Dr. Melissa Daly for data collection; Dr. Todd Pataky for guidance with regard to SPM; and Dr. Alyson Wilson for discussions of statistical analyses.
Footnotes
Conflict of interest
The authors have no conflicts of interest to declare.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Buckley MA, Yardley A, Johnson GR, Carus DA. Dynamics of the upper limb during performance of the tasks of everyday living--a review of the current knowledge base. Proc Inst Mech Eng H. 1996;210:241–247. doi: 10.1243/PIME_PROC_1996_210_420_02. [DOI] [PubMed] [Google Scholar]
- Chen W, Xiong C, Huang X, Sun R, Xiong Y. Kinematic analysis and dexterity evaluation of upper extremity in activities of daily living. Gait Posture. 2010;32:475–81. doi: 10.1016/j.gaitpost.2010.07.005. [DOI] [PubMed] [Google Scholar]
- Clark BC, Manini TM. Functional consequences of sarcopenia and dynapenia in the elderly. Curr Opin Clin Nutr Metab Care. 2010;13:271–6. doi: 10.1097/MCO.0b013e328337819e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daly M, Vidt ME, Eggebeen JD, Simpson WG, Miller ME, Marsh AP, Saul KR. Upper extremity muscle volumes and functional strength after resistance training in older adults. J Aging Phys Act. 2013;21:186–207. doi: 10.1123/japa.21.2.186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darling WG, Cooke JD, Brown SH. Control of simple arm movements in elderly humans. Neurobiol Aging. 1989;10:149–57. doi: 10.1016/0197-4580(89)90024-9. [DOI] [PubMed] [Google Scholar]
- Delp SL, Anderson FC, Arnold AS, Loan P, Habib A, John CT, Guendelman E, Thelen DG. OpenSim: open-source software to create and analyze dynamic simulations of movement. IEEE Trans Biomed Eng. 2007;54:1940–50. doi: 10.1109/TBME.2007.901024. [DOI] [PubMed] [Google Scholar]
- Dounskaia N. The internal model and the leading joint hypothesis: implications for control of multi-joint movements. Exp Brain Res. 2005;166:1–16. doi: 10.1007/s00221-005-2339-1. [DOI] [PubMed] [Google Scholar]
- Dutta GG, Freitas SMSF, Scholz JP. Diminished joint coordination with aging leads to more variable hand paths. Hum Mov Sci. 2013;32:768–784. doi: 10.1016/j.humov.2013.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Liddle PF, Frackowiak RS. Comparing functional (PET) images: the assessment of significant change. Journal of Cerebral Blood Flow and Metabolism. 1991;11:690–699. doi: 10.1038/jcbfm.1991.122. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Statistical parametric mapping: the analysis of functional brain images. Amsterdam; Boston: Elsevier/Academic Press; 2007. [Google Scholar]
- Frackowiak RSJ. Human brain function. Amsterdam; Boston: Elsevier Academic Press; 2004. [Google Scholar]
- Galloway JC, Koshland GF. General coordination of shoulder, elbow and wrist dynamics during multijoint arm movements. Exp Brain Res. 2002;142:163–180. doi: 10.1007/s002210100882. [DOI] [PubMed] [Google Scholar]
- Hogan N. The mechanics of multi-joint posture and movement control. Biol Cybern. 1985;52:315–31. doi: 10.1007/BF00355754. [DOI] [PubMed] [Google Scholar]
- Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Ann Biomed Eng. 2005;33:829–40. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- Holzbaur KR, Delp SL, Gold GE, Murray WM. Moment-generating capacity of upper limb muscles in healthy adults. J Biomech. 2007;40:2442–9. doi: 10.1016/j.jbiomech.2006.11.013. [DOI] [PubMed] [Google Scholar]
- Holzbaur KR, Murray WM, Gold GE, Delp SL. Upper limb muscle volumes in adult subjects. J Biomech. 2007;40:742–9. doi: 10.1016/j.jbiomech.2006.11.011. [DOI] [PubMed] [Google Scholar]
- Hortobagyi T, Mizelle C, Beam S, Devita P. Old adults perform activities of daily living near their maximal capabilities. J Gerontol A Biol Sci Med Sci. 2003;58:M453–60. doi: 10.1093/gerona/58.5.m453. [DOI] [PubMed] [Google Scholar]
- Hotelling H. The generalization of student’s ratio. Ann Math Statist. 1931;2(3):360–378. [Google Scholar]
- Hughes RE, Johnson ME, O’driscoll SW, An KN. Normative values of agonist-antagonist shoulder strength ratios of adults aged 20 to 78 years. Arch Phys Med Rehabil. 1999a;80:1324–6. doi: 10.1016/s0003-9993(99)90037-0. [DOI] [PubMed] [Google Scholar]
- Hughes RE, Johnson ME, O’driscoll SW, An KN. Age-related changes in normal isometric shoulder strength. Am J Sports Med. 1999b;27:651–7. doi: 10.1177/03635465990270051801. [DOI] [PubMed] [Google Scholar]
- Hughes VA, Frontera WR, Wood M, Evans WJ, Dallal GE, Roubenoff R, Fiatarone Singh MA. Longitudinal muscle strength changes in older adults: influence of muscle mass, physical activity, and health. J Gerontol A Biol Sci Med Sci. 2001;56:B209–17. doi: 10.1093/gerona/56.5.b209. [DOI] [PubMed] [Google Scholar]
- Ketcham CJ, Seidler RD, Van Gemmert AW, Stelmach GE. Age-related kinematic differences as influenced by task difficulty, target size, and movement amplitude. J Gerontol B Psychol Sci Soc Sci. 2002;57:P54–64. doi: 10.1093/geronb/57.1.p54. [DOI] [PubMed] [Google Scholar]
- Kiebel S, Holmes A. Introduction. In: Frackowiak RSJ, editor. Human Brain Function. Vol. 2. Amsterdam; Boston: Elsev Acad Pres; 2004. http://www.fil.ion.ucl.ac.uk/spm/doc/books/hbf2/ [Google Scholar]
- Kozak K, Ashton-Miller JA, Alexander NB. The effect of age and movement speed on maximum forward reach from an elevated surface: a study in healthy women. Clin Biomech (Bristol, Avon) 2003;18:190–6. doi: 10.1016/s0268-0033(02)00205-x. [DOI] [PubMed] [Google Scholar]
- Krutky MA, Trumbower RD, Perreault EJ. Effects of environmental instabilities on endpoint stiffness during the maintenance of human arm posture. Conf Proc IEEE Eng Med Biol Soc. 2009;2009:5938–41. doi: 10.1109/IEMBS.2009.5334751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landers KA, Hunter GR, Wetzstein CJ, Bamman MM, Weinsier RL. The interrelationship among muscle mass, strength, and the ability to perform physical tasks of daily living in younger and older women. J Gerontol A Biol Sci Med Sci. 2001;56:B443–8. doi: 10.1093/gerona/56.10.b443. [DOI] [PubMed] [Google Scholar]
- Lu TW, Chen HL, Chen SC. Comparisons of the lower limb kinematics between young and older adults when crossing obstacles of different heights. Gait Posture. 2006;23:471–9. doi: 10.1016/j.gaitpost.2005.06.005. [DOI] [PubMed] [Google Scholar]
- McDonagh MJ, White MJ, Davies CT. Different effects of ageing on the mechanical properties of human arm and leg muscles. Gerontology. 1984;30:49–54. doi: 10.1159/000212606. [DOI] [PubMed] [Google Scholar]
- Morgan M, Phillips JG, Bradshaw JL, Mattingley JB, Iansek R, Bradshaw JA. Age-related motor slowness: simply strategic? J Gerontol. 1994;49:M133–9. doi: 10.1093/geronj/49.3.m133. [DOI] [PubMed] [Google Scholar]
- Morley JE. Sarcopenia in the elderly. Fam Pract. 2012;29(Suppl 1):i44–i48. doi: 10.1093/fampra/cmr063. [DOI] [PubMed] [Google Scholar]
- Murray IA, Johnson GR. A study of the external forces and moments at the shoulder and elbow while performing every day tasks. Clin Biomech. 2004;19:586–594. doi: 10.1016/j.clinbiomech.2004.03.004. [DOI] [PubMed] [Google Scholar]
- Narici MV, Maffulli N. Sarcopenia: characteristics, mechanisms and functional significance. Br Med Bull. 2010;95:139–59. doi: 10.1093/bmb/ldq008. [DOI] [PubMed] [Google Scholar]
- Pataky TC. Generalized n-dimensional biomechanical field analysis using statistical parametric mapping. J Biomech. 2010;43:1976–82. doi: 10.1016/j.jbiomech.2010.03.008. [DOI] [PubMed] [Google Scholar]
- Pataky TC. One-dimensional statistical parametric mapping in Python. Comput Methods Biomech Biomed Engin. 2012;15:295–301. doi: 10.1080/10255842.2010.527837. [DOI] [PubMed] [Google Scholar]
- Pataky TC, Robinson MA, Vanrenterghem J. Vector field statistical analysis of kinematic and force trajectories. J Biomech. 2013;46:2394–401. doi: 10.1016/j.jbiomech.2013.07.031. [DOI] [PubMed] [Google Scholar]
- Pataky TC. SPM1D. 2014 http://www.spm1d.org/index.html.
- Perreault EJ, Kirsch RF, Crago PE. Effects of voluntary force generation on the elastic components of endpoint stiffness. Exp Brain Res. 2001;141:312–23. doi: 10.1007/s002210100880. [DOI] [PubMed] [Google Scholar]
- Ramsay JO, Silverman BW. Applied functional data analysis: methods and case studies. New York: Springer; 2002. [Google Scholar]
- Ramsay JO, Silverman BW. Functional data analysis. New York: Springer; 2005. [Google Scholar]
- Rankin JK, Woollacott MH, Shumway-Cook A, Brown LA. Cognitive influence on postural stability: a neuromuscular analysis in young and older adults. J Gerontol A Biol Sci Med Sci. 2000;55:M112–9. doi: 10.1093/gerona/55.3.m112. [DOI] [PubMed] [Google Scholar]
- Rosenberg IH. Sarcopenia: origins and clinical relevance. J Nutr. 1997;127:990S–991S. doi: 10.1093/jn/127.5.990S. [DOI] [PubMed] [Google Scholar]
- Row BS, Cavanagh PR. Reaching upward is more challenging to dynamic balance than reaching forward. Clin Biomech (Bristol, Avon) 2007;22:155–64. doi: 10.1016/j.clinbiomech.2006.06.003. [DOI] [PubMed] [Google Scholar]
- Saul KR, Hu X, Goehler CM, Vidt ME, Daly M, Velisar A, Murray WM. Benchmarking of dynamic simulation predictions in two software platforms using an upper limb musculoskeletal model. Comput Methods Biomech Biomed Engin. 2015a;18:1445–58. doi: 10.1080/10255842.2014.916698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saul KR, Vidt ME, Gold GE, Murray WM. Upper limb strength and muscle volume in healthy middle aged adults. Journal of Applied Biomechanics. 2015b;31:484–91. doi: 10.1123/jab.2014-0177. [DOI] [PubMed] [Google Scholar]
- Sayer AA, Syddall H, Martin H, Patel H, Baylis D, Cooper C. The developmental origins of sarcopenia. J Nutr Health Aging. 2008;12:427–32. doi: 10.1007/BF02982703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trumbower RD, Krutky MA, Yang BS, Perreault EJ. Use of self-selected postures to regulate multi-joint stiffness during unconstrained tasks. PLoS One. 2009;4:e5411. doi: 10.1371/journal.pone.0005411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai YJ, Lin SI. Reaching forward: effects of a preceding task and aging. Age (Dordr) 2015;37:9739. doi: 10.1007/s11357-014-9739-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vidt ME, Daly M, Miller ME, Davis CC, Marsh AP, Saul KR. Characterizing upper limb muscle volume and strength in older adults: a comparison with young adults. J Biomech. 2012;45:334–41. doi: 10.1016/j.jbiomech.2011.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Worsley KJ, Evans AC, Marrett S, Neelin P. A three-dimensional statistical analysis for CBF activation studies in human brain. Journal of Cerebral Blood Flow and Metabolism. 1992;12:900–918. doi: 10.1038/jcbfm.1992.127. [DOI] [PubMed] [Google Scholar]
- Wu G, Van Der Helm FC, Veeger HE, Makhsous M, Van Roy P, Anglin C, Nagels J, Karduna AR, Mcquade K, Wang X, Werner FW, Buchholz B International Society Of, B. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion--Part II: shoulder, elbow, wrist and hand. J Biomech. 2005;38:981–992. doi: 10.1016/j.jbiomech.2004.05.042. [DOI] [PubMed] [Google Scholar]