Abstract
Making decisions that factor the cost of time is fundamental to survival. Yet, while it is readily appreciated that our perception of time is intimately involved in this process, theories regarding intertemporal decision-making and theories regarding time perception are treated, largely, independently. Even within these respective domains, models providing good fits to data fail to provide insight as to why, from a normative sense, those fits should take their apparent form. Conversely, normative models that proffer a rationalization for why an agent should weigh options in a particular way, or to perceive time in a particular way, fail to account for the full body of well-established experimental evidence. Here we review select, yet key advances in our understanding, identifying conceptual breakthroughs in the fields of intertemporal decision-making and in time perception, as well as their limits and failings in the face of hard-won experimental observation. On this background of accrued knowledge, a new conception unifying the domains of decision-making and time perception is put forward (Training-Integrated Maximization of Reinforcement Rate, TIMERR) to provide a better fit to observations and a more parsimonious reckoning of why we make choices, and thereby perceive time, the way we do.
1 Introduction
Appreciating the cost of time is central to determining whether an offer of a later but larger reward affords a better opportunity than a smaller, but more immediate one. This is often due to the fact that the difference in time that must be invested to acquire the larger later reward may, potentially, be put to more profitable use. Therefore, when evaluating the relative worth of rewarding (or punishing) options, how should the cost of time invested to achieve an option’s outcome be weighed? Fields of study as diverse as economics, psychology, ecology, and neuroscience have struggled to measure, and to rationalize, how and why agents factor the cost of time the way they do. Below, we summarize prominent theories, their key contributions, and their experimentally determined limitations.
2 The problem of choice when factoring time: extant theories
There is a rich history of normative theories—theories that address the question of how behavior ought to be—of intertemporal decision making. Samuelson, from the field of economics, was the first to formally state how time should be factored in such intertemporal decision-making, postulating in his “Discounted Utility Theory” (DUT) the normative principle that decision-making should be stationary in time (that is, an option, having been determined to be of the greatest value remains so, all else being equal, with the passage of time)[1]. Under this constraint, the value of delayed rewards should appear as if discounted by an exponential function, with the exponent of discounting controlling its steepness (i.e. the agent’s sense of the cost of time, see Table 1). This formulation advanced the notion that time has a cost, that its specific form would derive from normative principles, and that it could account for observed behaviors. Yet, despite its appeal, experimental observation over the following decades would not well accord with this formalism. Rather, observations in psychological and behavioral science were largely found to be better fit by a hyperbolic form[2] of temporal discounting (wherein stationary time preference can be, and is, violated[2–8]).
Table 1.
| Theory | Normative Principle |
Decision Formula |
Discounting Form |
Steepness parameter |
|
|---|---|---|---|---|---|
| DUT | Stationary time preference |
Choose max(r(t)D(t)); D(t) = exp(−kt) |
Exponential | Free-fit | |
| OFT | Future reward-rate maximization |
Hyperbolic | Inter-trial interval |
||
| ERT | Local reward- rate maximization |
Hyperbolic | Delay to reward |
||
| TIMERR | Experientially- bounded reward-rate maximization |
Hyperbolic | Past integration interval |
While hyperbolic discounting provided a better fit to observation, it was from the fields of evolutionary biology and ecology that a normative theory rationalizing why agents should discount hyperbolically—and with a certain steepness—was forming. Under the principle that animals should forage so as to maximize their long-term reward rates[9], Optimal Foraging Theory (OFT) arose[10, 11]. When expressed as a discounting function (see Table 1), the form it takes is hyperbolic. Importantly, whereas the value of the parameter controlling the steepness of discounting in prior hyperbolic models lacked biological meaning, OFT asserted that this parameter is the reciprocal of the inter-trial interval (of the option chosen by the animal to maximize future reward). Though OFT proffered not only a normative theory of why temporal discounting should be hyperbolic but also why it should have a particular steepness, here too, experimentation was to show that intertemporal decision-making did not always abide by its prediction[2, 6, 7, 12–18], namely that agents would factor all the temporal delays associated with maximizing a future global reward rate. Given this, Ecological Rationality Theory (ERT) was then devised on the basis that animals, while seeking to maximize reward rates, factor only the temporal delays to acquire reward, arguing that rewards with differing post-reward delays are rarely encountered under natural conditions [11, 12] (see Table 1). In this way, the discounting function of ERT is a special case of OFT, wherein the post-reward delay—and therefore ERT’s discounting constant—is zero. Despite this reformulation, experiments consistently report discounting constants greater than zero, inconsistent with ERT [6, 7, 12–18].
The state of the field is then this: while proximate models have been proposed that well-fit experimental observations[19–22], as they do not arise from first principles, the meaning and/or justification of their terms and form are uncertain. Conversely, theories developed from normative principles, while addressing why a discounting function should take its apparent form, fare more poorly in capturing experimental observations. Nonetheless, collectively this work has provided deep insight into the problem of intertemporal decision-making, identifying, formalizing, and framing the issue that time has a cost, that the worth of an offer depends on the current state of affairs, and that agents should aim to gather the most reward while foraging in an environment. These insights have strong appeal, so what is wrong?
3 An experientially-constrained theory of intertemporal decision making: Training-Integrated Maximized Estimate of Reward Rate (TIMERR)
Consider an omniscient agent that can foresee the future disposition of reward options contingent upon whatever choice path it were to make. Such an agent, for the time it is allotted to foraging in an environment, could then determine the choice path that maximizes its reward intake over all possible future options. That is truly optimal, yet impossible. A real agent is limited in its ability to apprehend the availability of rewards into its future; hence, any theory regarding reward rate maximization must be constructed from the perspective of what is knowable by the agent. Given that the availability of future reward is unknowable, how should an agent evaluate the worth of a reward option, so as to maximize the reward acquired during foraging?
To appreciate whether a reward option is worth its cost in time, we have postulated that agents look back into their recent past to estimate their rate of experienced reward[23] (Figure 1a). An offer of reward is then evaluated by adding the experienced reward rate to the offered reward rate as in Figure 1a, and assessing whether the resulting rate of reward outstrips the rate that has already been achieved. This construction affords a manner of appreciating why some options should be foregone: their selection would needlessly decrease the achievable reward rate, as the experienced reward rate foretells of superior reward options to come. In the face of multiple offers, it also can determine which is the best and by how much. In this way, a reward option is thus evaluated in comparison to the estimated worth of the experienced environment as a whole and is the basis of our theory of intertemporal decision-making, named so to reflect that postulate: Training-Integrated Maximized Estimation of Reinforcement Rate (TIMERR) [23].
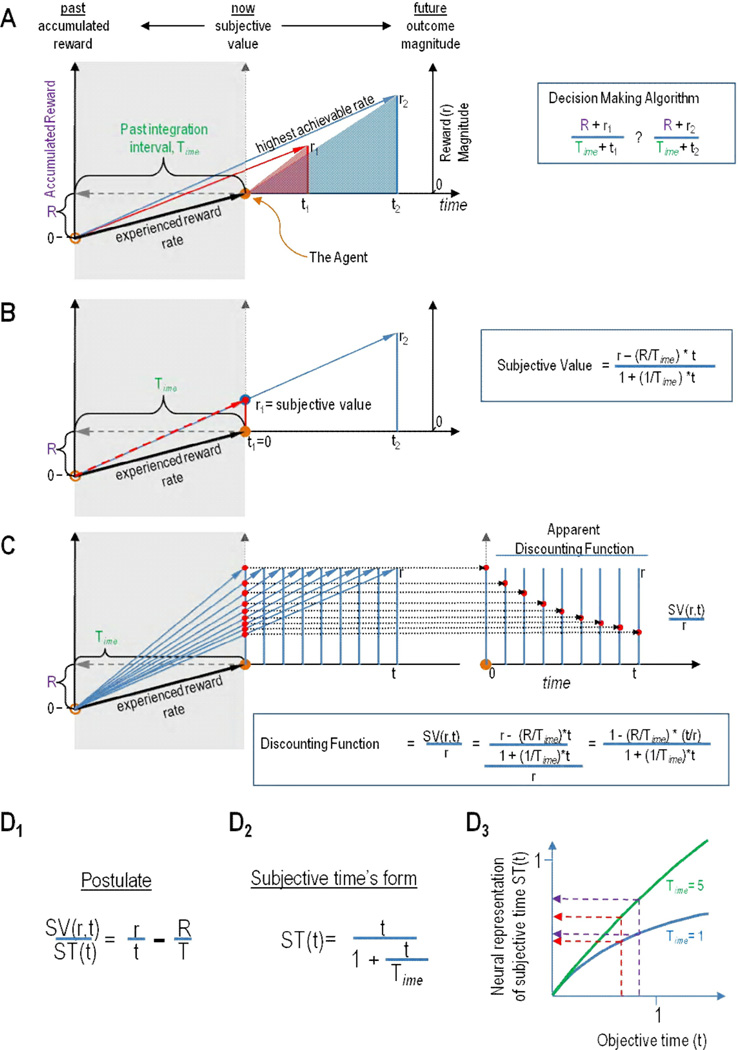
Figure 1.
A) The TIMERR decision-making algorithm (right) can be depicted graphically (left) so as to visualize how offers of given reward sizes (r) and delays (t) are evaluated. An agent (filled orange circle), by looking into its past over an interval Time, assesses the rewards accumulated (R), thereby appreciating the reward rate experienced in the environment up to that moment. The local reward rates associated with current offers of future reward (slopes of red and blue offers) are then added to the experienced reward rate so as to calculate respective reward rates that could be achieved, were the agent to pursue an offer.
B) The TIMERR decision-making algorithm can be used to derive an expression for the subjective value of an offer, by equating an immediate offer of reward with a delayed offer of greater size but which yields the same achievable reward rate. By rearranging for subjective value, it is then appreciated that the opportunity cost of time (R/Time* t) is subtracted from a reward option (right inset). Graphically, the subjective value of a delayed reward is the y-intercept “now” in time of the line depicting the achievable reward rate were the agent to pursue that reward option (left).
C) The TIMERR decision-making algorithm can also be re-expressed as a temporal discounting function in terms of the fraction of an offer’s magnitude as a function of time (inset). The discounting function can be visualized by re-plotting the subjective value of a reward that is delayed through time at the offered reward’s respective delay (left). The resulting function is hyperbolic.
D) The form of subjective time under TIMERR. D1) TIMERR postulates that the subjective reward rate of an offer should equal the difference between the local reward rate of an offer and the experienced reward rate. D2) Subjective representation of time (ST(t)) is then found by replacing the subjective value of a delayed reward of magnitude r and delay t, SV(r,t), with its equation in B, and solving for ST(t). D3) We hypothesize that the neural representation of time is ST(t) normalized by Time, as shown in the y-axis. This neural representation of subjective time yields a bounded, concave function from 0 (corresponding to zero delay) to 1 (corresponding to infinite delay). The smaller the past integration interval (Time), the more non-linear the neural representation of time (as visualized in D3).
TIMERR’s decision-making algorithm can be re-expressed as a statement of an offer’s subjective value (Figure 1b), or, as a discounting function (Figure 1c). While all are equivalent, these expressions of TIMERR provide additional insights into the consequences of TIMERR’s construction. For instance, in a world where one cannot pursue other rewards during the delay to a chosen reward, when an offer of reward of a given magnitude, r, and delay, d, is expressed in terms of its subjective value (SV[r,t]), it can be seen that an opportunity cost (the experienced rate of reward, R/Time, times the delay to the reward, t) is subtracted from the offered reward’s magnitude. Therefore, the degree to which an environment is rewarding is factored into the decision-making process by subtracting the amount of reward that would be expected to be received in lieu of pursuing the offer. The richer the reward environment, the less the subjective value of a given offer (and the more discerning the agent appears to be). In a setting where other rewards can indeed be pursued during the wait to a chosen option, the opportunity cost lowers to zero, but the hyperbolic form remains. By expressing TIMERR as a discounting function (see Figure 1c), it is perhaps most readily appreciated that the parameter controlling the steepness of temporal discounting is not a free-fit parameter of uncertain meaning (as in DUT and many psychological models), but rather is the reciprocal of the time that the agent looks back to estimate its experienced reward rate, (1/Time). The longer the agent looks back into its past, the greater the subjective value of an offer (and the more patient the agent appears to be). Therefore, the time an agent looks back (Time) to estimate its rate of reward, and what that experienced reward rate is (R/Time), controls how an offer of a given magnitude and delay is evaluated.
The merit of TIMERR rests, of course, on its ability to account for the breadth of well-established phenomenology in intertemporal decision-making. Key experimental observations in intertemporal decision-making are: hyperbolic discounting [2–8], that the steepness of discounting varies across individuals and even within individuals in varying contexts[2–8, 13, 24], that losses are discounted more steeply the larger the loss[25], that there is a differential treatment of losses[3], the Magnitude effect[26–29], the Sign effect[24, 27, 29], and relatedly, how increasing the size of outcomes diminishes how pronounced the Sign effect appears to be[3, 8, 29], when to forgo an option, and the delay-speedup effect[3, 29]. All of these observations are well-accounted for by TIMERR[23, 30–32]. Notably, and in addition, an agent employing the TIMERR decision rule will collect more long-term reward rate compared to one employing best fit exponential (DUT), hyperbolic (OFT & ERT), or hyperbolic-like (βδ) discounting [23].
4 The perception of time: extant theory and implementation
Above, we have considered how time is factored into decision-making. Since such choices require some comprehension of time, perhaps the vagaries of intertemporal decision making can be understood as arising from our sense of time? Indeed, it is on this basis that theories of temporal perception, in addition to accounting for distinctive features of timing behaviors, have been related to intertemporal decision-making. So, how do key theories of time perception explain why and/or how time perception expresses the errors? We will treat two kinds of errors, one in precision (spread in the temporal estimate) and one in accuracy (how close the temporal estimate is to the actual time interval).
Accounts of temporal imprecision
A core experimental observation in time perception is that errors in the precision of time perception are largely found to scale in proportion to the interval being timed. Leading theories of time perception[33–36] provide a framework as to how this oft observed characteristic[37–39], termed the “scalar timing property”, may come about. Scalar Expectancy Theory (SET) [36, 38] accounts for the temporal scalar property by asserting that a comparator operates on a ratio-rule in assessing whether the accumulation of a pacemaker matches a remembered interval. When the interval to be timed is the delay to a reinforcement, Behavioral Theory of Timing (BeT) can account for the scalar property by assuming that the rate of accumulation is inversely proportional to the rate of reinforcement (being the inverse of the delay to reward)[35]. These and related models of time perception [14, 33, 40–42] make connection to intertemporal decision-making in that they offer a rationale as to why agents may exhibit non-stationary time preferences: as two reward options separated by a given delay lie further into the future, their perceived delays increasingly approximate one another, leading to an increased likelihood of selecting the later, but larger, option. But, while these theories describe processes that would lead to scalar timing and, potentially, non-stationary time preferences, they don’t address why errors in timing should exhibit their observed relationship to the interval being timed.
Providing a proximate answer to this issue, it has been proposed that imprecision in timing may arise due simply to noise introduced by neural processing. Though a simple pacemaker-accumulator model that assumes Poisson-spiking of a single neuron can be constructed that produces the scalar timing property (mathematically mimicking BeT), a drift-diffusion model of timing comprised of a network of Poisson neurons provides a more biologically feasible account[43]. In this “Time-adaptive, opponent DDM” (TopDDM) model, it is assumed that two opponent Poisson processes (one excitatory and the other inhibitory) linearly sum to produce drift in the accumulator[44]. By this means, accumulation to a target threshold at rates tuned to the interval to be timed is shown to abide by the temporal scalar property. The above theories and implementation models posit how scalar timing comes about, and may thus offer a rationale as to why non-stationary time preference could be observed as imprecise perception at long delays might bias choices towards larger, later rewards. However, recent experimental observations [45, 46] run counter to the scalar timing account of non-stationary time preference. By its reckoning, improved time perception should result in reduced tolerance to delay; yet, improved time perception is correlated with a greater delay tolerance[45, 46]. Therefore, scalar timing is likely not the basis of non-stationary time preferences.
Accounts of temporal accuracy
In addition to the imprecision in timing, the accuracy of timing is yet another defining feature. Does subjective time (defined as the neuronal metric of the passage of time) accurately reflect objective time? Addressing this question requires a direct measure of subjective time and is thus, extremely difficult. However, psychologists attempt to infer the subjective representation of time by observing patterns in particular timing behaviors. To assess what form subjective time takes, the method of temporal bisection [47–49] is often used to determine the point of subjective equality (PSE) between two temporal intervals (ie, the intermediate interval equally mistaken as being short or long). Asserting that subjective time is linear, SET predicts that the PSE should be the geometric mean, which is consistent with many experimental observations [47, 50]. Yet, surveying temporal bisection experiments [48, 51, 52], the PSE can be found to range from the harmonic mean of the reference intervals to the arithmetic mean. This may either be because 1) the subjective representation of time is linear but the comparison of two intervals is performed by comparing their ratio against a standard (e.g. unity ratio within a measurement error implies equal intervals) or some other non-linear operation, or, 2) because the subjective representation of time itself is non-linear with the comparison of two intervals performed by comparing their difference (e.g. zero difference within a measurement error implies equal intervals). Therefore, while the form of subjective time can accord with objective time (under a ratio read-out rule), it also could deviate from objective time, apparently as some nonlinear, concave function[42]. Indeed, should subjective time be logarithmic, exponential temporal discounting in subjective time would then appear as hyperbolic, explaining non-stationary time preference as well as the scalar property[42, 53]. Nevertheless, these theories and implementation models do not speak to the purpose of why subjective time should take the form that it does, nor how or why the curvature of that form may, or should, change.
5 TIMERR and its reckoning of time perception
Postulating that the subjective reward rate of an option should reflect the change in objective reward rate it offers, we have recently derived, using TIMERR’s framework, an expression for the subjective representation of time (figure 1d1)[30–32]. This rationalizes why the representation of subjective time takes the form it does: so that the subjective reward rate accurately represents the change in objective reward rate. The key feature of representing subjective time in such a way is that it is a bounded, nonlinear concave function whose curvature is controlled, crucially, by Time (the past integration integral over which the animal estimates its experienced reward rate). In this way, TIMERR is able to account for the varying forms subjective time has been inferred to have through the method of temporal bisection. When the past integration interval becomes increasing large, the degree of nonlinearity between objective time and the subjective representation of time becomes diminishingly small, resulting in the PSE approaching the arithmetic mean of the reference intervals. As the past integration interval decreases, this non-linearity increases such that the PSE will come to accord with the geometric mean. Further decreasing the past integration interval toward zero results in this nonlinearity approaching its maximum, causing the PSE to approach the harmonic mean. Hence, TIMERR can reconcile divergent experimental observations regarding the form of subjective time, while addressing what purpose its form serves, but what of subjective time’s imprecision?
An implementation-level model of TIMERR that provides a mechanistic account of time perception and production is a drift-diffusion model (TIMERR-DDM), that assumes, like TopDDM, neurons that function as Poisson accumulators[30]. Poisson processes, by their very nature, produce errors that scale with the square root of their magnitude. How then do such accumulators result in timing errors that grow linearly with time? While TopDDM solves this problem by assuming that the accumulation is to a constant threshold with its rate tuned to be inversely proportional to the interval to be timed, TIMERR-DDM proposes a recurrent feedback onto the accumulator so as to represent the non-linear subjective time mentioned above. The TIMERR-DDM network accumulator model can produce near scalar invariance in timing[30], but importantly, also predicts, under certain conditions, systematic deviations from scalar timing, as have been observed experimentally [54, 55]. A defining feature of TIMERR-DDM is that the rate of integration is inversely proportional to the interval the agent looks back to estimate the rate of reward, Time, which controls this non-linearity in the accumulator. The distinctive prediction of TopDDM is that the ratio of skewness to CV of produced time intervals is exactly 3 [44]. Interestingly, while this distinguishes TopDDM from other accumulator models [30], TIMERR DDM makes very similar predictions. However, TIMERR-DDM makes additional falsifiable predictions. The most important such prediction is that the non-linearity of time perception will be tuned to be optimal for an interval to be timed. Since TIMERR predicts that the non-linearity of time perception is also tied to the rate of temporal discounting, this prediction implies that optimal timing of intervals will affect temporal discounting. This has not yet been appropriately tested, but it is known that there is strong correlation between temporal discounting and time perception, such that the greater the tolerance to delay, the greater the ability to perceive time[45, 46, 56, 57].
Summary
Why has the hunt for the perfect discounting function and a reckoning of time perception been so elusive? The accretion of thought and observation surveyed above argues that, with regards to intertemporal decision-making, evolutionarily motivated normative principles should underpin the decision-making process while being limited by what is knowable to the agent. In this light, TIMERR is a next step in rationalizing why temporal discounting takes its apparent form: so as to maximize reward rate within experiential constraints. From this perspective, error in subjective time can also then be understood as taking the form that it does in the service of maximizing reward rate, rather than simply being nature’s impoverished attempt at representing time as it is.
Highlights.
Intertemporal decision-making is not well-accounted for by prior normative theories
Prior theories of timing consider the perception of time to be independent of intertemporal decision-making
A new reward-rate maximizing theory (TIMERR) rationalizes observations in intertemporal decision-making & time perception
Acknowledgments
This work was funded by NIMH (R01 MH093665) to M.G.H.S.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Disclosures
Nothing declared.
References
- 1. Samuelson PA. A Note on Measurement of Utility. Review of Economic Studies. 1937;4:155–161. The first to formalize the cost of time in intertemporal decision-making, Samuelson conceives of a discounting function with an exponential decay under the normative principle that choices should be stationary with time.
- 2.Ainslie G. Specious reward: A behavioral theory of impulsiveness and impulse control. Psychological Bulletin. 1975;59:257–272. doi: 10.1037/h0076860. [DOI] [PubMed] [Google Scholar]
- 3.Benzion U, et al. Discount Rates Inferred from Decisions : An Experimental Study. Management Science. 1989;35:270–284. [Google Scholar]
- 4.Calvert AL, Green L, Myerson J. Delay discounting of qualitatively different reinforcers in rats. Journal of the Experimental Analysis of Behavior. 2010;93:171–184. doi: 10.1901/jeab.2010.93-171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Green L, Fristoe N, Myerson J. Temporal discounting and preference reversals in choice between delayed outcomes. Psychonomic Bulletin & Review. 1994;1:383–389. doi: 10.3758/BF03213979. [DOI] [PubMed] [Google Scholar]
- 6.Kobayashi S, Schultz W. Influence of reward delays on responses of dopamine neurons. The Journal of Neuroscience. 2008;28:7837–7846. doi: 10.1523/JNEUROSCI.1600-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rachlin H, Green L, Vi AD. Commitment, choice and self-control. Journal of the Experimental Analysis of Behavior. 1972;17:15–22. doi: 10.1901/jeab.1972.17-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Thaler R. Some empirical evidence on dynamic inconsistency. Economics Letters. 1981;8:201–207. [Google Scholar]
- 9.MacArthur RH, Pianka ER. On optimal use of a patchy environment. The American Naturalist. 1966;100:603–609. [Google Scholar]
- 10.Pyke GH. OPTIMAL FORAGING THEORY : A CRITICAL REVIEW. Annual Review of Ecology and Systematics. 1984;15:523–575. [Google Scholar]
- 11.Stephens DW, Krebs JR. Foraging Theory. 1986. [Google Scholar]
- 12.Bateson M, Kacelnik A. Rate currencies and the foraging starling: the fallacy of the averages revisited. Behavioral Ecology. 1996;7:341–352. [Google Scholar]
- 13.Blanchard TC, Pearson JM, Hayden BY. Postreward delays and systematic biases in measures of animal temporal discounting. Proceedings of the National Academy of Sciences of the United States of America. 2013;110:15491–15496. doi: 10.1073/pnas.1310446110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kacelnik A, Bateson M. Risky Theories—The Effects of Variance on Foraging Decisions. Integrative and Comparative Biology. 1996;36:402–434. [Google Scholar]
- 15.Louie K, Glimcher PW. Separating value from choice: delay discounting activity in the lateral intraparietal area. The Journal of Neuroscience. 2010;30:5498–5507. doi: 10.1523/JNEUROSCI.5742-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roesch MR, Calu DJ, Schoenbaum G. Dopamine neurons encode the better option in rats deciding between differently delayed or sized rewards. Nature neuroscience. 2007;10:1615–1624. doi: 10.1038/nn2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stephens DW, Anderson D. The adaptive value of preference for immediacy : when shortsighted rules have farsighted consequences. Behavioral Ecology. 2001;12:330–339. [Google Scholar]
- 18.Winstanley CA, et al. Contrasting roles of basolateral amygdala and orbitofrontal cortex in impulsive choice. The Journal of Neuroscience. 2004;24:4718–4722. doi: 10.1523/JNEUROSCI.5606-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.al-Nowaihi A, Dhami S. A general theory of time discounting : The reference-time theory of intertemporal choice. 2008 [Google Scholar]
- 20.Killeen PR. An additive-utility model of delay discounting. Psychological Review. 2009;116:602–619. doi: 10.1037/a0016414. [DOI] [PubMed] [Google Scholar]
- 21.Laibson D. Golden eggs and hyperbolic discounting. The Quarterly Journal of Economics. 1997;112:443–477. [Google Scholar]
- 22.McClure SM, et al. Separate neural systems value immediate and delayed monetary rewards. Science. 2004;306:503–507. doi: 10.1126/science.1100907. [DOI] [PubMed] [Google Scholar]
- 23. Namboodiri VMK, et al. A general theory of intertemporal decision-making and the perception of time. Frontiers in Behavioral Neuroscience. 2014;8:61. doi: 10.3389/fnbeh.2014.00061. A theory unifying intertemporal decision-making and time perception, TIMERR rationalizes decision-making as reward-rate maximization that occurs over a limited temporal interval that includes an immediate past integration interval and the delay to future reward. This past integration interval, in which experienced reward rate is estimated, controls the apparent steepness of temporal discounting and the non-linearity of the subjective representation of time.
- 24.Frederick S, et al. Time Discounting and Time Preference : A Critical Review. Journal of Economic Literature. 2002;40:351–401. [Google Scholar]
- 25.Hardisty DJ, Appelt KC, Weber EU. Good or Bad, We Want it Now : Fixed-cost Present Bias for Gains and Losses Explains Magnitude Asymmetries in Intertemporal Choice. Journal of Behavioral Decision Making. 2012 [Google Scholar]
- 26.Grace RC, Sargisson RJ, White KG. Evidence for a magnitude effect in temporal discounting with pigeons. Journal of Experimental Psychology. Animal Behavior Processes. 2012;38:102–108. doi: 10.1037/a0026345. [DOI] [PubMed] [Google Scholar]
- 27.Kalenscher T, Pennartz CMA. Is a bird in the hand worth two in the future? The neuroeconomics of intertemporal decision-making. Progress in Neurobiology. 2008;84:284–315. doi: 10.1016/j.pneurobio.2007.11.004. [DOI] [PubMed] [Google Scholar]
- 28.Kinloch JM, White KG. A concurrent-choice analysis of amount-dependent temporal discounting. Behavioural Processes. 2013;97:1–5. doi: 10.1016/j.beproc.2013.03.007. [DOI] [PubMed] [Google Scholar]
- 29.Loewenstein G, Prelec D. Anomalies in intertemporal choice: evidence and an interpretation. The Quarterly Journal of Economics. 1992;107:573–597. [Google Scholar]
- 30. Namboodiri VM, Mihalas S, Hussain Shuler MG. Analytical Calculation of Errors in Time and Value Perception Due to a Subjective Time Accumulator: A Mechanistic Model and the Generation of Weber’s Law. Neural Comput. 2015;28(1):89–117. doi: 10.1162/NECO_a_00792. This paper presents a full mechanistic and analytical treatment of the TIMERR algorithm, identifying not only the parameter regime in which Weber’s law is abided, but where it is violated. Critically, it also makes the prediction that the steepness of temporal discounting is affected by the precision required to time temporal intervals. Like TopDDM, it is composed in part by stochastic opponent processes, but unlike TopDDM, it can produce scalar timing representations during sensation without requiring the accumulation rate to be tuned.
- 31.Namboodiri VMK, Mihalas S, Hussain Shuler MG. Rationalizing decision-making: understanding the cost and perception of time. Timing & Time Perception Reviews. 2014;1:1–40. [Google Scholar]
- 32. Namboodiri VMK, Mihalas S, Hussain Shuler MG. A temporal basis for Weber’s law in value perception. Frontiers in Integrative Neuroscience. 2014;8:1–11. doi: 10.3389/fnint.2014.00079. This paper presents a drift-diffusion model of the TIMERR algorithm, showing a range of parameters over which errors in intertemporal decision-making and time perception approximate Weber’s law.
- 33.Bateson M. Interval timing and optimal foraging. In: Meck WH, editor. Functional and Neural Mechanisms of Interval Timing. Boca-Raton, Florida: CRC Press; 2003. pp. 113–141. [Google Scholar]
- 34. Gibbon J. Scalar Expectancy Theory and Weber’s Law in Animal Timing. Psychological Review. 1977;84:279–325. A dominant model of timing, Scalar Expectancy Theory (SET) proposes that a ratio-rule is used by a comparator when assessing whether the accumulation of a pacemaker matches a remembered interval, giving rise to the temporal scalar property.
- 35. Killeen PR, Fetterman JG. A behavioral theory of timing. Psychological Review. 1988;95:274–295. doi: 10.1037/0033-295x.95.2.274. Rather than building into the decision rule the property giving rise to temporal scalar property as in SET, BeT accounts for the scalar property by assuming that the rate of accumulation to a threshold is inversely proportional to the rate of reinforcement, itself being the inverse of the delay to reward.
- 36.Matell MS, Meck WH. Neuropsychological mechanisms of interval timing behavior. BioEssays. 2000;22:94–103. doi: 10.1002/(SICI)1521-1878(200001)22:1<94::AID-BIES14>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 37.Gibbon J, et al. Trial and intertrial durations in autoshaping. Journal of Experimental Psychology: Animal Behavior Processes. 1977;3:264–284. [Google Scholar]
- 38.Gibbon J, Church RM, Meck WH. Scalar timing in memory. In: Gibbon J, Allan L, editors. Timing and time perception. New York: New York Academy of Sciences; 1984. pp. 52–77. [DOI] [PubMed] [Google Scholar]
- 39.Wearden JH, Lejeune H. Scalar properties in human timing: Conformity and violations. The Quarterly Journal of Experimental Psychology. 2008;61:569–587. doi: 10.1080/17470210701282576. [DOI] [PubMed] [Google Scholar]
- 40.Cui X. Hyperbolic discounting emerges from the scalar property of interval timing. Frontiers in integrative neuroscience. 2011;5:24. doi: 10.3389/fnint.2011.00024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Stephens DW. Discrimination, discounting and impulsivity: a role for an informational constraint. Philosophical transactions of the Royal Society of London. Series B, Biological sciences. 2002;357:1527–1537. doi: 10.1098/rstb.2002.1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Zauberman G, et al. Discounting Time and Time Discounting : Subjective Time Perception and Intertemporal Preferences. Journal of Marketing Research. 2009;XLVI:543–556. [Google Scholar]
- 43. Simen P, et al. A model of interval timing by neural integration. The Journal of Neuroscience. 2011;31:9238–9253. doi: 10.1523/JNEUROSCI.3121-10.2011. A drift-diffusion model of timing is proposed based on the accumulation of opponent Poisson processes that linearly sum to a set threshold within an accumulator, producing the scalar timing property with a distinctive distribution of response times.
- 44.Balci F, Simen P. A decision model of timing. Current opinion in behavioral sciences. 2016;8:94–101. [Google Scholar]
- 45.Baumann AA, Odum AL. Impulsivity, risk taking, and timing. Behavioural Processes. 2012;90:408–414. doi: 10.1016/j.beproc.2012.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wittmann M, Paulus MP. Decision making, impulsivity and time perception. Trends in Cognitive Sciences. 2008;12:7–12. doi: 10.1016/j.tics.2007.10.004. [DOI] [PubMed] [Google Scholar]
- 47.Church RM, Deluty MZ. Bisection of temporal intervals. Journal of Experimental Psychology. Animal Behavior Processes. 1977;3:216–228. doi: 10.1037//0097-7403.3.3.216. [DOI] [PubMed] [Google Scholar]
- 48.Kopec CD, Brody CD. Human performance on the temporal bisection task. Brain and cognition. 2010;74:262–272. doi: 10.1016/j.bandc.2010.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Levy JM, Namboodiri VMK, Hussain Shuler MG. Memory bias in the temporal bisection point. Frontiers in Integrative Neuroscience. 2015;9:1–11. doi: 10.3389/fnint.2015.00044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Gibbon J. The structure of subjective time: How time flies. The Psychology of Learning and Motivation. 1986;20:105–135. [Google Scholar]
- 51.Killeen PR, Fetterman JG, Bizo L. Time’s Causes. In: Bradshaw CM, Szabadi E, editors. Advances in Psychology: Time and Behavior: Psychological and Neurobehavioral Analyses. Amsterdam: Elsevier; 1997. pp. 79–131. [Google Scholar]
- 52.Wearden JH. Do humans possess an internal clock with scalar timing properties? Learning and Motivation. 1991;22:59–83. [Google Scholar]
- 53.Takahashi T. Loss of self-control in intertemporal choice may be attributable to logarithmic time-perception. Medical Hypotheses. 2005;65:691–693. doi: 10.1016/j.mehy.2005.04.040. [DOI] [PubMed] [Google Scholar]
- 54.Bizo LA, et al. The failure of Weber’s law in time perception and production. Behavioural Processes. 2006;71:201–210. doi: 10.1016/j.beproc.2005.11.006. [DOI] [PubMed] [Google Scholar]
- 55.Lejeune H, Wearden JH. The Comparative Psychology of Fixed-Interval Responding : Some Quantitative Analyses. Learning and Motivation. 1991;22:84–111. [Google Scholar]
- 56.Heilbronner SR, Meck WH. Dissociations between interval timing and intertemporal choice following administration of fluoxetine, cocaine, or methamphetamine. Behavioral Processes. 2014;101:123–134. doi: 10.1016/j.beproc.2013.09.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Pine A, et al. Dopamine, time, and impulsivity in humans. The Journal of neuroscience : the official journal of the Society for Neuroscience. 2010;30:8888–8896. doi: 10.1523/JNEUROSCI.6028-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]