Mode switching of Inositol 1,4,5-trisphosphate receptor channel shapes the Spatiotemporal scales of Ca²⁺ signals

Abstract

The inositol 1,4,5-trisphosphate (InsP₃) receptor (InsP₃R) channel is crucial for the generation and modulation of highly specific intracellular Ca²⁺ signals performing numerous functions in animal cells. However, the single channel behavior during Ca²⁺ signals of different spatiotemporal scales is not well understood. To elucidate the correlation between the gating dynamics of single InsP₃Rs and spatiotemporal Ca²⁺ patterns, we simulate a cluster of InsP₃Rs under varying ligand concentrations and extract comprehensive gating statistics of all channels during events of different sizes and durations. Our results show that channels gating predominantly in the low activity mode with negligible occupancy of intermediate and high modes leads to single channel Ca²⁺ release event blips. Increasing occupancies of intermediate and high modes results in events with increasing size. When the channel has more than 50% probability of gating in the intermediate and high modes, the cluster generates very large puffs that would most likely result in global Ca²⁺ signals. The size, duration and frequency of Ca²⁺ signals all increase linearly with the total probability of channel gating in the intermediate and high modes. To our knowledge, this is the first study that quantitatively relates the modal characteristics of InsP₃R to the shaping of different spatiotemporal scales of Ca²⁺ signals.

Introduction

Cytosolic signals caused by Ca²⁺ released through inositol 1,4,5-trisphosphate (InsP₃) receptor (InsP₃R) Ca²⁺ channels from the endoplasmic reticulum (ER) regulate numerous cellular functions [1]. The secret of the universality and specificity of Ca²⁺ signals lies in the hierarchy of their dynamics. That is, information is encoded in the spatiotemporal patterning of Ca²⁺ transients. Despite its vital role, the mechanism behind the spatiotemporal patterning of Ca²⁺ signals remains misunderstood.

The InsP₃R is a Ca²⁺ - sensitive Ca²⁺ release channel having a bell-shaped equilibrium open probability (P _o) with respect to Ca²⁺ [2, 3]. It is more probable for the channel to be open in the presence of 2 μM Ca²⁺ on the cytosolic side of the membrane than it is for it to be open at 0.1 μM or 100 μM Ca²⁺. Opening of InsP₃R also requires the binding of second-messenger InsP₃, which is generated in the cytoplasm by the binding of extracellular ligands to the membrane receptors. Patch clamp data on Sf9 cells, an insect cell line derived from the moth Spodoptera frugiperda, show that InsP₃R gates in three distinct modes even if the concentrations of Ca²⁺ and InsP₃ are kept fixed [4]. The three modes are a low mode with P _o close to zero, an intermediate mode where the channel switches rapidly between closed and open states having P _o ∼0.25, and a high mode with P _o ∼0.85.

InsP₃Rs are distributed in clusters of a few channels per cluster in the membranes of intracellular compartments such as the ER. Experimental observations suggest a simultaneous opening of 6–10 channels during a Ca²⁺ puff (a Ca²⁺ release event caused by a simultaneous opening of more than one channel in a cluster) [5, 6] and a typical cluster diameter of about 0.5 μm [5, 7, 8]. We assume that the maximum number of simultaneously open channels ever observed at a given puff site represents the number of channels within the cluster giving a mean inter-channel spacing of about 100–150 nm depending on the size and number of channels within a cluster.

The Ca²⁺ feedback described above underlies a process of Ca²⁺ - induced Ca²⁺ release (CICR). Ca²⁺ liberation due to CICR may either remain restricted to a single channel opening, giving rise to a blip, cause the simultaneous opening of multiple channels in the cluster to generate a puff, or propagate as a salutatory intracellular Ca²⁺ wave sweeping across multiple clusters. It is this range of signaling patterns that makes Ca²⁺ a universal messenger [1]. Despite the fact that these spatiotemporal scales of Ca²⁺ signals have been the subject of intense research for a number of years, the gating behavior of InsP₃Rs during these scales of Ca²⁺ signals remains misunderstood.

To elucidate the complex spatiotemporal patterning of Ca²⁺ signals generated by InsP₃Rs, it is important to link the scales of observations summarized above. We need to understand the behavior of InsP₃R channels during different scales of Ca²⁺ signaling. In this paper, we use a computational framework to investigate the correlation between the gating behavior of InsP₃R with the wide range of statistical properties of elementary Ca²⁺ release events that are the building blocks for Ca²⁺ signaling in many animal cells and explore the behavior of the channel in the spatiotemporal dynamics of Ca²⁺ signaling. We recently employed a data-driven approach to develop a single channel model that can reproduce all observations about InsP₃R including P _o, response of the channel to rapid changes in the ligand concentrations [9] and characteristics of the channel during various modes [10]. We built our cluster model based on this single channel model and extracted comprehensive statistics of the gating properties of all channels during Ca²⁺ signals of different sizes and durations to see how the two correlate with each other.

Methods

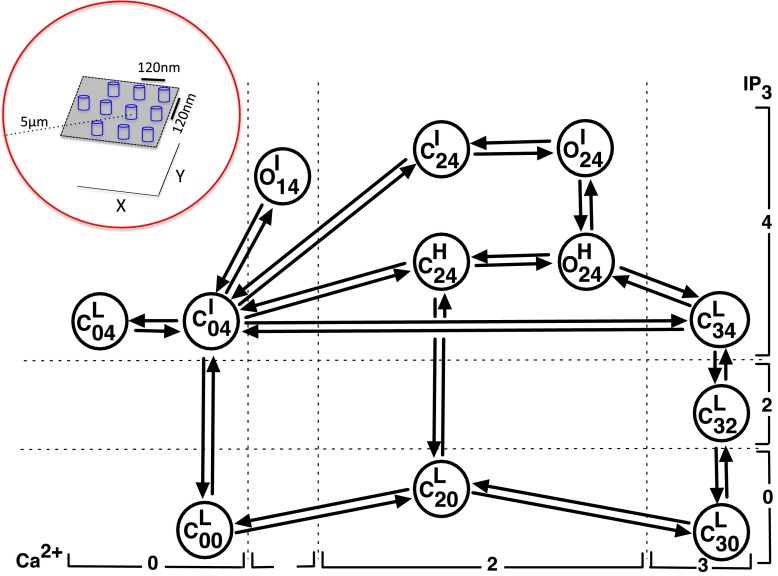
We modeled the gating of the single InsP₃R channel using the Markov chain shown in Fig. 1 that was originally developed in [10]. This model has 3 open and 9 closed states represented by the letters O and C respectively. The subscript of letter O or C indicates the number of ligands bound to the channel in the state. The first and second indexes respectively in the subscript correspond to the number of Ca²⁺ ions and InsP₃ molecules bound to the channel when in the given state. The model also takes into account the modal behavior of the channel. The superscript in each state represents the mode to which the state belongs. The letters L, I and H stand for low, intermediate and high activity mode respectively. Rates between various states are given in Table 1 and the various parameters used in the rates are given in Tables 2 and 3. Notice that some probability flux parameters given in Table 3 are different from those in [10] because here the transition rates ${\mathrm{C}}_{20}^{\mathrm{L}}\to {\mathrm{C}}_{24}^{\mathrm{H}}$ and ${\mathrm{C}}_{20}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{24}^{\mathrm{H}}$ are assumed to be the same as for ${\mathrm{C}}_{00}^{\mathrm{L}}\to {\mathrm{C}}_{04}^{\mathrm{I}}$ and ${\mathrm{C}}_{00}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{04}^{\mathrm{I}}$ respectively. Although not required for reproducing puffs, this simplification reduces the total number of parameters by two without qualitatively changing the fits to the data shown in [10]. We direct the interested reader to Ref. [10] for the fits to the single channel data. We also remark that this model successfully reproduces puffs provided that the Ca²⁺ concentration at the channel mouth is high enough (at least 100 μM), which comes naturally from the conversion of the channel current to Ca²⁺ flux (see below) [11, 12].

Fig. 1.

Kinetic scheme for the single-channel model. The model has nine closed states: ${\mathrm{C}}_{00}^{\mathrm{L}}$, ${\mathrm{C}}_{20}^{\mathrm{L}}$, ${\mathrm{C}}_{30}^{\mathrm{L}}$, ${\mathrm{C}}_{32}^{\mathrm{L}}$, ${\mathrm{C}}_{34}^{\mathrm{L}}$, ${\mathrm{C}}_{04}^{\mathrm{L}}$, ${\mathrm{C}}_{04}^{\mathrm{I}}$, ${\mathrm{C}}_{24}^{\mathrm{I}}$ and ${\mathrm{C}}_{24}^{\mathrm{H}}$ and three open states: ${\mathrm{O}}_{14}^{\mathrm{I}}$, ${\mathrm{O}}_{24}^{\mathrm{I}}$ and ${\mathrm{O}}_{24}^{\mathrm{H}}$. The inset shows the channel arrangement inside the cluster (not to scale). The channels are 120 nm apart in the X and Y directions

Table 1.

Transition rates between various states

Transition	Rates (ms−1)
${\mathrm{C}}_{04}^{\mathrm{I}}\to {\mathrm{C}}_{24}^{\mathrm{H}}$	$\mathrm{rsr}(j_{0414}\mathcal{C},j_{1424}{\mathcal{C}}^2)/K_{{\mathrm{C}}_{04}^{\mathrm{I}}}$
${\mathrm{C}}_{04}^{\mathrm{I}}\leftarrow {\mathrm{C}}_{24}^{\mathrm{H}}$	$\mathrm{rsr}(j_{0414}\mathcal{C},j_{1424}{\mathcal{C}}^2)/K_{{\mathrm{C}}_{24}^{\mathrm{H}}}{\mathcal{C}}^2$
${\mathrm{C}}_{24}^{\mathrm{H}}\to {\mathrm{O}}_{24}^{\mathrm{H}}$	$j_{2424}^{\text{HH}}/K_{{\mathrm{C}}_{24}^{\mathrm{H}}}$
${\mathrm{C}}_{24}^{\mathrm{H}}\leftarrow {\mathrm{O}}_{24}^{\mathrm{H}}$	$j_{2424}^{\text{HH}}/K_{{\mathrm{O}}_{24}^{\mathrm{H}}}$
${\mathrm{O}}_{24}^{\mathrm{H}}\to {\mathrm{C}}_{34}^{\mathrm{L}}$	$j_{2434}\mathcal{C}/K_{{\mathrm{O}}_{24}^{\mathrm{H}}}$
${\mathrm{O}}_{24}^{\mathrm{H}}\leftarrow {\mathrm{C}}_{34}^{\mathrm{L}}$	$j_{2434}/K_{{\mathrm{C}}_{34}^{\mathrm{L}}}$
${\mathrm{C}}_{04}^{\mathrm{I}}\to {\mathrm{C}}_{34}^{\mathrm{L}}$	$\mathrm{rsr}(j_{0414}^{\text{IL}}\mathcal{C},j_{1424}^{\text{IL}}{\mathcal{C}}^2,j_{2434}^{\text{IL}}{\mathcal{C}}^3)/K_{{\mathrm{C}}_{04}^{\mathrm{I}}}$
${\mathrm{C}}_{04}^{\mathrm{I}}\leftarrow {\mathrm{C}}_{34}^{\mathrm{L}}$	$\mathrm{rsr}(j_{0414}^{\text{IL}}\mathcal{C},j_{1424}^{\text{IL}}{\mathcal{C}}^2,j_{2434}^{\text{IL}}{\mathcal{C}}^3)/K_{{\mathrm{C}}_{34}^{\mathrm{L}}}{\mathcal{C}}^3$
${\mathrm{C}}_{04}^{\mathrm{I}}\to {\mathrm{O}}_{14}^{\mathrm{I}}$	$j_{0414}^{\text{II}}\mathcal{C}/K_{{\mathrm{C}}_{04}^{\mathrm{I}}}$
${\mathrm{C}}_{04}^{\mathrm{I}}\leftarrow {\mathrm{O}}_{14}^{\mathrm{I}}$	$j_{0414}^{\text{II}}/K_{{\mathrm{O}}_{14}^{\mathrm{I}}}$
${\mathrm{C}}_{24}^{\mathrm{I}}\to {\mathrm{O}}_{24}^{\mathrm{I}}$	$j_{2424}^{\text{II}}/K_{{\mathrm{C}}_{24}^{\mathrm{I}}}$
${\mathrm{C}}_{24}^{\mathrm{I}}\leftarrow {\mathrm{O}}_{24}^{\mathrm{I}}$	$j_{2424}^{\text{II}}/K_{{\mathrm{O}}_{24}^{\mathrm{I}}}$
${\mathrm{O}}_{24}^{\mathrm{I}}\to {\mathrm{O}}_{24}^{\mathrm{H}}$	$j_{2424}/K_{{\mathrm{O}}_{24}^{\mathrm{I}}}$
${\mathrm{O}}_{24}^{\mathrm{I}}\leftarrow {\mathrm{O}}_{24}^{\mathrm{H}}$	$j_{2424}/K_{{\mathrm{O}}_{24}^{\mathrm{H}}}$
${\mathrm{C}}_{04}^{\mathrm{I}}\to {\mathrm{C}}_{04}^{\mathrm{L}}$	$j_{0404}/K_{{\mathrm{C}}_{04}^{\mathrm{I}}}$
${\mathrm{C}}_{04}^{\mathrm{I}}\leftarrow {\mathrm{C}}_{04}^{\mathrm{L}}$	$j_{0404}/K_{{\mathrm{C}}_{04}^{\mathrm{L}}}$
${\mathrm{C}}_{32}^{\mathrm{L}}\to {\mathrm{C}}_{34}^{\mathrm{L}}$	$j_{3334}{\mathcal{I}}^2/K_{{\mathrm{C}}_{32}^{\mathrm{L}}}$
${\mathrm{C}}_{32}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{34}^{\mathrm{L}}$	$j_{3334}/K_{{\mathrm{C}}_{34}^{\mathrm{L}}}$
${\mathrm{C}}_{30}^{\mathrm{L}}\to {\mathrm{C}}_{32}^{\mathrm{L}}$	$j_{3132}{\mathcal{I}}^2/K_{{\mathrm{C}}_{30}^{\mathrm{L}}}$
${\mathrm{C}}_{30}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{32}^{\mathrm{L}}$	$j_{3132}/K_{{\mathrm{C}}_{32}^{\mathrm{L}}}$
${\mathrm{C}}_{20}^{\mathrm{L}}\to {\mathrm{C}}_{30}^{\mathrm{L}}$	$j_{2030}\mathcal{C}/K_{{\mathrm{C}}_{20}^{\mathrm{L}}}$
${\mathrm{C}}_{20}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{30}^{\mathrm{L}}$	$j_{2030}/K_{{\mathrm{C}}_{30}^{\mathrm{L}}}$
${\mathrm{C}}_{00}^{\mathrm{L}}\to {\mathrm{C}}_{04}^{\mathrm{I}}$	$\mathrm{rsr}(j_{0001}\mathcal{I},j_{0304}{\mathcal{I}}^4)$
${\mathrm{C}}_{00}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{04}^{\mathrm{I}}$	$\mathrm{rsr}(j_{0001},j_{0304}{\mathcal{I}}^3)/K_{{\mathrm{C}}_{04}^{\mathrm{I}}}{\mathcal{I}}^3$
${\mathrm{C}}_{20}^{\mathrm{L}}\to {\mathrm{C}}_{24}^{\mathrm{H}}$	same as that for ${\mathrm{C}}_{00}^{\mathrm{L}}\to {\mathrm{C}}_{04}^{\mathrm{I}}$
${\mathrm{C}}_{20}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{24}^{\mathrm{H}}$	same as that for ${\mathrm{C}}_{00}^{\mathrm{L}}\leftarrow {\mathrm{C}}_{04}^{\mathrm{I}}$

rsr is the reciprocal of a sum of reciprocals i.e., $\mathrm{rsr}(x_1,x_2,\cdots x_n)\equiv \frac{1}{{\sum }_{i=1}^n\frac{1}{x_i}}$

Table 2.

Parameters for occupancies of all states

Parameters	Values
$K_{C_{00}^L}$	1
$K_{C_{32}^L}$	1.4785×107 μM−5
$K_{C_{34}^L}$	7.76239×107 μM−7
$K_{O_{14}^I}$	1.20225×108 μM−5
$K_{C_{04}}=K_{{\mathrm{C}}_{04}^{\mathrm{L}}}+K_{{\mathrm{C}}_{04}^{\mathrm{I}}}$	2.18267×108 μM−4
$K_{C_{24}}=K_{{\mathrm{C}}_{24}^{\mathrm{H}}}+K_{{\mathrm{C}}_{24}^{\mathrm{I}}}$	6.1646×108 μM−6
$K_{O_{24}}=K_{{\mathrm{O}}_{24}^{\mathrm{H}}}+K_{{\mathrm{O}}_{24}^{\mathrm{I}}}$	2.04174×109 μM−6
p	0.8
r	0.95
$K_{C_{04}^L}$	$p{K}_{C_{04}}$
$K_{C_{04}^I}$	$(1-p)K_{C_{04}}$
$K_{O_{24}^H}$	$r{K}_{O_{24}}$
$K_{O_{24}^I}$	$(1-r)K_{O_{24}}$
$K_{C_{24}^H}$	$0.5K_{C_{24}}$
$K_{C_{24}^I}$	$(1-0.5)K_{C_{24}}$
$K_{C_{20}^L}$	$K_{C_{24}^H}/K_{C_{04}^I}$
$K_{C_{30}^L}$	$K_{C_{34}^L}/K_{C_{04}^I}$

Table 3.

Flux parameters used in the model

Parameters	Pathway	Values
j 0414	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{C}}_{24}^{\mathrm{H}}$	5.11487×105 μ M −5 ms −1
j 1424	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{C}}_{24}^{\mathrm{H}}$	9.88434×106 μ M −6 ms −1
j 2434	${\mathrm{O}}_{24}^{\mathrm{H}}\rightleftharpoons {\mathrm{C}}_{34}^{\mathrm{L}}$	5.08204×104 μ M −7 ms −1
$j_{0414}^{\text{IL}}$	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{C}}_{34}^{\mathrm{L}}$	6.55954×104 μ M −5 ms −1
$j_{1424}^{\text{IL}}$	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{C}}_{34}^{\mathrm{L}}$	1.00237×103 μ M −6 ms −1
$j_{2434}^{\text{IL}}$	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{C}}_{34}^{\mathrm{L}}$	8.06811×105 μ M −7 ms −1
j 2030	${\mathrm{C}}_{20}^{\mathrm{L}}\rightleftharpoons {\mathrm{C}}_{30}^{\mathrm{L}}$	8.95522×10−3 μ M −3 ms −1
$j_{0414}^{\text{II}}$	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{O}}_{14}^{\mathrm{I}}$	2.18273×105 μ M −5 ms −1
$j_{2424}^{\text{II}}$	${\mathrm{C}}_{24}^{\mathrm{I}}\rightleftharpoons {\mathrm{O}}_{24}^{\mathrm{I}}$	1.02087×107 μ M −7 ms −1
j 2424	${\mathrm{O}}_{24}^{\mathrm{I}}\rightleftharpoons {\mathrm{O}}_{24}^{\mathrm{H}}$	7.17650×105 μ M −6 ms −1
j 0404	${\mathrm{C}}_{04}^{\mathrm{I}}\rightleftharpoons {\mathrm{C}}_{04}^{\mathrm{L}}$	5.76225×104 μ M −4 ms −1
$j_{2424}^{\text{HH}}$	${\mathrm{C}}_{24}^{\mathrm{H}}\rightleftharpoons {\mathrm{O}}_{24}^{\mathrm{H}}$	6.46532×107 μ M −6 ms −1
j 3132	${\mathrm{C}}_{30}^{\mathrm{L}}\rightleftharpoons {\mathrm{C}}_{34}^{\mathrm{L}}$	5.01187 μ M −3 ms −1
j 3334	${\mathrm{C}}_{32}^{\mathrm{L}}\rightleftharpoons {\mathrm{C}}_{34}^{\mathrm{L}}$	2.00475×104 μ M −7 ms −1
j 0001	${\mathrm{C}}_{00}^{\mathrm{L}}\rightleftharpoons {\mathrm{C}}_{04}^{\mathrm{I}}$	0.0033 μ M −1 ms −1
j 0304	${\mathrm{C}}_{00}^{\mathrm{L}}\rightleftharpoons {\mathrm{C}}_{04}^{\mathrm{I}}$	8.019×105 μ M −4 ms −1

Superscripts are used to distinguish between different flux parameters that connect different pairs of states that have the same numbers of ligands bound. For example, in both transitions ${\mathrm{C}}_{24}^{\mathrm{I}}\rightleftharpoons {\mathrm{O}}_{24}^{\mathrm{I}}$ and ${\mathrm{C}}_{24}^{\mathrm{H}}\rightleftharpoons {\mathrm{O}}_{24}^{\mathrm{H}}$, ${\mathrm{C}}_{24}^{\mathrm{I}}$ and ${\mathrm{C}}_{24}^{\mathrm{H}}$ are bound to the same number of Ca²⁺ and InsP₃R and so are ${\mathrm{O}}_{24}^{\mathrm{I}}$ and ${\mathrm{O}}_{24}^{\mathrm{H}}$. However, the two transitions have different flux parameters

We placed a single cluster of 10 InsP₃R channels in a planar membrane separated by 120 nm in the X and Y directions (Fig. 1 inset) with each channel at the center of a 5 μm radius sphere. Thus each channel is first individually simulated by placing it at the center of a 5 μm radius sphere and finally the contributions of all channels to the spatial Ca²⁺ profile of a given channel are computed using the superposition of the individual Ca²⁺ profiles of all channels (see below). The gating of each channel is given by the 12 state model described above. We determined the state of the channel at a given time using a stochastic method described previously [12–14].

Ca²⁺ concentration on the cytoplasmic side of the cluster is controlled by diffusion; the flux coming out from the ER through InsP₃Rs, J _j; and the concentrations of free stationary buffers, free mobile buffers and free dye: b _s, b _m and b _d, respectively. Thus the rate equations for Ca²⁺ concentration at distance r _j and time t due to channel j, c ^j(r _j,t), and free Ca²⁺ buffers $b_s^j(r_j,t)$, $b_m^j(r_j,t)$, and $b_d^j(r_j,t)$ at distance r _j and time t from channel j are described as:

$$\begin{array}{rcll}\frac{\partial c^j(r_j,t)}{\mathrm{\partial t}}& =& D_c{\nabla }_j^2{c}^j+J_j+k_s^r(B_s-b_s^j)-k_s^f{c}^j{b}_s+k_m^r(B_m-b_m^j)-k_m^f{c}^j{b}_m^j& \\ & & +k_d^r(B_d-b_d^j)-k_d^f{c}^j{b}_d^j& \end{array}$$ 1

$$\begin{array}{rcll}\frac{\partial b_s^j}{\mathrm{\partial t}}& =& k_s^r(B_s-b_s^j)-k_s^f{c}^j{b}_s^j& \end{array}$$ 2

$$\begin{array}{rcll}\frac{\partial b_m^j}{\mathrm{\partial t}}& =& D_m{\nabla }_j^2{b}_m^j+k_m^r(B_m-b_m^j)-k_m^f{c}^j{b}_m^j& \end{array}$$ 3

$$\begin{array}{rcll}\frac{\partial b_d^j}{\mathrm{\partial t}}& =& D_d{\nabla }_j^2{b}_d^j+k_d^r(B_d-b_d^j)-k_d^f{c}^j{b}_d^j\mathrm{.}& \end{array}$$ 4

In the above equations B _i is the total concentration, $k_i^f$ the forward (binding) rate and $k_i^r$ reverse (unbinding) rate for the various buffers with i = s,m,d. D _c, D _m and D _d are the diffusion coefficients for Ca²⁺, mobile buffers and dye respectively. These evolution equations comprise an approximation analogous to the tight-binding model from solid state physics in which the consumption of buffers in the vicinity of the j ^th channel due to Ca²⁺ released by the i ^th channel (with i≠j) is neglected as the buffer consumed by a channel near its own pore is much higher than the buffer consumed by the same channel at the location of its neighbor [12]. As pointed out in [15], this may lead to underestimation of cytosolic Ca²⁺ concentration during the opening of channels and overestimation when all channels have closed, which makes this a crude approximation but not as crude as others have made in the field [16–18].

We consider a slow mobile buffer mimicking ethylene glycol tetraacetic acid (EGTA) and the fast mobile buffer 1,2-bis(o-aminophenoxy)ethane-N,N,N’,N’-tetraacetic acid (BAPTA). The term ‘slow’ refers to the binding kinetics of the buffer, not its mobility. We simulate the propagation of Ca²⁺ and buffers throughout a homogeneous 3D cytosolic space using fixed boundary conditions where ${\mathcal{C}}_i=50$ nM at the boundary. As presented in [15] these boundary conditions can be written in mathematical form as

$$\begin{array}{rcll}\underset{r_j\to 0}{lim}\left(-2\pi r_j^2{D}_c\frac{\delta c^j}{\delta r_j}\right)=\sigma ,c^j\left(R\right)=50\mathrm{n}\mathrm{M}\mathrm{.}& & & \end{array}$$ 5

where σ = I/(Z×F) is the source strength and R=5 μm is the radius of the simulating sphere. I, Z=2 and F represent the Ca²⁺ current passing through the channel, valence of Ca²⁺ and Faraday’s constant respectively. Previous studies have concluded that a single InsP₃R channel releases a current of about 0.05–0.5 pA [8, 19, 20]. Throughout this manuscript we will assume a standard single-channel current of I=0.05 pA when the channel is open, and zero otherwise.

The concentration of a given free buffer at the boundary of a sphere is fixed at its total concentration. For example, EGTA is fixed at 100 μM etc.

J _j = σ/δ V in (1) is the Ca²⁺ flux through the j ^th channel when open, where δ V is the volume of the hemisphere over the channel having a radius of 2.5 nm [21]. J _j=0 when the channel is closed. The various parameters used in (1–4) are given in Table 4.

Table 4.

Concentrations and rates

Quantity	Symbol	—	Numerical value	Reference
Resting Cytosolic Calcium	C a rest	=	50 nM	[22]
Stationary buffer	B s	=	100 μM	[23, 24]
Dye Buffer	B d	=	25,40 μM
EGTA	B EGTA	=	0,100 μM
BAPTA	B BAPTA	=	0,50 μM
C a 2+	D c	=	0.223 μ m 2/ms	[25]
Dye	D d	=	0.200 μ m 2/ms	[26]
Mobile Buffers	D m	=	0.200 μ m 2/ms	[26]
Stationary Buffer	$k_s^f$	=	0.2 μ M 2/ms	[22]
	$k_s^r$	=	0.4/m s	[22]
Dye Buffer	$k_d^f$	=	0.1 μM/ms	[22, 26]
	$k_d^r$	=	0.025/ms	[22, 26]
EGTA	$k_{\mathrm{EGTA}}^f$	=	0.006 μM/ms	[22, 26]
	$k_{\mathrm{EGTA}}^r$	=	0.001/ms	[22, 26]
BAPTA	$k_{\mathrm{BAPTA}}^f$	=	0.8 μM/ms	[22, 26]
	$k_{\mathrm{BAPTA}}^r$	=	0.2/ms	[22, 26]

The propagation of Ca²⁺ and buffers is simulated throughout a 3D cytosolic space. Considering the spherical symmetry around the channel, the Laplacian of Ca²⁺ and buffers in spherical coordinates is given as:

$$\begin{array}{rcll}{\nabla }_j^{2}X(r_j,t)=\frac{1}{r_j^2}\frac{\partial }{\partial r_j}\left(r_j^2\frac{\mathrm{\partial X}}{\partial r_j}\right)& & & \end{array}$$ 6

where X = c,b _m,b _d.

The set of differential equations (1–6) was solved implicitly on a spherical volume of radius 5 μm with a spatial grid size of 5 nm using the Tridiagonal Matrix (TM) solver for each channel and the contribution of all channels was summed for the instantaneous Ca²⁺ concentration at a given point in space [12]. The idea is that we are simulating the dynamics of a puff-site that is far from the plasma membrane, in essence a single puff-site in a semi-infinite medium. Under the simulated conditions the Ca²⁺ concentration at 5 μm does not change significantly. Thus we use 5 μm as the radius of the simulated volume. Increasing the radius of the simulated volume does not make an appreciable difference. The assumption that each channel has its own reservoir of buffers converts the 3D problem into N 1D problems, where N is the total number of channels. In this case, we solve 10 1D problems each with 1000 grid points. Solving this problem numerically with a similar resolution in Cartesian coordinates, for example, would require about a billion grid points, a very demanding computational job where thousands of puffs have to be simulated to extract statistics.

Finally, the Ca²⁺ concentration at the location of each channel i, ${\mathcal{C}}_i$, is updated by adding the contributions from other channels in the cluster

$$\begin{array}{rcll}{\mathcal{C}}_i=\sum _{j=1}^{10}{c}^j\left(r_{\mathrm{ij}}\right)& & & \end{array}$$ 7

where r _ji is the distance between channels i and j.

As we discussed in [12], this method is similar in spirit to the quasi-static approximation made by Nguyen et al. [16] where local Ca²⁺ experienced by channel i due to other channels was calculated as:

$$C_i={\sum }_{j=1}^N\frac{I_j{e}^{-r/\lambda }}{2\mathrm{\pi Dr}}\mathrm{.}$$

Here I_j, r, λ and D are the source amplitude of channel j, distance of channel j from channel i, buffer space constant and effective diffusion coefficient of Ca²⁺ respectively. I _j=0 when channel j is closed (see also [17]). The approximation made by [16, 17] is binary; an open channel contributes $\frac{I{e}^{-r/\lambda }}{2\mathrm{\pi Dr}}$ while a closed channel makes no contribution to the overall Ca²⁺ profile. We relax the binary static approximation made in these two studies. When a channel first opens the contribution to the overall Ca²⁺ profile is approximately

$$\frac{I{e}^{-r/\lambda }}{2\mathrm{\pi Dr}}\mathrm{.}$$

The contribution to the profile continues to evolve on a low time-scale. When an open channel first closes, its contribution to the overall profile rapidly drops to a low but nonzero level and then decays slowly to zero. Furthermore, when the first channel opens, the quasi-static approximation made by Nguyen et al. [16] fixes the first channel’s contribution to the Ca²⁺ concentration at the second channel. In reality, the first channel’s contribution to the Ca²⁺ concentration at the second channel will continue to increase as long as the first channel is open. Our approximation tracks these time-dependent contributions of the channels to the Ca²⁺ profile.

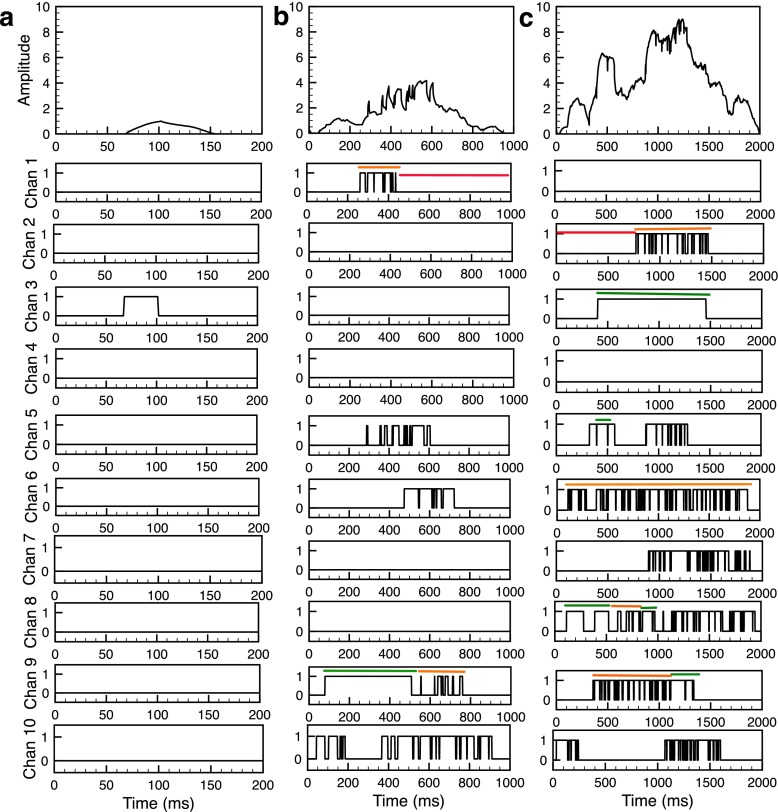
Fluorescence signals representing Ca²⁺ time-traces recorded by Total Internal Reflection Fluorescence (TIRF) microscopy shown in Fig. 2 (top panels) are estimated by the procedure outlined in [12, 19].

Fig. 2.

Time series of an elementary Ca²⁺ event from the model. Example of blip (a), intermediate puff (b) and large puff (c). Top panels in (a), (b) and (c) show the fluorescence signal caused by Ca²⁺ released during the event followed by 10 panels showing the gating of all channels in the cluster. Examples of the three different modes are shown by the lines over time traces, where the red, orange and green lines represent the low, intermediate and high mode respectively. InsP₃=100 nM, B _s=100 μM, B _d=25 μM, B _EGTA=100 μM, and B _BAPTA=0 μM

In [10] we derived analytical expressions for the modal characteristics of a single channel as a function of ligand concentrations using the Markov chain model in Fig. 1. However, in the present situation where ${\mathcal{C}}_i$ changes dynamically during the evolution of blips and puffs we use the algorithm developed in [4] to characterize the modal behavior of individual channels in the cluster. A detailed description of the algorithm is given in [4] and [14] and briefly described here. The channel makes a modal transition when two or more consecutive burst-terminating gaps (t _g) have t _g≤200 ms following at least one gap with t _g>200 ms but not when just one gap has t _g≤200 ms. However, a modal transition is recognized when a single burst-terminating gap with t _g>200 ms follows one or several consecutive gaps with t _g≤200 ms. Similarly, a modal transition is registered when a single channel burst has burst duration t _b>100 ms following a series of bursts with t _b≤100 ms: a modal transition is only registered when two consecutive channel bursts have t _b≤100 ms following a series of bursts with t _b>100 ms. After the modal transitions are identified, the channel is then classified as being in the I mode if t _g≤200 ms and t _b≤100 ms; in the H mode if t _g≤200 ms and t _b>100 ms; and in the L mode if t _g>200 ms and t _b≤100 ms.

We remark that although the single channel model shown in Fig. 1 does not include an open state when InsP₃R gates are in the L mode, the modal characterization algorithm discussed in the previous paragraph will detect an open state in the L mode when the criterion for the L mode is met while running the algorithm on the time traces obtained for each channel during blips and puffs. We would like to mention that the modal statistics can also be derived directly without using the algorithm described above by recording all twelve states for each channel as a function of time in the simulation, in which case one would not see an open state when a channel is gating in the L mode.

Results

The stochastic scheme outlined in the previous section allows us to simulate elementary Ca²⁺ release events. Examples of Ca²⁺ blips and puffs given by the model are shown in Fig. 2. The top panels in Fig. 2a, b, c show the event amplitudes in terms of fluorescence signal caused by Ca²⁺ release through the cluster, followed by 10 panels showing the gating of all 10 channels during the event. The blip shown in Fig. 2a is caused by the brief single opening of channel 3 in the cluster while all other channels remain closed. Thus all channels gate in low mode during the blip. During the small puff, five channels open, exhibiting short bursts that are reminiscent of intermediate mode (Fig. 2b). Only channel 9 briefly exhibits high mode followed by intermediate mode. The remaining five channels are in low mode. Eight out of ten channels open simultaneously during the longer puff (Fig. 2c). All open channels, except channel 6, spend some fraction of time in the high mode. Thus it is evident from Fig. 2 that, as the time spent by the channels in the intermediate and high modes increases, the size of the elementary Ca²⁺ release event increases.

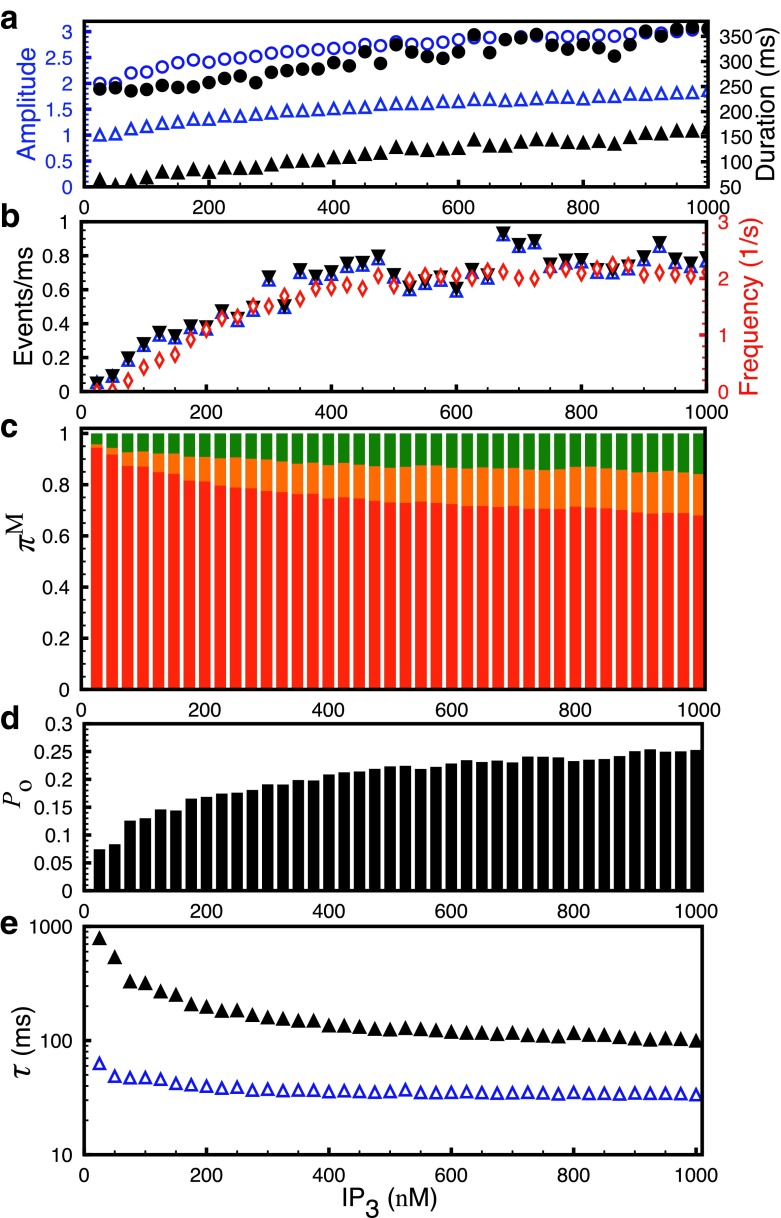
To analyze the single channel behavior during Ca²⁺ signals of different spatiotemporal scales, we increase the concentration of InsP₃. In experiments, modest InsP₃ concentration leads to spatially confined Ca²⁺ blips, confined Ca²⁺ blips and puffs [5, 27], while larger InsP₃R stimulus causes whole cell waves or oscillations [28–30]. Bearing in mind this transition from blips to puffs and waves as a function of InsP₃ concentration, we vary InsP₃ in the model from 25 nM to 1 μM and plot the average statistics of elementary Ca²⁺ events along with the modal characteristics of InsP₃R as shown in Fig. 3. For a given InsP₃R concentration, we run the simulation for 1000 seconds (real time) and compute the average statistical properties of blips and puffs based on several hundred events. Both the average amplitude defined as the maximum number of simultaneously open channels during the event (Fig. 3a, open triangles) and the duration (Fig. 3a, filled triangles) of the blips and puffs combined increase as we increase InsP₃ concentration. The cluster particularly leads to larger amplitude (Fig. 3a, open circles) and longer duration (Fig. 3a, filled circles) puffs for high InsP₃ concentration that would most likely recruit other puff sites leading to whole cell waves and oscillations [29, 31]. Similarly, the average rate of channel openings (Fig. 3b, open triangles) and closings during the events (Fig. 3b, filled triangles) increases as a function of InsP₃ concentration. The average rate of channel openings and closings was calculated by counting the total number of channels that opened or closed during the event and dividing the number by the duration of that event. Finally, the openings and closings per millisecond were averaged for all events. The frequency of puffs saturates after an initial rise as a function of InsP₃ concentration indicating a larger fraction of events with larger amplitude and longer life-time (Fig. 3b, diamonds). The change in the average rate of channel openings and closings indicates a change in the gating behavior or activity mode of InsP₃R and shows a relationship with the average statistics of elementary Ca²⁺ release events.

Fig. 3.

Statistics of elementary Ca²⁺ release events and single channel modal properties as a function of InsP₃ concentration. a Average amplitude of blips and puffs combined (empty triangles), puffs only (empty circles) and duration of blips and puffs combined (filled triangles), puffs only (filled circles). b mean channel openings (empty triangles) and closings (filled triangles) per millisecond during the puffs and frequency of puffs (empty diamonds). c Prevalence, π ^M, of the three modes. The superscript M is L for low mode (red), I for intermediate mode (orange) and H for high mode (green). d P _o and e τ _o (open triangles) and τ _c (filled triangles) of InsP₃R. B _s=100 μM, B _d=25 μM, B _EGTA=100 μM, and B _BAPTA=0 μM

Figure 3c shows the prevalences (the probability of the channel gating in a given mode) of three modes, π ^M, defined as the normalized probability that the channel is gating in a given mode. The prevalence of intermediate and high modes increases as we increase InsP₃R concentration, indicating a direct link between the modal behavior of the channel and Ca²⁺ patterning. The P _o, mean open (τ _o), and closed (τ _c) time of the channel are the other measures of the modal behavior of the channel. The average P _o of the channels in the cluster increases from a value representative of low mode to that higher than the intermediate mode (Fig. 3d). τ _o (Fig. 3e, open triangles) remains almost constant while τ _c (Fig. 3e, filled triangles) decreases by an order of magnitude as we increase InsP₃ concentration. The behavior of τ _o and τ _c shown here is again an indication of the change in the modal behavior of the channel. This is reminiscent of experimental data where τ _c of the channel was observed to drop from over a second for the low mode to less than 100 ms in intermediate and high modes [4, 14]. The τ _o on the other hand remained constant within a few milliseconds.

To further illustrate the relationship between Ca²⁺ patterning and the gating behavior of a single channel, we plot the average characteristics of elementary Ca²⁺ release events as a function of modal statistics (Fig. 4). The average amplitude, frequency and duration of blips and puffs increase as the total prevalence of intermediate and high modes increases (Fig. 4a, b). The average amplitude, frequency (Fig. 4c), and average life-time of puffs (Fig. 4d) decrease exponentially as a function of τ _c of a single channel.

Fig. 4.

Average statistics of elementary Ca²⁺ release events vary as a function of single channel modal characteristics. a Average amplitude (triangles), frequency (diamonds) and b mean duration of puffs as a function of total prevalence of I and H modes. c Average amplitude (triangles) and frequency (diamonds) and d mean duration of puffs (triangles) versus the mean closed time of a single channel. B _s=100 μM, B _d=25 μM, B _EGTA=100 μM and B _BAPTA=0 μM

So far we have been exploring the dependence of average statistics of elementary Ca²⁺ events on the modal characteristics of individual channels. To explore a more one-to-one relation of puffs with the modal behavior, we binned thousands of events according to their amplitude and computed the modal characteristics of all channels for each bin. Note that each bin contains many events having the same amplitude. Figure 5 shows the result of these simulations. A higher probability of low mode leads to blips; however, as the probability of intermediate and high modes increases, the amplitude of events increases. When the individual channels have more than 50% probability of being in the intermediate and/or high modes, on average nine out of ten channels in the cluster open during a puff, resulting in very large Ca²⁺ events that would most likely recruit neighboring puff sites, thus triggering global Ca²⁺ signals (Fig. 5a). The P _o of channels rise from the value close to the low mode to the range between intermediate and high modes (Fig. 5b). The τ _o remains constant except for an early rise as the amplitude increases (open triangles, Fig. 5c). The τ _c of the channel drops significantly, indicating a shift in the gating of channels from low to intermediate and high modes resulting in bigger puffs (filled triangles, Fig. 5c).

Fig. 5.

Modal properties of channels during events with different amplitudes. a Prevalence of low (red), intermediate (orange) and high (green) mode during puffs with different average amplitudes. b P _o and c τ _o (open triangles), τ _c (filled triangles) of InsP₃R during puffs with different average amplitudes. B _s=100 μM, B _d=25 μM, B _EGTA=100 μM, and B _BAPTA=0 μM

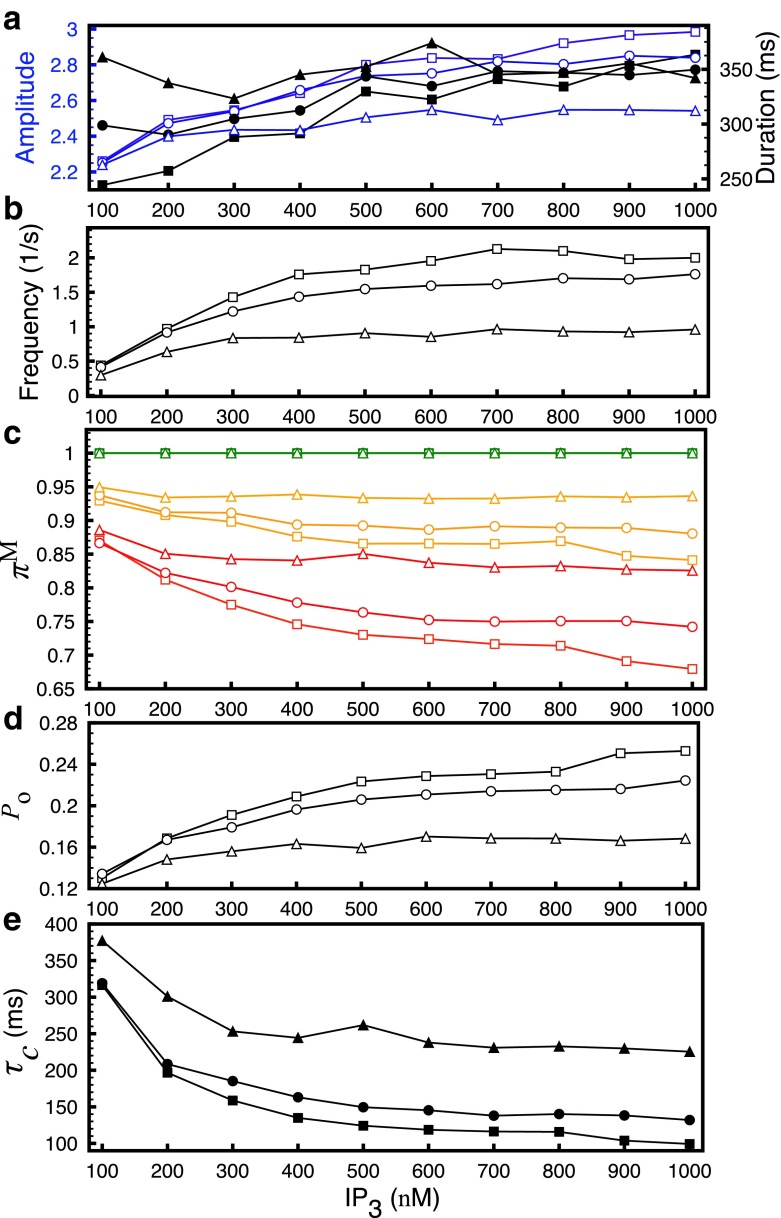
Next, we evaluate the effect of various buffers on the gating properties of a single InsP₃R inside the puff site and the statistics of puffs. We change the concentration of a single buffer at a time and compare our results with those from the control simulations discussed above (B _s=100 μM, B _d=25 μM, B _EGTA=100 μM and B _BAPTA=0 μM) (Fig. 6, squares). Increasing B _d from 25 μM to 40 μM (Fig. 6, circles) and B _BAPTA from 0 μM to 50 μM (Fig. 6, triangles) increases the duration of puffs (Fig. 6a, filled symbols), especially at lower InsP₃ concentration. The average amplitude of puffs at smaller InsP₃ concentration decreases slightly but has a significant drop at high InsP₃ concentration (Fig. 6a, open symbols). Thus increasing both dye and BAPTA lead to smaller puffs with longer lifetimes. The frequency of puffs also decreases significantly (Fig. 6b). This behavior of puffs can be explained by the change in the modal behavior of the channels where the prevalence of low mode increases and that of the high mode decreases as we increase dye and BAPTA concentrations (Fig. 6c). The prevalence of the intermediate mode on the other hand decreases slightly as we increase dye and BAPTA concentrations. Notice that the prevalence of high mode in (Fig. 6c) is given by the difference in the green and orange lines, while that of intermediate mode is given by the difference between the red and orange lines for a given parameter set (as in Fig. 3c). Consistent with our conclusion from Fig. 3, the change in modal behavior results in the decreased P _o (Fig. 6d) and increased τ _c (Fig. 6e) of the channel. The mean open time of the channel does not change significantly and is not shown here. Changing B _EGTA from 100 μM to 0 μM did not change the modal behavior of the single channel and the statistics of the puffs and is therefore not shown here.

Fig. 6.

Statistics of elementary Ca²⁺ release events and single channel modal properties as a function of InsP₃ concentration in the presence of different buffer concentrations. a Average amplitude (empty symbols) and duration of puffs (filled symbols), b frequency of puffs and c prevalence π ^M of the three modes. The superscript M is L for low mode (red), I for intermediate mode (orange) and H for high mode (green). d P _o and e τ _c of InsP₃R. Squares, circles and triangles are for control simulations from Fig. 3 (B _s=100 μM, B _d=25 μM, B _EGTA=100 μM, and B _BAPTA=0 μM), (B _s=100 μM, B _d=40 μM, B _EGTA=100 μM, and B _BAPTA=0 μM) and (B _s=100 μM, B _d=25 μM, B _EGTA=100 μM and B _BAPTA=50 μM) respectively

Conclusions

The opening of a single InsP₃R, the nearly simultaneous opening of more than one InsP₃R inside a single channel cluster, and the coordinated activation of multiple clusters on the intracellular stores underlie the spatiotemporal patterning of Ca²⁺ transients essential for regulating numerous highly specific cellular functions [1]. The gating behavior of individual channels in conjunction with the cluster architecture, inter-cluster spacing and buffered and free Ca²⁺ diffusion play a role in shaping these spatiotemporal scales. However, the cluster architecture and inter-cluster spacing do not change significantly over the time scale of these events [32]. Thus the gating behavior of the channel seems to be the main driving force for spatiotemporal patterning of Ca²⁺ signals. Despite many years of research, the limitations in experimental tools impair our ability to elucidate the single channel behavior during Ca²⁺ signals of different scales, which is the subject of this study.

We show that as the average channel behavior changes from gating in the low mode to gating in the intermediate and high modes the amplitude and duration of Ca²⁺ signals increase (Figs. 2 and 3). In fact, the mean amplitude, duration and frequency of Ca²⁺ signals all increase linearly as functions of total prevalence of intermediate and high modes (Fig. 4a, b). Channels gating predominantly in low mode lead to blips (Figs. 2a and 5). The size of the events increases from blips to small puffs as the probability of the channel gating in the intermediate and high mode begins to rise (Figs. 2b, c, and 5). When the prevalence of intermediate and/or high modes is very high, the cluster gives rise to very large puffs. For example, if the combined prevalence of intermediate and high modes is more than 50%, the puff site generates puffs where on average nine out of ten channels are open during the puff (Fig. 5). Although we do not simulate whole-cell Ca²⁺ waves and oscillations, these events with large amplitude and longer duration occurring at high frequency would most likely trigger global Ca²⁺ signals [31].

Consistent with the observations during single channel patch-clamp experiments [4] and recent modeling study [14], our results show that the transition of the channel behavior from gating predominantly in low mode during small events to gating in the intermediate and high modes during large events is due to the significant decrease in τ _c with a slight increase in τ _o of the channel (Figs. 3e and 5). Thus, the gating properties of InsP₃R leading to Ca²⁺ signals of different scales boil down to the change in τ _c of the channel.

It is worth noticing that our single channel model developed in Ref. [10] is not the only model that is driven by both stationary and nonstationary data on InsP₃R that also represents the modal behavior of the channel. Neither is ours the first instance where a model representing the modal behavior of InsP₃R is used for simulating puffs. Siekmann et al. developed a six-state model incorporating the modal behavior of the channel [33] that was shown to reproduce the statistics of puffs [34] and whole-cell oscillations [35]. Simplifying the six states to a two-state model by getting rid of the intra-modal structure and using the two versions of the model, Siekmann et al. [36] demonstrated that the fundamental process governing the generation of Ca²⁺ puffs and oscillations is primarily controlled by the inter-modal structure, not the intra-modal structure. This conclusion is in line with our observations where we found a direct relationship between the prevalence of the three modes and puff characteristics. Moreover, our study for the first time quantitatively relates the modal characteristics of InsP₃R to the generation of Ca²⁺ signals at different spatiotemporal scales.