PREDICTIVE MODELING OF CHOLERA OUTBREAKS IN BANGLADESH

Abstract

Despite seasonal cholera outbreaks in Bangladesh, little is known about the relationship between environmental conditions and cholera cases. We seek to develop a predictive model for cholera outbreaks in Bangladesh based on environmental predictors. To do this, we estimate the contribution of environmental variables, such as water depth and water temperature, to cholera outbreaks in the context of a disease transmission model. We implement a method which simultaneously accounts for disease dynamics and environmental variables in a Susceptible-Infected-Recovered-Susceptible (SIRS) model. The entire system is treated as a continuous-time hidden Markov model, where the hidden Markov states are the numbers of people who are susceptible, infected, or recovered at each time point, and the observed states are the numbers of cholera cases reported. We use a Bayesian framework to fit this hidden SIRS model, implementing particle Markov chain Monte Carlo methods to sample from the posterior distribution of the environmental and transmission parameters given the observed data. We test this method using both simulation and data from Mathbaria, Bangladesh. Parameter estimates are used to make short-term predictions that capture the formation and decline of epidemic peaks. We demonstrate that our model can successfully predict an increase in the number of infected individuals in the population weeks before the observed number of cholera cases increases, which could allow for early notification of an epidemic and timely allocation of resources.

1. Introduction

In Bangladesh, cholera is an endemic disease that demonstrates seasonal outbreaks [Huq et al., 2005, Koelle and Pascual, 2004, Koelle et al., 2005, Longini et al., 2002]. The burden of cholera is high in that country, with an estimated 352,000 cases and 3,500 to 7,000 deaths annually [International Vaccine Institute, 2012]. We seek to understand the dynamics of cholera and to develop a model that will be able to predict outbreaks several weeks in advance. If the timing and size of a seasonal epidemic could be predicted reliably, vaccines and other resources could be allocated effectively to curb the impact of the disease.

Specifically, we want to understand how the disease dynamics are related to environmental covariates. It is currently not known what triggers the seasonal cholera outbreaks in Bangladesh, but it has been shown that Vibrio cholerae, the causative bacterial agent of cholera, can be detected in the environment year round [Huq et al., 1990, Colwell and Huq, 1994]. Environmental forces are thought to contribute to the spread of cholera, evident from the many cholera disease dynamics models that incorporate the role of the aquatic environment on cholera transmission through an environmental reservoir effect [Codeçco, 2001, Tien and Earn, 2010]. One hypothesis is that proliferation of V. cholerae in the environment triggers the seasonal epidemic, feedback from infected individuals drives the epidemic, and then cholera outbreaks wane, either due to an exhaustion of the susceptibles or due to the deteriorating ecological conditions for propagation of V. cholerae in the environment. We probe this hypothesis using cholera incidence data and ecological data collected from multiple thanas (administrative subdistricts with a police station) in rural Bangladesh over sixteen years. There have been three phases of data collection so far, each lasting approximately three years and being separated by gaps of a few years; the current collection phase is ongoing. For a subset of these data, Huq et al. [2005] used Poisson regression to study the association between lagged predictors from a particular water body to cholera cases in that thana. This resulted in different lags and different significant covariates across multiple water bodies and thanas. Thus, it was hard to derive a cohesive model for predicting cholera outbreaks from the environmental covariates. Also, there is no easy way to account for disease dynamics in this Poisson regression framework. We want to measure the effect of the environmental covariates while accounting for disease dynamics via mechanistic models of disease transmission. Moreover, we want to see if we can make reliable short-term predictions with our model — a task that was not attempted by Huq et al. [2005].

Mechanistic infectious disease models use scientific understanding of the transmission process to develop dynamical systems that describe the evolution of the process [Bretó et al., 2009]. Realistic models of disease transmission incorporate non-linear dynamics [He et al., 2010], which leads to difficulties with statistical inference under these models, specifically in the tractability of the likelihood. Keeling and Ross [2008] demonstrate some of these difficulties; they use an exact stochastic continuous-time, discrete-state model which evolves Markov processes using the deterministic Kolmogorov forward equations to express the probabilities of being in all possible states. However, that method only works for small populations due to computational limitations. To overcome this intractability, Finkenstädt and Grenfell [2000] develop a time-series Susceptible-Infected-Recovered (SIR) model which extends mechanistic models of disease dynamics to larger populations. A similar development is the auto-Poisson model of Held et al. [2005]. To facilitate tractability of the likelihood, both of the above approaches make simplifying assumptions that are difficult to test. Moreover, these discrete-time approaches work only for evenly spaced data or require aggregating the data into evenly spaced intervals. Cauchemez and Ferguson [2008] develop a different, continuous-time, approach to analyze epidemiological time-series data, but assume the transmission parameter and number of susceptibles remain relatively constant within an observation period. Our current understanding of cholera disease dynamics leads us to think that this assumption is not appropriate for modeling endemic cholera with seasonal outbreaks.

To implement a mechanistic approach without these approximations, both maximum likelihood and Bayesian methods can be used. Maximum likelihood based statistical inference techniques use Monte Carlo methods to allow maximization of the likelihood without explicitly evaluating it [He et al., 2010, Bretó et al., 2009, Ionides et al., 2006, Bhadra et al., 2011]. Ionides et al. [2006] use this methodology to study how large scale climate fluctuations influence cholera transmission in Bangladesh. Bhadra et al. [2011] use this framework to study malaria transmission in India. They are able to incorporate a rainfall covariate into their model and study how climate fluctuations influence disease incidence when one controls for disease dynamics, such as waning immunity. Under a Bayesian approach, approximate Bayesian computation (ABC) techniques exist which avoid computation of the likelihood [Rubin, 1984]. Toni et al. [2009] use ABC to estimate parameters of dynamical models, and McKinley et al. [2009] utilize ABC in the context of epidemic models. Alternatively, particle Markov chain Monte Carlo (MCMC) methods have been developed which require only an unbiased estimate of the likelihood [Andrieu et al., 2010]. Rasmussen et al. [2011] use this particle MCMC methodology to simultaneously estimate the epidemiological parameters of a SIR model and past disease dynamics from time series data and gene genealogies. Using Google flu trends data [Ginsberg et al., 2008], Dukic et al. [2012] implement a particle filtering algorithm which sequentially estimates the odds of a pandemic. Notably, Dukic et al. [2012] concentrate on predicting influenza activity. Analyzing the same data, Fearnhead et al. [2014] also develop a predictive model for flu outbreaks using a linear noise approximation [van Kampen, N. G., 1992, Ferm et al., 2008, Komorowski et al., 2009]. Similarly, here we develop a model-based predictive framework for seasonal cholera epidemics in Bangladesh.

In this paper, we use a combination of sequential Monte Carlo and MCMC methods. Specifically, we develop a hidden Susceptible-Infected-Recovered-Susceptible (SIRS) model for cholera transmission in Bangladesh, incorporating environmental covariates. We use a particle MCMC method to sample from the posterior distribution of the environmental and transmission parameters given the observed data, as described by Andrieu et al. [2010]. Further, we predict future behavior of the epidemic within our Bayesian framework. Cholera transmission dynamics in our model are described by a continuous-time, rather than a discrete-time, Markov process to easily incorporate data with irregular observation times. Also, the continuous-time framework allows for greater parameter interpretability and comparability to models based on deterministic differential equations. We test our Bayesian inference procedure using simulated cholera data, generated from a model with a time-varying environmental covariate. We then analyze cholera data from Mathbaria, Bangladesh, similar to the data studied by Huq et al. [2005]. Parameter estimates indicate that most of the transmission is coming from environmental sources. We test the ability of our model to make short-term predictions during different time intervals in the data observation period and find that the pattern of predictive distribution dynamics matches the pattern of changes in the reported number of cases. Moreover, we find that the predictive distribution of the hidden states, specifically the unobserved number of infected individuals, clearly pinpoints the beginning of an epidemic approximately two to three weeks in advance, making our methodology potentially useful during cholera surveillance in Bangladesh.

2. SIRS model with environmental predictors

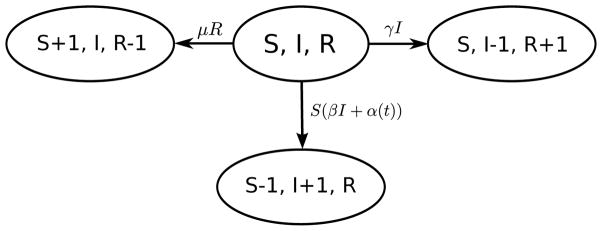
We consider a compartmental model of disease transmission [May and Anderson, 1991, Keeling and Rohani, 2008], where the population is divided into three disease states, or compartments: susceptible, infected, and recovered. We model a continuous process observed at discrete time points. The vector X_t = (S_t, I_t, R_t) contains the numbers of susceptible, infected, and recovered individuals at time t, and we consider a closed population of size N such that N = S_t +I_t +R_t for all t. Individuals move between the compartments with different rates; for cholera transmission we consider the transition rates shown in Figure 1. In this framework, a susceptible individual’s rate of infection is proportional to the number of infected people and the covariates that serve as proxy for the amount of V. cholerae in the environment. Thus, the hazard rate of infection, also called the force of infection, is βI_t+α(t) for each time t, where β represents the infectious contact rate between infected individuals and susceptible individuals and α(t) represents the time-varying environmental force of infection. Possible mechanisms for infectious contact include direct person-to-person transmission of cholera and consumption of water that has been contaminated by infected individuals. If I_t = 0, as it might between seasonal cholera epidemics, the hazard rate of infection is just α(t), so all of the force of infection comes from the environment. Infected individuals recover from infection at a rate γ, where 1/γ is the average length of the infectious period. Once the infected individual has recovered from infection, they move to the recovered compartment. Recovered individuals develop a temporary immunity to the disease after infection. They move from the recovered compartment to the susceptible compartment with rate μ, where 1/μ is the average length of immunity. Similar to Codeçco [2001] and Koelle and Pascual [2004], birth and death are incorporated into the system indirectly through the waning of immunity; thus, instead of representing natural loss of immunity only, μ also represents the loss of immunity through the death of recovered individuals and birth of new susceptible individuals.

Fig 1.

State transitions for Susceptible-Infected-Recovered-Susceptible (SIRS) model for cholera. S, I, and R denote the numbers of susceptible, infected, and recovered individuals. From the current state (S, I, R), the system can transition to one of three new states. These new states correspond to a susceptible becoming infected, an infected recovering from infection, or a recovered individual losing immunity to infection and becoming susceptible. The parameter β is the infectious contact rate, α(t) is the time-varying environmental force of infection, γ is the recovery rate, and μ is the rate at which immunity is lost.

Under this model, X_t is an inhomogeneous Markov process [Taylor and Karlin, 1998] with infinitesimal rates

$${\lambda }_{(S,I,R),(S^{\prime },I^{\prime },R^{\prime })}(t)=\{\begin{array}{ll}(\beta I+\alpha (t))S\hfill & \text{if}{S}^{\prime }=S-1,I^{\prime }=I+1,R^{\prime }=R,\hfill \\ \gamma I\hfill & \text{if}{S}^{\prime }=S,I^{\prime }=I-1,R^{\prime }=R+1,\hfill \\ \mu R\hfill & \text{if}{S}^{\prime }=S+1,I^{\prime }=I,R^{\prime }=R-1,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (1)

where X = (S, I, R) is the current state and X′ = (S′, I′, R′) is a new state. Because R_t = N − S_t − I_t, we keep track of only susceptible and infected individuals, S_t and I_t.

This type of compartmental model is similar to other cholera models in the literature. The time-series SIRS model of Koelle and Pascual [2004] also includes the effects of both intrinsic factors (disease dynamics) and extrinsic factors (environment) on transmission. King et al. [2008] examine both a regular SIRS model and a two-path model to include asymptomatic infections, and use a time-varying transmission term that incorporates transmission via the environmental reservoir and direct person-to-person transmission, but does not allow for feedback from infected individuals into the environmental reservoir. The SIWR model of Tien and Earn [2010] and Eisenberg et al. [2013] allows for infections from both a water compartment (W) and direct transmission and considers the feedback created by infected individuals contaminating the water. To allow for the possibility of asymptomatic individuals, Longini et al. [2007] use a model with a compartment for asymptomatic infections; that model only considers direct transmission. Codeçco [2001] uses an SIR model with no direct person-to-person transmission; infected individuals excrete directly into the environment and susceptible individuals are infected from exposure to contaminated water. Our SIRS model is not identical to any of the above models, but it borrows from them two important features: explicit modeling of disease transmission from either direct person-to-person transmission of cholera or consumption of water that has been contaminated by infected individuals and a time-varying environmental force of infection.

3. Hidden SIRS model

While the underlying dynamics of the disease are described by X_t, these states are not directly observed. The number y_t of infected individuals observed at each time point t is only a random fraction of the number of infected individuals. This fraction depends on both the number of infected individuals that are symptomatic and the fraction of symptomatic infected individuals that seek treatment and get reported (the reporting rate). Thus, y_ti, the number of observed infections at time t_i for observation i ∈{0, 1, …, n}, has a binomial distribution with size I_ti, the number of infected individuals at time t_i, and success probability ρ, the probability of infected individuals seeking treatment, so y_ti |X_ti = (S_ti, I_ti,R_ti), ρ ~ Binomial(I_ti, ρ). Given X_ti, y_ti is independent of the other observations and other hidden states.

We use a Bayesian framework to estimate the parameters of the hidden SIRS model, where the unobserved states X_t are governed by the infinitesimal rates in Equation (1). The parameters that we want to estimate are β, γ, μ, ρ, and the k + 1 parameters that will be incorporated into α(t), the time-varying environmental force of infection. We let C₁(t), …, C_k(t) denote the k time-varying environmental covariates, and we assume α(t) = exp (α₀ + α₁C₁(t) + ⋯ + α_kC_k(t)).

We assume independent Poisson initial distributions for S_t0 and I_t0, with means φ_S and φ_I. The population size N is assumed to be known, and we check sensitivity to this assumption. Parameters that are constrained to be greater than zero, such as β, γ, μ, φ_S, and φ_I, are transformed to the log scale. A logit transformation is used for the probability ρ. We assume independent normal prior distributions on all of the transformed parameters, incorporating biological information into the priors where possible.

We are interested in the posterior distribution Pr(θ|y) ∝ Pr(y|θ)p(θ), where y = (y_t0, …, y_tn), θ = (log(β), log(γ), log(μ), logit(ρ), α₀, …, α_k, log(φ_S), log(φ_I)), and

$$Pr(\mathbf{y}\mid \mathit{\theta })=\sum _{\mathit{X}}\left(\prod _{i=0}^{n}Pr(y_{t_i}\mid I_{t_i},\rho )\left[Pr({\mathit{X}}_{t_0}\mid {\phi }_S,{\phi }_I)\prod _{i=1}^{n}p({\mathit{X}}_{t_i}\mid {\mathit{X}}_{t_{i-1}},\mathit{\theta })\right]\right).$$

Here p(X_ti |X_ti−1, θ) for i = 1, …, n are the transition probabilities of the continuous-time Markov chain (CTMC). However, this likelihood is intractable; there is no practical method to compute the finite time transition probabilities of the SIRS CTMC because the size of the state space of X_t grows on the order of N². For the same reason, summing over X with the forward-backward algorithm [Baum et al., 1970] is not feasible. To use Bayesian inference despite this likelihood intractability, we turn to a particle marginal Metropolis-Hastings (PMMH) algorithm.

4. Particle filter MCMC

4.1. Overview

The PMMH algorithm, introduced by Beaumont [2003] and studied in Andrieu and Roberts [2009] and Andrieu et al. [2010], constructs a Markov chain that targets the joint posterior distribution π(θ,X|y), where X is a set of auxiliary or hidden variables, and requires only an unbiased estimate of the likelihood. To construct this likelihood estimate, we use a sequential Monte Carlo (SMC) algorithm, also known as a bootstrap particle filter [Doucet et al., 2001]. Thus, the PMMH algorithm proceeds as follows: at each Metropolis-Hastings step [Metropolis et al., 1953, Hastings, 1970], a new θ^* is proposed from the proposal distribution q(·|θ), an SMC algorithm is used to estimate the marginal likelihood of the data given the proposed set of parameters, p̂(y|θ^*), and to obtain a sample ${\mathit{X}}_{{\mathit{t}}_{0:n}}^{\ast }~\widehat{p}(·\mid \mathit{y},{\mathit{\theta }}^{\ast })$, and θ^*, ${\mathit{X}}_{{\mathit{t}}_{0:n}}^{\ast }$, and p̂(y|θ^*) are accepted with a Metropolis-Hastings acceptance ratio which uses the estimated likelihood. An SMC algorithm is used to generate and weight K particle trajectories corresponding to the hidden state processes using the proposed parameter set θ^* as follows. Let the superscript k ∈{1, …, K} denote the particle index, where K is the total number of particles, and the subscript t_i ∈{t₀, …, t_n} denote the time; thus, ${\mathit{X}}_{t_i}^k$ denotes the kth particle at time t_i, and ${\mathit{X}}_{{\mathit{t}}_{0:i}}^k=({\mathit{X}}_{t_0}^k,\dots ,{\mathit{X}}_{t_i}^k)$. At time t_i = t₀, we simulate initial states ${\mathit{X}}_{t_0}^k=(S_{t_0}^k,I_{t_0}^k)$ for k = 1, …, K from the initial density of the hidden Markov state process, specifically from Poisson distributions with means φ_S and φ_I. We compute the k weights $w({\mathit{X}}_{t_0}^k):=Pr(y_{t_0}\mid {\mathit{X}}_{t_0}^k,{\mathit{\theta }}^{\ast })$, and set $W({\mathit{X}}_{t_0}^k)=w({\mathit{X}}_{t_0}^k)/{\sum }_{k^{\prime }=1}^{K}w({\mathit{X}}_{t_0}^{k^{\prime }})$. For i = 1, …, n, we resample ${\overline{\mathit{X}}}_{t_{i-1}}^k$ from ${\mathit{X}}_{t_{i-1}}^k$ with weights $W({\mathit{X}}_{t_{i-1}}^k)$. We sample K particles ${\mathit{X}}_{t_i}^k$ from $p(·\mid {\overline{\mathit{X}}}_{t_{i-1}}^k)$. We assign weights $w({\mathit{X}}_{t_i}^k):=Pr(y_{t_i}\mid {\mathit{X}}_{t_i}^k,{\mathit{\theta }}^{\ast })$, compute normalized weights $W({\mathit{X}}_{t_i}^k)=w({\mathit{X}}_{t_i}^k)/{\sum }_{k^{\prime }=1}^{K}w({\mathit{X}}_{t_i}^{k^{\prime }})$, and set ${\mathit{X}}_{{\mathit{t}}_{0:i}}^k=({\overline{\mathit{X}}}_{{\mathit{t}}_{0:i-1}}^k,{\mathit{X}}_{t_i}^k)$.

The marginal likelihood is estimated by summing the weights of the SMC algorithm, since

$$\widehat{p}(y_{t_i}\mid {\mathit{y}}_{{\mathit{t}}_{0:i-1}},{\mathit{\theta }}^{\ast })=\frac{1}{K}\sum _{k=1}^{K}w({\mathit{X}}_{t_i}^k)$$

is an approximation to the likelihood p(y_ti |y_t0:i−1, θ^*), and therefore an approximation to the total likelihood is

$$\widehat{p}(\mathit{y}\mid {\mathit{\theta }}^{\ast })=\widehat{p}(y_{t_0}\mid {\mathit{\theta }}^{\ast })\prod _{i=1}^n\widehat{p}(y_{t_i}\mid {\mathit{y}}_{{\mathit{t}}_{0:i-1}},{\mathit{\theta }}^{\ast }).$$

A proposed ${\mathit{X}}_{{\mathit{t}}_{0:n}}^{\ast }=({\mathit{X}}_{t_0}^{\ast },\dots ,{\mathit{X}}_{t_n}^{\ast })$ trajectory is sampled from the K particle trajectories based on the final particle weights of the SMC algorithm, and the proposed θ^* and ${\mathit{X}}_{{\mathit{t}}_{0:n}}^{\ast }$ are accepted with probability $min\left\{1,\frac{\widehat{p}(\mathit{y}\mid {\mathit{\theta }}^{\ast })}{\widehat{p}(\mathit{y}\mid \mathit{\theta })}\frac{p({\mathit{\theta }}^{\ast })}{p(\mathit{\theta })}\frac{q\{\mathit{\theta }\mid {\mathit{\theta }}^{\ast }\}}{q\{{\mathit{\theta }}^{\ast }\mid \mathit{\theta }\}}\right\}$, where p(θ) is the prior distribution for θ. To sample X_ti from p(·| X̄_ti−1), we simulate from a cholera transmission model with a time-varying environmental force of infection. CTMCs which incorporate time-varying transition rates are inhomogeneous. The details of the discretely-observed inhomogeneous CTMC simulations are now described.

4.2. Simulating inhomogeneous SIRS using tau-leaping

Gillespie developed two methods for exact stochastic simulation of trajectories with constant rates: the direct method [Gillespie, 1977] and the first reaction method [Gillespie, 1976]. Details of these methods are given in Appendix A. The exact algorithms work for small populations, but for large state spaces these methods require a prohibitively long computing time. This is a common problem in the chemical kinetics literature, where an approximate method called the tau-leaping algorithm originated [Gillespie, 2001, Cao et al., 2005]. This method simulates CTMCs by jumping over a small amount of time τ and approximating the number of events that happen in this time using a series of Poisson distributions. As τ approaches zero, this approximation theoretically approaches the exact algorithm. The value of τ must be chosen such that the rates remain roughly constant over the period of time; this is referred to as the “leap condition”.

Specifically, for our simulation, using the methods outlined in Cao et al. [2005], we define the rate functions h₁(X_t) = (βI_t + α(t)) S_t, h₂(X_t) = γI_t, and h₃(X_t) = μR_t, corresponding to the infinitesimal rates of the CTMC. Then k₁ ~ Poisson(h₁(X_t)τ) represents the number of infections in time [t, t+τ), k₂ ~ Poisson(h₂(X_t) τ) represents the number of recoveries in time [t, t + τ), and k₃ ~ Poisson(h₃(X_t) τ) represents the number of people that become susceptible to infection in time [t, t + τ). We make the assumption that the time-varying force of infection, α(t), remains constant each day. We define daily time intervals A_i := [i, i + 1) for i ∈{t₀, t₀ + 1, …, t_n − 1}, and α(t) = α_Ai for t ∈ A_i. Using τ ≤ 1 day, our rates now remain constant within each tau jump. See Appendix A for details regarding the selection of τ.

4.3. Metropolis-Hastings proposal for model parameters

Our implementation of the PMMH algorithm consists of a pilot run with a burn-in and a post-burn-in period, and a final run. Both the pilot burn-in and the post-burn-in periods use independent normal random walk proposal distributions for the parameters. The pilot burn-in period is thrown away; from the pilot run post-burn-in period, we calculate the approximate posterior covariance of the parameters and scale it by a factor to construct the covariance of the multivariate normal random walk proposal distribution in the final run of the PMMH algorithm. In all runs, parameters are proposed and updated jointly. Proposal covariance matrices are scaled such that acceptance rates for all final runs were between 15% and 20%.

4.4. Prediction

One of the main goals of this analysis is to be able to predict cholera outbreaks in advance using environmental predictors. To assess the predictive ability of our model, we estimate the parameters of the model using a training set of data and then predict future behavior of the epidemic process. We examine the posterior predictive distributions of cholera counts by simulating data forward in time under the time-varying SIRS model using the accepted parameter values explored by the particle MCMC algorithm and the accepted values of the hidden states S_T and I_T at the final observation time, t = T, of the training data. Under each set of parameters, we generate possible future hidden states and observed data, and we compare the posterior predictive distribution of observed cholera cases to the test data. In the analyses below, the PMMH output is always thinned to 1000 iterations for prediction purposes by saving only every kth iteration, where k depends on the total number of iterations.

5. Simulation results

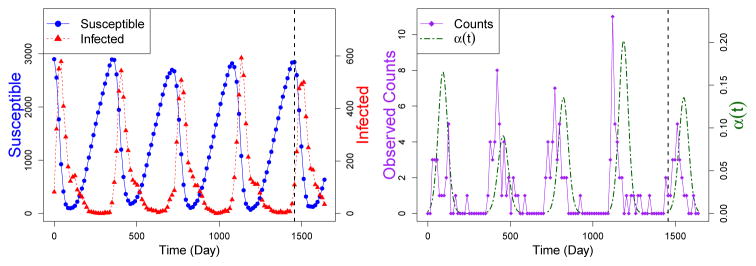
To test the PMMH algorithm on simulated infectious disease data, we generate data from a hidden SIRS model with a time-varying environmental force of infection. We then use our Bayesian framework to estimate the parameters of the simulated model and compare the posterior distributions of the parameters with the true values. To simulate endemic cholera where many people have been previously infected, we start with a population size of N = 10000 and assume independent Poisson initial distributions for S_t0 and I_t0, with means φ_S = 2900 and φ_I = 84. The other parameters are set at β = 5 × 10⁻⁵, γ = 0.12, and μ = 0.0018. All rates are measured in the number of events per day. The average length of the infectious period, 1/γ, is set to be 8 days, and the average length of immunity, 1/μ, is set to be about 1.5 years. Parameter values are chosen such that the simulated data are similar to the data collected from Mathbaria, Bangladesh. We use the daily time intervals A_i := [i, i + 1) for i ∈{t₀, t₀ + 1, …, t_n − 1}, as in Section 4.2, and define α(t) = α_Ai for t ∈A_i where α_Ai = exp [α₀ + α₁C(i)]. Here C(i) = a(z) sin (2πi/365) for 365(z − 1) < i ≤ 365z and z ∈ (1, 2, 3, 4, 5), where a(1) = 2.1, a(2) = 1.8, a(3) = 2, a(4) = 2.2, and a(5) = 2. The intercept α₀ and the amplitude α₁ are parameters to be estimated. The frequency of the sine function is set to mimic the annual peak seen in the environmental data collected from Bangladesh. For the simulations we set α₀ = −6 and α₁ = 2. Using the modified Gillespie algorithm described in Appendix A, we simulate the (S_t, I_t) chain given in the left plot of Figure 2. The observed number of infections y_t ~ Binomial(I_t, ρ), where ρ = 0.009 and is treated as an unknown parameter.

Fig 2.

Plots of simulated hidden states (counts of susceptible, S_t, and infected, I_t, individuals) and the observed data (number of observed infections = y_t ~ Binomial(I_t, ρ)) plotted over time, t. Simulation with seasonally varying α(t) generates data with seasonal epidemic peaks. The dashed vertical black line represents the first cut off between the training sets and the test data. Data before the line are used to estimate parameters, and we use those estimates to predict the data after the line. Other data cut offs are shown in Figure 3

We simulate four years of training data. There is not enough information in the data to estimate the means of the Poisson initial distributions, φ_S and φ_I, since estimation of these parameters is only informed by the very beginning of the observed data. We set these parameters to different values and compare parameter estimation and prediction between models with parameter assumptions which differ from the truth. We also assume that we know the population size, N = 10000.

We assume independent normal prior distributions for the elements of θ, with means and standard deviations chosen such that the mass of each prior distribution is not centered at true value of the parameter in this simulation setting. We use relatively uninformative, diffuse priors for log(β), α₀, and α₁, centered at log(1.25×10⁻⁴), −8, and 0, respectively, and with standard deviations of 5. The prior distribution for logit(ρ) is centered at logit(0.03) and has a standard deviation of 2. For log(γ), the prior is centered at log(0.1) with a relatively small standard deviation of 0.09, since this value is well studied for cholera. The prior for log(μ) is centered at log(0.0009) with a standard deviation of 0.3. Thus, a priori 1/γ falls between 8.4 to 11.9 days with probability 0.95, and 1/μ falls between 1.7 and 5.5 years.

Using these data, the PMMH algorithm starts with a pilot run with a burn-in period of 30000 iterations, a pilot post-burn-in period of 20000 iterations, and a final run of 400000 iterations. To thin the chains, we save only every 10th iteration. We use K = 100 particles in the SMC algorithm. We compare results from models with different assumptions on the values of φ_S and φ_I : assumed φ_S/N and φ_I/N are above the true values (0.39 and 0.0168), at the true values (0.29 and 0.0084), below the true values (0.19 and 0.0042), or further below the true values (0.095 and 0.0021). Marginal posterior distributions for the parameters of the SIRS model from the final runs of these PMMH algorithms are in Appendix B. The posterior distributions are similar, regardless of assumed values for φ_S and φ_I. Trace plots, auto-correlation plots, bivariate scatterplots, and effective sample sizes for the posterior samples under the situation in which the true values of φ_S and φ_I were assumed are also given in Appendix B. We report β × N and ρ × N, since in sensitivity analyses we found these to be robust to assumptions about the total population size N. From the posterior distributions, it is clear that the algorithm is providing good estimates of the true parameter values, though estimates of the parameters μ and ρ × N are slightly different than the truth when φ_S and φ_I are not set at the true values.

5.1. Prediction results

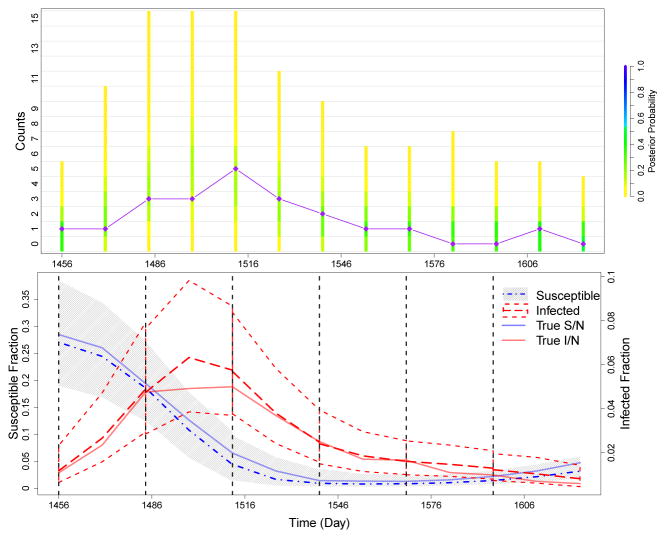
To test the predictive ability of the model, we use multiple cut off times to separate our simulated data into staggered training sets and test sets. The simulated observed data are shown in the right plot of Figure 2. For each cut off time, parameters were drawn from the posterior distribution based on the training data. These parameter values were then used to simulate possible realizations of reported infections after the training data until the next cut off, 28 days later. The distributions of these predicted reported cases are shown in the top plot of Figure 3. The test data are denoted by the purple diamonds, connected by straight lines to help visualize ups and downs in the case counts. Case counts are observed once every 14 days. On each observation day, the colored bar represents the distribution of predicted counts for that day. The distributions of predicted counts on the cut off days come from the accepted values of the hidden states S_T and I_T at the final observation time, t = T, of the training data. As desired, the posterior predictive distribution shifts its mass as time progresses to follow the case counts in the test data. The plot of the predicted hidden states in the bottom row of Figure 3 also shows that our model is capturing the formation and decline of the epidemic peak well, as seen in the trajectory of the predicted fraction of infected individuals. This plot shows that the predictive distributions are capturing the true simulated fraction of susceptible and infected individuals and illustrates the interplay of the hidden states of the underlying compartmental model. During an epidemic, the fraction of susceptibles decreases while the fraction of infected individuals quickly increases. Afterwards, the fraction of infected individuals drops and the pool of susceptibles slowly begins to increase as both immunity is lost and more susceptible individuals are born.

Fig 3.

Summary of prediction results for simulated data. We run PMMH algorithms on training sets of the data, which are cut off at each of the dashed black lines in the bottom plot. Cut off times occur at days 1456, 1484, 1512, 1540, 1568, and 1596. Future cases are then predicted until the next cut off. The top plot compares the posterior probability of the predicted counts to the test data (diamonds connected by straight purple lines). The coloring of the bars is determined by the frequency of each set of counts in the predicted data for each time point. The bottom plot shows how the trajectory of the predicted hidden states changes over the course of the epidemic. The gray area and the dot-and-dash line denote the 95% quantiles and median, respectively, of the predictive distribution for the fraction of susceptibles. The short dashed lines and the long dashed line denote the 95% quantiles and median, respectively, of the predictive distribution for the fraction of infected individuals. The solid blue and red lines denote the true simulated fraction of susceptible and infected individuals.

These predictions were made under the assumption that φ_S and φ_I are set to the true values. To test sensitivity to these assumptions, we compare predictions made from models that assume other values; these are shown in Appendix D. Predicted distributions are similar for all values of φ_S and φ_I. In addition, we study the effects of misspecification of the data generating process on estimation and prediction. We simulate data from a more biologically realistic model for cholera transmission, and fit the parameters of the SIRS model to this simulated data. Despite the model misspecification, we find that we can still predict outbreaks well. See Appendix G for details.

6. Using cholera incidence data and covariates from Mathbaria, Bangladesh

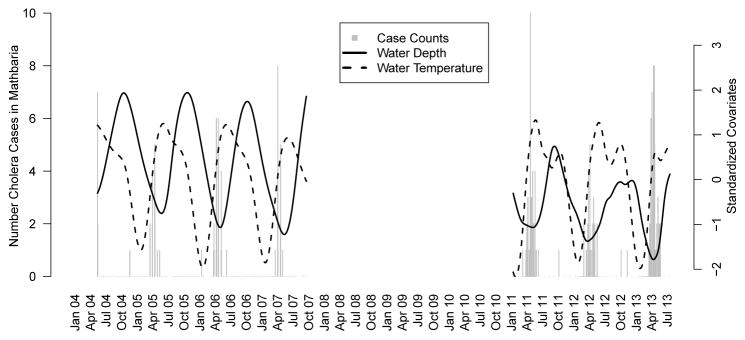
Huq et al. [2005] found that water temperature (WT) and water depth (WD) in some water bodies had a significant lagged relationship with cholera incidence. Therefore, we use these covariates and cholera incidence data from Mathbaria, Bangladesh collected between April 2004 to September 2007 and again from October 2010 to July 2013. Between April 2004 and September 2007, physicians made bimonthly visits to the thana health complex in Mathbaria and counted the number of cholera cases that were observed on each day during a three day period. Environmental data were also collected approximately every two weeks from multiple water bodies in the area. Water bodies include rivers, lakes, and ponds. From October 2010 to July 2013, physicians made three day visits weekly during periods in which seasonal outbreaks were expected and made monthly three day visits when few cases were expected. Environmental data were collected from multiple water bodies on the same schedule, approximately once a week during seasonal outbreaks and monthly between outbreaks. Further details of the clinical and environmental surveillance are given by Sack et al. [2003] and Huq et al. [2005]. We use data from five to six water bodies in each phase of data collection. To get a smooth summary of the covariates using data from the water bodies, we fit a cubic spline to the covariate values. We then slightly modify our environmental force of infection to allow for a lagged covariate effect. Let κ denote the length of the lag. We consider the daily time intervals A_i := [i, i + 1) for i ∈{t₀, t₀ + 1, …, t_n − 1} and define the environmental force of infection α (t) = α_Ai for t ∈A_i and t ≥ κ where α_Ai = exp [α₀ + α₁C_WD(i − κ) + α₂C_WT (i − κ)]. Here the covariates are the smoothed standardized daily values $C_{WT}(i)=(WT(i)-\overline{WT})/s_{WT}$ and $C_{WD}(i)=(WD(i)-\overline{WD})/s_{WD}$, where X̄ is the mean of the measurements for all i and s_X is the sample standard deviation. We consider and compare results from models assuming three different lags: κ = 14, κ = 18, and κ = 21. Predictions from all three models are similar, so we report only results from the model assuming κ = 21, in order to receive the earliest warning of upcoming epidemics; see Appendix C for details and prediction comparisons. The smoothed, standardized, 21 day lagged covariates and cholera incidence data are shown in Figure 4.

Fig 4.

Barplot of cholera case counts in Mathbaria, Bangladesh and the standardized covariate measurements over time. The covariates are shown with a lag of three weeks. No data were collected from October 2007 through November 2010. The ranges of the unstandardized smoothed covariates are 1.4 to 2.8 meters for water depth and 21.6 to 33.1°C for water temperature.

The population size N, which quantifies the size catchment area for the medical center, is assumed to be 10000 for computational convenience. We do not know the true value of N, but 10000 is a reasonable estimate and is small enough that simulations run quickly. We studied sensitivity to this assumption by setting N to different values, obtaining similar results. We also again set φ_S and φ_I to various values and the results were insensitive. See Appendix D for details.

In these analyses, we use relatively uninformative, diffuse normal prior distributions on the time-varying environmental covariates α₁ and α₂, centered at 0 and with standard deviations of 5. The diffuse normal prior distributions on the transformed parameter values log(β) and α₀ are centered at log(1.25 × 10⁻⁷) and −8, respectively, with standard deviations of 5. We know that the average infectious period for cholera, 1/γ, should be between 8 and 12 days. Thus, the transformed parameter log(γ) is given a normal prior distribution with mean log(0.1) and standard deviation 0.09 to give 0.95 prior probability of 1/γ falling within the interval (8, 12). In addition, we know that a reasonable length of immunity under this model should be between one and six years. We use a normal prior distribution for log(μ) centered at log(0.0009) with a standard deviation of 0.3, giving a 0.95 prior probability of 1/μ falling between 1.7 and 5.5 years. We also know that ρ should be very close to zero, since only a small proportion of cholera infections are symptomatic and a smaller proportion will be treated at the health complex [Sack et al., 2003]. Thus, the transformed parameter logit(ρ) is given a normal prior distribution with mean logit(0.0008) and standard deviation equal to 2, to give 0.95 prior probability of ρ falling within the interval (1.6 × 10⁻⁵, 0.04).

We run the PMMH algorithm with a pilot run with a burn-in period of 30000 iterations, a pilot post-burn-in period of 20000 iterations, and a final run of 400000 iterations. We again save only every 10th iteration and use K = 100 particles in the SMC algorithm. We check sensitivity to the number of particles, using 1000 particles instead of 100 and obtaining similar results; see Appendix D for details. Posterior medians and 95% Bayesian credible intervals for the parameters β × N, γ, μ, α₀, α₁, α₂, and ρ × N generated by the final run of the PMMH algorithm are given in Table 1. We report β × N and ρ × N since we found these parameter estimates to be robust to changes in the population size N during sensitivity analyses. For more details, see Appendix D. The credible intervals for α₁ and α₂ do not include zero, so both water depth and water temperature have a significant relationship with the force of infection. Decreasing water depth increases the force of infection, likely due to the higher concentration and resulting proliferation of V. cholerae in the environment; increasing water temperature increases the force of infection [Huq et al., 2005].

Table 1.

Posterior medians and 95% equitailed credible intervals (CIs) for the parameters of the SIRS model estimated using clinical and environmental data sampled from Mathbaria, Bangladesh.

Coefficient	Estimate	95% CIs
β × N	0.47	(0.33, 0.65)
γ	0.12	(0.1, 0.14)
μ	0.002	(0.001, 0.002)
(β × N)/γ	3.92	(2.84, 5.19)
α0	−6.49	(−7.39, −5.41)
α1	−1.94	(−2.49, −1.37)
α2	2.35	(1.85, 2.98)
ρ × N	37.1	(27.2, 50.2)

The basic reproductive number, R₀, is the average number of secondary cases caused by a typical infected individual in a completely susceptible population [Diekmann et al., 1990]. In Table 1, we report (β × N)/γ, the part of the reproductive number that is related to the number of infected individuals in the population under our model assumptions. Our estimate of 3.92 is fairly large; it is very similar to the reproductive number of 5 (sd=3.3) estimated by Longini et al. [2007] using data from Matlab, Bangladesh. However, posterior median values for α(t) range from 0.000003 to 0.27, while posterior median values for βI_t only range from 0 to 0.04, suggesting that the epidemic peaks in our model are driven mostly by the environmental force of infection. During epidemic peaks, when I_t is largest, the posterior median for α(t) is larger than the posterior median for βI_t. See Appendix F for more details. However, the infectious contact rate is not zero and is not negligible compared to the environmental force of infection.

6.1. Prediction Results

For the data collected from Mathbaria, we begin prediction at multiple points around the time of the two epidemic peaks that occur in 2012 and 2013. Figure 4 shows the full cholera data with smoothed and standardized covariates. Figure 5 shows the posterior predictive distribution of observed cholera cases (top row) and hidden states from the time-varying SIRS model (bottom row). Parameters used to simulate the SIRS forward in time have been sampled using the PMMH algorithm applied to the training data, with data being cut off at different points during the 2012 and 2013 epidemic peaks. From each of these cut offs, parameter values are then used to simulate possible realizations of the test data. Predictions are run until the next cut off point, with cut off points chosen based on the length of the lag κ. Realistically, at time t we have covariate information to use for prediction only until time t + κ, where κ is the covariate lag. Since the smallest lag considered is 14 days, we make only 14 day ahead predictions where possible to mimic a realistic prediction set up. Due to the sparse sampling between epidemic peaks (June 2012 to February 2013), we use longer prediction intervals for these cut-offs than would be possible in real time data analysis in order to evaluate our model predictions.

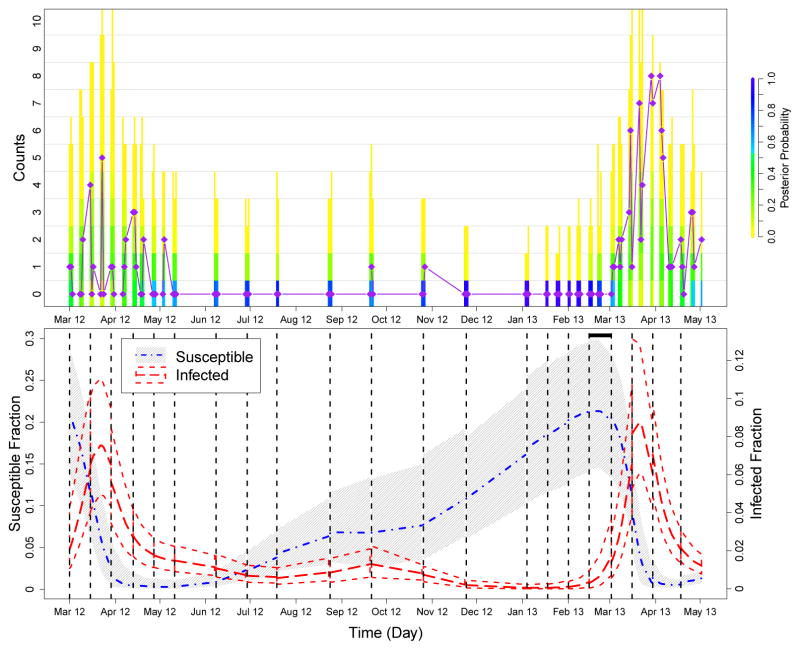
Fig 5.

Summary of prediction results for the second to last and last epidemic peaks in the Bangladesh data. We again run PMMH algorithms on training sets of the data, which are cut off at each of the dashed black lines in the bottom plot, and future cases are predicted until the next cut off. The top plot compares the posterior probability of the predicted counts to the test data (purple diamonds and line), and the bottom plot shows how the trajectory of the predicted hidden states changes over the course of the epidemic. See the caption of Figure 3 for more details. The black horizontal bar at the top of the bottom plot marks where our model predicts an increase in the fraction of infected individuals, warning of the upcoming epidemic. This increase is predicted weeks before an increase can be seen in the case counts.

In the top row of Figure 5, the coloring of the bars again represents the distribution of predicted cases. Between the two peaks of case counts (June 2012 to February 2013), the frequency of predicted zero counts is very high, so we conclude that the model is doing well with respect to predicting the lack of an epidemic. During the epidemics, the distribution of the counts shifts its mass away from zero. The plot in the bottom row of Figure 5 again illustrates the periodic nature and interplay of the hidden states of the underlying compartmental model. When the fraction of infected individuals quickly increases during an epidemic, the fraction of susceptibles decreases. Afterwards, the fraction of infected individuals drops to almost zero and the pool of susceptibles is slowly replenished. When the fraction of infected individuals is low, there is more uncertainty in the prediction for the fraction of susceptibles (September 2012 to March 2013). The fraction of infected individuals increases to a slightly higher epidemic peak 2013 (March 2013 to May 2013) than in 2012 (March 2012 to May 2012), as observed in the test data for those years. The predicted fraction of infected people in the population increases before an increase can be seen in the case counts, which could allow for early warning of an epidemic.

We also use a quasi-Poisson regression model similar to the one used by Huq et al. [2005] to predict the mean number of cholera cases (Appendix E). Although the quasi-Poisson model predicts reasonably well the timing of epidemic peaks, it appears to overestimate the duration of the outbreaks. The predicted means under both the quasi-Poisson and SIRS models most likely underestimate the true mean of the observed counts, with the quasi-Poisson model performing slightly better. However, the SIRS predicted fraction of infected individuals — a hidden variable in the SIRS model — provides a more detailed picture of how cholera affects a population. By providing not only accurate prediction of the time of epidemic peaks, but also the predicted fraction of the population that is infected, the SIRS model predictions could be used for efficient resource allocation to treat infected individuals. See Appendix E for additional details.

7. Discussion

We use a Bayesian framework to fit a nonlinear dynamic model for cholera transmission in Bangladesh which incorporates environmental covariate effects. We demonstrate these techniques on simulated data from a hidden SIRS model with a time-varying environmental force of infection, and the results show that we are recovering well the true parameter values. We also estimate the effect of two environmental covariates on cholera case counts in Mathbaria, Bangladesh while accounting for infectious disease dynamics, and we test the predictive ability of our model. Overall, the prediction results look promising. Based on data collected, the predicted hidden states show a noticeable increase in the fraction of infected individuals weeks before the observed number of cholera cases increases, which could allow for early notification of an epidemic and timely allocation of resources. The predicted hidden states show that the fraction of infected individuals in the population decreases greatly between epidemics, supporting the hypothesis that the environmental force of infection triggers outbreaks. Estimates of βI_t are low, but not negligible, compared to estimates of α(t), suggesting that most of the transmission is coming from environmental sources.

Computational efficiency is an important factor in determining the usefulness of this approach in the field. We have written an R package which implements the PMMH algorithm for our hidden SIRS model, available at https://github.com/vnminin/bayessir. The computationally expensive portions of the PMMH code are primarily written in C++ to optimize performance, using Rcpp to integrate C++ and R [Eddelbuettel and François, 2011, Eddelbuettel, 2013]; however there is still room for improvement. Running 400000 iterations of the PMMH algorithm on the six years of data from Mathbaria takes 3 days on a 4.3 GHz i7 processor. Since we can predict three weeks into the future using a 21 day covariate lag, we do not think timing is a big limitation for using our model predictions in practice.

Plots of residuals over time, shown in Appendix C, show that we are modeling well case counts between the epidemic peaks but not the epidemic peaks themselves, either due to missing the timing of the epidemic peak or the latent states not being modeled accurately. This possible model misspecification might be fixed by including more covariates, using different lags, or modifying the SIRS model. Also, we assume a constant reporting rate, ρ, rather than using a time-varying ρ_t [Finkenstädt and Grenfell, 2000]. With better quality data we might be able to allow for a reporting rate that varies over time; we will try to address these model refinements in future analyses. Another related assumption of this model is that individuals act independently. However, these data come from a carefully conducted observational study of cholera over many years with strict protocol across time and locations. Thus, it is unlikely that there would be systematic differences in reporting or treatment seeking behaviors of people. We tested this using a basic split of the data, altering our SIRS model to include a separate reporting rate for each phase of data collection, and found no significant difference between the two reporting rates. Also, there is no evidence that people do not act independently, at least with respect to their treatment seeking behavior. Surveys currently in the field will allow us to test these assumptions in future work.

In the future, we will extend this analysis to allow for variable selection over a large number of covariates. This will allow us to include many covariates at many different lags and incorporate information from all of the water bodies in a way that does not involve averaging. In the current PMMH framework, choosing an optimal proposal distribution to explore a much larger parameter space would be difficult. We want to include a way of automatically selecting covariates or shrinking irrelevant covariate effects to zero with sparsity inducing priors. The particle Gibbs sampler, introduced by Andrieu et al. [2010], would allow for such extensions. Approximate Bayesian computation is also an option for further model development [McKinley et al., 2009]. In addition, the available data consist of observations from multiple thanas during the same time period. Future analyses will look into sharing information across space and time and accounting for correlations between thanas. Another challenging future direction involves exploring models which incorporate a feedback loop from infected individuals back into the environment to capture the effect of infected individuals excreting V. cholerae into the environment. To accomplish this, we could add a water compartment to our SIRS model that quantifies the concentration of V. cholerae in the environment, similar to the model of Tien and Earn [2010]. However, adding an additional latent state leads to identifiability problems, even with fully observed data [Eisenberg et al., 2013], so such an extension will require rigorous testing and fine tuning.