Abstract
An inexpensive, reliable method for protein sequencing is essential to unraveling the biological mechanisms governing cellular behavior and disease. Current protein sequencing methods suffer from limitations associated with the size of proteins that can be sequenced, the time, and the cost of the sequencing procedures. Here, we report the results of all-atom molecular dynamics simulations that investigated the feasibility of using graphene nanopores for protein sequencing. We focus our study on the biologically significant phenylalanine-glycine repeat peptides (FG-nups)—parts of the nuclear pore transport machinery. Surprisingly, we found FG-nups to behave similarly to single stranded DNA: the peptides adhere to graphene and exhibit step-wise translocation when subject to a transmembrane bias or a hydrostatic pressure gradient. Reducing the peptide’s charge density or increasing the peptide’s hydrophobicity was found to decrease the translocation speed. Yet, unidirectional and stepwise translocation driven by a transmembrane bias was observed even when the ratio of charged to hydrophobic amino acids was as low as 1:8. The nanopore transport of the peptides was found to produce stepwise modulations of the nanopore ionic current correlated with the type of amino acids present in the nanopore, suggesting that protein sequencing by measuring ionic current blockades may be possible.
Keywords: maximum five, not capitalized, plural, separated by commas, no full stop
1. Introduction
Starting with the pioneering study of RNA translocation through α-hemolysin [1], nanopores in biological and synthetic membranes have been used to detect and characterize a variety of analytes at the single-molecule level [2–4]. In a typical measurement, a thin membrane containing a single nanopore separates an ionic solution into two compartments. A trans-membrane bias is applied to capture and transport analytes from one side of the membrane to the other through the nanopore. The presence of analyte molecules in the nanopore disrupts the flow of ions through the nanopore; the duration, amplitude and frequency of the ionic current disruptions report on the presence, chemical structure and concentration of the analytes. More recently, nanopores have shown promise not only for detection, but also for sequencing of DNA molecules [5–7]. Experiments have demonstrated that each type of DNA nucleotide produces a characteristic modulation of the ionic current [8–11]. With the help of a DNA processing enzyme [12–14] and a signal deconvolution algorithm [15], MspA, a biological nanopore, has been used to determine the nucleotide sequence of a natural DNA polymer [16].
There is much excitement surrounding the possibility of applying the nanopore method to sequence proteins. Results of several experimental studies have already shown the utility of nanopores for single-molecule detection and characterization of proteins [17–33]. The proteins can either be driven through a wide nanopore (wider than the proteins) by electric field and the solvent flow, or stripped off of a DNA molecule by a narrower pore [34]. The nanopore detection principle has been used to identify proteins [17, 23, 27] including single amino acids [35], and distinct conformational states of the same protein [17, 23, 31, 36]. Nanopores have also been used to characterize the binding of proteins to DNA [20, 21, 24, 25]. A biological nanopore has been combined with a protein processing enzyme to unfold proteins while pushing them through a nanopore [30], suggesting the possibility of developing a protein sequencing system analogous to the one used in DNA sequencing.
Synthetic materials, such as silicon nitride membranes, have robust mechanical properties [37], a broad range of pore sizes [38, 39], and better scalability of production that is needed to create multiplexed devices. However, conventional solid-state membranes are too thick to detect single amino acids [40], which are only 1 nm in size. The development of 2D materials, offers a solution to this spatial imprecision [41]. A particularly attractive material is graphene [42]—an atom-thick layer of carbon—that is both robust enough to withstand changes in environmental conditions and thin enough to potentially distinguish neighboring nucleotides or amino acids. Nanopores in graphene membranes have already been used to experimentally detect the translocation of double- and single-stranded DNA [43–50]; additionally, modeling work suggests possible uses for DNA sequencing [51–55].
In this study, we employ all-atom molecular dynamics (MD) simulations to explore the feasibility of protein sequencing using graphene nanopores. Our simulations characterize the behavior of unfolded proteins in contact with a graphene membrane and the process of nanopore translocation driven by either a transmembrane bias or a hydrostatic pressure difference. By measuring nanopore ionic current at different stages of the translocation process, we assess the feasibility of determining the amino-acid composition of the peptides via ionic current recording. The results of our simulations suggest that protein sequencing using graphene nanopores may be possible.
2. Results and discussion
2.1. Unfolded peptides adhere to graphene
To model the behavior of unfolded proteins in proximity to a graphene nanopore, we constructed several all-atoms systems each containing a 48 residue unfolded peptide chain, a three-layer graphene membrane, and 1 M KCl solution. Each system featured a 2.2 nm diameter nanopore; the unfolded peptides were initially threaded through the nanopore, Figure 1a. One of the systems contained a 48 amino acid fragment of the α-hemolysin protein. Three additional systems were built by mutating the amino acids of the α-hemolysin fragment into FG-Nup repeat peptides of the prescribed amino acid sequence. For this set of simulations, we chose negatively charged (−12e, (FDFG)12), positively charged (+12e, (FKFG)12) and electrically neutral (0e, (FGFG)12) peptides. Hereafter we denote the charge of a proton with e and the amino acid content of the peptides with the one letter code. Water and ions were added so that the concentration of the solution was 1 M KCl. Upon assembly, the systems were minimized and equilibrated; the details of the simulation protocols are provided in the Materials and Methods; Table S1, and Table S2, and Table S3 provide the complete list of performed simulations.
Figure 1.
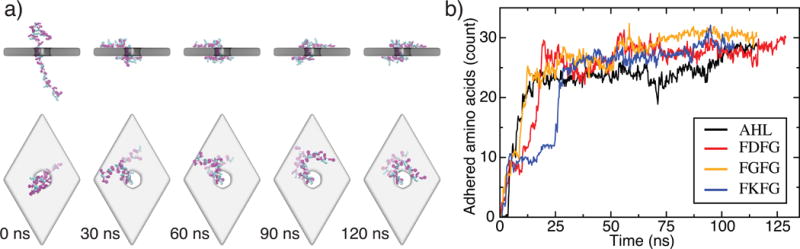
Equilibrium conformations of unfolded proteins threaded through a nanopore in a three-layer graphene membrane. (a) Equilibration simulation of the (FKFG)12 peptide. The sequence of snapshots illustrates the microscopic conformations of the peptide during the equilibration simulation. Graphene is shown as a gray transparent molecular surface The protein is shown using the licorice representation, with phenylalanine shown in magenta, lysine shown in teal, and glycine shown in white. At the beginning of the simulation, the protein is threaded through the nanopore and extended away from the membrane. The protein collapses onto the membrane in less than 30 ns and remains in contact with the membrane, diffusing along the membrane’s surface. (b) The number of amino acids adhered to the graphene membrane. Here, an amino acid is considered adhered to the membrane if its center of mass is located within 7 Å of the nearest carbon layer of the membrane, and it is not within the nanopore. Data are shown for a 48 residue fragment of α-hemolysin, negatively charged (FDFG)12, neutral (FGFG)12, and positive charged (FKFG)12 FG-Nups repeats. Each data point in this plot indicates a 200 ps block average of data sampled every 18-ps.
During a 120 ns equilibration simulation (without an applied electric field), the (FKFG)12 peptide was seen to collapse from an initially extended conformation onto the graphene surface within 30 ns, Figure 1a; three other peptides, the α-hemolysin fragment, (FGFG)12, and (FDFG)12, behaved similarly. Thus, we found that both naturally occurring and designer peptides adhere to the surface of graphene in a manner similar to that of single-stranded DNA (ssDNA) [53, 54]. The degree of adsorption was comparable among the random-sequence (α-hemolysin fragment) and repeat-sequence peptides and did not appreciably depend on the charge of the peptides. Once adsorbed, the peptides continued to move along the surface of the graphene membrane, performing a 2D diffusion reminiscent of the behavior of ssDNA [53, 54]. To quantitatively assess the degree of adhesion, we plot in Figure 1b the number of adsorbed amino acids for the four peptides as a function of simulation time. After initial collapse, all four peptides adhere even more tightly to the membrane through the remainder of the equilibration. The hydrophobic residues were most completely adsorbed to the surface of the graphene, with ~ 75% of phenylalanine residues adsorbed. Only ~ 25% of the charged residues were found adsorbed to graphene at the end of the equilibration runs; the number of adsorbed glycines was about half of their total number.
2.2. Electrophoretic transport of charged peptides is stepwise
To determine the character of the electrophoretic motion of our FG-Nup peptides through a graphene nanopore, we carried out MD simulations of the peptide/graphene nanopore systems under an applied electric field [56] using, as initial conditions, the microscopic conformations obtained at the end of the equilibration simulations. Figure 2a shows a representative conformation of the (FDFD)12 system during an applied electric field simulation. In this particular peptide, the negatively charged aspartic acid chains are interspersed with phenylalanine aromatic rings, resembling the charged backbone-hydrophobic base repeat structure of ssDNA.
Figure 2.
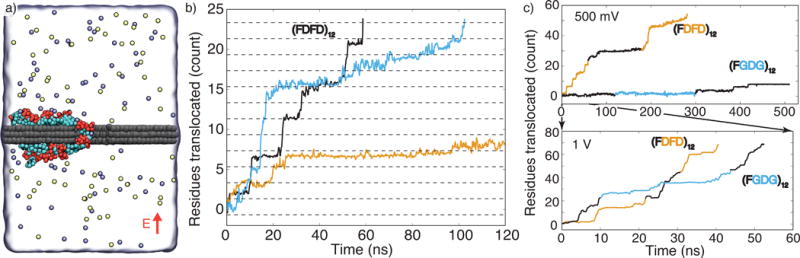
Electric field-driven transport of charged peptides. (a) An illustration of a typical simulation system. Atoms of the graphene membrane are shown as gray spheres; a part of the membrane is removed to reveal the nanopore. The (FDFD)12 peptide chain is shown using the molecular bonds representation, F and D amino acids are shown in cyan and red, respectively. The electrolyte solution is shown as a semitransparent surface, potassium and chloride ions are shown as yellow and light blue spheres, respectively; only one in ten ions is shown for clarity. A uniform electric field (red arrow) is applied normal to the membrane, producing a transmembrane bias of a desired magnitude [56]. (b) Representative permeation traces of the (FDFD)12 peptide driven by a 500 mV membrane bias. The permeation is characterized by counting the number of amino acids transported through the mid-plane of the membrane in the direction opposite to that of the applied electric field. The spacing between the dashed lines corresponds to two residues, which is the smallest repeat unit of the (FDFD)12 peptide. (c) Permeation traces of the (FDFD)12 and (FGDG)12 peptides at 500 mV (top) and 1 V (bottom) biases. The alternate coloring of the traces indicate data from independent simulations that were combined to produce a total permeation trace.
Subject to a 500 mV transmembrane bias, the negatively charged peptide chain was observed to move against the electric field without losing the adhesion contact with the graphene membrane. The translocation process consisted of short, quick steps interspersed between long (in relation to the duration of the steps) stationary periods, Figure 2b. Similar behavior was observed in two replicate simulations of the same system, Figure 2b; Supplementary Movie 1 illustrates one such simulation trajectory. Although not every residue of the peptide was charged and the charge was localized at the ends of the flexible side chains, the translocation rate of the (FDFD)12 peptide was surprisingly similar to that of ssDNA observed in our previous studies at the same conditions [53, 54].
Such a stepwise motion of peptide chains is of interest to protein sequencing applications of graphene nanopores. By pausing in one position for a longer time, a longer ionic current measurement can be gathered, thus allowing better identification of the contents of the pore. Furthermore, predictable pausing of nanopore translocation can be useful in deducing the peptide sequence from the ionic current data [15]. Indeed, in the three independent simulations of the same (FDFD)12 peptide, the peptides’ translocation was frequently observed to halt after the same number of amino acids traveled through the nanopore, Figure 2b.
To determine how the rate of the peptide transport depends on the applied bias, we repeated our simulations of the (FDFD)12 peptide at 1V, Figure 2c. In comparison to the 500 mV simulations, the translocation rate increased by a factor of 10, while the translocation kinetics maintained its stepwise character but exhibited larger, on average, translocation steps. An even more dramatic effect of the transmembrane voltage was observed in the case of the (FGDG)12 peptide, which contained only one negatively charged amino acid in every four amino acids of the peptides: the translocation rate increased by a factor of 80, Figure 2c. Thus, the rate of the electrophoretic transport of adsorbed peptides exponentially depends on the applied voltage, increasing by at least an order of magnitude with a twofold increase in the bias. The exponential dependence of the translocation rate on the bias could be explained by considering each translocation step as a barrier crossing event associated with unbinding of the hydrophobic group from the graphene membrane—a required step for peptide translocation. Extrapolating to 100 mV bias, one could expect the translocation pauses to last at least hundreds of microseconds, and the translocation step length to approach the spacing between the consecutive charges of the peptide.
2.3. Sequence-dependent translocation rate
To determine the effect of the membrane thickness on the peptides’ translocation rate, we created four additional systems containing a carbon membrane made of either one, two, three, or five layers; each membrane had a (DGG)16 peptide threaded through a 2.2 nm-diameter nanopore, Figure 3a. When a 500 mV bias was applied, the (DGG)16 peptide moved through the single- or double-layer graphene nanopores 6 and 4 times faster than through the three-layer membrane, respectively, Figure 3b,c. Further increasing the membrane thickness (to five layers) did not considerably change the peptide translocation rate, which could be expected as the total force experienced by a charged polymer in a solid-state nanopore does not depend on the membrane thickness as long as the membrane thickness is considerably greater than the spacing between the consecutive charges of the polymer. The faster peptide translocations through thinner graphene membranes could be explained by the absence of friction forces associated with binding of the peptide’s amino acids to the nanopore surface. The opposite trend was observed for ssDNA: the nanopore transport through a single layer graphene membrane was slower than through the double or triple layer membranes [53]. Thus, electric field-driven transport of a membrane-adsorbed charged biopolymer sensitively depends on the distance between its charged and hydrophobic groups.
Figure 3.
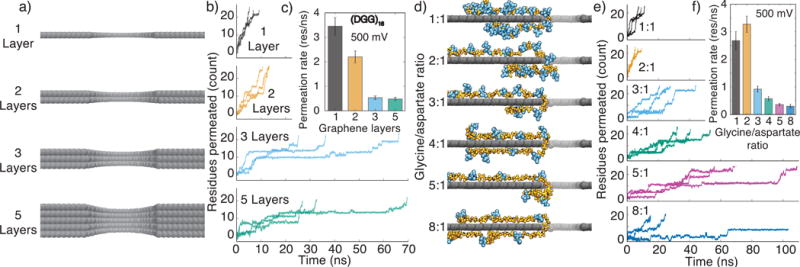
Influence of graphene thickness and peptide charge density on translocation rate of glycine– aspartate repeat peptides. (a) Atomic representations of graphene nanopores in one-, two-, three- and five-layer graphene membranes. (b) Electric field-driven translocation of a (DGG)16 peptide through a 2.2-nm-diameter nanopore in one-, two-, three- and five-layer graphene membranes. Three independent simulations were performed for each membrane thickness; the transmembrane bias was 500 mV. (c) The average rate of (DGG)16 translocation versus the membrane thickness. The average translocation rate was computed by splitting the corresponding MD trajectories into 1 ns blocks, finding the average translocation rate for each block and averaging over the blocks. The error bars represent the standard error of the translocation rate among the 1 ns blocks. (d) Typical conformations of (DGm)n peptides threaded through a 2.2-nm-diameter nanopore in a single layer graphene membrane. The ratio of glycine to aspartate residues, m, increases from 1:1 (top), to 8:1 (bottom). The quotient of 48 divided by (m+1) is n; the sequence of the 1:5 and 1:8 systems contains a terminal DGG fragment. (e) Permeation traces of (DGm)n peptides. Three independent simulations were performed for each glycine-to-aspartate ratio; the transmembrane bias was 500 mV in each simulation. (f) The average permeation rate of the (DGm)n peptide. The average translocation rate was computed using the method described in the caption to panel c.
To systematically investigate the dependence of the peptides’ translocation rate on the peptide’s charge density, we built six additional single-layer graphene systems containing a poly-glycine peptide chain with aspartic acid side chains introduced every second, third, fourth, fifth, sixth and ninth amino acid, Figure 3d. Each system was equilibrated for over 16 ns, followed by three independent simulations under an applied electric field corresponding to a 500 mV transmembrane bias. The resulting peptide translocation traces, Figure 3e, indicate a pronounced dependence of the translocation rate on the peptide charge density. As expected, more densely charged peptides moved faster through the nanopore, Figure 3f. The higher peptide charge density makes it more likely for the charged part of the polymer to wander into the nanopore where it experiences the electrophoretic pull of the transmembrane bias driving the translocation.
The diffusive component of the translocation mechanism is negligible for the systems where the distance between the charges along the peptide is less than or comparable to the effective nanopore length (such as our (DGDG)12 and (DGG)16 systems), which was estimated to be approximately 1 nm for single layer graphene [46].
The diffusive motion, however, can facilitate unidirectional transport of rather sparsely charged peptides. Thus, the (DGGGGGGGG)n peptide was observed to move unidirectionally through the pore in the direction prescribed by the transmembrane bias, Figure 3e (bottom). In this system, the charged tip of the aspartic acid side chain would eventually approach the nanopore by diffusion and be pulled through the nanopore by the electric field. Supplementary Movie 2 illustrates the translocation process. Thus, even a sparsely charged peptide could be unidirectionally driven through a graphene nanopore as long as the peptide’s side chains carry charges of the same sign.
2.4. Sequence-dependent translocation rate
To determine the effect of specific amino acids on the translocation rate, we simulated electric field translocation of several peptide variants through a three-layer graphene nanopore. Similar to our previous findings, Figure 2c and Figure 3d, reducing the charge density of the peptides from two charged residues per every four amino acids (as in (FDFD)12) to one charged residue per every four amino acids (as in (FDFG)12) reduced the translocation rate by a factor of ten, Figure 4a. Replacing the negatively charged aspartic acid side chain with a positively charged lysine side chain (producing (FKFK)12 and (FKFG)12) reversed the direction of the peptide translocation without substantially altering the average translocation rate or its dependence on the peptide charge density, Figure 4a. Thus, the rate of a peptide’s translocation appears to be controlled by the interaction of hydrophobic phenylalanine side chain with graphene. Indeed, replacing all aspartate residues in (FDFG)12 with glutamate (E) residues, which have the same negative charge as aspartate but has a one-carbon longer side chain, did not change the peptide’s translocation rate, Figure 4b. In contrast, replacing all lysine residues in (FKFG)12 with arginines (R) considerably retarded the translocation process, Supplementary Figure S1a. The latter result could be expected because, in addition to carrying a positive charge, arginine side chains are known to engage in hydrophobic interactions [57, 58], which, in our simulations, strengthened adhesion of the peptide to graphene, slowing the translocation process.
Figure 4.
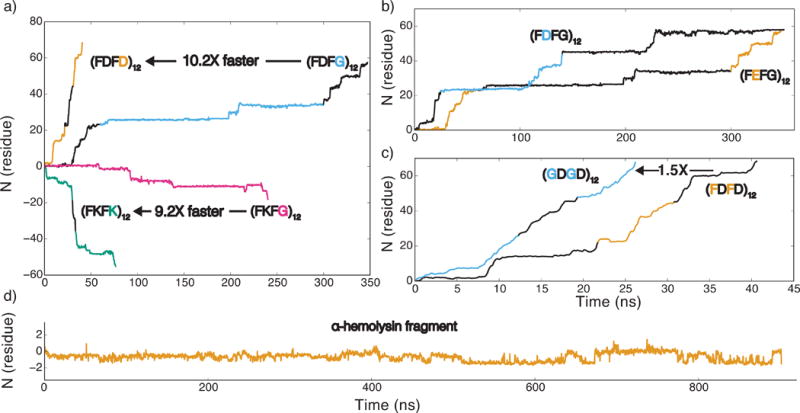
The effect of amino acid content on electrophoretic transport of peptides through a graphene nanopore. (a) The effect of the peptide charge. The number of residues translocated through a 2.2-nm-diameter nanopore in a three-layer graphene membrane is plotted versus simulation time. Just like in all other figures of this article, a positive number of translocated residues indicates translocation in the direction opposite to that of the applied electric field. Positively charged strands, (FKFK)12 and (FKFG)12 (green and magenta), move with the electric field, and negatively charged strands (FDFD)12 and (FDFG)12 (orange and blue), move against the electric field. All translocation traces reported in this figure were obtained under a 1 V transmembrane bias. (b) The effect of aspartic acid (blue)/glutamic acid (orange) substitution. (c) The effect of hydrophobic amino acids on the translocation rate of a charged peptide. The peptide containing glycine (GDGD)12 (blue) moves 1.5 times faster through the nanopore than the peptide containing phenylalanine (FDFD)12 (orange) (d) The translocation of a 48-residue fragment of α-hemolysin. Supplementary Table S1 lists the amino acid sequence of the fragment; the RNSIDTKE part of the fragment is threaded through the nanopore. In all panels, traces of alternating colors indicate data from independent simulations.
To directly evaluate the effect of phenylalanine stacking on the translocation rate, we replaced all phenylalanines in (FDFD)12 with glycines. The resulting (GDGD)12 peptide was observed to translocate ~1.5 times faster than (FDFD)12 at the same transmembrane bias, Figure 4c. A stronger effect was observed in the case of more sparsely charge peptides: the translocation of (FDFG)12 (Figure 4b) was approximately 10 times slower than that of (FGDG)12 (Figure 2c) at the same transmembrane bias (1 V). Replacing a glycine residue with a bulkier and polar glutamine residue (Q) in either (FDFG)12 (see Supplementary Figure S1b) or in (FKFG)12 (compare panels a and d of Figure 6) was observed to considerably reduce the translocation velocity.
Figure 6.
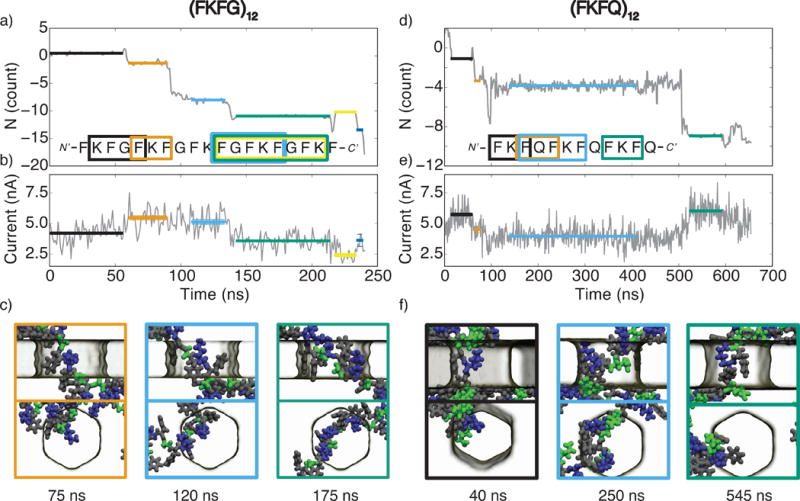
Ionic current blockades produced by peptide translocation through a graphene nanopore. (a) The permeation trace of the (FKFG)12 peptide. The number of amino acids passing through the midplane of the graphene membrane is plotted versus simulation time; positive values indicate translocation in the direction of the applied electric field. The colored horizontal lines highlight individual permeation steps and indicate the parts of the trajectory used for the ionic current calculations. The sequence of amino acids confined to the nanopore at a particular translocation pause is indicated by a rectangle of matching color overlaid with the nucleotide sequence of the peptide. (b) The ionic current passing through a graphene nanopore as the (FKFG)12 peptide translocates through the nanopore. The current was sampled at 18 ps intervals and block averaged in 1 ns blocks. The average value of the ionic current for each translocation pause is indicated by a horizontal line; the color and the length of the line matches that from the permeation trace (panel a). (c) Snapshots illustrating the typical conformations of the (FKFG)12 peptide during the second, third, and fourth translocation pauses highlighted in orange, blue, and green, respectively, in panels a and b. Phenylalanine is shown in grey, lysine is shown in blue, and glycine is shown in green. The top and bottom rows show the side and top views of the same molecular conformation. (d–f) Same as in panels a–c but for the (FKFQ)12 peptide. In panel f, the snapshots illustrate the peptide conformation corresponding to the first (black), third (blue), and fourth (green) translocation pauses; phenylalanine is shown in grey, lysine is shown in blue, and glutamine is shown in green. All simulations reported in this figure were carried out under a 1 V transmembrane bias and a 2.2-nm-diameter nanopore in a three-layer graphene membrane.
Despite its overall net charge of −4e, the 48-residue fragment of α-hemolysin did not exhibit unidirectional translocation during a microsecond simulation under a 1 V transmembrane bias, Figure 4d. The lack of translocation is explained by clustering of opposite charges within the fragment, rendering the overall charge of the peptide fragment residing within a nanopore neutral. A similar outcome (no translocation at a 1 V bias) was recorded for neutral peptides (FGFG)12 and (FKDG)12, Supplementary Figure S2a,b show the respective translocation traces. Although the three peptides did not move unidirectionally in the applied field, they were observed to undergo small amplitude (< 1 amino acid) stochastic displacements at the nanosecond time scale, interspersed with occasional larger amplitude (1–2 amino acids) displacements through the nanopore.
2.5. Water flow-directed nanopore transport of uncharged peptides
We have demonstrated that charged peptides can be driven through a graphene nanopore by a transmembrane voltage. However, uncharged or sparsely charged peptides containing side chains of opposite charge did not move under electric field substantially or unidirectionally. In the next set of simulations, we explored the possibility of using a drag force from a water flow to unidirectionally transport peptides regardless of their charge. In experiment, such water flow can be produced by applying a gradient of hydrostatic pressure across the membrane [59]. In our simulation, the water flow was produced by applying a small force to the oxygen atom in each water molecule [60]. Figure 5a provides a schematic illustration of our simulation protocol.
Figure 5.
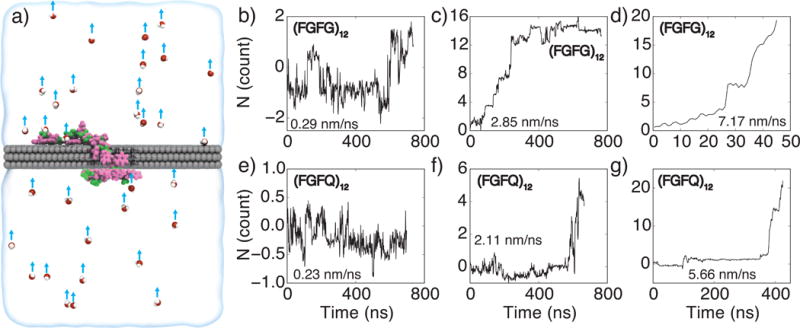
Water flow-driven translocation of uncharged peptides through a nanopore. (a) Illustration of a simulation setup. Atoms of the graphene membrane are shown as gray spheres, the peptide chain, (FGFG)12, is shown in a licorice representation, with the phenylalanine (F) shown in pink, and glycine (G) shown in green. The semitransparent surface illustrates the volume of electrolyte solution in a unit simulation cell. A small number of water molecules are explicitly shown as spheres (oxygen in red and hydrogen in white). A flow of water through the nanopore is instilled by applying a small force to all water molecules in the system (blue arrows). (b–g) Flow-induced translocation of peptide chains through a graphene nanopore. The top/bottom panels characterize translocation of (FGFG)12/(FGFG)12 peptides, respectively. The water velocity within the nanopore volume was 0.29 (b), 2.85 (c), 7.17 (d), 0.23 (e), 2.11 (f), and 5.66 (g) nm/ns.
To examine the possibility of using water flow to move peptides through a graphene nanopore, we created and equilibrated two systems, each containing a 3-layer graphene membrane, 1M KCl solution and one of either (FGFG)12 or (FQFQ)12 peptide. The systems were simulated by applying the same constant force, directed normal to the membrane, to every water molecule in the system, producing a net water flow through the nanopore. Three values of water flow-generating forces were explored: 0.005 pN (Figure 5b,e), 0.05 pN (Figure 5c,g) and 0.12 pN (Figure 5d,g); the average velocity of the resulting water flow in the nanopore varied from 0.23 nm/ns for the smallest applied force up to 7.17 nm/ns for the largest force. For the same applied force value, water was found to flow faster through the nanopore blocked by the (FGFG)12 peptide than through the nanopore blocked by the (FQFQ)12 peptide because of the smaller excluded volume of the former.
Clear, distinct steps can be seen in the translocation trace of the (FGFG)12 peptide under the 2.85 nm/ns flow condition, Figure 5c, with three 1-residue steps, two 2-residue steps, and one 4-residue step occurring within the first 250 ns of the simulation; Supplementary Movie 3 illustrates this simulation trajectory. The duration of the translocation pauses between the stops range from 7 to 71 ns. At a higher flow rate, 7.17 nm/ns, the peptide transport occurs considerably faster: 24 residues pass through the nanopore within 50 ns, Figure 5g. The translocation of the (FQFQ)12 peptide occurs considerably slower: only five residues pass through the nanopore under the 2.11 nm/ns flow conditions in almost 700 ns, Figure 5g. However, at 5.66 nm/ns, 24 residues pass through the nanopore in 426 ns; the permeation trace features a long pause of over 200 ns, Figure 5g, and has a clear stepwise character. At the lowest water flow conditions, neither (FGFG)12 nor (FQFQ)12 peptide was seen to move unidirectionally through the nanopore, Figure 5b,e. Thus, the rate of flow-induced peptide transport through graphene nanopores sensitively depends on the magnitude of the flow.
Overall, the results of the above simulations suggest the possibility of using water flow to unidirectionally transport neutral peptides through a graphene nanopore. Water flow in the range of 0.25 nm/ns was reported experimentally by Majumder and associates [61] through carbon nanotubes subjected to a 1 bar hydrostatic pressure. While our simulations did not show peptide translocations at that flow rate, Figure 5b,e, this is likely the consequence of the simulation time scales. Thus, reading the amino acid sequence of a neutral peptide may be possible by using a hydrostatic pressure gradient [59, 62] to produce stepwise translocation of the peptide through the nanopore and a transmembrane bias to produce ionic current that reports on the amino acid content of the peptide fragment confined to the nanopore.
2.6. Ionic current reports on the type of amino-acid confined to the nanopore
We have used MD trajectories of the (FKFG)12 and (FKFQ)12 systems to evaluate the feasibility of protein sequencing by measuring the ionic current passing through the pore. The permeation trace of the (FKFG)12 peptide, Figure 6a, has several well-defined translocation pauses that last long enough for the nanopore ionic current to reach a well-defined value. Figure 6b characterizes the changes in the nanopore ionic current during the 250 ns simulation of the (FKFG)12 peptide translocation. Coincidentally with the steps in the translocation trace, the nanopore ionic current is seen to change, most dramatically, between the first and second pauses with the ionic current increasing by 30%, and between the third and fourth steps, with the ionic current decreasing by 30%. The length of the peptide fragment confined within the nanopore as well as the amino acid sequence of the fragment varied from one translocation step to the other, Figure 6a. The highest blockade current was recorded for the three-amino acid FKF fragment at step 2 (orange), and the lowest when a 8-amino acid fragment FGFKFGFK blocked the nanopore at step 5 (yellow). Although it is natural to assume that a greater number of amino acids in the nanopore produces a deeper current blockade, the opposite is also possible. For example, when comparing the ionic currents in the first (black) and the third (blue) translocation pauses (Figure 6a,b), addition of a phenylalanine residue appears to increase the blockade current. Furthermore, the same peptide fragment (FGFKFGFK) can produce two distinct ionic current levels (compare pauses 4 and 5 in Figure 6a) because of a conformational change. The permeation trace of the (FKFQ)12 peptide, Figure 6d, also features several prominent pauses in the translocation process. The first (black) and fourth (green) translocation pauses bring to the nanopore different FKF amino acid fragments of the (FKFQ)12 peptide. Encouragingly, the average blockade currents in the first and the third pauses are close to one another: 5.7 nA and 6.0 nA, respectively, Figure 6e. Such good agreement of the currents is perhaps a result of the two peptide fragments adopting a similar conformation in the nanopore: the peptides appear to be hugging the nanopore’s edge, Figure 6f. Furthermore, a similar magnitude blockade current (5.5 nA) was also observed in the simulations of the (FKFG)12 peptide when an FKF fragment of that peptide was localized within the nanopore (Figure 6b, second translocation pause).
All of the above suggest that stepwise translocation of an unfolded peptide through a graphene nanopore can produce an ionic current signature that carries information about the amino acid sequence of the peptide. What confounds the possibility of determining the position of amino acids solely from the ionic current is the uncontrolled accumulation (jamming) of the amino acids within the nanopore. This could perhaps be ameliorated by some form of peptide stretching [49] to keep the number of amino acids in the pore low and constant.
3. Conclusion
The interaction of proteins with graphene has been the subject of several computational [55, 63] and experimental [28] studies. Both simulation and experiment have found folded proteins to adsorb to graphene, leading to their partial denaturing or unfolding. The adhesive interactions of protein and graphene are often regarded as detrimental to achieving the goal of protein sequencing and several approaches have been proposed to minimize such adhesive interactions [28, 47, 55].
In agreement with previous studies, we find unfolded peptides to adhere to graphene in our MD simulations. We also find, however, that such adhesion makes transport of peptides through graphene nanopore stepwise. Peptide chains that contain a mixture of neutral and charged residues of the same sign could be driven unidirectionally through the nanopore by a transmembrane bias, akin to nanopore translocation of DNA. Neutral peptides or peptides containing oppositely charged residues could be unidirectionally driven through nanopores by a drag force of solvent flow, which, in experiment, can be produced by a hydrostatic pressure difference or electroosmosis. The rate of peptide transport in both cases sensitively depends on the magnitude of the driving force, suggesting that slow stepwise translocations can be produced at moderate driving forces. In the case of an arbitrary protein, the adhesion-assisted stepwise nanopore transport may be realized by combining chemical denaturing with highly acidic or highly basic pH conditions that can render protein residues to have electrical charge of the same sign without affecting hydrophobic adhesion of unfolded protein to graphene.
With regard to the possibility of amino acid sequence detection, the results of our simulation indicate potential feasibility of the ionic current measurement to report the amino acid content of the peptide fragment confined to the nanopore. The practical realization of the method will require, however, that the number of amino acid residues confined to the nanopore is maintained at a low, constant number throughout the translocation process. Stretching peptide chains by either solvent flow [59], local heating [64] or hydrophobic adhesion [49] may accomplish that without affecting the stepwise character of the translocation process.
4. Materials and Methods
4.1 MD simulations
All MD simulations were performed using NAMD [65], a 2 fs integration timestep and periodic boundary conditions. Multiple time stepping was used to calculate local interactions every time step and full electrostatics every three time steps. SETTLE [66] and RATTLE [67] algorithms were applied to covalent bonds that involved hydrogen atoms in water and protein, respectively. The CHARMM36 force field [68] was used for proteins, graphene, water and ions, with type CA atoms used for graphene [53, 68], and custom NBFIX corrections for ions [69]. The particle mesh Ewald algorithm [70] was used to evaluate long-range electrostatic interactions over a 0.1 nm-spaced grid. Van der Waals interactions were evaluated using a smooth 7–8 Å cutoff. The temperature was maintained at 295 K using a Lowe-Anderson thermostat [71] with a cutoff radius of 2.7 Å and the Lowe-Anderson collision rate of 50 ps−1.
4.2 All-atom models of graphene systems
An all-atom model of a three-layer graphene membrane was generated using VMD’s [72] Inorganic Builder plugin [73]. A circular nanopore was created by removing all atoms satisfying the condition x2 + y2 < R2, where x and y are the coordinates of the atoms and R is the target radius of the pore, which in this study was 11 Å. The graphene membrane was then solvated using VMD’s Solvate plugin. The initial model of a protein chain was created by extracting a 48-residue protein fragment from α-hemolysin [74], residue 92 to 130. Three other protein structures, (FGFG)12, (FDFG)12 and (FKFG)12 were obtained from that chain by mutating amino acids according to the prescribed sequence. The protein chains were then combined with the solvated graphene nanopore model such that the chains were threaded through the nanopore. Overlapping solvent molecules were removed from the system, and each system was then ionized and neutralized to 1 M KCl using the Autoionize plugin in VMD. Each final system was a hexagonal prism, ~ 49 Å inner radius and 130 Å height, and contained approximately 112,000 atoms.
Upon assembly, each system was minimized for 10,000 steps, applying harmonic restraints of 1 (kcal/mol·Å2) to each atom of the protein. The systems were then each equilibrated for over 100 ns applying a Nosé-Hoover Langevin piston in the z direction only to keep the pressure and temperature constant at 1 atm and 295 K, respectively. During the equilibration simulations, one residue of the protein located in the middle of the nanopore was harmonically restrained. In all simulations, each atom of the graphene membrane was restrained to its initial coordinates using a 10 (kcal/mol·Å2) harmonic spring. All other peptide systems were created via side chain replacement using the final frames of the equilibration trajectories, see Supplementary Table 1.
Production simulations under applied electric field were performed at constant volume, with the dimensions specified by the average dimensions of the system during equilibration. Harmonic restraints of 10 kcal/mol·Å2 were applied only to the atoms of the graphene membrane holding them to their initial positions; all restraints were removed from the proteins. The electric field strength was set to E = −V/Lz, where V is the target transmembrane bias and Lz is the length of the simulation cell in the z direction [56]. In the simulations of flow-induced peptide translocation, the water flow was produced by applying a constant force on each water molecule present in the system [60].
4.3 Analysis
The number of translocated amino acids Np, was calculated by counting the number of amino acids on the upper (cis) side of the membrane at each recorded microscopic state of the MD trajectory. If an amino acid had partially crossed the plane, the fraction of heavy atoms in the backbone of the protein above the plane was added to Np. The permeation rate was calculated as the slope of Np over time. When Np did not change more than 1 residue over several nanoseconds when block averaged to 200 ps blocks, that section was deemed a pause in the trajectory.
Instantaneous ionic currents were calculated by summing up ion displacements (of ions within 1 nm of the graphene membrane) between consecutive frames of an MD trajectory and dividing by the time between frames [56]. The time series were then block-averaged to 1 ns blocks to decrease noise.
Supplementary Material
Acknowledgments
This work was supported by the grants from the National Science Foundation (NSF) (DMR-0955959), the National Institutes of Health (R01-HG007406) and through a cooperative research agreement with the Oxford Nanopore Technologies. Z.H. was supported through the Undergraduate Fellowship of the Center for the Physics of Living Cells via NSF grant PHY-1430124; L.S. was supported through the University of Illinois Research Experience for Undergraduates program via NSF grant PHY-1359126. We gladly acknowledge supercomputer time provided through XSEDE Allocation Grant MCA05S028 and the Blue Waters petascale supercomputer system (UIUC).
Footnotes
Supporting Information
Supporting Information is available from the Wiley Online Library or from the author.
Contributor Information
Dr. James Wilson, Department of Physics, University of Illinois Urbana-Champaign, Urbana, IL 61801, USA
Leila Sloman, McGill University, 845 Rue Sherbrooke O, Montreal, QC H3A 0G4, Canada.
Zhiren He, Department of Physics, University of Illinois Urbana-Champaign, Urbana, IL 61801, USA.
Prof. Aleksei Aksimentiev, Email: aksiment@illinois.edu, Department of Physics, University of Illinois Urbana-Champaign, Urbana, IL 61801, USA.
References
- 1.Kasianowicz JJ, Brandin E, Branton D, Deamer DW. Characterization of individual polynucleotide molecules using a membrane channel. Proc Natl Acad Sci USA. 1996;93:13770–13773. doi: 10.1073/pnas.93.24.13770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kasianowicz JJ, Robertson JWF, Chan ER, Reiner JE, Stanford VM. Nanoscopic Porous Sensors. Annu Rev Anal Chem. 2008;1:737–766. doi: 10.1146/annurev.anchem.1.031207.112818. [DOI] [PubMed] [Google Scholar]
- 3.Howorka S, Siwy ZS. Nanopore Analytics: Sensing of Single Molecules. Chem Soc Rev. 2009;38:2360–2384. doi: 10.1039/b813796j. [DOI] [PubMed] [Google Scholar]
- 4.Wanunu M. Nanopores: A journey towards DNA sequencing. Phys Life Rev. 2012;9:125–158. doi: 10.1016/j.plrev.2012.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Branton D, Deamer DW, Marziali A, Bayley H, Benner SA, Butler T, Di Ventra M, Garaj S, Hibbs A, Huang X, et al. The potential and challenges of nanopore sequencing. Nat Biotech. 2008;26:1146–1153. doi: 10.1038/nbt.1495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Timp W, Mirsaidov UM, Wang D, Comer J, Aksimentiev A, Timp G. Nanopore Sequencing: Electrical Measurements of the Code of Life. IEEE Tran Nanotechnol. 2010;9:281–294. doi: 10.1109/TNANO.2010.2044418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Venkatesan BM, Bashir R. Nanopore sensors for nucleic acid analysis. Nat Nanotech. 2011;6:615–624. doi: 10.1038/nnano.2011.129. [DOI] [PubMed] [Google Scholar]
- 8.Akeson M, Branton D, Kasianowicz JJ, Brandin E, Deamer DW. Microsecond Time-Scale Discrimination Among polycytidylic Acid, Polyadenylic Acid, and Polyuridylic Acid as Homopolymers or as Segments Within Singe RNA Molecules. Biophys J. 1999;77:3227–3233. doi: 10.1016/S0006-3495(99)77153-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Meller A, Nivon L, Brandin E, Golovchenko J, Branton D. Rapid nanopore discrimination between single polynucleotide molecules. Proc Natl Acad Sci USA. 2000;97:1079–1084. doi: 10.1073/pnas.97.3.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Clarke J, Wu H-C, Jayasinghe L, Patel A, Reid S, Bayley H. Continuous Base Identification for Single-Molecule Nanopore DNA Sequencing. Nat Nanotech. 2009;4:265–270. doi: 10.1038/nnano.2009.12. [DOI] [PubMed] [Google Scholar]
- 11.Manrao EA, Derrington IM, Pavlenok M, Niederweis M, Gundlach JH. Nucleotide Discrimination with DNA Immobilized in the MspA Nanopore. PLoS ONE. 2011;6:e25723. doi: 10.1371/journal.pone.0025723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cockroft SL, Chu J, Amorin M, Ghadiri MR. A Single-Molecule Nanopore Device Detects DNA Polymerase Activity with Single-Nucleotide Resolution. J Am Chem Soc. 2008;130:818–820. doi: 10.1021/ja077082c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Manrao EA, Derrington IM, Laszlo AH, Langford KW, Hopper MK, Gillgren N, Pavlenok M, Niederweis M, Gundlach JH. Reading DNA at single-nucleotide resolution with a mutant MspA nanopore and phi29 DNA polymerase. Nat Biotech. 2012;30:349–353. doi: 10.1038/nbt.2171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cherf GM, Lieberman KR, Rashid H, Lam CE, Karplus K, Akeson M. Automated Forward and Reverse Ratcheting of DNA in a Nanopore at 5-°A Precision. Nat Biotech. 2012;30:344–348. doi: 10.1038/nbt.2147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Timp W, Comer J, Aksimentiev A. DNA Base-Calling from a Nanopore Using a Viterbi Algorithm. Biophys J. 2012;102:L37–L39. doi: 10.1016/j.bpj.2012.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Laszlo AH, Derrington IM, Ross BC, Brinkerhoff H, Adey A, Nova IC, Craig JM, Langford KW, Samson JM, Daza R, et al. Decoding Long Nanopore Sequencing Reads of Natural DNA. Nat Biotech. 2014;32:829–833. doi: 10.1038/nbt.2950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Movileanu L, Howorka S, Braha O, Bayley H. Detecting protein analytes that modulate transmembrane movement of a polymer chain within a single protein pore. Nat Biotech. 2000;18:1091–1095. doi: 10.1038/80295. [DOI] [PubMed] [Google Scholar]
- 18.Xie H, Braha O, Gu LQ, Cheley S, Bayley H. Single-molecule observation of the catalytic subunit of cAMP-dependent protein kinase binding to an inhibitor peptide. Chem Biol. 2005;12:109–120. doi: 10.1016/j.chembiol.2004.11.013. [DOI] [PubMed] [Google Scholar]
- 19.Movileanu L, Schmittschmitt JP, Bayley H. Interactions of Peptides with a Protein Pore. Biophys J. 2005;89:1030–1045. doi: 10.1529/biophysj.104.057406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Hornblower B, Coombs A, Whitaker RD, Kolomeisky A, Picone SJ, Meller A, Akeson M. Single-molecule analysis of DNA-protein complexes using nanopores. Nat Mater. 2007;4:315–317. doi: 10.1038/nmeth1021. [DOI] [PubMed] [Google Scholar]
- 21.Zhao Q, Sigalov G, Dimitrov V, Dorvel B, Mirsaidov U, Sligar S, Aksimentiev A, Timp G. Detecting SNPs Using a Synthetic Nanopore. Nano Lett. 2007;7:1680–1685. doi: 10.1021/nl070668c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Mohammad M, Prakash S, Matouschek A, Movileanu L. Controlling a Single Protein in a Nanopore through Electrostatic Traps. J Am Chem Soc. 2008;130:4081–4088. doi: 10.1021/ja710787a. [DOI] [PubMed] [Google Scholar]
- 23.Talaga DS, Li J. Single-molecule Protein Unfolding in Solid State Nanopores. J Am Chem Soc. 2009;131:9287–9297. doi: 10.1021/ja901088b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dorvel B, Sigalov G, Zhao Q, Comer J, Dimitrov V, Mirsaidov U, Aksimentiev A, Timp G. Analyzing the Forces Binding a Restriction Endonuclease to DNA Using a Synthetic Nanopore. Nucleic Acids Res. 2009;37:4170–4179. doi: 10.1093/nar/gkp317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kowalczyk SW, Hall AR, Dekker C. Detection of Local Protein Structures along DNA Using Solid-State Nanopores. Nano Lett. 2010;10:324–328. doi: 10.1021/nl903631m. [DOI] [PubMed] [Google Scholar]
- 26.Yusko EC, Johnson JM, Majd S, Prangkio P, Rollings RC, Li J, Yang J, Mayer M. Controlling protein translocation through nanopores with bio-inspired fluid walls. Nat Nanotech. 2011;6:253–260. doi: 10.1038/nnano.2011.12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Freedman KJ, Bastian AR, Chaiken I, Kim MJ. Solid-State Nanopore Detection of Protein Complexes: Applications in Healthcare and Protein Kinetics. Small. 2012;9:750–759. doi: 10.1002/smll.201201423. [DOI] [PubMed] [Google Scholar]
- 28.Shan YP, Tiwari PB, Krishnakumar P, Vlassiouk I, Li WZ, Wang XW, Darici Y, Lindsay SM, Wang HD, Smirnov S, et al. Surface modification of graphene nanopores for protein translocation. Nanotech. 2013;24:495102. doi: 10.1088/0957-4484/24/49/495102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Rotem D, Jayasinghe L, Bayley H. Protein Detection by Nanopores Equipped with Aptamers. J Am Chem Soc. 2012;134:2781–2787. doi: 10.1021/ja2105653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nivala J, Marks DB, Akeson M. Unfoldase-mediated protein translocation through an α-hemolysin nanopore. Nat Biotech. 2013;31:247–250. doi: 10.1038/nbt.2503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rodriguez-Larrea D, Bayley H. Multistep protein unfolding during nanopore translocation. Nat Nanotech. 2013;8:288–295. doi: 10.1038/nnano.2013.22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Plesa C, Kowalczyk SW, Zinsmeester R, Grosberg AY, Rabin Y, Dekker C. Fast Translocation of Proteins through Solid State Nanopores. Nano Lett. 2013;13:658–663. doi: 10.1021/nl3042678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Larkin J, Henley RY, Muthukumar M, Rosenstein JK, Wanunu M. High-Bandwidth Protein Analysis Using Solid-State Nanopores. Biophys J. 2014;106:696–704. doi: 10.1016/j.bpj.2013.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Comer J, Ho A, Aksimentiev A. Toward Detection of DNA-Bound Proteins Using Solid-State Nanopores: Insights From Computer Simulations. Electrophoresis. 2012;33:3466–3479. doi: 10.1002/elps.201200164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhao Y, Ashcroft B, Zhang P, Liu H, Sen S, Song W, Im J, Gyarfas B, Manna S, Biswas S, et al. Single-molecule spectroscopy of amino acids and peptides by recognition tunnelling. Nat Nanotech. 2014;9:466–473. doi: 10.1038/nnano.2014.54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rosen CB, Rodriguez-Larrea D, Bayley H. Single-molecule site-specific detection of protein phosphorylation with a nanopore. Nat Biotech. 2014;32:179–181. doi: 10.1038/nbt.2799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Striemer CC, Gaborski TR, McGrath JL, Fauchet PM. Charge- and size-based separation of macromolecules using ultrathin silicon membranes. Nature. 2006;445:749–753. doi: 10.1038/nature05532. [DOI] [PubMed] [Google Scholar]
- 38.Storm AJ, Chen JH, Ling XS, Zandbergen HW, Dekker C. Fabrication of solid-state nanopore with single-nanometre precision. Nat Mater. 2003;2:537–540. doi: 10.1038/nmat941. [DOI] [PubMed] [Google Scholar]
- 39.Heng JB, Ho C, Kim T, Timp R, Aksimentiev A, Grinkova YV, Sligar S, Schulten K, Timp G. Sizing DNA using a Nanometer-Diameter Pore. Biophys J. 2004;87:2905–2911. doi: 10.1529/biophysj.104.041814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dekker C. Solid-State Nanopores. Nat Nanotech. 2007;2:209–215. doi: 10.1038/nnano.2007.27. [DOI] [PubMed] [Google Scholar]
- 41.Arjmandi-Tash H, Belyaeva LA, Schneider GF. Single molecule detection with graphene and other two-dimensional materials: nanopores and beyond. Chem Soc Rev. 2016;45:476–493. doi: 10.1039/c5cs00512d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, Grigorieva IV, Firsov AA. Electric field effect in atomically thin carbon films. Science. 2004;306:666. doi: 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- 43.Schneider GF, Kowalczyk SW, Calado VE, Pandraud G, Zandbergen HW, Vandersypen LMK, Dekker C. DNA Translocation through Graphene Nanopores. Nano Lett. 2010;10:3163–3167. doi: 10.1021/nl102069z. [DOI] [PubMed] [Google Scholar]
- 44.Merchant CA, Healy K, Wanunu M, Ray V, Peterman N, Bartel J, Fischbein MD, Venta K, Luo Z, Johnson ATC, et al. DNA Translocation through Graphene Nanopores. Nano Lett. 2010;10:2915–2921. doi: 10.1021/nl101046t. [DOI] [PubMed] [Google Scholar]
- 45.Garaj S, Hubbard W, Reina A, Kong J, Branton D, Golovchenko JA. Graphene as a subnanometre trans-electrode membrane. Nature. 2010;467:190–193. doi: 10.1038/nature09379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Garaj S, Liu S, Golovchenko JA, Branton D. Molecule-Hugging Graphene Nanopores. Proc Natl Acad Sci USA. 2013;110:12192–12196. doi: 10.1073/pnas.1220012110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schneider GF, Xu Q, Hage S, Luik S, Spoor JNH, Malladi S, Zandbergen HW, Dekker C. Tailoring the hydrophobicity of graphene for its use as nanopores for DNA translocation. Nat Commun. 2013;4:3619. doi: 10.1038/ncomms3619. [DOI] [PubMed] [Google Scholar]
- 48.Traversi F, Raillon C, Benameur SM, Liu K, Khlybov S, Tosun M, Krasnozhon D, Kis A, Radenovic A. Detecting the Translocation of DNA through a Nanopore Using Graphene Nanoribbons. Nat Nanotech. 2013;8:939–945. doi: 10.1038/nnano.2013.240. [DOI] [PubMed] [Google Scholar]
- 49.Banerjee S, Wilson J, Shim J, Shankla M, Corbin EA, Aksimentiev A, Bashir R. Slowing DNA Transport Using Graphene–DNA Interactions. Adv Funct Mater. 2015;25:936–946. doi: 10.1002/adfm.201403719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Walker MI, Weatherup RS, Bell NAW, Hofmann S, Keyser UF. Freestanding graphene membranes on glass nanopores for ionic current measurements. Appl Phys Lett. 2015:106. [Google Scholar]
- 51.Postma HWC. Rapid sequencing of individual DNA molecules in graphene nanogaps. Nano Lett. 2010;10:420–425. doi: 10.1021/nl9029237. [DOI] [PubMed] [Google Scholar]
- 52.Saha K, Drndi’c M, Nikoli’c BK. DNA base-specific modulation of microampere transverse edge currents through a metallic graphene nanoribbon with a nanopore. Nano Lett. 2012;12:50–55. doi: 10.1021/nl202870y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wells DB, Belkin M, Comer J, Aksimentiev A. Assessing Graphene Nanopores for Sequencing DNA. Nano Lett. 2012;12:4117–4123. doi: 10.1021/nl301655d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Shankla M, Aksimentiev A. Conformational Transitions and Stop-and-Go Nanopore Transport of Single-Stranded DNA on Charged Graphene. Nat Commun. 2014;5:5171. doi: 10.1038/ncomms6171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Hoshin Kim, Y GY, Sabrina M. Huang Sequence dependent interaction of single stranded DNA with graphitic flakes: atomistic molecular dynamics simulations. MRS Advances. 2016:1–7. [Google Scholar]
- 56.Aksimentiev A, Heng JB, Timp G, Schulten K. Microscopic Kinetics of DNA Translocation Through Synthetic Nanopores. Biophys J. 2004;87:2086–2097. doi: 10.1529/biophysj.104.042960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Bhattacharya S, Derrington IM, Pavlenok M, Niederweis M, Gundlach JH, Aksimentiev A. Molecular Dynamics Study of MspA Arginine Mutants Predicts Slow DNA Translocations and Ion Current Blockades Indicative of DNA Sequence. ACS Nano. 2012;6:6960–6968. doi: 10.1021/nn3019943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Guallar V, Borrelli KW. A binding mechanism in protein–nucleotide interactions: Implication for U1A RNA binding. Proc Natl Acad Sci USA. 2005;102:3954–3959. doi: 10.1073/pnas.0500888102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lu B, Hoogerheide DP, Zhao Q, Zhang H, Tang Z, Yu D, Golovchenko JA. Pressure-Controlled Motion of Single Polymers through Solid-State Nanopores. Nano Lett. 2013;13:3048–3052. doi: 10.1021/nl402052v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zhu F, Tajkhorshid E, Schulten K. Pressure-induced water transport in membrane channels studied by molecular dynamics. Biophys J. 2002;83:154–160. doi: 10.1016/S0006-3495(02)75157-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Majumder M, Chopra N, Andrews R, Hinds BJ. Nanoscale hydrodynamics: enhanced flow in carbon nanotubes. Nature. 2005;438:44–44. doi: 10.1038/43844a. [DOI] [PubMed] [Google Scholar]
- 62.Gadaleta A, Biance A-L, Siria A, Bocquet L. Ultra-sensitive flow measurement in individual nanopores through pressure–driven particle translocation. Nanoscale. 2015;7:7965–7970. doi: 10.1039/c4nr07468h. [DOI] [PubMed] [Google Scholar]
- 63.Bonome EL, Lepore R, Raimondo D, Cecconi F, Tramontano A, Chinappi M. Multistep Current Signal in Protein Translocation through Graphene Nanopores. The Journal of Physical Chemistry B. 2015;119:5815–5823. doi: 10.1021/acs.jpcb.5b02172. [DOI] [PubMed] [Google Scholar]
- 64.Belkin M, Maffeo C, Wells DB, Aksimentiev A. Stretching and Controlled Motion of Single-Stranded DNA in Locally Heated Solid-State Nanopores. ACS Nano. 2013;7:6816–6824. doi: 10.1021/nn403575n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Phillips JC, Braun R, Wang W, Gumbart J, Tajkhorshid E, Villa E, Chipot C, Skeel RD, Kale L, Schulten K. Scalable Molecular Dynamics with NAMD. J Comput Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Miyamoto S, Kollman PA. SETTLE: An Analytical Version of the SHAKE and RATTLE Algorithm for Rigid Water Molecules. J Comput Chem. 1992;13:952–962. [Google Scholar]
- 67.Andersen HC. RATTLE: A “Velocity” Version of the SHAKE Algorithm for Molecular Dynamics Calculations. J Comput Phys. 1983;52:24–34. [Google Scholar]
- 68.MacKerell AD, Jr, Bashford D, Bellott M, Dunbrack JrRL, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, et al. All-atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 69.Yoo J, Aksimentiev A. Improved Parametrization of Li+, Na+, K+, and Mg2+ Ions for All-Atom Molecular Dynamics Simulations of Nucleic Acid Systems. J Phys Chem Lett. 2012;3:45–50. [Google Scholar]
- 70.Darden TA, York D, Pedersen L. Particle Mesh Ewald: An N log(N) Method for Ewald Sums in Large Systems. J Chem Phys. 1993;98:10089–92. [Google Scholar]
- 71.Koopman EA, Lowe CP. Advantages of a Lowe-Andersen Thermostat in Molecular Dynamics Simulations. J Chem Phys. 2006;124:204103. doi: 10.1063/1.2198824. [DOI] [PubMed] [Google Scholar]
- 72.Humphrey W, Dalke A, Schulten K. VMD: Visual Molecular Dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 73.Aksimentiev A, Brunner R, Cruz-Chu ER, Comer J, Schulten K. Modeling transport through synthetic nanopores. IEEE Nanotechnol Mag. 2009;3:20–28. doi: 10.1109/MNANO.2008.931112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Song L, Hobaugh MR, Shustak C, Cheley S, Bayley H, Gouaux JE. Structure of Staphylococcal α-Hemolysin, a Heptameric Transmembrane Pore. Science. 1996;274:1859–1865. doi: 10.1126/science.274.5294.1859. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


