Evolution‐development congruence in pattern formation dynamics: Bifurcations in gene expression and regulation of networks structures

ABSTRACT

Search for possible relationships between phylogeny and ontogeny is important in evolutionary‐developmental biology. Here we uncover such relationships by numerical evolution and unveil their origin in terms of dynamical systems theory. By representing developmental dynamics of spatially located cells with gene expression dynamics with cell‐to‐cell interaction under external morphogen gradient, gene regulation networks are evolved under mutation and selection with the fitness to approach a prescribed spatial pattern of expressed genes. For most numerical evolution experiments, evolution of pattern over generations and development of pattern by an evolved network exhibit remarkable congruence. Both in the evolution and development pattern changes consist of several epochs where stripes are formed in a short time, while for other temporal regimes, pattern hardly changes. In evolution, these quasi‐stationary regimes are generations needed to hit relevant mutations, while in development, they are due to some gene expression that varies slowly and controls the pattern change. The morphogenesis is regulated by combinations of feedback or feedforward regulations, where the upstream feedforward network reads the external morphogen gradient, and generates a pattern used as a boundary condition for the later patterns. The ordering from up to downstream is common in evolution and development, while the successive epochal changes in development and evolution are represented as common bifurcations in dynamical‐systems theory, which lead to the evolution‐development congruence. Mechanism of exceptional violation of the congruence is also unveiled. Our results provide a new look on developmental stages, punctuated equilibrium, developmental bottlenecks, and evolutionary acquisition of novelty in morphogenesis. J. Exp. Zool. (Mol. Dev. Evol.) 326B:61–84, 2016. © 2015 The Authors. Journal of Experimental Zoology Part B: Molecular and Developmental Evolution Published by Wiley Periodicals, Inc.

Possible relationships between the development of multicellular organisms and their evolution have been searched for over a century. About 200 years ago, von Baer proposed laws of development, based on observations of development across species, which mainly claimed that the early embryo is mostly conserved across species, while embryonic changes through ontogeny move from a general form common to many species, to species‐specific forms (von Baer, 1828). Charles Darwin and other biologists of his time interpreted these laws as proof of evolution from a common ancestor (Darwin, 1859; Müller, 1869; Hall, 2000). Thus, changes in embryos from a common to a specialized form are regarded as a reflection of evolutional history. Development has been studied in an evolutionary context, and thus some relationships between evolution and development are expected. The most popular concept might be Ernst Haeckel's recapitulation theory, or simply the statement “Ontogeny recapitulates phylogeny” which assumes that development is literally the accelerated evolution, i.e., embryo in development is the same as one of an adult of its ancestors and during development, embryo changes from one ancestor to another according to the evolutional order (Haeckel, 1900). This idea, of course, is not acceptable today, as there are also many counterexamples against it. Indeed, we know that genome itself is not affected during development. However, its modern thesis on possible recapitulation at the gene expression pattern needs to be tested. Although existence of some kind of evo‐devo relationship has been widely supposed and gathered much interest, contemporary evolutional‐developmental biology still cannot provide alternative general concept for it (Gould, 1977; Hall, 1999; Richardson and Keuck, 2002).

GLOSSARY.

Dynamical systems:

Mathematical formulation of temporal change of state variables. Dynamical system formulates the temporal change of state by how a point in the state space moves according to the fixed rule for time development. The rule gives a flow on the state space.

Application to biology: Consider a cell whose state is represented by a set of (protein) concentrations of k species, x ₁(t), …, x_k(t), i.e., expression level of each gene. Then the cellular state is represented by a point in a k‐dimensional state space, each of which axis gives expression level of each gene (protein). According to the reaction process involving gene regulation, the cellular state changes in time giving a trajectory in this state space, as formulated by a dynamical system.

Attractor:

After some time, the state in dynamical systems is attracted into, and remains at, a certain portion of state space. This region is called an attractor. Sometimes, temporal change in the state ceases after sometime, i.e., a fixed state is reached. This is called a fixed point attractor. For some attractor, the state oscillates periodically in time known as a limit‐cycle attractor.

Nullcline:

A line (or plane) in the state space in which one variable does not change in time, i.e., the flow in the direction of one axis is null. Nullcline is useful in depicting the flows in the state space, while fixed‐points are obtained as the intersection of nullclines for all the variables.

Bifurcation:

Dynamical systems include control parameter(s) that determine the rule of temporal change. Often, the attractor changes continuously against the change in a parameter, without qualitative/topological change. However, when a parameter reaches some value, qualitative change in the attractor occurs; for example, change from one fixed‐point attractor to another, or change to a limit‐cycle attractor. Such change is termed as bifurcation.

Pattern:

Besides the intra‐cellular dynamics of a cell, cells that are aligned in space interact with each other via diffusion. Thus the protein concentration forms a pattern in space, which changes in time. This pattern dynamics is represented by coupled dynamical systems in which cells with intracellular dynamical systems are spatially aligned.

Feedforward (Network):

With the gene regulation network, each protein expression mutually influences, with activation or inhibition. When the expression of gene A influences B but there is no influence from B to A, (i.e., there is no loop between A and B), the structure from A to B is called as feedforward.

Feedback (Network):

In contrast, if the two genes influence on each other's expression, i.e., if there is a loop between two genes, it is termed as feedback network. When A activates B and B inhibits A (or vice versa), the feedback structure can generate oscillatory gene expression, as adopted in segmentation clock.

Epoch (the term introduced in the present paper):

The short period of time in which pattern changes drastically, where the expression of output gene (state) exhibits a distinct change. Here distinct change means that the expression level of output gene changes between ∼0 and ∼1 within the time scale of the output gene 1/γ (which is usually ∼1) for development, and within a single generation for the evolution (see Methods for algorithmic definition).

In development: In the present system, some variables change slowly in time, during a quasi‐stationary regime. Its time span is much longer than the epoch with the drastic change. If this slow change influences the output pattern, it is regarded to work as a control parameter. Then the drastic change of output occurs as a result of bifurcation against this control parameter.

In evolution: Mutation causes the change in gene regulation network, leading to the change in the reaction path and accordingly the rule of dynamical systems. With this change, the pattern shows a drastic change, which, as will be shown, is represented also as bifurcation.

Previously, this type of research was hindered by a lack of quantitative arguments. To transcend the century‐long controversies associated with this research, efforts are being made to quantitatively analyze the evolution‐development (“evo‐devo”) relationship by using gene expression and genome sequence data. For example, a developmental bottleneck among species in some phylum is discussed, where differences in gene expressions among several species from the same progenitor decreases at the same developmental stage (Hazkani‐Covo et al., 2005; Domazet‐Lošo and Tautz, 2010; Kalinka et al., 2010; Irie and Kuratani, 2011; Quint et al., 2012; Levin et al., 2012; Wang et al., 2013). In spite of these advances, however, a quantitative relationship between evolution and development remains to be unveiled owing to the limitations in available data on developmental processes along the evolutionary course.

In experimental studies, comparisons are made among current species on phylogenic trees, as schematically shown in Figure 1. On the other hand, a comparison over species along a single phylogenetic chain from ancestor to offspring as shown in Figure 1, if available, gives more straightforward information on relationship between development and evolution. This comparison is hardly possible in practice, as fossil data usually do not include information on developmental processes. However, there is an alternative approach in evo‐devo, which uses in silico evolution. Indeed, several numerical evolution of developmental process has been recently carried out. The models in these studies consider the spatial arrangements and behaviors of cells that are subject to morphogenic input. Protein expression levels within the cells change over time by intra‐cellular gene expression dynamics and also by cell‐to‐cell interaction. The developmental processes of cellular states are represented by these gene expression dynamics to form a spatial pattern of expressions, while the gene regulation networks associated with these dynamics evolve through modifications by genome changes. By establishing a fitness condition of making pattern with particular features, the evolution of the network to generate such a pattern can be studied quantitatively. Indeed, with the fitness condition of rewording segment number, recent studies of in silico evolution have suggested basic mechanisms for stripe formation through development and accessed plausible evolutionary scenarios (Salazar‐Ciudad et al., 2001a,2001b; François et al., 2007; Fujimoto et al., 2008; Ten Tusscher and Hogeweg, 2011).

Figure 1.

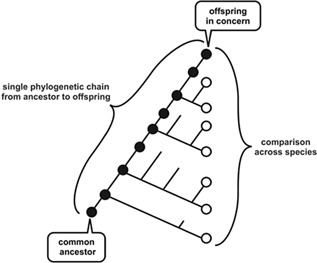
Schematic representation of single‐chain phylogeny and comparison across species in phylogenic tree. Schematic representation of the comparisons along single‐chain phylogeny and across species. In the phylogenic tree shown here, the currently existing species represented by the right‐end circles, are diverted from a common ancestor. Branching from a common ancestor leads to establishment of some new species, while some are terminated by extinction. The comparison of developmental processes across species is made over the existing species. On the other hand, a single phylogenic chain, which we focused in this study, is given as the line from the common ancestor to the offspring in concern. From the species in concern, ancestors are uniquely traced back. The comparison of developmental processes along this chain is possible at least in theory or simulations, which provides fundamental information on possible relationship between development and evolution.

OUR STRATEGY

Following the earlier theoretical studies for the development to form stripes, we focus here on uncovering evo‐devo relationship and understand them in dynamical‐systems and network analysis. Cells are aligned in 1‐dimensional space, each of which consists of a set of proteins. The cellular state is thus represented by a set of protein concentrations whose temporal changes are governed by intra‐cellular gene regulation network and cell‐to‐cell interaction via diffusion of some proteins. (Note that reaction‐diffusion formulation is rather general which, for example, covers pattern formation by mechanical stress (Murray, 2002).

We introduced the fitness so that the gene expression of a given output gene in space approaches a prescribed spatial pattern. The fitness is higher, as the developed pattern is closer to the prefixed target pattern. Accordingly, our evolution is under strongly purifying selection. With this fitness evolution simulation, we can trace how a certain pattern is evolved on single‐chain phylogeny of ancestor to descendant, which is different than species‐wide comparison in experiments (Fig. 1).

Comparing the developmental processes to shape a given gene expression pattern through an evolutionary course under mutation, we examine the developmental dynamics of offspring achieving high fitness and evolutionary change in the patterns. For the majority of simulations, we found parallelism between evolution and development along the single‐chain phylogeny, as is named as evo‐devo congruence. This is distinguishable from the standard version of recapitulation, as it adopts not the species‐wide but single‐chain‐phylogeny comparison, and it is based on quantitative gene‐expression pattern. Analyses are provided in terms of dynamical‐systems theory and network analysis (Strogatz, 1994, Hirsch et al., 2004, Alon, 2006, Kaneko, 2006). For experimentalists who may not be familiar with the theory, here we provide brief description of key terms as glossary table so that one can come back to it later.

The organization of the present paper is as follows.

In the present paper, after presenting the numerical evidences for evolution‐development congruence, we explain its origin in terms of dynamical systems.

We will be showing that both development and evolution adopt the same type of bifurcation, while the structure in gene regulation networks to support the congruence is understood as a combination of upstream feedforward network with downstream feedforward‐ or feedback‐networks. In rare examples, however, evo‐devo congruence is found to be violated, whose mechanisms are also elucidated. After examining extensive numerical results to support the above conclusion, its relevance to developmental and evolutionary biology will be discussed.

RESULTS

We numerically evolved gene regulatory networks governing development in order to study evo‐devo relationship. Here each organism consisted of M cells (where M = 96), aligned in onedimensional space, where maternal factors were supplied from each end of the space. Each cell had N genes (proteins) (where N = 16) whose expression dynamics were governed by expression levels of other genes through a given gene regulatory network (GRN), while interaction between neighboring cells was mediated via diffusion of expressed proteins. These conditions defined the developmental dynamics of the study. We prepared 100 individuals with slightly modified GRNs (See Table 1 in the Method section for further information for parameters and initial settings for the simulation). After each gene expression level reached a stationary value through development, we computed fitness from the expression of a prescribed output gene.

Table 1.

Parameters and initial settings for the simulation

Numbers of network nodes	16 (fixed)
Total cell number (space size)	96 (fixed)
Numbers of average edges in the initial network	16
Range of γ (randomly selected)	[0:1]
Range of D (randomly selected)	[0:1]
Range of θ (randomly selected)	[0:1]
Degree of nonlinearity of the reaction term β	40
Population size	100 (fixed)
Mutation rate μ	1/256
Degree of evolutionary fluctuation of parameter σ	0.01

Fitness was defined as the difference between this output expression pattern in space and a prescribed target pattern, with the highest fitness values defined by the best match. We used a genetic algorithm to select the individuals with higher fitness by introducing mutations in the GRN (see Fig. 2 for schematic representation and the Methods section for details).

Figure 2.

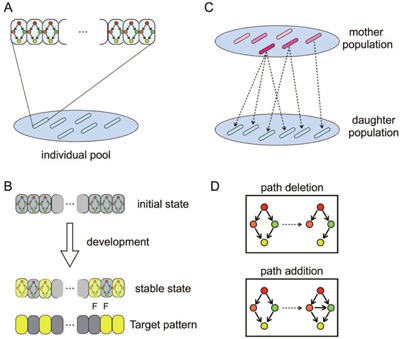
Schematic representation of simulation procedure. (A) There are 100 individuals in a pool for each generation. Each individual consists of 96 uniform cells, which share a common GRN, while the GRN differs slightly between individuals. (B): Each individual develops from the same initial state in which genes are not expressed (i.e., with x < 0) except for genes receiving the maternal gradient. Over time, individuals develop into stable states. Colors of cells indicate the expression level of the output genes; yellow is high, gray is low. After reaching a stable state, the expression pattern of the output gene was compared with the predefined target pattern. The fitness level was then elevated as the stable expression of the output gene approached the target pattern (see the Methods section for detail). (C) After the fitness of every individual was calculated, the population for the next generation was created. Each individual was selected as a mother with a probability proportional to its fitness. In the figure, the degree of red color indicates the fitness. (D) The GRN of a daughter is slightly different from the mother's, with a given mutation rate. The mutation involves deletion or addition of paths in the mother's GRN, and a change in characteristic parameters in expression dynamics and the diffusion constant (see the Methods section for details).

Most evolved networks, after few thousand generations, were capable of generating predefined target patterns. An example of the developmental time course to shape such a pattern is shown in Figure 3A, where the space‐time diagram of the expression level of the output gene is displayed with the horizontal axis as the developmental time and the vertical axis as the cellular index (i.e., spatial axis). As shown, the target pattern (Fig. 3C) is shaped after several developmental stages for stripe formations. (Unless otherwise mentioned, development after evolution is plotted for the fittest individual at 2,000th generation.) Next, we examined how the output gene pattern had evolved, by tracing the final output pattern of the ancestors successively.

Figure 3.

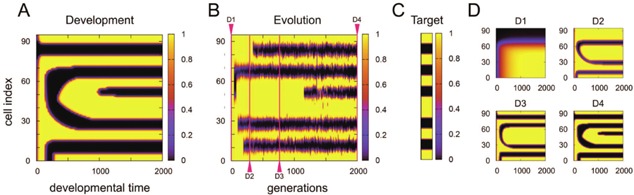
An example of space‐time diagram of evolution and development. (A) The expression level of the output gene is shown with developmental time as the horizontal axis and cell index (spatial position) as the vertical axis. The expression level of the output gene of the corresponding cell at a given time is color coded, (sidebar) with black indicating the lowest and yellow indicating the highest expression levels. Development consists of a few epochs with rapid changes in the pattern, separated by quasi‐stationary regimes with little change in the pattern, until the target pattern is shaped by development. (B) The spacetime diagram of the evolutionary course, corresponding to (A). The expression level of the final output gene (at time = 2000) is shown with evolutionary generation as the horizontal axis and cell index (spatial position) as the vertical axis. This figure shows how the pattern is acquired through evolution. At each generation, the final pattern of the direct ancestor of the next generation is shown. The evolution of the developed output pattern consists of quasi‐static regimes sandwiched by epochs with rapid change resulting from mutation, until the target pattern is evolved. (C) The predefined target pattern adopted in the present simulation. (D) Space‐time diagram of the developmental process for several generations in (B). Each figure shows the development of the ancestral expression pattern at each generation, 0(D1), 300(D2), 750(D3), and 2000(D4). For reference, these generations are each marked by a red triangle at the top or bottom in (B).

The output pattern after development of the ancestor at each generation is plotted in Figure 3B, where the color code and spatial axis are identical to those in Figure 3A, while the horizontal axis represents the generation (evolution time) in Figure 3B. The similarity between the developmental (Fig. 3A) and evolutionary (Fig. 3B) spacetime diagrams are clearly discernible.

For reference, we have also plotted the developmental course at intermediate (1, 300, 750, 2,000) generations in Figure 3D. With successive generations, novel stripes are acquired, moving the system toward the target pattern.

DEVELOPMENT WITH EPOCHS THAT CORRESPOND TO THOSE DERIVED THROUGH EVOLUTION

Correspondence between developmental and evolutionary space‐time diagrams was commonly observed in our simulations (Fig. 3). Additional examples are provided in Fig. 4 and in Supplemental Fig. S1.

It is remarkable that the pattern formation progressed in a stepwise manner, with respect to both evolution and development. Each stripe emerges not gradually, but discretely at some step in development and in evolution.

More interestingly, the correspondence between evolutionary and developmental diagrams is supported by the correspondence of epochs in the two diagrams. This correspondence is valid for a large portion of our simulations. Furthermore, we generally observed good agreement between development and evolution modes, based on the topology of stripe formation: i.e., how later stripes branched from earlier stripes (Figs. 3 and 4, Supplemental Fig. S1).

Figure 4.

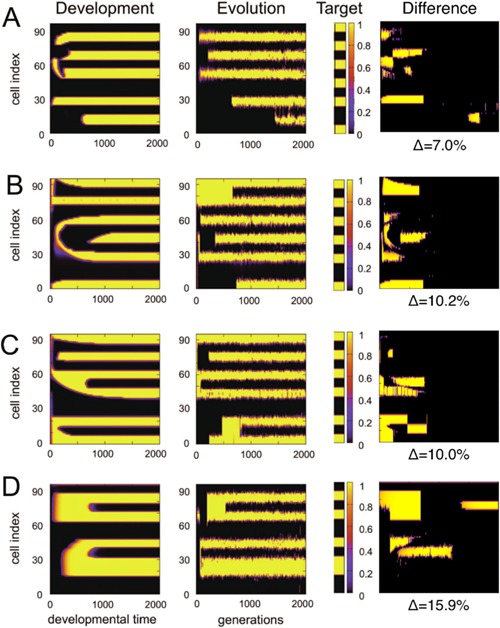
Four additional examples of evo‐devo congruence. (A)–(D) Each row shows space‐time diagrams of evolution and development, in the same way as Figure 3, for different target patterns as displayed, the difference pattern between evolution and development as defined in Figure 5. See Supplemental Information for additional examples.

To quantitatively evaluate the correspondence between evolutionary and developmental space‐time diagrams, we measured the overlap between the diagrams of the output expression levels. The procedure to compute the overlap is shown in Figure 5A. For both diagrams, we took only the temporal regime in which the pattern formation progressed, i.e., we discarded both the early stages where the output gene was not expressed in all cells (i.e., x _output(l,t) = 0), and the final stage after emergence of the stationary pattern, when no additional changes were observed. The distances between the output expression levels for both the diagrams were then averaged over all space‐time pixels, Δ, thus allowing us to compute the differences between the two diagrams. The distribution of Δ from approximately 500 evolution trials for different target patterns is shown in Figure 5B, with a peak distribution located at approximately 8%. Note that if the difference between the two diagrams is one stripe over all of the space‐time pixels, Δ here is evaluated to be 8.2% (Fig. 5B). Hence, the peak value in the distribution is mostly just one stripe difference over all space‐time. Thus for most examples, the space‐time diagrams between developmental and evolutionary processes show remarkable similarity. These results suggest that the correspondence between evolution and development is not an accident, but is a general outcome for most evolution samples.

Figure 5.

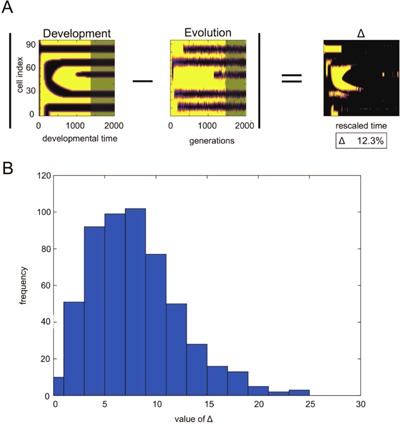
Quantitative analysis of the degree of evo‐devo congruence. (A) Schematic diagram illustrating quantitative analysis of the similarity between evolution and development. The differences between development and evolution were computed by subtracting expression levels at each pixel. By taking the absolute value of difference, and averaging the space‐time pixels, the average difference was computed. To avoid over‐estimating similarity, the region before the emergence of the first stripe and after the final pattern was ignored for both development and evolution. For example, the gray‐masked region of the development and evolution figures does not include data for the calculation. If one stripe is completely shifted in time, is approximately 8%. (B) Histogram of the distribution of the Δ values. The abscissa is the Δ value computed via the procedure described in (A). The ordinate is the frequency of touch Δ values determined by bin size 2. Distribution was obtained from 500 runs with different target patterns.

Furthermore, the distribution of Δ over time, as shown in Figure 6, shows that deviation is more frequent as earlier time scale. At later stages, the congruence is higher, which suggests that degree of changes decreases at later stage as dynamics depend on network structures pre‐existing from earlier stage.

Figure 6.

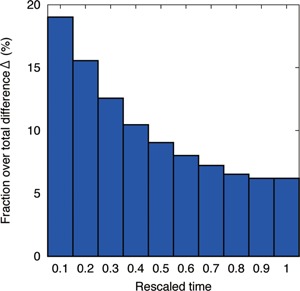
Time distribution of the difference Δ between evolution and development. We computed the difference Δ in space‐time pixel. Then we obtained the distribution of Δ over all simulation results, by using the histogram with the time bin of 1/10 of rescaled time between 0 (initial) and 1 (final). Difference in evolution and development is more frequent at earlier stages.

MECHANISMS OF EVO‐DEVO CONGRUENCE

Emergence of Slowly Changing Gene Expressions

During each epoch, patterns change within a short span for both evolution and development, whereas the pattern remains quasi‐stationary between epochs (Figs. 3 and 4). Evo‐devo congruence is a direct consequence of the congruence of these epochs between evolution and development. Thus, we study first how such epochal pattern formation is possible for both evolution and development.

The epoch formation in evolutionary courses is trivial. Since the evolution undergo with strongly purifying selection, only neutral mutations or beneficial mutations remain during evolution. Generally, appearance of the relevant mutations to beneficial to pattern change require some generations. Furthermore, accumulation of neutral mutations is often needed for the beneficial mutation to work (indeed, for 80% of epochs, they are needed). Thus the evolutionary course of the developed pattern consists of a quasi‐stationary regime and requires several epochs to change the stripe pattern. This epochal pattern change in evolution has previously been coined as “punctuated equilibrium” (Eldredge and Gould, 1972).

Correspondingly, we have observed a long quasi‐stationary period in development between epochs of rapidly changing stripe patterns. However, this is not self‐evident. In this section, we focus on how epochal pattern formation is possible in development. In Figure 7, we show the change in gene expression at the site marked in Figure 7A, which presents the space‐time diagram of the output gene expression. Figure 7B shows the expression dynamics in the marked cells in Figure 7A. Each colored line indicates the expression dynamics of a given gene. As shown, the expression of the output gene (red line) switched between on and off at the time denoted by the crossed red lines in Figure 7A. This switch corresponds to an epoch. As seen in Figure 7B, expression of a subset of genes changes over time, before and after an epoch. Even though the expression change in most genes, including the output gene, was rather fast to support the epoch, there exists a subset of genes whose expression level changes slowly over time (blue line).

Figure 7.

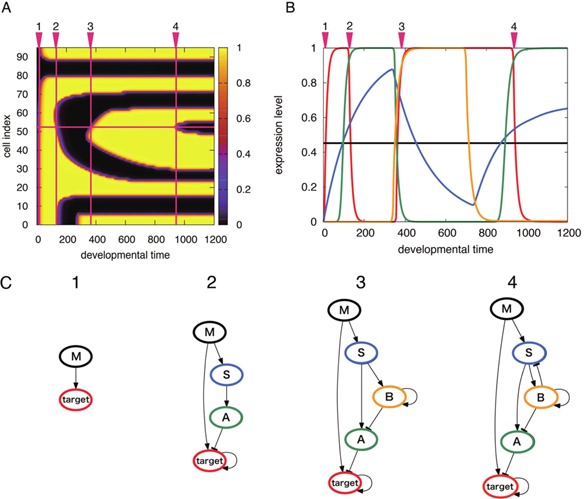
An example of developmental dynamics with several epochs for a single cell. (A) Developmental space‐time diagram of the output expression level. The developmental time up to 1,200 in Figure 3 is zoomed, in order to clearly distinguish epochs. There are four epochs associated with one cell, marked by crossing of the red lines. (B) Gene expression dynamics at the cell highlighted by red horizontal line in (A). The time series of the expression level is plotted where the line color corresponds to that of network node in (C), which representing each gene. Most genes change their expression level within each epoch, except for the gene S represented by the blue line. (C) The working networks that function to switch the output expression at each epoch. These networks are derived from analyses on gene expression dynamics (see the Method section). Arrow edges indicate positive regulation while the headed edges indicate negative regulation.

To understand the role of genes with slowly varying expression, a core part of the GRN, which is responsible for stripe formation at each epoch, was extracted (see the Methods section). The core network at each epoch is termed the “working network”, as shown in Figure 7C.

From the working network, it is clear that slowly changing gene expression serves as a control variable for the switch in output gene expression dynamics. The input to the output gene was beyond or below its threshold level at the times marked by crossed red lines in Figure 7A. This change was driven by the on/off switch of gene A, seen in Figure 7C, while the switching in gene A was mainly driven by the slow change in input, denoted by gene S in Figure 7C. The slow change in the expression of gene S served as a control cue, providing the timing of the epoch. The morphogen concentration acting on cells was fixed, as indicated by the black horizontal line in Figure 7B. Morphogens initially activated the output gene that provides the first epoch. However, they simultaneously activated gene S, whose expression level increased at a slower rate than that of the output gene. When it exceeded the threshold for the expression level of gene A, the suppression of the output gene was dominant, leading to decreased output gene expression and thereby generating the second epoch. Indeed, the third and fourth epochs were controlled by a slowly varying input in the same manner (data not shown).

We examined several other examples, and found that the working network after evolution always includes a gene with slowly varying expression at the corresponding epoch. The slow gene expression did not give a direct input for the output gene, but gave an input to a gene that gives an input to the target (i.e., gene A and B, Fig. 7). We then carried out statistical analyses to confirm that control via slow expression changes is a general outcome of evolution.

In our model, the input term for each expression has a dynamic range given by the threshold (θ_i) and the slope (β) of the input–output relationship (see the Methods section). If the input for a gene is out of the dynamic range (i.e., −2/β < Input − θ < 2/β), the expression of the gene is either 0 or 1. Thus, the time span required for the input to pass through the dynamic range provides an indicator of the time‐scale for the control of the input. We computed the timescale of the input to both the output gene and the other genes. In Figure 8, the evolutional changes of these two time scales are plotted (for the latter time scale, the slowest change among all genes that have a path to the output gene is added). As shown, the time scales are nearly equal at the first generation, indicating the absence of slow expression control. Throughout evolution, the timescale of the output gene was not altered, which also supported the notion of epochs with a short time span of change. In contrast, the time scales of other genes increased, such that the ratio of the target timescale to that of others decreased, reaching 1/5 of the average. Thus the relative timescale of input gene expression to the change in target expression was slower during evolution. Hence, the results of Figure 8 support the emergence of epochs by the slow genetic control.

Figure 8.

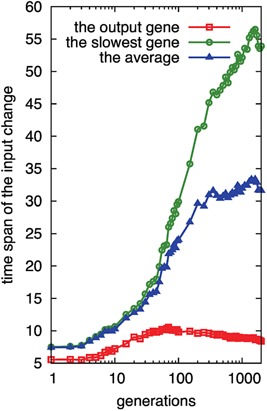
Evolution of the time scale for the input for the output and other genes. By taking genes whose expression level change between on and off for each developmental epoch, the time scales are computed as the time span that the input for the gene passes through the dynamic range during each development. The red square gives the time span for the input of the output gene, and the blue triangle (green circle) denotes the average (the largest) of the time span among the genes that have a path to the output gene, respectively. The time spans are computed from the average of 500 samples of evolution simulations.

The Origin Of Slowness in Expression

Questions remained regarding the origins of such slow expression dynamics. Following analysis of all examples, we concluded that they could be attributed to the following two mechanisms:

1. The existence of genes with small rate constants γ_i associated with expression change: The expression dynamics in our model includes a parameter 1/γ_i, representing the time constant for change. Hence, if some gene i has a small γ_i value, expression changes slowly. It should be noted that the rate parameters γ_is after evolution are distributed by gene i, and some genes have smaller γ_i values. Therefore, the expression levels of genes with small γ_i values function as a slow variable. Indeed, in the example presented in Figure 6, γ_i for the gene S is 0.063; a full order of magnitude smaller than the others. Through evolution, genes with distinctively small γ_i values appear, even though we initially established nearly uniform γ_i values for all genes.

2. Expression levels near the threshold: The expression dynamics here have a threshold θ_i. If the input to the gene is larger (or smaller) than θ_i, it is expressed (or suppressed), respectively. When the input term from other genes to the gene i is close to θ_i, then, the expression level can be balanced at an intermediate value between 0 and 1. Indeed, if the deviation of input from θ_i is smaller than 1/β, the inverse of sensitivity, then the expression level of x_i(l,t) is no longer attracted to 0 or 1. In this case, this stationary state is less stable than those closer to 0 or 1 (see Supplemental text S1 for the mathematical explanation using the Jacobian matrix). Hence, the time‐scale around this fixed point is longer in duration.

This slow relaxation to the stationary state as a single‐cell dynamics is extended through the entire space, mediated by the diffusion interactions with other cells. With diffusion, the slow expression change of a certain cell can propagate spatially to other sites, to change their expression levels slowly.

Mechanisms for Pattern Formation and Their Dependency

Now, we show how stripes (valleys) are formed in developmental process here, based on gene regulation dynamics, cell‐to‐cell diffusion, and morphogen gradient. Through extensive analysis of 500 samples of the evolved pattern‐formation, we confirmed that the stripe formation process is reduced to only two basic mechanisms in gene expression dynamics with corresponding GRN structures. In fact, these two mechanisms have previously been identified and studied extensively, which are known as feedforward and feedback regulations (Salazar‐Ciudad et al., 2001a,2001b; Alon, 2006; François et al., 2007; Fujimoto et al., 2008; Cotterell and Sharpe, 2010; Ten Tusscher and Hogeweg, 2011).

Feedforward

The classic mechanism for stripe formation, which was analyzed in the segmentation process in Drosophila, is feedforward regulation. This mechanism has been analyzed both theoretically and experimentally (von Dassow et al., 2000; Jaeger et al., 2004; Ishihara et al., 2005). In this case, a gene “reads” the morphogen gradient for spatial information, to establish an “on/off” response under a given threshold level, so that the gene is expressed on the one side of space, and non‐expressed on the other side. Another “downstream” gene receives positive (or negative) input from this gene, and negative (or positive) input from the morphogen, and responds to create another segmentation in space, if the threshold parameters satisfy a suitable condition. By combining this feedforward regulation, more stripes are formed for the downstream gene. The corresponding GRN does not require feedback regulation, or cell‐to‐cell interaction by diffusion; only unidirectional, feedforward regulation from morphogen input to downstream genes is required. This feedforward regulation frequently exists in our evolved GRN, and is used to generate at least some stripes.

Feedback Oscillation Within a Boundary

The other mechanism for stripe formation, commonly observed in the present simulations, takes advantage of feedback regulation to produce a temporal oscillation in the expression level. This temporal oscillation at a single‐cell level is then fixed into a spatial periodic pattern by the diffusion among cells. A typical core network structure and expression dynamics are shown in Figure 9A. Here, gene A activates the expression of both itself and gene B, while gene B suppresses the expression of gene A. As this network is just a typical negative feedback loop, it produces a temporally oscillating expression when the parameter values are appropriate. Now, with the diffusion of B under an appropriate boundary condition, this temporal oscillation is fixed into a spatially periodic pattern (Fig. 9B).

Figure 9.

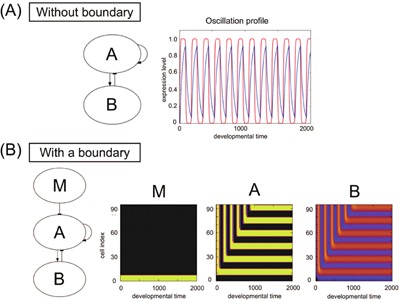
Feedback oscillation and its fixation. (A) Without boundary: minimal network for oscillatory expression with the time series of the expression for a specific cell. Gene A activates the expression of gene B and itself, and gene B suppresses A. In the plotted time series, developmental time is plotted as the abscissa, and the expression levels of A (red) and B (blue) are plotted as the ordinate. (B) With a boundary: the input from gene M, which was influenced by the maternal factor, was included in the oscillatory network. The space‐time diagram of genes M, A, and B illustrate how oscillatory expressions of gene A and gene B were fixed to form stripes. Gene M was expressed near the boundary.

Consider a case where the input from the morphogen M suppresses the activation of A at the boundary. Again, without input from M at the boundary, there appears temporal oscillation in the expression of A and B. At this boundary, the expression of gene B is also suppressed. Then the protein B at the adjacent upper site diffuses to this boundary. Subsequently, the expression of B at the site is decreased, so that the suppression of A is relaxed (Fig. 9B, bottom). Then the expression of gene A is fixed to a higher level, instead of oscillating. This also leads to an increase in the expression of B. At the next upper sites, oscillation still remains. When the expression of A is low, the diffusion of protein B from the lower site suppresses the activation of A, so that the increase of the expression of A no longer occurs. Thus, the expression level of A is fixed at a lower level. With this process, temporal oscillation of one period is mapped into one spatial stripe. The same fixation process is repeated with the subsequent oscillation at further upper sites. Thus, the temporal oscillation is recursively fixed to a spatially periodic pattern. With this mechanism, the stripe pattern in space is formed and fixed (for detailed theoretical analysis, see Supplemental Figs. S2 and S3).

This mechanism is analogous to the classic Turing pattern in which case the suppression of B to itself is necessary to exclude a spatially homogeneous, temporally oscillating state. Here, the diffusion of the inhibitor gene B works in the same way as the Turing pattern (Turing, 1952), but the mechanism here adopts temporally oscillatory dynamics, and is understood as Turing–Hopf bifurcation (De Wit et al., 1996). In an interacting two‐cell system, this differentiation from the oscillatory state is understood as a saddle node bifurcation on invariant cycle (SNIC) (Goto and Kaneko, 2013).

We note two points. The mechanism here uses the suppression at a boundary to fix a pattern, instead of the inhibition of B to itself, and thus the boundary condition is important. Next, the mechanism resembles Meinhardt's model or a classic wavefront mechanism, where the temporal oscillation is fixed into a spatial periodic pattern through input from the morphogen gradient (the growth of the system size) (Meinhardt, 1982). In those mechanisms, however, diffusion (or cell‐to‐cell interaction) is not essential, in contrast to our mechanism. In our case, not the gradient but only the information at the boundary is needed, and further stripe formation progresses spontaneously by the diffusive cell‐to‐cell interaction.

Stripe Formation Order by the Combination of the Two Mechanisms

All of the potential stripe formation processes evolved in our model could be generated by a combination out of four possible ways of combining these two developmental mechanisms, sequentially. However, for the feedback mechanism to work, the boundary depending on the morphogen has to be established in advance, to fix the temporal oscillations to spatial stripes. Thus, the feedforward mechanism to read the external morphogen is needed to produce the boundary. Otherwise, no stripe will be formed, so that such networks will not remain in the evolutionary simulation. Hence, we consider only two combinations: feedforward–feedforward and feedforward–feedback. Indeed, these two cases are the bases for all of the possible developmental processes evolved in our simulation.

Sequential Feedforward Mechanisms

Stripe formations involving the combination of feedforward mechanisms have been extensively studied. In some examples, the developmental processes evolved here are achieved by sequentially combining feedforward processes, where cell‐to‐cell interaction is not needed. Consider a new feedforward mechanism, added at some point downstream from an upstream feedforward circuit. As long as the upstream mechanism is not affected by the downstream mechanism (which is true if there is no feedback from the latter to the former), the stripe formation progresses first by the upstream mechanism, and then, at a later epoch, the stripe is generated by the downstream mechanism. This ordering in the developmental process agrees with the order of evolution, since the downstream mechanism is acquired later in the evolutionary course. Hence, in this simple, sequential feedforward mechanism, the evo‐devo correspondence is a natural outcome. Since the evolved GRN typically has slower gene expression dynamics that control the downstream expression as already shown, the stripe formation will occur sequentially in developmental time, with some delay, in agreement with evolutionary time course.

The evolved network illustrated in Figure 10A consists of a combination of sequential feedforward networks and a downstream feedback network. Through evolution, first the feedforward network via gene 10 and 3 (Fig. 10D) is acquired at around the 10th generation. Then, a domain in the middle space is shaped in development as shown in Figure 10B and E. Later, at the 88th generation, another feedforward network via gene 12 is attached downstream through evolution (Fig. 10F). With this attached network, a domain is shaped in the interior of the earlier domain as seen in Figure10F and G, right after the earlier domain formation is shaped. The shaping of domains is successfully completed at an early stage of development. This leads to the evo‐devo congruence. Later, this modified domain in the middle works as a boundary condition for the subsequent feedback network to be discussed.

Figure 10.

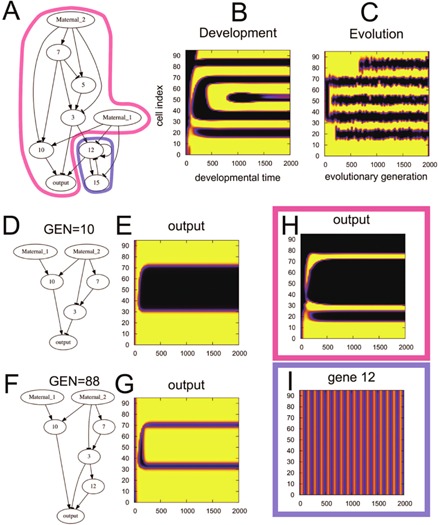
Example of evo‐devo congruence with network structures. (A) An example of a core part of the GRN at the 2,000th generation, evolved to achieve the target pattern. From the maternal factors, the feedforward networks is surrounded by magenta, while the network module for feedback oscillation, consisting of genes 12 and 15, is surrounded by blue. Here, genes and paths that are not essential to the output pattern formation were eliminated. (B, C) Space‐time diagrams of the output gene expression for development (B) and evolution (C) or the GRN are displayed together to show the degree of similarity between them. The vertical axis denotes the space (cell index), and the horizontal axis denotes either evolutionary generation (evolution) or developmental time (development). For this example, the Δ value is 8.0%. (D) An example of the core part of the GRN at the 10th generation (i.e., very early generation) and the corresponding space‐time expression diagrams of the output. (E) Feedforward structure of the GRN is evolved at this early stage of evolution. The vertical axis of the phase diagram denotes the space (cell index), and the horizontal axis denotes developmental time. This expression is observed at a very early stage of development in (B), at approximately the 10th generation. (F) The network structure at the 88th generation. Through evolution, feedforward structures are sequentially acquired in the downstream region of the core part of the GRN. (G) Developmental space‐time diagram of the expression of the output gene for the network F. This expression profile provides the top and bottom stripes in (B). (H) Developmental space‐time diagram of the output expression of the 2,000th generation where the feedback oscillation module is eliminated. Without feedback, only part of (B) is generated. (I) Developmental space‐time diagram of the expression of gene 12, one of the feedback modules in (A), which produces a spatially homogeneous and temporally periodic oscillation if constant activation is applied by gene 3. The combination of this feedback oscillation and the boundary condition provided by gene 12 shown here produces the three internal stripes in (B).

Feedback‐Oscillation Mechanism Attached Downstream of the Feedforward Network

The upstream feedforward network is indeed necessary for the feedback mechanism to work as already explained. In development, the stripe formation by the feedback mechanism cannot work without a boundary, and only after the appropriate boundary condition is generated by the feedforward mechanism. On the other hand, the feedforward circuit is first acquired in the earlier stage of evolution to increase fitness, and later the feedback‐oscillation is obtained to create further stripes using the former feedforward stripe as a boundary. Hence, evo‐devo congruence is resulted.

An example of evo‐devo congruence caused by feedback‐oscillation down‐stream of the feedforward mechanism is displayed in Figure 10A–C. Evo‐devo congruence is detected, in particular between the third and fourth upper stripes. These two stripes are generated by the oscillation‐fixation mechanism generated by the feedback loop (Fig. 10A), attached downstream of gene 3, which is a component of the feedforward network from a maternal morphogen. This feedback module is inhibited by two morphogens and gene 5, so that this oscillation does not start without an input for activation. The only activation input for this feedback module is gene 3, which is expressed only in a domain restricted by the upstream feedforward network. Thus, the oscillation starts after the expression level of the gene 3 is sufficiently high (Fig. 10I), and thus is bounded within the domain, maintaining the expression of gene 3 (Fig. 10H). Following the mechanism discussed in the next section, a stripe is generated in this domain. This feedback oscillation is regulated by the upstream feedforward network but does not disturb upstream feedforward expression.

Parallelism Between the Working GRNs of Evolution and Development

The results in the last section suggest that the ordering of working networks over epochs is in agreement with development and evolution, and that both progress from feedforward‐based networks to networks including feedback loops in addition to feedforward networks. We examined the validity of this ordering statistically.

We first examined whether a working network includes a feedback loop, and computed the fraction of purely feedforward networks that do not include a feedback loop at each epoch.

First, as the working network size for the i‐th epoch k_i increases, the probability of a network without feedback loops is expected to decrease as estimated by $f^{k_i/k_1}$, where f is the ratio of the number of purely feedforward network (that do not include feedback) to the total sample at the first epoch. The observed decrease rate without feedback loops is much higher than this estimate (Fig. 11A). Hence, the fraction of feedforward networks is significantly higher during the first epoch, while the fraction with feedback loops increases faster than that estimated by using the increase in network size (network size was computed from a randomly generated network by removing genes that was not included in a path from the morphogen to the target gene).

Figure 11.

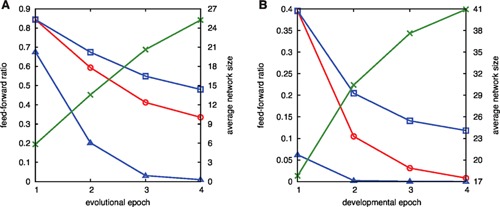
Feedforward ratio. (A) The red circle denotes the fraction of working networks that do not include a feedback loop, plotted as a function of evolutional epoch. The fraction is computed from 500 samples of evolution simulations. For reference, the probability estimated from the value at the first epoch only as a result of the increase in the network size is plotted as the blue square, while the blue triangle denoted such probability computed from 2 × 10⁶ random networks of the corresponding size, generated only under the constraint that there are paths from the morphogens, and to the target. The average size of the network computed from the simulation is also plotted as green cross with the second vertical axis. (B) Ratio of the feedforward network as a function of each developmental epoch, computed in the same manner as (A) and plotted with the same use of symbols. Here both for evolution and development, the target pattern is mostly reached with four or less bifurcations so that we plot the case up to 4 epochs.

Next, the feedforward ratio is close to 1 at the first epoch (<0.85), and it decreases in later evolutionary epochs. In comparison, we also plotted the fraction of pure feedforward networks from random networks of corresponding size. The fraction in the evolved network was much larger. Thus, the feed‐forward network was preferentially selected.

We also checked whether the ancestral network is conserved by computing the fraction of networks preserved in later epochs (see the Methods section). This overlap ratio is shown in Figure 12A as a function of evolutionary epochs. The data demonstrate that over 75% of the ancestral working networks were preserved during evolution. In summary, the results shown in Figures 11A and 12A indicate that ancestral working networks mostly consisted of feedforward networks, and were well conserved throughout evolution. Additionally, later in evolution, feedback loops were added.

Figure 12.

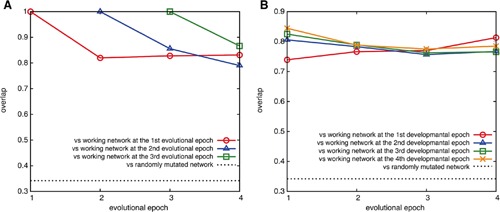
Network overlap. (A) The overlap of the working network at each epoch with its ancestral network. The overlap of the 1st (○), the 2nd (△), and the 3rd (□) epochs with the offspring network at later epochs are plotted. See the Method section for the definition of the overlap, which is computed as a statistical average from 500 samples of evolution. Dashed line is the average overlap between randomly generated network and the same network that underwent 2,000 steps of random mutations. (B) The overlap of the working networks at the 1st (○), the 2nd (△), the 3rd (□), and the 4th (×) developmental epoch with the ancestral networks at each evolutional epoch represented by the abscissa. Dashed line is the average overlap between randomly generated network and the same network that underwent 2,000 steps of random mutations.

The fraction of pure feed‐forward networks in the working network is plotted against the developmental epochs in Figure 11B. The network size was large at the first epoch, such that the ratio at the first epoch was small. Still, the decay of the fraction is much larger than that expected by the probability calculations due to the increase in network size.

Finally, we checked the overlap ratio of the working networks between evolution and development. As shown in Figure 12B, the overlap remains high throughout the epochs, indicating that the working networks in evolution and development correspond with each other. Thus, the same pattern formation dynamics are adopted in the same order between evolution and development.

A Slowly Varying Expression Level Works as a Bifurcation Parameter to Produce a Developmental Epoch

So far we have uncovered the existence of slow expression change working as a control for the output gene expression and the combination of feedforward and feedback networks. These are important for evo‐devo correspondence in pattern formation and gene‐expression ordering, but we need to understand how these two features lead to fast switch‐like change in target patterns at epochs, and how these are correlated in development and evolution. Here we describe this issue, in terms of bifurcation in dynamical‐systems theory.

Consider the example of the network shown in Figure 7, with a slowly changing expression of gene S. When the expression level of gene S (slow variable) increases slowly and reaches a certain level, the expression level of gene A increases from ∼0 to ∼1. Input changes to gene B may then lead to bifurcation. Here the morphogen (gene M) activates gene S and B, while gene S activates A, and gene A subsequently inhibits gene B. If the expression level of gene S is smaller than the total activation input to gene B, the dynamics of expressions of gene A and B are given by the row as shown in Figure 13 (upper left). The nullcline of gene B forms z‐like structure in this phase space, which crosses the perpendicular nullcline of gene A, at coordinates near (0,1). As the expression level of gene S increases, the nullcline for the expression of gene A moves horizontally, so that the fixed point at (x_A, x_B)∼(1,0) disappears and is replaced by the fixed point at (x_A, x_B)∼(0,1), as seen in Figure 13 (bottom left). Thus, the bifurcation between fixed point attractors occurs with a change in the expression level of gene S as the bifurcation parameter.

Figure 13.

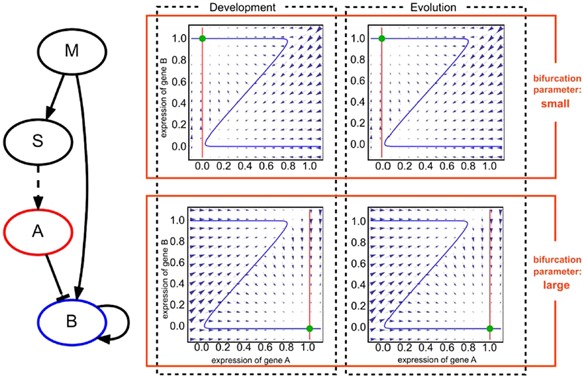
Evolution and development as bifurcation. The network structure where the expression level of gene S changes slowly (left). Phase space diagrams plotting the expression levels of gene A (horizontal access) and gene B (vertical access). The blue line represents the nullcline of gene A, and the red line represents the nullcline of gene B (right). The green circle denotes the final stable cell state from the initial conditions in each of the diagrams. Development (left column): expression level of the slow variable works as a bifurcation parameter. While the expression of gene S is lower than the threshold of gene A, the stable fixed point can be found at approximately (x _A∼0, x _B∼1) (upper left). As development progresses, the expression level of gene S increases, and after the expression of gene 1 exceeds the threshold of gene A, the nullcline of gene A shifts slightly to the right, indicating a higher value (lower left). Gene A inhibits the expression of gene B, so that the fixed point is changed to (x _A∼1, x _B∼0). Evolution (right column): phase diagram representing the expression levels of gene A (horizontal axis) and gene B (vertical axis). The blue line represents the nullcline of gene A and the red line represents the nullcline of gene B. The activation strength from gene A to gene B is regarded as a continuous value here. If the activation strength is low, the expression level of gene 1 is low, so that the stable fixed point is observed at approximately (x _A∼0, x _B∼1) (upper right). When the strength is sufficiently large, the expression level of gene 1 assumes a higher value so that the fixed point is observed at approximately (x _A∼1, x _B∼0) (lower right). Note that by comparing these two columns, a strong correspondence is observed in bifurcation between evolution and development.

Bifurcation Behind Evo‐Devo Correspondence

Similar to the developmental dynamics, the evolutionary process also consisted of a quasi‐stationary regime prior to the emergence of a relevant mutation to increase the fitness. Indeed, such mutations change the gene expression dynamics drastically to form a new stripe, which again is regarded as a bifurcation. At a certain generation, a mutation occurs to add an inhibition path from gene S to A (Fig. 13). This mutation occurs in a discrete manner: whether a path exists or not, it is not represented as a continuous change in a parameter value. However, we can introduce a continuous strength parameter that changes from 0 to ±1, which can be regarded as a bifurcation parameter. Then with this continuous change, an on/off discrete change appears at a certain value of path strength that depends on the threshold of gene A.

Dynamics of the expression of gene A and B are represented in the two‐dimensional state space in Figure 13 (right column). At a lower strength in the path, the nullcline of gene B expression changes so that the former stable fixed point (1,0) exhibits a saddle‐node bifurcation, to move to another fixed point (0,1). Hence, the mutational change in the network leads to a bifurcation. As shown in Figure 13, this bifurcation through the evolutionary process agrees with that observed during development.

After examining hundreds of numerical evolution simulations, the results for pattern formation were summarized as follows: development: slow change during expression works as a bifurcation parameter, and bifurcation in the expression dynamics generates a novel state, which gives rise to an epoch. Evolution: search for mutation resulting in relevant change to a new state. Epoch in evolution is also generated by the same bifurcation. In this way, evo‐devo correspondence is achieved through bifurcation.

Violation of Evo‐Devo Correspondence

Although evo‐devo correspondence was frequently observed and was discussed as a natural outcome of the combination of network motifs for development, small, but non‐negligible portions of the simulation runs exhibited deviation from this evo‐devo correspondence. An example of such an exception is shown in Figure 14A (see also Supplemental Figs. S4 and S5 for additional examples). In this example, the developmental and evolutionary diagrams differ distinctly, not only in the timing of the formation of the second and third upper stripes, but also in the topology in their branching. During the course of evolution, there is a drastic change in the final pattern, at approximately 1272–1273 generations. Here, only a single mutation occurred in a GRN (addition of a single path). In this example, the feedback oscillation of gene 5 was responsible for the output gene expression, in particular for the second and third stripes, while the expression of gene 6, which lies upstream of gene 5, acted as a boundary for the feedback oscillation, which also contributed to the expression of the output gene. In Figure 14B, the gene expression dynamics of the selected genes 5 and 6, as well as the output gene, are displayed for generations before and after this mutation, in the left and right rows, respectively. Here, the mutation occurred upstream of gene 6, and reduced the range in which the gene was expressed, accordingly. The expression around sites 60–70 was subsequently suppressed, allowing for the formation of an additional stripe near site 70, while at lower sites (around site 60) the expression level continued to oscillate, forming a stripe much later. Hence the temporal ordering of the formation of the second (near site 80) stripe and that of the third (near site 70) stripe was reversed by this mutation. Indeed, before the mutation, the third and fourth stripes were generated together (while the second stripe did not exist), and after this mutation, the second and fourth stripes were generated together, and the third stripe was shaped later. Thus, the ordering and topological branching of stripes were altered by the mutation, which led to a violation of the evo‐devo correspondence.

Figure 14.

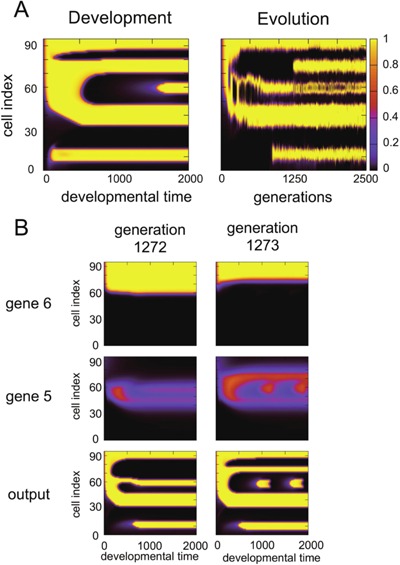
Violation of evo‐devo congruence. (A) Evolution: the expression level of the final output gene (at time = 2000) is shown with the generation (horizontal axis) and cell index (vertical axis). The color scale is presented as a side bar, as in Figure 3B. According to the figure, the second upper stripe is acquired at the most recent stage of evolution, and the first, third, and fourth upper stripes branch from the same root, so that the second stripe emerges from the first upper valley. Development: space‐time diagram of the expression with developmental time (horizontal axis) and cell index (vertical axis). The third upper stripe emerges at the most recent stage of development. Unlike evolution, the first, second, and fourth upper stripes branch from the same root, and the third stripe emerges from the second upper valley. Here, evo‐devo congruence is topologically violated. (B) Developmental diagrams plotted for generations 1,272 and 1,273. These genes show drastic change in their expression between the two generations. Gene 6 provides a feedforward regulation to the output, and inhibits the expression of gene 5, which is a component of the feedback loop to generate oscillatory expression. A mutation, which adds a path to gene 6, occurs between the two generations, which inhibits the expression of gene 6. Through this mutation, the expression of gene 6 is suppressed, thus shrinking the resulting stripe, and producing an additional stripe for gene 5. With this change, the ordering of the expression of the output gene is altered.

To summarize, the violation of the correspondence was due to an upstream expression change resulting from mutation, which caused a change in the boundary condition for the feedback oscillation of the downstream expression gene. We have studied several other examples that showed a violation of evo‐devo correspondence, and confirmed that differences in the topology in stripe branching between development and evolution is caused by mutation upstream of the feedforward mechanism acting as a boundary of the feedback mechanism (see Supplemental Information for additional examples).

DISCUSSION

Summary

Potential relationship between phenotypic dynamics to shape phenotypes and evolution in genotypes has been the focus of the evo‐devo field, since the time when genetic assimilation was first proposed by Waddington (Waddington, 1957). The relationship has been investigated in RNA evolution (Ancel and Fontana, 2000) and gene expression dynamics (Ciliberti et al., 2007; Kaneko, 2007), as also summarized in recent reviews (Wagner, 2005; Kaneko, 2006; Soyer, 2012). Still, studies to establish relationships between multicellular pattern formation dynamics and evolutionary processes that shape the pattern remain premature both in theory and experiment.

Here, we carried out extensive simulations to evolve gene regulatory networks subject to strongly purifying selection, in order to generate a predefined target pattern for the expression of a given output gene. The main results of the present paper are summarized as follows:

1. Epochs of development as bifurcation by slow expression dynamics: the developmental course of the expressions of the output gene, after evolution, consisted of a few epochs characterized by rapid temporal change in gene expression and a quasi‐stationary regime with slow temporal change between the epochs. The slow quasi‐stationary regime is due to expression levels of some genes that vary slowly over time, while the drastic change is due to a bifurcation in the expression dynamics. The slowly varying expressions always emerge as a result of evolution, and they work as bifurcation parameters to control the fast change in the expression of the output gene.

   If we mutate the timescale of the slow gene γ_i to a smaller value, development can be accelerated, but with a further change, the original pattern is collapsed by bifurcation in the dynamics leading to destruction or branching of stripes. In fact, such bifurcation could also occur by changing the time scale of a gene with faster time scale, but it is less frequent and needs much larger change in the time scale. Thus, the pattern is more sensitive to change in slower genes. Hence, acquiring slower genes accelerates the evolution to novel pattern formation. Indeed, François and Siggia, (2010) reported that the existence of a gene with slower expression, termed as “timer gene”, controls the evolution of somitogenesis, and discussed its relevance to short‐germ/long‐germ transition.

2. Punctuated equilibrium in the evolution of morphology as bifurcation: likewise, the evolutionary course of expression dynamics consists of a few epochs with a drastic change, and a quasi‐stationary regime between the epochs. The drastic change is again represented by a bifurcation, which is caused by mutations in the gene regulation network.

3. Evo‐devo congruence through common bifurcations: in most cases, we observed good agreement between development and evolution when evaluating epoch changes from one pattern to another, as well as the ordering of epochs. Indeed, the same bifurcations occurred for both, and thus the evo‐devo congruence was due to the common bifurcation at each epoch.

4. The combination of feedforward and feedback gene regulation networks to support developmental epochs: the combination of feedforward and feedback modules in gene regulation networks provides successive bifurcations at epochs. The upstream feedforward network converted the external gradient of the maternal factor into an output pattern, while the feedback loop converted the temporal oscillation of gene expression into a spatial stripe, under a given boundary condition provided by the feedforward expression dynamics. The evo‐devo correspondence was preserved as long as the upstream feedforward network was maintained.

5. Violation of evo‐devo correspondence through modification of upstream feedforward regulation under downstream feedback mechanism: in rare examples, we observed violations of evo‐devo congruence. These violations were always associated with a structure of the upstream feedforward network and a downstream feedback loop, in which modification of the upstream feedforward network changed the boundary condition of the downstream feedback. This then raised questions as to why the sequential feedforward network was excluded therein, and whether the violation always involved the feedforward‐feedback combination. The feedforward mechanism reads the morphogen gradient of a maternal factor, so that the feedforward‐feedforward process transfers spatial information of the maternal gradient sequentially, from upstream to downstream. This flow of information is unidirectional, so that the downstream genes could not generate new stripes on their own. Since each stripe location was defined by the expression of the upstream genes, the downstream genes could not translate their stripe location in parallel. For the violation of evo‐devo congruence to occur without the loss of fitness, at least two mutations, one to delete a stripe and one to add a stripe, had to occur at the same time, otherwise, downstream stripe formation would be damaged, and fitness would decrease. As such simultaneous multi‐mutations are less probable, the violation of evo‐devo congruence under feedforward‐feedforward network rarely occurred. Conversely, in the case of the feedforward‐feedback network, the downstream feedback loop maintained the stripe formation mechanism by its own, and the upstream changes affected only the boundary condition. Hence, as a result of a single mutation, the stripe position could be shifted without destroying it. In this instance, only a single mutation was needed, which is why the violation of evo‐devo congruence we observed was always in association with the feedforward‐feedback network rather than through a sequential feedforward network.

Relevance of Our Results to Developmental and Evolutionary Biology

Now we discuss the relevance of our results to evolution and development of biological patterns, corresponding to the points noted above.

• (1)Note that the developmental process evolved in our simulation involved slow change in concentrations of some chemical controlling the dynamics. Slow gradual changes in the concentrations of several chemicals are known to play an important role in the developmental process, which may involve some signal molecules, hormones, and morphogens (Carroll et al., 2009). The developmental process is generally believed to consist of successive stages, each of which involves time spans with slow gradual change, and epochs involving drastic change leading to the next stage. Novel dynamical processes are necessary for such epochal changes (Carroll et al., 2009). This empirical fact in development is consistent with our observations, while our bifurcation scheme provided an interpretation for commonly observed developmental stages. Because processes that generate such drastic changes are not fully understood so far in developmental biology, it will be relevant to analyze such changes in terms of dynamical systems, in particular, by bifurcation against slow change in some concentration of chemicals.
• (2)The existence of a quasi‐stationary regime and rapid change in evolution is consistent with punctuated equilibrium (Eldredge and Gould, 1972), suggested from morphological changes in fossil data. Our results suggest that such temporal modes can be explained as bifurcation. Indeed, research has suggested that novel developmental events are acquired in evolution as a result of bifurcations (i.e., evolution as bifurcation) (François and Siggia, 2012; Jaeger et al., 2012).

  From fossil data, it is difficult to confirm this bifurcation viewpoint. Alternatively, we expect that a novel morphological pattern may be achieved by imposing suitable changes in gene expression dynamics that might correspond to evolutionary change. For example, by introducing a hormone and over‐expressing a single gene, Freitas et al. succeeded in inducing fin distal expansion and fin fold reduction in zebrafish, which conceivably represented a prototype of vertebrate appendages (Freitas et al., 2012). The induced epigenetic change leads to a novel gene expression pattern, thereby generating a stripe pattern. This may correspond to bifurcation of a spatial pattern due to genetic change of expression dynamics in our study.

• (3)Correspondence between evolution and development through common bifurcation is difficult to check directly from experimental data, since the morphology is not easily traced through an evolutionary course, while the comparison of phylogeny and ontogeny usually involves of the morphology only of present organisms diverged from common ancestral species (Fig. 1). However, if the morphological novelty is a result of bifurcation, different novel morphologies are expected to be diverged from a common ancestral pattern, through different bifurcations. This viewpoint is consistent with von Baer's third law of embryology, which claims that a common basic morphological feature of the group emerges in advance of special features for each species. If we assume that ancestral features are basic for the group, our result suggests that von Baer's third law is valid for strongly purifying selection during evolution.
• (4.1)The importance of feedforward and feedback regulations in development has now gained more extensive recognition. The relevance of the successive combination of feedforward networks has been recognized in long‐germ segmentation processes in Drosophila, together with theoretical analyses (von Dassow et al., 2000; Jaeger et al., 2004; Ishihara et al., 2005). On the other hand, the relevance of a feedback loop to form temporal oscillations has been revealed for several decades (Goodwin, 1963; Chance et al., 1967; Cooke and Zeeman, 1976; Horikawa et al., 2006; Masamizu et al., 2006). Here, it is often believed that short‐germ organisms adopt feedback mechanisms with gene‐expression oscillation. However, this does not necessarily mean that there is no feedforward mechanism to read the external gradient at the upstream of the feedback network. Rather, our results may suggest the existence of feedforward mechanism at the upstream of the feedback loop for the oscillation.

  How evolution between the short‐ and long‐germ organisms progressed remains an unsolved question. Considering the simplicity in the gene‐regulation network needed for the former, one might expect the evolution from the short‐germ to the long‐germ, while no direct evidence from the feedback to feedforward network was obtained in the numerical evolution (Fujimoto et al., 2008). In this context, existence of upstream feedforward network might be beneficial for the evolution from short‐ to long‐germ organisms.

• (4.2)In vertebrates, somitogenesis is achieved by mapping this temporal oscillation to a spatial stripe formation, where a wavefront model is applicable (Palmeirim et al. 1997; Pourquiè, 2003). Our mechanism to fix the temporal oscillation to the spatial pattern is similar to the wavefront model, but uses neither the morphogen gradient nor the size growth, but a combination of cell‐to‐cell interaction with diffusion and oscillation leads to stripe formation under the boundary conditions provided by upstream feedforward gene regulation. This distinction will be experimentally verifiable by determining whether the cell‐to‐cell interaction is essential to stripe formation.
• (4.3)Here we also demonstrated the importance of the feedforward‐feedback combination. Complex gene regulatory networks in the present organisms often include a combination of feedforward‐feedback networks (Carroll et al., 2009), although their functional roles have not been fully uncovered. It will be important to elucidate the role of the feedforward network as a boundary‐maker and the role of the feedback loop in robust patterning, as suggested here.
• (5)As for experimental confirmation of the violation of evo‐devo congruence through modification of the upstream feedforward network, with a conserved downstream feedback loop, we propose to examine whether morphological novelty arises as a result of modification of upstream feedforward regulation under feedback regulation. It will be possible to evaluate our feedforward‐feedback hypothesis by externally destroying the upstream feedforward network while retaining the feedback loop.

Future Issues

The present study is an initial step toward resolving the larger issue of evo‐devo relationships. Even within the present model, a number of issues remain to be clarified, as follows:

1. Even though we have confirmed that our result is independent of the details in the model, such as the cell number, gene number, model parameters, and the form of the external morphogen profile, further study is necessary to confirm the universal applicability of our results. In particular, dependence on the fitness condition is of interest. In the earlier theoretical studies on the evolution of segmentation, the evo‐devo congruence was not noted explicitly (Salazar‐Ciudad et al., 2001a,2001b; François et al., 2007; Fujimoto et al., 2008; François and Siggia, 2010; Ten Tusscher and Hogeweg, 2011). In these studies, fitness condition does not include the information on the absolute location of segments, as, for example, given by the number of segments or cell types. Indeed, we found that the congruence is much worse when just the number of stripes is adopted as fitness function. In our case, the fitness given as a function of fixed (non‐periodic) spatial pattern. How much does the evo‐devo congruence depend on the strength of purifying selection?

2. We have not observed the classic Turing mechanism (Turing, 1952) in the developmental process by evolved networks. Under the influence of a morphogen gradient, it may be natural to use the maternal information effectively with respect to evolution. It is then an open question whether without the external information (but by imposing only the boundary condition instead), the Turing‐pattern mechanism can evolve dominantly.

3. How do evolutionary reachability of the target and complexity in the developmental process depend on the predefined target pattern? It may be expected that as the target pattern is more complex, it takes more time to evolve GRN to produce such patterns, and development involves more epochs, but is there a way to quantitatively characterize such complexity?

4. It is not yet clear whether quantitative congruence exists beyond the correspondence of epochs. For example, does the time span for the quasi‐stationary regime between two epochs correlate between development and evolution? In other words, if the evolutionary search time to generate a relevant mutation for the next epoch is longer, then, is the quasi‐stationary regime before the epoch also longer in development? Our preliminary results suggest that this correlation exists for cases where small Δ values are observed, while further analysis is required to clarify the conditions and mechanisms for such congruence.

5. Extension of our model for higher spatial dimensions, introduction of size (cell number) growth through development, and inclusion of recombination in a genetic algorithm will be important in future studies. Furthermore, it is important to note that real morphogenesis in multi‐cellular organisms is far more complex than these models, and is not necessarily governed only by the reaction‐diffusion mechanism. Cell rearrangement under mechanical stress could also play an important role, and inclusion of development mechanisms will be important. Still, we also note that macroscopically represented, stress‐induced pattern formation can also be represented by equations of the reaction‐diffusion type (Murray, 2002). Hence, the present conclusions on evo‐devo congruence through bifurcations may be applicable beyond development based on a reaction‐diffusion system.

6. Last but not least, the implications of our single‐chain‐phylogeny study on species‐wide comparison have to be explored. For example, by adding population division and speciation process with imposing different target pattern to the model, species‐wide extension will be available. That future study will be important not only for the validation of our results, but also for further understanding of evo‐devo relationship in species‐wide comparison.

Concluding Remark

In contrast to recent advances in experiments aimed toward analyzing the evo‐devo relationship at a quantitative level, theoretical studies based on dynamical systems and statistical physics are still in their infancy. While we acknowledge that our current model may be oversimplified, we hope that the present work can act as a springboard to launch future cooperative efforts in the field of evo‐devo between theories and experiments.

METHODS

Gene Regulation Network (GRN) Model for Pattern Formation

A cell's state is represented by the expression levels of k genes/proteins, x_i(l,t), involving the protein expression levels of the i‐th gene in the l‐th cell at time t, representing N genes (i = 1, …, N) and M cells, aligned in a 1‐dimensional space. A protein expressed from each gene either activates, inhibits, or does not influence, the expression of other genes, in addition to itself. For simplicity, we assumed that the change in the i‐th protein expression level is given by the equation:

$$\frac{\partial x_i(l,t)}{\partial t}={\gamma }_i\left(F(i,l,t)-x_i(l,t)\right)+D_i\frac{{\partial }^2{x}_i(l,t)}{\partial l^2},$$ (1)

with

$$F(i,l,t)=f\left(\underset{j}{\mathrm{\Sigma }}{J}_{i,j}{x}_j(l,t)-{\theta }_i\right),$$ (2)

where the term –x_i(l,t) in Eq. (1) provides a measure of the degradation of the i‐th protein with γ_i as its rate (Glass and Kauffman, 1973; Mjolsness et al., 1991; Salazar‐Ciudad et al., 2001a,2001b). The expression level is scaled so that the maximum level is unity. The function f(x) is similar to a step function, where the function approaches 1 as x is increased to a positive side, and approaches 0 as x_i(l,t) is decreased to a negative side: In other words, if the term ${\mathrm{\Sigma }}_j{J}_{i,j}{x}_j(l,t)$, is sufficiently larger than the threshold θ_i, then F(i,l,t) < 1, which indicates that the gene is fully expressed, and if it is smaller than the θ_i, then F(i,l,t) < 1, which indicates that the gene expression is suppressed. Here, we chose, f(x) = 1/(1 + e ^−βx), where β, which was set to 40, denoting the sensitivity of the expression at the threshold. Roughly speaking, it is proportional to the Hill coefficient.

The gene regulation network was introduced to our model based on work reported in earlier studies. In Figure 2, each node of the network represents a gene, and the edge of the network represents the interaction between genes, given by N × N matrix J = {J_i,j}: where J_i,j is 1, if gene j activates the expression of the gene i, −1 if it suppresses the expression, and 0 if there is no connection. All cells have an identical regulatory network, with the same parameter values, which are determined by genetic sequence in the genome.

Finally, the last term in Eq. (1) shows the diffusion of a protein, between neighboring cells, with D_i as the diffusion constant. For the majority of the simulations described here, we set M = 96, and N = 16, while preliminary simulations adopting larger values for these did not alter the conclusion in the present paper.

Initial/Boundary Condition

As an initial condition, the expression levels of all genes were set to 0. Furthermore, external morphogens, which are denoted as the proteins 0 and 1, are supplied externally. Fixed linear morphogens are induced from both sides for cellular use, so that x ₀(l,t) = x ₀(t) = (M − l)/M and x ₁(l,t) = x ₁(t) = −l/M. We also evaluated a case involving a gradient with an exponential dependence in space, as ∝ exp(–1/ξ), but this condition did not alter the conclusions presented in this study. Discrete Neumann boundary conditions were adopted at both ends for this study, i.e., x(1) = x(2) and x(M) = x(M − 1).

Algorithm to Define an Epoch

Both in evolution and development, if the change in expression level of the output gene at a given site exceeds 0.9 within 50 time steps, it is regarded as an epoch.

Definition of Fitness

To study the evolution of morphogenesis, we imposed a fitness condition to generate a given specific target pattern, for the expression of a given output gene. By setting a target pattern as T(l), the fitness f for a given individual was defined as the sum of the distance between this target pattern and output gene expression at each cell, as:

$$f=\underset{i}{\mathrm{\Sigma }}(1-\left|T\left(l\right)-x_{output}\left(l\right)\right|)$$

where l is a cellular index. From the equation, the smaller the distance, the higher the fitness is. Here the output gene pattern was defined after a given transient time, which was chosen to be large enough to reach a stationary pattern. For each genotype (i.e., GRN and a set of parameter values), the fitness was thus computed, after simulating each set of pattern dynamics.

For this analysis, we chose 100 individuals with different genotypes. Among these individuals, those who had higher fitness values were preferred to be selected for the next generation. Selection of the individual i with a fitness value of f_i was defined by

$$p_i=\frac{e^{f_i}}{{\mathrm{\Sigma }}_k{e}^{f_k}}$$

The denominator summation of index k is aimed for all individuals in the population.

To generate the offspring, each genotype was slightly modified. A path in GRN was added, eliminated, or its sign was flipped with the probability 1/N ². Also, the parameter values γ_i, D_i, θ_i were modified by adding a random number from a Gaussian distribution $\eta \left(x\right)=\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{x^2}{2{\sigma }^2})$, while restricting these values to the set [0,1]. We set σ = 0.01.

Extracting Working Network

Although the GRN is uniform for each cell in an individual, working gene expression dynamics differ from cell to cell. Additionally, the expression level of most genes changes discretely between epochs, indicating that the regulation of the output gene is different between epochs. Thus, it is difficult to describe gene expression regulation in one cell for a given epoch, because the whole GRN has too many edges, which may work for other cells during other epochs. To identify which regulations are essential at a certain location and time, we extracted part of the GRN that works at a certain location during a certain period by adopting the following systematic method.

1. We fixed a cell to analyze and trace the dynamics of the input to the output gene in that cell. The developmental time was divided into epochs by checking the changes in the input to the target, which are responsible for the epoch. In practice, we defined the time span during which the input goes out of the range [–2/β:2/β], which is the dynamic range for the reaction term in the reaction diffusion equation (see equations (1) and (2)). Epochs are defined as the time span.

2. Fix the epoch to analyze and trace the dynamics of other genes during the epoch. If a gene is not expressed at all throughout the period, the regulation from and to the gene does not work. Hence, both input and output edges to such genes are eliminated.

3. Even if a gene is expressed for a certain time during the period, it does not necessarily mean that paths connecting to the gene are essential for the expression dynamics of the output gene. To check this point, we examines gene j's expression as the input of another gene i with J_i,j  ≠ 0. We then, checked whether changes in gene j's expression contributed to the expression of the gene i as an input, while the latter's change stayed within the dynamic range [–2/β:2/β]. If this contribution, defined below, was larger than a certain threshold value, then the edge j→i is assumed to work. Otherwise the edge was eliminated.

   The specific procedure is as follows: Consider an edge j→i. For a given cell, let Δx_k(t) as the expression change of gene k.

   If $\left|{\mathrm{\Sigma }}_k{J}_{i,j}\mathrm{\Delta }{x}_k\left(t\right)\right|>0$, and $-\frac{2}{\beta }<{\mathrm{\Sigma }}_k{J}_{i,j}\mathrm{\Delta }{x}_k\left(t\right)<\frac{2}{\beta }$, check whether $\frac{J_{i,j}\mathrm{\Delta }{x}_j\left(t\right)}{{\mathrm{\Sigma }}_k{J}_{i,j}\mathrm{\Delta }{x}_k\left(t\right)}>\mathit{\text{threshold}}$, where ${\mathrm{\Sigma }}_k{J}_{i,j}\mathrm{\Delta }{x}_k\left(t\right)$, is the net input change of gene i. The threshold was 0.01. Delete all the edges j→i that do not satisfy the above condition.

4. Last, delete all the edges on genes that did not have a route from morphogens or to the output gene.

Overlap Ratio

The overlap between two networks A = {a_{i ,j}} and B = {b_{i ,j}} was computed as follows:

$$overlap=\frac{\mathrm{\Sigma }\theta (A,B,i,j)}{\min \left(\mathrm{\Sigma }\varphi (A,i,j),\mathrm{\Sigma }\varphi (B,i,j)\right)}$$

where

$$\theta (A,B,i,j)=\{\begin{array}{cc}\hfill 1\hfill & \hfill \text{if}{a}_{i,j}=0\hfill \\ \hfill 0\hfill & \hfill \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\hfill \end{array},\varphi (A,i,j)=\{\begin{array}{cc}\hfill 0\hfill & \hfill \text{if}{a}_{\mathrm{i},\mathrm{j}}=0\hfill \\ \hfill 1\hfill & \hfill \mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}\hfill \end{array}$$

The numerator is the number of common edges between the two networks, while the denominator is the size of the smaller network. The overlap is 1 when a smaller network is completely included in the larger network and is 0 when the two networks do not have common edges.

Supporting information

Additional supporting information may be found in the online version of this article at the publisher's web‐site.

Supplemental Fig. S1.

Supplemental Fig. S2.

Supplemental Fig. S3.

Supplemental Fig. S4.

Supplemental Fig. S5.

Supplemental Figure Legends.

Kohsokabe T, Kaneko K. 2016. Evolution‐development congruence in pattern formation dynamics: bifurcations in gene expression and regulation of networks structures. J. Exp. Zool. (Mol. Dev. Evol.) 326B: 61–84.