High-throughput measurement of single-cell growth rates using serial microfluidic mass sensor arrays

Abstract

Methods to rapidly assess cell growth would be useful for many applications, including drug susceptibility testing, but current technologies have limited sensitivity or throughput. Here we present an approach to precisely and rapidly measure growth rates of many individual cells simultaneously. We flow cells in suspension through a microfluidic channel with 10–12 resonant mass sensors distributed along its length, weighing each cell repeatedly over the 4–20 min it spends in the channel. Because multiple cells traverse the channel at the same time, we obtain growth rates for >60 cells/h with a resolution of 0.2 pg/h for mammalian cells and 0.02 pg/h for bacteria. We measure the growth of single lymphocytic cells, mouse and human T cells, primary human leukemia cells, yeast, Escherichia coli and Enterococcus faecalis. Our system reveals subpopulations of cells with divergent growth kinetics and enables assessment of cellular responses to antibiotics and antimicrobial peptides within minutes.

Single cells vary widely in their growth rate, a fundamental phenotype that reflects biochemical and biophysical differences between cells and ultimately may govern their relative abundance within a population. From bacteria to unicellular eukaryotes to metazoan cells, even genetically identical cells may grow at extremely different rates, owing to a combination of intrinsic molecular noise and various deterministic behavioral programs^1–5. This variation is not observable via population-based growth assays, yet it has important consequences for human health. For example, cancer cells within an individual may vary drastically in proliferative potential, with subsets capable of continuous cycling and others primarily arrested⁶. Similarly, growth rate variation in bacterial populations can dictate the efficacy of antibiotic treatments, as slow- or non-growing cells tend to be more resistant to antibiotics^7–9. Despite its importance, precisely and rapidly quantifying single-cell growth rates remains technically challenging. One approach is to measure a cell’s outline in a microscopic image and then calculate its volume based on assumptions about its three-dimensional shape - e.g. measuring the length of rod-shaped bacteria and assuming the cross-section stays constant^9–12 or measuring yeast cell boundaries and assuming the cell is a prolate ellipsoid¹³. However, it is unclear how often these shape assumptions are violated, and these methods are generally not usable for irregularly-shaped cells. Another approach known as quantitative phase microscopy can be used to estimate a cell’s dry mass over time^14,15 but, like other available platforms, it cannot perform precise, single-cell growth measurements on a variety of samples with high temporal resolution.

Recently, inertial methods for measuring single-cell growth have been developed based on resonating micromechanical structures^16–18 that provide much higher precision than microscopy but are hindered by low throughput. These methods exploit the fact that a micromechanical resonator’s natural frequency depends on its mass. Adding cells to a resonator alters the resonator’s mass and causes a measurable change in resonant frequency. One such class of resonator mass sensors are suspended microchannel resonators (SMRs), which consist of a sealed microfluidic channel that runs through the interior of a cantilever resonator. The cantilever itself is housed in an on-chip vacuum cavity, reducing damping and improving frequency (and thus mass) resolution¹⁹. As a cell in suspension flows through the interior of the cantilever, it transiently changes the cantilever’s resonant frequency in proportion to the cell’s buoyant mass – i.e. the cell’s mass minus the fluid mass it displaces. In water, a cell’s buoyant mass is roughly proportional to (and is typically about one-quarter of) its dry mass²⁰. SMRs are very precise, weighing single mammalian cells with a resolution of 0.05 pg (0.1% of a cell’s buoyant mass) or better^15–17. By repeatedly flowing a cell back and forth through the cantilever, SMRs can be used to measure a cell’s growth rate, but are limited to measuring one cell at a time. This limitation in throughput has prevented the wider application of SMRs across a range of biological and clinical efforts.

Here we introduce an SMR-based technique for high-throughput growth rate measurements that retains the SMR’s mass and growth rate precision. We use an array of SMRs fluidically connected in series and separated by “delay” channels between each cantilever (Fig. 1A,B). These delay channels give the cell time to grow as it flows between cantilevers. After a cell exits a cantilever, other cells are free to enter it and be weighed. As a result, we are not limited to flowing only one cell through the array at a time, but can have many cells flowing in a queue. This enables high-throughput precision growth measurements across a wide array of suspended cell types. Here we demonstrate a proof-of-concept serial SMR array and show that it can measure E. coli, E. faecalis, S. cerevisiae, lymphoid cell lines, primary murine T cells and primary human lymphocytes and acute myeloid leukemia cells. We demonstrate previously unrecognized variability in growth kinetics and perform ultra-rapid assessment of susceptibility to antibiotics and antimicrobial peptides.

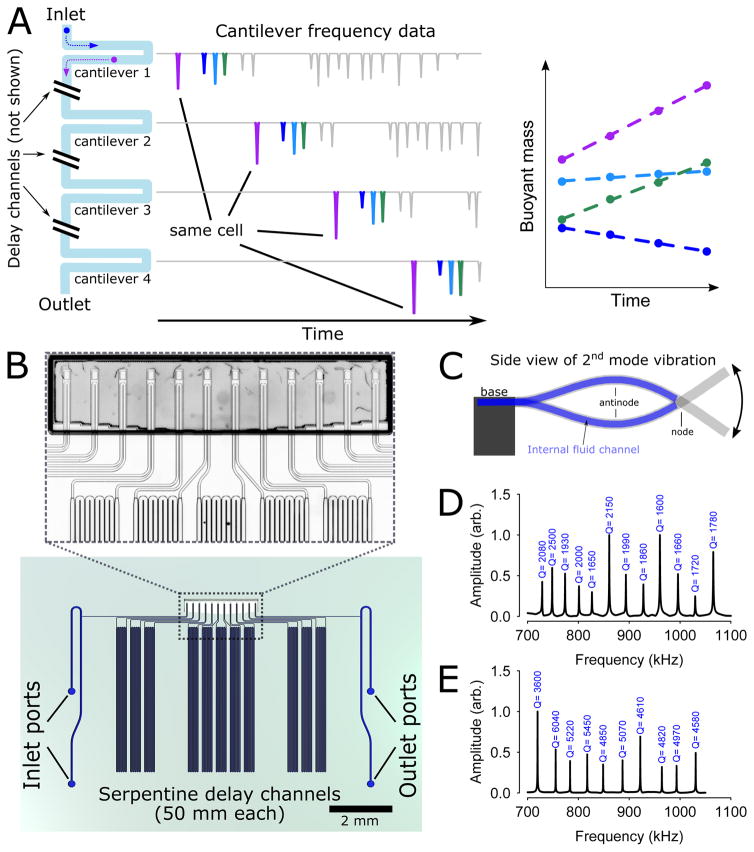
Figure 1. Design and implementation of the serial SMR array.

(A) Simulated data showing frequency peaks originating from single cells flowing through a series of SMRs separated by delay channels. Cells grow as they traverse the array. After grouping frequency peaks originating from the same cell, that cell’s mass accumulation rate can be obtained by regressing its buoyant mass versus time. Because many cells can traverse the array simultaneously, this device can achieve much higher throughput than a single SMR device. (B) Rendering of a large-channel serial SMR array device, showing delay channels and the cantilevers (magnified in inset micrograph). (C) To prevent cells from getting trapped at the end of the cantilever by large centrifugal forces, the internal microfluidic channel extends only to the node of the second eigenmode. (D) Transfer function amplitude measured a large-channel serial SMR array, demonstrating frequency spacing of approximately 30 kHz and typical quality factors of 1500–2500. (E) Transfer function for a small-channel serial SMR array.

Results

Device design

Before designing the serial SMR arrays, we first considered how the number of buoyant mass (referred to hereafter simply as mass) measurements, k, the measurement resolution, σ_mass, and the time between each measurement, Δt, affect mass accumulation rate resolution. We derived a simple relationship for the mass accumulation rate standard error (resolution) in terms of these three quantities:

$${\sigma }_{\text{mass}\text{accumulation}\text{rate}}\approx \frac{{\sigma }_{\text{mass}}\sqrt{12}}{k^{1.5}\mathrm{\Delta }t}$$ (1)

(see Supplementary Note 1 for derivation).

For serial SMR arrays, the time between measurements (Δt) can be controlled by adjusting the flow rate. Therefore, apart from guiding our designs, equation (1) also illustrates that we can easily tune the device’s behavior to trade throughput for resolution by changing the flow rate, i.e. faster flow yields higher throughput but poorer resolution, and conversely for slower flow (see Supplementary Note 1).

In this work, we designed and validated two serial SMR arrays with two different channel dimensions – one for larger cells (mammalian cells and yeast, 15 by 20 μm in cross-section) and one for bacteria (3 by 5 μm). Despite the differences in scale, operation and design concepts are essentially identical for these two device types.

For studying mammalian and yeast cells, which often accumulate mass at rates between 1–10 pg/h¹⁶, we sought a mass accumulation rate resolution of less than 1 pg/h. Using the expected mass noise (σ_mass ~ 0.05 pg for similar single SMR devices), we designed a device consisting of twelve SMRs fluidically connected in series by roughly 50 mm-long delay channels (Fig. 11B). At typical SMR flow rates, Δt would be about 1.5 minutes and thus the expected mass accumulation rate resolution would be 0.17 pg/h, resulting in a relative precision of 1–10%. We designed our small-channel devices similarly, but with 10 cantilevers and with the expectation of operating at faster flow rates (Δt ~ 30 seconds between SMRs).

To obtain the best possible mass resolution (σ_mass), we excited our cantilevers in the second bending mode so that the measured mass does not depend on the cell’s flow path²¹, a fundamental error source for SMRs operated in the first mode. However, because the second mode is at a higher frequency and the tip follows an arc with a shorter radius than in the first mode, cells often became trapped at the cantilever tip due to centrifugal force^22,23. This problem was exacerbated at the low flow rates (and therefore reduced drag forces) necessary for sufficient delay time between cantilevers. To overcome the trapping problem, we shortened the interior channel to extend only as far as the vibration node, where the centrifugal force is minimal (Fig. 11C).

So that each cantilever can be individually operated without coupling or interacting with other cantilevers, we used frequency-division multiplexing. We designed each cantilever with a unique resonant frequency roughly 30 kHz apart from its neighbors (Fig. 1D, E), which we controlled by varying cantilever lengths from 380 to 470 μm (large-channel devices) or 180–215 μm (small-channel devices). This frequency spacing is conservative, as we estimate based on Carson’s rule²⁴ that the spacing could be reduced to less than 1 kHz in future devices, enabling operating hundreds of cantilevers simultaneously within the frequency band used here (700–1100 kHz).

Device operation and data analysis

To simultaneously measure the resonant frequency of all k cantilevers in the array, we first required a way to measure the superposition of all the cantilever deflection signals. We employed two approaches: i) an optical lever setup in which all cantilevers are simultaneously illuminated and a single photodetector measures the superposition of their deflection signals (Supplementary Fig. 1), or ii) devices with piezoresistors doped into the base of each cantilever^22,25, which are wired in parallel and their combined resistance measured via a Wheatstone bridge-based amplifier. The resulting deflection signal, which consists of the sum of k signals from the cantilever array, goes to an array of k phase-locked loops (PLLs) where each PLL locks to the unique resonant frequency of a single cantilever. Therefore there is a one to one pairing between cantilevers and PLLs. Each PLL determines its assigned cantilever’s resonant frequency by demodulating its deflection signal²⁶ and then generates a sinusoidal drive signal at that frequency. The drive signals from each PLL are then summed and used to drive a single piezo actuator positioned directly underneath the chip, completing the feedback loop (Supplementary Fig. 1). Each PLL is configured such that it will track its cantilever’s resonant frequency with a bandwidth of 50 or 100 Hz (see Methods and Supplementary Fig. 2).

After acquiring the frequency signals for each cantilever, we convert them to mass units via each cantilever’s sensitivity (Hz/pg), which must be known precisely. Although cantilever mass sensitivity should theoretically scale with the resonant frequency to the power three-halves (see Supplementary Note 2), we found that the actual sensitivities occasionally deviated from the expected values, and in some cases changed by up to 5% between days (Supplementary Fig. 3). To account for this, we measured the cantilever sensitivities during each experiment by spiking in inert monodisperse polystyrene particle size standards into all samples. Because the particles are highly uniform (~1% coefficient of variation in diameter), we can easily distinguish them even when they are of similar size to the cell sample of interest.

The final step in extracting individual cell mass accumulation rates is to identify the frequency peaks in each cantilever that originate from the same cell. This is trivial if the cells stay in exactly the same order as they flow through the entire array. In practice however, cells may occasionally change order, divide, drop out of the queue (via adhering to a channel wall or getting physically stuck in the channel), and potentially re-enter the queue at a later time. We approach the task of matching frequency peaks to the cell that generated them using a probabilistic model based on our assumptions about the expected time for a cell to traverse a delay channel and about the fastest rates at which cells can change mass. We assume that mass accumulation rates are nearly constant on the timescale of our measurements which constitute a small fraction of a cell cycle^16,17 (see Supplementary Note 3 and Supplementary Fig. 4). We then apply the Hungarian algorithm²⁷ to find a maximally-likely way of matching all the cell events observed in cantilever 2 with the cells that have been observed in cantilever 1, followed by matching the cells observed in cantilever 3 with the cells observed in cantilevers 1 and 2, and so on. At concentrations used here, the matching is quite robust (better than 99% for simulated data, Supplementary Fig. 5), and can be manually verified for accuracy. At higher cell concentrations, the risk of incorrect matching increases, but outliers of interest can still be manually verified.

Device characterization

As these devices represent the first chips implementing SMR arrays, we asked whether operating 10–12 cantilevers simultaneously would decrease the performance of each individual cantilever. We measured the frequency noise for 12 large-channel cantilevers operating simultaneously using an optical-lever based measurement system and observed minimal frequency noise (in terms of Allan deviations²⁸) of 20–30 parts per billion at averaging times of 200–500 ms (Supplementary Fig. 6). Slightly lower Allan deviations were observed for small-channel devices (Supplementary Fig. 6), with optimal noise at shorter averaging times (30–100 ms). In both cases, these noise magnitudes are comparable to what can be routinely achieved with single-cantilever devices, but could potentially be further reduced an order of magnitude or more before reaching thermomechanical limits (Supplementary Fig. 6).

To assess the devices’ ability to resolve a cell’s mass accumulation rate, we first analyzed mixtures of polystyrene particles, spanning 4–12 μm in diameter (large-channel devices), and 1.0–2.5 μm (small-channel devices). Our measurements clearly show that these particles’ masses are not changing, and the standard deviations of the observed rates (an estimate for our mass accumulation rate resolution) were 0.32 pg/h (large-channel device, Supplementary Fig. 7), and 0.022 pg/h (small-channel device, Supplementary Fig. 8). We also tested large-channel device with fixed cells, which also were not changing in mass and exhibited a similarly low mass accumulation rate standard deviation of 0.18 pg/h (Supplementary Fig. 9). These are in good agreement with what we would have predicted from equation (1) based on the experimental flow rates and measured buoyant mass resolution.

Measuring growth rates of living cells

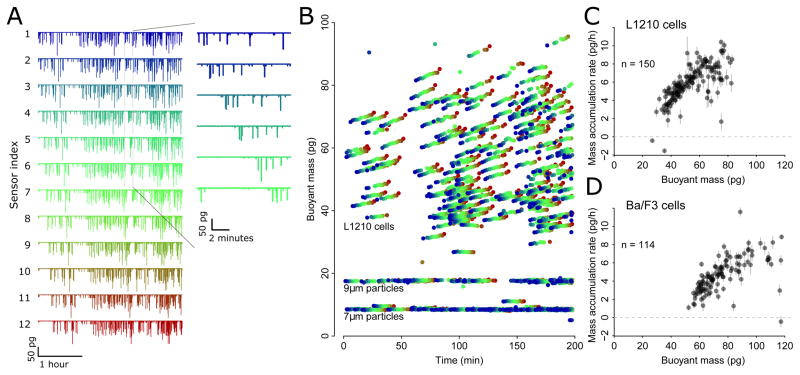
We used the large-channel serial SMR array to monitor the growth of steady-state L1210 cells (Fig. 2), a mouse lymphoblast cell line previously studied with SMRs^16,17. In a 200-minute experiment, we measured the size and mass accumulation rate of 150 cells. In contrast, a single SMR measuring each cell for 20 minutes could measure less than 10 cells as it takes some time to switch between cells. As seen previously, these cells’ mass accumulation rates are size-dependent and are higher for larger cells (Fig. 2C). We also measured BCR-ABL-expressing-Ba/F3 pro-B-cells under the same conditions and found a similar correlation between mass and mass accumulation rate (Fig. 2D). As previously noted for L1210 cells¹⁷ but not studied in Ba/F3 cells, the mass accumulation rate per unit cell mass is lower for smaller cells compared to larger cells, suggesting that Ba/F3 cells also deviate from purely exponential growth in a manner similar to L1210s.

Figure 2. Experiments measuring the growth of lymphoid cell lines.

(A) Data from twelve cantilevers, demonstrating continuous operation over roughly three hours with L1210 cells, at a flow rate of roughly two minutes between each cantilever (inset). (B) Buoyant mass data extracted from frequency shifts of cantilevers, color-coded by cantilever (blue is first cantilever, green is 6th cantilever, red is 12th cantilever). 7 and 9 μm inert polystyrene particles are added as calibration and negative control, respectively. (C) Buoyant mass versus mass accumulation rate for the L1210 cells in (B), extracted via an automated peak-matching algorithm (Supplementary Note 3). Error bars are standard errors of the slope estimated directly from the fit, not from equation 1. (D) Buoyant mass vs mass accumulation rate for Ba/F3 cells, showing a profile similar to L1210s but at larger cell sizes.

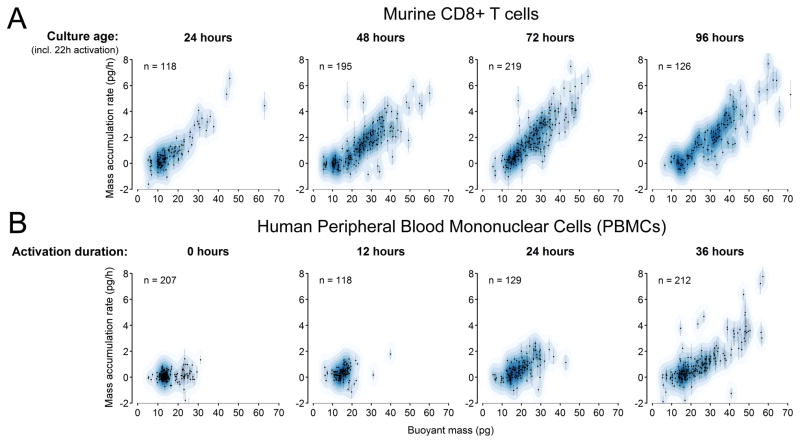
We next investigated whether we could measure primary cells, beginning with mouse CD8+ T cells. In response to stimulation, CD8+ T cells are known to drastically alter their metabolic activity and begin to grow²⁹. However, current methods for studying this transition often rely on bulk or single time-point measurements which make it difficult to characterize heterogeneity in this phenotypic response over time. To this end, we activated murine CD8+ T cells in vitro and assayed their single-cell growth behavior daily for four days. Whereas the cumulative cell population grew robustly between each daily measurement, the serial SMR consistently revealed a sizable non-growing subpopulation (Fig. 3A) composed of the lowest weight fractions (5–15 pg buoyant mass). Between 24 and 48 hours, the growing subpopulation increased relative to the non-growers and stayed roughly constant after 48h. As with L1210 and Ba/F3 cells, although the mass accumulation rate covaried with the size in all cases, it was not directly proportional but was instead proportional to the mass minus an offset. This departure from exponential growth is similar to that seen for the L1210 and Ba/F3 cells.

Figure 3. Measuring single immune cell growth patterns and activation dynamics.

(A) Mouse CD8+ T cells activated with anti-CD3 and anti-CD28 show an initial increase in the growing fraction between 24 and 48 hours, followed by a consistent mass-growth profile over the next three days. Error bars are standard errors of the slope, estimated directly from the regression fit. Points are overlaid on corresponding kernel density estimates (blue). (B) Measuring lymphocyte activation by quantifying mass and growth of single human PBMCs. After the initial loss of a presumed monocyte subpopulation between 20–30 pg (likely due to adherence to the culture well), we observed the emergence of a subpopulation containing larger and correspondingly faster-growing cells.

Our measurements of murine CD8+ T cells suggested we could rapidly assess human lymphocyte activation as an alternative to existing clinical techniques such as the lymphocyte transformation test^30,31. This assay measures proliferation via DNA synthesis – typically via incorporation of tritiated thymidine – and requires several days to quantify bulk proliferation in response to activation. In contrast, we demonstrate that we can directly observe activated lymphocytes within a population of unlabeled PBMCs within 24–36 hours of stimulation. We obtained peripheral blood mononuclear cells (PBMCs) from whole blood, activated them for varying durations and then immediately measured their growth. Although naïve (t = 0 hours) PBMCs show a clear subpopulation of cells between 20–30 pg, this subpopulation vanished after 12 hours of activation, consistent with monocyte adherence to the culture dish³². By 24 hours, larger growing cells are present (putative activated T cells), and by 36 hours, this population has expanded to even larger sizes and faster mass accumulation rates. The ability to assess growth within 36 hours by mass accumulation of individual cells suggests the serial SMR array could provide a substantially faster method for assessing lymphocyte transformation than existing approaches that measure proliferation. Furthermore, access to cell-to-cell heterogeneity could be used to identify responsive clones in a population of generally unresponsive cells. This functionality is particularly promising for fields such as cancer immunotherapy where the characterization of rare, responsive lymphocytes may offer crucial insight for the identification of tumor neoantigens.

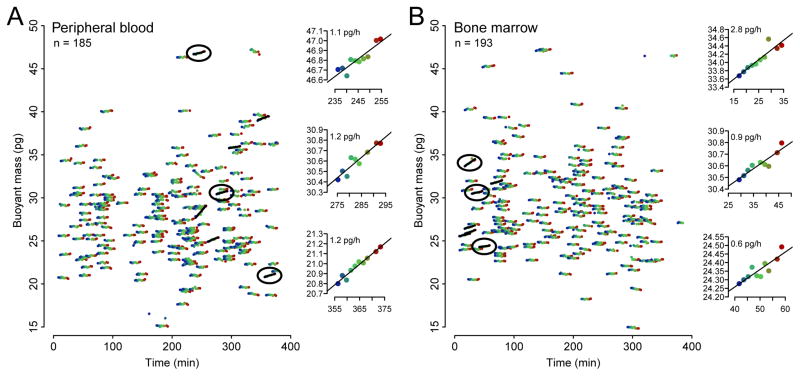
To further explore the capabilities of the system for studying primary cell growth kinetics, we asked whether we could detect growth in single putative cancer cells from patients. We enriched acute myeloid leukemia cells from the peripheral blood or bone marrow of two distinct patients by flow sorting hCD15/hCD33 double positive cells (Supplementary Fig. 10, Supplementary Table 1), which were then maintained in serum-supplemented media. In neither case was the tumor immunophenotype known in advance, so the collected cell populations were heterogeneous owing to the conservative sorting strategy. Although no growth was visible at the population level over the first 48 hours (Supplementary Fig. 11), we detected a rare subpopulation of cells (~4% of each sample) that were accumulating mass when we analyzed these samples on the serial SMR array 3–9 hours post-sample-acquisition (Fig. 44, growing cells are denoted by black lines). These cells typically grew between 0.2 and 1 pg over the 20 minute measurement, which would correspond to less than a 1% change in diameter. We also noted another rare subpopulation of cells losing mass, which may be cells in the process of dying. These data – though exploratory – show that the serial SMR can resolve heterogenous growth patterns in primary patient samples.

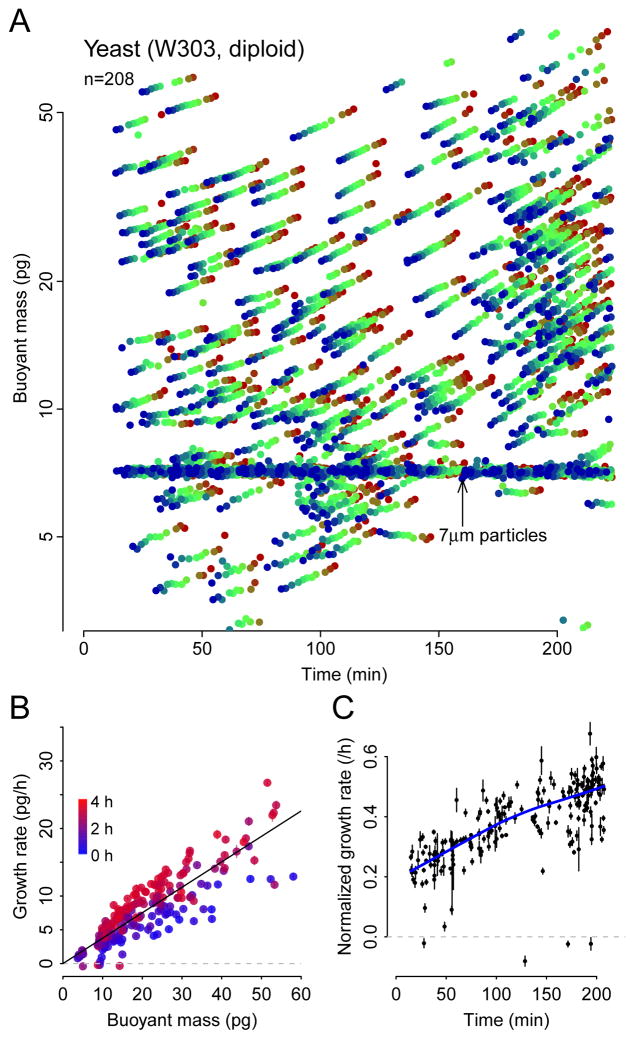
We next investigated whether the large-channel serial SMR array could be used to study S. cerevisiae, a model organism of interest in studies of growth rate control and size homeostasis^3,13. We measured the growth of single yeast cells in lag phase – a brief period of slow or no growth following transfer from spent media to fresh media. In a 3.5 hour experiment, we measured the mass accumulation rates of 208 cells (or cell clumps, as daughters often remain adhered to mothers following division), as shown in Fig. 55. Here we’ve plotted these cells’ mass on a logarithmic scale because single yeast cells grow exponentially^3,16. On a semilog plot, the slope of a cell’s mass trajectory may be interpreted as an exponential growth rate, which is equivalent to its mass accumulation rate per unit mass. In the following we will refer to this as the cell’s growth rate. Throughout the first several hours, cells gradually increase their growth rates towards their maximal rate of approximately 0.5/h (Fig. 5B,C). Notably, the initial growth rate immediately after inoculation into fresh medium was not zero, but rather started at around 0.2/h, showing that yeast in stationary phase remain primed to immediately begin growing should conditions become favorable, albeit at a sub-maximal rate.

Figure 5. Lag-phase yeast culture time-resolved growth dynamics measured at single-cell resolution.

(A) Semilog plot of buoyant mass trajectories of yeast cells in rich media. Data from SMR nine is not used here due to very high noise. We expect that particles between 5–20 pg are mostly single cells and that 20+ pg particles are mostly clumps of cells, as mother and daughter cells often remain weakly adhered to each other after cytokinesis. (B) Buoyant mass versus mass accumulation rate. Colors indicate time from blue at time zero to red at the end of the experiment. Error bars are standard error of the slope estimated from each regression of buoyant mass versus time. (C) Mass accumulation rate per unit mass (interpretable as exponential growth rate) versus time. Error bars are standard error of the slope divided by the cell’s buoyant mass. Blue line shows lowess curve to clarify trend.

We next asked whether serial SMR arrays designed for bacteria could provide rapid and precise measurements of bacterial growth. We first investigated the growth of single log-phase E. coli (Fig. 6A). In rich media (LB) at 37 C, we found that the average growth rate of individual bacteria was 2.14 ± 0.02/h (mean ± standard error, 19.4 minute doubling time) with a coefficient of variation of 7.4% excluding four outlying small cells (Fig. 6A), in good agreement with other recent measurements¹². However, it is notable that we are measuring growth on a much shorter timescale (four minutes instead of a full 20 minute cell cycle), and that the biological variation on this timescale is no larger than at longer timescales. We were also able to measure growth of the gram-positive coccus E. faecalis (Supplementary Fig. 12). This strain behaved similarly to the gram-negative rod E. coli in the serial SMR array, growing at easily-detectable rates with a mean growth rate of 1.86 ± 0.02/h. The serial SMR array can thus provide high-resolution and rapid growth measurements of single gram-positive and gram-negative bacteria of varying morphologies, including clinically relevant species.

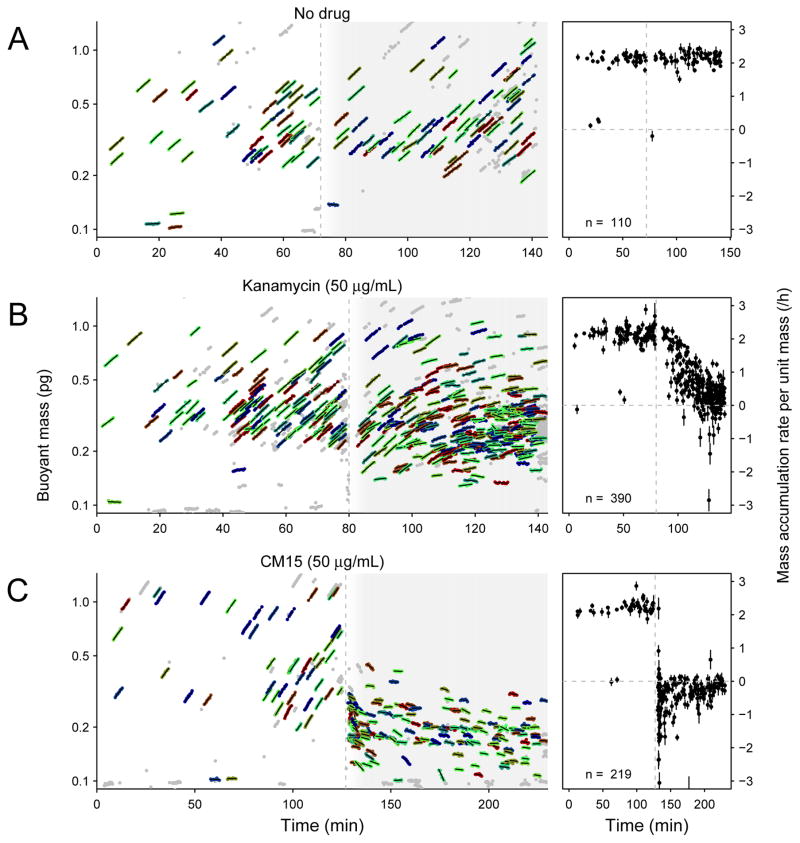
Figure 6. E. coli growth and drug response measured on a small-channel serial SMR array.

Left plots show serial SMR array buoyant mass measurements. Polystyrene particles used for calibration have been omitted from these plots for clarity. Colored dots with overlaid lines indicate cells included in the analysis at right, and grey dots indicate data for which less than six mass measurements could be linked together or the automated matching was uncertain. Right hand plots show mass accumulation rate per unit mass versus time for colored cells at left. Error bars are standard errors of regression parameter for normalized growth rate. In both left and right plots, vertical dashed line indicates the time at which a drug was added (A, nothing; B, kanamycin; C, CM15).

We next asked whether we could observe the effects of antibiotics on bacterial growth. We added kanamycin to an E. coli culture in the middle of the experiment (Fig. 6B), and observed a rapid drop in growth rates to near zero over less than half an hour. This result demonstrates the potential for rapidly assessing antibiotic susceptibility and quantifying killing kinetics on an unprecedented timescale. Furthermore, we noted variation in the timescale of growth arrest – after 20 minutes of exposure to kanamycin, some cells had nearly stopped growing, while others continued growing near their maximal rate.

Finally, we asked whether we could observe the growth-arresting effects of an antimicrobial peptide CM15³³, which is known to permeabilize cells on short timescales but does not change the overall cell size as measured by microscopy³⁴. When we added CM15 to the culture, we observed an immediate decrease in mean cell mass and an immediate cessation of mass accumulation (Fig. 6C). While most cells appeared to be neither growing nor decreasing in mass, we witnessed several cells rapidly losing mass immediately following peptide addition and even up to nearly an hour later.

Discussion

We have shown that the serial SMR array can measure single cell mass accumulation rates precisely for up to 60 mammalian and 150 bacterial cells per hour. This enables observations of the full distribution of growth behaviors – including rare cells behaving quite unlike the average cell - on short timescales. This method is compatible with a variety of cell types from cell lines to primary blood cells to yeast and bacteria, and can be used to profile the response of cells in culture to perturbations, including small molecule therapeutics and peptides. We envision that this device will be applicable in many areas of research and potentially in a clinical setting. The ability to detect rare growing cells in complex mixtures from patients suggests the possibility of correlating these types of measurements to disease states, and ultimately assessing drug susceptibility in these rare cells. Outside of medical applications, the serial SMR system could be used to quantify cellular heterogeneity and ultimately determine how cell growth is intrinsically tied to a broad array of molecular-scale phenomena.

Compared to microscopy, which has long been a mainstay for studying cell growth, our system has both benefits and drawbacks. Small-channel serial SMR arrays provide at least 10-fold higher precision as compared to a recent quantitative phase microscopy study³⁵ (Supplementary Note 4 and Supplementary Fig. 13). Furthermore, at slower flow rates, the precision increases by another 2–3 fold to a level achievable with dynamic trapping measurements performed on a single SMR (Supplementary Fig. 13). Likely as a result of this higher resolution, we observe substantially less cell-to-cell variability (Supplementary Fig. 13B,D). This high precision applies to cells in flow, including motile cells, which is advantageous for automated clinical assays such as antibiotic susceptibility testing. However, there are drawbacks to our method. The serial SMR array is currently not suitable for measuring growth of cells that are attached to a surface. Furthermore, unlike microscopy, we are only able to capture short “snapshots” of single-cell growth, though the length of this snapshot may increase in the future with increasing SMR parallelization. Finally, microscopes are more widely available and are easier to operate than the current version of our serial SMR system.

In future work, the serial SMR approach described here could be optimized further. Improving the actuation and detection schemes might reasonably enable an order of magnitude improvement in mass accumulation rate precision (Supplementary Fig. 6), and this extra precision can be exchanged directly for higher throughput by increasing the flow rates of cells transiting the array (see Supplementary Note 1 and Supplementary Fig. 14). Another possibility is further parallelizing by implementing many serial SMR arrays on a single chip, enabling measuring cells under many conditions simultaneously – for example, bacteria in several different concentrations of antibiotic. Other future advancements could include integration with fluorescence microscopy and the ability to sort cells based on growth rates, both of which would greatly expand the potential for correlative assays that link growth kinetics with underlying biology.

Methods

Device design and fabrication

Devices were fabricated using previously described methods^22,36. Large-channel devices used with optical-lever readout were fabricated at MIT’s Microsystems Technology Laboratories and Innovative Micro Technology (Santa Barbara, CA) and large-channel devices with embedded piezoresistors for readout were fabricated at CEA/LETI (France). Notably, the large devices designed for optical-lever readout did not include a getter layer, but the cavity surrounding the cantilevers remained in vacuum. Large-channel devices had cantilever interior channels of 15 by 20 μm in cross-section, and delay channels 20 by 30 μm in cross-section. Only human PBMC measurements were carried out on large-channel devices fabricated at CEA/LETI, all other mammalian cell and yeast experiments were on devices fabricated at Innovative Micro Technology without piezoresistors. Small-channel devices had cantilever channels 3 by 5 μm in cross-section, and delay channels 4 by 15 μm in cross-section. The tips of the cantilevers in the array are aligned (Fig. 1) so that a single line-shaped laser beam can be used for optical-lever readout (Supplementary Fig. 1). The cantilevers are arrayed such that the shortest (and therefore most sensitive) cantilevers are at the ends of the array. Before use, the device is first cleaned with piranha (3:1 sulfuric acid to 50% hydrogen peroxide) and the channel walls are passivated with polyethylene glycol (PEG) grafted onto poly-L-lysine (SuSoS, Switzerland).

System setup

Supplementary Fig. 1 shows a full schematic and picture for the device setup using optical-lever based detection. A piezo-ceramic actuator seated underneath the device is used for actuation. The custom-made low-noise photodetector, wheatstone bridge-based amplifier (for piezoresistor readout) and high-current piezo-ceramic driver are detailed elsewhere³⁷. It is worth noting that in previous readout systems designed for a single cantilever, signal distortion (via electronic saturation, or optical interference patterns) typically does not contribute to system noise, as the distortion generates spectral components at integer multiples of the carrier frequency which are easily filtered out. However, in a channel carrying many signals, nonlinear distortion (especially saturation) will generate noise near the carrier signals (Supplementary Fig. 15). Therefore, care must be taken to ensure that no signals become saturated. To avoid the effects of optical interference between signals from different cantilevers (producing harmonics at the difference frequency), we used a low-coherence-length light source (675 nm superluminescent diode, 7 nm full-width half maximum spectral width, Superlum, Ireland) for our optical lever. After the custom photodetector converts the optical signal to a voltage signal, that signal is fed into an FPGA board, for which implementation details are as published previously ²⁶. Briefly, the FPGA implements 12 parallel second-order phase-locked loops which each both demodulate and drive a single cantilever. The FPGA is a Cyclone IV FPGA (Altera) on a DE2-115 development board (Terasic Inc.), operating on a 100 MHz clock (AOCJY2 oven-controlled crystal oscillator, Abracon). I/O was via a high-speed AD/DA card (DCC HSMC card, Terasic Inc.) operating 14-bit analog-to-digital and digital-to-analog converters at 100 MHz.

System operation

To operate all cantilevers in the array, we first measure the resonator array transfer function by sweeping the driving frequency and recording the amplitude and phase of the array response. We next calculate parameters for each PLL, such that each cantilever-PLL feedback loop has a 50 or 100 Hz FM-signal bandwidth. We then adjust the phase-delay for each PLL to maximize the cantilever vibration amplitude. Finally, we measure the FM-signal transfer function for each cantilever-PLL feedback loop to confirm sufficient measurement bandwidth (in case of errors in setting the parameters). This transfer function relates the measured cantilever-PLL oscillation frequency to a cantilever’s time-dependent intrinsic resonant frequency. Frequency data for each cantilever are collected at 500 Hz, and are transmitted from the FPGA via ethernet to a personal computer where they are saved via custom LabView software (National Instruments).

As in previous SMR systems, the device is placed on a copper heat sink/source connected to a heated water bath, maintained at 30°C (yeast) or 37°C (mammalian cells and E. coli) for the duration of the experiment. The sample is loaded into the device from vials pressurized under air (yeast and E. coli) or air with 5% CO₂ (all mammalian cells) (Supplementary Fig. 1), through 0.009 inch inner-diameter FEP tubing. The pressurized vials are seated in a temperature-controlled sample-holder throughout the measurement. FEP tubing allows us to flush the device with piranha solution for cleaning, as piranha will damage most non-fluorinated plastics. To measure a sample of cells, we initially flush the device with filtered media, and then flush the sample into one bypass channel. NIST traceable polystyrene beads are added to the sample as an internal calibration standard. For experiments on large-channel devices, we typically apply between one and two psi across the entire array, yielding flow rates on the order of 0.5 nL/s (the array’s calculated fluidic resistance is approximately 3×10¹⁶ Pa/(m³/s), calculated via³⁸). For small-channel devices, we apply 4–5 psi across the array, yielding flow rates around 0.1 nL/s. Additionally, every several minutes we flush new sample into the input bypass channel to prevent particles and cells from settling in the tubing and device. Between experiments, devices were cleaned with either filtered 2% tergazyme, filtered 10% bleach, or piranha solution.

Data analysis

We first rescale the recorded frequency signals from each cantilever by applying a rough correction for the different sensitivities of the cantilevers. Cantilevers differing in only their lengths should have mass sensitivities proportional to their resonant frequencies to the power three-halves. Therefore we initially divide each frequency signal by its carrier frequency to the power three-halves such that the signals are of similar magnitude. To detect peaks, we first filter the data with a third order Savitzky-Golay lowpass filter³⁹, followed by a nonlinear highpass filter (subtracting the results of a moving quantile filter from the data). We find peak locations as local minima that occur below a user-defined threshold. After finding the peak locations, we estimate the peak heights by fitting the surrounding baseline signal (to account for a possible slope in the baseline that was not rejected by the highpass filter), fitting the region surrounding the local minima with a fourth-order polynomial, and finding the maximum difference between the predicted baseline and the local minima polynomial fit. Because this process occasionally makes errors (it sometimes detects noise, particles that got stuck in the cantilever, and particles that passed through the cantilever at the same time as another particle), for each cantilever we reject peaks that are very unlike the typical peak. We do this by first calculating the robust Mahalanobis distance for each peak in terms of a number of its estimated characteristics (baseline slope, time between sequential antinode peaks, minimum value between sequential peaks, and difference in heights of sequential peaks), and rejecting those with large distances above a user-specified threshold. We then identify the peaks corresponding to the calibration particles, and precisely estimate the mass sensitivity for each cantilever, such that the modal mass for the particles is equal to the expected modal mass according to the manufacturer’s datasheet. Finally we match up peaks at different cantilevers that originate from the same cell to extract single-cell growth information (more details in Supplementary Note 3). Figs. 2–5 show the mass accumulation rates of automatically-matched cells that were observed at least seven times. For E. coli (Fig. 6), because the cell concentrations were higher, we required both that the cell have been measured at least six out of ten times and that the root-mean-square-error of a linear fit (buoyant mass vs time) was less than 5 fg, as a greater fitting error suggests a possibly-incorrect matching.

Cell culture

E. coli strain 25922 (ATCC) were grown overnight in LB broth (Miller, Difco) at 37°C. Saturated overnight cultures were diluted 10,000-fold in LB broth supplemented with 0.2% Tween-80 (this prevents particles from sticking to the device walls), and incubated 1.5–2.5 h in a shaker incubator at 37°C prior to loading them onto the serial SMR array. The CM15 peptide (sequence KWKLFKKIGAVLKVL; Biosynthesis) was ordered as a crude synthesis and suspended in water by weight. Kanamycin (Sigma-Aldrich) and CM15 were prepared as stock solutions at 50 mg/mL in water, and 1μL of these stock solutions were added to 1 mL of culture at the times indicated.

E. faecalis (ATCC strain 29212) was grown overnight in Brain Heart Infusion (BHI, Difco) at 37°C. Saturated overnight cultures were diluted 100,000-fold in BHI broth with 0.2% Tween-80, and incubated 3 h in a shaker incubator at 37°C prior to loading onto the serial SMR array.

Yeast (strain W303, diploid) were a gift from Angelika Amon’s lab and were maintained on YPD agar plates and grown in YPD broth at 30°C.

L1210 cells were a gift from Marc Kirschner’s lab and no further cell line validation was performed. BaF3-BCR-ABL were created from the parental BaF3 cell line obtained from the RIKEN BioResource Center. Both cell lines tested negative for mycoplasma. L1210 and Ba/F3 cells were cultured in filtered RPMI 1640 supplemented with 10% FBS and streptomycin and penicillin at 37°C under 5% CO₂. Ba/F3 cells were cultured under identical conditions, and were IL-3 independent due to a BCR-ABL insertion.

Murine CD8+ T cells were obtained from a 14-week old female C57BL/6J mouse. Animals were cared for in accordance with federal, state, and local guidelines following a protocol approved by the Department of Comparative Medicine (DCM) at MIT. Cells were obtained from a mouse spleen and two lymph nodes, which were ground through a filter, subjected to ACK lysis, purified with a CD8a+ T Cell Isolation Kit (Miltenyi), and then immediately seeded into wells and activated in RPMI 1640 with 10% FBS, 1X streptomycin/penicillin, and 55 μM β-mercaptoethanol (Gibco), using surface-bound anti-CD3 (Biolegend 145-2C11, coated at 5μg/mL) and soluble anti-CD28 (Biolegend, 37.51, 2 μg/mL) at 37°C under 5% CO₂ for 22 h. After 22 h cells were transferred to new medium containing IL-2 (100 U/mL) and from there on passaged daily to a concentration of roughly 200,000 cells/mL, 2–3 hours prior to each measurement.

Human blood buffy coat was obtained from Research Blood Components (Boston, MA) and PBMCs were isolated with Ficoll-Paque Plus (GE) using the manufacturer’s recommended protocol. The PBMC layer was isolated, subjected to ACK lysis (Thermo Fisher) and washed three times with RPMI 1640 supplemented with 10% FBS. Cells were then seeded in a 96 well plate (Corning High Bind microplate) at a concentration of 1.5×10⁶ mL⁻¹ with 5 μg/mL surface-bound anti-CD3 (BioLegend, HIT3a clone), 2 μg/mL soluble anti-CD28 (BioLegend, CD28.2 clone), and 100 U/mL soluble IL-2 (PeproTech) at 37°C under 5% CO₂. Immediately before measurement, cells were harvested from the well by gently pipetting to suspend weakly-adhered cells, and were diluted into RPMI 1640 supplemented with 10% FBS and IL-2, then loaded into the serial SMR array.

All studies involving primary patient samples were approved by the Dana-Farber/Harvard Cancer Center Institutional Review Board. Informed consent was obtained in accordance with the Declaration of Helsinki. Diagnostic peripheral blood or bone marrow specimens were obtained from patients with acute myeloid leukemia (Supplementary Table 1), subject to erythrocyte lysis (Qiagen, #158904), and stained with antibodies targeting human CD45 (eBiosciences, #17-9459-42) and CD15 (eBiosciences, #12-0159-42). Leukemia cells were enriched by sorting for CD45/CD15 double-positive cells on a FACSAria II SORP fluorescence activated cell sorter (BD Biosciences) (Supplementary Fig. 8). Sorted cells were seeded at a density of 1e6/mL and cultured at 37 C in a humidified 5% CO2 incubator in RPMI (Gibco) supplemented with 10% fetal calf serum (Gibco), 2 mM L-glutamine (Gibco), and 50 IU/ml-50 μg/mL penicillin-streptomycin (Fisher Scientific) prior to dilution and loading on the SMR.

Figure 4. Measured growth dynamics of single hCD15+/hCD33+ AML cells taken from two patients.

Cells with statistically significant growth (one-sided T-test for slope > 0, p-value < 0.001) are marked with black lines, and three growing cells are highlighted for each sample (insets). 7 μm (~8.5 pg) particles were included in these samples for calibration but are not shown. Data from the first cantilever was not used in this analysis due to abnormally high noise. (A) Cells taken from a peripheral blood draw. (B) Cells taken from bone marrow (different patient than in (A)).