Increasing Generality and Power of Rare-Variant Tests by Utilizing Extended Pedigrees

Abstract

Recently, multiple studies have performed whole-exome or whole-genome sequencing to identify groups of rare variants associated with complex traits and diseases. They have primarily utilized case-control study designs that often require thousands of individuals to reach acceptable statistical power. Family-based studies can be more powerful because a rare variant can be enriched in an extended pedigree and segregate with the phenotype. Although many methods have been proposed for using family data to discover rare variants involved in a disease, a majority of them focus on a specific pedigree structure and are designed to analyze either binary or continuously measured outcomes. In this article, we propose RareIBD, a general and powerful approach to identifying rare variants involved in disease susceptibility. Our method can be applied to large extended families of arbitrary structure, including pedigrees with only affected individuals. The method accommodates both binary and quantitative traits. A series of simulation experiments suggest that RareIBD is a powerful test that outperforms existing approaches. In addition, our method accounts for individuals in top generations, which are not usually genotyped in extended families. In contrast to available statistical tests, RareIBD generates accurate p values even when genetic data from these individuals are missing. We applied RareIBD, as well as other methods, to two extended family datasets generated by different genotyping technologies and representing different ethnicities. The analysis of real data confirmed that RareIBD is the only method that properly controls type I error.

Introduction

Human genetics rapidly adopts sequencing technology as a method of choice in studies of complex traits.^{1, 2} Sequencing studies uncover rare variants invisible to genome-wide association studies (GWASs)^{3, 4, 5} that employ microarray-based genotyping. Although the role of rare variants in the unaccounted “missing” heritability remains debatable,^{6, 7} it is anticipated that rare-variant studies would deliver functionally interpretable alleles of larger effect sizes amenable to the experimental manipulation.^{8, 9, 10, 11}

To identify rare variants associated with traits, several statistical methods called “burden” or “collapsing” approaches have been proposed.^{12, 13, 14, 15} Because it is statistically difficult to identify an effect of a single rare variant, these approaches combine effects of multiple rare variants in one gene or region to increase statistical power. Several studies have recently applied burden approaches to sequencing and exome-chip data mostly by utilizing case-control designs, similar to the GWAS approach.^{16, 17} However, they have had limited success at identifying previously uncharacterized genes associated with traits. This could be mainly due to limited statistical power given that several studies^{7, 18, 19, 20} have shown that using burden approaches to identify rare variants associated with a disease requires tens of thousands of individuals.

An alternative approach to finding rare variants involved in diseases is to use family-based studies, which offer several advantages over case-control studies. First, genetic variants that are rare in the general population could be enriched in certain extended families, which allows family-based studies to achieve higher power to detect rare-variant associations than case-control studies.²¹ Second, segregation of variants with the phenotype, even if imperfect, provides an additional source of information. Third, sequencing errors can be detected through violations of Mendelian inheritance in families, and moreover, these errors can be corrected by statistical approaches.^{22, 23, 24} This reduces erroneous calls made by sequencing and hence increases the power of rare-variant analysis by correctly calling rare variants. Lastly, family-based studies can be designed to be robust to population structure that could introduce false findings in case-control studies.²⁵

Several burden approaches have been proposed for using family data to detect rare variants involved in a disease. However, some methods can be applied to only small families such as trios and nuclear families,^{26, 27, 28} some are designed only for quantitative traits,^{29, 30, 31} and some methods lack software implementation.³² Thus, very few methods can be applied to extended families, to both binary and quantitative traits, and to affected-only pedigrees. As we also show, current methods for large extended families^{21, 33} have inflated false-positive rates (FPRs) when founders are not genotyped, which happens frequently in large families.

Here, we propose RareIBD for detecting rare variants underlying the phenotype in extended families. Our approach looks for a rare variant whose segregation pattern among affected and unaffected individuals is different from the predicted distributions based on Mendelian inheritance and computes a statistic measuring the difference. To increase statistical power, our statistic combines variants per gene and across multiple families. The method can be applied to any large pedigree, including those that include only affected individuals, and can incorporate both binary and quantitative traits. Our method also considers the case where not all founders are genotyped. Simulations suggest that the proposed method achieves higher power than existing approaches for the analysis of extended families. When founders are not genotyped, our approach maintains a correct FPR with greater power improvement over currently available techniques.

In this study, we applied RareIBD to two extended family datasets. One is a whole-exome sequencing dataset of families with members affected by severe, early-onset chronic obstructive pulmonary disease (EOCOPD). This dataset contains 347 individuals. The other dataset is from the Cleveland Family Study (CFS), which collected a family-based cohort to identify the genetic basis of sleep apnea and related traits. The CFS consists of 632 individuals with African American (AA) ancestry³⁴ and 710 individuals with European ancestry (EA) who were genotyped with genome-wide SNP microarrays and exome chips. Both family datasets consist of multiple extended families, and not all founders were genotyped. We show that our method generates p values that are closer to the expected null distribution and are much more uniform than those from other approaches in both datasets. This suggests that our approach generates correct p values regardless of pedigree structure and missing founders.

Material and Methods

RareIBD

The main idea of our approach is that causal rare alleles are enriched among affected individuals and depleted among unaffected individuals. First, we assume that only one founder carries a rare mutation in a family for a given rare variant. This is true for a majority of rare variants because it is very unlikely that two or more founders have the same rare variant in a family. This means that any non-founders in the same family who inherit this rare allele share the allele identically by descent. We are interested in the segregation of this allele in the family. We compute a statistic that measures enrichment of this allele among affected pedigree members and depletion among unaffected members. Lastly, we adopt a burden-test approach that aggregates these statistics across multiple rare variants and multiple families for a given gene and tests whether rare variants in this gene are associated with a disease or a quantitative trait.

We assume that we have N families and M rare variants in gene g. To determine whether a variant is rare or common, we utilize allele-frequency information from both external sources, such as 1000 Genomes¹ and the Exome Aggregation Consortium (ExAC) Browser,² and internal sources, such as allele frequency estimated from only founders and/or all individuals in N families. We assume for now that all individuals, including founders, are genotyped in a family. (We will discuss how our approach can be extended to missing founders in the next section.) For each rare variant, we check whether it is present only in one founder. For variant i in family j, where only one founder carries this variant, let $a_{+}^{ij}$ be the number of affected individuals with the variant and $u_{-}^{ij}$ be the number of unaffected individuals without the variant. Our statistic $S_{\text{RareIBD}}^{ij}$ is defined as follows:

$$S_{\text{RareIBD}}^{ij}=a_{+}^{ij}+u_{-}^{ij}.$$ (Equation 1)

We are then interested in finding the value of $S_{\text{RareIBD}}^{ij}$ under the uniform distribution of inheritance vectors (IVs), which is similar to the null distribution. An IV consists of 2n binary values, where n is the number of non-founders.³⁵ Each non-founder has two binary values (0 and 1) for two chromosomes such that each value indicates a transmission of the grandpaternal or grandmaternal allele. We enumerate all possible IVs to estimate the mean and SD of our statistic under the uniform distribution of IVs. Let k be the founder with the rare mutation, and let μ^k and σ^k be our statistic’s mean and SD, respectively, estimated from enumerating all IVs under the assumption that founder k has the mutation. Then, we can estimate the Z score as follows:

$$Z_{ij}^{\text{OneF}}=\frac{S_{\text{RareIBD}}^{ij}-{\mu }^k}{{\sigma }^k}.$$ (Equation 2)

We call this Z score “OneF” because it is estimated with the mean and SD of one founder. Lastly, we take a weighted sum of Z scores across all rare variants and all families in gene g:

$$Z_g^{\text{OneF}}=\frac{{\sum }_i^M{\sum }_j^N{w}_i{Z}_{ij}^{\text{OneF}}}{\sqrt{{\sum }_i{\sum }_j{w}_i^2}}.$$ (Equation 3)

w_i is the weight of each rare variant, and this will be discussed in detail in the next section. We can compute a p value of $Z_g^{\text{OneF}}$ from the standard normal distribution or a gene-dropping approach, which we will discuss in the next section.

Improvements in RareIBD

Missing Founders in Extended Families

Missing founders introduce two challenges in our approach. First, we might not know whether only one founder carries the variant, and it is not clear whether we should include this variant in our statistic or not. To solve this problem, we check to see whether at least one non-founder carries a mutation because we are not interested in a variant for which no non-founder has a mutation. If the minor allele frequency (MAF) estimated from the external and internal sources indicates that this is a rare variant, we assume that only one founder has a mutation for this variant.

The other challenge is that we might not know which founder mean (μ^k) and SD (σ^k) to use when estimating the Z score (Equation 2). To solve this problem, we estimate μ and σ for every founder in each family. We can estimate μ and σ even though a founder is not genotyped by assuming that only the founder in the family has a mutation. We then compute a Z score for each founder and average the scores. Let F^j be the number of founders in family j. Our new statistic is defined as follows:

$$Z_{ij}^{AllF}=\left(\underset{k}{\sum ^{F^j}}\frac{S_{\text{RareIBD}}^{ij}-{\mu }^k}{{\sigma }^k}\right)/F^j$$ (Equation 4)

$$Z_g^{\text{AllF}}=\frac{{\sum }_i^M{\sum }_j^N{w}_i{Z}_{ij}^{\text{AllF}}}{\sqrt{{\sum }_i{\sum }_j{w}_i^2}}.$$ (Equation 5)

We call this approach “AllF” because it uses the Z scores of all founders. It is important to note that this approach is computationally efficient because we can independently compute μ and σ for all founders in every family. We estimate μ^k and σ^k by assuming that founder k has the mutation, and it needs to be estimated only once as a pre-processing step.

Estimating the Mean and SD of RareIBD Statistics

When estimating μ and σ of our statistic for each founder, we need to enumerate all IVs. The time complexity of this computation is exponential (O(2²ⁿ)) in the number of non-founders. For example, the number of all possible IVs is about 10²⁴ when the number of non-founders is 40. To reduce the computational time to estimate μ and σ, we decided to perform a fixed number of random IV samplings. In each sampling, we randomly chose 0 or 1 for 2n chromosomes. In our simulation and real datasets, we performed 100,000 random IV samplings. We found that μ and σ from the 100,000 samplings were very similar to those from all 2²ⁿ IVs (data not shown).

Estimating p Values

One approach to obtaining a p value from our Z score ($Z_{ij}^{\text{AllF}}$ and $Z_{ij}^{\text{OneF}}$) is using the standard normal distribution. This approach is very efficient and simple, but it is known to be inaccurate,³⁵ and we found empirically that this approach often yields an overly conservative p value (data not shown), which leads to a loss of power. Also, as will be discussed next, we estimate weights from data. Then, the weighted sum of Z scores is no longer asymptotically normal, and hence the standard normal approximation does not hold.

To solve this problem, we adopt a gene-dropping approach to estimate a p value. Below are steps showing how a standard gene-dropping approach is applied.

• 1.For each family, genotypes of founders are randomly generated according to the allele frequency of a variant.
• 2.Genes (or haplotypes) are randomly “dropped” to non-founders.
• 3.A statistic of interest (e.g., $S_{\text{RareIBD}}^{{ij}^{\prime }}$) is computed.
• 4.IVs are enumerated for estimating the mean and SD of the statistic under the uniform distribution.
• 5.A Z score (e.g., $Z_{ij}^{{\text{AllF}}^{\prime }}$ or $Z_{ij}^{{\text{OneF}}^{\prime }}$) is computed.
• 6.Steps 1–5 are repeated for all families, and a weighted sum of Z scores (e.g., $Z_g^{{\text{AllF}}^{\prime }}$ or $Z_g^{{\text{OneF}}^{\prime }}$) is computed.
• 7.Steps 1–6 are repeated many times, and a p value is a proportion of $Z_g^{\text{AllF}}>Z_g^{{\text{AllF}}^{\prime }}$.

This standard gene-dropping approach is computationally very expensive because of step 4, which estimates the mean and SD by enumerating IVs. Because we assume that only one founder has a rare allele, we can simplify the gene-dropping approach and greatly increase its efficiency with the following modifications. In step 1, we consider only families with a rare variant because our statistic is computed from only such families. For rare variant i in family j, we assign a mutation to one of the founders randomly. This implicitly assumes that there is no linkage disequilibrium (LD) among rare variants in each family because each rare variant is assigned to a founder independently. This assumption is violated if a founder has more than one rare variant in a haplotype. For example, let’s assume that there are two rare variants, rv₁ and rv₂, in the same haplotype of a founder. This haplotype will be inherited to the same set of non-founders if we assume that there is no recombination in the gene, which means that rv₁ and rv₂ are in perfect LD. rv₂ can be considered a duplicate variant of rv₁, and rv₂ does not provide additional information to our statistic. Hence, we consider only rv₁ in our statistic. In our method, if all individuals in a family have the same genotypes across multiple variants, we consider them to be duplicate variants and use only one from those variants. In step 4, because we already computed the mean and SD for all founders independently in a pre-processing step, it is not necessary to enumerate IVs, and we use pre-computed values. This gene-dropping approach is computationally efficient, and we also use the adaptive permutation approach, whereby we stop the gene dropping once p values are clearly non-significant.

Weighting Rare Variants

Several approaches have been proposed for weighting rare variants. One of them is to weight variants by allele frequency, whereby rare variants are assigned higher weights than common variants.^{13, 14} Another approach is to use estimated effect sizes and to weight variants with larger effects more heavily.³⁶ The third approach is to use functional variant information that assigns higher weights to more deleterious variants.³⁷ The functional information can be obtained from several bioinformatics tools, such as PolyPhen-2 (PP2)³⁸ and SIFT.³⁹ Our approach incorporates all three weighting schemes.

First, we use the estimated regression coefficient (EREC) approach³⁶ for the effect-size-based weight. We compute the odds ratio (OR) for each rare variant from individuals in all families by assuming that they are unrelated and add a constant to it: w_i = log(OR_i) + δ in Equations 3 and 5. We use δ = 2 because we found empirically that it yields the highest power (data not shown). When estimating OR, we add a pseudocount of 1 to every term in the two-by-two frequency table. Second, for the frequency-based weight, we utilize the variable-threshold (VT) approach.¹³ Some rare-variant methods use a fixed-threshold approach that sets the weight of a variant (w_i) to 0 if the variant’s MAF is greater than a certain threshold (e.g., 1%). The VT method varies this threshold and finds the maximum Z score among all thresholds. Let T_i denote the minor allele count (MAC) among founders in all families for variant i. If founders are not genotyped, there are two approaches. If there is an accurate estimation of MAF of a variant, as in our simulations, we can compute the expected MAC by using the MAF and the number of founders. Otherwise, we use the MAC among non-founders, which is the approach we use in real datasets. Let Ω be the sorted list of $\left\{T_1,T_2,\dots ,T_M\right\}$ and Ω_i be the i^th element in the list. Our new statistic is as follows:

$$Z_g^{\text{AllF}}\left({\text{Ω}}_i\right)=\frac{{\sum }_i^M{\sum }_j^N{w}_i{Z}_{ij}^{\text{AllF}}}{\sqrt{{\sum }_i{\sum }_j{w}_i^2}},\{\begin{array}{c}{w}_i=\text{log}\left({\text{OR}}_i\right)+2\text{if}{T}_i\le {\text{Ω}}_i\\ w_i=0\text{if}{T}_i>{\text{Ω}}_i\end{array}$$ (Equation 6)

$$Z_g^{\text{AllF}}=\text{max}\left(Z_g^{\text{AllF}}\left({\text{Ω}}_1\right),Z_g^{\text{AllF}}\left({\text{Ω}}_2\right),\dots ,Z_g^{\text{AllF}}\left({\text{Ω}}_M\right)\right)$$ (Equation 7)

It is important to note that the same weighting scheme needs to be applied in the gene-dropping approach to ensure the validity of the gene dropping. Lastly, as for the weights reflecting the functional information, we utilize PP2 scores where a nonsense variant has a weight of 1, a missense variant has a weight equal to the probability that a variant is damaging according to PP2 (the minimum weight is set to 0.3), and all other annotations have a weight of 0.1. This functional weight is multiplied by the original weight (w_i in Equation 6) and used only in the real-data analyses.

Extension to Affected-Only Families and Quantitative Traits

RareIBD can be extended to compute its statistic for families with only affected individuals and quantitative traits. For affected-only families, the $u_{-}^{ij}$ term in Equation 1, which is the number of unaffected individuals without a mutation, is not considered. Hence, our statistic $\left(S_{\text{RareIBD}}^{ij}\right)$ consists of only $a_{+}^{ij}$, the number of affected individuals with a mutation. In this case, we test whether a rare allele is enriched among affected individuals. For a quantitative trait, we want to test whether a rare allele increases or decreases the trait. To test this, our statistic can be defined as $S_{\text{RareIBDq}}^{ij}={\left(r_{+}^{ij}-r_{-}^{ij}\right)}^2$, where $r_{+}^{ij}$ and $r_{-}^{ij}$ are the average trait values among individuals with a mutation and without a mutation, respectively. We can enumerate IVs to estimate the mean and SD of this statistic and estimate a p value by using the gene-dropping approach.

Simulation Framework

To measure the FPR and power of RareIBD and other approaches, we generate simulated data for extended families. We consider three pedigree structures: wide, deep, and small families (Figure S1). The number of individuals in wide, deep, and small families is 30, 36, and 12, respectively, and the number of families is 24, 20, and 60 for wide, deep, and small families, respectively, which means a total of 720 individuals in all three family types. First, we create haplotypes of unrelated individuals by using COSI software.⁴⁰ We assume EA ancestry, a gene length of 20,000 bp, and an exon length of 5,000 bp. We generate 50,000 haplotypes by using COSI and estimate the MAF of each variant. Then, one million haplotypes are generated with the estimated MAF. Those haplotypes are split into two groups: rare haplotypes and non-rare haplotypes. Rare haplotypes contain at least one rare variant, and non-rare haplotypes do not. (Throughout the paper, a rare variant is defined as a variant whose MAF is less than 1% unless otherwise specified.) We randomly choose one haplotype from the rare haplotypes and 2F − 1 haplotypes from the non-rare haplotypes (F is the number of founders). We assign the rare haplotype to one chromosome among 2F founder chromosomes, and the remaining founder chromosomes are the 2F − 1 non-rare haplotypes. We then randomly drop chromosomes from founders to non-founders. Once we have haplotypes for all individuals in a family, we determine their disease status. Let P(A = 1) be the probability that individual A is affected. In FPR simulation, P(A = 1) = 50%. In power simulation, this probability is determined with the logistic regression model:

$$P\left(A=1\right)=\frac{\text{exp}\left({\beta }_0+X^T\beta \right)}{1+\text{exp}\left({\beta }_0+X^T\beta \right)}.$$

${\beta }_0=\text{log}\left(W/(1-W)\right)$, where W is the baseline prevalence, $\beta =\left\{{\beta }_1,{\beta }_2,\text{..},{\beta }_M\right\}$, where ${\beta }_i=\text{log}\left({\text{OR}}_i\right)$ for i^th variant, and X is the genotype vector for M variants. Assuming that non-rare variants have a null effect, we use a baseline prevalence of 40% and an OR of 2 for variants with a MAF < 1% and use an OR of 1 for variants with a MAF ≥ 1%. The baseline prevalence is the prevalence of a disease in a family; we assume high prevalence in simulations because studies usually collect families with many affected individuals. Each variant also has c_i, which is the probability that variant i is causal. We consider five different levels of c_i: 10%, 20%, 30%, 40%, and 50%. Hence, not all rare variants are causal in the simulations. We limit the number of affected individuals per family such that the minimum is one-third of the family size and the maximum is two-thirds. We keep only families with the desired number of affected individuals in our simulation and repeat this procedure until we have the desired number of families. We generate 10,000 replications for false-positive simulations and 2,000 for power simulations. We perform 10,000 gene-dropping permutations to estimate p values in simulations. Once we have phenotype and genotype information for all families, we test two other approaches in addition to RareIBD: (1) family-based functional principal-component analysis (FPCA), which includes five methods: FPCA, ChiPerm, ChiMin, T², and combined multivariate and collapsing (CMC);²¹ and (2) Pedgene, which includes two methods: kernel and burden.³³ They can both be applied to any large extended family with binary traits.

EOCOPD Whole-Exome Sequencing Dataset

This dataset contains high-coverage whole-exome sequencing data of 347 individuals in 49 extended families sequenced at the University of Washington Center for Mendelian Genetics for the Boston EOCOPD Study. ^{41, 42, 43} The Genome Analysis Toolkit⁴⁴ with multisample calling was used to call variants. For initial quality control (QC), individuals who were outliers according to sex concordance and ethnicity were removed. We also checked expected relatedness by using $\hat{\pi }$ and removed five individuals whose $\hat{\pi }$ values did not match the pedigree structure. We removed variants with a missing rate >1%, Hardy-Weinberg equilibrium (HWE) p value <10⁻⁸, Mendelian transmission errors, and average sequence depth <12, as well as monomorphic variants. Additional QC included setting genotypes whose genotype-quality scores were ≤20 to missing and removing variants whose missing rates were greater than 5% and monomorphic variants. To correct additional Mendelian errors (MEs) and to impute missing data (RareIBD requires that no data be missing), we applied Polymutt,²³ which uses pedigree structure to refine and imputes genotypes. After Polymutt was applied, there were no MEs or missing genotypes. We considered 115,361 variants in autosomes for our analysis. We estimated the MAF of each variant by using the following sources: (1) all individuals, (2) unrelated individuals, (3) the NHLBI Exome Sequencing Project (ESP) Exome Variant Server, (4) dbSNP,⁴⁵ and (5) 1000 Genomes.¹ If the MAF was less than 1% in any of the previous sources, we considered the variant to be rare. In our analysis, we included 12,092 genes that had at least three rare variants. Individuals with Global Initiative for Chronic Obstructive Lung Disease (GOLD) spirometry grades of 2 (moderate chronic obstructive pulmonary disease [COPD]), 3 (severe COPD), and 4 (very severe COPD) were considered affected individuals, and individuals with normal spirometry were considered unaffected. There were 155 affected, 148 unaffected, and 44 unassigned individuals according to these criteria. Table S3 describes detailed information on the family structure of this dataset, such as the average number of individuals in each family and the percentage of individuals who were sequenced. We obtained institutional-review-board (IRB) approval and signed informed consent for all participants.

CFS Microarray and Exome-Chip Dataset

The CFS is a family-based longitudinal study designed to examine the genetic basis of sleep apnea in AA and EA individuals studied between 1990 and 2006. Index probands with confirmed sleep apnea, along with additional family members and neighborhood control families, were recruited from sleep centers in northern Ohio.⁴⁶ Over four waves of data collection over 16 years, a total of 2,534 individuals from 356 families underwent measurements for sleep apnea, anthropometry, and other related phenotypes. Sleep apnea was assessed prior to 2000 with a type 3 home sleep-apnea test (Eden Trace). In the last examination conducted between 2000 and 2006, sleep apnea was assessed by 14-channel overnight polysomnography (Compumedics E-Series) obtained in a clinical research unit. For both studies, apneas and hypopneas were scored on the basis of reduction of airflow or chest-wall movement with an associated 3% more desaturation. Data used in the analysis were based on 632 individuals with AA ancestry and 710 individuals with EA ancestry who had both genotype data and sleep data. IRB approval and signed informed consent were obtained for all participants.

Individuals with AA ethnicity were genotyped with the Affymetrix 6 and Illumina Exome chip, and those with EA ancestry were genotyped with the Illumina OmniExpress and Exome chip. Before QC, there were 632 AA individuals with 1,127,887 SNPs and 710 EA individuals with 963,502 SNPs. We performed the following QC. First, we removed individuals with a missing rate > 5% and set all MEs to missing. We then again removed individuals with a genotype missing rate > 5%, SNPs with a missing rate > 2%, SNPs with a HWE p value < 0.001, and monomorphic SNPs. We computed estimates of identity by descent (IBD, $\hat{\pi }$) between every pair of individuals by using PLINK software⁴⁷ and identified pairs whose estimated $\hat{\pi }$ values were not consistent with coefficients of relationship. We removed the fewest number of individuals among those pairs such that $\hat{\pi }$ values of remaining pairs were consistent with coefficients of relationship. Using EIGENSTRAT software,⁴⁸ we performed principal-component analysis on founders with 1000 Genomes as a reference panel to identify population outliers. We removed those outliers and their children. We applied ShapeIt software⁴⁹ to phase and impute missing genotypes because it can incorporate family relationships for phasing. After applying ShapeIt, we removed SNPs with at least one ME and removed families with only one individual and families with only founders. After QC, the number of individuals was 563 and 665 in AA and EA datasets in 119 and 114 families, respectively. The number of SNPs in autosomes was 874,622 and 692,422 in AA and EA datasets, respectively. Table S3 describes detailed information on the family structure of both datasets.

We focused on the primary clinical measure of sleep-apnea severity, the apnea-hypopnea index (AHI), which is the average number of breathing pauses (apnea plus hypopneas) per hour of sleep. Given the strong age dependency of the AHI, we defined disease on the basis of an age-specific cutoff for analysis of dichotomous traits. Specifically, individuals were defined as having sleep apnea if their AHI values were greater than or equal to 5, 10, 15, and 20 for ages <21, 21–44, 45–64, and ≥65 years, respectively. There were 217 affected and 346 unaffected individuals in the AA dataset and 218 affected, 444 unaffected, and 3 missing individuals in the EA dataset. We used four sources of MAF information: (1) all individuals, (2) unrelated individuals, (3) the ExAC Browser,² and (4) 1000 Genomes.¹ We included genes with at least three rare variants, and there were 7,267 and 6,110 such genes in AA and EA datasets, respectively.

Results

Effect of Weighting Variants and AllF Approach on Power of RareIBD

Our method, RareIBD, incorporates weighting schemes and the AllF approach to include all founders (see Material and Methods). We quantified the effect of these improvements on statistical power. Our weighting scheme consists of both frequency-based and effect-size-based weights. In the OneF approach, our Z score is calculated with the mean and SD of one founder who carries a mutation, whereas in the AllF approach, it is calculated with the mean and SD of all founders. We generated our simulated data as discussed in the Material and Methods, and we considered three pedigree structures: (1) wide, (2) deep, and (3) small families (Figure S1). We assumed that all individuals are genotyped in this simulation and considered three different versions of our approach: (1) weighted AllF, (2) weighted OneF, and (3) unweighted OneF.

Results show that all three approaches have correct FPR in all three types of families (Table S1). Results of our power simulations show that weighting variants increases statistical power and that weighted OneF consistently has higher power than unweighted OneF in all three families at all c_i values (the probability that a rare variant is causal) (Figure S2). Surprisingly, the weighted AllF approach achieves significantly higher power than the weighted OneF approach even though all founders are genotyped in this simulation (Figure S2). This could be because using information from all founders provides more stable and accurate estimation of Z scores, which is similar to model averaging. The AllF approach also has another advantage in that it can be applied to families with missing founders, whereas the OneF approach cannot. Hence, we used the weighted AllF approach in the rest of our simulations and in the real datasets.

Comparison between RareIBD and Other Approaches when Founders Are Genotyped

Here, we use simulations to compare the FPR and power of RareIBD with those from two other methods: FPCA²¹ and Pedgene.³³ They are among the few methods that can be applied to extended families with binary traits. All individuals, including founders, are genotyped in this simulation, and the same three pedigree structures are used for measuring the FPR and power of each method. Results of FPR simulation show that some methods provided by FPCA software do not have correct FPRs; FPCA has an overly conservative FPR, whereas ChiMin and T² have inflated FPRs (Table 1). Hence, these three methods are excluded from the power simulation. All other approaches including RareIBD have a correct FPR.

Table 1.

Comparison of the FPR between RareIBD and Other Approaches for Three Different Pedigree Structures: Wide, Deep, and Small

Software	Method	All Founders Genotyped			Top Two Generations Missing
		Wide	Deep	Small	Wide	Deep	Small
RareIBD	RareIBD	0.0475	0.0466	0.0517	0.0477	0.0435	0.0533
FPCA	FPCA	1.00 × 10−4	0.0019	7.00 × 10−4	4.00 × 10−4	0.0015	9.00 × 10−4
	ChiPerm	0.0544	0.0475	0.0366	0.0519	0.0494	0.0472
	ChiMin	0.5375	0.2981	0.4395	0.5196	0.2569	0.1976
	T2	0.0838	0.0643	0.1138	0.0922	0.0645	0.1906
	CMC	0.056	0.0586	0.0459	0.0596	0.0553	0.0557
Pedgene	kernel	0.0233	0.0345	0.0064	0.0263	0.0382	0.0158
	burden	0.0449	0.0456	0.0472	0.0604	0.0566	0.0883

We tested FPCA and Pedgene software in addition to RareIBD. FPCA has five methods (FPCA, ChiPerm, ChiMin, T², and CMC), and Pedgene has two methods (kernel and burden). We also considered two simulation scenarios: (1) all individuals in a family are genotyped, and (2) individuals in the top two generations are not genotyped, which simulates families with missing founders. The FPR was measured at α = 0.05 from 10,000 replications of simulations. See Figure S1 for a description of each pedigree type.

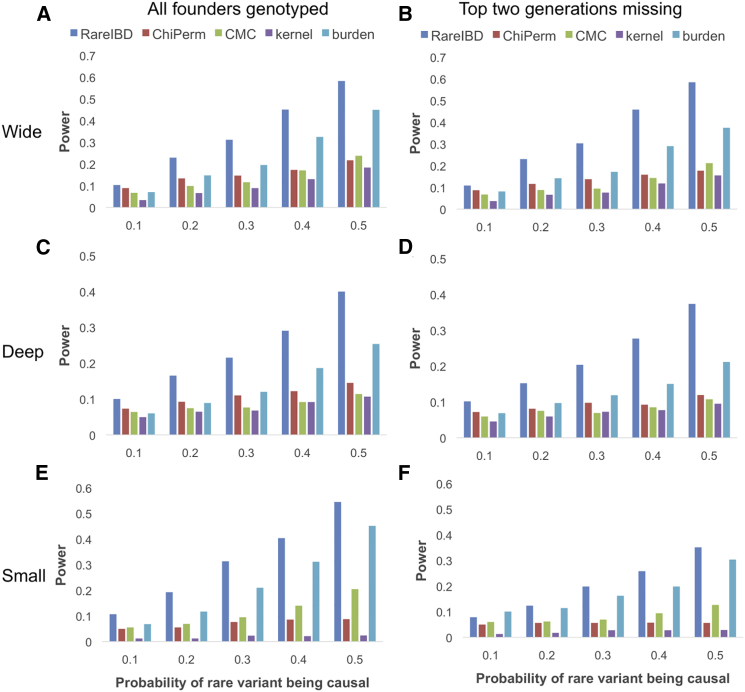
According to power simulations, RareIBD outperforms all other approaches in the three types of families at every c_i level (Figures 1A, 1C, and 1E). The power improvement of RareIBD over other approaches is substantial given that our power is at least 9% higher than the second-best approach—the burden approach from Pedgene when c_i ≥ 30% in three families. For wide and deep families at c_i = 50%, our method achieves 13%–14% higher power than the burden approach. RareIBD gains higher power in these two types of families because enrichment of a causal rare allele among affected individuals and its depletion among unaffected individuals are more prominent in these larger families. Our method also has higher power in relatively “small” families and can be applied to any extended family.

Figure 1.

Power Comparison between RareIBD and Other Approaches

Pedigree structures include wide families (A and B), deep families (C and D), and small families (E and F) (Figure S1). ChiPerm and CMC are from FPCA,²¹ and kernel and burden are from Pedgene.³³ The x axis indicates the c_i of a variant (there are five levels) and the probability that each rare variant is causal. We also considered two simulation scenarios: (1) all individuals in a family are genotyped (A, C, and E), and (2) the individuals in the top two generations are not genotyped, which simulates families with missing founders (B, D, and F). Power was measured at α = 0.05 from 2,000 replications of simulations.

Comparison between RareIBD and Other Approaches when Founders Are Missing

The previous simulation framework, where all individuals in a family are genotyped, is an ideal scenario in real data but is often unlikely because of the inability to obtain DNA from some individuals in top generations. To mimic this scenario, we remove all individuals in the top two generations in all three family types and measure the FPR and power. In RareIBD, we assume that we know whether a variant is rare or common and hence know whether only one founder carries a mutation for each variant because it is not possible to know this information when some or all founders are missing. In real data, we use MAF estimated from several sources to determine whether a variant is rare or not.

RareIBD has a correct FPR when the top two generations are missing (Table 1). However, the burden approach from Pedgene and the CMC approach from FPCA, which had a correct FPR when everyone was genotyped, now have inflated FPRs. Results of the power simulation show that RareIBD offers a substantial power improvement over other approaches; our method achieves 20.9% and 16.2% higher power than the burden approach in wide and deep families, respectively, when c_i = 50% (Figures 1B and 1D). It is important to note that the burden approach has an inflated FPR, and its true power would be lower than one reported in Figure 1, meaning that the power improvement of our method would be higher.

Another important observation is that when we compare the power across methods for situations when all individuals are genotyped and when the top two generations are missing, power loss due to the missing individuals is much smaller in RareIBD than in other approaches for wide and deep families. For example, for c_i = 50%, RareIBD has 0.15% higher power in wide families and 2.6% lower power in deep families when the two generations are missing. However, power loss due to two missing generations in the burden approach is 7.4% and 4.2% for wide and deep families, respectively. This result is expected because the top two generations do not provide much information on how a causal allele is inherited and shared in extended families, which is the information that RareIBD uses to detect rare variants involved in a disease. Missing the top two generations, however, greatly reduces the power of other association approaches whose power depends on the overall number of individuals. In small families, both RareIBD and the burden approach suffer high power loss because removing the top two generations could eliminate half of the individuals in a family.

FPR of RareIBD when Two Rare Variants Are Present in a Family

One main assumption of our approach is that only one founder in a family carries a rare variant in a given gene. When all founders are genotyped, it is straightforward to check this assumption. When some founders are missing, we utilize MAF information estimated from several sources and assume that only one founder has a mutation if it is a rare variant according to the MAF information. However, in larger families, this assumption could be violated. In this simulation, we want to check FPRs of RareIBD when two founders have the same rare variant. We assume that the top two generations are missing, and each family has a 30% probability that two founders have a mutation for a rare variant. RareIBD knows which variants are rare but assumes that only one founder has a mutation for all rare variants.

Results show that our method has small inflation of test statistics in deep and small families (Table S2). At the α = 0.05 level, the FPR of RareIBD is 0.0528, 0.0585, and 0.0631 for wide, deep, and small families, respectively. The reason we have small inflation is because we estimate a p value by using the gene-dropping approach, which assumes that only one founder has a mutation. However, the inflation of test statistics of RareIBD is smaller than that of the burden approach, whose FPR is as high as 10% in small families. It is also very unlikely that two founders will have a mutation for 30% of rare variants, and we expect that this percentage is much lower in real data. Inflation of test statistics of RareIBD would then be small.

Comparison of Power for Protective Rare Variants

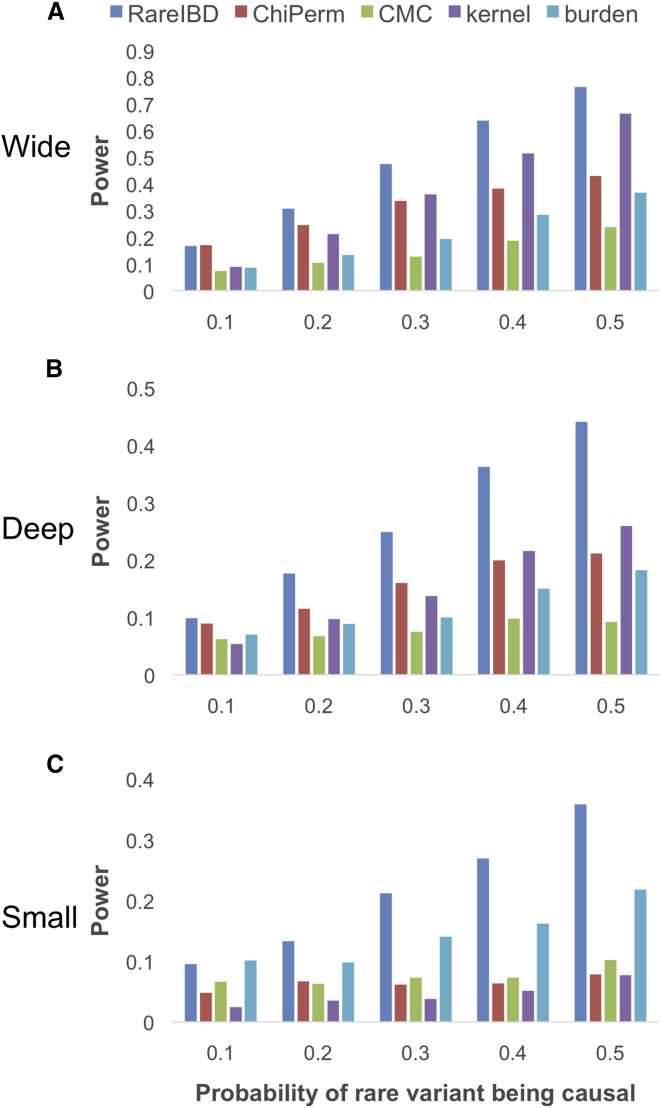
Previous simulations assumed that causal rare variants are all deleterious; the OR of causal variants is 2. To measure the power of RareIBD and other methods when protective rare variants are present in a gene, we generate simulations in which 40% of rare variants are protective with an OR of 0.25 and 60% of variants are deleterious with an OR of 4. The top two generations are missing in this simulation. It is known that the kernel approach from Pedgene, which is similar to SKAT,¹⁵ achieves high power when a gene has a mixture of deleterious and protective variants. Our results confirm this phenomenon given that the kernel approach has higher power than the burden approach in wide and deep families (Figure 2). Our method still outperforms the kernel approach in all families, and its power improvement over the kernel approach is substantial; RareIBD has 10% and 18.1% higher power than the kernel approach in wide and deep families, respectively. In small families, the kernel approach has lower power than RareIBD and the burden approach, most likely because of the limited information related to the small sample size in each family.

Figure 2.

Power Comparison between RareIBD and Other Approaches when Protective Variants Are Present

Pedigree structures include wide families (A), deep families (B), and small families (C) (Figure S1). In this simulation, 40% of rare variants are protective with an OR of 0.25, whereas 60% are deleterious with an OR of 4. We assume that individuals in the top two generations are not genotyped. Power was measured at α = 0.05 from 2,000 replications of simulations.

Application to EOCOPD and CFS Family Datasets

We applied RareIBD to two family datasets, EOCOPD and CFS, to analyze the COPD and sleep-apnea dichotomous traits, respectively. Whole-exome sequencing was performed on 347 individuals in extended families affected by EOCOPD, and microarray and exome chip were used for genotyping individuals in CFS families. The CFS includes two race groups, which we analyzed separately. We performed stringent QC and also used several methods to ensure no MEs or missing genotypes (see Material and Methods). After QC, both datasets contained no MEs and no missing genotypes. We considered only rare variants, defined as having a MAF less than 1% in any of several sources of allele-frequency information (see Material and Methods). Only genes with at least three rare variants were included in our analysis, and there were 12,092, 7,267, and 6,110 such genes in the EOCOPD, CFS-AA, and CFS-EA datasets, respectively. For RareIBD, to estimate p values of genes, we performed 10,000 gene-dropping permutations for all genes, one million permutations for genes with a p value less than 0.05, and 100 million permutations for genes with a p value less than 5 × 10⁻⁴. We also used PP2³⁸ to annotate variants and incorporate PP2 scores for missense variants into our weight. We present results with and without PP2 score weighting. Our frequency- and effect-size-based weights were applied to both approaches.

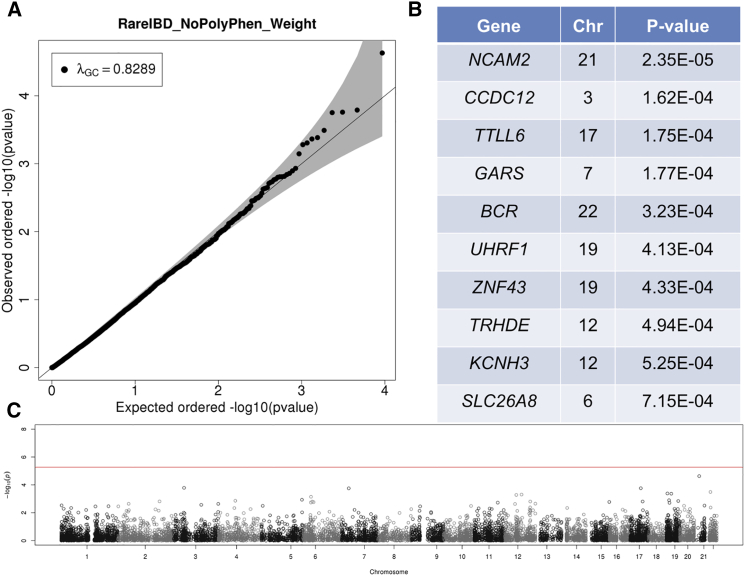
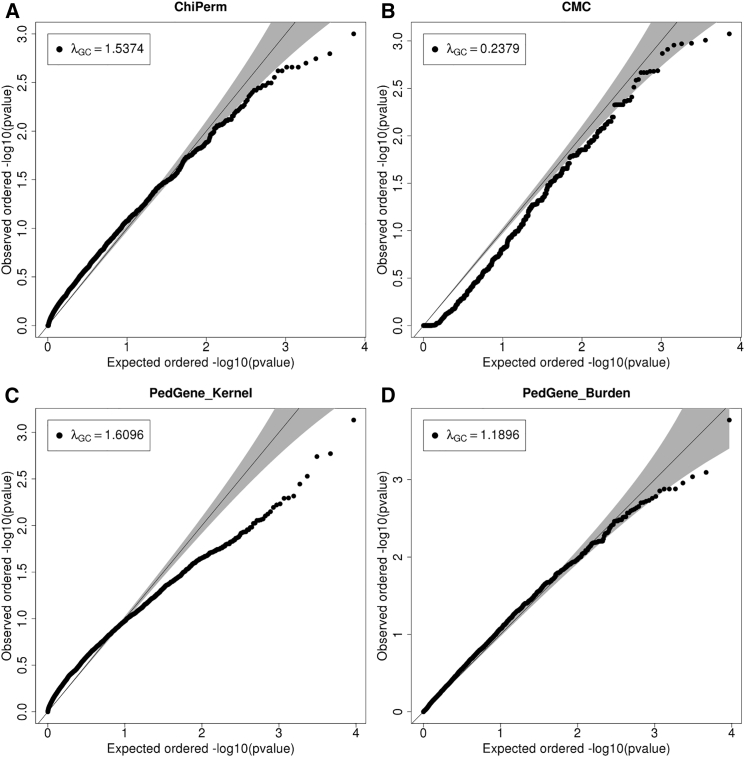
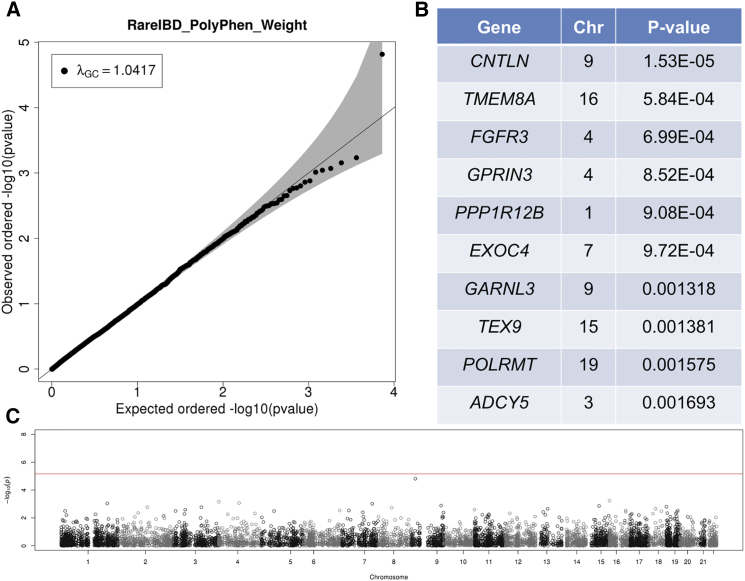
According to quantile-quantile (Q-Q) plots and inflation factors (λ_GC), RareIBD had a uniform distribution of p values in the EOCOPD dataset, although test statistics were modestly deflated both with PP2 weighting (λ_GC = 0.81; Figure S3A) and without weighting (λ_GC = 0.829; Figure 3A). This result is anticipated because of the relatively small sample size of the EOCOPD dataset (n = 303 after QC). However, other approaches had very severely inflated or deflated test statistics (Figure 4). For example, λ_GC values of the ChiPerm and CMC approaches from FPCA software were 1.537 and 0.238, respectively (Figures 4A and 4B), whereas the kernel approach from Pedgene was λ_GC = 1.61 with a very non-uniform distribution of p values according to its Q-Q plot (Figure 4C). The burden approach generated more uniformly distributed p values (Figure 4D), but its λ_GC was 1.19, which is somewhat high given the small sample size. None of the methods, including RareIBD, detected a significant gene in this dataset, although there was one gene close to a genome-wide significance level in RareIBD without PP2 weighting (Figures 3B and 3C).

Figure 3.

Results of Applying RareIBD without PP2 Weighting to Whole-Exome Sequencing Data of Extended Families in the EOCOPD Dataset

This dataset includes 347 individuals.

(A) Q-Q plot shows the distribution of p values of 12,092 genes that contain at least three rare variants, and it also indicates λ_GC values.

(B) Top ten genes with the most significant p values.

(C) Manhattan plot of p values along the chromosomes.

Figure 4.

Results of Applying FPCA and Pedgene to Whole-Exome Sequencing Data of Extended Families in the EOCOPD Dataset

Q-Q plots from ChiPerm of FPCA (A), CMC of FPCA (B), kernel approach of Pedgene (C), and burden approach of Pedgene (D). All Q-Q plots include λ_GC values.

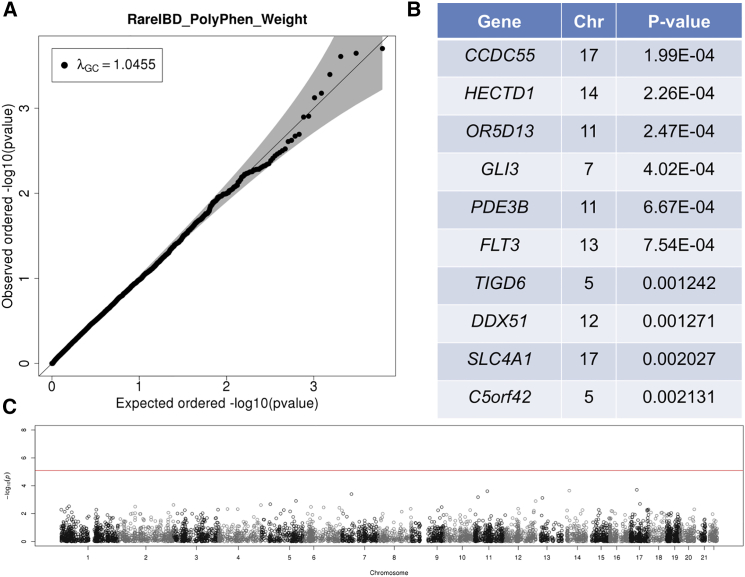
We then applied RareIBD to the CFS-AA dataset. p values of RareIBD followed the expected null distribution both with PP2 weighting (Figure 5) and without weighting (Figure S4). RareIBD with PP2 weighting found one chromosome 9 gene whose p value nearly reached the genome-wide significance level (Figures 5B and 5C), and this gene was also the top gene without PP2 weighting, although its p value was not as significant as one with weighting (Figures S4B and S4C). ChiPerm and CMC approaches had severely deflated test statistics (Figures S5A and S5B). There was one genome-wide-significant gene according to CMC, although this finding is most likely spurious given the non-uniform distribution of p values. The kernel approach from Pedgene had somewhat high inflation of test statistics (Figure S5C), whereas the burden approach generated uniformly distributed p values without inflation (Figure S5D). RareIBD had a similar distribution of p values and λ_GC values in the CFS-EA dataset (Figures 6 and S6). As with the CFS-AA dataset, ChiPerm and CMC showed deflation of test statistics in the CFS-EA dataset (Figures S7A and S7B). The kernel and burden approaches, however, had much higher λ_GC in the CFS-EA dataset than in the CFS-AA dataset (Figures S7C and S7D). Both approaches detected one gene whose p value was very close to the genome-wide significance level, but it could have been due to the highly inflated test statistics.

Figure 5.

Results of Applying RareIBD with PP2 Weighting to Microarray and Exome-Chip Data of CFS-AA Individuals

This dataset includes 632 individuals.

(A) Q-Q plot shows the distribution of p values of 7,267 genes that contain at least three rare variants, and it also indicates λ_GC values.

(B) Top ten genes with the most significant p values.

(C) Manhattan plot of p values along the chromosomes.

Figure 6.

Results of Applying RareIBD with PP2 Weighting to Microarray and Exome-Chip Data of CFS-EA Individuals

This dataset includes 710 individuals.

(A) Q-Q plot shows the distribution of p values of 6,110 genes that contain at least three rare variants, and it also indicates λ_GC values.

(B) Top ten genes with the most significant p values.

(C) Manhattan plot of p values along the chromosomes.

Robustness to Population Structure

There are two main scenarios in which population stratification can arise in families: the first is within families, and the other is between families. The first scenario is when founders in the same family are from different populations. For example, a majority of founders in a family have EA ancestry, whereas one founder has AA ancestry. In this scenario, the founder with AA ancestry could have more rare variants than other founders. Founders with multiple rare variants in a gene could violate the assumption of our gene-dropping approach that rare variants are independent because multiple rare variants in the same haplotype from the founder are inherited by the same set of non-founders, which creates perfect LD. These “duplicate” variants do not contribute to the overall statistic and could cause inflated test statistics. We avoid this problem by removing variants that are in perfect LD with another variant in a family and consider only one rare variant from such variants (see Material and Methods). This ensures the independence among rare variants in a family and correctness of our gene-dropping approach. To demonstrate the robustness of our approach to the within-family population structure, we performed simulations where we randomly selected one founder in each family and assigned four times more rare variants to this individual than other founders. We assumed that all individuals are genotyped and generated 10,000 replications for false-positive simulations. Results demonstrate that RareIBD has a correct or slightly higher FPR in the three pedigree structures (0.0502, 0.0557, and 0.0574 in the wide, small, and deep families, respectively). This simulation scenario, in which all families have one founder with four times more rare variants than other founders, is a somewhat extreme case. In real data, we expect that only a fraction of families will consist of founders with different ancestries and expect a smaller difference in the number of rare variants among founders. RareIBD will then have a more accurate FPR in small and deep families. Hence, population structure caused by founders with many more rare variants than other founders does not cause inflation of our test statistics.

Another scenario of population stratification is structure between families: this occurs when families with different ancestries are analyzed together. This, however, does not inflate our test statistic because our method can be thought of as a meta-analysis across many families. We estimate the Z score of each family on each rare variant and take a weighted sum of Z scores, similarly to the fixed-effects model of meta-analysis.⁵⁰ Because our statistic $\left(S_{\text{RareIBD}}^{ij}\right)$ is computed per family and not across whole families, our method does not suffer from population stratification across families. We demonstrated this by merging CFS-AA and CFS-EA datasets and applying RareIBD. Results show that our approach has a uniform distribution of p values even when two very different populations are merged and analyzed jointly (Figure S8). Therefore, estimating a statistic for each family independently, along with our LD-pruning procedure to remove perfectly correlated variants in a family, makes RareIBD robust to population structure both within and between families.

Discussion

We developed a general and powerful approach called RareIBD to identify a group of rare variants that influence disease susceptibility by utilizing extended families. Statistical power to detect an association of rare variants could be higher in family-based studies than in case-control studies because a causal rare allele could be enriched in extended families, which increases its allele frequency and hence the power to detect its effect. However, many of the currently available rare-variant methods for family-based analysis are not adequate for large extended families with binary traits because they are designed for small families or quantitative traits. We have shown in simulations that even methods that support large families with binary traits do not have correct FPRs when founders are missing. Also, to the best of our knowledge, no association methods for binary traits can be applied to extended families with only affected individuals. RareIBD is a very general approach that does not have any restrictions on how large families are, what types of traits are collected, whether founders are genotyped, or whether unaffected individuals are genotyped in families.

Another advantage of our approach is that it has accurate FPRs and remains powerful for detecting an association of rare variants even when some or many of the individuals in top generations of families are missing, which happens frequently in large extended families. In simulations where individuals in the top two generations were not genotyped, our method had a correct FPR, whereas other approaches had inflated FPRs. More importantly, in the same simulations, RareIBD did not suffer the large power loss that other methods experienced. Our method also had higher power than all other approaches when founders were genotyped. Our method gained additional power with the weighting schemes and the AllF approach. We weighted rare variants on the basis of both allele frequency¹³ and effect size³⁶ and used information from all founders to compute the Z score. For the real-data analysis, we included the functional information³⁸ of variants in our weights to incorporate the deleteriousness of genetic variants.

We compared our method to two existing software tools^{21, 33} that include FPCA, CMC, burden, and kernel approaches for rare variants. Another approach to analyzing a family dataset is the family-based association test (FBAT), which computes its statistic by considering each offspring separately and conditioning on parent genotypes. For an extended pedigree, the FBAT splits a family into several trios and computes its statistic from these trios. Our method, however, considers a whole family in our statistic and captures the inheritance pattern of a casual allele among all affected and unaffected individuals in a family. This means that our approach is likely to be more powerful than the FBAT in a large family because RareIBD fully utilizes information of an extended pedigree structure, whereas the FBAT uses limited information captured in trios. Also, the FBAT cannot be applied if parents are not genotyped, and RareIBD does not have this restriction. For example, the wide and small families in our simulation do not have any parents genotyped if the top two generations are missing, and one cannot use the FBAT for these families. Therefore, the fact that the FBAT requires parents to be genotyped limits its applicability in an extended pedigree.

We applied RareIBD to two family datasets. Although our method did not find significant genes in either dataset, it identified two genes very close to genome-wide significance levels, which will require further validation. The lack of significance might be because the sample size in the EOCOPD dataset is small, and for the CFS dataset, exome chip might not capture all rare variants present in a family. However, importantly, we observed that similar to our simulations, our method consistently generated uniformly distributed p values that followed the expected null distribution, whereas other methods had highly inflated or deflated test statistics.

Our method is inspired by non-parametric linkage (NPL) analysis, which finds IBD sharing among affected relative pairs (S_pairs) or among all affected relatives (S_all).⁵¹ One major difference between RareIBD and NPL is that we assume that only one founder has a rare minor allele, and our method is interested in finding IBD sharing of this minor allele among affected relatives, whereas NPL is more general such that it considers all founder alleles. NPL, however, requires computationally expensive operations to estimate IBD sharing, and it is often not scalable to large extended families. In contrast, when only one founder has the rare allele, any non-founders who have this allele share it identically by descent, which greatly simplifies estimation of IBD sharing. This enables RareIBD to compute its statistic efficiently and, moreover, to evaluate the significance of its statistic by using the gene-dropping approach, which generates very accurate p values. Because the standard gene-dropping approach is prohibitively computationally expensive, we took advantage of our main assumption and considerably increased the approach’s efficiency. With this improvement, we were able to apply RareIBD to the two family datasets on a genome-wide scale without computational difficulty.

The main assumption in our approach is that only one founder in a family has a mutation for a rare variant. It is important to note that a family can have multiple rare variants in a gene. For a specific rare variant, however, we assume that the rare allele is inherited from only one founder. This assumption might fail in rare circumstances. Our simulations showed that RareIBD had slightly inflated statistics when the assumption was violated for a subset of rare variants. We note that test statistics of other approaches were more inflated than those of our method. To protect against this issue, our software checks for violations of our assumptions. For example, our software checks whether any nonfounder carries two copies of a rare allele. Also, we check whether any unrelated individuals in a family share the rare allele. In these cases, there must be more than one founder with the rare allele, and hence this variant is not included in our analysis. In the presence of consanguinity, a non-founder might have two copies of a rare allele, although only one founder carries one copy of the allele. We remove this variant from analysis because when founders are missing, it is not known whether a non-founder has two alleles as a result of consanguinity or as a result of two founders with a rare variant. Another approach to ensuring that only one founder carries a mutation is to impute missing founders with family imputation software such as GIGI.⁵² Although this approach is not very accurate for individuals who are not genotyped, it could provide additional information to confirm whether our assumption holds.

Before our method is applied to real data, one important requirement is that genotype data should contain no MEs or missing genotypes. Although some MEs might be de novo mutations, they are extremely rare, and most MEs represent genotyping errors. These requirements allow greater computational efficiency. Before performing the gene-dropping approach, we pre-compute the mean and SD of our statistic for all founders. During this process, we assume that genotyped individuals have no missing genotypes. This requirement for no MEs or missing genotypes can be met without difficulty by one of several statistical approaches developed to refine genotypes on the basis of pedigree structure. For example, Polymutt²³ can correct a majority of MEs and impute missing genotypes for sequencing data. For microarray data, ShapeIt⁴⁹ phases genotypes by using family information and imputes missing genotypes. This requirement also increases the quality of genotype data and reduces the chance of detecting false associations.

We have designed several enhancements in RareIBD, including applicability to families with only affected individuals. Some family studies⁵³ focus mostly on affected individuals because NPL statistics do not require genotypes of unaffected individuals. Therefore, it is important that a method for family-based studies can be applied to affected-only families. We tested our method for affected-only families by performing simulations in which everyone was genotyped and found that it had correct FPRs in all three families (Table S1). The power of the affected-only approach is, however, lower than that of RareIBD, which uses both affected and unaffected individuals (Figure S2). This is expected because unaffected individuals also provide important information regarding IBD sharing. We tested other approaches on affected-only families, but either they failed to generate p values or they generated p values that were not available, 1, or infinity. This result indicates that our method can identify a gene with rare variants involved in a disease from affected-only families in a sample of sufficient size. In addition, our method is robust to population structure. We have shown that population structure both within and between families does not cause inflation of test statistics.

Published: September 22, 2016

Web Resources

• 1000 Genomes, http://www.1000genomes.org

• ExAC Browser, http://exac.broadinstitute.org/

• NHLBI Exome Variant Server (ESP) Exome Variant Server, http://evs.gs.washington.edu/EVS

• RareIBD, http://genetics.bwh.harvard.edu/rareibd/

• RareIBD, Jae Hoon Sul lab, http://jaehoonsullab.semel.ucla.edu/rareibd/