Summary of Human Ankle Mechanical Impedance During Walking

Abstract

The human ankle joint plays a critical role during walking and understanding the biomechanical factors that govern ankle behavior and provides fundamental insight into normal and pathologically altered gait. Previous researchers have comprehensively studied ankle joint kinetics and kinematics during many biomechanical tasks, including locomotion; however, only recently have researchers been able to quantify how the mechanical impedance of the ankle varies during walking. The mechanical impedance describes the dynamic relationship between the joint position and the joint torque during perturbation, and is often represented in terms of stiffness, damping, and inertia. The purpose of this short communication is to unify the results of the first two studies measuring ankle mechanical impedance in the sagittal plane during walking, where each study investigated differing regions of the gait cycle. Rouse et al. measured ankle impedance from late loading response to terminal stance, where Lee et al. quantified ankle impedance from pre-swing to early loading response. While stiffness component of impedance increases significantly as the stance phase of walking progressed, the change in damping during the gait cycle is much less than the changes observed in stiffness. In addition, both stiffness and damping remained low during the swing phase of walking. Future work will focus on quantifying impedance during the “push off” region of stance phase, as well as measurement of these properties in the coronal plane.

Only recently have researchers been able to quantify how the mechanical impedance of the ankle varies during walking. This communication unifies the results of the first two studies measuring ankle mechanical impedance in the sagittal plane during walking, where each study investigated differing regions of the gait cycle. Rouse et al. measured ankle impedance from late loading response to pre-swing, where Lee et al. quantified ankle impedance from initial swing to early loading response. While the stiffness component of impedance increases significantly as the stance phase of walking progresses, the change in damping during the gait cycle is much less than the changes observed in stiffness.

Download video file ^{(2.2MB, mp4)}

I. Introduction

Biped walking is mechanically unstable. Feedback control may actually increase rather than decrease instability due to the inherent time-delay in the neural close-loop control. Stability might be achieved instead by controlling mechanical impedance [1], [2]. We focused on measuring the mechanical impedance of the ankle during walking because the ankle is critical for propulsion, shock absorption, and balance during standing and walking. The ankle is the largest source of mechanical power during terminal stance [3]. The ankle plantarflexors contribute as much as 50% of positive mechanical work in a single stride to enable forward propulsion [4]. In pre-swing, ankle plantarflexors also act to advance the leg into swing phase while promoting knee flexion at toe-off [5]. Additionally, the ankle helps maintain body-weight support during gait and balance [6], [7]. Finally, the ankle dorsiflexor musculature helps absorb impact forces during foot strike to enable controlled landing and foot-floor swing clearance at toe off.

Extensive previous work estimating ankle impedance has provided a rich characterization of these properties during stationary, non-moving conditions [8]–[14]. When investigated in the sagittal plane, ankle joint impedance has been shown to vary with many factors, including mean ankle torque, ankle position, perturbation amplitude, and muscle fatigue [8]. The research showed that modulation of these factors can vary the stiffness component of impedance by up to three orders of magnitude. Few studies have focused on characterizing ankle impedance during non-stationary conditions, which are more relevant to locomotion. These studies use changes in ankle torque or position in combination with time-varying system identification techniques to estimate ankle impedance [15]–[17]. Rather than using a perturbation, researchers have instead focused on measuring the instantaneous slope of the ankle’s torque-angle profile during locomotion, known as the “quasi-stiffness” [18], [19]. These studies has provided important insight into how torque and angle co-vary at a joint during locomotion [20]. However, because the agonist and antagonist muscles that cross human joints are capable of producing net-positive mechanical work, joint torque and angle can be varied independently of joint stiffness. Thus, there is no causal relationship between quasi-stiffness and joint impedance [19], and these concepts are decoupled. Ultimately, a perturbation is required to assess the joint impedance that characterizes the underlying system dynamics.

The mechanical impedance of the human ankle plays a critical role in locomotion, and has broad applications in assistive technologies, such as robotic prostheses and exoskeletons, as well as humanoid robotics [21]. For the first time, the previous studies have been merged to provide a comprehensive representation of how joint impedance varies throughout the entire gait cycle. Specifically, we have examined the work of Lee and Hogan [24] and Rouse et al. [23] to characterize ankle impedance from pre-swing to terminal stance. The purpose of this study is to show how ankle impedance varies throughout the gait cycle, and discuss the implications of the results in the context of the whole gait cycle. This study motivates many changes in the development of future assistive technologies, as well as a new understanding of neuromuscular pathologies, and the neural mechanisms that underlie these disorders.

II. Methods

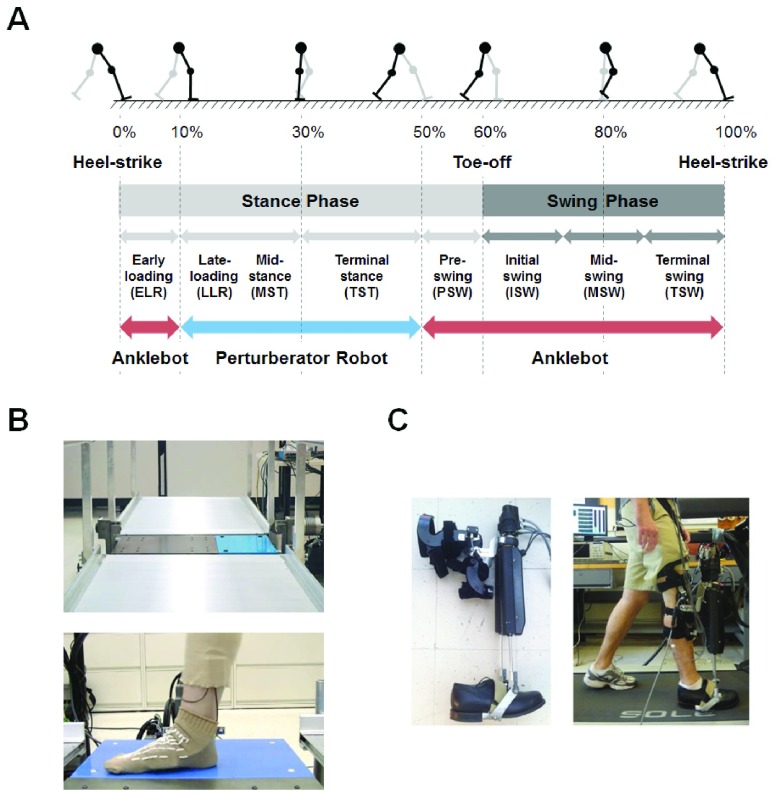
Two different approaches were used to construct a trajectory of ankle impedance modulation during walking. A mechatronic platform and a wearable ankle robot were utilized to quantify ankle impedance from late-loading response to terminal stance phase and from pre-swing phase to early-loading response, respectively (Fig. 1A). Brief descriptions on each approach are as follows.

FIGURE 1.

Two robotic platforms to estimate ankle impedance during walking. A: From late-loading response to terminal stance phase, i.e, when the foot was flat to the ground, ankle impedance was estimated by a mechatronic platform, recessed into a walkway (B). From pre-swing phase through the entire swing phase to early-loading response, i.e, when the toe and/or heel were off the ground, ankle impedance was estimated by a wearable ankle robot (C). B: The Perturberator robot was comprised of a force platform coupled to a gear-motor that was controlled by a servodrive and microcontroller. C: The Anklebot was mounted onto the knee brace and its end-effectors were connected to a rigid U-shaped bracket attached to the bottom of a shoe (left). The robot was properly attached to the subjects’ right leg, and subjects were instructed to walk on a treadmill with the robot (right).

A. Ankle Impedance Estimation from Late-Loading Response to Terminal Stance Phase

1). Apparatus

Joint impedance was estimated using perturbations and data recorded from a mechatronic platform, termed the Perturberator Robot (Fig. 1B), validated and previously described in detail in [22]. The mechatronic platform was comprised of a multi-axis force platform coupled to a gear-motor that received position commands from a servodrive and microcontroller. The mechatronic platform was recessed into a walkway and the platform section of the robot was flush with the walkway surface. The total length of the walkway was 5.25 m.

2). Experimental Protocol

Ten healthy, able-bodied subjects participated in this experimental protocol. Subjects’ right ankles were instrumented with an electrogoniometer that recorded ankle angle. Subjects walked at a self-selected pace that ranged from 85 – 90 steps per minute across the walkway that included the recessed mechatronic platform. When subjects stepped on the mechatronic platform, a 2.0° ramp perturbation was randomly applied with a probability of 50% in either the dorsiflexion or plantarflexion directions. The duration of the ramp part of the perturbation was 75 ms. One hundred perturbation trials were recorded at each timing point, and approximately 400 trials were recorded where no perturbation occurred, totaling approximately 800 walking trials. Subjects were encouraged to rest after every 40 perturbation trials. Perturbations were applied at four timing points, ranging from 20–70% of the stance phase of walking, chosen randomly during each trial. The mid-stance region of stance phase was chosen because it is a critical part of the gait cycle when the body is supported by a single leg. Additionally, during mid-stance, the perturbation caused changes in the ankle’s angle, rather than deformations of the mid-foot, improving the accuracy of our estimation.

3). Estimation Methods

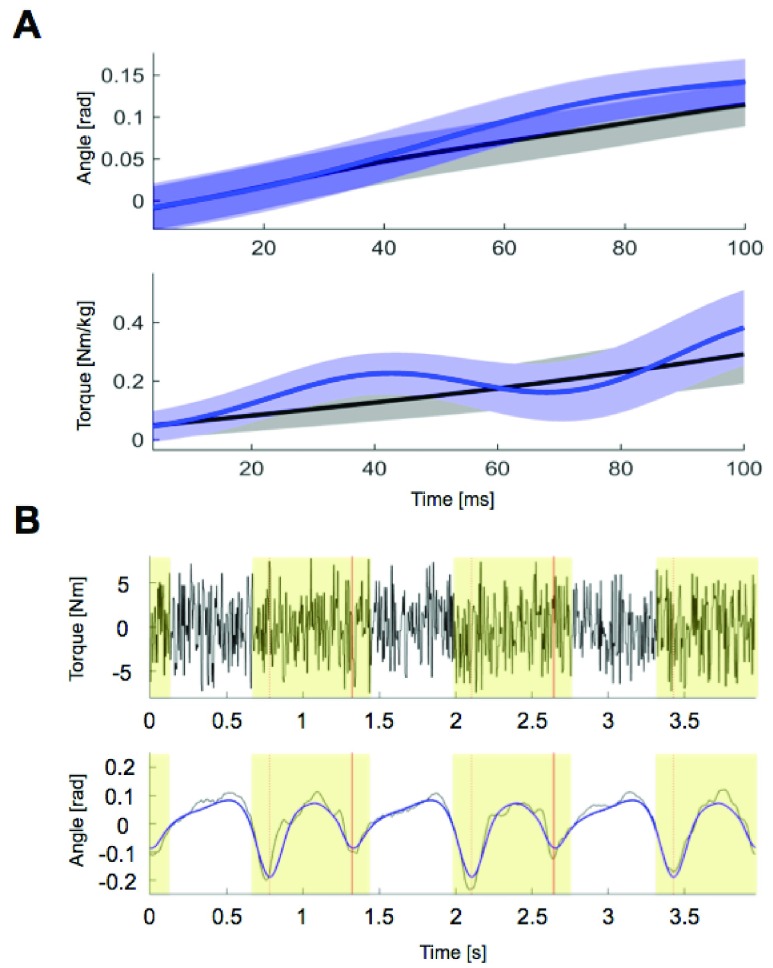
Data were low-pass filtered at 20 Hz and segmented to include the 100 ms window beginning with the perturbation onset. To obtain ankle torque, ground reaction force data were resolved to the equivalent force-torque couple at the ankle’s center of rotation. The ankle’s center of rotation was identified from high-definition video obtained during the experiment. A second-order model consisting of stiffness, damping, and inertia was used to estimate ankle impedance. The stiffness, damping, and inertia describe the position, velocity, and acceleration dependent components of response torque, respectively. Prior to estimation, a bootstrapping procedure was used to provide a more reliable estimate of the parameter variability. The bootstrapping procedure involved included the following steps: a random selection of 60% of the torque and angle profiles from perturbed trials were chosen and averaged. The mean non-perturbed torque and angle profile (Fig. 2A black lines) was then subtracted from the mean of the perturbed torque and angle profiles (Fig. 2A blue lines), resulting in the profiles caused by the perturbation alone. The joint impedance was then estimated from these resultant profiles using the optimal least squares estimate [25], with a constraint that the estimated parameters be greater than zero. This process was repeated one hundred times for each perturbation direction and time point. In summary, the purpose of the bootstrapping procedure was to remove the torque and angle changes that occurred simply as a result of walking, while preserving the variability of the parameter estimates that were subsequently obtained.

FIGURE 2.

Samples of inputs and outputs for the estimation of ankle impedance. A: Data during the analysis window (100 ms) from the Perturberator Robot. Time window begins with onset of the perturbation. Black: non-perturbed, Blue: perturbed. B: Sampled measurements from the Anklebot (3 gait cycles). Random torque inputs (top) and the corresponding angles (black curve - blue curve; bottom). The blue curve is the nominal angle trajectory. Only the data in the shaded region (from pre-swing phase to early-loading response) were used. Red bars represent heel-strike.

The aforementioned methods that were used to estimate ankle impedance during locomotion were previously validated and shown to provide highly accurate estimates of ankle stiffness [24]. The stiffness of a passive prosthetic foot was estimated during locomotion at four time points and compared to values obtained independently using a materials testing machine. The stiffness component of impedance was shown to be accurate within 5% on average during walking.

A correction has been applied to the data from [23], which updated the inertia estimates. The stiffness and damping values did not change significantly, however, the data presented here reflect the updated values.

B. Ankle Impedance Estimation from Pre-Swing Phase to Early-Loading Response

1). Apparatus

A wearable ankle robot, Anklebot, was used to estimate ankle impedance from pre-swing phase before toe-off to early-loading response right after heel-strike. The robot was designed to have very low intrinsic mechanical impedance at the interaction port, i.e, the ankle [11]. This made possible highly back-drivable operations, allowing subjects to have movements with minimal resistance. The robot was mounted onto the knee brace and its end-effectors were connected to a rigid U-shaped bracket attached to the bottom of a shoe.

2). Experimental Protocol

Thirteen healthy, able-bodied subjects participated in this experimental protocol. The robot was properly attached to the subjects’ dominant leg, and subjects were instructed to walk on a treadmill to familiarize themselves with the experimental setup and select their preferred walking speed. In a main experiment, subjects walked with the Anklebot on a treadmill for 13 minutes while the robot continuously applied mild random torque perturbations (band-limited white noise with stop frequency 100 Hz) to the ankle. The magnitude of perturbations was determined low enough not to disturb normal walking but strong enough to perturb the ankle. The resulting ankle displacements due to the mild perturbations were 1.6° (root-mean-square value) and −4.1° −3.9° (peak-to-peak value; negative and positive denote plantarflexion and dorsiflexion, respectively) when averaged across subjects.

3). Estimation Methods

Ankle impedance was estimated based on ensemble-based linear time-varying system identification. This is an effective and robust system identification technique when repetitive and periodic data are available. In this study, more than 500 realizations for ensemble sets were generated from human walking, where each realization was defined by a gait cycle that begins with heel-strike of one foot and ends with another heel-strike of the same foot. Input and output ensemble sets contain torque perturbations (Fig. 2B top) and the resulting ankle displacements (Fig. 2B bottom), respectively. By applying correlation-based system identification approach [17] to the ensemble sets, measured dynamics were estimated along the time axis (at 2 ms intervals) in the form of finite impulse response functions (IRF). The IRF estimates were further approximated by second order models consisting of inertia, damping, and stiffness. Finally, ankle parameters (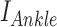, , 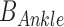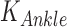) were obtained by compensating actuator dynamics. As the ankle and the robot share the same displacement, ankle impedance was calculated by subtracting impedance of the robot (also approximated as a second order model consisting of inertia, damping, and stiffness) from the measured impedance [9]. While impedance was estimated every 2 ms, representative ankle parameters were calculated at five sub-gait phases, ranging from 0–10% (early-loading response: ELR), 50–60% (pre-swing phase: PSW), 60–73% (initial swing phase: ISW), 74–86% (mid-swing phase: MSW), and 87–100% (terminal swing phase: TSW) of the gait cycle by averaging estimated parameters within each sub-gait phase into single values. Detailed descriptions of the methods and validation are provided in [22].

III. Results

A. Ankle Impedance Modulation Across a Gait Cycle

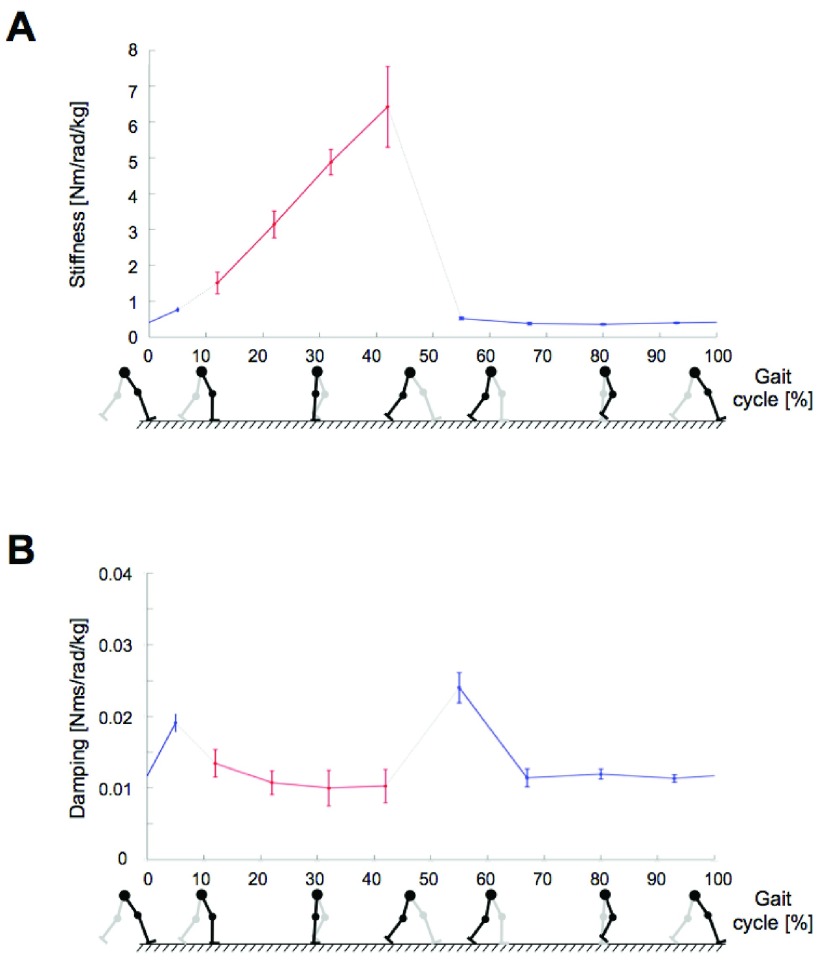
Based on the aforementioned two methods, ankle impedance was estimated for the whole gait cycle. Time-varying ankle stiffness and damping were summarized at nine timing points (Fig. 3). First, ankle stiffness linearly increased from loading response to terminal stance; the correlation coefficient (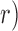 between the gait phase and the corresponding ankle stiffness was 0.998. Ankle stiffness substantially decreased at the end of the stance phase, remained relatively constant through the entire swing phase, and increased again around heel-strike (Fig. 3A). Stiffness in the swing phase was comparable with results from a previous steady-state study of matched muscle activation [10]. The change in damping during the gait cycle is much less than the changes observed in stiffness (Fig. 3B) – stiffness: 0.35–6.42 Nm/rad/kg, damping: 0.010–0.024 Nms/rad/kg. The inertia estimates were different depending on the measurement methods. Inertia estimates by the Anklebot were rather invariant throughout the gait phase around 0.008 kgm², consistent with previous findings [26], [27]. Although also generally invariant throughout the gait cycle, inertia estimates by the Perturberator Robot were approximately 0.027 kgm², differing by a factor of three. This is likely a result of residual inertia of the mechanism structure and other coupled body segments.

FIGURE 3.

Time-varying ankle mechanical impedance during walking.Ankle stiffness and damping were summarized at nine timing points. The stance and swing phases account for approximately 60% and 40% of the gait cycle. Ankle stiffness (A) and damping (B) were normalized by bodyweight. Red and blue colors denote results from the Perturberator Robot and Anklebot, respectively. Dashed black lines indicate the regions where no results were available. Asterisks and error bars denote the mean and standard error, respectively.

The quality of estimation by second order models was demonstrated by high percentage variance accounted for (%VAF) between measurements and estimates by the models. When averaged across subjects and timing points from late-loading response to terminal stance phase, the %VAF between torque measurements and estimates by second order models was 92±6.3% (mean±standard deviation). For timing points from pre-swing phase to early-loading response, the %VAF between angle measurements and predicted outputs by input torques and estimated second order models was 85.7±4.5%.

IV. Discussion

For the first time, we were able to provide an estimate of the ankle impedance in the sagittal plane during the complete gait cycle. We demonstrated that the stiffness and damping do not remain constant. Especially, stiffness increases from heel strike to terminal stance, remaining low during the swing phase. This modulation of ankle mechanical impedance parallels functional need to prevent foot slap following heel strike, increase stability demands during stance and metabolic savings during the swing phase. It goes beyond coarse correlations between anthropometric measures with intrinsic ankle [28] or prior studies showing that humans adjust leg stiffness to accommodate surface changes [29]. We speculate that proper modulation of ankle impedance is part of the learning process of human biped walking and it is an important aspect when assessing neurological deficits, aging, and determining proper therapeutic interventions as well as designing prosthetics.

This study highlights the need to incorporate joint impedance in the design of future wearable robotic technologies, including prostheses and exoskeletons. Historically, the development of wearable robotic technologies has only used the torques and angles of lower limb joints to define the design criteria, and accompanying metrics of success [30]–[32]. However, the present study demonstrates that joint impedance is also regulated during gait, and must be included in the future design and control of wearable robotic systems that can truly mimic the system dynamics of the healthy neuromuscular system. The impedance control law proposed in Rouse et al. has been implemented in a robotic prosthetic leg, which led to more natural locomotor behavior in amputees [33]. Additionally, a quasi-passive prosthetic ankle has been developed that can provide the natural joint impedance relationship during gait [34], which will be soon be tested in amputees.

Because impedance is at the interface between the neural controller and the world, we further speculate that inappropriate impedance may interfere with neuro-recovery process. One implication of our working model is that restoring appropriate impedance occurs concurrently with recovery. In a preliminary study Krebs and colleagues found that the ankle quasi-stiffness of neurologically impaired subjects was significantly different from that of age-matched healthy subjects [28], [35]. They also found that seated (‘open-chain’) robot-aided therapy successfully resolved this abnormality and—most important—this therapy resulted in a 20% improvement of over-ground walking speed [36]. The identification techniques described here will allow rehabilitation therapy to be targeted toward the specific deficits in the mechanical impedance and its modulation that each individual exhibits. We will alter the adaptive algorithm developed in 2003 to compensate also for impedance abnormalities [37]. It will include time-varying impedance that depends on arm reaching or gait phase and aims to normalize the patient’s impedance with respect to unimpaired impedance (suitably scaled).

While the stiffness and quasi-stiffness are distinct entities in general [19], linearly increasing stiffness from loading response to terminal stance in this study are remarkably similar to those from the slope of the ankle’s torque-angle profile [23], which was not previously known. However, despite their similar magnitudes, the joint stiffness and quasi-stiffness have different meanings and, therefore also different interpretations. Moreover, we do not yet know if these properties are similar for other joints or regions of the gait cycle. Future work will focus on potential mechanisms that underlie this behavior.

The methods used to identify ankle impedance rely on several assumptions. Most notably, the identification procedures assume a linear, time-invariant behavior of the ankle within a short period of time; the procedure with the Perturberator Robot used data within the 100 ms window beginning with the perturbation onset, and the procedure with the Anklebot used data within the 40 ms window for IRF estimation [22]. Furthermore, the system structure was assumed to be second order, consisting of stiffness, damping and inertia. The rationale for this assumption was based on previous findings that the human ankle was accurately described as a second order system over a wide range of ankle positions and muscle activation [8], [10]. Even with these assumptions, the methods were valid under the given experimental conditions, supported by the high %VAF between measurements and predicted outputs across the gait cycle.

This study used two distinct approaches to complete a trajectory of ankle impedance modulation throughout the gait cycle. To estimate ankle impedance, we should apply external energy to the ankle and analyze the corresponding responses. In the entire swing phase and when the toe or heel were off the ground, a wearable device is proper to provide accurately controlled perturbations to the ankle. However, when weight bearing is substantial during stance phase, i.e., when the foot was flat to the ground, a wearable device is less desirable. Due to high weight bearing, mild perturbations are not strong enough for the purpose of identification. Strong perturbations from the wearable device are not desirable either; they will significantly change the normal gait or may cause slippage at the interface of the lower-limb and the device. On the other hand, a robotic platform recessed into a walkway can provide strong perturbations to the ankle without disturbing the normal gait. However, this approach can be used only when solid contact exists between the foot and the device. Thus, we would argue that the current best practice to estimate ankle impedance across the full gait-cycle could be achieved through the combination of two distinct experimental setups: a wearable ankle device and an instrumented walkway.

It is important to discuss the effects of the added mass on gait. The Anklebot used in this study weighs 3.6 kg [11]. However it is important to note that the robot is not mounted at the ankle, but mounted proximally to the leg and anterior to the shank to minimize perception of loading [38]. We further examined the effects of asymmetric or unilateral loading of the limb during task-oriented gait in adults both healthy and stroke (9 chronic stroke patients) [39]. Specifically, we sought to assess the effects of the added inertia and friction of unpowered ankle robot on gait parameters, interlimb symmetry, and lower extremity joint kinematics. In summary, our results demonstrated that the added inertia anterior to the shank (above knee) had no statistically significant effect on spatiotemporal parameters of gait, including paretic and nonparetic step time and stance percentage, in both overground and treadmill conditions. Noteworthy, interlimb symmetry as characterized by relative stance duration was greater on the treadmill than overground regardless of loading conditions.

The current study utilized a treadmill in estimating ankle impedance from pre-swing phase to early-loading response. The primary reason for this is to minimize the duration of the experiment in a limited space. We collected more than 500 gait cycles in 15 minutes of treadmill walking. In fact, it is possible to extend the current study to overground walking. One recent study has demonstrated that the Anklebot could be well used for overground walking [40]. Since dynamics of treadmill walking may be significantly different from those of overground walking, it is important to compare the modulation of ankle impedance in these two conditions.

As a limitation of this study, the analysis methods presented do not attempt to separate intrinsic and reflex components of joint impedance. However, it is presumed that impedance measurements by both systems are dominated by the intrinsic components of the ankle joint, supported by the time course of short latency reflexes that occur approximately 40 ms following the onset of an imposed movement [41], [42] and an additional 60 ms delay in subsequent force production [43], [44]. It was also demonstrated that the influence of random perturbations by the Anklebot on muscle activity is small; the change of muscle activation due to perturbations was less than 0.5% MVC of each of the major ankle muscles [22]. Together, it is presumed that reflex contribution to ankle impedance measurements is minimal in this study.

This study lays the groundwork for various future studies. The current results are limited to the characterization of ankle impedance in the dorsi-plantarflexion direction. We plan to expand this work and measure healthy young subjects’ ankle mechanical impedance in all 2-D directions during walking, including dorsi-plantarflexion and inversion-eversion directions. We will employ the Anklebot described above and the MIT-Skywalker [45] or a new multi-axis robotic platform [46] during stance to implement in 2-D what the Perturberator Robot did in 1-D. In addition, it is possible to extend the current study to characterize ankle impedance in different walking conditions, such as walking in different speeds and slopes.

Biographies

Hyunglae Lee (M’13) received the B.S. (summa cum laude) and M.S. degrees in mechanical engineering from Seoul National University, Seoul, in 2002 and 2004, respectively, and the Ph.D. degree in mechanical engineering with the Massachusetts Institute of Technology in 2013. He is an Assistant Professor with the School for Engineering of Matter, Transport, and Energy, Arizona State University, and the Director of Neuromuscular Control and Human Robotics Laboratory. He worked as a Post-Doctoral Fellow with the Sensory Motor Performance Program, Rehabilitation Institute of Chicago (RIC). He also worked at the Korea Institute of Science and Technology from 2006 to 2008 and LG Electronics from 2004 to 2006 as a Researcher in the field of human-computer interaction, human-robot interaction, and mechanical design. His current research interest includes physical human-robot interaction, rehabilitation robotics, and neuromotor control. He is a recipient of Samsung Scholarship and has been awarded the 2014 Sarah Baskin Award for Excellence in Research (first place) from RIC.

Elliott J. Rouse (S’10–M’12) received the B.S. degree in mechanical engineering from The Ohio State University, Columbus, OH, USA, in 2007, the M.S. and Ph.D. degrees in biomedical engineering from Northwestern University, Evanston, IL, USA, in 2009 and 2012. Subsequently, he joined the Massachusetts Institute of Technology (MIT), Cambridge, MA USA, where he was a Post-Doctoral Fellow with the Biomechatronics Group, MIT Media Lab, until 2014. He is an Assistant Professor with the Department of Physical Medicine and Rehabilitation, Northwestern University, with appointments in the Department of Mechanical Engineering and Department of Biomedical Engineering, Northwestern University. He directs the Neurobionics Lab in the Center for Bionic Medicine at the Rehabilitation Institute of Chicago, Chicago, IL, USA. His current research focuses on understanding locomotion through the lens of system dynamics and control and how pathology affects these dynamics. The goal of this understanding is to develop a new class of wearable robotic technologies that impact the lives of the disabled. Applications include robotic prostheses, exoskeletons, and technologies that augment human motor performance. He serves as an Associate Editor for the journal Assistive Technology.

Hermano Igo Krebs (F’14) joined the Mechanical Engineering Department, Massachusetts Institute of Technology, in 1997, where he is a Principal Research Scientist and Lecturer with the Newman Laboratory for Biomechanics and Human Rehabilitation. He also holds an affiliate position as an Adjunct Professor at Department of Neurology, University of Maryland School of Medicine, and as a Visiting Professor at the Department of Physical Medicine and Rehabilitation, Fujita Health University; Institute of Neuroscience, Newcastle University; and Department of Mechanical Science and Bioengineering, Osaka University. He is one of the Founders and Chairman of the Board of Directors of Interactive Motion Technologies, a Massachusetts-based company commercializing robot technology for rehabilitation. He was nominated by two of the IEEE societies: the IEEE Engineering in Medicine and Biology Society and the IEEE Robotics and Automation Society to this distinguished engineering status for contributions to rehabilitation robotics and the understanding of neuro-rehabilitation. He has published and presented extensively on rehabilitation robotics. His work goes beyond Stroke and has been extended to Cerebral Palsy for which he received The 2009 Isabelle and Leonard H. Goldenson Technology and Rehabilitation Award, from the Cerebral Palsy International Research Foundation. In 2015, he received the IEEE-INABA Technical Award for Innovation leading to Production for contributions to medical technology innovation and translation into commercial applications for Rehabilitation Robotics. His goal is to revolutionize the way rehabilitation medicine is practiced today by applying robotics and information technology to assist, enhance, and quantify rehabilitation.

Funding Statement

This work was supported in part by NIH under Grant R01 HD069776, the Toyota Motor Corporation’s Partner Robot Division, Samsung Scholarship, the U.S. Army Telemedicine and Advanced Technology Research Center under Award W81XWH-09-2-0020, the NIH National Institute of Neurological Disorders and Stroke under Award F31NS074687, and the National Institute of Child Health and Human Development under Award T32HD007318.