Ccoffinn: Automated Wave Tracking in Cultured Cardiac Monolayers

Abstract

Cardiac arrhythmias are one of the most frequent causes of death worldwide. A popular biological model used to study arrhythmogenesis is the cultured cardiac cell monolayer, which provides a good trade-off between physiological relevance and experimental access. Excitation wave patterns are imaged using high-bandwidth detectors, producing large data sets that are typically analyzed manually. To make such analysis less time consuming and less subjective, we have designed and implemented a toolkit for segmentation and tracking of cardiac waves in optical mapping recordings. The toolkit is optimized for high-resolution detectors to accommodate the growing availability of inexpensive high-resolution detectors for life science imaging applications (e.g., scientific CMOS cameras). The software extracts key features of propagating waves, such as wavefront speed and entropy. The methods have been validated using synthetic data, and real-world examples are provided, showing a difference in conduction velocity between two different types of cardiac cell cultures.

Introduction

Cardiac arrhythmias such as ventricular or atrial fibrillation are a major factor in the occurrence of cardiac arrest, one of the most frequent causes of death worldwide, claiming 300,000–400,000 deaths annually in the United States alone (1). Despite recent advances and decades of research, a precise insight into the mechanics of fibrillation is lacking (2). A popular experimental model of arrhythmogenesis, or, more generally, signal propagation in excitable media, is cultured cardiac monolayers (CCMs) (3). CCMs can be grown in a controlled manner, allowing for manipulation of their spatial and functional organization. For example, CCMs can give insight into the origins of reentrant waves and can be used to determine conditions that allow different wave topologies to occur (4). Despite being structurally different from in vivo tissue, CCMs remain popular models of cardiac conduction due to their simplicity, controllability of growth, and ease of experimental access due to very little movement of the tissue and the absence of deep 3D structure. CCMs therefore allow researchers to perform experiments that would not be practical in vivo.

Optical mapping techniques are used to observe wave propagation in CCMs. Two types of optical mapping, dye based and dye free, are used. Typically, cell activity is recorded using fluorescence imaging, using either voltage-sensitive or calcium-sensitive dyes (5). Although these techniques directly measure key biophysical properties, they tend to suffer from two major drawbacks, phototoxicity and photobleaching, rendering longer recording of tissue nearly impossible. An alternative approach is based on dye-free visualization of contraction of cardiac cells, using either phase imaging (6) or off-axis illumination (7). Although dye-free techniques do not capture membrane voltage or calcium concentration, they allow direct visualization of wave patterns without the drawbacks associated with fluorescent-imaging approaches.

All the optical mapping techniques are capable of producing a large quantity of image data, but the analysis of such data is still frequently done manually (8), or largely manually (9), which is subjective and time-consuming. An automated analysis of wave propagation in optically mapped tissue would be less prone to operator bias and has the potential to increase throughput. However, most of the existing automated methods for analyzing optical mapping data focus on the properties of single cells or patches of tissue, rather than macroscopic behavior of the tissue.

There are automated approaches to the analysis of higher-level activity (e.g., waves), but their focus seems to be mainly on the analysis of data from electrode arrays (10, 11); an example task being solved is keeping track of the number of waves in a recording, recording the events of splitting and fusion (12, 13). Such electrophysiological recordings are characterized by an excellent temporal resolution of >1 kHz, a low amount of noise, and relatively poor spatial resolution (e.g., the 22 × 23 and 24 × 21 arrays used in (10)). These techniques have been successfully applied to voltage-sensitive dye recordings collected by specialized low-resolution high-speed detectors (14).

Recently, relatively inexpensive high-resolution, low-noise sCMOS sensors with moderate frame rates have been made widely available for biomedical research (15). These detectors yield data sets with relatively poor temporal resolution of up to 100 Hz, and signals typically have a lower signal/noise ratio (SNR), but their high spatial resolution offers several advantages. Such an increase in spatial resolution may be used to measure detailed properties of wave propagation, such as the distribution of wavefront speeds for different parts of a wave, or to track small and short-lived wavelets (16), which cannot be achieved with lower-resolution devices. The gold standard for measuring conduction properties is the method by Bayly et al. (10), developed for conduction-velocity estimation in electrophysiological recordings, also used in the toolkit Rhythm (14). However, in our experience, the method is not ideally suited for processing high-resolution, heterogeneously conducting tissue; a discussion of its shortcomings and a comparison with the methods developed by us can be found in Section S7 in the Supporting Material.

Because of the lack of suitable software for analysis of the behavior of waves in high-spatial-resolution data sets, particularly for recordings where the activation is not a continuous pattern (such as obtained using conventional calcium imaging) but a discrete one, we designed the toolkit Ccoffinn (Cardiomyocyte Cultures Optically-mapped: Fast Feature extractIoN and trackiNg), presented in this text; the code (with user guide and sample data) is available from https://ccoffinn.dpag.ox.ac.uk/. The approach is based on the segmentation of single cells or groups of neighboring cells, using the information of their activity to construct a representation of waves and track their movement. After these steps, features are extracted that describe the quantitative properties of the observed waves, such as wavefront speed, wavefront smoothness (or lack thereof), or several measures of order in the recorded activity. The presented methods are validated using synthetic data and used as a proof of concept to demonstrate the difference in conduction properties of myocyte cultures and cocultures of myocytes and cardiac neurons. The whole process of segmentation, tracking, and feature extraction, is implemented mainly in Matlab, and it is relatively high throughput, allowing for processing hundreds of data sets per day on a personal computer. Although the software was designed for data sets obtained using a dye-free imaging approach, we demonstrate that it also can be directly applied to data sets collected using fluorescence techniques with a continuous pattern of activation.

Materials and Methods

This section briefly sketches the functionality of Ccoffinn, describing the process of wave segmentation, tracking, and subsequent feature extraction.

Wave segmentation and tracking

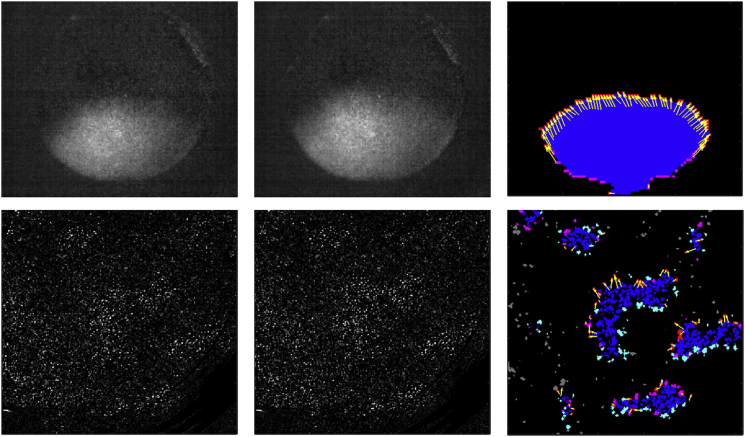
The main aim of the wave segmentation is to estimate which parts of tissue are firing in a synchronized manner in each frame of a source video. In addition to simple wave segmentation, we also propose a method for detection of a wavefront (the part of a wave that advances forward). Using the methods for segmenting waves, we can then track movement of wavefronts and extract features describing the waves. An example output of Ccoffinn for both dye-free and calcium imaging is shown in Fig. 1. Below is a more detailed description of the algorithms used to get from a source video to extracted features. Furthermore, Sections S3–S5 in the Supporting Material give an overview of parameters, a description of the synthetic and experimental data used, and notes on implementation, respectively.

Figure 1.

An example output of wave segmentation and tracking. Each row contains two consecutive frames of a recording, with segmentation and annotation by Ccoffinn in the third column. In the first row is a straight wave imaged using a calcium dye at 200 fps. The second row is a case of dye-free imaged wavelets at 50 fps with spurious activity (which is the most difficult type of activity to process). The colors in the images encode the roles of blobs within the waves. Blue represents the area inside the waves, cyan the borders of waves that are not in the upstroke phase, magenta the wavefront blobs (border blobs in the upstroke phase), red the wavefront blobs that were not wavefront in the previous frame (“became-wavefront”), and yellow the tracking arrows linking border blobs from the first shown frame to those that “became wavefront” in the second shown frame.

Blob segmentation

The aim of this step is to estimate locations of pixel clusters that are activated at the same time (given available temporal resolution). This can be single cells or clusters of cells, depending on the spatial resolution used. Using the off-axis-illumination dye-free imaging, active cells or groups of cells manifest as bright blobs; thus, the segmentation of the cell culture is reduced to blob detection. The segmentation is greatly simplified, as the blobs in monolayers do not change their location throughout the recording. Therefore, we can average all the frames of the video, obtaining an image with an excellent SNR that contains all the blobs that were active. The averaged image is then segmented using the four-connected version of the SeNeCA algorithm (17), chosen for its computational simplicity and its ability to cope with data with uneven background brightness, which is a common feature in our data sets. The parametrization of SeNeCA is described in Section S3 in the Supporting Material.

For cases of data where the imaged tissue does not manifest clear blobs (e.g., macroscopic calcium imaging), an alternative segmentation method based on filtered binning is included in Ccoffinn. Using this approach, a frame of the video is binned into squares with a chosen side length (parameter $binningSize$; see Section S3 in the Supporting Material). Using the whole source video, the SNR is measured for each of the brightness traces of the squares using the Matlab snr function. Optionally, the squares with SNR smaller than a given threshold (parameter $minSNR$) are discarded. The remaining squares are then considered to be segmented blobs in a manner similar to segmentation using the default approach.

Determining times of blob activity

Once the blobs have been segmented, the next task is to determine which blobs are active at which frame of the recording. Simple thresholding of intensities performed poorly on our data, given the wide range of brightness and/or SNR of blob traces. We did not want to use shape-specific methods (such as template matching), as our aim was to keep the method flexible with respect to different imaging modalities and species-specific action-potential morphologies. Methods based on the derivative of the measured intensity, which is often used as a surrogate for the rate of change of membrane voltage (14), cannot be used solely, because the derivative of intensity only provides the time of the upstroke and not information such as action-potential duration (APD). We designed a simple spike-mining algorithm that uses the derivative of intensity to detect spikes as events and then uses temporal surroundings of the detected event to extract the start and end of the particular spike. The detailed description of the algorithm is given in Section S1.1 in the Supporting Material.

Wave segmentation

Here, we aim to detect waves in each frame. Informally, a wave is defined as a “sufficiently large group of active blobs which are sufficiently dense.” Our approach works frame by frame, and in each frame, it takes all the blobs active in that particular frame, considers them in areas of dense-enough activation (see Section S1.2 in the Supporting Material for details), and divides them into groups using a recursive criterion: blobs a and b belong to the same wave $\iff$ a and b are close enough or if there exist blobs c and d so that a is close enough to c, b is close enough to d, and c and d belong to the same wave (the case when $a=c$ or $b=d$ is allowed).

The blobs are then further segmented according to their “roles”: blobs within a wave, blobs at the border of the wave, and blobs that are at the border and are furthermore wavefront blobs (i.e., the wave is propagating across them, as opposed to, e.g., border blobs that are at the tail of the wave and are ceasing to be active rather than becoming active). The whole process of wave segmentation is described in detail and illustrated in Section S1.2 in the Supporting Material.

Wavefront tracking

After the blobs are segmented into various types according to their position in waves, the next step is to track the movement of the wavefronts throughout the recording. The tracking information may be then used to estimate wavefront-related features of interest. Unlike in traditional tracking of blobs, the blobs are stationary in our data and only the pattern of their activation is tracked. This means that the number of tracked objects (wavefront blobs) is highly variable throughout the recording and waves tend to disappear completely unless they are reentrant.

For wavefront tracking, Ccoffinn uses a novel algorithm, to our knowledge, based on solving a minimum-cost bipartite matching problem to link wavefront blobs of a wave with the border blobs of the same wave in the previous frame. This approach is optimal in the total distance between the linked cells and is sufficiently fast for recordings with <10,000 segmented blobs. The detailed explanation of the algorithm is given in Section S1.3 in the Supporting Material. Alternatively, we have implemented the method of Bayly et al. (10), which may be used for smoothly conducting recordings.

Feature extraction

Rather than to observe wave segmentation and tracking in a video visually, it may be more convenient to extract several features that describe the data set using an automated method. Furthermore, an automated approach avoids operator bias, which can occur if researchers are free to select regions manually, possibly causing false-positive results (18). Ultimately, an automated analysis is more easily scaled to high-throughput applications (e.g., drug screening). For the purpose of the automated description of the recorded behavior, we have designed several features that either simply describe the data or may serve as a way of showing a difference between two groups of data. Most features are actually multisets, which can be further summarized, e.g., averaged over time (producing a spatial map) or over space (producing a development over time), or both (producing a single number). The features extracted are given below, with precise definitions in Section S2 in the Supporting Material.

• •Conduction-oriented: wavefront speed (conduction velocity), wavefront roughness
• •Organization-oriented: entropy, perimeter/area ratio
• •Spike properties: APD, interspike duration, beating frequency
• •Structural: number of blobs, sparseness of blobs (spatial)

Results

We made two comparisons using the available dye-free data (more details on the data are provided in Section S4.2 in the Supporting Material). First, we manually divided the recordings into organized waves (target, spiral, or straight) and disorganized waves (wavelets or chaotic activity). We then compared the features extracted from organized waves to those from disorganized waves. Second, we compared the properties of organized waves in myocyte cultures to organized waves in cocultures of myocytes and neurons. In both comparisons, we used the rank sum test to compare features of the groups of recordings. Furthermore, an evaluation of Ccoffinn using synthetic data is given in Section S6 in the Supporting Material.

The results of comparing the recordings of organized and disorganized activity are given in the upper part of Table 1. The disorganized cultures had a significantly higher perimeter/area ratio and wavefront roughness. This is an expected result, as these two features are mainly aimed at orderliness of propagation in tissue. The third feature aimed at orderliness, entropy, failed to discern between the two classes of data, supporting the opinion, based on the evaluation of synthetic data, that it is not a useful feature. Wavefront speed was significantly increased in the group containing organized activity, which is an expected result as well.

Table 1.

Comparisons of Recordings of Organized and Disorganized Activity and of Organized Activity in Myocyte Cultures and Myocyte-Neuron Cocultures

Organized versus Disorganized Activity
Feature	Org Median (IQ range)	Dis Median (IQ range)	p value
Number of cells	4678 (4138–5087)	4890 (4318–5573)	0.1909
Wavefront speed (mm/s)a	11.3 (7.6–20.8)	5.9 (5.2–7.4)	0.0024
Interspike period (ms)	443.2 (331.8–564.3)	372.1 (341.9–466.1)	0.2673
APD (ms)	138.5 (112.1–180.4)	138.2 (103.6–150.3)	0.3286
Cell sparseness (m)	170.2 (152.8–204.6)	192.4 (168.5–210.7)	0.3453
Wavefront roughness (°)a	27.1 (23.3–30.9)	37.7 (32.7–38.9)	0.0010
Beat frequency (Hz)	0.838 (0.606–1.403)	1.173 (0.894–1.437)	0.1694
Entropy	0.322 (0.034–2.130)	0.127 (0.060–0.509)	0.7281
Perimeter/area ratioa	0.139 (0.093–0.162)	0.188 (0.161–0.229)	0.0022
Organized Activity in Myocyte Cultures versus Myocyte-Neuron Cocultures
Feature	Myo Median (IQ range)	Co Median (IQ range)	p value
Number of cells	4956 (4751–5313)	4411 (4127–4835)	0.1471
Wavefront speed (mm/s)a	6.5 (5.3–9.5)	17.8 (11.1–21.5)	0.0110
Interspike period (ms)a	564.3 (432.9–643.1)	366.3 (307.7–464.6)	0.0420
APD (ms)	180.4 (134.4–204.5)	133.5 (107.3–151.3)	0.0559
Cell sparseness (m)	184.3 (159.5–204.8)	169.3 (146.1–204.4)	0.7925
Wavefront roughness (°)	29.6 (24.1–38.6)	26.6 (23.1–29.3)	0.2635
Beat frequency (Hz)	0.599 (0.516–0.929)	0.947 (0.815–1.891)	0.0559
Entropy	0.667 (0.306–2.081)	0.168 (0.003–2.179)	0.3676
Perimeter/area ratio	0.152 (0.135–0.192)	0.117 (0.084–0.162)	0.2198

For each feature (or mean of feature), the median and interquartile range are given. Org, organized recordings (target, spiral, or straight wave); Dis, disorganized activity (wavelets); IQ, interquartile; Myo, cultures of myocytes; Co, cocultures of myocytes and neurons.

^aFeatures that differ significantly $\left(p<\alpha =0.05\right)$ between the respective groups.

The results of comparing recordings of organized activity in myocyte cultures and cocultures of myocytes and neurons are given in the lower part of Table 1. The most striking result is the large increase of wavefront speed in cocultures compared to myocyte cultures. At the same time, the perimeter/area ratio is not significantly different between the two groups of data; thus, the difference in wavefront speed and wavefront roughness is unlikely to be caused by different morphology of waves. Also, we can observe a borderline-significantly faster beat rate in cocultures (this trend is further bolstered by shorter APD and interspike period, consistent with more frequent spiking).

To link the results using real data to the analysis of synthetic data (Section S6 in the Supporting Material), we have estimated the noise standard deviation in the real data using the method by Immerkær (19). The mean over recordings of standard deviation of the noise was 0.1063 with a standard deviation of 0.0583, suggesting that the results presented in this section should not be affected too severely by the presence of noise.

Discussion

In this work, we present the toolkit Ccoffinn, a novel approach, to our knowledge, to segmentation and wave tracking in optically mapped tissue, with subsequent feature extraction, focused on the analysis of high-resolution recordings with heterogeneously conducting tissue. The method was validated using synthetic data and applied to a large cardiac culture data set, where it successfully detected significant differences in properties of two types of cell cultures.

Our software toolkit has the following advantages: the ability to extract many different features from data sets, describing various properties of the imaged tissue that, to our knowledge, have not been analyzed automatically before (e.g., wavefront roughness); computational efficiency; and freely available code. The code is written in Matlab in a modular fashion using static classes and subprograms to allow users to easily incorporate different methods in Ccoffinn while still being able to use the toolkit’s core functionality (e.g., the current spike-mining algorithm can be seamlessly replaced without disrupting Ccoffinn’s tracking, visualization, and feature-extraction functionality).

The main limitation of Ccoffinn is the offline nature of the software; this is very convenient for blob segmentation tasks, but having a real-time implementation might be also very useful. Implementing a real-time version of the toolkit is feasible, provided that no complex visualization of the segmentation is needed. The main change needed would be an alternative algorithm for determining which cells are active and which are not. A frame-by-frame use of the SeNeCA algorithm might be an option, as this has been validated in (17).

We believe that the main future use of the toolkit will be to discover and quantify the effects of pharmacological agents on cardiac propagation, or for determining functional differences between tissue types, similar to the proof-of-concept application presented in this text. A second use might be to explore the relationships between features in a very large data set, for example, the homogeneity of distribution of cells and the propagation velocity. When the real-time version of our approach is implemented, a third possible use is for optogenetic applications (20), allowing the automated control of illumination for feedback applications that depend on wavefront location or velocity. Ccoffin could greatly improve the reaction time to experimental events and could allow the application of patterns of stimulation that are well beyond the capabilities of human operators.

Author Contributions

J.T. designed the new algorithms used, wrote and assembled the code, and performed the analyses using real and synthetic data. R.A.B.B. produced real dye-free data used in the article and provided consultancy and information on the data to J.T. G.B. supervised the project, wrote the initial design document (which features to extract, etc.), and consulted the algorithms used with J.T.

Editor: Andrew McCulloch.