Fast fMRI can detect oscillatory neural activity in humans

Significance

A major challenge in neuroscience is our limited ability to image neural signals noninvasively in humans. Oscillations in brain activity are important for perception, attention, and awareness, and progress in cognitive neuroscience depends on localizing these patterns. fMRI is thought to be too slow to measure brain oscillations because it depends on slow changes in blood flow. Here, we use recently developed imaging techniques to show that fMRI can measure faster neural oscillations than previously thought, and responses are 10 times larger than expected. With computational modeling and simultaneous electroencephalography we show that vascular responses are surprisingly fast when brain activity fluctuates rapidly. These results suggest that fMRI can be used to track oscillating brain activity directly during human cognition.

Abstract

Oscillatory neural dynamics play an important role in the coordination of large-scale brain networks. High-level cognitive processes depend on dynamics evolving over hundreds of milliseconds, so measuring neural activity in this frequency range is important for cognitive neuroscience. However, current noninvasive neuroimaging methods are not able to precisely localize oscillatory neural activity above 0.2 Hz. Electroencephalography and magnetoencephalography have limited spatial resolution, whereas fMRI has limited temporal resolution because it measures vascular responses rather than directly recording neural activity. We hypothesized that the recent development of fast fMRI techniques, combined with the extra sensitivity afforded by ultra-high-field systems, could enable precise localization of neural oscillations. We tested whether fMRI can detect neural oscillations using human visual cortex as a model system. We detected small oscillatory fMRI signals in response to stimuli oscillating at up to 0.75 Hz within single scan sessions, and these responses were an order of magnitude larger than predicted by canonical linear models. Simultaneous EEG–fMRI and simulations based on a biophysical model of the hemodynamic response to neuronal activity suggested that the blood oxygen level-dependent response becomes faster for rapidly varying stimuli, enabling the detection of higher frequencies than expected. Accounting for phase delays across voxels further improved detection, demonstrating that identifying vascular delays will be of increasing importance with higher-frequency activity. These results challenge the assumption that the hemodynamic response is slow, and demonstrate that fMRI has the potential to map neural oscillations directly throughout the brain.

Neuronal information processing is shaped by ongoing oscillatory activity, which modulates excitability in neuronal populations and supports the coordination of large-scale brain networks (1–3). In particular, the occurrence of low-frequency dynamics (0.1–2 Hz) within specific cortical regions has been suggested as a key mechanism underlying perception, attention, and awareness (4, 5), because conscious processes typically evolve on the timescale of hundreds of milliseconds (6) and may depend on cortical dynamics in this frequency range. Localizing >0.1-Hz oscillatory dynamics in the human brain is an essential step toward understanding the mechanisms of the many high-level cognitive processes that occur on these timescales. Studies of the spatial properties of neural oscillations in human subjects have been fundamentally limited by the ill-posed inverse problem of electromagnetic recordings: It is not possible to reconstruct the neural generators of EEG and magnetoencephalography (MEG) signals unambiguously, and signals from deep subcortical structures are rarely detected. Noninvasive neuroimaging approaches that can detect >0.1-Hz oscillations with higher spatial resolution are needed to advance studies of large-scale brain network function.

We hypothesized that recent technical advances in fMRI could potentially enable direct localization of neural oscillations in the human brain. fMRI measures brain function by tracking focal changes in blood flow and oxygenation and therefore is an indirect measure of neuronal activity, with spatial and temporal specificity intrinsically limited by the precision and responsiveness of the coordinated regulation of blood delivery in the brain (7, 8). Typical fMRI experiments use stimuli or tasks designed to elicit large, easily detectable hemodynamic responses, which lag the onset of neuronal activation by several seconds, suggesting that these hemodynamic signals are too slow to capture many aspects of ongoing neuronal activity. However, new MRI technologies available in recent years, such as ultrahigh magnetic field systems, provide boosts in sensitivity, enabling more naturalistic stimulation paradigms that perturb the vasculature only weakly.

In addition to improvements in sensitivity, the recent development of methods for simultaneous multislice (SMS) imaging (9–13) allows whole-brain fMRI to be performed at relatively fast acquisition rates (<1 s). However, the temporal resolution of fMRI has generally been thought to be limited by the sluggishness of the hemodynamic response itself rather than by data-acquisition rates. The slow dynamics of the hemodynamic response function (HRF) result in strong attenuation of high-frequency neural activity (14). In addition, rapidly repeating neural stimuli typically result in smaller fMRI responses (15–20), further limiting the detectability of neural oscillations.

The detection of patterns that are periodic in nature, rather than irregular, is particularly challenging (14). The fMRI response to periodic (nonjittered) stimuli declines rapidly with increasing frequency and has been detected down to a limit of a 6.7-s (21) or 4-s (22) period. Because of the strong attenuation of high-frequency oscillatory signals, event-related fMRI paradigms that use relatively short interstimulus intervals (ISIs) typically either jitter the ISIs or alternate between different stimulus conditions (14, 23). These experimental design choices are made in part to lower the fundamental frequency being studied. In general, the fact that fMRI temporal resolution is limited by slow neurovascular coupling has restricted the majority of fMRI studies to studying dynamics in the <0.1-Hz range, because periodic oscillations above that frequency range are expected to be vanishingly small.

Despite this evidence, recent studies performed during the resting state have suggested that there are significant neuronally driven blood oxygenation level-dependent (BOLD) contributions to fMRI signals at frequencies above 0.1 Hz (24–27). However, a challenge in interpreting fMRI oscillatory dynamics measured during the resting state is that the underlying brain activity is not known. Electrophysiology studies have demonstrated a link between infraslow (<0.1 Hz) EEG activity and the fMRI signal (28, 29), but such studies have not been performed at higher frequencies. In the absence of neurophysiological recordings, it is difficult to ascertain the degree to which the >0.1-Hz fMRI signals are generated by >0.1-Hz neural activity or instead reflect other hemodynamic and physiological processes.

This study aimed to determine whether fMRI signals contain neurally generated oscillatory content above 0.2 Hz and to determine the frequency response to ongoing periodic neural activity. To link the dynamics of the fMRI signal to underlying neural activity, we examined the fMRI response in the context of a known, stimulus-induced neural oscillation and used rapid data acquisition [repetition time (TR) <300 ms] to sample the fMRI oscillatory response directly. We found that fMRI oscillations of up to 0.75 Hz can be detected and that the amplitude of these oscillations is an order of magnitude larger than predicted by canonical models. Using simultaneous EEG–fMRI and model-based simulations, we studied the link between neural activity, neurovascular coupling, and the BOLD signal to determine how fast fMRI responses are generated.

Results

Canonical Linear Models Predict Undetectable fMRI Oscillations at 0.5 Hz.

We used a flickering checkerboard stimulus whose luminance contrast oscillated at a frequency of interest, driving neuronal oscillations in human primary visual cortex (V1) and enabling us to quantify the fMRI response to a controlled oscillation with a known frequency (Fig. 1A).

Fig. 1.

Linear canonical models predict that the fMRI response to oscillatory neural activity will decrease exponentially as the oscillation frequency increases. (A) Diagram of the visual stimulus. The luminance contrast of a flickering radial checkerboard was modulated at 0.2, 0.33, 0.5, or 0.75 Hz. (B) Time course of the HRFs used for simulations. (C) Example of the predicted fMRI response to sinusoidally oscillating neural activity. As the frequency increases, the predicted response reaches a stable plateau, and the oscillation amplitude around that plateau becomes small. (D) Predicted fMRI response across stimulation frequencies. The predicted response declines exponentially for all HRFs. (E) The predicted fMRI response on a log scale for a linear system and for a sample set of nonlinear parameters shows that nonlinear adaptation effects would be expected to reduce the fMRI response amplitude further at high stimulus frequencies.

We first performed simulations of the predicted fMRI response to neural oscillations at each frequency by convolving the idealized neuronal activity (the sinusoidal stimulus waveform) with either the canonical two-gamma HRF used in SPM software, a single-gamma function, or the double-gamma HRF (Fig. 1B) described by Glover (30). The predicted response was estimated as the amplitude of the convolved response once it reached a plateau value (Fig. 1C), discarding the initial transient response. The predicted response amplitude declined exponentially with increasing frequency for all three models (Fig. 1D and Fig. S1A). The amplitude of the fMRI response to a 0.5-Hz neural oscillation was predicted to be 0.8–1.3% of the response to a 0.2-Hz oscillation, suggesting that resolving fMRI signals at delta-range frequencies could be quite challenging. We next added nonlinear effects to the hemodynamic model, because at short ISIs the fMRI response becomes both smaller in amplitude and broader (15, 16, 20), and observed that this nonlinearity is predicted to yield even more temporal smoothing and a further reduction in fMRI signal at higher frequencies (Fig. 1E). However, these models were developed to describe task-evoked activity in response to individual stimuli with long durations during block-design experiments, whereas periodic continuous neural activity, which may be closer to that observed in typical naturalistic contexts, could potentially elicit different hemodynamic responses.

Fig. S1.

Phase-shift properties of the fMRI response. (A) Simulation with a canonical model. The oscillation around the plateau is expected to become extremely small when the stimulus frequency is 0.5 Hz. (B) Schematic of expected phase delays. When the HRF is convolved with oscillatory neural activity, and the period of neuronal activity fluctuations is short relative to the duration of the HRF, the phase of the response can shift substantially relative to the input oscillation. a.u., arbitrary units. (C) Simulation of the expected response at different stimulation frequencies with a range of HRFs. For each HRF, the phase of the response differs across stimulation frequencies, because the phase wraps relative to the stimulation frequency. The phase shifts induced by these physiologically plausible hemodynamics are in the same range as those we observed in the data, with precise values varying depending on the shape of the HRF.

fMRI Oscillations at 0.5 Hz Are an Order of Magnitude Larger than Expected.

To test whether fMRI can detect neural oscillations directly, we acquired fMRI data at 3 T using fast temporal sampling (TR ≤280 ms) and analyzed the mean response in V1 during the oscillatory visual stimulus (Fig. 2 A and B). We averaged the mean time series across all voxels in the region of interest (ROI) on every cycle of the stimulus contrast oscillation, discarding the first 3–10 cycles to avoid transient effects (SI Methods). The resulting plot shows a stimulus-triggered average of the fMRI data. In experiment 1, we found a robust oscillation in response to the visual stimulation at 0.2 Hz, with an amplitude of 0.73% [95% confidence interval (CI) 0.55, 0.92] (Fig. 2C). As the stimulus frequency increased, we continued to find significant oscillatory responses, with an amplitude of 0.21% (CI 0.09, 0.33) at 0.33 Hz (Fig. 2D) and an amplitude of 0.06% at 0.5 Hz (CI 0.04, 0.09) (Fig. 2E). The induced oscillations also could be seen in the power spectrum of the V1 BOLD signal (Fig. S2), although the evoked analysis (Fig. 2C) enabled a better estimation of oscillation amplitude because it reduced the contribution of non–phase-locked noise. To ensure the replicability of these responses, we conducted a second experiment using SMS imaging to double the number of slices acquired. We again found robust induction of oscillatory responses in V1 when stimulation was delivered at 0.2, 0.33, or 0.5 Hz (Fig. 2 F–H) at similar amplitudes (0.2 Hz = 1.05%, CI 0.83, 1.31; 0.33 Hz = 0.28%, CI 0.15, 0.41; 0.5 Hz = 0.08%, CI 0.04, 0.13). The phase of the response was shifted at higher frequencies, as expected because of the filtering induced by the hemodynamic response (Fig. S1 B and C). Although the response amplitude was small at higher frequencies (Fig. 2I), it nevertheless was substantially larger than predicted by the canonical linear model in every subject studied (Fig. 2J), eliciting a mean response within individual subjects that was 10.1% the size of the 0.2-Hz condition rather than the 1.3% ratio predicted by the SPM model (P = 0.0005, Wilcoxon signed-rank test). The response amplitude was very similar (10.7%) when edge slices were excluded from the analysis, suggesting that these observations were not driven by inflow effects. The fMRI response at 0.5 Hz was therefore an order of magnitude larger than predicted, suggesting that delta-range neuronal oscillations are detected more easily with fMRI than originally thought.

Fig. 2.

Oscillatory fMRI responses in V1 acquired at 3 T can be detected at each stimulus frequency and are an order of magnitude larger than predicted. (A) An example of slice positioning in experiment 1 (five slices). (B) An example of the V1 ROI in a single subject. (C) Stimulus-triggered mean response in V1 in experiment 1, locked to the stimulation cycle at 0.2 Hz. The shaded area shows the SE across runs. (D) As in C, runs at 0.33 Hz. (E) As in C, runs at 0.5 Hz. (F–H) Mean response in V1 in experiment 2. (I) Amplitude of the fMRI response across stimulus frequencies, compared with the linear model using the SPM HRF. Error bars are 95% CIs (bootstrap). (J) Ratio of the fMRI response at 0.2 Hz to the response at 0.5 Hz across all subjects who participated in both conditions: Each individual subject had a larger response to the 0.5-Hz stimulus than predicted by the canonical linear model with the SPM HRF (black dashed line).

Fig. S2.

Induced oscillations in the V1 ROI. (A–C) Mean spectrum of the V1 ROI across all subjects in experiment 1. A peak induced by the stimulus is visible at each frequency (red arrow); however, by 0.5 Hz (C) the peak is quite small. The power-based approach therefore can prove more challenging than the stimulus-triggered averages, which show only phase-locked evoked activity rather than all power at any given frequency. The shaded area shows the SE across subjects. (D and E) Examples of the V1 spectrum in a single run, single session at 3 T. The peaks around 0.4 Hz and 1.1 Hz are physiological noise, and the stimulus frequencies can be well separated from them. However, the noise comes close to obscuring the 0.5-Hz peak in E. The shaded areas show theoretical 95% CIs. (F) Mean spectrum at 7 T during the 0.2-Hz stimulus. (G) Mean spectrum at 7 T during the 0.75-Hz stimulus. The amplitude of the induced oscillation is too low to be observed directly in the spectrum, because the noise amplitude is relatively large in this frequency band. In this case the phase-locked evoked analysis is needed to detect the 0.75-Hz oscillation by averaging out the noise contributions in this frequency band and thereby revealing significant stimulus-locked oscillations.

Neural and Vascular Mechanisms Underlying the Unexpectedly Large fMRI Response.

The large fMRI response could indicate either that the underlying neural activity is stronger at 0.5 Hz than at 0.2 Hz and therefore drives a larger hemodynamic response, or that the linear canonical hemodynamic model is not a good fit for periodic neural activity. To investigate the first possibility, we recorded EEG simultaneously with fMRI in four subjects to obtain an electrophysiological measure of response amplitude. The evoked response was concentrated in occipital channels (Fig. 3A), consistent with previous studies suggesting that the steady-state visual evoked potential (SSVEP) is generated largely by visual cortex with strong contributions from V1 (31–33). The cross-correlation between the V1 fMRI signal and the 12-Hz amplitude in the occipital EEG demonstrated a clear correlation (Fig. 3B), in line with these previous reports that V1 is a major generator of the SSVEP. The cross-correlation for both stimulus conditions overlapped with a lag of ∼3.5 s, suggesting a more rapid hemodynamic response than in canonical models but within a physiologically plausible range.

Fig. 3.

Simultaneous EEG recordings suggest that the large fMRI responses are not explained by increased amplitude of neural oscillations at higher frequencies. (A) The SSVEP to the 0.5-Hz sinusoidal stimulus localizes primarily to occipital channels, consistent with previous studies. (B) Cross-correlation of the 12-Hz amplitude in channel OZ and the fMRI signal in the V1 ROI. Both stimulus conditions induce a peak with a lag of ∼3.5 s, indicating that the V1 fMRI signal correlates with EEG power at a plausible physiological lag (n = 3 subjects, 6 runs at 0.2 Hz, 15 runs at 0.5 Hz). (C) Mean EEG across runs with sinusoidal contrast modulation at 0.5 Hz (n = 4 subjects, 19 runs) shows an SSVEP at 12 Hz in channel OZ. (D) Amplitude envelope of the 12-Hz EEG oscillation across runs at 0.5 Hz (n = 4 subjects, 19 runs). (E) The amplitude envelope of the 12-Hz EEG across runs at 0.2 Hz has the same magnitude (n = 4 subjects, 12 runs).

To determine whether increased neural activity could have contributed to the large fMRI oscillations we observed, we tested how the SSVEP dynamics changed across stimulus frequencies. The stimulus-triggered mean EEG (Fig. 3C) contained an evoked signal at 12 Hz (corresponding to the checkerboard contrast inversion frequency), with amplitude modulation of either 0.2 Hz or 0.5 Hz (corresponding to the luminance contrast modulation). The amplitude of the EEG response to the 0.5-Hz stimulus was not larger than the response to the 0.2-Hz stimulus (0.2 Hz = 3.12 μV; 0.5 Hz = 2.99 μV; difference = −0.08; CI −1.4, 1.2) (Fig. 3 D and E). This finding suggested that the magnitude of the neural response was similar across conditions and that the HRF to ongoing oscillatory neural activity must differ from the classic models developed for transient task activity.

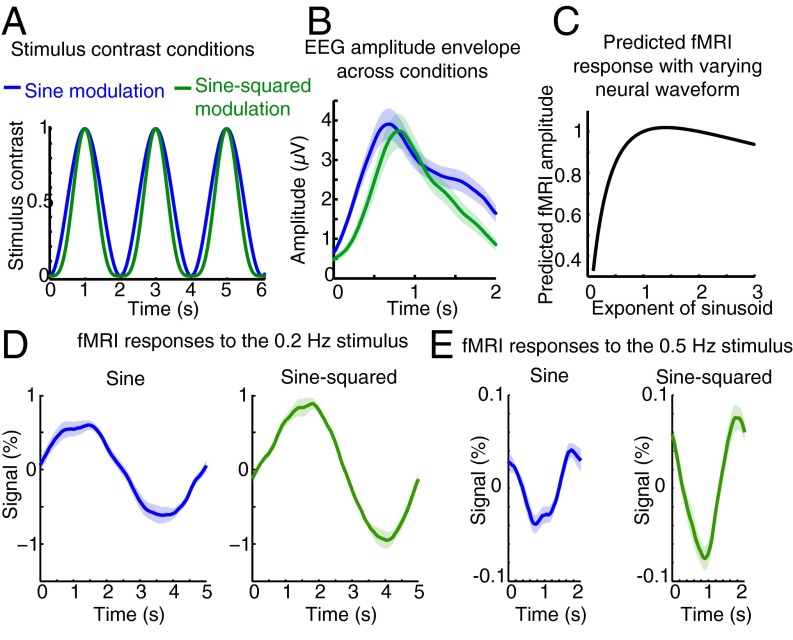
Although the magnitude of neural activity appeared similar across conditions, the duration of neural activity in the 0.5-Hz condition was substantially shorter (Fig. 3 D and E). fMRI responses are known to exhibit nonlinear dependence on stimulus duration, with briefer stimuli inducing larger responses than expected from a linear system (17, 34, 35). To test the role of stimulus duration explicitly, we presented stimuli with luminance contrast varying as the square of a sinusoidal function, yielding a narrower stimulus waveform than the sinusoidal case (Fig. 4A). The EEG recordings in the sine-squared condition had the same magnitude as in the sinusoidal condition (amplitude = 3.12 μV) but had a narrower waveform (Fig. 4B), suggesting that this stimulus paradigm successfully elicited neural activity of similar magnitude but briefer temporal dynamics. Simulations predicted that the sine-squared stimulus would elicit a 15% larger fMRI response than the sine stimulus at either stimulus frequency (Fig. 4C). In contrast, the measured fMRI response to the sine-squared stimulus was 49% larger (CI 24%, 81%) than the response to the sinusoidal stimulus in the 0.2-Hz stimulus condition (Fig. 4D) and was 93% larger (CI 21%, 399%) in the 0.5-Hz stimulus condition (Fig. 4E). We concluded that ongoing oscillatory activity can produce relatively large fMRI responses if the waveform of that activity is narrow.

Fig. 4.

Continuous and rapidly varying neural activity can elicit faster hemodynamic responses. (A) Schematic of the contrast modulation used in the sine vs. sine-squared conditions. In the sine-squared case, the same range of contrasts is used, but the waveform shape is narrower. (B) Envelope of the EEG signal. As expected, the magnitude of the EEG is similar across conditions, but the waveform of the EEG response is narrower in the sine-squared case, suggesting successful modulation of the waveform of the underlying neural oscillation. (C) The predicted fMRI response to oscillating neural activity varies with its waveform but is expected to change less than 15% in the range of our stimulus parameters. (D) The fMRI response to a sine-squared wave at 0.2 Hz is 49% larger than the response to a sine wave. (E) Similarly, the fMRI response to a sine-squared wave at 0.5 Hz is 93% larger than the response to a sine wave, demonstrating that narrower neural oscillations drive larger fMRI signals. The shaded region shows the SE across runs.

What mechanism could underlie the production of a large fMRI response to >0.1-Hz oscillatory neural activity? A recent study proposed that a faster HRF should be used for resting-state fMRI signals (25). We hypothesized that a fast HRF also should be used for task-driven activity when neural activity varies rapidly and continuously. To test whether a similar modification to the HRF could account for our data, we simulated the predicted fMRI response using HRFs with different shapes. Narrower HRFs produced larger responses at high stimulus frequencies: An HRF peaking at 2.5 s predicted a response at 0.5 Hz that is five times larger than the canonical SPM HRF (Fig. S3 A and B). In addition, the 93% increase in fMRI signal observed for the sine-squared vs. sine modulation at 0.5 Hz could be generated if the HRF shape depends on the duration of the neural activity, because an additional reduction of the HRF width would generate this increase (Fig. S3B). A single parsimonious model in which the temporal dispersion of the HRF is linked to the timescale of neural activity could therefore explain these data.

Fig. S3.

Modeling the predicted response to oscillatory stimuli dependent on the HRF. (A) Example of a range of HRF waveforms with differing parameters used for convolution. (B) Frequency response at 0.5 Hz using each HRF, normalized to the frequency response obtained with the SPM HRF. (C) The flow input to the balloon model was a single cycle of a sinusoid of different frequencies. (D) When τ_v (the time constant for the viscoelastic effects) is set to zero, the predicted response has wide dispersion for all input durations. (E) When τ_v is set to 30 s, briefer stimuli elicit sharper BOLD responses. (F) When the mean transit time (τ_MTT) is decreased, the BOLD response again becomes sharper, and dispersion is reduced.

Biophysical Modeling of Oscillatory fMRI Responses.

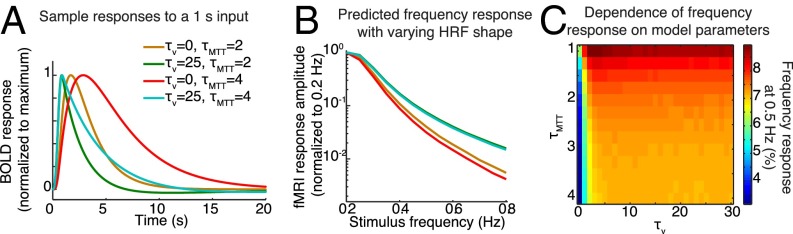
To test whether this narrower shape for the HRF is physiologically plausible during task-evoked neural activity, we implemented the balloon model (36–38) and examined its responses to a brief input. We considered two possible factors that could contribute to a faster HRF in this experiment: (i) whether brief neural activity induces a narrower fMRI response, as suggested by Fig. 4, and (ii) whether continuous, rather than transient, activity would affect the shape of the response. To test the first possibility, we examined the predicted responses to a single cycle of a sinusoidal flow input with increasing frequency (Fig. S3C). We varied the time constant for the viscoelastic effect, in which blood volume transiently lags before achieving steady state. Setting this time constant to zero, as in the original model, yielded slow BOLD responses similar to the canonical HRF (Fig. 5A and Fig. S3D). However, when this time constant was set to physiologically plausible nonzero values (37), the BOLD response to stimuli of shorter duration was both faster (time-to-peak) and narrower (FWHM) (Fig. 5A and Fig. S3E). These sharper dynamics demonstrate that when cerebral blood volume (CBV) lags changes in cerebral blood flow (CBF) rather than maintaining a steady-state relationship, the fMRI response to high frequencies or brief activity is expected to increase.

Fig. 5.

Modeling suggests that the vasculature can respond relatively quickly to oscillatory neural activity. (A) Predicted responses to a 1-s sine flow input using different parameters for the balloon model. (B) The predicted frequency response demonstrates that modifying the time constants within physiological values is expected to lead to an order-of-magnitude increase in fMRI oscillatory responses. (C) The predicted amplitude at 0.5 Hz (normalized to 0.2 Hz), depending on balloon model parameters. Low but still plausible values for the mean transit time (τ_MTT) and the increased viscoelastic constant (τ_v) lead to values closer to the data (∼8%, orange/red region of the plot).

Another possibility is that continuous periodic stimuli may shift the system to a new steady state in which baseline flow is higher and the system can respond more rapidly to changes in neural activity. Higher baseline flow would reduce the mean transit time, used as a time constant in the balloon model. Varying this parameter demonstrated that higher baseline flow would speed up the BOLD response (Fig. S3F), although the effects were less than those seen when the viscoelastic parameter was varied. However, values near 2 s, which would be consistent with prior reports (39), were sufficient to replicate the responses we observed, suggesting that as long as the mean transit time is relatively short at baseline, these oscillations could be expected.

When using the modified balloon model with these parameter settings to simulate the response to the visual stimulus, we obtained predictions much closer to the data: The model predicted that the fMRI response amplitude to a 0.5-Hz stimulus should be 7.5% of the response to a 0.2-Hz stimulus (Fig. 5 B and C), compared with ∼8–10% in the data (whereas the canonical model predicted 1.3%). These analyses demonstrated that a physiologically grounded model can produce the responses we observed, through viscoelastic effects that cause blood volume to lag while changes in flow vary more rapidly, leading to a sharpened HRF waveform when neural activity is brief. The large fMRI responses we observed therefore may be explained by a shift in the shape of the HRF, with continuous and rapidly varying neural activity inducing a sharper HRF and thereby leading to rapid fMRI responses.

Extending Detection of Oscillatory Activity up to 0.75 Hz.

This model also allowed us to extrapolate and generate predictions of the fMRI response at even higher frequencies, predicting that stimuli at 0.75 Hz would elicit a response 1.9% as large as the response at 0.2 Hz (as opposed to 0.14% predicted by the linear convolutional model). Our experiments at 3 T were unable to detect a significant neural response to the 0.75-Hz oscillation (amplitude, 0.02%; CI –0.02, 0.06), because the noise was larger than the predicted signal. To increase the signal-to-noise ratio, we conducted a third experiment at 7 T. We found a significant fMRI oscillation during 0.75-Hz stimulation (Fig. 6 A and B) with an amplitude of 0.021% (CI 0.009, 0.034). This value corresponded to 1.46% of the signal at 0.2 Hz, i.e., slightly below the balloon model prediction but an order of magnitude larger than the canonical model. The phase of the response again was shifted within a range that would be expected with physiologically plausible models (Fig. S4). To control for the possibility that the detected oscillation was caused by a physiological or motion artifact rather than by neural activation, we analyzed a control gray matter region that was not visually driven and observed no significant oscillation (amplitude, 0.002%; CI –0.006, 0.010) (Fig. 6 C and D). In addition, the 0.75-Hz oscillation in V1 was still detectable when physiological noise was reduced through nuisance regression of white matter and ventricle signals (Fig. S5). The magnitude of the observed response was small but nevertheless was detectable within a single session of scanning at 7 T, suggesting that the fMRI response is measurable and larger than predicted even at 0.75 Hz.

Fig. 6.

fMRI responses can be detected reliably up to 0.75 Hz. (A) In experiment 3, at 7 T, oscillatory stimuli at 0.2 Hz evoked consistent and large responses. (B) At 0.75 Hz, the evoked oscillations were still statistically detectable and were ∼1% of the amplitude of the 0.2-Hz signal. (C and D) A non-visually activated gray matter control ROI does not show oscillatory responses, suggesting that the detected oscillation is caused by neural activity rather than by motion or physiological noise. In all panels, the shaded region shows the SE across runs.

Fig. S4.

Physiologically plausible HRFs produce phase shifts close to the data. Both the SPM HRF and an example of a simulated faster HRF are expected to induce phase shifts close to those observed in the fMRI responses, with slightly closer matches from the fast HRF in this case. Because the best HRF cannot be analytically identified, this plot shows only a single example of an HRF with faster dynamics; other waveforms may also perform well.

Fig. S5.

Results are very similar after correcting for physiological noise. The triggered oscillation amplitude is similar when nuisance regressors from ventricles and white matter are applied before analysis, because these stimulus frequencies do not overlap with cardiac or respiratory signals. (A) Response at 0.2 Hz in experiment 3. The oscillation amplitude is 1.45% (CI 0.98, 1.86). (B) Response at 0.75 Hz in experiment 3. The oscillation amplitude is 0.02% (CI 0.009, 0.033).

Accounting for Vascular Delays Improves Resolution of Neural Oscillations.

The analyses described up to this point were averaged across all visually responsive voxels in V1, assuming similar response properties throughout that region. However, HRFs vary across the brain (40), and the structure of local vasculature can alter the timing of responses in individual voxels by hundreds of milliseconds (41). As stimulation frequencies approach 0.5 Hz (i.e., a period of 2 s), these delays can introduce cancellation into fMRI signals when averaging is performed across voxels. We therefore examined the response phase in individual voxels. In the localizer run, we selected voxels with the earliest peak response (in the 0–33rd percentile) and voxels with the latest peak response (in the 67th–100th percentile, median lag 635 ms). We then analyzed the response of these voxels on the other functional runs (Fig. 7A). In the 3-T experiments, the late-responding voxels exhibited a signal 97% larger than the early-responding voxels in the 0.2-Hz condition (P = 0.0004) and 54% larger in the 0.5-Hz condition (P = 0.02). Late and large-amplitude responses typically correspond to larger draining veins (41), suggesting that even large veins can contain periodic oscillatory signals at frequencies 0.2 Hz.

Fig. 7.

Accounting for vascular lags can further improve the resolution of fMRI oscillations. (A) Responses of early-responding and late-responding voxels across stimulus frequencies in an individual subject. The phase delays persist across conditions, and the fMRI response is larger in the later-responding voxels. (B) Early- and late-responding voxels plotted for a subject in experiment 3. At 0.75 Hz, the lags across voxels introduce phase cancellation of the fMRI response. The shaded region shows the SE across cycles. (C) The mean oscillatory response across all subjects in experiment 3 declines more in late-responding voxels and is stronger in early-responding voxels at high frequencies. The black dashed line is the prediction of the canonical linear model. (D) Mean time series across subjects in experiment 3 demonstrates that analyzing the early voxels separately results in larger oscillations than are detectable when averaging across the whole V1 ROI (n = 5 subjects, 60 runs). The shaded region is standard error across runs. (E) Heterogeneous spatial distribution of lags in individual voxels. The image is from a representative subject. Color indicates the phase lag in each voxel in the localizer run.

The phase delays across voxels suggest that identifying and correcting for hemodynamic delays could further improve the detection of oscillatory signals. In the 0.75-Hz condition, separating early- and late-responding voxels had a large impact, because these lags introduced major phase cancellation when averaged across all voxels (Fig. 7B). The mean signal amplitude in the early-responding voxels alone was 0.033%, 45% larger than the results from averaging across all voxels within the ROI (Fig. 7C). Furthermore, this result was better aligned with the model prediction from the data generated at lower frequencies (0.027%). Overall, late-responding voxels exhibited a more severe drop-off in signal as stimulus frequency increased, and early-responding voxels exhibited slightly larger responses at 0.75 Hz (Fig. 7D), suggesting that high-frequency oscillatory activity may be detected more easily in voxels with rapid response onset. The oscillations in early-responding voxels were also significant (P < 0.05) within a single scan session in three of the five subjects, in addition to the mean being significant across the group. The early- and late-responding voxels were spatially intermixed (Fig. 7E), suggesting that avoiding spatial smoothing during preprocessing and then grouping individual voxels according to their lags in a localizer run before analysis can further improve the detectability of high-frequency oscillations.

SI Methods

Study Participants.

All experimental procedures were approved by the Massachusetts General Hospital Institutional Review Board. We conducted two separate imaging studies (experiment 1 and experiment 2) using the same 3-T scanner and similar stimulus paradigms but different imaging acquisition parameters. We conducted experiment 3 on a 7-T scanner. For experiment 1, we enrolled 10 subjects (four female). One subject was later excluded because of substantial motion that caused the target region to move out of the field of view (FOV) of the acquired slices; one subject was excluded after falling asleep in the scanner; and one subject was excluded because of the failure to identify the V1 ROI in the functional localizer (see ROI Selection below). Therefore a total of seven subjects were analyzed. Three of these subjects returned for a second session on a different day. For experiment 2, we enrolled 11 subjects (six female). We excluded all data from one subject because of severe motion artifacts and excluded imaging data (but not EEG data) from one subject because of failure to identify V1 in the functional localizer scan. Two of the subjects returned for a second session on a different day. For experiment 3, we enrolled seven subjects (four female), one of whom returned for a second session on a different day. One subject was excluded because of severe motion artifact, and one was excluded because of failure of the localizer. One of the subjects in experiment 2 was also a participant in experiment 1, and two of the subjects in experiment 2 were also participants in experiment 3.

Visual Stimulus.

Visual stimuli were programmed in Matlab and Psychtoolbox (57, 58) and were presented with a digital light processing (DLP) Projector (Psychology Software Tools) with a synchronized frame rate. Subjects viewed the projection on a screen fixed at the back of the scanner bore, through a mirror fixed in front of the eyes. Each run lasted 254 s; the first 14 s were a gray screen, and the following 240 s consisted of a 12-Hz counterphase flickering radial checkerboard presented for the remainder of the run (Fig. 1A). To evoke a continuous oscillation in the visual cortex, the luminance contrast of the checkerboard was modulated in time as either a sinusoidal (experiments 1 and 2) or sine-squared (experiments 2 and 3) wave of 0.2 Hz, 0.33 Hz, 0.5 Hz, or 0.75 Hz, leading to a stimulus that varied smoothly between uniform gray and high-contrast checkerboard. Each subject participated in one to three runs of the 0.2-Hz sinusoidal modulation. Not all subjects viewed every frequency and modulation pattern, because multiple runs of the same stimulus frequency were used in the same subjects to improve detection. Subjects who viewed the 0.33-Hz stimulus did so for two or three runs, subjects who viewed the 0.5-Hz sinusoidal or sine-squared stimulus did so for three to eight runs, and subjects who viewed the 0.75-Hz stimulus did so for 6–10 runs. The sine vs. sine-squared comparison was done as part of experiment 2, and all subjects who viewed a sine-squared stimulus also viewed the sinusoidal stimulus so within-subject amplitude comparisons could be made. In experiment 3, all subjects viewed the sine-squared 0.75-Hz stimulus, and one subject also viewed a sinusoidal stimulus. For this subject the sine and sine-squared conditions were averaged together in the analysis because no difference in response timing was observed. In experiment 1, subjects passively viewed the stimulus, except for one subject who performed the same fixation task used in experiment 2. In experiments 2 and 3, a red dot was positioned at the center of the screen to assist with fixation. The brightness of the dot alternated between light and dark, with switching times drawn from a uniform distribution of (0.8, 3) s. Subjects were asked to press a button as soon as they detected a change in brightness, and responses were recorded to track performance. The size of the dot was adjusted initially in a practice run performed just before starting the functional scans, targeting a detection rate of 80%, and was adjusted further between runs if a subject’s performance changed substantially throughout the session.

Imaging Acquisition.

In experiments 1 and 2, subjects were scanned on a 3-T Siemens TIM Trio scanner (Siemens Healthcare) with the vendor-supplied 32-channel head coil. Anatomical images were acquired with a 1-mm isotropic multiecho magnetization-prepared rapid gradient-echo (MPRAGE) protocol (59) with TR = 2,510 ms, echo time (TE) = 1.64, 3.5, 5.36, 7.22 ms, 7° flip angle, bandwidth = 651 Hz per pixel, FOV = 256 × 256 × 176 mm, and R = 2 acceleration. For functional runs, oblique-axial slices were positioned to target the calcarine sulcus. In experiment 1, functional scans acquired five oblique unaccelerated interleaved single-shot gradient-echo echo-planar imaging (EPI) slices with 2.5-mm isotropic resolution, TE of 28 ms, echo-spacing of 0.52 ms, 30° flip angle, FOV = 190 × 190 mm, and a TR of 246 ms. In experiment 2, functional scans acquired 10 interleaved oblique slices using single-shot gradient-echo blipped-controlled aliasing in parallel imaging (CAIPI) SMS EPI (12) with multiband factor = 2, CAIPI shift = FOV/3, FOV = 190 × 190 mm, with 2.5-mm isotropic resolution, TE of 28 ms, 30° flip angle, echo-spacing of 0.58 ms, and TR of 280 ms. No dummy scans were used, and the transient before steady-state was discarded during the data-processing stage. A whole-brain reference scan (consisting of 55–70 EPI slices to cover the brain) using the same image-encoding parameters was acquired at the end of the session to assist with anatomical registration.

In experiment 3, subjects were scanned on a 7-T Siemens whole-body scanner with a custom-built 32-channel head coil. The first scan acquired anatomical images with a 0.75-mm isotropic multiecho MPRAGE protocol with TR = 2,530 ms, TE = 1.76, 3.7 ms, flip angle = 7°, acceleration = 2, bandwidth = 651 Hz per pixel, FOV = 240 × 240 × 168 mm (59). Functional runs were acquired as single-shot gradient-echo blipped-CAIPI SMS-EPI (12) with 15 interleaved oblique slices with 2-mm isotropic resolution targeting the calcarine sulcus, using R = 2 acceleration with fast low-angle excitation echo-planar technique for auto-calibration signal (FLEET-ACS) (60), multiband factor = 3, matrix = 120 × 120, CAIPI shift = FOV/3, TR = 227 ms, TE = 24 ms, echo-spacing = 0.59 ms, and flip angle = 30°. The flip angle was selected to achieve the value closest to the Ernst angle calculation while remaining within the scanner specific absorbance rate (SAR) limits. As above, a whole-brain reference scan using the same image-encoding parameters was acquired at the end of the session to assist with anatomical registration.

fMRI Preprocessing.

All localizer runs were motion corrected with AFNI software (https://afni.nimh.nih.gov/) using the middle frame in the time series as the reference. No spatial smoothing was applied. All further preprocessing for the localizer run was implemented in FSL (fsl.fmrib.ox.ac.uk/fsl/fslwiki/). To remove the transient signal change at the beginning of each run caused by stimulus onset, the first ∼24 s were discarded (the first 98 volumes were discarded in experiment 1 localizer runs, the first 86 volumes were discarded in experiment 2 localizer runs, and the first 106 volumes were discarded in experiment 3 localizer runs). A high-pass temporal filter of 30 s was used. The remaining functional runs were slice-timing corrected, motion corrected to the middle frame using AFNI, and detrended using piecewise quadratic splines with knots every 20 s in Matlab. A high-pass finite impulse response filter was applied to filter runs with a 0.2-Hz stimulus above 0.1 Hz, runs with a 0.33- to 0.5-Hz stimulus above 0.2 Hz, and runs with a 0.75-Hz stimulus above 0.5 Hz. The data then were upsampled to 20 Hz using cubic spline interpolation to facilitate stimulus-locked averaging.

ROI Selection.

All analyses were performed within the individual subject’s native space rather than in a common atlas space. In each session, a single run in which the sinusoidal 0.2-Hz stimulus was presented was used as a functional localizer to select visually responsive voxels. A general linear model (GLM) was fit in FSL using two custom basis functions, a sine and cosine wave with a period of 5 s, to detect periodic activation. The F-statistic for the combined fit to both basis functions was transformed to a z-score, and voxels with a z-score above 3 were selected for further analysis. A z-score threshold of 4 was used for experiment 3 to take advantage of the higher signal-to-noise ratio that can be achieved at 7 T. ROIs were selected for each subject from the functional localizer run, and this run then was registered to the anatomical data using boundary-based registration (61) to identify a rigid transformation (six degrees of freedom), using the reference scan as an intermediate template. Each subject’s cortical surface reconstruction was generated automatically from the MPRAGE volumes using FreeSurfer (62), and the boundaries of V1 were computed automatically from the cortical folding pattern (63, 64). Only EPI voxels corresponding to the automatically generated V1 labels provided by FreeSurfer (labels were assigned from the white matter surface to the pial surface) were retained. If fewer than 10 voxels were identified in the functional localizer, the subject was excluded from further analysis (as described in Study Participants above, this criterion excluded one subject in experiment 1, one subject in experiment 2, and one subject in experiment 3). The selected voxels in the localizer run then were mapped to each of the other functional runs in the session by registering all runs to the anatomical scan and concatenating the inverse of the resulting per-run registration matrices with the functional localizer registration matrix. To generate an ROI in nonactivated gray matter for the control analyses, ROIs were hand-drawn to include voxels within the lateral occipital cortex with negligible activation on the localizer run, and then these voxels were mapped to the functional runs as described above.

Detection of Periodic Activation.

The ROI identified in the localizer run was applied to the remaining runs by registering each run to the subject’s cortical surface reconstruction. To analyze the periodic response to the periodic contrast modulation, stimulus-triggered plots were computed by averaging the mean time series across the whole ROI on each cycle of the stimulus (i.e., every 5 s during 0.2-Hz modulation, every 3 s at 0.33 Hz, and every 2 s at 0.5 Hz). The first few cycles of the stimulus were excluded to minimize transient effects (three cycles for 0.2 Hz, five cycles for 0.33 Hz, seven cycles for 0.5 Hz, and 10 cycles for 0.75 Hz). Activation is reported as percent signal change, where baseline is defined as the mean signal value in the second half of the run.

Linear Model Simulations.

The predicted fMRI response was modeled by convolving a sinusoidal stimulus with an HRF. For initial modeling, the predicted amplitude with a canonical SPM double-gamma HRF, a single-gamma HRF (shape = 6, scale = 1), and the auditory impulse response HRF characterized by Glover (30) were used. The predicted response was defined as the amplitude of the predicted oscillation once the response reached a steady plateau. In analyses exploring the possibility of a narrower HRF, narrower functions were generated by reducing the scale parameter of the first gamma in the double-gamma function. In analyses demonstrating predicted nonlinear effects (simulations in Fig. 1E), the HRF was scaled according to the parameters reported in Liu et al. (20), taking the predicted reduction in amplitude for a given ISI and applying it to a visual stimulus with the same period.

fMRI Signal Amplitude Statistics.

To ensure that our statistics were valid when studying small signals near the noise floor, we computed oscillation amplitudes using a resampling-based procedure, reducing the required assumptions about the statistical properties of the data. The reported fMRI response amplitude is the magnitude of the sine wave fit to the average response through linear regression. The statistics on the fMRI response amplitude were computed using a nonparametric bootstrap and were averaged in circular space. One thousand bootstrap samples were calculated; each calculation consisted of five steps: (i) drawing a new sample of sessions; (ii) drawing a new sample of trials within those sessions, in which each stimulus cycle is considered to be a trial; (iii) computing a mean stimulus-triggered time series from the resampled data; (iv) estimating the magnitude and phase of the best-fit sine wave to the resampled time series using linear regression against a sine and cosine wave; (v) vectorially projecting the resampled sine wave onto the mean sine wave computed on the original dataset and storing the projection magnitude as the bootstrap statistic. This procedure resulted in 1,000 bootstrapped estimates of the signal amplitude at a given oscillation phase, and the 95% CI was drawn from the 2.5th and 97.5th percentiles. When amplitudes for an individual subject session were computed, the same procedure was used, but the first step was omitted because only a single session was analyzed for each individual-level statistic.

Physiological Noise Correction.

Control analyses demonstrating results after physiological noise correction (Fig. S5) were performed using ventricle and white matter nuisance regressors. The ventricle and white matter ROIs were first identified automatically from the anatomical data using FreeSurfer. These labels then were eroded using a 3-mm cube kernel to ensure that no boundary voxels were accidentally included and then were transformed into the functional space using the registration matrix calculated as described above. The mean of each nuisance ROI was then high-passed with the same parameter settings as the V1 ROI, and the cleaned V1 signal was recalculated by regressing out the ventricle and white matter ROI time series from the V1 ROI time series. These cleaned V1 time series were fed into the analysis procedure as described above in fMRI Signal Amplitude Statistics.

Spectral Analysis.

Power spectral densities for the V1 ROI were calculated by first identifying the V1 ROI as described above in ROI Selection. All voxels within the ROI then were spline detrended with knots placed every 20 s and were normalized to percent signal change. The time series used for spectral analysis was the mean across voxels within the ROI of each run; the first 25 s of data were discarded to avoid transient effects. The Chronux toolbox (chronux.org) (65) was used to compute the spectra, using five tapers, and theoretical error bars were computed using alpha = 0.05.

EEG Acquisition.

EEG was acquired simultaneously with fMRI in four subjects who participated in experiment 2. The EEG was recorded with an MR-compatible Geodesic 400 MR System (Electrical Geodesics, Inc.) using a 256-channel net. Data were sampled at 1,000 Hz and referenced to the Cz electrode. EEG acquisition was synchronized to the scanner’s 10-MHz clock to align data sampling with the gradient artifact. A trigger was recorded in the EEG system at the beginning of each volume acquisition to mark the onset of each gradient artifact. To assist with ballistocardiogram artifact removal, an ECG was also acquired using two MR-compatible disposable ECG leads (InVivo Corp.) positioned diagonally on the chest across the heart.

EEG Analysis.

Gradient switching artifacts were cleaned using a 10-sample moving average subtraction, and ballistocardiogram artifacts were cleaned using optimal basis sets (66) implemented in NetStation (Electrical Geodesics, Inc.). To assess the neural response to the flickering checkerboard, the signal from channel OZ was selected in each volunteer. The raw time series was extracted on each cycle of the stimulus, detrended, and then averaged across all cycles and all subjects, resulting in a mean triggered EEG time series for each run. Two runs were excluded for having an SD above 500 μV because of failure of the gradient-cleaning algorithm. The amplitude envelope for each run then was extracted by applying a finite impulse response filter of length 1,500 samples to bandpass between 11.6 and 12.4 Hz to the mean triggered EEG in that run, taking the Hilbert transform, and computing the magnitude. Reported figures show EEG time series averaged across runs and the mean amplitude envelope at 12 Hz averaged across runs. The CI for the difference in amplitude across runs was computed with a nonparametric bootstrap that resampled the runs and recomputed the difference in amplitude 1,000 times.

To compute cross-correlation of the EEG-induced signal and the fMRI signal in V1, the 12-Hz amplitude envelope in channel OZ was detrended and downsampled to match the sampling rate and filtering of the fMRI data. The first 100 time points in each signal were dropped to avoid transient effects. Any time points with amplitude above 20 μV were discarded as artifact and replaced with the mean amplitude over the time series. The cross-correlation between the OZ amplitude at 12 Hz and the mean V1 signal (from the ROI defined in the functional localizer as described above) then was computed over 40 lags, normalizing so that the autocorrelation of each signal was equal to 1.

EEG Spatial Plots.

For the spatial plot of EEG amplitude (Fig. 3A), all channels first were rereferenced to the common average to minimize spatial biases from the Cz electrode used as a reference during acquisition. Channels positioned on the cheeks were excluded from the analysis and were excluded from the common reference computation because of large ballistocardiogram artifacts in this region. Data then were filtered between 0.1 Hz and 35 Hz using a finite impulse response filter of length 2,000 samples, and were downsampled to 200 Hz. For each channel, the SSVEP was computed as the mean stimulus-locked EEG across all cycles. The triggered results were filtered between 11.6 and 12.4 Hz, Hilbert transformed, and the absolute value was taken, resulting in a measure of instantaneous amplitude in the frequency band of interest. Channels with a maximum amplitude larger than 25 μV were rejected as noisy. The maximum amplitude of the 12-Hz signal averaged across subjects was plotted onto the standard 256-channel net electrode coordinates provided by Electrical Geodesics, using EEGLAB (67).

Balloon Model Simulations.

The balloon model was implemented in Matlab using the equations described by Buxton et al. (37), and the parameter set was varied within previously reported physiologically plausible ranges (25, 37, 38, 68). To simulate the BOLD signal resulting from stimuli of different lengths, a single cycle of a sine wave at varying frequencies was entered as the blood flow input to the balloon model. To simulate the response to neural oscillations, neural activity with a 14-s baseline followed by a 240-s sinusoidal oscillation (identical to the stimulus waveform) was input to the model and then passed through neurovascular coupling equations (69) to determine the flow input (Fig. 5 B and C). All equations and parameter settings for the balloon model simulations are provided in SI Appendix.

Voxel-Dependent Phase Analysis.

The voxel-dependent phase analyses included only subjects with at least 30 responsive voxels. A template for each voxel’s response was defined as a sinusoidal wave with a frequency of 0.2 Hz over 5 s. A mean time course for each voxel was computed by calculating stimulus-triggered averages, as described above, from the functional localizer run. The time course of each voxel selected in the localizer run was correlated with the template sine wave at 40 lags ranging from −1 to 1 s, and the lag with highest correlation was taken as the estimate of that voxel’s lag. The voxels were sorted according to lag: The earliest 33% were defined as the early-responding voxels, and the latest 33% were defined as the late-responding voxels. Then the amplitude of responses in early- vs. late-responding voxels was computed on other runs, excluding the localizer run. The amplitude was computed as described above, by resampling the trials and projecting the resampled data onto the best-fit sine wave. The phase lag between early- and late-responding voxels was computed by estimating the phase of response on each resampled dataset as the arctangent of the sine and cosine regressor estimates and subtracting the phases of the early-responding voxels from the phase of the late-responding voxels to obtain 1,000 bootstrapped samples of the phase lag. To determine the amplitude of the fMRI response across different groups of voxels, the phase of the response in this analysis was allowed to vary across subjects (because the lags were not identical in different subjects). The median amplitude was computed as described above, except that the response magnitude was computed for the within-subject amplitude, and these magnitudes then were averaged across subjects. The ratio in amplitudes is reported as the median ratio across subjects, and P values were calculated using the Wilcoxon signed-rank test to test a paired difference of late- and early-responding voxels within each subject.

Discussion

We conclude that the fMRI response to oscillatory neural activity is detectable up to at least 0.75 Hz within a single 7-T scan session in individual subjects, and higher frequencies may be detectable with future gains in MRI sensitivity. The amplitude of the fMRI signal at high frequencies is an order of magnitude larger than predicted by canonical linear models, suggesting that fMRI could provide a new method for noninvasively localizing oscillatory neural activity in the human brain. The strong oscillatory responses result from the faster dynamics of the BOLD response when neural activity is continuous and rapidly varying, suggesting that different models of the hemodynamic response should be used in studies seeking to analyze ongoing periodic activity or rapidly fluctuating activity rather than large, transient task-evoked activations. The HRFs derived from these conventional block-design stimulation paradigms do not represent a true “impulse response” in the strict sense of the term; instead, for rapid stimulus presentations, the shape of the HRF varies as a function of the stimulus duration. The slow canonical hemodynamic response functions may reflect the slow experimental paradigms used to obtain them, whereas hemodynamic responses to rapidly fluctuating neural activity are, in fact, fast. This interpretation also could explain the observations of previous studies that have reported nonlinear fMRI responses to short-duration stimuli (17, 25, 34, 42). We suggest that, rather than representing a problem for fMRI because of the failure of the canonical linear models, these fast responses in fact mean that fMRI has an unexpectedly strong ability to measure naturalistic, rapidly varying neural activity. Updated models with faster HRFs may provide a generally better representation of the true hemodynamic response during high-level cognitive tasks, because it is likely that cortical activity typically is ongoing at fluctuating rates rather than slowly alternating between the silent and high firing rates that can be induced in primary sensory cortices through a blocked experimental design.

Our model suggests that both viscoelastic effects and a new vascular baseline state during rapid neural activity could contribute to the fast dynamics we observed. The fact that increasing the variability in neural firing rates through a narrower stimulus waveform (Fig. 4) increased the fMRI response amplitude suggests that the HRF waveform depends on the dynamic activity patterns of the neurons. The important influence of viscoelastic effects suggests that classic block designs induce steady-state dynamics with a slow HRF, whereas uncoupling of CBF and CBV during dynamic neural activity leads to a sharper HRF and stronger frequency response. Although we could not directly measure the CBF responses to these fast oscillations because of the limited temporal resolution and sensitivity of arterial spin-labeling methods, previous experiments have demonstrated that the CBF–CBV coupling is altered during dynamic stimulation (43) and have suggested that the CBV lags during dynamic neural activity; this suggestion is consistent with our proposed model. Further studies will be needed to assess the mechanism underlying our results more conclusively. Experiments manipulating total flow using hypercapnia or caffeine have found that the shape of the hemodynamic response changes in a counterintuitive manner that does not match model predictions (44, 45); however, these agents also influence neuronal activity and oxygen consumption (46, 47) and may act through different pathways than neuronal activity (48). Directly manipulating CBF and/or neural activity would be valuable for testing the underlying mechanism. Although selectively manipulating a single parameter of the vasculature is not feasible in humans, studies in animal models could manipulate either local neuronal activity or local vessel dilation while performing simultaneous flow and neuronal imaging to test these mechanisms causally.

We also show that the impact of hemodynamic delays is severe when studying signals above 0.1 Hz, because the delays typically seen in vasculature can be hundreds of milliseconds (41, 42, 49), large enough to cause phase cancellation in rapidly oscillating signals. Spatial smoothing can therefore attenuate oscillatory fMRI signals substantially, because the delay in neighboring voxels can differ according to their local vascular anatomy. Analysis methods that take local vascular delays into account (15, 50–52) will be essential when analyzing fast fMRI activity. Smaller voxel sizes also could improve the resolution of higher frequencies, although fMRI’s spatial resolution is also limited by its point spread function. Ultimately, high-spatial-resolution scans are expected to yield better results when studying fast neural activity, because they would minimize smoothing across regions with different phase delays. Current fMRI analyses are weighted toward the large (and hence slow) signals from draining veins, and shifting to focus selectively on the rapidly responding voxels, which exhibited less attenuation at high frequencies, may enhance the detection of faster neural dynamics.

Our results suggest that fMRI now can be used to measure oscillatory neural activity on the timescale of many high-level cognitive processes, in the hundreds of milliseconds. Even higher frequencies potentially could be attained when averaging across sufficient numbers of subjects and sessions, and animal studies directly imaging the vasculature could test the upper limit of hemodynamic oscillatory responses. The temporal resolution of fMRI undoubtedly will still be limited, because it seems unlikely the vasculature follows rapid neural oscillations (e.g., >10 Hz), but our results suggest it could be useful for measuring dynamics in the slow-delta range. In particular, this approach could be used to measure endogenous low-frequency oscillations and <1-Hz modulations of gamma power, dynamics that are key to modulating attention and states of consciousness (4, 53–55). Intracranial recordings in human subjects (54, 56) have demonstrated that slow oscillatory activity is often spatially isolated, but these invasive methods can access only restricted cortical regions and are limited to patient populations. Similarly, amplitude modulation of high-frequency oscillations occurs locally and on timescales of hundreds of milliseconds, putting it in the range of phenomena that can be measured and spatially localized using this approach. Fast fMRI studies potentially could resolve the spatial distribution of these dynamics across the entire cortex and in subcortical structures simultaneously, yielding new insight into the role of oscillatory neural dynamics in human cognition.

Methods

Written informed consent was obtained from all subjects, and all experimental procedures were approved by the Massachusetts General Hospital Institutional Review Board. Experiment 1 included data from seven subjects, and experiment 2 included data from nine subjects, using a Siemens Tim Trio 3T scanner and similar stimulus paradigms but different imaging acquisition parameters. Experiment 3 included five subjects and was conducted on a Siemens Magnetom whole-body 7-T scanner. For four subjects in experiment 2 we also acquired a simultaneous EEG using an Electrical Geodesics 256-channel system. Visual stimuli consisted of a 12-Hz (inversion rate) flickering checkerboard with luminance contrast modulation oscillating at the frequency of interest. Displayed fMRI time series show the mean fMRI data triggered on each cycle of the visual stimulus. Statistics for the magnitude of the fMRI oscillation were computed using a nonparametric bootstrap to estimate the 95% CIs. Full details of acquisition and analysis procedures are provided in SI Methods.