Characterization of Mg²⁺ Distributions around RNA in Solution

Abstract

Binding of metal ions is an important factor governing the folding and dynamics of RNA. Shielding of charges in the polyanionic backbone allows RNA to adopt a diverse range of folded structures that give rise to their many functions within the cell. Some RNA sequences fold only in the presence of Mg²⁺, which may be bound via direct interactions or occupy the more diffuse “ion atmosphere” around the RNA. To understand the driving forces for RNA folding, it is important to be able to fully characterize the distribution of metal ions around the RNA. In this work, a combined Grand Canonical Monte Carlo-Molecular Dynamics (GCMC-MD) method is applied to characterize Mg²⁺ distributions around folded RNA structures. The GCMC-MD approach identifies known inner- and outer-shell Mg²⁺ coordination, while also predicting new regions occupied by Mg²⁺ that are not observed in crystal structures but that may be relevant in solution, including the case of the Mg²⁺ riboswitch, for which alternate Mg²⁺ binding sites may have implications for its function. This work represents a significant step forward in establishing a structural and thermodynamic description of RNA–Mg²⁺ interactions and their role in RNA structure and function.

Introduction

RNA serves many important cellular functions, including information transfer, catalysis, and regulation of gene expression.¹⁻³ This functional diversity is due to the variety of structures that the polynucleotide chain may adopt. Although the charge density of a polynucleotide is high as every nucleotide bears a −1 charge, RNA can adopt numerous distinct, compact folds that are important for their biological function.⁴⁻⁶ Toward this end, metal ions play an important role in stabilizing RNA folds by shielding the repulsive backbone charges. In particular, divalent magnesium (Mg²⁺) is commonly bound to RNA, and some RNA fold only in the presence of Mg²⁺.⁷⁻¹⁰ The role of Mg²⁺ in stabilizing RNA conformations includes both indirect and direct interactions. The former involves Mg²⁺ occupying the so-called “ion atmosphere” around RNA in solution,⁸ in which mobile ions are not specifically bound to any RNA functional group, but they are attracted by the electric field arising from the anionic RNA.¹¹ Mg²⁺ in this environment may participate in water-mediated, or outer-shell, interactions with RNA. Direct interactions are associated with the high charge density of Mg²⁺ that allows it to bind to RNA directly through inner-shell coordination, including to tight turns in the RNA structure as well as simultaneously ligating multiple phosphate groups in the RNA backbone, thereby directly stabilizing specific folded conformations. To better understand the role of these various Mg²⁺–RNA interactions on RNA conformation, it is necessary to fully characterize the distribution of Mg²⁺ around RNA.

The high charge density of Mg²⁺ that allows it to play a central role in RNA conformation complicates efforts to study that role on an atomic level. Identifying Mg²⁺ binding sites on folded or unfolded RNA structures remains challenging, yet essential for understanding the forces governing RNA folding, stability, and biological function. Whereas directly coordinated Mg²⁺ can often be resolved experimentally using methods such as X-ray diffraction and solution NMR, diffuse and indirectly coordinated Mg²⁺ are more difficult to characterize. To overcome this, theoretical methods hold great potential.

Previous theoretical efforts have found limited success in reproducing known crystal structure positions for Mg²⁺.¹²⁻¹⁵ These methods have relied on static structures, electrostatic surface calculations, and/or continuum representation of solvent, thus ignoring dynamics, ion correlation effects, and the influence of water structure around the ions, including the corresponding configurational entropy contribution. Thus, it is attractive to use more rigorous simulation methods, such as explicit-solvent molecular dynamics (MD) simulations, to evaluate RNA structures for possible Mg²⁺ binding sites and to relate these binding events to subsequent local shifts in conformational dynamics. However, there is a large activation energy for partial desolvation of Mg²⁺,^16,17 which makes sampling the distribution of Mg²⁺ in and around RNA largely intractable on the time scales typically accessible to traditional MD.

Toward a greater understanding of the interactions of Mg²⁺ with folded RNA, we present a theoretical investigation into the distribution of Mg²⁺ in and around four structurally distinct RNAs¹⁸⁻²¹ using a combined Grand Canonical Monte Carlo-MD (GCMC-MD) approach.²² The approach involves the use of explicit solvent for both GCMC sampling of Mg²⁺ around folded RNAs and MD, to refine the GCMC-identified ion distribution by allowing the RNA structure and aqueous environment to respond to changes in the Mg²⁺ position. Use of GCMC overcomes the use of MD alone, as exchange rates of Mg²⁺ coordinating water are on the order of μs¹⁷ and exchanges of Mg²⁺ with anionic phosphate groups are on the ms time scale.^23,24 The RNA structures used in this work represent a large range of sizes (26–161 nucleotides) and a variety of tertiary structures and contain both inner- and outer-shell Mg²⁺ coordination by RNA functional groups, allowing an analysis of the competition between fully and partially hydrated ions and the ability of the GCMC-MD protocol to distinguish between both.

Results and Discussion

Identification of Experimental Mg²⁺ Binding Sites

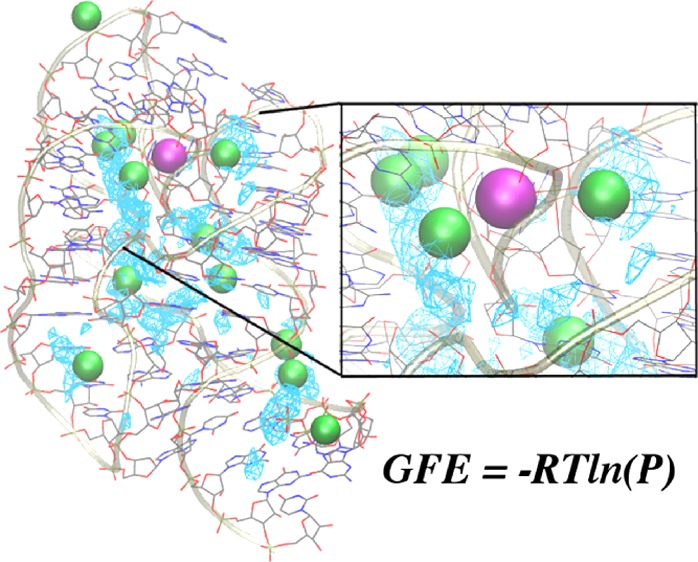
To address the initial objective of assessing the ability of GCMC-MD to reproduce experimentally identified Mg²⁺ binding sites, we computed the occupancy of Mg²⁺ over the surface of the four RNA structures. These occupancies were converted to “grid free energies” (GFE)²⁵ according to G = −k_BT ln(P), where P is the probability of occupying a voxel (1 Å cubic unit of volume) on the RNA surface relative to the voxel occupancy of the same species in bulk solution, k_B is the Boltzmann constant, and T is the temperature (298 K). Thus, the GFE provides a quantitative measure of the affinity of a given species (in this case, Mg²⁺ ions) for different regions across the RNA surface, which can be used to both evaluate the relative affinity of known Mg²⁺ binding sites and predict new ones. The GFE maps can be further discretized to identify Mg²⁺ binding sites using the so-called “Site-Identification by Ligand Competitive Saturation (SILCS) pharmacophore” method described elsewhere.²⁶ Briefly, an energetic cutoff value, −3 kcal mol^–1 in this study, is used as an upper limit to determine the most favorable regions within the GFE maps, and the voxel GFE values are clustered to yield cationic pharmacophore features representative of Mg²⁺ binding sites. The GFE maps themselves can be used to score the experimentally assigned Mg²⁺ sites as a way to evaluate the favorability of these sites, as affinity for specific Mg²⁺ sites will be different in a crystal environment versus in aqueous solution.

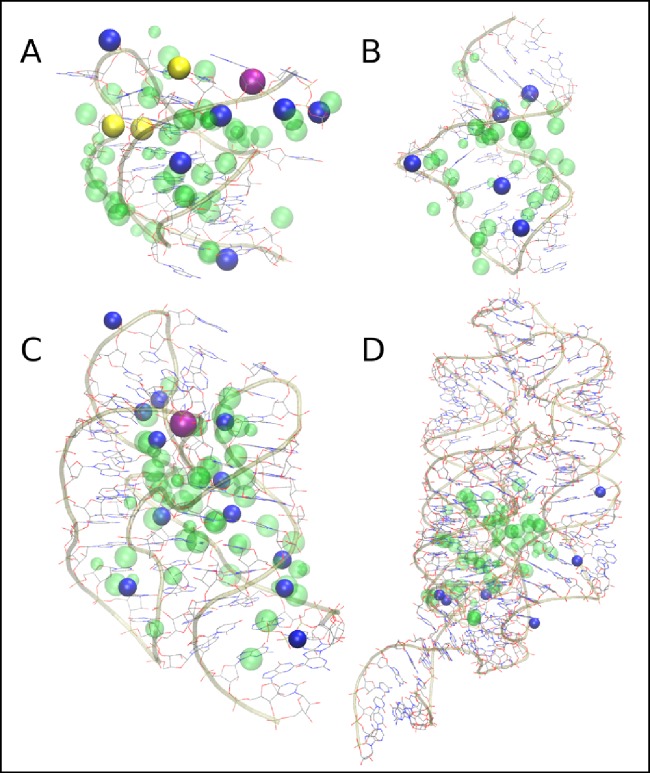
Figure 1 shows the predicted binding sites for Mg²⁺ superimposed on the crystal or NMR structures of each of the RNAs considered here, constructed by discretizing the GFE maps shown in Figure S1 of the Supporting Information. Overall, the binding sites overlap well with the experimentally identified Mg²⁺ sites (Table 1), including both direct and diffuse binding, with few exceptions (discussed below). On the basis of the minimum distance between each experimental Mg²⁺ position and predicted binding sites (Table 1), it is clear that that GCMC-MD approach was able to identify the locations of Mg²⁺ ions at favorable sites that coincide with the experimental assignments. The intervals of MD refined the positions identified by GCMC, as can be seen by comparing the Mg²⁺ maps from GCMC alone (Figure S2), which cover a larger portion of each RNA surface and those generated during the subsequent MD simulations (Figure S1), which show more defined regions of favorable occupancy. MD simulations from the same starting configurations, without intervals of GCMC sampling, show only partial coverage of experimental Mg²⁺ binding sites and sparse occupancy of the occluded volume (Figure S3), consistent with the slow exchange rates of Mg²⁺ discussed above.

Figure 1.

Mg²⁺ binding sites based on SILCS pharmacophore maps of Mg²⁺ distributions (green spheres) at a cutoff of −3 kcal mol^–1 from GCMC-MD superimposed on the crystal or NMR structures of the RNA molecules considered in the present work: (A) BWYV pseudoknot, (B) VS ribozyme stem-loop VI, (C) 23S rRNA, and (D) Mg²⁺ riboswitch. RNA atoms are colored by element (C = gray, H = white, N = blue, O = red, P = gold), and experimental positions of Mg²⁺, Na⁺, and K⁺ ions identified in the crystal or NMR structures are shown as dark blue, yellow, and magenta spheres, respectively. The radius of each pharmacophore sphere reflects the number of voxels included in the assigned cluster, with larger spheres indicating larger clusters. The locations of Os³⁺ ions used experimentally to resolve additional hydrated Mg²⁺ binding sites in panel (C) are represented as Mg²⁺.

Table 1. Minimum Distance between SILCS Pharmacophore-Identified Mg²⁺ Binding Sites and Experimentally Assigned Mg²⁺ Sites, and the Atomic GFE Scores for the Experimental Mg²⁺ Sites^a.

system/site	minimum distance (Å)	atomic GFE (kcal mol–1)
Beet Western Yellow Virus (BWYV) Pseudoknot
Mg-29	2.01	–4.47
Mg-34	6.95	+1.64
Mg-38	2.82	–1.58
Mg-45	2.25	–2.19
Mg-52	2.58	–1.86
Mg-59	3.34	+1.64
Varkud Satellite (VS) Ribozyme SLVI
Mg-101	2.34	–0.16
Mg-102	4.18	–0.88
Mg-103	3.52	–3.03
Mg-104	0.91	–3.44
Mg-105	2.94	–1.47
23S rRNA
Mg-159	1.23	–3.19
Mg-160	3.58	–1.24
Mg-161	1.75	–2.40
Mg-163	1.70	–3.14
Mg-164	2.60	+1.64
Mg-165	16.10	+0.22
Mg-166	6.28	–0.16
Mg-167	1.13	–3.11
Mg-168	2.63	+0.22
Mg-172	3.26	–2.28
Mg-173	1.53	–3.26
Mg-174	2.94	–2.49
Mg2+ Riboswitch
Mg-201	1.96	–1.31
Mg-202	2.09	–3.00
Mg-203	5.08	–0.90
Mg-204	12.21	–1.07
Mg-205	6.16	–0.99
Mg-206	14.32	0.00

^aMg²⁺ residue labels are shown as they are listed in each PDB file.

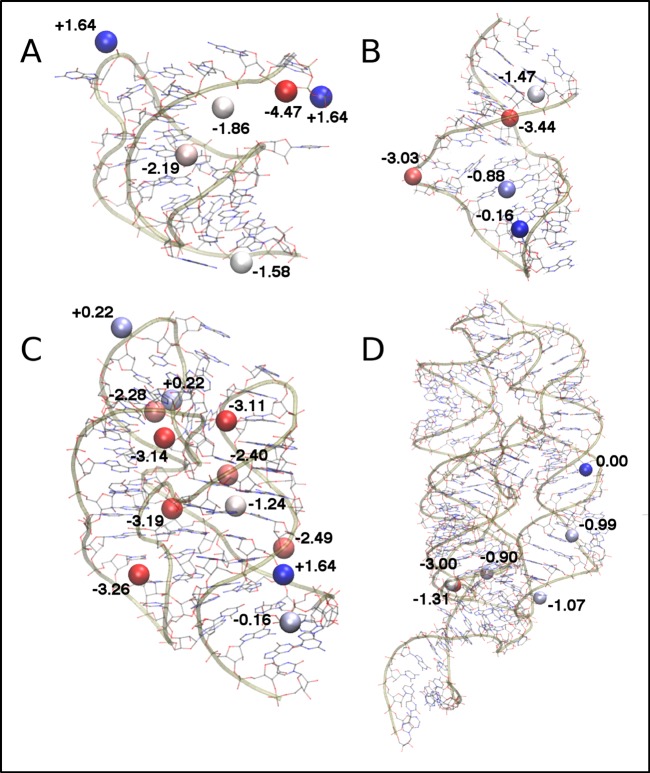
Experimental Mg²⁺ positions were scored in terms of their overlap with the GFE maps to provide a quantitative estimate of the relative affinity of Mg²⁺ for these sites. Figure 2 shows the scores for each experimentally identified Mg²⁺ ion, and their distances from the nearest predicted binding site are listed in Table 1. The scoring of the Mg²⁺ positions indicates that nearly all of the experimentally identified sites are favorable, with a few exceptions. An important consideration in evaluating these results is Mg²⁺ coordination between adjacent RNA molecules in the crystal structures. The four peripheral Mg²⁺ in the BWYV structure are all mediated by crystal contacts, and the 5′-terminal guanosine triphosphate cap is artificial;²¹ thus, the occupancy of these sites in aqueous solution remains an open question. Two of these sites have favorable atomic GFE scores, −4.47 and −1.58 kcal mol^–1, though the former will not be relevant to the real BWYV pseudoknot as it is bound to the artificial cap. Two sites are coordinated via crystal contacts²¹ and have unfavorable atomic GFE scores (+1.64 kcal mol^–1), indicating that these sites are not likely to be occupied in solution. One Mg²⁺ on the 23S rRNA¹⁹ has an unfavorable score of +0.22 kcal mol^–1 and has no nearby predicted binding site (Figure 1C, top-left ion), but given that it is coordinated between neighboring RNA molecules in the crystal, it is unlikely to be relevant to Mg²⁺ occupancy for RNA in solution. Similarly, the other two poorly scoring ions (with scores of +0.22 and +1.64 kcal mol^–1, respectively) are not specifically coordinated by any RNA group, and thus, their positions may reflect unique features of the crystal packing environment that do not extend to a solvated state. Notably, the GCMC-MD comprehensively sampled the major groove of the BWYV structure in the region occupied by two Mg²⁺ ions that are bound only via interactions with one RNA molecule of the crystal structure (Figure 1). One of these Mg²⁺ is known to be critical for BWYV pseudoknot stability, as its dissociation leads to unfolding.²¹ Its atomic GFE score of −2.19 kcal mol^–1 indicates that the GFE maps correctly identify this site as being very favorable for interacting with Mg²⁺. The VS ribozyme stem-loop VI structure was determined using solution NMR¹⁸ and therefore does not suffer from complications associated with crystal contacts. The GCMC-MD sampling predicts that all of the experimentally identified sites are favorable within the GFE maps, though two ions occupy regions of comparatively weak affinity (−0.16 and −0.88 kcal mol^–1). Both of these sites are fully hydrated in the NMR structure and interact primarily via water-mediated hydrogen bonding to nucleobase atoms. These sites were not sampled at all during a 100 ns unbiased MD simulation (Figure S3). The results of our relative affinity scoring are similar to those obtained by Misra and Draper,²⁷ who used a series of nonlinear Poisson–Boltzmann calculations in continuum solvent at varying salt concentrations to determine the affinity of several experimentally assigned Mg²⁺ to an RNA hairpin and the Escherichia coli 23S rRNA, which differs by only one base (U1061A) from the Bacillus stearothermophilus structure studied here. They found that at 1 mM Mg²⁺, the free energy of binding for diffuse ions bound to the 23S rRNA was on the order of −0.3 to −0.8 kcal mol^–1. Extrapolating to 50 mM Mg²⁺ used in our GCMC-MD sampling, these binding free energies fall in the range of −1 to −3 kcal mol^–1, in good agreement with the relative affinities we have calculated in the present work.

Figure 2.

Atomic GFE scores for all experimentally assigned Mg²⁺ sites. Each Mg²⁺ ion is colored on a gradient from blue (least favorable) to red (most favorable) according to its atomic GFE score (labeled) for the studied systems: (A) BWYV pseudoknot, (B) VS ribozyme stem-loop VI, (C) 23S rRNA, and (D) Mg²⁺ riboswitch.

Predictions of Mg²⁺ Binding Sites

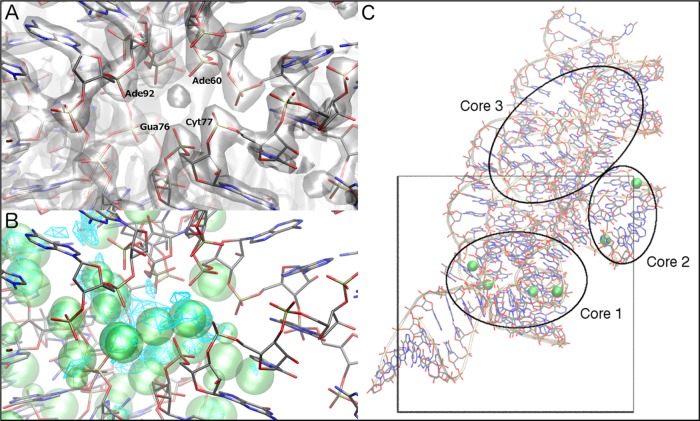
In addition to reproducing the known Mg²⁺ binding sites, our GCMC-MD approach uncovered additional regions on each RNA surface to which Mg²⁺ can bind. Most of these are near known sites, but in some cases they are completely new (Figure 1) and represent predicted sites with which Mg²⁺ can favorably interact in solution to modulate RNA structure and dynamics. This outcome is particularly evident in the case of the Mg²⁺ riboswitch. Scoring the experimental positions indicates that five of the six crystallographic Mg²⁺ sites are favorable when compared to the GFE maps (Figure 2D); the final site was outside the defined GCMC box and, thus, not sampled. The remaining sites all occupy what is known as “core 1” of the M-box riboswitch structure (Figure 3C),^20,28 the region located closest to sequences that participate in terminator or antiterminator helix formation and therefore most immediately responsible for Mg²⁺-induced structural changes. Importantly, the GCMC-MD sampling also indicates that Mg²⁺ can favorably occupy regions of the riboswitch close to “core 3” (Figures 1 and 3C) that have previously been proposed using Mn²⁺ competition²⁸ and phosphorothioate nucleotide substitution experiments.²⁹ Although occupancy of these sites is not observed at all in the crystal structure,²⁰ these additional locations may play an important role in modulating the stability of the folded state and the dynamics of the Mg²⁺ riboswitch under different Mg²⁺ concentrations and therefore are predicted to be important to its function as a Mg²⁺ sensor.²⁹ Wakeman et al.²⁹ proposed additional Mg²⁺ binding sites that were not identified in the Mg²⁺ riboswitch crystal structure,²⁰ including one coordinated by Cyt89 and Gua91. GCMC-MD produced Mg²⁺ sampling near these nucleotides, agreeing with their hypothesis based on phosphorothioate substitution. However, whereas Wakeman et al. proposed that strong interference at Ade101 and Ade105 was not likely due to Mg²⁺ binding, but rather steric clashes associated with the introduction of sulfur into the backbone, we observe Mg²⁺ sampling in this region. As such, putative coordination by Ade101 and Ade105 should not be dismissed without further experimental evidence. Additionally, our approach indicated that Mg²⁺ sampled a pocket with considerable negative charge density formed by the backbone phosphate groups of Ade60, Gua76, Cyt77, and Ade92 (Figure 3). In the crystal structure, the density in this region (part of the interface between helices P4 and P5) is assigned to a water molecule, with distances to the nearest nonbridging phosphate oxygen atoms in the range of 3.0–4.4 Å. This site could easily accommodate a partially dehydrated Mg²⁺ ion, as our sampling predicts. As the packing of helices P4 and P5 against helix P2 is proposed to be important to the structural change as a function of Mg²⁺ concentration,²⁰ binding of Mg²⁺ at this newly identified site may also be important for stabilizing the P4–P5 interface during the structural interconversion of the Mg²⁺ riboswitch.

Figure 3.

Predicted Mg²⁺ binding site at the P4–P5 interface of the Mg²⁺ riboswitch. (A) Crystallographic electron density at the interface (gray surface) with residues ligating the crystallographic assigned water molecule labeled. (B) GFE maps (cyan mesh) and predicted Mg²⁺ binding sites (green spheres) at this site. (C) Three “core” Mg²⁺ binding regions of the M-box Mg²⁺ riboswitch according to Wakeman et al.²⁹ are indicated. The GCMC sampling box is mapped onto the structure.

In conclusion, we have shown that by applying GCMC sampling in combination with conventional MD simulations, it is possible to comprehensively sample Mg²⁺ occupancy around complex RNA structures to give a realistic picture of the thermodynamics of ion sampling around RNA. The method produces both inner- and outer-shell Mg²⁺ coordination by RNA moieties (Figure S4) in agreement with experimentally assigned Mg²⁺ occupancy using a computationally efficient additive force field model.³⁰⁻³² By including MD simulations between intervals of GCMC sampling, a fully dynamical picture of RNA–Mg²⁺ interactions can be generated. The implications of these interactions on local RNA dynamics are currently being investigated. Importantly, the present study shows that it is possible to reproduce known Mg²⁺ binding sites and to quantify the relative affinity for these sites in the context of solvated systems. Additionally, our approach is the first of its kind in predicting new Mg²⁺ sites that may be relevant to the RNA structure and dynamics in solution, an outcome that previous methods and crystal structure analysis cannot provide. This is particularly evident in the case of the Mg²⁺ riboswitch, which senses cellular Mg²⁺ concentration to regulate the expression of Mg²⁺ transport proteins. Whereas the primary region of sampling was in core 1, as in the crystal structure, numerous additional sites throughout the central region of the RNA structure were identified as putative Mg²⁺-binding sites. As the shift in conformational ensemble in response to Mg²⁺ is directly related to its function in gene regulation, these predictions merit additional study, particularly with respect to the effects on dynamics. Whereas previous GCMC studies have focused on highly ordered crystalline DNA systems³³ or static, ideal structures in implicit solvent,³⁴⁻³⁶ the present work is the first of its kind in addressing Mg²⁺ sampling around RNA with an explicit solvent representation of the aqueous solution and has achieved qualitative and quantitative agreement with experiments, while simultaneously yielding new predictions for Mg²⁺ occupancy in solution under ambient conditions. We expect that application of the GCMC-MD method to a wider range of folded and unfolded RNA will yield critical insights into the stabilizing forces of Mg²⁺ ions and provide a more complete thermodynamic description of interactions between ions and nucleic acids. In addition, given the limitations in the use of additive force fields for treatment of Mg²⁺ due to the absence of polarization and charge-transfer effects,³⁷⁻³⁹ we anticipate that force fields that include such contributions may yield further improvements in the description of Mg²⁺ distributions around RNA⁴⁰ when combined with the presented GCMC-MD approach.

Computational Methods

RNA Structures

The RNA structural models used in this work, from both X-ray crystallography¹⁹⁻²¹ and NMR spectroscopy,¹⁸ are listed in Table 2. The structures chosen include both canonical (helical) and noncanonical RNA structural elements, as well as both inner- and outer-shell Mg²⁺ coordination. To prepare the systems for GCMC-MD, all Mg²⁺ ions and waters present in the initial structures were removed. Other ions (Na⁺ and K⁺) were retained in their assigned positions, except in the case of the Mg²⁺ riboswitch, which was capable of adopting its folded structure in the absence of K⁺.²⁰ For the VS ribozyme stem-loop VI solution NMR structure, the first model (out of 20 in the NMR ensemble) was used. For the 23S rRNA fragment, the bound protein was removed because it has no effect on the RNA structure¹⁹ and only one RNA chain was used, as both RNA chains superimpose with <0.5 Å nonhydrogen atom RMSD. Os³⁺ ions identified in the crystal structure were also removed as [Os·(NH₃)₆]³⁺ is used to mimic hydrated Mg²⁺ ions.

Table 2. RNA Structures Used in the Present Work.

PDB ID	notes and references	size (nt)	experimental method	resolution (Å)	Mg2+ coordination (inner/outer)
1HC8	23S rRNA19	58	X-ray	2.80	4/8a
2QBZ	Mg2+ riboswitch20	161	X-ray	2.60	6/0
1L2X	BWYV pseudoknot21	28	X-ray	1.25	3/3
2MIS	VS ribozyme stem-loop VI18	26	solution NMR	N/A	2/3

^aThe two RNA chains in the crystal structure have 10 identical Mg²⁺ binding sites plus 2 [Os·(NH₃)₆]³⁺ sites that are experimental surrogates for hydrated Mg²⁺ binding sites. [Os·(NH₃)₆]³⁺ sites are considered as outer-shell Mg²⁺ in the enumeration of inner- and outer-shell Mg²⁺.

GCMC-MD Protocol

Parameters for RNA and ions were taken from the Chemistry at HARvard Macromolecular Mechanics 36 (CHARMM36) additive force field.³⁰⁻³² The water model was CHARMM-modified TIP3P.⁴¹⁻⁴³ All RNA molecules were centered in cubic boxes of sufficient size to allow addition of 50 mM total [Mg²⁺] and neutralizing Cl^– ions. Mg²⁺ ions were inserted in the GCMC exchanges in two forms in equimolar amounts: a “bare” ion and a trihydrate, [Mg·(H₂O)₃]²⁺. Several preliminary simulations were conducted, and it was found that bare Mg²⁺ (n = 0) as the sole source of Mg²⁺ in the system led to excessive rejections of the MC moves and inefficient sampling. This outcome was due to the small size of the divalent ion allowing it to be placed in nearly any accessible space in the simulation box, leading to a large number of rejections. To overcome this problem, the insertion of hydrated Mg²⁺ was considered and tested. In principle, any hydrate (1 ≤ n ≤ 6, see Figure S5) could be chosen as the species for GCMC sampling. A fully solvated (n = 6) complex would prevent direct coordination from being sampled and was too large to be efficiently inserted in the GCMC sampling region. The trihydrate form (n = 3) was found to give good sampling and could participate in both direct and indirect coordination. Results were not significantly different with n = 2, 4, or 5, so the trihydrate was chosen as the consensus representation of exchangeable, hydrated Mg²⁺ ions. The topology of the trihydrate was designed such that the oxygen atoms of the coordinating water molecules were restrained within 2.1 Å of the Mg²⁺ ion, but no coordination geometry was enforced, allowing the waters to reorganize in response to the surrounding environment. In conjunction with bare Mg²⁺, a reasonable acceptance rate (between 2 and 8% per species) was obtained without needing to use an impractical number of GCMC steps.

GCMC exchanges were performed in 60 Å cubic boxes (sufficient to cover the entire surface of the RNA) in the cases of the BWYV pseudoknot, VS ribozyme stem-loop VI, and 23S rRNA. For the Mg²⁺ riboswitch, the 60 Å cubic box encompassed the entire Mg²⁺-binding region (cores 1 and 2, Figure 3C), as it was computationally intractable to sample the entire surface of this large structure. GCMC sampling was performed using a method described previously.²² In each round of GCMC, 100 000 MC moves (insertions, deletions, translations, and rotations) were attempted, evenly divided between all four species—bare Mg²⁺, [Mg·(H₂O)₃]²⁺, water, and bare Cl^–. For species with only a single particle (bare Mg²⁺ and Cl^–), only insertions, deletions, and translations were attempted, as rotations of these particles result in no change to the configuration. A GCMC move was accepted if the energy of the generated configuration decreased, or if the Metropolis criterion was satisfied, otherwise the move was rejected. GCMC energy calculations were carried out using a simple atom-based truncation scheme within 12 Å for electrostatics and van der Waals interactions. As such, there is a small difference between the energy evaluation between GCMC and the subsequent MD simulations (see below). Because short-range electrostatic interactions are expected to dominate interactions involving ions, the absence of long-range electrostatics and the use of a hard cutoff for the van der Waals interactions should not significantly influence the outcome.

For GCMC, the excess chemical potential (μ_ex) of each species was set to its hydration free energy (ΔG_hydr). For bare Mg²⁺ and [Mg·(H₂O)₃]²⁺, the ΔG_hydr values were determined using a free-energy perturbation method described previously,⁴⁴ yielding values of −430.33 and −267.13 kcal mol^–1, respectively. The full list of complexes for which the ΔG_hydr values were determined is given in Table S1. During GCMC sampling, the μ_ex values are allowed to oscillate by a set window (Δμ_ex) to better drive sampling, therefore the method is more accurately described as “oscillating-μ_ex GCMC-MD”, and the ensemble is “GCMC-like.”²² For the Mg²⁺ species and Cl^– (μ_ex = −79.4 kcal mol^–1), Δμ_ex was set to ±20 kcal mol^–1, and for water (μ_ex = −5.8 kcal mol^–1) Δμ_ex was ±2 kcal mol^–1. We confirmed that this approach was valid by allowing μ_ex to vary freely in performing GCMC sampling of bulk solutions of several [Mg·(H₂O)_n]²⁺ hydrates, targeting a concentration of 50 mM. As shown in Figure S6, these μ_ex values converge to the value of ΔG_hydr, confirming the robustness of our approach.

Following GCMC, MD simulations were conducted using Groningen MAchine for Chemical Simulation (GROMACS), version 5.0.⁴⁵ Nonbonded interactions were calculated using the Verlet cutoff scheme,⁴⁶ with a minimum neighbor list cutoff of 12 Å. Short-range van der Waals forces were switched to zero from 10–12 Å, and an isotropic dispersion correction was applied to account for finite truncation of van der Waals interactions. Electrostatic interactions were calculated using the smooth particle mesh Ewald method,^47,48 with the real-space contribution to the Coulombic forces truncated at 12 Å. Bonds involving hydrogen atoms were constrained using P-LINCS,⁴⁹ allowing an integration time step of 2 fs. Periodic boundary conditions were applied in all three spatial dimensions.

Before MD, the configurations produced by GCMC were subjected to steepest descent minimization, followed by 100 ps of NPT equilibration at a temperature of 298 K and 1 bar of pressure, applying harmonic restraints (k = 2.4 kcal mol^–1 Å^–2) to all RNA nonhydrogen atoms, as well as bound Na⁺ and K⁺ ions, if present. Temperature was regulated using the velocity rescaling thermostat of Bussi et al.⁵⁰ and pressure using the Parrinello–Rahman barostat.^51,52 Production simulations were carried out for 500 ps under an NPT ensemble with harmonic restraints (also set to k = 2.4 kcal mol^–1 Å^–2) on RNA phosphorus atoms and crystallographic Na⁺ or K⁺ ions, if present. Such restraints allow for local flexibility of the RNA while still preserving the overall tertiary structure, as the present study is focused on the distribution of Mg²⁺ ions around the RNAs rather than comprehensive conformational sampling of the RNAs. Similarly, the maintenance of Na⁺ and K⁺ ions in the experimental locations was to allow for sampling of Mg²⁺ ions into an environment similar to that obtained experimentally, thereby facilitating comparison of the calculated and experimental Mg²⁺ distributions. During production simulations, the temperature was regulated using the Nosé–Hoover thermostat^53,54 and pressure using the Parrinello–Rahman barostat.^51,52 For each run, 200 cycles of GCMC-MD were performed, and each RNA system was subjected to 10 independent runs for a total sampling of 2 × 10⁷ GCMC steps and an MD simulation time of 1 μs.

Map Analysis

Occupancy maps were calculated from the distribution of Mg²⁺ around each RNA structure. The overlap coefficient (OC) between occupancy maps is calculated as

1

where N is the number of voxels in the GCMC region, and Q_i¹ and Q_i are the occupancies of voxel i by fragments 1 and 2 (here, Mg²⁺ ions). The values of OC range from 0 to 1, with 1 indicating exact overlap. The OC exhibits nonlinear behavior, as even small differences in the maps result in values of ∼0.8, whereas values >0.6 indicate strong similarity (Figure S7). The OC is used principally as a measure of convergence of the simulations; temporal and spatial convergence of the OC were calculated from the first 100 and last 100 cycles in each run and the first and last five runs for each structure, respectively, and are listed in Table S2. Given the similarity of the OC values during the first and last half of each run, and across the 10 independent runs, the obtained results are deemed adequately converged, such that 200 cycles of GCMC-MD is sufficient for sampling each RNA system.

Binding Site Analysis

Using the SILCS pharmacophore approach,²⁶ the GFE maps from GCMC-MD were discretized into clusters based on GFE, yielding predicted binding sites. Predicted binding sites are derived by considering only regions of the GFE maps more favorable than −3 kcal mol^–1. The spherical SILCS pharmacophore sites have radii depending on the number of voxels clustered together, with larger radii indicating greater continuous regions of similar GFE values (Figure 1). To quantitatively assess the agreement between experimentally assigned Mg²⁺ positions and the predicted binding sites, we calculated the minimum distance between the experimental position and the sphere centers along with the atomic GFE scores (see above) of the experimental Mg²⁺ positions.

Atomic GFE Calculations

Scoring of the experimentally assigned Mg²⁺ positions in the field of the GFE maps was carried out by assigning an atomic GFE value. The experimental coordinates were overlaid onto the GFE map for a given RNA structure, and for each Mg²⁺ ion, its distance to each voxel in the GFE map was calculated. If the distance was less than 1.0 Å (the resolution of the GFE maps), then the GFE score at that voxel was assigned to the Mg²⁺ ion. Thus, the nearest GFE voxel describes the favorability of the RNA surface for Mg²⁺ at a given volume and does not represent the free energy of binding of a Mg²⁺ ion.

As three of the structures used in this study were resolved using X-ray crystallography, such an evaluation is critical for understanding differences in Mg²⁺ occupancy in the crystal environment and in aqueous solution. It is important to note that these scores are not absolute free energies of binding at these locations, rather they are relative affinity scores based on the overlap of a single point in space with the GFE maps. Calculating the absolute binding free energy of Mg²⁺ to complex, folded RNA is a considerable challenge due to the heterogeneity of interactions in the bound state and is beyond the scope of this work.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsomega.6b00241.

• GFE maps; radial distribution function of Mg²⁺; geometries of [Mg·(H₂O)_n]²⁺ hydrates; convergence of μ_ex for selected [Mg·(H₂O)_n]²⁺ hydrates in bulk solution, starting from μ_ex= 0 kcal mol^–1; graphical representation of OC (Figures S1–S7); ΔG_hydr (μ_ex, kcal mol^–1) values of [Mg·(H₂O)_n]²⁺ complexes; OC values for Mg²⁺ occupancy maps over the first and last 100 cycles of all runs, and over all cycles of runs 1–5 and 6–10 (Tables S1 and S2) (PDF)

The authors declare the following competing financial interest(s): A.D.M., Jr. is co-founder and Chief Scientific Officer of SilcsBio LLC.