Reliability of measuring regional callosal atrophy in neurodegenerative diseases

Abstract

The Corpus Callosum (CC) is an important structure connecting the two brain hemispheres. As several neurodegenerative diseases are known to alter its shape, it is an interesting structure to assess as biomarker. Yet, currently, the CC-segmentation is often performed manually and is consequently an error prone and time-demanding procedure. In this paper, we present an accurate and automated method for corpus callosum segmentation based on T1-weighted MRI images.

After the initial construction of a CC atlas based on healthy controls, a new image is subjected to a mid-sagittal plane (MSP) detection algorithm and a 3D affine registration in order to initialise the CC within the extracted MSP. Next, an active shape model is run to extract the CC. We calculated the reliability of most popular CC features (area, circularity, corpus callosum index and thickness profile) in healthy controls, Alzheimer's Disease patients and Multiple Sclerosis patients. Importantly, we also provide inter-scanner reliability estimates.

We obtained an intra-class correlation coefficient (ICC) of over 0.95 for most features and most datasets. The inter-scanner reliability assessed on the MS patients was remarkably well and ranged from 0.77 to 0.97.

In summary, we have constructed an algorithm that reliably detects the CC in 3D T1 images in a fully automated way in healthy controls and different neurodegenerative diseases. Although the CC area and the circularity are the most reliable features (ICC > 0.97); the reliability of the thickness profile (ICC > 0.90; excluding the tip) is sufficient to warrant its inclusion in future clinical studies.

Highlights

• •A completely automated segmentation of the Corpus Callosum
• •Both traditional features and the thickness profile using Laplace's equation are calculated.
• •Excellent reproducibility and accuracy in healthy controls
• •Excellent reproducibility and accuracy in Alzheimer's Dementia and Multiple Sclerosis patients
• •Excellent inter-scanner reliability enabling the pooling of multi-center data

1. Introduction

The Corpus Callosum (CC) is the most important fibre bundle relaying information between homologous cortical areas. The mid-sagittal CC Area (CCA) is considered an indicator of the number of small-diameter fibres involved in higher order cognitive functions [Aboitiz, 1992] and a larger CCA has been hypothesized to reflect improved interhemispheric communication [Luders et al., 2007]. Consequently, several studies have found a positive correlation between CCA and intelligence scores [Luders et al., 2007, Luders et al., 2009, Park et al., 2008]. These findings were further corroborated by a post-mortem study of Albert Einstein's brain [Men et al., 2014], in which a significant increase in width – especially in the splenium – was found when compared to healthy controls. In contrast to these findings, some studies have also shown a negative correlation between CCA and intelligence [Ganjavi et al., 2011].

Alterations to the CC morphometry have been shown to be present in different (neurodegenerative) pathologies. An increased CC Area (CCA) was observed in children affected with Autism Spectrum Disorder [Wolff et al., 2015] and smaller CCAs were found in Schizophrenia patients [Bachmann et al., 2003, Rotarska-Jagiela et al., 2008]. Regional CC atrophy was observed in patients affected by Alzheimer's disease [Frederiksen et al., 2011, Hallam et al., 2008, Di Paola et al., 2010], in patients with Huntington's dementia [Di Paola et al., 2012, Rosas et al., 2010], in a sample of patients with mesial temporal lobe epilepsy [Schneider et al., 2014] and in patients with bipolar disorder [Sarrazi et al., 2015].

In Multiple Sclerosis, a neuro-inflammatory disease with a neurodegenerative component, correlations have been established between the Corpus Callosum Area (CCA) and the Expanded Disability Status Scale (assessing physical handicap) and the Symbol Digit Modalities Test (assessing information processing speed) [Granberg et al., 2015]. In addition - in the same study - the CCA outperformed whole-brain, lesion, white and grey matter volume in discriminating between healthy controls (HC) and MS patients. Finally, CC atrophy during the first year of treatment was found to be the best predictor (comparing to T1 and T2 lesion volumes and, brain parenchymal fraction and atrophy) of disability and its increase in a large and long-running (9 years) follow-up study [Vaneckova et al., 2012].

Due to the increasing interest in analysing the regional influence of different (neurodegenerative) pathologies on the CC, recent research has included the corpus callosum thickness profile as an important feature [Walterfang et al., 2009]; e.g. a recent study found that the regional thickness could predict the conversion from mild cognitive impairment to Alzheimer's disease [Lee et al., 2016].

Although most thickness profile generation methods rely on the orthogonal projection outward from a midline [Adamson et al., 2011], overlap between adjacent streamlines may lead to biased results inflating the thickness in more curved CC. As presented in [Adamson et al., 2014], the use of a continuous thickness calculation based on an artificial Laplacian field bypasses this limitation. Furthermore, it provides a biologically plausible model as the resulting thickness profiles are similar to the underlying organisation of the connections from the CC [Adamson et al., 2011, Hofer and Frahm, 2006] and omits the need of subdividing the CC using different partition schemes [Luders et al., 2007] (e.g. the Witelson partition [Witelson, 1989]).

Several strategies have been developed to segment the mid-sagittal plane (MSP) CC from T1-weighted magnetic resonance images. These strategies can be roughly divided into three categories [Herron et al., 2012]: a first set of methods is based on whole-brain registration to one (or multiple) common space(s) [Adamson et al., 2014, Ardekani et al., 2005, Chaim et al., 2007, Wang et al., 2009]. While the main advantage of these methods is that the CC does not need to be delineated in individual images (but only on the template), these methods lack the flexibility to capture the large inter individual differences in CC shape and require manual intervention in up to 20% of the cases [Adamson et al., 2011, Ardekani et al., 2014, Wang et al., 2009]. Furthermore, the robustness of more advanced deformation-based techniques is not clear [Herron et al., 2012], especially with respect to neurodegenerative diseases.

A second strategy relies on pre-defined rules. However, these methods seem to be vulnerable to segmentation errors (e.g. the fornix and pericallosal arteries [Herron et al., 2012]) and may not be suitable to segment the CC in various neurodegenerative diseases.

As we expected that neither deformation-based techniques, neither rule-based techniques could be reliably applied to the segmentation of the CC in patients affected by neurodegenerative diseases, we developed a method that belongs to the boundary based methods, that rely on a set of manually delineated CCs that are fed into an active shape model. As such, the variations observed in the training set limit the shape variations allowed in test-images. While the main disadvantage of these boundary-based methods seems to be the necessity to develop specific training sets for every (neurodegenerative) population, we aim at assessing to what extent this disadvantage is justified.

In this paper, we provide accuracy (comparison to manual segmentations), repeatability (subject stayed within the scanner) and reproducibility (patient was repositioned for a new scan) estimates for the most commonly used CC features (area, circularity, corpus callosum index [Figueira et al., 2007]) and the thickness profile calculated using Laplace's equation, both in healthy controls and in two neurodegenerative populations. Our aim is to provide an insight into the reliability of the different CC features and to assess whether the thickness profile – which can be easily calculated and provides more detailed information than the commonly used CC features – can be as reliably extracted as more robust features like the CC area.

2. Methods

2.1. Datasets

2.1.1. Dataset 1. Healthy controls and Alzheimer's patients from the OASIS database

The OASIS database consists of 416 subjects aged between 18 and 96 years old. For each subject, 3 or 4 individual T1-weighted MRI scans obtained in single-scan sessions were included. The scans were acquired on a 1.5-T Vision scanner (Siemens). All subjects are right-handed and female. Out of the 416 scanned subjects, 100 have been clinically diagnosed with very mild to mild Alzheimer's disease (AD) according to the Clinical Dementia Rating [Marcus et al., 2007, Morris et al., 2001]. Additionally, a reliability dataset of 20 non-demented subjects imaged on a subsequent visit within 90 days of their initial session was provided (oasis-brains.org). For more information, cf. [Marcus et al., 2007].

From the OASIS database we applied the algorithm to the 216 healthy controls that were not used for training and 100 patients affected by very mild to mild Alzheimer's Disease. For these patients, 3 to 4 scans are available. Rather than averaging the different scans to increase the signal-to-noise ratio, we processed the different scans independently. This allowed us to assess the repeatability of our algorithm. The 216 healthy controls are referred to as “OASIS_HC”, the 100 AD patients as “OASIS_AD”.

Furthermore, 20 non-demented subjects had been scanned twice within 90 days. These patients are denoted as “OASIS_HC_TRT”.

2.1.2. Dataset 2. Multiple sclerosis patients

Ten MS patients participated in a study at University Hospital UZ Brussel, Brussels, Belgium. The study was approved by the local ethics committee and all patients signed informed consent forms. MR imaging was performed for each patient twice on 3 3T whole body scanners from 3 different manufacturers (GE Medical Systems Discovery MR750 MW, SIEMENS Skyra, Philips Medical Systems Achieva). The patient was re-positioned between the first and the second scan. The GE scanner protocol contained, among others, a 3D T1-weighted FSPGR sequence (TR 7.32 ms, TE: 3.144 ms, FA 12°, 220 × 220 mm² FOV, 328 sagittal slices, 0.4297 × 0.4297 × 0.5 mm³ voxel resolution). The SIEMENS scanner protocol contained a 3D-T1-weighted MPRAGE sequence (TR: 2300 ms, TE: 2.29 ms, FA 8°, 240 × 240 mm² FOV, 176 sagittal slices, 0.9375 × 0.935 × 0.94 mm³ voxel resolution) and the PHILIPS scanner protocol contained a 3D T1-weighted FPSR sequence (TR 4.936 ms, FA 8°, 230 × 230 mm² FOV, 310 sagittal slices, 0.5324 × 0.5324 × 0.5 mm³ voxel resolution).

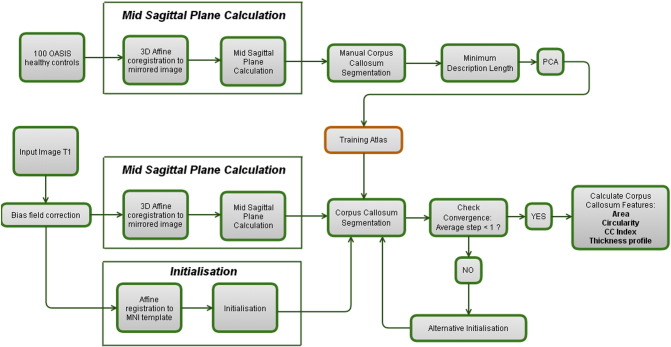
2.2. Construction of a CC training atlas

The training set consisted of 100 images from the OASIS dataset for which the corpora callosa were manually delineated on their respective Mid Sagittal Planes (MSPs). Next, a minimum description length algorithm was applied in order to solve the point correspondence problem (i.e. ensuring maximal correspondence between the n'th point on the CC boundary among the different images) [Thodberg, 2003]. The subjects used in this step are excluded from the analysis in which repeatability of the different CC features is assessed.

As a CC shape consisted of > 3000 edge points, that – in theory – could all move independently, a principal component analysis on these shapes was performed to retain 99% of the observed variance in the constructed atlas (corresponding to 16 principal components). The shape variations along the first 3 principal components are depicted in Fig. S1. Once a new image is entered in the pipeline, these 16 principal components will ensure a regularisation on the possible shapes and will ensure that the fornix is not included in the segmentation.

This way, we have constructed a training atlas (cf. Fig. 1) containing the average shape and the principal components of the shape variations observed in this sample of healthy controls. Furthermore, it contains the average pixel intensities (and their principal components) along the normal over every point on the CC edge. This atlas will serve as the input when a new image is segmented.

Fig. 1.

Overview of the segmentation pipeline.

2.3. Mid sagittal plane detection and corpus callosum segmentation

When a test-image is provided, two algorithms should be run before the actual 2D segmentation algorithm can start. First, the MSP is calculated through a 3D affine registration to the image mirrored to the current MSP. Next, a 3D-registration to a 3D T1 MNI atlas is used to estimate the initial position of the CC.1 Finally, given the MSP and the initialisation of the CC within this plane, the 2D segmentation algorithm is run. The pipeline is depicted in Fig. 1.

2.3.1. Mid sagittal plane extraction

The MSP was determined by calculating the transformation of three non-colinear points during a mirroring operation around the current MSP, followed by a 3D affine coregistration (NiftyReg, [Ourselin et al., 2002]) to the original image. The midpoints between the original and the transformed points determine the MSP. The voxel values of the MSP were calculated through trilinear interpolation.

2.3.2. Corpus callosum initialisation

The corpus callosum segmentation algorithm was initialised by the result of an affine coregistration between the subject and standard MNI-space. The resulting transformation matrix allowed to calculate the approximate location of the subject's CC. In this cross-sectional design, this affine transformation allows to transfer and rotate the average CC (averaged over all subjects used for training) to an initial position (cf. Fig. 2. A-C Green lines).

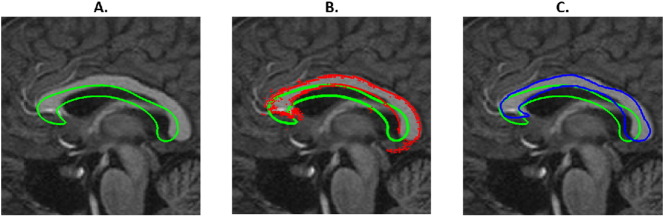
Fig. 2.

After an affine 3D registration, an average CC is initialised on to the MSP (A – Green line). For every point on the boundary, the optimal translation is calculated along the local normal by matching the intensity profile with intensity profiles observed in the training set at that point. This results in the whimsical shape (Fig. 2.B. Red dots). This shape is projected onto the first N eigenvectors observed in the training data (C. Green line: initial shape, Blue line: result after one iteration), which is used as the starting point of the following cycle. The algorithm continues until convergence (mean movement of red dots < 0.5 mm) or until the maximum number of iterations is reached. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.3.3. Corpus callosum extraction

Next, an active shape model [Cootes, 2000] was run according to the following algorithm: for every point on the edge, intensity values were sampled along the normal (using linear interpolation) and the optimal translation for that edge point was calculated by minimizing the sum of Mahalanobis distances with the eigenvectors obtained in the training-set at that same point (and saved in the CC atlas). Once this procedure is applied for all points, a whimsical CC emerges (Fig. 2.B. red points) that is subsequently projected on the 16 principal components previously found during the training of the atlas. That projection is used to rebuild the CC shape from a linear combination of the eigenvectors (Fig. 2.C. blue shape). This way, the continuity of the boundary and the exclusion of the fornix is guaranteed.

As can be seen in Fig. 2.C., the projected (blue) shape sometimes lies further from the true edge than the whimsical red dots in Fig. 2.B. Therefore, the same procedure is repeated until convergence. In order to speed up convergence, a two-step procedure was applied (in the first step the image was down-sampled to 256 × 256 voxels). More information on the method can be found in [Van Ginneken et al., 2002, Kroon, 2012].

2.3.4. Alternative optimisations

As there is a substantial interindividual variance in CC shape and as the algorithm failed to detect highly curved CC automatically, we were able to improve the performance by a second initialisation (when the first initialisation had not reached convergence) in which the initial shape was the mean CC as obtained from the training images, but elongated along the superior-inferior axis.

2.4. Morphometric feature calculation

2.4.1. Corpus Callosum area (CCA)

The CCA was calculated by applying Green's theorem on the resulting contour:

$$\text{Area}={\displaystyle \iint }\mathrm{dA}=\frac{1}{2}{\displaystyle \oint }\left(\mathrm{xdy}-\mathrm{ydx}\right)$$

This method has the advantage of fully exploiting the continuous nature of the edges obtained by the active shape model and bypasses the partial volume effects as it does not require every pixel to be classified as either CC or not CC. This results into slightly smaller CC areas than those found when deciding for each voxel individual whether or not it is contained in the CC. Obviously, the difference reduces with decreasing pixel size.

2.4.2. Circularity (CIRC)

In Alzheimer's disease, it has been suggested that the death of cells in the grey matter leads to Wallerian degeneration, which in turns leads to a reduced CCA. In [Ardekani et al., 2014], Ardekani et al. argue that CCA alone may not capture the effect of ventricular dilation and therefore suggested circularity as an appropriate measure to follow AD patients. Circularity is defined as $4\pi \frac{\mathit{CCA}}{P^2}$, with P being the perimeter calculated as the sum of the Cartesian distances between all subsequent points. CIRC therefore reduces both when the CCA reduces or the perimeter increases. As CIRC (in contrast to CCA) showed the ability to discriminate between very mild and mild AD patients, Ardekani et al. concluded that circularity should be included in future studies. In this paper, the perimeter is calculated as the sum of squared distances between subsequent boundary points.

2.4.3. Corpus Callosum Index (CCI)

In order to calculate the CCI, one needs to determine the greatest anterior-posterior diameter (cf. Fig. S2, AB′). The 3 line segments under consideration are those where the AB’ line (or the normal constructed on the middle point of AB′) crosses the corpus callosum. As this measure is sometimes used as an easy-to-calculate measure (e.g. [Yaldizli et al., 2014]), we report its reproducibility and repeatability.

2.4.4. Thickness profile generation

The Corpus Callosum Thickness profile generation was performed using Laplace's equation, based on [Adamson et al., 2011]. First, a scalar field is calculated between the inferior and superior part of the CC that needs to be Laplacian (i.e. $\frac{{\text{∂}}^2\phi }{\text{∂}{x}^2}+\frac{{\text{∂}}^2\phi }{\text{∂}{y}^2}=0$). The inferior and superior part can be easily separated by the use of the active shape model, that allows to reliably select equivalent points in different CCs.

Next, the midline is found as the line where the Laplacian field assumes the mean value of the two extremes imposed on the inferior and posterior edge. Finally, 50 equidistant points are calculated on this line and streamlines are calculated from this midline to both the inferior and posterior edge. Similar to [Adamson et al., 2014], we used the first-order Euler approximation to the gradient of the Laplacian field in order to construct the streamlines. The sum of the distances covered by these streamlines is the thickness at that point. In Fig. 3 we depict 50 equidistant (along the midline) streamlines.

Fig. 3.

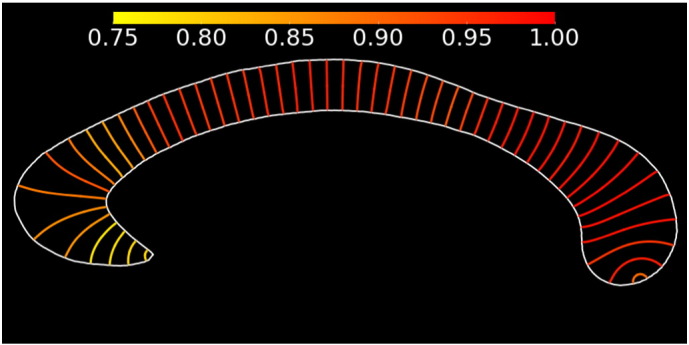
Evolution of the repeatability (ICC) over the CC thickness profile, calculated in 215 healthy control subjects. The colour indicates the repeatability (scale from 0.75 to 1.00). The plotted CC is the average CC obtained in the training set (for illustration purposes only).

2.5. Accuracy, repeatability and reproducibility

In order to assess the accuracy, repeatability and reproducibility, we selected a subset of 50 subjects from the OASIS database. After calculation of the MSP, the CC were manually delineated by two experts. One expert delineated the same image twice, another expert delineated two images of the same subject. All images were given a coded name in order to minimise potential biases. This way we are able to assess the intra- and interrater variability and the (manual) repeatability.

The accuracy was assessed by calculating the Dice similarity index between manually delineated and automated segmentations. The Dice similarity index [Dice, 1945] is defined as the ratio between the number of voxels where both segmentations agree to the mean number of voxels labelled by either method.

With respect to the repeatability and reproducibility, we used the definitions provided by Bartlett and Frost [Bartlett and Frost, 2008]:

• -“Repeatability of measurements refers to the variation in repeat measurements made on the same subject under identical conditions”.
• -“Reproducibility refers to the variation in measurements made on a subject under changing conditions.”

Therefore we make a distinction between scans from the same subject without (repeatability) and with (reproducibility) repositioning. The algorithm itself is deterministic. Therefore, different runs on the same image return the exact same segmentation.

Throughout the paper, we have applied the agreement intra-class correlation coefficient (ICC, [Koch, 1982]) as the measure to compare multiple observations of the same quantity.

3. Results

3.1. Comparison to manual segmentations

The accuracy was assessed by calculating the dice coefficient with manual segmentations for 50 randomly selected subjects from the OASIS_HC dataset, resulting in a mean dice coefficient of 0.904. The dice coefficient calculated for the MS dataset was 0.908, for the AD dataset (calculated on 20 randomly selected patients) 0.913.

The intra- and interrater dice coefficients are 0.959 and 0.909 respectively. The manual repeatability dice coefficient was 0.977.

3.2. Repeatability and reproducibility

The results for the repeatability (subject is not repositioned) and reproducibility (subject is repositioned) for the different CC features are summarized in Table 1.

Table 1.

Repeatability and reproducibility estimates.

	Repeatability		Reproducibility
	OASIS_HC	OASIS_AD	OASIS_HC_TRT	MS
				Philips 3T	Siemens 3T	GE 3T
# failed segm./# scans	0/432	2/200	0/40	0/17	0/18	0/17
% failed segm.	0.0	1.0	0.0	0.0	0.0	0.0
# Subjects	216	99	20	8	9	8
DICE	0.965	0.945	0.934	0.938	0.954	0.945
Area	0.981	0.980	0.986	0.996	0.996	0.971
Circularity	0.985	0.985	0.978	0.989	0.997	0.981
Corpus Callosum Index	0.966	0.956	0.923	0.912	0.972	0.961
Thickness profile	0.953	0.949	0.944	0.945	0.964	0.867

Given the available datasets, repeatability could be assessed in 216 healthy controls (OASIS_HC) and 100 patients affected by very mild to mild Alzheimer's Disease (OASIS_AD).

Reproducibility was assessed on 20 healthy controls (OASIS_HC_TRT) for whom at least 2 scanning sessions (separated by a maximum of 90 days) were available. Reproducibility with respect to repositioning and manufacturer was assessed in 10 MS patients, who have been scanned at least twice on 3 different scanner types.

For two MS patients, one (out of six) T1 images was missing. One other MS patient was excluded as the size of the black holes effectively partitioned the CC in separate parts, impeding the convergence of our contour based segmentation algorithm.

Intra-class correlation coefficients for the different populations and features. Segm = segmentations. Only subjects with 2 available scans on which the algorithm converged correctly could be included.

As the ICC of the CC thickness profile did show an important variation, we provide a more detailed result in Fig. 3 for the 205 healthy controls from the OASIS dataset. Repeatability is highest in the posterior regions, while the thickness is more difficult to estimate in the CC tip.

For every feature, we assessed the absolute difference between the two measurements and normalised this difference to the mean of the two available measurements (cf. Table 2).

Table 2.

Normalised and absolute reliability.

	Repeatability		Reproducibility
	OASIS_HC	OASIS_AD	OASIS_HC_TRT	MS
				Philips 3T	Siemens 3T	GE 3T
Normalised difference – median [IQR]
Area	1.40 [0.6–2.7]	1.39 [0.7–2.7]	0.87 [0.2–2.0]	1.11 [0.6–1.9]	0.65 [0.4–2.3]	3.61 [1.7–4.6]
Circularity	1.40 [0.6–2.5]	1.55 [0.6–2.7]	1.06 [0.6–2.3]	1.31 [0.7–2.5]	0.89 [0.5–1.6]	3.04 [2.6–3.3]
Corpus Callosum Index	1.27 [0.6–3.3]	1.44 [0.6–2.7]	1.7 [1.6–6.0]	3.06 [1.4–4.8]	1.02 [0.8–4.9]	1.95 [1.4–3.1]
Thickness profile	2.64 [1.2–4.8]	2.89 [1.4–5.2]	2.4 [1.1–4.4]	3.32 [1.8–5.0]	2.82 [1.5–5.0 ]	5.68 [3.4–9.1]
Absolute difference – median
Area (mm2)	8.06	6.78	5.85	6.9	3.6	19.2
Circularity (−)	0.003	0.002	0.002	0.002	0.001	0.004
Corpus Callosum Index (−)	0.004	0.004	0.007	0.011	0.004	0.007
Thickness profile (mm)	0.14	0.12	0.14	0.14	0.12	0.24

Median of the normalised (%) and absolute difference for the different features in the different datasets. IQR = Inter Quartile Range. For every streamline of the thickness profile, the median (normalised or absolute) was calculated. Next, those results were averaged over all streamlines.

3.3. Inter-scanner reproducibility (Re3T – MS)

In Table 3, we list the reproducibility estimates obtained for the different features obtained on different scanners. The inter-scanner reproducibility is highest for CIRC (all > 0.94).

Table 3.

Inter-scanner reproducibility.

	CCA			CIRC			CCI
	Philips 3T	Siemens 3T	GE 3T	Philips 3T	Siemens 3T	GE 3T	Philips 3T	Siemens 3T	GE 3T
Philips 3T		0.863	0.982		0.944	0.965		0.890	0.927
Siemens 3T			0.831			0.956			0.893

Inter-scanner reproducibility obtained on the dataset of 10 MS patients who have been scanned twice on 3 different scanners.

4. Discussion

In this paper we have shown that an active shape model is capable of accurately segmenting the CC, both in a cohort of healthy controls and in two patient cohorts representing two important neurodegenerative diseases (Alzheimer's disease and Multiple Sclerosis). For both diseases, 3D T1-weighted images are already regularly collected and therefore the presented procedure may warrant the inclusion of several CC features in future large-scale studies and even regular clinical reporting. Furthermore, we have shown that the CC thickness profile may be reliably estimated providing more detailed information on callosal atrophy.

The accuracy was assessed by calculating the dice coefficient with manual segmentations. We obtained dice coefficients of 0.904, 0.908 and 0.913 for a subset of the healthy controls, the AD and MS patients respectively. The obtained dice coefficients in both the repeatability and reproducibility datasets outperform the (manual) interrater reliability (0.909) and are very similar to the manual repeatability (0.977) and the intra-rater reliability (0.959) obtained by manually segmenting 50 randomly selected controls. We obtained a high (mostly > 0.97) repeatability and reproducibility for all calculated features (CCA, CIRC, CCI, CC thickness profile) as assessed by the ICC. Finally, we showed that – in a dataset of 9 MS patients scanned at 3 different scanners on the same day – a high inter-scanner reliability (ICC ≫ 0.8) could be obtained.

The repeatability and reproducibility results for area and circularity outperform the inter-rater reliability reported by manual segmentations in [Tepest et al., 2010] (intra-rater correlation coefficient = 0.99, inter-rater correlation coefficient = 0.7) and are comparable to the results reported in [Ballmaier et al., 2008] (inter-rater ICC = 0.97). In this regard it should be noted that inter-rater reliability in those studies start from the same MSP and only assess the inter-rater variability due to the manual segmentation, while the repeatability and reproducibility reported in this study can only be negatively influenced by small changes in MSP detection, i.e. our procedure is high reliable for both MSP detection and CC segmentation.

An important advantage of our active shape algorithm is the availability of an easy convergence-parameter (the average step a point on the edge would like to do during each iteration) allowing us to easily monitor the algorithm's performance. For this algorithm, we observed that a mean step of 0.5 mm during the CC iteration scheme corresponded with an accurate and reliable segmentation. Images on which the algorithm did not converge, were marked as “failed” and occur only in very rare cases (cf. Table 1).

As our CC segmentation input parameters do not need to be tuned to the images' acquisition parameters and as we obtain relatively high inter-scanner reproducibility estimates, this pipeline enables the pooling of data in large multicentre studies. The ability of pooling data over multiple scanner types is an important asset in clinical studies. Although the inter-scanner reproducibility is lower for all calculated features as compared to the intra-scanner reproducibility, our results in 8 MS patients (ICC: 0.77–0.97) compare to the ICCs obtained on total brain, cerebellum, lateral and third ventricle, grey matter and white matter volume in 6 healthy controls (ICC: 0.21–0.96) [Schnack et al., 2004] and to the between-site ICC (grey and white matter volume, thalamus, hippocampus, amygdala and caudate) reported in [Keshavan et al., 2016]. The difference in dice coefficients (0.91 for Philips, 0.89 for Siemens and 0.93) is small and may be due the different acquisition parameters.

As in every study, some limitations should be noted. First, although we feel that a dataset of 8–9 patients scanned on the same day on three different scanners constitutes a unique dataset of a comparable sample size as studies in healthy controls [Keshavan et al., 2016, Schnack et al., 2004], the number of patients is low and results should be interpreted with caution. Next, lesions are frequently observed in CC of MS patients [Evangelou et al., 2000]. Although a possible solution could be performing an automated lesion filling (cf. [Jain et al., 2015]) before starting the CC segmentation, we prefer to post-process the CC as (small) hypo-intensities do not influence the algorithm's convergence and can be easily detected in the final image. Importantly, features that rely on the full CC like CIRC and CCI cannot be trusted in those cases.

Furthermore, it has to be noted that our segmentation failed on one MS patient due to a significant atrophy, partitioning that patient's CC in different disconnected parts. While this limits the application of any boundary-based method in a cross-sectional design, we would like to note that this active shape model is ideally suited for longitudinal follow-up as the outcome of the previous scan can be easily used as the starting CC shape (instead of the average CC). Therefore, if a previous scan would be available, that contour could be used to initialise the convergence of the next scan.

5. Conclusion

In summary, we have constructed an algorithm that reliably detects the CC in 3D T1-weighted images in a fully automated way in healthy controls and two important neurodegenerative diseases. Although the CC area (dice > 0.934, ICC > 0.97) and the circularity are the most reliable features (ICC > 0.98), the reliability of the thickness profile (ICC > 0.90; excluding the tip) is sufficient to warrant its inclusion in future clinical studies. Furthermore, our algorithm can be applied to imaging data from different scanners enabling multi-centre study designs.

Appendix A. Supplementary data

Supplementary figures.