SUMMARY
Using exact, analytic results for the average power of the Benjamini-Hochberg (1995) procedure, we provide example power analyses useful for scientists planning studies involving multiple comparisons. The power results are based on the distribution of the p-value under the alternative for the Pearson’s χ2, and for the Hotelling-Lawley trace, the Wilks’ lambda, and the Pillai-Bartlett trace, all tests for the general linear multivariate model. Detailed example power analyses are given for a planned mammography experiment with categorical data and a study that tests the association of a single nucleotide polymorphism with insulin resistance and visceral adiposity.
Keywords: Power, multiple comparisons
1. INTRODUCTION
A Type I error is a rejection of the null hypothesis when the null hypothesis is true. Typically, the Type I error rate is denoted by α, which is often fixed at 0.05. When multiple tests are performed in the experiment, the family-wise error rate (FWER) is the probability that at least one Type I error occurs during hypothesis testing. The FWER increases as a function of the number of hypotheses tested in the experiment. The increasing chance of making an error is called the multiple comparison problem (Curran-Everett, 2000).
The multiple comparison problem arises in clinical trials, laboratory studies, microarray experiments, and observational studies. A variety of statistical procedures have been suggested to control the multiple comparison problem. See Westfall et al. (1999) for an overview.
Benjamini and Hochberg (1995) introduced a multiple comparison technique that controls the expected value of the false discovery rate (FDR). This is the proportion of all rejections that are rejections of null hypotheses, i.e. rejections that are made in error. Pounds and Cheng (2005) provide an approximate method for power under the Benjamini and Hochberg (1995) procedure. Exact power for the Benjamini and Hochberg (1995) procedure is derived in Glueck et al. (2008). In this paper, we give two detailed examples of how to conduct power analyses for the Benjamini and Hochberg (1995) procedure using methods from Glueck et al. (2008). The two tests we consider in this paper are among the most commonly used tests in statistics, namely the Pearson’s χ2 and the F test for the general linear multivariate model (GLMM). Since we will use approximate inputs for Glueck et al. (2008), we will assess the accuracy of the exact power computation. We will also provide guidance as to when it is appropriate to use the methods of this paper.
In Section 2 we discuss power calculations for the Benjamini and Hochberg (1995) procedure. In Section 3 we review previous work on the distribution of p-values under the null and alternative, and derive the approximate distributions of the p-value under the alternative for the Pearson χ2 test and for three tests for the general linear multivariate model. In Section 4 we discuss the accuracy of the power approximations for the Benjamini and Hochberg (1995) procedure. In Section 5 we provide the results of two example power analyses, one using the Pearson χ2 for a mammography experiment and one using the general linear multivariate model for genetic association with diabetes related outcomes. In Section 6 we discuss the advantages and limitations of the example power analyses and further areas of research.
2. BENJAMINI AND HOCHBERG PROCEDURE AND POWER
Given α ∈ [0, 1], null hypotheses H0i, i = 1, 2 …, m, with independent but not necessarily identically distributed p-values Pi, and corresponding order statistics P(i) (the p-values Pi sorted in non-decreasing order), the Benjamini and Hochberg (1995) procedure produces a non-decreasing sequence of rejection bounds bi = iα*/m ∈ [0, 1]. When k is the largest number for which P(k) ≤ bk, the k null hypotheses H0(i), i = 1, 2, …, k, k ≤ m, are rejected, and the other null hypotheses are not rejected.
Benjamini and Liu (1999) define average power as the expected value of the ratio of correct rejections, K − J, and the number of non-true null hypotheses, m − n, so
| (2.1) |
As summarized in Table 1, given m hypotheses with m − n true alternatives, fixed α and known test statistics and distribution of p-values, Glueck et al. (2008) derive the exact joint distribution of the total number of rejections and the number of false rejections in terms of sums of the joint distribution function of the order statistics of the p-values. Glueck et al. (2008) thus calculate the exact average power given in Equation (2.1).
Table 1.
Summary of possible hypothesis rejection and non-rejection scenarios. m is the total number of hypotheses tested. K is the total number of rejections of which J are false rejections.
| Decision | |||
|---|---|---|---|
| Do Not Reject | Reject | ||
| Null Hypothesis True | n − J | J | n |
| Alternative Hypothesis True | (m − n) − (K − J) | K − J | m − n |
| m − K | K | m | |
3. DISTRIBUTION OF p-VALUES UNDER THE ALTERNATIVE
In order to calculate average power using the method of Glueck et al. (2008), it is necessary to know the exact distribution of the un-ordered p-values under the alternative. Denote PHA to be the p-value when the alternative hypothesis is true. Thus, for a right-tailed test with a generic test statistic X, PHA = P(X ≥ XOBS | HA is true). Note then even if the alternative hypothesis is true the p-value is still calculated assuming a true null hypothesis. In general, the distribution of the PHA has been considered by authors such as Hung et al. (1997), who derived the result for the normal case, Sackrowitz and Samuel-Cahn (1999), who considered expected p-values, and Bhattacharya and Habtzghi (2002), who focused on median p-values. Although Ruppert et al. (2007) gave the general form of the distribution of PHA, the distribution of PHA has not been derived for the Pearson χ2 test of independence nor for multivariate F tests for the GLMM. We derive the distribution of PHA for those two cases in the next two sections.
3.1 PEARSON’S χ2 TEST
Pearson’s χ2 test (Pearson, 1904) is commonly used in clinical research situations to assess whether two binary outcome variables are independent. Kroll (1989) and Agresti (1992) provide a thorough summary of the statistical literature on the 2×2 table. The observed data for two binary outcome random variables can be summarized as in Table 2. The underlying population probabilities under the null hypothesis are defined in Table 3.
Table 2.
Observed data for two binary outcome random variables. Here n11 is the number of subjects for whom both variable 1 and variable 2 take on the values 1. n10 is the number where variable 2 is 1 and variable 1 is 0, and n01 and n00 are defined similarly. The total number of observations is N = n11 + n10 + n01 + n00. The row and column marginals are N1+ = n11 + n10, N0+ = n01 + n00, N+1 = n11 + n01 and N+0 = n10 + n00.
| Variable 1 | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| Variable 2 | 1 | n11 | n10 | N1+ |
| 0 | n01 | n00 | N0+ | |
| N+1 | N+0 | N | ||
Table 3.
Population probabilities under the null hypothesis for two binary random variables. π11 is the probability that a subject will have both Variable 1 and Variable 2 take on the value 1. π10, π01, and π00 are defined similarly.
| Variable 1 | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| Variable 2 | 1 | π11 | π10 | π1+ |
| 0 | π01 | π00 | π0+ | |
| π+1 | π+0 | |||
The null hypothesis for Pearson’s χ2 test of independence (Agresti, 1990, p. 47) is
| (3.1.1) |
for all i, j ∈ {0, 1}.
The usual test statistic is the Pearson’s χ2 test (Pearson, 1904). As in Upton (1982) let
| (3.1.2) |
We will assume fixed marginal totals. Under this assumption, when the null hypothesis is true, the exact probability distribution of the test statistic (and of the 2 × 2 table) is the hypergeometric distribution (Agresti, 1992, p. 134, Equation 1.2). For ease of calculation, under the null, the exact distribution is typically approximated by the central χ2 with one degree of freedom. The approximation is usually accurate enough when the expected cell counts are all greater than 5 (Rosner, 2006, p. 396). While the exact test allows one-sided hypothesis testing, the Pearson’s χ2 is always a two-sided test. The approximate two-sided p-value for the Pearson’s χ2 test is given by
| (3.1.3) |
Since n11, n00, n01 and n10 are not observed until an experiment has occurred the p-value is a random variable.
For power analysis, we are interested in the distribution of PHA. The alternative hypothesis is
| (3.1.4) |
for all i, j ∈ {0, 1}, where the population probabilities under the alternative hypothesis are shown in Table 4. Define
| (3.1.5) |
Under the alternative hypothesis, the exact distribution of the test statistic is the noncentral hypergeometric distribution (Agresti, 1992, p. 134, Equation 1.2). This can be approximated by a noncentral χ2 (1,ω) distribution (Cohen, 1988). For 0 < p < 1, an asymptotic form of the cumulative distribution function of PHA is given by
| (3.1.6) |
which is a special case of Ruppert et al.[(2007, Equation 5]. Note that under a true null hypothesis Equation (3.1.6) reduces to a continuous uniform(0,1) distribution.
Table 4.
Population probabilities under the alternative hypothesis for two binary random variables. δ11 is the probability that a subject will have both Variable 1 and Variable 2 take on the value 1. δ10, δ01, and δ00 are defined similarly.
| Variable 1 | ||||
|---|---|---|---|---|
| 1 | 0 | |||
| Variable 2 | 1 | δ11 | δ10 | δ1+ |
| 0 | δ01 | δ00 | δ0+ | |
| δ+1 | δ+0 | |||
In order to confirm the result given in (3.1.6), we performed an enumeration experiment to calculate the empirical cumulative distribution function for the approximate two-sided p-value for the Pearson’s χ2 test. The overall sample size, N and the marginal totals were fixed and all possible tables, i, within the fixed N and marginal totals were enumerated. Table probabilities under the null hypothesis were calculated using the central hypergeometric distribution (Agresti, 1992, p. 134, Equation 1.2). To calculate the probability of Table i under the alternative, the tables were listed in ascending order using the test statistic for each table. The table probability under the alternative was then calculated as
| (3.1.7) |
with Q given in (3.1.2) and ω given in (3.1.5). The table probability under the alternative for the table with the largest test statistic was calculated as 1 − Fχ2 [Qmax(i)−1; 1,ω]. Let i index the tables, with corresponding p-values pi and probabilities under the alternative given by Xi. The empirical cumulative distribution function was calculated as
| (3.1.8) |
We compared the empirical cumulative distribution function to the approximate cumulative distribution of the p-value (3.1.6) using the following steps. 1) Fix N, N1+, N0+, N+0, and N+1; 2) Fix the null hypothesis so that the odds ratio is 1; 3) Fix the alternative hypothesis so that the odds ratio is greater than 1. Note that values for N and the alternative hypotheses were chosen to provide a range of non-centrality parameters, ω, which is a function of the sample size and the effect size; 4) Enumerate all possible tables with the fixed setup; 5) Calculate p-values for each table; 6) Calculate probabilities for each table under the null and alternative hypothesis; 7) Calculate the empirical distribution function and compare it to the theoretical distribution function.
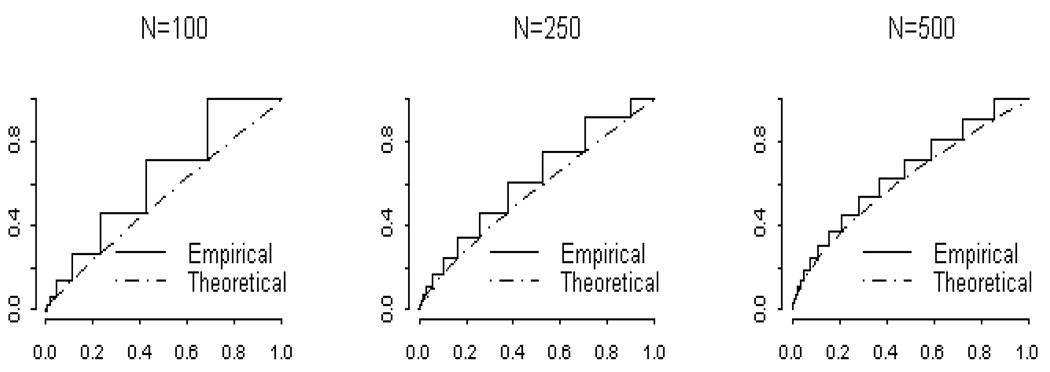
Figure (1) shows the empirical and theoretical p-value distributions when the odds ratio under the alternative was 1.2. The approximate distribution of PHA increases in accuracy as the sample size increases. As shown in Figure (1), the empirical cumulative distribution function is a step function, while the approximate cumulative distribution function is continuous. As the sample size increases, the step size decreases, and the empirical function is better approximated by approximate cumulative distribution function.
Figure 1.
Comparison of the empirical and theoretical χ2 p-value distributions under the alternative hypothesis when the odds ratio under the alternative hypothesis is 1.2. Population parameters under the null were π11 = 0.25, π10 = 0.25, π01 = 0.25, π00 = 0.25 and under the alternative were δ11 = 0.26, δ10 = 0.24, δ01 = 0.24, δ00 = 0.26.
Although Figure (1) shows convergence between the approximate and empirical cumulative distribution function, the functions are significantly different by the Kolmogorov-Smirnov test (Daniel 1990). To further explore the effect of odds ratio on the strength of the approximation, we also considered odds ratios under the alternative hypothesis of 2.3 and 5.4. The accuracy of the approximation depended on both the sample size and the size of the odds ratio under the alternative. For example, the Kolmogorov-Smirnov test showed no difference between the empirical and approximate p-value distribution for N = 500, and odds ratio = 5.4; N = 500, odds ratio = 2.3, and N = 250, and odds ratio = 2.3. However, for N = 500, and odds ratio = 1.2, and for N = 100, and odds ratio = 2.3, the empirical and approximate distribution results were significantly different. The results of our enumeration experiment were similar to those observed by Bayarri and Berger (2000), who compared the approximate and exact cumulative distribution functions under the null. Unfortunately, as is shown later, the divergence between the empirical and approximate p-value distributions can have adverse effects on power estimates.
3.2 MULTIVARIATE F TESTS
The general linear multivariate model (GLMM) is used when multiple outcome measurements are taken for each subject. Because there is no uniformly most powerful test for the GLMM, a variety of test statistics are in use. Three of the most common tests are Wilks’ lambda (W), the Pillai-Bartlett trace (B), and the Hotelling-Lawley trace (L) (see Equations 7.20, 7.21 and 7.22 for definitions). Although there are no exact results, the distributions of the test statistics under the null (given in Equation 7.19) are well approximated by a central F distribution (Muller et al. 1992). Under the alternative, Muller and Peterson (1984) give non-central F approximations (shown in Equation 7.24).
For power analysis, we are interested in the distribution of PHA. Let 𝒯(z) be the scalar transformation of test statistic z (details in Appendix A), and 𝒟(z) be the denominator degrees of freedom for the F approximation for that test. The approximate p-value, which is a random variable, is given by
| (3.2.1) |
The approximate cumulative distribution function of PHA is
| (3.2.2) |
for 0 < p < 1. This is a special case of Equation (5), Ruppert et al. (2007).
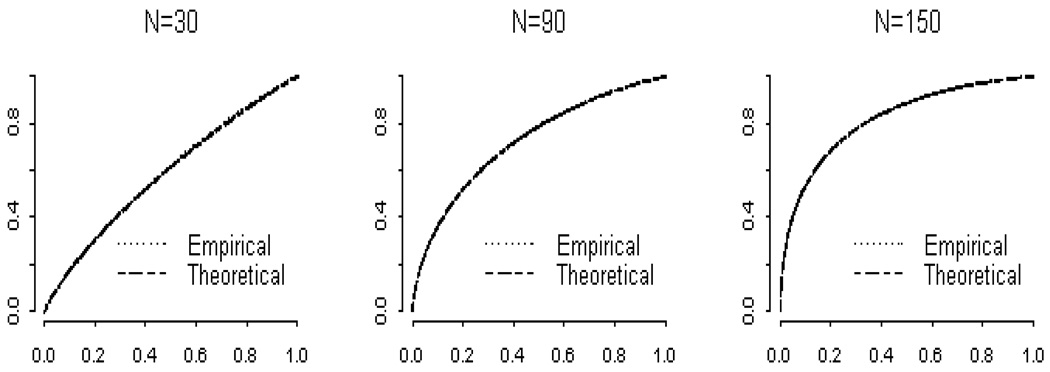
A simulation experiment showed that the approximation for the cumulative distribution function of the p-value given in Equation 3.2.2 is very accurate. For the simulation, we fixed N, β, and Σ, and repeated these steps 10,000 times: 1) generating ℰ so that [rowi (ℰ)]′ ~ N (0, Σ), independently; 2) calculating Y = Xβ + ℰ; 3) performing the Pillai-Bartlett trace, Wilks’ lambda and the Hotelling-Lawley trace, and 4) finding the empirical cumulative distribution function of the p-values. As shown in Figure 2, the approximate and empirical cumulative distribution functions essentially coincide. Similar results were obtained for the Pillai-Bartlett trace and the Hotelling-Lawley Trace. The one-sample Kolmogorov-Smirnov test (Daniel 1990) showed that there was no difference between the empirical and exact cumulative distribution functions for all but the smallest values of ω(z) and the smallest sample sizes.
Figure 2.
Comparison of empirical and theoretical p-value distributions for Wilks’ Lambda for sample sizes of N = 30, 90 and 150 with δ = 0.2, where δ measures the difference between treatment group means.
4. ASSESSING ACCURACY OF THE POWER APPROXIMATION
The results of Glueck et al. (2008) give exact average power. Using the previously described power formulas with approximate PHA distributions produces approximate average power estimates.
A simulation experiment showed that the average power for the Benjamini and Hochberg (1995) procedure was accurate to the second decimal place using the F test and to the first decimal place using Pearson’s χ2. We verified the accuracy of the power approximation using the following steps: 1) We fixed whether the null or the alternative hypothesis was true within and across experiments, the sample size, and parameters under the null and alternative hypotheses for three independent experiments. These parameters were fixed to provide a variety of non-centrality parameters, ω, which is a function of the sample size and the effect size; 2) We used a stochastic approach to generate data, a test statistic (either χ2 or one of the multivariate F tests), and a p-value for each experiment; 3) We conducted the Benjamini and Hochberg (1995) procedure to determine the number of hypothesis rejections; 4) We counted the number of rejections of the null when the null was actually true; 5) We repeated this process 10,000 times for the F. For the χ2 we formed all possible three table combinations given fixed N and fixed table margins. 6) We calculated empirical average power as
| (4.1) |
where
| (4.2) |
for the F and
| (4.3) |
for the χ2, i.e., the empirical joint probability mass is a function of k, the number of rejections, and j, the number of false rejections. 7) We calculated the distribution of PHA given in Equation (3.1.6), for the χ2, or Equation (3.2.2), for the appropriate general linear multivariate model test; 8) We used the p-value distribution to calculate the theoretical average power result by the methods of Glueck et al. (2008). The theoretical result is exact when the p-value distribution is exact. Because the distributions of PHA given in Equation (3.1.6) and Equation (3.2.2) is approximate, our calculations of the theoretical average power will also be approximate.
The results of an example simulation for the Pearson’s χ2 test are shown in Table (5). The largest difference between the empirical average power and theoretical average power for any χ2 test was 0.131. The inaccuracy in the power result is due to errors in the approximation for the distribution of PHA. The power approximation is accurate for small and large values of power, but inaccurate for values around 0.5.
Table 5.
Comparison of empirical and theoretical average power for the Benjamini-Hochberg (1995) procedure. Results are for three independent χ2 hypothesis tests. The sample size for each experiment is N ∈ {100, 250, 500}. The odds ratio under the alternative is δ ∈ {1.2, 2.3 and 5.4}.
| δ | N | Empirical Average Power |
Theoretical Average Power |
Absolute Difference |
|---|---|---|---|---|
| 1.2 | 100 | 0.064 | 0.028 | 0.036 |
| 250 | 0.076 | 0.045 | 0.031 | |
| 500 | 0.096 | 0.077 | 0.019 | |
| 2.3 | 100 | 0.567 | 0.436 | 0.131 |
| 250 | 0.896 | 0.876 | 0.020 | |
| 500 | 0.996 | 0.994 | 0.002 | |
| 5.4 | 100 | 0.992 | 0.978 | 0.014 |
| 250 | 1.000 | 1.000 | 0.000 | |
| 500 | 1.000 | 1.000 | 0.000 |
The results of an example simulation for the three multivariate F tests, and its comparison to the theoretical results are given in Tables (6), (7) and (8). The empirical average power and theoretical average power did not differ widely for any case examined. The largest difference between the empirical average power and theoretical average power for any F test was 0.069 and occurred in the smallest sample size. The majority of cases had absolute differences of less than 0.01. Given the uncertainty of parameter selection for power analysis, errors in the estimation of average power on the order of 0.01 should make no difference in clinical or experimental design.
Table 6.
Comparison of empirical and theoretical average power for the Benjamini and Hochberg (1995) procedure. Results are for three independent general linear multivariate models. Each hypothesis is tested with the Wilks’ lambda. The sample size for each experiment is N ∈ {30, 90, 150}.The difference between treatment group means under the alternative is δ ∈ {0.2, 0.5 and 0.8}.
| δ | N | Empirical Average Power |
Theoretical Average Power |
Absolute Difference |
|---|---|---|---|---|
| 0.2 | 30 | 0.043 | 0.046 | 0.003 |
| 90 | 0.153 | 0.157 | 0.004 | |
| 150 | 0.318 | 0.315 | 0.003 | |
| 0.5 | 30 | 0.350 | 0.342 | 0.008 |
| 90 | 0.953 | 0.944 | 0.009 | |
| 150 | 0.999 | 0.998 | 0.001 | |
| 0.8 | 30 | 0.861 | 0.825 | 0.036 |
| 90 | 1.000 | 1.000 | 0.000 | |
| 150 | 1.000 | 1.000 | 0.000 |
Table 7.
Comparison of empirical and theoretical average power for the Benjamini and Hochberg (1995) procedure. Results are for three independent general linear multivariate models. Each hypothesis is tested with the Pillai-Bartlett trace. The sample size for each experiment is N ∈ {30, 90, 150}. The difference between treatment group means under the alternative is δ ∈ {0.2, 0.5 and 0.8}.
| δ | N | Empirical Average Power |
Theoretical Average Power |
Absolute Difference |
|---|---|---|---|---|
| 0.2 | 30 | 0.036 | 0.047 | 0.011 |
| 90 | 0.148 | 0.157 | 0.009 | |
| 150 | 0.312 | 0.314 | 0.002 | |
| 0.5 | 30 | 0.311 | 0.333 | 0.022 |
| 90 | 0.951 | 0.933 | 0.018 | |
| 150 | 0.998 | 0.997 | 0.001 | |
| 0.8 | 30 | 0.838 | 0.769 | 0.069 |
| 90 | 1.000 | 1.000 | 0.000 | |
| 150 | 1.000 | 1.000 | 0.000 |
Table 8.
Comparison of empirical and theoretical average power for the Benjamini and Hochberg (1995) procedure. Results are for three independent general linear multivariate models. Each hypothesis is tested with the Hotelling-Lawley trace. The sample size for each experiment is N ∈ {30, 90, 150}. The difference between treatment group means under the alternative is δ ∈ {0.2, 0.5 and 0.8}.
| δ | N | Empirical Average Power |
Theoretical Average Power |
Absolute Difference |
|---|---|---|---|---|
| 0.2 | 30 | 0.054 | 0.045 | 0.009 |
| 90 | 0.158 | 0.156 | 0.002 | |
| 150 | 0.323 | 0.316 | 0.007 | |
| 0.5 | 30 | 0.376 | 0.348 | 0.028 |
| 90 | 0.954 | 0.953 | 0.001 | |
| 150 | 0.999 | 0.999 | 0.000 | |
| 0.8 | 30 | 0.875 | 0.864 | 0.011 |
| 90 | 1.000 | 1.000 | 0.000 | |
| 150 | 1.000 | 1.000 | 0.000 |
5. EXAMPLE POWER ANALYSES FOR THE BENJAMINI AND HOCHBERG PROCEDURE
We conducted two example power analyses using the Benjamini and Hochberg (1995) procedure. The first one is for a set of independent χ2 tests, and the second is for a set of independent multivariate tests for the general linear multivariate model. We give detailed power analyses for each experiment.
5.1 PEARSON’S χ2 TEST
The first example is for a proposed meta-analysis, designed to answer the question whether hormone replacement therapy (HRT) affects the detection of cancer by digital mammography. Meta-analysis is useful because it combines several, smaller studies into a study that has a larger number of subjects and as a result has increased power to detect the difference of interest. Hormone replacement therapy (HRT) has been implicated both in increasing the number of breast cancers (Collaborative Group, 1997), and in making breasts more mammographically dense (Greendale et al. 1999), which can hide developing cancers. Lewin et al. (2002), Skaane et al. (2003) and Pisano et al. (2005) compared the diagnostic accuracy of digital and film mammography. Although none of these clinical trials were designed to look at the effect of hormone replacement therapy on breast cancer detection, the data from these trials could be used to answer the question.
Data for women with breast cancer in each study was used to form three 2 × 2 tables. The tables show women with cancer cross-classified by two binary variables: use or non-use of HRT, and detection or non-detection by digital mammography. Each 2 × 2 table will yield a Pearson’s χ2 test. The null hypothesis is no association between hormone replacement therapy and whether the cancer is detected by digital mammography.
With three studies, the risk of making at least one Type 1 error is more than 0.14. All the studies are independent, as they were conducted in different locations, with different subjects and investigators. Thus, we can use the Benjamini and Hochberg (1995) procedure to control the multiple comparisons problem. We then use the methods of Glueck et al. (2008) to calculate the exact average power for Benjamini and Hochberg (1995) procedure. To conduct an average power analysis, there are four main steps.
First, we need to choose α*, which is the level at which we wish to control the false discovery rate. Recall that the false discovery rate is the expected number of rejections when the null is true, divided by the total number of rejections. By analogy to the Type 1 error rate, this is conventionally set at α* = 0.05.
Second, to calculate power using the methods of Glueck et al. (2008), we need to specify the number of hypothesis tests for which the null is actually true. In this case, since we have three studies that all test the same hypothesis, either all the null hypotheses are true, or none of them are. It makes no sense to conduct the study if we truly believe that all the null hypotheses are true, so we will assume that the number of hypothesis tests for which the null is true is zero. When no null hypotheses are true, average power can be interpreted as the fraction of hypotheses that should be rejected that are rejected. Note that the assumption of none of the three null hypotheses being true is not essential to use the methods of Glueck et al. (2008) but is made for logical reasons.
Third, we need to specify the sample size for each hypothesis test. There were N = 42, 31 and 335 total breast cancer cases in Lewin et al. (2002), Skaane et al. (2003) and Pisano et al. (2005) respectively. Digital mammography detected 27, 23 and 185, respectively.
Finally, we need to specify the population proportions under both the null and the alternative hypotheses. It is important to note here that we never know these answers well until the experiment is run. The best we can do is to estimate the population parameters from previous studies, or from clinical knowledge. In any power analysis, it is important to note where we are uncertain, and to conduct sensitivity analyses, to see if the sample size is fairly stable to different input parameters. We show here how we estimated the proportions under the null and alternative for this example.
In the Collaborative Group (1997) paper, 33% of the 53,865 women in the main analysis had used hormone replacement therapy at some point. In the Pisano et al. (2005) study, 55% of the cancers were detected digitally. We fixed the margins at these values. Assuming no association between the rows and columns, πij = πi+π+j. Thus, under the null, we obtain π11 = 0.18, π10 = 0.15, π01 = 0.37, π00 = 0.30 as reasonable values for the population parameters.
With the fixed margins, we calculated the power for clinically interesting odds ratios. If we choose the alternative hypotheses of δ11 = 0.10, δ10 = 0.23, δ01 = 0.45, δ00 = 0.22 for all three experiments, women who take hormone replacement therapy are 0.21 times as likely to get their cancer detected by a digital mammogram, and the average power is 0.67. Similarly, if we choose an the alternative hypotheses of δ11 = 0.07, δ10 = 0.26, δ01 = 0.48, δ00 = 0.19, women who take hormone replacement therapy are 0.08 times as likely to get their cancer detected by a digital mammogram, and the average power is 0.86. This means that with the sample sizes observed in Lewin et al. (2002),Skaane et al. (2003) and Pisano et al. (2005), we would expect to reject 86% of the three hypotheses.
As in single hypothesis power analysis, one wants average power to be as high as possible. The interpretation of a 86% average power is that there is a large chance of getting all three rejections in the meta-analysis, while controlling the false discovery rate at 0.05.
5.2 MULTIVARIATE F TESTS
As a second example, we now give an example of using an average power analysis to choose sample size for an experiment with three independent general linear models. Links between visceral fat accumulation, increased insulin sensitivity and Type 2 diabetes have been explored. (Lewis et al. 2002). Visceral fat accumulation and insulin sensitivity may be linked to Type 2 diabetes by a single nucleotide polymorphism (SNP).
A typical genome wide association study can result at least 300,000 hypothesis tests, and a large multiple comparison problem. Because the exact power methods of Glueck et al. (2008) work only for a small number of hypotheses, assessing average power for a genome wide association study is beyond the scope of this paper. Instead, we examine another common problem, a confirmatory study.
Suppose a genome wide association study has identified three independently inherited SNPs which are strongly associated with the outcomes of interest. We assume that each SNP is expressed in a dominant genetic manner. We will also assume that each study subject will only have no more than one of the three SNPs. This is a reasonable assumption if the SNPs are rare in the population. With control of the false discovery rate, we wish to assess the association between each SNP and the bivariate outcomes of visceral fat accumulation and insulin sensitivity, controlling for age. Since visceral fat and insulin sensitivity are measured in different scales we will also assume they have been scaled so that are of the same order of magnitude.
Suppose we collect information on visceral fat volume and insulin sensitivity in four groups of different people: group 1 with SNP 1; group 2 with SNP 2; group 3 with SNP 3; and the last group with none of the implicated SNPs. We wish to compare the difference in average visceral adiposity and insulin sensitivity between each group.
We now use the methods of Glueck et al. (2008) to calculate the exact average power for Benjamini and Hochberg (1995) procedure. To conduct an average power analysis, there are four main steps.
First, we choose α* = 0.05 to control the false discovery rate. Second, we specify the number of hypothesis tests for which the null is actually true. Here, we suppose that each SNP is in fact related to the outcomes, and thus no null is true. Third, we set up the models, and null and alternative hypotheses. We calculate average power as a function of the parameters and sample sizes, and use the average power values to choose a sample size for the study.
With xi indicating the ith subject’s age, the X and β matrices for each of the SNP models are:
| (5.2.1) |
with associated β matrix given by
| (5.2.2) |
The null hypothesis that there is no difference between the normal population, and those carrying SNP i is
| (5.2.3) |
The C, U and Σ matrices for this hypothesis are
| (5.2.4) |
| (5.2.5) |
| (5.2.6) |
As with one hypothesis power, multiple hypothesis average power depends on the hypothesis being tested and the sample size. In this case it also depends on what assumption is made regarding the prevalence of individuals with a SNP of interest in each study. Define κ to be the proportion of the study population that has one of the SNP being studied. Let ϕ represent the difference between the normal population, and those with any SNP in both visceral adiposity and insulin sensitivity. Also, define N to be the sample size for each hypothesis test.
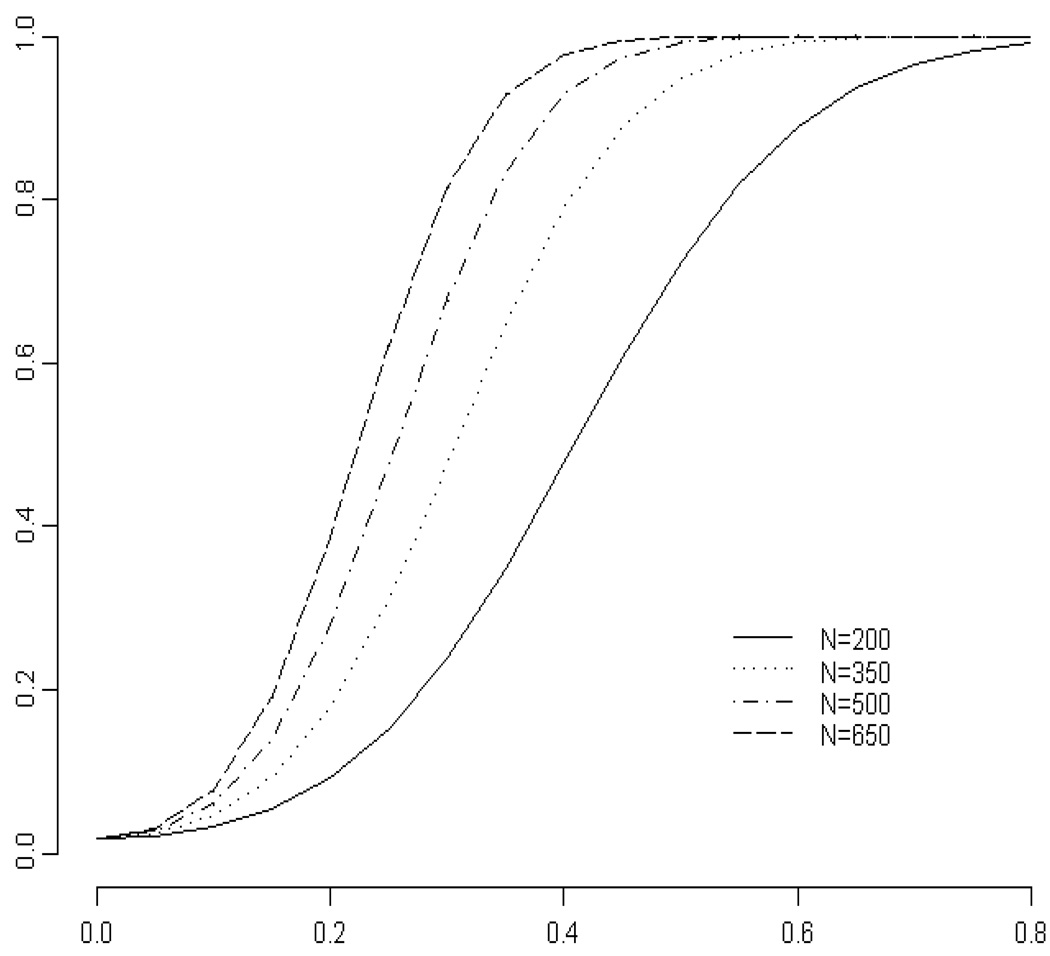
Figure 3 shows the average power curve for three single SNP models. Here, κ = 0.10. The difference,ϕ, in both visceral adiposity and insulin sensitivity between the normal population and those with a SNP was allowed to vary between 0 and 0.8. With sample size of 500 per hypothesis, κ of 0.10 and ϕ of 0.25, the average power is nearly 50%. With sample size of 500 per hypothesis, κ of 0.10 and ϕ of 0.4, the average power is over 90%. Thus the proposed genetics studies should provide adequate average power to answer the question as to which of the SNPs are associated with visceral adiposity and insulin resistance, while controlling the false discovery rate at 0.05. The interpretation of average power for the Benjamini and Hochberg (1995) procedure is the fraction of hypotheses that should be rejected that are rejected. Power of 90% shows that on average, all three hypotheses will be rejected 90% of the time.
Figure 3.
Average power curve for the Benjamini and Hochberg (1995) procedure for three independent studies using the general linear multivariate model. Here the Hotelling-Lawley trace, the Pillai-Bartlett trace and Wilks’ lambda test coincide. The hypothesis for each study is that there is no association between a single nucleotide polymorphism and visceral adiposity and insulin sensitivity. The false discovery rate was set at 0.05. The population proportion of individuals in each study of individuals with the SNP of interest was set at 0.10. The difference between the normal population and those with any SNP in both visceral adiposity and insulin sensitivity was varied to examine the effect on power.
For this example power analysis, the values of κ and ϕ were set somewhat arbitrarily. In a grant application, one would use previously published literature, or clinical knowledge to choose reasonable values of κ and ϕ. A graph similar to Figure 3 is useful for clinicians and granting agencies so that they can see the effects of changes in population value and sample sizes on the power of the study.
6. DISCUSSION
This paper develops the necessary components for performing average power calculations for small numbers of hypotheses when using the Benjamini and Hochberg (1995) procedure to adjust for multiple comparisons. The Benjamini and Hochberg (1995) procedure can be used in clinical trials, experimental studies and grant proposals whenever the hypotheses are independent. The examples presented here show how to conduct power and sample size analysis based on the Benjamini and Hochberg (1995) procedure for two commonly used tests. These methods also would be useful to investigators submitting grants and as another way to perform a meta analysis. We hope that our examples will aid study designers and statisticians in both computing and interpreting average power results.
All power analysis depends on knowledge of population parameters that are in fact impossible to know before the study is completed. The best power analysis uses information from previously published studies, or from clinical knowledge. Because there is uncertainty in these estimates, even the best power analysis is subject to error. The error in the power estimates is compounded by using approximations to the distributions of PHA.
This paper discusses average power for the Pearson’s χ2 test of independence and three tests for the general linear multivariate model. The methods of this paper can be extended to calculate Benjamini and Hochberg (1995) power for other statistical tests. This paper assumes independent hypotheses that are necessary for the Benjamini and Hochberg (1995) procedure. Often however, hypotheses are correlated. While not explored in this paper, Benjamini and Yekutieli (2001) explores using the Benjamini and Hochberg (1995) procedure under conditions of non independent hypotheses. The methods of this paper could thus be extended using Benjamini and Yekutieli (2001) to allow for situations where the assumption of hypothesis independence can be relaxed.
Table 10.
Denominator degrees of freedom for three multivariate test statistics.
| Name, (z) | Denominator degrees of Freedom, 𝒟 (z) |
|---|---|
| Wilks’ Lambda (W) | g [(N − r) − (b − a + 1)/2] − (ab − 2) /2 |
| Pillai-Bartlett Trace (PB) | s [(N − r) − b + s] |
| Hotelling-Lawley Trace (HL) | s [(N − r) − b − 1] + 2 |
APPENDIX
In this appendix, we give definitions, and approximate distributions under the null and the alternative for three multivariate tests. The discussion is condensed from Muller et al., (1992) and is reproduced here for the readers’ convenience.
The general linear multivariate model is
| (7.1) |
where Y and ℰ are N × p, X is N × q, and β is q × p with rank(X)= r. We assume that each row of ℰ is independent and identically distributed as N(0, Σ) (Muller et al 1992).
Define two contrast matrices, C and U, and a hypothesis matrix θ so that
| (7.2) |
The multivariate general linear null hypothesis is
| (7.3) |
All test statistics are functions of the observed data. Let s = min(a, b). As in Muller et al (1992), define
| (7.4) |
| (7.5) |
| (7.6) |
| (7.7) |
| (7.8) |
| (7.9) |
The alternative hypothesis is of the form
| (7.10) |
Under the alternative hypothesis, we calculate
| (7.11) |
| (7.12) |
| (7.13) |
Define the test statistic for Wilks’ lambda as
| (7.14) |
Define the test statistic for the Pillai-Bartlett trace as
| (7.15) |
Define the test statistic for the Hotelling-Lawley trace as
| (7.16) |
A scalar measurement of multivariate association, 𝒯 (ẑ) for each observed test statistic z ∈ {Ŵ, B̂, L̂} appears in Table 9. Muller et al., (1992) gave single F approximations under the null and the alternative for the multivariate tests. Let
| (7.17) |
The denominator degrees of freedom for three multivariate tests are given in Table 11. Define for each test statistic z
| (7.18) |
Then for each multivariate test under the null,
| (7.19) |
where FF [ab, 𝒟(z)] is the central F distribution with numerator degrees of freedom ab and denominator degrees of freedom 𝒟(z). Under the alternative hypothesis, the distribution of test statistic becomes noncentral. For the purposes of defining the non-centrality parameter, define the test statistic under the alternative for Wilks’ lambda as
| (7.20) |
the test statistic under the alternative for the Pillai-Bartlett trace as
| (7.21) |
and the test statistic under the alternative for the Hotelling-Lawley trace as
| (7.22) |
A scalar measurement of multivariate association under the alternative, 𝒯 (z) for each test statistic z ∈ {W, B, L} appears in Table 11. Define the non-centrality parameter ω as
| (7.23) |
This is the value that the scalar test statistic would have taken on if we observed θ̂=θA and Σ̂=ΣA For each multivariate test under the alternative we have
| (7.24) |
where FF [ab, 𝒟(z), ω (z)] is the noncentral F distribution with ab numerator degrees of freedom, 𝒟(z) denominator degrees of freedom, and noncentrality w (z).
Table 9.
Scalar measurements of multivariate association for three multivariate tests.
| Name, (z) | Transformation, 𝒯 (ẑ) |
|---|---|
| Wilks’ Lambda (Ŵ) | 1 − |
| Pillai-Bartlett Trace (B̂) | B̂/s |
| Hotelling-Lawley Trace (L̂) | (L̂/s) (1 + L̂/s)−1 |
Table 11.
One-to-one transformations for three multivariate test statistics.
| Name, (z) | Transformation, 𝒯 (z) |
|---|---|
| Wilks’ Lambda (W) | 1 − |
| Pillai-Bartlett Trace (B) | B/s |
| Hotelling-Lawley Trace (L) | (L/s) (1 + L/s)−1 |
Footnotes
Glueck was supported by NCI K07CA88811.
REFERENCES
- Agresti A. Categorical Data Analysis. New York: John Wiley & Sons; 1990. [Google Scholar]
- Agresti A. A Survey of Exact Inference for Contingency Tables. Statistical Science. 1992;V.7(No. 1):131–153. [Google Scholar]
- Bayarri MJ, Berger JO. P-Values for Composite Null Models. Journal of the American Statistical Association. 2000;V.95(No. 452):1127–1142. [Google Scholar]
- Benjamini Y, Hochberg J. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. Journal of the Royal Statistical Society: Series B. 1995;V.57(No. 1):289–300. [Google Scholar]
- Benjamini Y, Liu W. A Step-Down Multiple Hypotheses Testing Procedure that Controls the False Discovery Rate under Independence. Journal of Statistical Planning and Inference. 1999;82:163–170. [Google Scholar]
- Benjamini Y, Yekutieli D. The Control of the False Discovery Rate in Multiple Testing Under Dependency. The Annals of Statistics. 2001;29(No 4):1165–1188. [Google Scholar]
- Bhattacharya B, Habtzghi D. Median of the p-value Under the Alternative Hypothesis. The American Statistician. 2002;56(3):202–206. [Google Scholar]
- Cohen J. Statistical Power Analysis for the Behavioral Sciences. 2nd edition. New York: Lawrence Erlbaum Associates; 1988. [Google Scholar]
- Collaborative Group on Hormonal Factors in Breast Cancer. Breast Cancer and Hormone Replacement Therapy: Collaborative Reanalysis of data from 51 Epidemiologic Studies of 52,705 Women with Breast Cancer and 108,411 Women Without Breast Cancer. Lancet. 1997;350:1047–1059. [PubMed] [Google Scholar]
- Curran-Everett D. Multiple Comparisons: Philosophies and Illustrations. American Journal Physiology - Regulatory, Integrative and Comparative Physiology. 2000;279:R1–R8. doi: 10.1152/ajpregu.2000.279.1.R1. [DOI] [PubMed] [Google Scholar]
- Daniel WW. Applied Nonparametric Statistics. United States: Duxbury Thomson Learning; 1990. [Google Scholar]
- Glueck DH, Mandel J, Karimpour-Fard A, Hunter L, Muller KE. Exact Calculations of Average Power for the Benjamini-Hochberg Procedure. The International Journal of Biostatistics. 2008;Vol. 4(Iss. 1) doi: 10.2202/1557-4679.1103. Article 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greendale GA, Reboussin BA, Sie A, Singh HR, Olson LK, Gatewood O, Bassett LW, Wasilauskas C, Bush T, Barrett-Connor E. Effects of Estrogen and Estrogen-Progestin on Mammographic Parenchymal Density. Annals of Internal Medicine. 1999;130:262–269. doi: 10.7326/0003-4819-130-4_part_1-199902160-00003. [DOI] [PubMed] [Google Scholar]
- Hung HMJ, O’Neill RT, Bauer P, Koehne K. The Behavior of the P-Value When the Alternative Hypothesis is True. Biometrics. 1997;53:11–22. [PubMed] [Google Scholar]
- Kroll NEA. Testing Independence in 2×2 Contingency Tables. Journal of Educational Statistics. 1989;Vol. 14(No. 1):47–79. [Google Scholar]
- Lewin JM, D’Orsi CJ, Hendrick RE, Moss LJ, Isaacs PK, Karellas A, Cutter GR. Clinical Comparison of Full-Field Digital Mammography and Screen-Film Mammography for Detection of Breast Cancer. American Journal of Roentgenology. 2002;179:671–677. doi: 10.2214/ajr.179.3.1790671. [DOI] [PubMed] [Google Scholar]
- Lewis FL, Carpentier A, Adeli K, Giacca A. Disordered Fat Storage and Mobilization in the Pathogenesis of Insulin Resistance and Type 2 Diabetes. Endocrine Reviews. 2002;23(2):201–229. doi: 10.1210/edrv.23.2.0461. [DOI] [PubMed] [Google Scholar]
- Muller KE, LaVange LM, Ramey SL, Ramey CT. Power Calculations for General Linear Multivariate Models Including Repeated Measures Applications. Journal of the American Statistical Association. 1992;Vol 87(No. 420):1209–1226. doi: 10.1080/01621459.1992.10476281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller KE, Peterson BL. Practical Methods for Computing Power in Testing the Multivariate General Linear Hypothesis. Computational Statistics and Data Analysis 2. 1984:143–158. [Google Scholar]
- Pearson K. Mathematical contributions to the theory of evolution XIII: On the Theory of Contingency and its Relation to Association and Normal Correlation. Draper’s Co. Research Memoirs. In: Karl Pearson’s Early PapersPearson ES, editor. Biometric Series. No. 1. Cambridge: Cambridge University Press; 1904. (Reprinted in, 1948) [Google Scholar]
- Pisano ED, Gatsonis C, Hendrick E, Yaffe M, Baum JK, Acharyya S, Conant EF, Fajardo LJ, Bassett L, D’Orsi CD, Jong Roberta, Rebner M. Diagnostic Performance of Digital versus Film Mammography for Breast-Cancer Screening. The New England Journal of Medicine. 2005;353(No. 17):1773–1783. doi: 10.1056/NEJMoa052911. [DOI] [PubMed] [Google Scholar]
- Pounds S, Cheng C. Sample Size Determination for the False Discovery Rate. Bioinformatics. 2005;V.21(No 17):4263–4271. doi: 10.1093/bioinformatics/bti699. [DOI] [PubMed] [Google Scholar]
- Rosner B. Fundamentals of Biostatistics. 6th Edition. New York: Brooks-Cole; 2006. [Google Scholar]
- Ruppert D, Nettleton D, Hwang JTG. Exploring the Information in P-Values for the Analysis and Planning of Multiple-Test Experiments. Biometrics. 2007;63:483–495. doi: 10.1111/j.1541-0420.2006.00704.x. [DOI] [PubMed] [Google Scholar]
- Sackrowitz H, Samuel-Cahn E. P-Values as Random Variables - Expected P-Values. The American Statistician. 1999;53(4):326–331. [Google Scholar]
- Sant M, Allemani C, Capocaccia R, Hakulinen T, Aareleid T, Coebergh JW, Coleman MP, Grosclaude P, Martinez C, Bell J, Youngson J, Berrino F the Eurocare Working Group. Stage at Diagnosis is a Key Explanation of Differences in Breast Cancer Survival Across Europe. International Journal of Cancer. 2003;106:416–422. doi: 10.1002/ijc.11226. [DOI] [PubMed] [Google Scholar]
- Skaane P, Young K, Skjennald A. Population-based Mammography Screening: Comparison of Screen-File and Full-Field Digital Mammography with Soft-Copy Reading - Oslo I Study. Radiology. 2003;229:877–884. doi: 10.1148/radiol.2293021171. [DOI] [PubMed] [Google Scholar]
- Upton GJG. A Comparison of Alternative Tests for the 2×2 Comparative Trial. Journal of the Royal Statistical Society. Series A. 1982;V. 145(No. 1):86–105. [Google Scholar]
- Westfall PH, Tobias RD, Rom D, Wolfinger RD, Hochberg Y. Multiple Comparisons and Multiple Tests Cary. North Carolina: SAS Institute; 1999. [Google Scholar]