A Practical Bayesian Design to Identify the Maximum Tolerated Dose Contour for Drug Combination Trials

Abstract

Drug combination therapy has become the mainstream approach to cancer treatment. One fundamental feature that makes combination trials different from single-agent trials is the existence of the maximum tolerated dose (MTD) contour, i.e., multiple MTDs. As a result, unlike single-agent phase I trials, which aim to find a single MTD, it is often of interest to find the MTD contour for combination trials. We propose a new dose-finding design, the waterfall design, to find the MTD contour for drug combination trials. Taking the divide-and-conquer strategy, the waterfall design divides the task of finding the MTD contour into a sequence of one-dimensional dose-finding processes, known as subtrials. The subtrials are conducted sequentially in a certain order, such that the results of each subtrial will be used to inform the design of subsequent subtrials. Such information borrowing allows the waterfall design to explore the two-dimensional dose space efficiently using a limited sample size, and decreases the chance of overdosing and underdosing patients. To accommodate the consideration that doses on the MTD contour may have very different efficacy or synergistic effects due to drug-drug interaction, we further extend our approach to a phase I/II design with the goal of finding the MTD with the highest efficacy. Simulation studies show that the waterfall design is safer and has higher probability of identifying the true MTD contour than some existing designs. The R package “BOIN” to implement the waterfall design is freely available from CRAN.

1. Introduction

Drug combination therapy has become the cornerstone of cancer treatment. A unique feature that distinguishes drug combination dose-finding trials from conventional single-agent trials is the existence of the MTD contour in the two-dimensional dose space. In the single-agent trial, there is only one MTD under the assumption of monotonicity (i.e., toxicity monotonically increases with the dose), whereas in the combination trial, multiple MTDs (i.e., the MTD contour) may exist in the dose matrix. Depending on the study objective, phase I drug-combination trials may aim to find a single MTD or the MTD contour in a prespecified dose combination matrix.

Numerous dose-finding designs have been proposed for finding a single MTD of drug combinations. Conaway, Dunbar, and Peddada [1] proposed a drug combination dose-finding method based on the order of the restricted inference. Yin and Yuan [2, 3] proposed Bayesian dose-finding designs based on latent contingency tables [2] and a copula-type model [3] for drug combination trials. Braun and Wang [4] developed a dose-finding method based on a Bayesian hierarchical model. Wages, Conaway and O’Quigley [5] extended the continuous reassessment method (CRM) [6] based on partial ordering of the dose combinations. Braun and Jia [7] generalized the CRM to handle drug combination trials. Riviere et al. [8] proposed a Bayesian dose-finding design based on the logistic model. Cai, Yuan and Ji [9] and Riviere et al. [10] proposed Bayesian adaptive designs for drug combination trials involving molecularly targeted agents, among others.

The aforementioned designs are devised for finding a single MTD in the drug combination matrix. They are not suitable for finding the MTD contour due to several reasons. First, most of these designs make the decision of dose assignment and selection based on parametric dose-toxicity models, and in practice the assumed models are more likely to be misspecified than correctly specified. When our goal is to find a single MTD, model misspecification is not of a particular concern. This is because as long as the assumed model provides a good local fit around a MTD, it often leads to correct identification of that MTD, even though the global fit of the model is poor and biased [9, 11]. However, when our goal is to find the MTD contour, model misspecification can be disastrous and lead to misidentification of the MTD contour. This is because in order to correctly identify the MTD contour, we must precisely estimate the whole dose-toxicity surface, which typically is not possible under misspecified models. In other words, finding the MTD contour is much more susceptible to the influence of model misspecification than finding a single MTD. Second, the dose finding algorithms used in the existing designs are typically myopic in the sense that they assign the next new (cohort of) patient to the dose that has the toxicity estimate closest to the target toxicity rate. As a result, these designs tend to concentrate the patient allocation at a certain local region (e. g., one of the MTDs) and thus loses the opportunity to learn about other regions of the dose space. Without adequately learning about the whole dose space, it is generally not possible to accurately identify the whole MTD contour.

Several designs have been developed for finding the MTD contour. Thall et al. [12] proposed a six-parameter model-based design to find three MTDs; however, that design assumes that the doses are continuous and can be freely changed during the trial, which is not common in practice. Wang and Ivanova [13] proposed a design to find the MTD contour based on a parametric model, assuming that the logarithm of the toxicity probability of a drug combination is a linear function of the doses of the two drugs. As discussed previously, to find the MTD contour, these model-based designs are susceptible to model misspecification. Yuan and Yin [14] proposed a sequential method to find the MTD contour by converting two-dimensional dose finding into a series of one-dimensional dose findings. Adrian et al. [15] recently proposed a product of independent beta probabilities escalation (PIPE) design to find the MTD contour based on Bayesian model averaging, without assuming a parametric form on the dose-toxicity curve.

In this article, we propose a simple, practical dose-finding design to find the MTD contour for drug combination trials. Our design adopts the sequential dose-finding strategy proposed by Yuan and Yin [14] which divides the original trial into a series of subtrials. Within each subtrial, the investigational doses are fully ordered. The key feature of the new design is that the subtrials are conducted sequentially in a certain order, such that the results of each subtrial will be used to inform the design (e.g., the dose range and the starting dose) of subsequent subtrials. Such information borrowing allows the proposed design to explore the two-dimensional dose space efficiently using a limited sample size, and also decrease the chance of overdosing and underdosing patients. We further extend our approach to phase I/II designs to accommodate the consideration that even when doses on the MTD contour have similar toxicity, they may have very different efficacy or synergistic effects due to drug-drug interaction. Simulation studies show that the proposed design is robust and outperforms existing designs. The new design is implemented in R package “BOIN” and available from CRAN.

The remainder of this article is organized as follows. In Section 2, we propose the new design based on the divide-and-conquer strategy and extend it to phase I/II trials. We briefly describe the software to implement the waterfall design in Section 3. In Section 4, we investigate the operating characteristics of the proposed design based on simulation studies. In Section 5, we conclude with a brief discussion.

2. Methods

2.1. Divide and conquer

Finding the MTD contour is substantially more challenging than finding a single MTD in the two-dimensional dose combination space. To find a single MTD, we do not need to learn the whole dose space. Once the dose finding algorithm settles down in a region that contains a MTD, we only need to learn that local region in order to correctly find that MTD. In contrast, in order to find all MTDs (i.e., the MTD contour) existing in the dose matrix, we must explore and learn the whole dose matrix, otherwise there is always a risk of missing or misidentifying some MTDs. The challenge is how to use a very limited sample size, a characteristic of phase I trials, to learn the whole dose matrix and find the MTD contour.

A general strategy for handling a difficult task, such as finding the MTD contour, is to divide it into several small tasks that are easy to complete. Taking that strategy, Yuan and Yin [14] proposed to partition the dose matrix into a series of blocks (i.e., groups of doses), within which the doses are fully ordered, and then find the MTD within each block. In other words, the strategy is to divide the two-dimensional dose-finding problem into a series of simpler one-dimensional dose-finding problems. Each of these one-dimensional dose-finding problems is referred to as a “subtrial.” When we have used that design in practice, the clinicians have raised several practical issues. First, the design starts the trial at the second lowest dose, A₂B₁, rather than at the lowest dose. In practice, clinicians strongly favor starting the trial at the lowest dose, A₁B₁, for safety considerations. Second, to improve trial efficiency, the design of Yuan and Yin [14] continuously shrinks the search space by removing some doses on the basis of the MTD identified in the previous subtrial. However in practice, that rule may be too stringent. Due to the small sample size, the MTD identified in a subtrial may be incorrect. As a result, the true MTD may be incorrectly removed from the subsequent subtrials. Third, Yuan and Yin [14] did not provide detailed guidance on when and how to switch from one subtrial to the next one. This is a critical issue when implementing the design and requires careful consideration.

To address these concerns, we introduce a new dose-finding design, the waterfall design. The “waterfall” characterizes the process of sequentially finding the MTD contour, moving from the top of the dose matrix to the bottom, as described later. A new partition scheme is used to partition the dose matrix into blocks such that the trial always starts with the lowest dose. In addition, the results from the prior subtrial are used only to set the starting dose rather than to directly shrink the dose space for the subsequent trial, which gives the design more flexibility to move around and identify the MTD more precisely. We also propose a practical rule to determine when to switch from one subtrial to the next.

2.2. Waterfall design

Consider a trial combining J doses of drug A, A₁ < ··· < A_J, with K doses of drug B, B₁ < ··· < B_K, and let A_jB_k denote the combination of A_j with B_k. Given the J × K dose matrix, finding the MTD contour is equivalent to finding an MTD, if it exists, in each row of the dose matrix. Without loss of generality, we assume that J ≤ K such that the dose matrix is in a “landscape” orientation (i.e., more columns than rows). If drug A has more dose levels than drug B (i.e., J > K), we recommend rotating the dose matrix to make it in the “landscape” orientation. As shown below, arranging the dose matrix in the “landscape” orientation leads to fewer subtrials, which simplifies the practical implementation of the waterfall design.

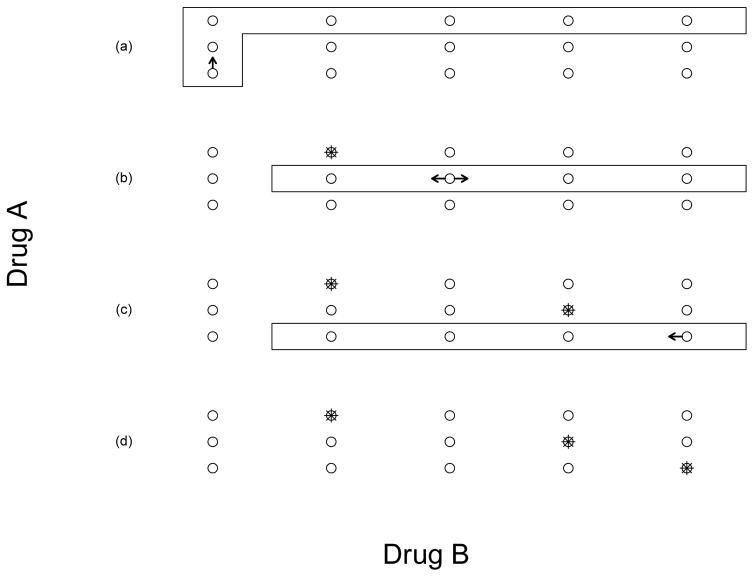
As illustrated in Figure 1, the waterfall design partitions the J × K dose matrix into J subtrials (or blocks), within which the doses are fully ordered. These subtrials are conducted sequentially from the top of the matrix to the bottom, which is why we refer to the design as the waterfall design. The waterfall design can be described as follows:

Figure 1.

Illustration of the waterfall design for a 3 × 5 combination trial. The doses in the rectangle form a subtrial, and the asterisk denotes the candidate MTD. As shown in panel (a), the trial started by conducting the first subtrial with the starting dose A₁B₁. After the first subtrial identified A₃B₂ as the candidate MTD, we conducted the second subtrial with the starting dose A₂B₃ (see panel (b)). After the second subtrial identified A₂B₄ as the candidate MTD, we conducted the third subtrial with the starting dose A₁B₅ (see panel (c)). After all the subtrials were completed, we selected the MTD contour based on the data from all the subtrials, as shown in panel (d).

1. Divide the J × K dose matrix into J subtrials S_J, ···, S₁, according to the dose level of drug A:

   $$\begin{array}{lll}\hfill S_J& =\hfill & \{A_1{B}_1,\cdots ,A_J{B}_1,A_J{B}_2,\cdots ,A_J{B}_K\},\hfill \\ \hfill S_{J-1}& =\hfill & \{A_{J-1}{B}_2,\cdots ,A_{J-1}{B}_K\},\hfill \\ \hfill S_{J-2}& =\hfill & \{A_{J-2}{B}_2,\cdots ,A_{J-2}{B}_K\},\hfill \\ \hfill \cdots & \hfill & \hfill \\ \hfill S_1& =\hfill & \{A_1{B}_2,\cdots ,A_1{B}_K\}.\hfill \end{array}$$

   Note that subtrial S_J also includes lead-in doses A₁B₁, A₂B₁, ···, A_JB₁ (the first column of the dose matrix) to impose the practical consideration that the trial starts at the lowest dose. Within each subtrial, the doses are fully ordered with monotonically increasing toxicity.

2. Conduct the subtrials sequentially using a one-dimensional (or single-agent) dose-finding method as follows:

   1. Conduct subtrial S_J, starting from the lowest dose combination A₁B₁, to find the MTD. We call the dose selected by the subtrial the “candidate MTD” to highlight that the dose selected by the individual subtrial may not be the “final” MTD that we will select at the end of the trial. The final MTD selection will be based on the data collected from all the subtrials. The objective of finding the candidate MTD is to determine which subtrial will be conducted next and the corresponding starting dose.

   2. Assuming that the current subtrial S_j, j = J, ···, 2, selects dose A_j^*B_k^* as the candidate MTD, next, conduct subtrial S_j^*−1 with the starting dose A_j^*−1B_k^*+1. That is, the next subtrial to be conducted is the one with the dose of drug A that is one level lower than the candidate MTD found in the previous subtrial. After identifying the candidate MTD of subtrial S_j^*−1, the same rule is used to determine the next subtrial and its starting dose. See Figure 1 for an example.

   3. Repeat step (ii) until subtrial S₁ is completed.

3. Estimate the toxicity probability R(A_jB_k) based on the toxicity data collected from all the subtrials using matrix isotonic regression [16]. For each row of the dose matrix, select the MTD as the dose combination that has the estimate of toxicity probability closest to the target toxicity rate ϕ_T, unless all combinations in that row are overly toxic.

As described previously, the major challenge of finding the MTD contour is the conflict between the desire to use as few patients as possible to run phase I trials and the fact that, in order to find the MTD contour, we must adequately explore and learn the whole dose matrix, which requires a large sample size. The waterfall design tackles this challenge by borrowing information across subtrials to efficiently explore the two-dimensional dose space. Specifically, in step 2, the waterfall design utilizes the results of the current subtrial to inform the design of subsequent subtrials, e.g., the doses range and the starting dose. In step 2(ii), the reason that subtrial S_j^*−1 starts with dose A_j^*−1B_k^*+1 rather than the lowest dose in that subtrial (i.e., A_j^*−1B₂) is that A_j^*−1B_k^*+1 is the lowest dose that is potentially located at the MTD contour, and starting from that dose allows us to quickly reach the MTD for that subtrial. Using Figure 1 as an example, the first subtrial S₃ identified the dose A₃B₂ as the MTD, and thus the second subtrial S₂ starts from the dose A₂B₃. It is not desirable to start from the lowest dose, A₂B₂, because by monotonicity we know that A₂B₂ is below the MTD. Starting at the lowest dose in this example will waste patient resources and expose patients to low doses that may be subtherapeutic.

We note that the “waterfall” sequencing is not the only possible sequence to construct the subtrials. We choose the “waterfall” sequencing because it has the following desirable properties: (1) the waterfall sequencing starts the trial from the lowest dose A₁B₁, which addresses the practical concern for the previous design by Yuan and Yin [14] that the trial does not start from the lowest dose; (2) the waterfall sequencing allows us to use the results of current subtrial to inform the design of subsequent subtrials (e.g., the doses range and the starting dose) in a simple and efficient way. Such information borrowing allows our design to explore the two-dimensional dose space efficiently using a limited sample size, and also decrease the chance of underdosing and overdosing patients. In addition, it is easy to show that the “waterfall” sequencing renders the design the consistency property as follows:

Theorem 1

The waterfall design is consistent for identifying the MTD contour if the method used for running the subtrial is consistent.

In what follows, we discuss a method to run the subtrial, which has such a consistency property.

2.3. Conducting subtrials using the BOIN design

Although any reasonable single-agent dose-finding trial design can be used to conduct the subtrials, here, we focus on the BOIN design [17] because of its implementation simplicity and good performance. The BOIN design can be implemented in a simple way that is similar to that of the traditional algorithm-based designs, such as “3+3” design, but yields good operating characteristics that are comparable to those of the CRM [17]. Coupled with BOIN, the resulting waterfall design is simple to implement in practice. In addition, as the BOIN design is consistent [17], the resulting waterfall design is also consistent.

Specifically, using the BOIN design, a subtrial with L doses can be described as follows.

1. Patients in the first cohort are treated at the lowest dose level or at a prespecified intermediate dose.

2. At the current dose level ℓ, we assume that a total (or the cumulative number) of n_ℓ patients have been treated, and m_ℓ of them have experienced toxicity. Let p̂_ℓ = m_ℓ/n_ℓ denote the observed toxicity rate at dose level ℓ. To assign a dose to the next cohort of patients,

   • if p̂_ℓ ≤ λ₁, we escalate the dose level to ℓ + 1;

   • if p̂_ℓ ≥ λ₂, we de-escalate the dose level to ℓ − 1;

   • otherwise, i.e., λ₁ < p̂_ℓ < λ₂, we retain the same dose level, ℓ.

   where λ₁ and λ₂ are prespecified dose escalation and de-escalation boundaries.

3. This process continues until the maximum sample size is reached or the trial is terminated due to excessive toxicity, as described below.

Table 1 provides the values of λ₁ and λ₂ for common target toxicity rates. For example, given the target DLT rate of 30%, the corresponding escalation threshold λ₁=0.236 and the de-escalation threshold λ₂=0.358. For ease of use, these thresholds can be converted to discrete decision boundaries as shown in Table 2. The theory and derivation of λ₁ and λ₂ can be found in Liu and Yuan [17].

Table 1.

Escalation and de-escalation boundaries λ₁ and λ₂ for the BOIN design under different target toxicity rates

Boundaries	Target toxicity rate ϕT
	0.15	0.2	0.25	0.3	0.35	0.4
λ1	0.118	0.157	0.197	0.236	0.276	0.316
λ2	0.179	0.238	0.298	0.358	0.419	0.479

Table 2.

Discrete escalation and de-escalation boundaries for target toxicity rate ϕ_T = 0.3 with cohort size of 3.

Action	Number of patients treated at the current dose
	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Escalate dose if the number of DLTs≤	0	0	0	0	1	1	1	1	2	2	2	2	3	3	3	3
De-escalate dose if the number of DLTs ≥	1	1	2	2	2	3	3	3	4	4	4	5	5	6	6	6

To protect patients from overly toxic doses, we impose the following dose elimination rule during trial conduct:

$$\begin{array}{c}\text{If}\text{pr}(p_{\ell }>{\varphi }_T\mid m_{\ell },n_{\ell })>0.95\text{and}{n}_{\ell }\ge 3,\text{dose}\text{levels}\ell \text{and}\text{higher}\text{are}\text{eliminated}\\ \text{from}\text{the}\text{trial},\text{and}\text{the}\text{trial}\text{is}\text{terminated}\text{if}\text{the}\text{first}\text{dose}\text{level}\text{is}\text{eliminated},\end{array}$$

where pr(p_ℓ > ϕ_T|m_ℓ, n_ℓ) > 0.95 can be evaluated on the basis of a beta-binomial model, assuming that m_ℓ follows a binomial distribution (with size and probability parameters n_ℓ and p_ℓ) and p_ℓ follows a vague beta prior, e.g., p_ℓ ~ beta(1, 1). The eliminated doses cannot be used to treat patients and are not selected as the MTDs.

For the waterfall design, one key issue is to determine when to end the current subtrial and initiate the next one. We recommend the following stopping/starting rule for the subtrials:

At any time during the subtrial, if the total number of patients treated at the current dose reaches a certain prespecified number of patients, say n_stop, we stop the subtrial, select the candidate MTD and initiate the next subtrial.

The rationale for the stopping rule is that when the patient allocation concentrates at a given dose, it indicates that the dose finding might have converged to the MTD, and thus we can stop the trial and claim the MTD. This stopping rule allows the sample size of the subtrials to be automatically adjusted according to the difficulty of the dose finding. Another attractive feature of the above approach is that it automatically ensures that a certain number of patients are treated at the MTD. Conventionally, we achieve this by adding cohort expansion after identifying the MTD. In practice, we recommend n_stop > 9 to ensure reasonable operating characteristics.

An alternative stopping rule is based on the confidence interval (CI) of the estimate of toxicity probabilities. For example, stop the subtrial when the CI of a dose contains the target toxicity probability ϕ_T and its width is narrower than a certain value. Our numerical study shows that after appropriate calibration, these two approaches have virtually the same performance (results are not shown). This is somewhat expected because the width of the CI is essentially determined by the sample size (i.e., n_stop). Thus, we recommend the stopping rule that is based on the number of patients treated because it is more transparent, in particular to clinicians, and is easy to implement.

Although the above stopping rule provides an automatic, reasonable way to determine the sample size for the trial, the resulting sample size is random. In practice, it is often desirable to put a cap on the maximum sample size of the subtrials. This can be done by adding an extra stopping rule as follows:

$$\text{Stop}\text{the}j\text{th}\text{subtrial}\text{if}\text{its}\text{sample}\text{size}\text{reach}\mathrm{a}\text{prespecified}\text{maximum}\text{sample}\text{size}{N}_j^{\mathit{max}}.$$

As a rule of thumb, we recommend $N_j^{\mathit{max}}=4\times (\text{the}\text{number}\text{of}\text{doses}\text{in}\text{the}j\text{th}\text{subtrial})$, for j = 1, ···, J. This means that given a J × K dose combinations, the maximum total sample size for the trial is 4 × J × K. For example, for a 3×5 combination, as shown in Figure 1, the first subtrial contains 7 doses, and the second and third subtrials contain 4 doses each. The recommended sample sizes are 28, 16 and 16 for three subtrials, respectively, resulting a total sample size of 60 patients. This may seems large, however given that there are a total of 15 doses, 60 patients actually is not a very large sample size. To see this, considering a single-agent trial with 15 doses, the maximum sample size under the 3+3 design is 90 patients. In practice, the recommended sample sizes n_stop and $N_j^{\mathit{max}}$ should be further calibrated using simulation until attaining desirable operating characteristics, which can be readily done using R package “BOIN” described later.

2.4. Extension to phase I/II trial

Doses on the MTD contour have similar toxicity, but may have rather different efficacy or synergistic treatment effects due to drug-drug interaction. Thus, it is of great practical interest to identify which MTD has the highest efficacy or synergistic effect. The waterfall design can be easily extended to achieve this goal using the (seamless) phase I/II trial design framework [18].

Our phase I/II waterfall design consists of a phase I part and a phase II part, which are seamlessly connected. Both toxicity and efficacy data are collected throughout the trial. The phase I part uses the waterfall design as described previously to find the MTD contour on the basis of only toxicity. Once the MTD contour is identified, these MTDs are seamlessly moved to phase II to evaluate efficacy. Suppose that R MTDs are identified in phase I and moved to phase II for evaluating efficacy. We equally randomize patients into the R MTDs. Let π_r denote the response rate of the rth MTD, r = 1, ···, R, and y denote the binary response indicator. We model π_r using a beta-binomial model

$$\begin{array}{lll}\hfill y\mid {\pi }_r& ~\hfill & \mathit{binomial}({\pi }_r)\hfill \\ \hfill {\pi }_r& ~\hfill & \mathit{beta}(0.05,0.05).\hfill \end{array}$$

Assume that at an interim decision time, n_r patients have been treated at the rth MTD, and s_r patients experienced efficacy. Note that n_r patients include those treated in phase I. Given interim data 𝒟 = (n_r, s_r), the posterior distribution of π_k is pr(π_k|𝒟 ) = beta(0.05 + s_k, 0.05 + n_k − s_k).

During phase II, we monitor efficacy and remove futile doses based on the following rule: drop the rth MTD if pr(π_r < π|𝒟 ) > c, where π is the lower bound on efficacy and c is a probability cutoff (e.g., c = 0.9). Such monitoring can be done in a group sequential way (e.g., after 1/3 and 2/3 patients are enrolled) when efficacy takes a relatively long time to be scored, e.g., using RECIST criteria. Patient accrual may be paused during the interim analysis. Alternatively, we can model efficacy as a time-to-event outcome [19] or unobserved efficacy outcomes as missing data [20, 21] to allow continuous monitoring of efficacy. Meanwhile, we also monitor toxicity based on the BOIN dose escalation/de-escalation rule. An important feature of the proposed phase I/II design is that during phase II, in light of the accumulating data, we still allow for dose escalation and de-escalation based on the rule of the BOIN design. Dose escalation and de-escalation will be restricted to the subtrial in which that dose is originally assigned. For example, suppose that A₂B₃ was selected as a candidate MTD after phase I and moved forward to phase II to evaluate efficacy. Assume that the new toxicity data collected from phase II suggest that A₂B₃ is actually overly toxic. In this case, we de-escalate the dose to A₂B₂ and evaluate that new dose’s efficacy and toxicity. Such flexibility is important because it allows us to continuously refine our estimate of the MTDs. In addition, because it uses all cumulated data from both phases I and II, it provides more accurate evaluation of the toxicity and efficacy of the doses. These features make our phase I/II design different from the approach of simply attaching phase II to phase I. After the prespecified maximum sample size is reached, we stop the trial and select the dose with the highest posterior estimate of efficacy as the recommended dose. Yuan and Yin [22] proposed a different, model-based phase I/II drug-combination designs, where the phase I part finds all safe doses, rather than the MTD contour, for evaluating efficacy in the phase II part.

3. Software

The waterfall design can be easily implemented using the R package “BOIN”, which is freely available from CRAN. A statistical tutorial and protocol template for using this package to design drug combination trials can be found in http://odin.mdacc.tmc.edu/~yyuan/index_code.html. Here, we provide a brief overview of the related functions.

• get.boundary(···); This function is used to generate escalation and de-escalation boundaries for conducting subtrials.

• next.subtrial(···); This function is used to obtain the starting dose for the next subtrial when the current subtrial is completed.

• select.mtd.comb(···); This function (with argument mtd.contour = TRUE) is used to select the MTD contour at the end of the trial based on isotonically transformed estimates.

• get.oc.comb(···); This function (with argument mtd.contour = TRUE) is used to generate the operating characteristics of the waterfall design for drug combination trials.

• get.oc.comb.phase12(···); This function is used to generate the operating characteristics of the phase I/II waterfall design for drug combination trials.

One important practical advantage of the proposed waterfall design is that it is simple and fast to implement. Simulating 1,000 trials using our R package took only about 1.5 minutes.

4. Simulation Studies

4.1. Waterfall design

We investigated the operating characteristics of the proposed waterfall design using simulation studies. The target toxicity probability ϕ_T = 0.3. Patients were treated in cohort sizes of 3. To end the current subtrial and initiate the next one, we set n_stop = 12 and $N_j^{\mathit{max}}=4\times (\text{the}\text{number}\text{of}\text{doses}\text{in}\text{the}j\text{th}\text{subtrial})$. We simulated 1000 trials under each of 14 scenarios (see Table 3). We compared the waterfall design with the PIPE design [15] and matched the sample sizes for the two designs under each simulation scenario. The PIPE design was implemented using the software provided by Adrian et al. [15]. We noted problems with the way the PIPE software reports the selection percentage. Specifically, let u_jk denote the number of times that A_jB_k is selected as the MTD across 1000 simulated trials. The PIPE software calculates the selection percentage for A_jB_k as

Table 3.

True toxicity probabilities for fourteen scenarios. The MTD contours are in boldface.

Drug A	Drug B
	1	2	3	4	5	1	2	3	4	5
	Scenario 1					Scenario 2
2	0.10	0.30	0.50			0.30	0.48	0.60
1	0.03	0.10	0.28			0.12	0.30	0.48
	Scenario 3					Scenario 4
2	0.32	0.45	0.60			0.42	0.49	0.55
1	0.10	0.15	0.30			0.30	0.40	0.50
	Scenario 5					Scenario 6
4	0.53	0.58	0.63	0.70		0.31	0.59	0.64	0.69
3	0.30	0.42	0.54	0.62		0.12	0.30	0.56	0.63
2	0.12	0.28	0.49	0.57		0.06	0.11	0.27	0.61
1	0.06	0.12	0.30	0.52		0.01	0.07	0.08	0.30
	Scenario 7					Scenario 8
4	0.55	0.63	0.69	0.73		0.56	0.62	0.68	0.75
3	0.50	0.53	0.57	0.64		0.48	0.52	0.58	0.65
2	0.30	0.42	0.54	0.66		0.30	0.45	0.55	0.60
1	0.05	0.28	0.48	0.61		0.01	0.05	0.15	0.30
	Scenario 9					Scenario 10
3	0.07	0.10	0.30	0.48	0.54	0.10	0.30	0.51	0.57	0.63
2	0.03	0.05	0.13	0.30	0.50	0.06	0.14	0.27	0.52	0.61
1	0.01	0.04	0.11	0.15	0.30	0.01	0.03	0.05	0.12	0.31
	Scenario 11					Scenario 12
3	0.28	0.49	0.61	0.68	0.73	0.49	0.51	0.57	0.64	0.77
2	0.06	0.10	0.31	0.51	0.57	0.30	0.41	0.52	0.61	0.73
1	0.01	0.05	0.07	0.11	0.30	0.01	0.03	0.30	0.45	0.52
	Scenario 13					Scenario 14
3	0.52	0.55	0.66	0.71	0.75	0.51	0.57	0.65	0.73	0.79
2	0.30	0.42	0.54	0.60	0.65	0.30	0.45	0.52	0.66	0.70
1	0.01	0.03	0.15	0.30	0.45	0.09	0.28	0.48	0.60	0.65

$$q_{jk}=\frac{u_{jk}}{{\sum }_{j=1}^J{\sum }_{k=1}^K{u}_{jk}}.$$ (1)

The issue is that q_jk indicates that among the selected doses, how likely it is that A_jB_k. It does not reflect what we really care about in practice, which is, across 1000 trials, how likely it is that we select A_jB_k as the MTD, i.e.,

$$Pr(\text{selecting}{A}_j{B}_k\text{as}\text{MTD})=\frac{u_{jk}}{1000}.$$ (2)

Actually, using q_jk to measure the design performance can be misleading. We use scenario 1 to illustrate this and assume that there are two designs. The first design has perfect performance. In each of the 1000 simulated trials, it always correctly selects A₁B₃ and A₂B₂ as the MTDs. For the second design, in 500 simulated trials, it correctly selects A₁B₃ and A₂B₂ as the MTDs, but in the remaining 500 simulated trials, it incorrectly claims that there was no MTD and does not select any dose as the MTD. If we use q_jk as the measure of MTD selection, we will conclude that these two designs have the same performance, with selection percentages of 100% for each of A₁B₃ and A₂B₂. Therefore, in our simulation study, we use (2) as the definition of the MTD selection percentage for drug combinations.

Table 4 shows the selection percentage for each dose combination based on 1000 simulated trials. The waterfall design outperformed the PIPE design. For example, in scenario 1, the MTD contour is A₁B₃ and A₂B₂. The selection percentage was above 59% for each of the two target doses under the waterfall design, whereas it was below 45% under the PIPE design. Note that the sum of the selection percentages across all dose combinations can be larger than 100% because the designs may select more than one combination as the MTD in a simulated trial. In scenarios 2 and 3, the MTD contours are at different locations (i.e., A₁B₂ and A₂B₁ in scenario 2, and A₁B₃ and A₂B₁ in scenario 3). The selection percentages for these doses under the waterfall design were above 53% for each of the target doses, however they were below 43% under the PIPE design. Scenario 4 considers the case in which there is only one MTD (i.e., incomplete MTD contour). The selection percentage of the MTD (i.e., A₁B₁) under the waterfall design was 12% more than that under the PIPE (i.e., 56.5% versus 44.5%). Scenarios 5 to 8 consider the 4 × 4 combinations, and Scenarios 9 to 14 consider the 3 × 5 combinations. The waterfall design again outperformed the PIPE design. For example, in scenario 7, the selection percentages of the two MTDs (A₁B₂ and A₂B₁) were 56.3% and 67.2%, respectively, under the waterfall design, while those under the PIPE design were respectively 31.3% and 30.4%.

Table 4.

Selection percentage of each dose combination under the PIPE and waterfall designs. The selection percentages of the true MTDs are shown in boldface.

Sc.	Drug A	Drug B
		Waterfall					PIPE
		1	2	3	4	5	1	2	3	4	5
1	2	21.1	59.8	18.5			56.9	35.2	1.3
	1	0.3	15.5	84.2			0.1	34.5	44.1
2	2	58.5	18.7	1.0			41.1	3.0	0.0
	1	18.2	55.9	25.5			30.5	42.6	5.1
3	2	53.6	19.7	2.8			37.9	6.3	0.4
	1	6.5	28.8	64.5			9.2	49.3	33.0
4	2	23.4	5.9	0.3			10.7	0.5	0.0
	1	56.5	24.4	6.9			44.5	13.5	1.2
5	4	9.6	1.6	0.0	0.0		9.6	0.8	0.0	0.0
	3	60.1	15.5	1.2	0.0		37.2	18.1	1.5	0.0
	2	20.6	54.1	23.1	1.3		15.2	39.0	9.8	1.3
	1	9.7	15.8	54.3	20.2		0.1	13.8	42.0	8.8
6	4	66.4	7.7	0.0	0.0		42.6	2.2	0.0	0.0
	3	20.3	65.2	13.0	0.2		24.6	45.1	2.3	0.0
	2	9.6	13.1	66.4	10.8		0.2	21.7	52.4	1.9
	1	8.8	0.8	15.6	74.8		0.0	0.0	22.2	46.6
7	4	1.1	0.0	0.0	0.0		5.7	0.4	0.0	0.0
	3	13.6	0.5	0.2	0.0		15.7	4.4	0.4	0.0
	2	67.2	15.7	1.5	0.0		30.4	19.6	2.8	0.5
	1	14.3	56.3	26.7	2.7		12.1	31.3	20.7	4.4
8	4	1.3	0.1	0.0	0.0		7.2	1.0	0.0	0.0
	3	17.4	0.8	0.1	0.0		19.2	6.1	1.7	0.0
	2	69.1	15.2	1.6	0.2		26.4	21.0	9.5	2.7
	1	8.3	2.4	32.9	56.4		0.1	4.8	36.8	47.1
9	3	1.6	21.7	61.4	15.1	0.0	3.2	51.3	40.3	4.2	0.1
	2	0.0	0.3	17.5	67.1	15.1	0.0	0.0	27.1	45.6	3.7
	1	0.0	0.0	0.8	19.8	79.4	0.0	0.0	0.2	23.7	45.0
10	3	20.0	65.9	12.8	0.1	0.0	47.1	44.0	5.4	0.4	0.0
	2	1.1	13.6	67.3	17.3	0.7	0.1	20.7	49.4	8.1	0.2
	1	0.1	0.1	0.6	22.1	77.1	0.0	0.0	2.1	47.1	42.1
11	3	69.6	17.5	0.8	0.0	0.0	48.9	10.0	0.9	0.0	0.0
	2	1.5	20.3	62.3	14.7	1.2	1.3	43.4	42.7	6.3	0.7
	1	0.2	0.0	1.1	22.1	76.6	0.0	0.0	2.5	44.6	46.5
12	3	14.7	2.1	0.2	0.0	0.0	15.7	5.3	0.4	0.0	0.0
	2	64.8	20.1	2.1	0.2	0.0	29.4	19.3	6.9	1.7	0.2
	1	4.7	14.5	54.7	21.8	4.3	0.0	29.7	34.9	17.3	6.5
13	3	12.0	0.7	0.0	0.0	0.0	13.3	3.3	0.6	0.0	0.0
	2	69.5	15.1	1.8	0.1	0.0	31.8	21.6	6.9	2.5	0.1
	1	4.8	1.0	26.8	45.9	21.5	0.0	6.3	33.3	41.2	15.1
14	3	13.3	1.1	0.0	0.0	0.0	12.2	1.8	0.0	0.0	0.0
	2	63.8	15.8	0.9	0.0	0.0	35.5	15.8	4.0	0.3	0.0
	1	16.7	61.5	19.9	1.7	0.2	15.5	34.8	16.3	6.5	0.4

Table 5 shows the percentage of correct selection (PCS) of the MTD contour. That is, the percentage of times the design correctly selected all MTDs simultaneously in 1000 simulated trials. For example, in scenario 1, the PCS is the percentage of times that the design selected A₁B₃ and A₂B₂ simultaneously. In terms of selecting the MTD contour, the advantage of the waterfall design is more obvious. The PCS of the MTD contour was usually higher than 30% (12 out of 14 scenarios) under the waterfall design; whereas it was usually less than 16% (11 out of 14 scenarios) under the PIPE design. Across 14 scenarios, the average PCS under the waterfall design was 35.2%, which was 2 times greater than that of the PIPE design (i.e., 14.8%). Note that by the play of randomness, simultaneously identifying all MTDs in the dose matrix is a much more challenging task than identifying a single MTD, especially given the small sample size of phase I trials. For example, suppose that there are 3 MTDs, and for each of them the PCS is 70%. If the selection of each of the MTDs is independent, the probability of simultaneously selecting 3 MTDs is merely 0.7³ = 34.3%. Therefore, the PCS for the MTD contour is substantially lower than the PCS for each individual MTD.

Table 5.

The percentage of correct selection of the MTD contour, and the percentage of patients treated above and at the MTD contour.

Design	Scenario
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
	% correct selection of the MTD contour
Waterfall	50.4	36.4	35.1	48.5	18.7	27.7	36.8	36.0	30.7	32.6	33.8	35.9	31.3	38.4
PIPE	20.5	19.6	10.2	44.5	8.9	6.1	12.5	12.5	11.9	10.1	10.9	12.2	11.6	15.8
	% of patients treated above the MTD contour
Waterfall	9.4	25.0	12.7	51.7	30.0	16.2	34.4	24.6	14.2	16.0	15.7	33.2	26.2	36.0
PIPE	5.8	16.7	8.6	40.4	51.7	25.8	62.0	46.6	18.4	24.4	30.2	51.1	46.7	54.9
	% of patients treated at the MTD contour
Waterfall	51.3	50.1	47.8	48.3	44.1	53.6	48.0	39.3	45.7	46.2	48.0	42.6	39.5	47.0
PIPE	48.0	59.2	51.5	59.6	37.4	54.5	27.4	29.1	47.2	43.3	43.1	31.2	28.8	34.0
	Sample size (matched between two designs)
	27	27	27	18	48	60	36	36	60	60	60	42	42	39

Table 5 also reports the percentage of patients treated at doses above the MTD contour under the two designs, as a measure of design safety, and the percentage of patients treated at the MTD contour. We can see that, in general, the waterfall design was safer than the PIPE design because it assigned a lower percentage of patients to doses above the MTD contour. In addition, the waterfall design assigned higher percentages of patients to the MTDs than the PIPE. The sample sizes of two designs were matched and provided in Table 5. The patient allocation to each of the dose combinations can be found in Table S1 in the Appendix.

4.2. Phase I/II waterfall design

We also briefly evaluated the performance of the proposed phase I/II waterfall design via simulation studies. The toxicity upper limit ϕ_T was 0.30, and the efficacy lower limit π was 0.2. The maximum sample size was 36 for phase I and 72 for the whole trial. The cohort size was 3. We considered 8 toxicity-efficacy scenarios (see Table 6). The target (or optimal) dose is defined as the most efficacious dose combination in the MTD contour. We simulated 1000 trials under each scenario.

Table 6.

Selection probability and number of patients treated at each dose combination using the proposed phase I/II waterfall design, with the target dose combinations in boldface.

Sc.	Drug A	Drug B						Simulation results
		True pr(toxicity)			True pr(efficacy)			Selection percentage			No selection†	Number of patients
		1	2	3	1	2	3
1	2	0.10	0.30	0.50	0.25	0.35	0.55	7.5	20.2	0.9	0.5	11.6	19.5	4.9
	1	0.03	0.10	0.28	0.20	0.30	0.50	0.1	20.2	50.6		3.5	9.1	22.2
2	2	0.10	0.30	0.50	0.20	0.30	0.40	23.5	42.0	0.9	11.0	11.3	18.8	5.0
	1	0.03	0.10	0.28	0.07	0.12	0.20	0.0	3.3	19.3		3.5	7.9	22.3
3	2	0.10	0.30	0.50	0.25	0.50	0.60	7.9	36.1	0.9	0.5	12.0	19.3	4.9
	1	0.03	0.10	0.28	0.20	0.32	0.50	0.3	14.4	39.9		3.5	8.6	22.3
4	2	0.10	0.30	0.50	0.04	0.07	0.10	1.1	5.7	0.3	92.5	7.5	12.5	4.7
	1	0.03	0.10	0.28	0.01	0.03	0.05	0.0	0.0	0.4		3.4	4.3	15.4
5	2	0.30	0.48	0.60	0.40	0.45	0.49	36.0	2.6	0.0	10.9	18.6	5.4	0.7
	1	0.12	0.30	0.48	0.20	0.40	0.60	16.2	32.1	2.2		13.3	21.0	5.4
6	2	0.30	0.48	0.60	0.36	0.50	0.60	51.9	2.8	0.0	42.6	19.3	5.5	0.7
	1	0.12	0.30	0.48	0.01	0.06	0.10	2.0	0.6	0.1		8.8	16.6	5.0
7	2	0.32	0.45	0.60	0.50	0.55	0.63	45.6	4.7	0.1	47.7	18.0	5.9	0.9
	1	0.10	0.15	0.30	0.01	0.02	0.03	1.9	0.0	0.0		7.8	9.3	14.1
8	2	0.42	0.49	0.55	0.17	0.33	0.55	3.4	0.6	0.1	88.9	6.8	1.6	0.2
	1	0.30	0.40	0.50	0.06	0.22	0.39	2.4	4.4	0.2		12.8	5.8	1.4

^†“No selection” is the percentage that the method did not select any dose-combination as the optimal dose.

As shown in Table 6, scenarios 1–4 share the same MTD contour (i.e., A₁B₃ and A₂B₂), but have different optimal doses. Specifically, in scenario 1, A₁B₃ is the optimal dose. The PCS of A₁B₃ was 50.6%, and the design allocated the largest number of patients (i.e., 22.2) to that dose. In scenario 2, the optimal dose is A₂B₂, and the PCS of that dose was 42.0%. Scenario 3 has two optimal doses (i.e., A₁B₃ and A₂B₂) due to the toxicity and efficacy equivalence contours. Both optimal doses had high PCS and more patients were assigned to those two doses than to the others. In scenario 4, all doses have efficacy that is below the lower limit of efficacy, thus there is no optimal target dose. In this case, our design stopped the trial early 92.5% of the time. Scenarios 5–7 show more cases with different toxicity and efficacy profiles. The results are similar; that is, the proposed design yielded high PCS and allocated a large percentage of patients to the target doses. In scenario 8, there is no optimal dose because the safe dose (i.e., A₁B₁) is not efficacious and the other doses are efficacious but not safe. In that scenario, our proposed design stopped the trial 88.9% of the time.

We note that in scenarios 6 and 7, the proposed design had 42.6% and 47.7% of chance of not choosing any dose as the optimal dose. This seems high, but actually is a reasonable behavior when we examine the PCS of the optimal dose in phases I and II. Specifically, in scenarios 6 and 7, at the end of phase I, the PCS of moving the optimal dose (i.e., A₂B₁) to phase II was 59.8% and 57.8%, respectively; and in phase II, the PCS of the optimal dose was 86.8% and 78.9%, respectively. These PCS are pretty reasonable for phase I and II trials, leading to the overall phase I/II PCS of 59.8% × 86.8% = 51.9% and 57.8% × 78.9% = 45.6%, respectively, for scenarios 6 and 7. In the case that we missed the optimal dose, the most appropriate action is not to select any dose, which results in high percentages of no selection in these scenarios.

5. Discussion

We have proposed a new design, the waterfall design, to find the MTD contour for drug combination trials. Taking the divide and conquer strategy, the waterfall design divides the problem of finding the MTD contour into a series of subtrials that are easy to implement. The subtrials are conducted sequentially in a certain order, such that the results of each subtrial will be used to inform the design of subsequent subtrials. Such information borrowing allows the waterfall design to explore the two-dimensional dose space efficiently using a limited sample size, and decreases the chance of overdosing and underdosing patients. As the doses in the MTD contour may have different efficacy due to drug-drug interaction, we extended the waterfall design to phase I/II combination trials, aiming to find the MTD that has the highest efficacy.

One important advantage of the waterfall design is that it is very easy to implement and meanwhile yields excellent operating characteristics. The dose escalation/deescalation rule of the waterfall design is laid out before the onset of the trial. During the trial conduct, there is no complicated model fitting and statistical computing. The trial can be carried out in a simple fashion similar to the 3+3 design. More importantly, such simplicity does not come at the cost of the design performance. Simulation studies show that the waterfall design substantially outperforms some existing, more complicated dose-finding designs. The freely available R package “BOIN” and detailed documentations coming with the package further facilitate the use of the design in practice.

We should note that in general, finding the MTD contour is much more difficult than finding a single MTD. In order to find all MTDs (i.e., the MTD contour), we must explore the whole J × K dose matrix; otherwise, we risk missing some MTDs. In contrast, to find a single MTD, experimenting at a local region that contains a MTD is often adequate. As a result, finding the MTD contour requires a larger sample size than combination trials that aim to find a single MTD. In the waterfall design, the results of current subtrial are used to inform the starting dose and dose range of subsequent subtrials to allow the design to quickly reach the MTDs and thus decrease the required samples size. Even though, the required sample size for finding the MTD contour is still larger than typical single-agent phase I trials. As a rule of thumb, in order to obtain robust performance, we recommend a sample size of 4 × J × K or more for a J × K combination trial, as described previously.

One limitation of the waterfall design is that it assumes that toxicity is binary and can be assessed quickly. Extending the waterfall design to handle late-onset toxicity is of great practical interest. One possible approach is to use Bayesian data augmentation [20, 21] or the expectation-maximization algorithm [23] to predict the unobserved late-onset toxicity data, so that adaptive decisions can be made in real time without observing all toxicity outcomes.