Multivariate Analysis of Longitudinal Rates of Change

Abstract

Longitudinal data allow direct comparison of the change in patient outcomes associated with treatment or exposure. Frequently, several longitudinal measures are collected that either reflect a common underlying health status, or characterize processes that are influenced in a similar way by covariates such as exposure or demographic characteristics. Statistical methods that can combine multivariate response variables into common measures of covariate effects have been proposed by Roy and Lin [1]; Proust-Lima, Letenneur and Jacqmin-Gadda [2]; and Gray and Brookmeyer [3] among others. Current methods for characterizing the relationship between covariates and the rate of change in multivariate outcomes are limited to select models. For example, Gray and Brookmeyer [3] introduce an “accelerated time” method which assumes that covariates rescale time in longitudinal models for disease progression. In this manuscript we detail an alternative multivariate model formulation that directly structures longitudinal rates of change, and that permits a common covariate effect across multiple outcomes. We detail maximum likelihood estimation for a multivariate longitudinal mixed model. We show via asymptotic calculations the potential gain in power that may be achieved with a common analysis of multiple outcomes. We apply the proposed methods to the analysis of a trivariate outcome for infant growth and compare rates of change for HIV infected and uninfected infants.

1. Introduction

Longitudinal studies frequently collect measurements from multiple outcome domains, and changes in one response variable may be similar to changes in other outcomes. For example, in studies of interventions for low back pain serial measures of both disability and pain are routinely collected to assess improvement in health status. Factors such as pharmacologic treatment or surgery that influence change in pain are also expected to impact change in function. Also, pediatric studies of growth and development commonly collect multiple related measures of infant size such as height, weight, and head circumference. When multiple longitudinal measures are separately analyzed there may be a loss of power as compared to a joint analysis that can focus inference on a common treatment effect. The goal of this manuscript is to detail new statistical methods that can provide a common effect estimate and associated test for the impact of an exposure or intervention on the rate of change across multiple outcome measures.

Two common approaches for modeling multivariate longitudinal data exist: linking outcomes through a longitudinal, latent variable; and estimating a common group parameter across separately specified outcome models. Methods that use latent variables to model multivariate longitudinal data have been proposed by Roy and Lin [1], and Proust-Lima, Letenneur and Jacqmin-Gadda [2]. Under the latent variable approach, each outcome characterizes the behavior of an unmeasured latent variable. For example, in autism research, several behavioral outcome measures exist that characterize the severity of repetitive behavior in children with autism. Roy and Lin [1] propose use of a hierarchical model for making inference on the latent variable that is assumed to drive the measured outcomes. A two part model is constructed where a longitudinal model structure is assumed for the latent variable representing the underlying “state”, and a second, measurement model structure is assumed for each outcome linked to the latent variable. Roy and Lin [1] outline the use of mixed effect models for both the longitudinal, latent variable structure and the multivariate outcome measurement structure when all outcomes are continuous. Let Y_ijk denote the observed measurement of the kth outcome for individual i at time t_j, and let U_ij denote the latent variable for the related outcomes. Given a fixed effect design matrix X_ij and random effect design matrix Z_ij, Roy and Lin [1] express the latent variable model and the measured outcomes model as follows:

$$\begin{array}{cc}\hfill U_{ij}=& {\mathbf{X}}_{ij}^{\prime }\alpha +{\mathbf{Z}}_{ij}^{\prime }{\mathbf{a}}_i+{ϵ}_{ij}\hfill \\ \hfill Y_{ijk}=& {\beta }_{0k}+U_{ij}{\beta }_{1k}+b_{ik}+e_{ijk}.\hfill \end{array}$$

By combining the two mean structures together, the association between the covariates of interest and the latent variable can be estimated. Proust-Lima, Letenneur and Jacqmin-Gadda [2] also propose methodology for a longitudinal latent variable model where the multivariate outcome consists of a mixture of continuous and categorical outcomes. When direct inference on the underlying latent variable is of interest, the latent variable approach will characterize each covariates effect. However, in many applications with multivariate longitudinal data, interest is in inference on the measured outcome even when an underlying latent variable may describe longitudinal and multivariate dependence. For example, clinical studies of patients recovering from back pain are focused on direct improvements in pain and function although both outcomes are dimensions of a patient's quality of life. When inference on each outcome is of primary interest, it is often beneficial to allow for separate structures for each outcome since a uniform longitudinal and multivariate structure may be difficult to justify. Further discussion comparing latent variable models to other multivariate longitudinal methods in a more general setting has been made by Verbeke et. al. [4].

A second approach to analysis of multivariate longitudinal data is to allow each outcome to be modeled separately, but to link each outcome model by a common parameter that describes shared differences between groups defined by a covariate of interest [3, 5–7]. By generating a common, or global, estimate for this parameter across each outcome, a global test for group differences across the multivariate outcome can be constructed. We refer to such models as global shared parameter models which can generally be expressed as

$$E[Y_{ijk}\mid X_i=x,t_{ij}=t]=f_k\{\lambda \left(x\right),{\beta }_k\left(t\right)\}$$ (1)

where the global parameter is denoted by λ for a grouping variable X_i and is fixed across all outcomes, k = 1, ··· , K. A global test for multivariate longitudinal data based on a global shared parameter model was proposed by Gray and Brookmeyer [3,5] using accelerated time (AT) models. In AT models, the time scale of a longitudinal outcome is assumed to differ across groups. Coinciding with the notation in Equation (1), the mean structure for the AT model under a third degree polynomial time structure is given by the equation

$$E[Y_{ijk}\mid X_i=x,t_{ij}=t]={\beta }_{0k}+{\beta }_{1k}\left({\lambda }^{x}t\right)+{\beta }_{2k}\left({\lambda }^{x}t\right)+{\beta }_{3k}{\left({\lambda }^{x}t\right)}^3.$$

The interpretation of shared parameter, λ, in this instance is that longitudinal progression of an outcome is accelerated or decelerated across groups of interest. The multivariate AT method introduced by Gray and Brookmeyer [3, 5] allows separate specification for the time structure of each outcome, but estimates a global group parameter that alters the time scale uniformly across outcomes. Travison and Brookmeyer [7] proposed a global test for a treatment across multivariate outcomes by linking the marginal distributions of treatment groups by a shared treatment parameter across outcomes. The treatment parameter is used to relate the marginal distribution for observations on treatment to the marginal distribution of control observations in a manner that allows the use of estimation from survival analysis methodology. Jia and Weiss [6] constructed a multivariate longitudinal model with common additive effects for covariates of interest. The linear combination of covariates for the additive model is multiplied by a unique parameter for each outcome that accounts for the scale of the outcome.

Existing global shared parameter approaches focus on different types of association between a multivariate outcome and covariate-defined groups: group differences in the time scale [3,5], group differences in the quantiles of the marginal distribution [7], and scaled mean level group differences [6]. In this paper, we propose a new global shared parameter model that estimates group differences in the rate of change of a multivariate longitudinal outcome. The proposed methodology is an extension of the longitudinal rate regression (LRR) model developed by Bryan and Heagerty [8] for a univariate longitudinal outcome. The LRR method characterizes longitudinal change across groups through direct structuring of longitudinal rates of change. The LRR method links rates of change across groups by assuming a Proportional Rate (PR) assumption where rates differ across groups by a constant proportion over time. A mean model is then induced based on the rate assumptions coupled with a flexible specification for a reference time trend. Bryan and Heagerty [8] demonstrated potential advantages of a direct approach to modeling rates of change as compared to linear mixed effects model approach when the underlining time trend is non-linear. The LRR method is similar to the AT model developed by Gray and Brookmeyer [3,5] in that each approach estimates differences in rates of change across covariate-defined groups. However, the AT model assumes a fixed range or magnitude for the outcome, and focuses on potential accelerations and decelerations in the progression of an outcome along a common trajectory. In contrast, the LRR model directly links covariates to the magnitude of longitudinal change and does not assume a common, bounded trajectory.

Our proposed multivariate longitudinal data extension to the LRR model permits estimation of a global shared parameter representing the difference in the rate of change associated with covariate-defined groups. We maintain a separate specification for the reference time trend and adjustment for baseline covariates for each outcome. In Section 2, we detail methodology for the Multivariate Longitudinal Rate Regression (MLRR) model both for estimating separate rate differences for each outcome and a global rate difference across all outcomes, and discuss options for specifying a multivariate longitudinal covariance structure. In Section 3, the asymptotic power of the MLRR model using a global shared parameter is compared to the power for testing for differences in the rate of change for each outcome separately. We illustrate the MLRR method in Section 4 on a study of growth among infants exposed to HIV infection. Finally, in Section 5, we offer discussion and concluding remarks for studying differences in rates of change for multivariate longitudinal data.

2. Methods

2.1. Regression Models for Rates of Change

We use the notation Y_ijk to denote the kth outcome of individual i observed at time t_ijk for i = 1, . . . , N, j = 1, . . . , m_ik, and k = 1, . . . , K. Further denote $M_i={\sum }_{k=1}^K{m}_{ik}$, the total number of outcome measures for the ith individual. We use X_i = (X_i1, . . . , X_iQ) to denote a vector of covariates. We are interested in detecting differences in the rate of change of Y_ijk across groups defined by X_i. Let

$$E[Y_{ijk}\mid {\mathbf{X}}_i=\mathbf{x},t_{ij}=t]=g_k\left(\mathbf{x}\right)+{\mu }_{\mathbf{x}k}\left(t\right)$$

where g_k(·) is a function dependent only on X and μ_xk(·) denotes some function of t for given values of X with the constraint that μ_x(0) = 0 for all values of X. The function g_k(·) describes the mean level and all covariate-defined differences in the mean of Y_ijk at a time origin, or time zero. The function μ_xk(t) specifies the change in the expected value of the kth outcome over time from baseline for a given X_i = x. We generalize the Proportional Rate (PR) assumption proposed by Bryan and Heagerty [8] to the multivariate outcome setting which can be expressed as

$$\frac{\partial {\mu }_{\mathbf{x}k}\left(t\right)}{\partial t}=(1+{\theta }_k^{\prime }\mathbf{x})\frac{\partial {\mu }_{0k}\left(t\right)}{\partial t}$$

where μ_0k(·) is the time function for the kth outcome for some preselected reference group, defined by X_i = 0. Thus, the MLRR method that jointly models correlated longitudinal outcomes assumes that the rate of change in the expected value for each outcome, Y_ijk, for given values of X_i = x, relative to the reference group (X_i = 0), is given by $(1+{\theta }_k^{\prime }\mathbf{x})$ for all times t_ijk. Thus, the difference in the rate of change for the kth outcome associated with changes in the covariates in X_i is captured by θ_k = (θ_1k, . . . , θ_Qk).

In order to borrow information across outcome for estimating an overall differences in the rate of change for the multivariate outcome Y_ij = (Y_ij1, . . . , Y_ijK), we further modify the multivariate PR assumption to a Global Multivariate Proportional Rate (GMPR) assumption where we will assume that θ_k = θ for k = 1, . . . , K. Hence, the difference in the rate of change associated with a given covariate is assumed to be the same across all outcomes. We can interpret the rate parameters, θ, as the global difference in the rate of change in the mean of Y_ij associated with a unit difference in the covariates, X_i. That is, the parameter θ_q is interpreted as the percent increase (decrease) in the rate of change in the mean of Y_ij when X_iq = (x + 1) relative to when X_iq = x. Throughout this paper, we will refer to this modeling approach as the MLRR model with GMPR assumption or simply the global MLRR model. The remainder of the methods section will be framed under this modeling approach, but we will also use the MLRR model without the GMPR assumption as a comparison model in later sections which we refer to simply as the joint MLRR model. Both of these MLRR models may also be constructed using a non-proportional rate assumption. Doing so requires incorporating time varying covariates into the modeling framework in order to allow cut points in the time trajectory for which the rate structure is able to change for a given covariate. The necessary modifications to the methodology for including time varying covariates has been described in detail by Bryan and Heagerty [8] for the univariate case, and the same approach can be used for this multivariate setting. We emphasize that this non-proportional model allows the effect of each covariate on the rate to vary across fixed time periods, but we still may assume that the difference in the rate of change within each of these time periods is the same for each outcome. For the remainder of this paper, we assume a proportional rate assumption is valid in order to focus evaluation on the additional assumption of a global rate parameter imposed by the GMPR assumption.

A full mean structure for the MLRR model with GMPR assumption can be constructed by integrating over a given time interval, [0, t]. For outcome Y_ijk, the full mean structure is specified as

$$E(Y_{ijk}\mid {\mathbf{X}}_i=\mathbf{x},t_{ij}=t)=g_k\left(\mathbf{x}\right)+(1+{\theta }^{\prime }\mathbf{x}){\mu }_{0k}\left(t\right).$$ (2)

For the model defined by Equation (2), we refer to the functions g_k(·) and μ_0k(·) respectively as the baseline function and the reference time function for the kth outcome. We emphasize that both the baseline function g_k(·) and the reference time function μ_0k(·) are allowed to differ across outcomes; only the rate parameters are assumed to be common across outcomes. Both parametric and non-parametric approaches can be considered when specifying the reference time structure for each outcome in the MLRR model. For either approach, we can specify the reference time structure for the kth outcome as a linear combination of functions of times: ${\mu }_{0k}\left(t_{ijk}\right)={\beta }_k^{\prime }{\mathbf{T}}_{ijk}$ where T_ijk is a vector of functions evaluated at t_ijk. The distinction between a parametric versus a non-parametric approach is whether a small time basis is used and maximum likelihood estimation is carried out or a large basis is used and a penalized likelihood estimation approach is adopted. See Bryan and Heagerty [8] for a detailed discussion of parametric versus non-parametric estimation of the reference time structure in the univariate case. An important consideration is that the non-parametric estimation approach will add increased complexity in the multivariate case since multiple penalty terms will be included in the estimation, one for each outcome where the reference time trend is estimated non-parametrically. For this paper, the baseline function of covariates for each outcome will be specified as a linear combination of the covariates: $g_k\left({\mathbf{X}}_i\right)={\alpha }_k^{\prime }{\mathbf{X}}_i$ though other covariate structures can be considered.

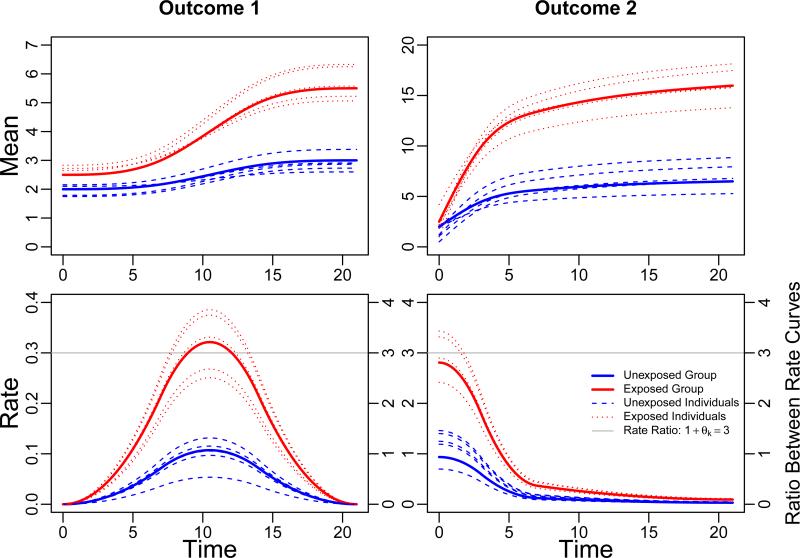
The modeling assumptions assumed for the rate structure by the MLRR method are illustrated in Figure 1. The longitudinal trajectory of two outcomes for two exposure groups (e.g. binary treatment variable) are plotted both in terms of the mean and the rate of change (time derivative). The curves illustrate a basic proportional rate assumption as proposed by Bryan and Heagerty [8]. For example, although each outcome has a unique reference time profile the comparison of treatment groups is structured such that they have a common proportional difference in the the rate of change, both across all times and over both outcomes. This proportional difference can be observed in the lower two plots depicting the rate of change over time. For both plots, the value of the rate of change for the exposed group (solid red line) is three times the value of the rate of change for the unexposed group (solid blue line) at each time point. By focusing inference on the rate of change for each outcome, the relative comparison across groups can be evaluated in terms of percentage difference in rates of change which does not depend on the scale of the outcome. The basic proportional rates assumption assumes that for each outcome the group difference can be captured by a single parameter: θ₁ for outcome 1; and θ₂ for outcome 2 (see Figure 1). For the MLRR model, we may impose an additional assumption that the rate differences across treatment groups are the same for each outcome which yields the full GMPR assumption. In Figure 1, this assumption is equivalent to assuming that θ₁ = θ₂, which is true by construction for this example with θ₁ = θ₂ = 2. The common θ_j = 2 is equivalent to a 200% increase in the rate of change for the exposed group relative to the unexposed group for both outcomes. When appropriate to adopt the GMPR assumption, power can be gained to detect group differences in the rate of change associated with exposure.

Figure 1.

An illustration of the mean and rate structure assumed by a basic proportional rate assumption for an example of two longitudinally measured outcomes and a single binary exposure. The solid blue line represents the mean and rate longitudinal trajectory of the unexposed group for each outcome. Mean and rate trajectory for the exposed group is captured by the solid red line. The dashed blue line and dotted red line represent the individual curves for select unexposed and exposed individuals respectively as would be captured by a random effects variance structure. The rate plots include a grey line to represent the ratio between the two rate curves (the exposed curve divided by the unexposed curve) which is assumed to be equal to a single proportion under the basic proportional rate assumption (1+ θ_k; for k = 1, 2). The MLRR model with GMPR assumption further assumes the rate difference due to exposure is the same across outcomes, i.e. θ₁ = θ₂, which was constrained to be true in this illustration.

A necessary secondary aspect to multivariate longitudinal modeling is the structuring of the covariance to account for correlation across time and across outcomes. When using a latent variable modeling structure, Roy and Lin [1] and Proust-Lima, Letenneur and Jacqmin-Gadda [2] discuss an approach to modeling the covariance structure using hierarchical linear mixed effects. Part of the hierarchical covariance structure of the latent variable models includes random effects specified at the latent variable level. Since we focus on global shared parameter methods which do not incorporate latent variables, a hierarchical linear mixed effects model will not be directly applicable. Previous work [9] has structured a dynamic correlation for functional longitudinal data with multivariate outcomes. Alternatively, the covariance specification approach we consider apply to studies where the outcomes are measured discretely in time as is often done in designed clinical studies.

2.2. A Mixed Model for Rates of Change

For the MLRR approach with GMPR assumption, we model the covariance structure for multiple longitudinal outcomes by incorporating longitudinal random effects that are correlated across outcomes. The use of a mixed effects structure to specify a covariance structure is a common approach for modeling multivariate longitudinal data [10]. For a mixed effects structure, we specify the longitudinal structure of outcome k with individual intercepts and rates of change as follows:

$$\frac{\partial {\mu }_{{\mathbf{X}}_{i}k}\left(t_{ij}\right)}{\partial t_{ij}}=(1+{\theta }^{\prime }{\mathbf{X}}_i+b_{1ik})\frac{\partial {\mu }_{0k}\left(t_{ij}\right)}{\partial t}$$ (3)

$$Y_{ijk}=\{g_k\left({\mathbf{X}}_i\right)+b_{0ik}\}+(1+{\theta }^{\prime }{\mathbf{X}}_i+b_{1ik}){\mu }_{0k}\left(t_{ij}\right)+{ϵ}_{ijk}$$ (4)

where, for outcome k, the vector of random effects for individual i, b_ik = (b_0ik, b_1ik)′, is normally distributed with mean 0 and covariance R_kk and the vector of random errors for individual i, ϵ_ik = (ϵ_i1k, . . . , ϵ_imikk), is normally distributed with mean 0 and covariance ${\sigma }_k^2{I}_{m_{ik}}$. The covariance is then connected across outcomes by assuming that Cov(b_ik, b_ik*) = R_kk* for k ≠ k*. Therefore, the mixed effects model for the MLRR method characterizes individual variation both in the mean level at baseline and in the rate of change, and this variation is correlated across outcomes. The multivariate longitudinal mixed effects modeling approach is analogous to the LRR mixed effects model proposed by Bryan and Heagerty [8] for the univariate longitudinal case. The mixed effects structure is illustrated in Figure 1 where individual mean and rate trajectories are depicted for a selection of individuals from the unexposed and exposed groups.

Using random effects to structure the multivariate longitudinal covariance structure provides an intuitive interpretation of the model at the individual level with each subject having their own baseline value and rate of change. The disadvantage of a mixed effects approach is that four additional variance parameters are introduced by the across outcome covariance matrix for each pair of outcomes modeled. More explicitly, given K outcomes, the mixed effects multivariate structure requires the estimation of $3K+4\frac{K(K-1)}{2}$ variance parameters for the random effects. If we instead model the outcomes separately in independent models using random effects, we would only estimate 3K parameters for the random effects. Thus, the general random effects modeling approach for the MLRR method requires the estimation of 2K(K – 1) additional variance parameters compared to the collection of univariate models.

In contrast, the number of mean parameters estimated by the MLRR model, when the GMPR assumption is assumed, will be reduced relative to the univariate models. For an MLRR model with a single rate covariate, the number of rate parameters being estimated is reduced by K – 1 compared to the univariate approach. Thus, taking into account both mean and variance components, the multivariate mixed effects modeling approach would estimate 2K² – 3K + 1 more parameters than when using a univariate model for each outcome when a single rate covariate has a globally estimated rate effect. More generally, for a MLRR model with Q rate covariates all of which have globally estimated rate effects, the total difference in the number of parameters compared to a univariate approach is given by the quantity 2K(K – 1) – Q(K – 1). Hence, when the number of globally estimated rate covariates is double that of the number of outcomes, e.g. Q = 2K, the number of parameters estimated by the multivariate and univariate approaches is the same. The multivariate model will estimate fewer parameters when Q > 2K. This relationship between the parameter dimension of the multivariate and univariate model approach remains the same regardless of the specification of the baseline functions, g_k(·), and the reference time functions, μ_k(·), for each outcomes since the number of parameters in these components are the same for each approach. Therefore, in addition to potential gains in power discussed in the next section, a global shared parameter approach to modeling multivariate longitudinal data can be a useful means for addressing the increasing dimensionality of the multivariate model.

The increase in model parameters is a common issue with modeling multivariate longitudinal outcomes, but can also be advantageous for maintaining flexibility for modeling the covariance structure. By specifying an unstructured cross outcome random effect covariance matrix, the mixed effects model can robustly model a correlation structure that differs across outcome. The challenges in using a random effects structure in a multivariate longitudinal context are discussed in detail by Fieuws and Verbeke [11] and Verbeke et. al. [4]. To reduce computational burden of the multivariate random effects model, Fieuws and Verbeke [11] propose an estimation approach where pairwise bivariate models are fit for each pair of outcomes and parameter estimates are averaged across the pairwise models in order to make inference on parameters in the multivariate model. An alternative for simplifying estimation is to reduce the complexity of the structure of the random effects matrix. One approach could be to assume that the cross-outcome covariance matrix is the same for all (k, k*) pairs, R_kk* = R (equivalent to an exchangeable assumption). A less extreme simplification that is similar in character to the overall MLRR model with GMPR assumption is to assume a common rate random effect for each individual across all outcomes, b_1i, while maintaining separate random intercepts across outcomes, b_0ik. Computational time is an issue of important consideration for multivariate longitudinal data, and modifications such as these may need to be employed in situation when the number of outcomes and/or sample size is large. Further exploration of these concerns is left for future work, and thus, all calculations and results presented in this paper were derived directly via a standard maximum likelihood approach using an unstructured random effects matrix.

The incorporation of random effects to model a multivariate longitudinal covariance structure is particularly challenging for the MLRR model from an implementation stand point. Due to the inclusion of a random rate effect into the model for each outcome, the mean and variance components are not orthogonal to each other. Thus, mean and variance parameters cannot be independently estimated for the MLRR model which is a common technique used in the estimation of generalized linear models. The mean-variance dependence is not unique to the multivariate setting. Bryan and Heagerty [8] provide discussion of this issue as well as score and Hessian equations that can be used for estimation in the univariate longitudinal setting. We have provided extensions of these equations to the multivariate setting plus further details of the estimation procedure in an appendix to this paper. Such an estimation approach will provide full maximum likelihood estimates for the proposed model, but will likely increase computation time relative to other semi-parametric or pairwise estimating approaches particularly as the level of complexity and size of the dataset increases [4,11]. However, the ability to estimate the proposed model using a full maximum likelihood approach is a major advantage over other non-linear mixed modeling approach which require estimation via numerical integration since this estimation approach can scale to multiple outcomes much more easily than models that require numerical integration for each random effect. To illustrate the computational speed of the proposed algorithm, we note that for the global MLRR model described in Section 4 for three outcomes and three rate covariates on 616 individuals, estimation of model results was completed within 14 minutes on a standard desktop computer. By comparison, the joint MLRR model on the same dataset reached convergence in about 12 minutes, and the estimation time for the three univariate LRR models ranged between 7 and 30 seconds. Though the run time is largely related to the complexity and size of the data, it can also depend on the accuracy of the initial values provided for the Newton-Raphson algorithm described in the appendix. The estimation approach was implemented using R version 3.1.0.

3. Power Associated with Multivariate Analysis

As a general evaluation of the power obtained from a global multivariate outcome approach, we calculated and compared the power of MLRR model with GMPR assumption under various data generating scenarios. A primary goal of the global shared parameter model is to gain power to detect group differences by borrowing information across outcomes. For the MLRR model in particular, the global shared parameter of interest is the group difference in the rate of change. Specifically, we hope to gain power to detect group differences in the rate of change for a multivariate outcome compared to examining group differences for each outcome separately. To evaluate this potential gain in power, we compare the global test for group differences using the global MLRR model to two alternatives: a test for differences in the rate of change for one pre-selected outcome using the univariate LRR model; and testing for differences in the rate of change for each outcome in multivariate setting using the MLRR model with separate rate parameters for each outcome (e.g. the joint MLRR). The univariate LRR model approach represents an investigator selecting a single outcome for testing e.g. the outcome of greatest scientific interest or the outcome most anticipated to show a difference across groups. Alternatively, an investigator may decide to test all outcomes, but not assume the difference in the rate of change is the same for each outcome. In this case, the joint MLRR model would be appropriate although power to detect group differences may be sacrificed since each rate parameter tested results in additional degrees of freedom.

We compare the power of the three modeling approaches using three correlated, continuous outcome and a single binary covariate for comparing rates of change. The reference time trend is modeled using a cubic polynomial equation, and the covariance matrix was structured using the mixed effects model approach outlined in Subsection 2.2. The three models for each comparison can generally be expressed as

$$\begin{array}{cc}\text{Univariate LRR (for outcome k = 1)}:\hfill & E(Y_{ij1}\mid X_i=x,t_{ij}=t)={\alpha }_{01}+{\alpha }_{11}x+(1+{\theta }_{1}x)({\beta }_{11}t+{\beta }_{21}{t}^2+{\beta }_{31}{t}^3)\hfill \\ \text{Joint MLRR}:\hfill & E(Y_{ijk}\mid X_i=x,t_{ij}=t)={\alpha }_{0k}+{\alpha }_{1k}x+(1+{\theta }_{k}x)({\beta }_{1k}t+{\beta }_{2k}{t}^2+{\beta }_{3k}{t}^3)\hfill \\ \text{Global MLRR}:\hfill & E(Y_{ijk}\mid X_i=x,t_{ij}=t)={\alpha }_{0k}+{\alpha }_{1k}x+(1+\theta x)({\beta }_{1k}t+{\beta }_{2k}{t}^2+{\beta }_{3k}{t}^3)\hfill \end{array}$$

where k = 1, 2, 3. Thus, the univariate LRR model will test the null hypothesis of θ₁ = 0, the joint MLRR model will test the strong null that θ_k = 0 for k = 1, 2, 3, and the global MLRR model will test the global rate parameter θ = 0. Each test was carried out at the .05 significance level. Except for the rate structure which changed across each set of calculations, the mean structure was assumed to be the same for each of the three outcomes up to a change in intercept. For each outcome, the main effect for the exposure variable x was 3 and the coefficients for the time function were 3, −0.3, and 0.01. The intercept values for each outcome were 40, 50, and 30 respectively. The measurement error for each outcome was assumed to have a variance of 0.1, and correlation structure for the random effects is given by the matrix:

$$\mathbf{R}=\left(\begin{array}{cccccc}\hfill 1\hfill & \hfill 0.158\hfill & \hfill 0.05\hfill & \hfill 0.003\hfill & \hfill 0.05\hfill & \hfill 0.003\hfill \\ \hfill 0.158\hfill & \hfill 0.1\hfill & \hfill 0.003\hfill & \hfill 0.005\hfill & \hfill 0.003\hfill & \hfill 0.005\hfill \\ \hfill 0.05\hfill & \hfill 0.003\hfill & \hfill 1\hfill & \hfill 0.158\hfill & \hfill 0.05\hfill & \hfill 0.003\hfill \\ \hfill 0.003\hfill & \hfill 0.005\hfill & \hfill 0.158\hfill & \hfill 0.1\hfill & \hfill 0.003\hfill & \hfill 0.005\hfill \\ \hfill 0.05\hfill & \hfill 0.003\hfill & \hfill 0.05\hfill & \hfill 0.003\hfill & \hfill 1\hfill & \hfill 0.158\hfill \\ \hfill 0.003\hfill & \hfill 0.005\hfill & \hfill 0.003\hfill & \hfill 0.005\hfill & \hfill 0.158\hfill & \hfill 0.1\hfill \end{array}\right).$$

Each subject was assumed to be observed 12 times for each outcome over the study period with measurements at time points denoted by the values 1, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, and 21. The similarities between the assumed structure for the three outcomes was used to simplify implementation of the following calculations. In practice, both multivariate models are amenable to using different time trend functions and baseline design matrices for each outcome in the model. However, the comparison of interest in these calculations is on the rate structure which we do assume is the same for each outcome in order for global multivariate model to be a valid approach. The relative comparison in power for the rate parameters is expected to be similar in cases where the time trend and baseline design matrix differ across outcomes.

We consider scenarios for the true data generating mechanism where the GMPR assumption is correct and where the assumption is incorrect. When the GMPR assumption is correct, the rate parameters for each outcome is the same, θ_k = θ for k = 1, 2, 3, and all three models are correctly specified. Hence, asymptotic power for the three models is based directly on the Hessian of the log-likelihood. When the GMPR assumption is incorrect, the rate parameters differ among the outcomes, θ_k ≠ θ_j for k ≠ j, and the global MLRR model is mis-specified. The univariate LRR model and the joint MLRR model are still correctly specified since we still assume that the rate of change for each outcome is proportional across groups. Power for the univariate LRR model and the joint MLRR model are again generated using the Hessian equations. To calculate the power for the global MLRR model, we use results for the asymptotic behavior of longitudinal estimates under model mis-specification characterized by White [12] and Heagerty and Kurland [13]. The asymptotic global rate difference and its corresponding sandwich standard error under mis-specification were estimated using Monte Carlo methods consisting of 10⁴ individuals as described by Heagerty and Kurland [13]. Based on 10 replicated samples of this size, we estimate that the Monte Carlo procedure produced a power curve that has maximum point-wise standard deviation of approximately 3%.

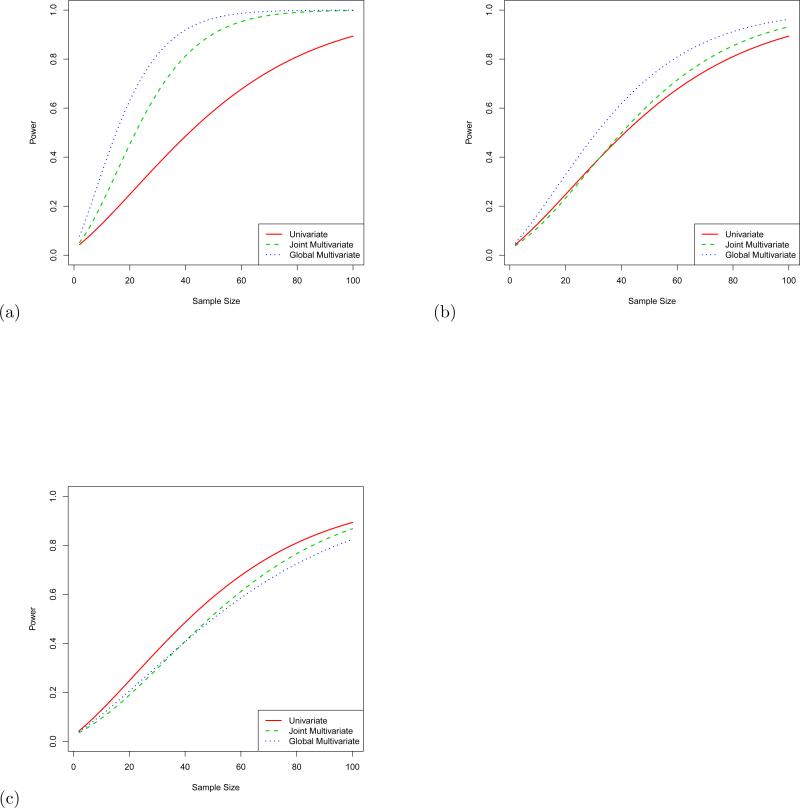
Figure 2 displays three plots of power curves comparing the three modeling approaches. For all three plots, the value of the rate parameter for the outcome tested using the univariate LRR model is the same (that is, θ₁ = 0.25 for all scenarios), and is greater than or equal to the rate effect for the outcomes that are not tested by the univariate LRR model. Therefore, the curve for the univariate LRR model is identical in each plot. In Figure 2(a), the curves were calculated where the true rate parameter was the same for all outcomes, θ_k = 0.25 for k = 1, 2, 3. When the GMPR assumption is true, the two MLRR models show a clear advantage over the univariate LRR model for detecting group difference. Estimating a global rate parameter is advantageous compared to estimating separate rate parameters which was expected since the global rate model is correct in this scenario. Figures 2(b) and 2(c) depict scenarios where the GMPR assumption is incorrect. The rate parameter for the first outcome is again assumed to be 0.25, but the second and third outcomes have a reduced rate of two-thirds and one-third respectively relative to the effect for the first outcome (e.g. θ₂ = 0.25 × 2/3 and θ₃ = 0.25/3) for the power curves depicted in Figure 2(b). Based on the Monte Carlo approach describe previously, the global rate parameter for the global MLRR model in this misspecified scenario was projected to have an asymptotically normal distribution with a mean of 0.17 and a standard deviation of 0.18. The MLRR models show a substantial reduction in power in Figure 2(b) relative to Figure 2(a). The joint MLRR model had roughly the same power to detect group differences as the univariate model. The global MLRR model still showed gains in power for detecting group differences relative to the competing models. In Figure 2(c), the rate parameter for each outcome was 0.25, 0.125, and 0 respectively, equivalent to a 50% and a 100% reduction in the effects for the second and third outcomes relative to the effect for the first outcome. For this scenario, the asymptotic distribution for the global rate parameter was projected to have a mean of 0.13 and a standard deviation of 0.17. The power to detect group differences suffers for both MLRR models relative to the chosen univariate LRR model under this scenario. For the largest sample sizes, the global MLRR model tended to perform the worst of the three models.

Figure 2.

Power curves for testing group differences in the rate of change for three outcomes between two groups for the univariate LRR model (solid red), the MLRR model with separate rate parameters for each outcome (dashed green), and the MLRR model with a global rate parameter (dotted blue). (a) The true data was generated from a model where the rate parameter for each outcome was the same and the GMPR assumption was correct. The global rate effect size is 25%. (b) The true data was generated from a model where the rate parameters for the second and third outcomes respectively were two-thirds and one-third the size of the rate parameter for the first outcome. The rate effect sizes for the each outcome was 25%, 16.7%, and 8.3%. (c) The true rate parameter for the second and third outcomes respectively were reduced by half and to zero relative to the rate parameter of the first outcome. The rate effect sizes for each outcome was 25%, 12.5%, and 0%. The power curve for the univariate LRR model was generated from testing the first outcome whose rate effect was 25% in each scenario.

The power curve results illustrate the potential gains in power of the global shared parameter MLRR model when the rate parameter is the same across outcomes and how these gains are negated as the difference between the rate parameters for each outcome is increased. The illustrated advantage of the global MLRR model over the univariate LRR model is likely conservative since in each scenario the univariate analysis always used the outcome with the largest effect size. We could instead introduce a probability distribution on which outcome was selected for the univariate LRR model where there was a non-zero probability of selecting the outcome with the small effect size. If this were the case, the power curve for the univariate LRR model would be reduced in the second and third scenarios. Therefore, the global MLRR model is also advantageous over a univariate approach since it avoids the need for outcome selection.

The results of the calculated power curves are encouraging for showing that gains in efficiency can be obtained even when the rate parameters are not the same, but still similar in direction. Defining what sufficiently similar means for a given application will be dependent on rate parameter effect size and the values of the variance components. We examine and discuss the potential impact of changes in the covariance structure on the power of these multivariate models in supplementary materials available online. The example provided in the supplemental document illustrates how the global MLRR model may be less advantageous compared to univariate approach under violations of the GMPR assumption when correlation across the measured outcomes is high. In addition, the joint MLRR model exhibits positive performance in this setting which speaks to the complexity of assessing power under varying covariance structures in a multivariate setting. Such behavior has been observed previously in a simplified multivariate setting when using MANOVA [14]. The relationship between power and the covariance structure is particularly complex for models such as the MLRR model where the mean and variance components are non-orthogonal due to the assumed random effects structure. Thus, an area of future work will explore the interaction between power and the covariance structure in order to better understand the complexities of their relationship in a multivariate setting.

4. Application

The infant growth study is a secondary study from the HIVNET 012 clinical trial focusing on prevention of mother-to-child HIV transmission. Mothers were recruited during pregnancy and randomized to receive either zidovudine (AZT) or nevirapine (NEV). The first infant born of the pregnancy was then followed and tested for HIV infection. Details and results for the primary aim of the clinical trial are presented in Jackson et al. [15]. As a secondary aim, growth among the infants was measured longitudinally. Infants were followed for 5 years from birth and measured as many as 16 times for weight (Kg), crown-heel length (cm), and head circumference (cm). We use the data from this study of growth to illustrate the MLRR method using all three growth outcomes. A global MLRR model was constructed to examine global differences in rates of change for growth outcomes among the 616 infants with complete data across groups defined by sex (312 Females, 304 Males), treatment (302 AZT, 314 NEV), and whether HIV infection was detected. To avoid confounding of treatment and HIV infection and to use HIV status as a baseline covariate, we categorize infants as HIV positive if infection was detect pre- or peri-natally defined by detection within 6 weeks from birth. This definition of baseline HIV status resulted in 59 cases of HIV for this sample.

Table 1 presents coefficient estimates and 95% confidence intervals for the global MLRR model for weight and crown-heel length. The three covariates were used to estimate both mean level and rate level differences. The reference time function was modeled using a natural cubic spline with knots at 150, 500, and 1100 days for each outcome. The same reference time function was used due to the similar shape of the growth trajectory of these three outcomes. In general, using the same time structure as well as the same design matrix for the baseline covariates for each outcome is not required for the MLRR model. The mixed effects model described in subsection 2.2 was used to structure the covariance matrix. For the variance components, the global MLRR model estimated variance of the measurement error for each outcome to be 0.35, 2.18, and 0.51 respectively. The estimated covariance and correlation matrix of the random effects were

$$\left(\begin{array}{cccccc}\hfill 0.33\hfill & \hfill 0.00\hfill & \hfill 0.92\hfill & \hfill -0.01\hfill & \hfill 0.45\hfill & \hfill -0.02\hfill \\ \hfill 0.00\hfill & \hfill 0.03\hfill & \hfill -0.01\hfill & \hfill 0.01\hfill & \hfill 0.02\hfill & \hfill 0.01\hfill \\ \hfill 0.92\hfill & \hfill -0.01\hfill & \hfill 3.65\hfill & \hfill -0.03\hfill & \hfill 1.45\hfill & \hfill -0.06\hfill \\ \hfill -0.01\hfill & \hfill 0.01\hfill & \hfill -0.03\hfill & \hfill 0.01\hfill & \hfill -0.01\hfill & \hfill -0.01\hfill \\ \hfill 0.45\hfill & \hfill 0.02\hfill & \hfill 1.45\hfill & \hfill -0.01\hfill & \hfill 1.17\hfill & \hfill -0.01\hfill \\ \hfill -0.02\hfill & \hfill 0.01\hfill & \hfill -0.06\hfill & \hfill 0.01\hfill & \hfill -0.01\hfill & \hfill 0.01\hfill \end{array}\right)\left(\begin{array}{cccccc}\hfill 1.00\hfill & \hfill -0.05\hfill & \hfill 0.85\hfill & \hfill -0.15\hfill & \hfill 0.73\hfill & \hfill -0.31\hfill \\ \hfill -0.05\hfill & \hfill 1.00\hfill & \hfill -0.02\hfill & \hfill 0.82\hfill & \hfill 0.12\hfill & \hfill 0.67\hfill \\ \hfill 0.85\hfill & \hfill -0.02\hfill & \hfill 1.00\hfill & \hfill -0.15\hfill & \hfill 0.70\hfill & \hfill -0.32\hfill \\ \hfill -0.15\hfill & \hfill 0.82\hfill & \hfill -0.15\hfill & \hfill 1.00\hfill & \hfill -0.06\hfill & \hfill 0.62\hfill \\ \hfill 0.73\hfill & \hfill 0.12\hfill & \hfill 0.70\hfill & \hfill -0.06\hfill & \hfill 1.00\hfill & \hfill -0.14\hfill \\ \hfill -0.31\hfill & \hfill 0.67\hfill & \hfill -0.32\hfill & \hfill 0.62\hfill & \hfill -0.14\hfill & \hfill 1.00\hfill \end{array}\right).$$

Table 1.

Group differences in the rate of change for growth outcomes among infants exposed to HIV infection based on a MLRR model with GMPR assumption. Covariates were included for mean level and rate level differences. A natural cubic spline with knots at 150,500, and 1100 days was used as a reference time trend for all outcomes. The covariance structure was specified using a mixed effects model. Main effect estimates and time trend coefficient estimates are provided for each outcome. A global rate effect was estimated for each covariate.

	Weight (Kg)		Crown-Heel Length (cm)		Head Circumference (cm)
	Estimate	95% CI	Estimate	95% CI	Estimate	95% CI
Main Effects
Intercept	3.51	(3.41, 3.60)	49.90	(49.61, 50.20)	36.04	(35.87, 36.20)
Sexa	0.34	(0.24, 0.44)	1.25	(0.93, 1.57)	0.78	(0.60, 0.96)
Treatmentb	−0.14	(−0.24, −0.03)	−0.38	(−0.71, −0.06)	−0.32	(−0.50, −0.15)
HIV Statusc	−0.03	(−0.21, 0.14)	0.44	(−0.12, 1.00)	−0.01	(−0.31, 0.30)
Time Trend
Basis 1	5.5	(5.4, 5.7)	25.1	(24.7, 25.5)	10.4	(10.2, 10.6)
Basis 2	8.8	(8.6, 8.9)	36.4	(35.9, 36.9)	10.7	(10.6, 10.9)
Basis 3	16.0	(15.7, 16.3)	64.7	(63.8, 65.6)	21.9	(21.6, 22.2)
Basis 4	10.3	(10.1, 10.4)	43.2	(42.6, 43.8)	9.2	(9.1, 9.4)
Rate Effects		Estimate			95% CI
Sexa		−0.00			(−0.01, −0.01)
Treatmentb		0.01			(−0.01, 0.02)
HIV Statusc		−0.06			(−0.09, −0.04)

^aParameter estimates for males relative to females.

^bParameter estimates for infants exposed to nevirapine relative to those exposed to zidovudine.

^cParameter estimates for HIV positive infants relative to HIV negative infants.

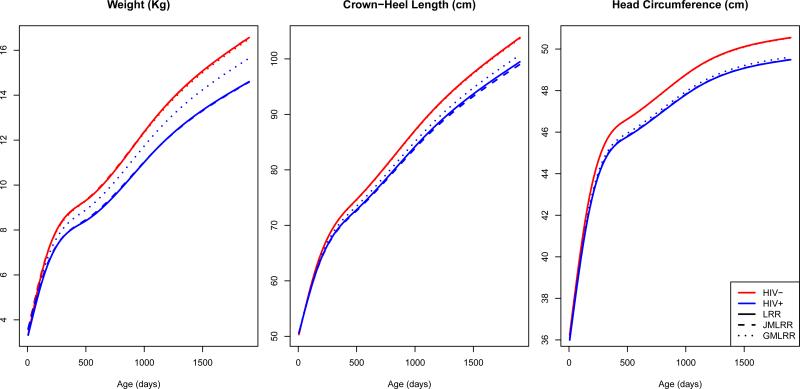
Separate estimates were produced for main effects and time trend coefficients associated with each outcome, and global estimates were produced for rate effects of the MLRR model. In Table 1, the main effect estimates for the global MLRR model showed large mean differences at birth due to sex and treatment. Males were estimated to be 0.34 Kg (95% CI = (0.24, 0.44)) heavier, 1.25 cm (95% CI = (0.93, 1.57)) taller, and increased head circumference of 0.78 cm (95% CI = (0.60, 0.96)) at birth on average compared to females. Infants whose mothers were assigned to nevirapine were estimated to have lower weight (Mean Diff. = −0.12 Kg, 95% CI = (−0.19, −0.06)), crown-heel length (Mean Diff. = −0.36 cm, 95% CI = (−0.54, −0.18)), and head circumference (Mean Diff. = −0.32 cm, 95% CI (−0.50, 0.15)) at birth on average compared to those on zidovudine. There was little evidence that infants who tested HIV positive differed in weight (Mean Diff. = −0.04 Kg, 95% CI = (−0.21, 0.14)), height (Mean Diff. = 0.44 cm, 95% CI = (−0.12, 1.00)), or head circumference (Mean Diff. = −0.01 Kg, 95% CI = (−0.31, 0.30)) at birth compared to infants who tested negative. The time trend for each outcome is illustrated in Figure 3 which presents fitted lines from the global MLRR model for the HIV negative and positive groups as well as the fitted line from the univariate LRR model for each outcome and the MLRR model without a global rate parameter assumption. The figure illustrates that the estimated time trend for the global MLRR model was fairly similar to that of the other models. Most of the differences shown in the figure are a result of differing estimates for the rate of growth of HIV positive children across the three models. The differences in the fitted lines between the three modeling approaches was most apparent for the HIV positive group since this group is substantially smaller (59 HIV positive infants) and thus more subject to change across various modeling approaches. The global rate effects estimated a small difference in the rate of change in the two growth outcomes due to sex and treatment with essentially no difference in growth between males and females, and a 1% faster rate of change for infants on nevirapine compared to zidovudine. There was strong evidence for a difference in the rate of change in growth outcomes due to HIV infection status with infants infected with HIV estimated to have 6% decrease in the rate of change (95% CI = (−9%, −4%)) compared to non-infected infants. Therefore, the model shows evidence that weight, crown-heel length, and head circumference differ across groups defined by sex and treatment at the mean level primarily where as HIV infection status primarily impacted the rate of change for these outcomes.

Figure 3.

Plots of fitted lines for the models of rate differences in the trivariate outcome of weight, crown-heel length, and head circumference across groups defined by sex, treatment, and HIV status. Separate plots have been generated for each outcome with the mean fitted line for HIV negative (red) and HIV positive (blue) infants for three longitudinal rate regression models. Fitted lines were plotted for the univariate LRR model (solid line) for each outcome, the MLRR model with separate rate effects for each outcome (dashed line), and the MLRR model with GMPR assumption (dotted line)

The presented model results are based on a complete case analysis of the data. Missing values were present in the data for all three outcomes. In particular, there were fewer measurements of crown-heel length and head circumference since these were measured less consistently than weight and were not measured at the initial visit. The complete dataset for the univariate weight model alone consisted of 7,643 observation on a total of 622 infants. Thus, the additional missing data for crown-heel length and head circumference resulted in 6 fewer infants with a total of 6,964 observations. In addition, much of the missing outcome values were result of drop out from the study which was primarily a result of infant mortality [15]. Since death is likely associated with HIV status, the missing data mechanism likely does not conform to a missing completely at random assumption. However, the advantage of the random effects estimation approach employed in this application is that such approaches have been shown to consistently estimate model parameters under a missing at random assumption (see Chapter 13 of Diggle et. al. [16] and Chapters 15 and 16 of Verbeke and Molenberghs [17]). Such an analysis targets estimation of the longitudinal profiles toward what would have been observed in the absence of death which is a hypothetical construct [18]. In addition, though no covariate values were missing in this dataset, the MLRR model is amenable to accounting for missing covariate values under flexible missing data assumptions via conventional approaches such as multiple imputation.

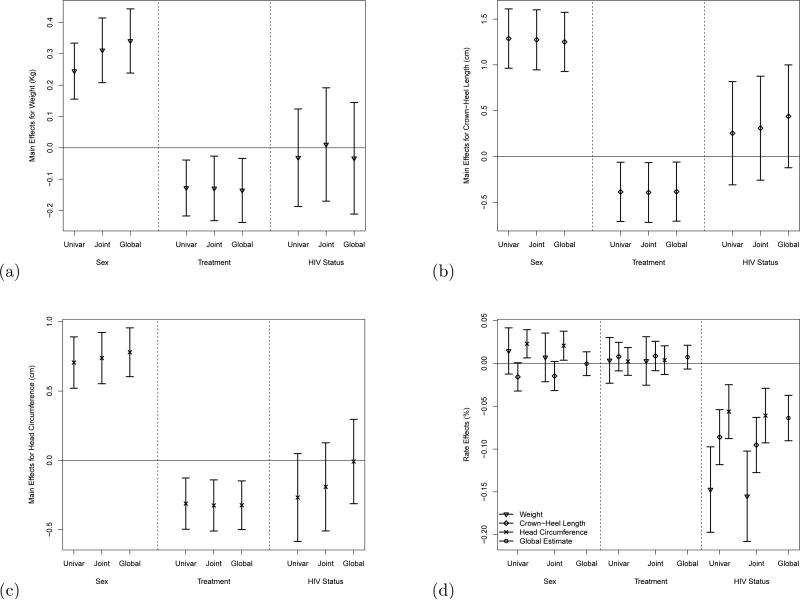
We illustrate the impact of the GMPR assumption on model estimates in Figure 4 by comparing the confidence intervals for the global MLRR model presented in Table 1 to the confidence intervals from the equivalent univariate LRR models and joint MLRR models which does not assume GMPR. Confidence intervals for the main effect estimates are provided for each outcome in Figure 4(a), (b), and (c). The level of precision for the main effect estimates was relatively similar between the three models and only mild to moderate differences were present between each estimate across the models. There were also some mild differences between estimates and confidence intervals for the intercept (not shown). The global rate effect for each covariate exhibited modest gains in precision compared to the separate estimates from the univariate LRR model and joint MLRR model (see Figure 4(d)). The largest difference in the rate estimates across outcomes were observed for HIV status with the rate of change for weight being most impacted followed by crown-heel length and head circumference. The rate estimates for HIV in the global MLRR model were intermediate to the rate estimates for crown-heel length and head circumference provided by the univariate LRR and joint MLRR models with closer proximity to the estimates for head circumference. The global estimate were likely dominated by crown-heel length and head circumference since the standard error for the rate estimates were smaller for these outcomes compared to the standard error for weight. Also, the variation in the random effects and measurement error for the global MLRR model was smallest for head circumference which could account for the global estimates being more similar to the separate effect of head circumference compared to crown-heel length. Though this property may be unfavorable in some instances such as this where the global effect may be dominated by outcomes with smaller rate differences that have smallest standard error for these differences, in general, such a characteristic is desirable that the global estimate should tend toward the individual estimates where the difference in the rate of change between groups was the most consistent across the sample. Similar properties are achieved for other metrics used to combine estimates such as weighted means. In fact, a simple weighted mean of the rate effects from the joint MLRR model results in a value of −0.09 which is similarly intermediate to the separate rate effects for crown-heel length and head circumference. The global effect is much closer to the separate effect for head circumference compared to the weighted mean, but there are other possible explanations for this occurring. One such explanation is that the global model is combining effects across three covariates (sex, treatment, and HIV status) and the interplay between these three covariates may account for the additional differences between the global effect and the weighted mean.

Figure 4.

Parameter estimates and 95% confidence intervals are plotted for the longitudinal rate regression models for estimating group differences in growth outcomes for infants exposed to HIV infection. Each model regressed the growth outcome(s) against sex, treatment, and HIV infection status. Results are provided for univariate LRR models for weight, crown-heel length, and head circumference; a MLRR model with separate rate estimates for each outcome; and a MLRR model with GMPR assumption. (a) Main effect estimates and confidence intervals for group differences in weight (Kg). (b) Main effect estimates and confidence intervals for group differences in crown-heel length (cm). (c) Main effect estimates and confidence intervals for group differences in head circumference (cm). (d) Rate effect estimates and confidence intervals for the three growth outcomes. Each estimate and interval is indicated for whether they correspond to weight, crown-heel length, head circumference, or all three in the case of the global rate parameter.

Diagnostic plots and testing procedures for validating the PR assumption for the LRR model have been proposed by Bryan and Heagerty [8]. These procedures may also be used to evaluate the proportionality of rates for the MLRR model. Figure 5 depicts residual plots which may be used to evaluate the proportional rate assumption across each rate covariate for the global MLRR model. The residuals for the model have been plotted over time separately within each covariate group. Any violations in the proportional rate assumption over time across a given covariate would be depicted as deviations from 0 in the over all trend in the residuals over time within covariate groups. Lowess smooth lines have been included within each plot to illustrate the time trend within each subgroup. These plots show little deviation from 0 over time which implies there is little evidence of concern for the proportional rate assumption. The spread of the residuals over time within each plot indicates a slight increase in variation over time. Such behavior in the residuals is anticipated since heteroskadasticity is common to observe when measuring growth outcomes in children. The heteroskadastic behavior in the data is likely accounted for by the random effects structure, specifically the random slope for each outcome, but the plotted residuals have not removed the individual variability explained by the random effects. Residuals can be calculated that remove this individual variation to evaluate how well the non-constant variation has been captured. Such residuals could also be used to evaluate the proportional rate assumption, but would likely result in the same conclusion as from the plots presented in Figure 5. Additionally, we can also evaluate the global rate parameter assumption for the global MLRR model using diagnostic tests. One way to test the global parameter assumption for the infant growth data is based on the joint MLRR model estimates where the point estimates and covariance matrix for the rate effect for each covariate across the three outcomes can be combined into a Wald statistic in order to test for equivalence. This Wald test approach suggested a significant difference in the rate effects across growth outcomes for sex (P-value < 0.001) and HIV (P-value < 0.001). There was no evidence for a difference in the rate effects associated with treatment (P-value = 0.20). These test support violations of the global shared parameter assumption and suggest that the MLRR model with separate rate effect estimates may be more appropriate for this application. Alternative testing metrics could be considered such as using a score test which would avoid the need for running both the joint and the global MLRR models. However, even when the global MLRR model is the primary result of interest, most studies would likely construct the joint MLRR model as well in order to fully characterize the relationship between the outcomes and the rate covariates. Thus, the Wald testing approach described here would be easily applicable in most settings.

Figure 5.

Plots of residuals over time for the MLRR model with GMPR assumption for modeling rate differences in weight, crown-heel length, and head circumference across sex, treatment, and HIV status. Residuals capture the difference between the population mean and the observed value and do not account for individual variation explained by the random effects structure. Separate plots are include for each covariate group with a lowess curve to characterize the trend over time.

5. Discussion

Methodology for multivariate longitudinal data has received limited attention in the statistical literature. Since the routine collection of detailed longitudinal data is becoming more common in the scientific community, more applications where multivariate longitudinal methods are potentially advantageous will likely arise. The methodology presented here has focused on utilizing multivariate longitudinal data to model group differences. Comparing longitudinal changes across groups is a common scientific aim, and established methodology has separately shown the utility of longitudinal data and multivariate data for making inference. Using both data types presents challenges, but also provides gains in power and precision that counter the added model complexity.

We proposed an extension to the LRR model that was introduced by Bryan and Heagerty [8]. The LRR method directly and parsimoniously models differences in rates of change for longitudinal data. The model allows for a flexible time structure and a simple interpretation for the difference in the rate of change which makes the LRR method advantageous when the underlying time trend is non-linear. The extended MLRR model allows separate specifications for baseline covariate adjustment and reference time trend for each outcome. The mean of each outcome is linked by a global parameter for the difference in the rate of change for the multivariate outcome. Group differences can then be interpreted as global or overall difference in the rate of change of the multivariate outcome associated with the group. Though our approach is similar to other global shared parameter model [3, 5–7], we did not make any direct comparisons with these approaches since each was designed for very different applications. The MLRR will be most appropriate for application interested in differences in rates of change or rates of growth for a collection of outcomes. Among the other global shared parameter models, only that proposed by Gray and Brookmeyer [3, 5] is concerned with differences in rates, but in contrast to the MLRR model, this model focuses on rate differences characterized by an acceleration of the time trend. Thus, Gray and Brookmeyer's approach will be best suited for applications where the progression of the outcomes are the primary concern.

We compared the power to detect group differences using the global shared parameter MLRR approach versus testing using only a single outcome, or using multiple outcomes with a separate rate parameter for each outcome. A global testing approach will be more powerful when it is reasonable to assume that the rate effect is the same for each outcome. Furthermore, when correlation between outcomes is low, gains in power may still be obtained using MLRR when the true difference in the rate of change varies across outcomes but maintains a common direction. Using a multivariate comparison of rates of change will lose power relative to an optimally chosen univariate comparison when major differences exist between the rate effects for each outcome. In particular, if some covariates increase the rate of change for certain outcomes and decrease the rate of change for other outcomes, a global shared parameter model would not be appropriate. Therefore, for applications where group differences in the rate of change is expected to be similar across mildly correlated outcomes a global shared parameter MLRR model will be beneficial for increasing power and precision of the group comparison. We also explored testing options when the multivariate outcomes have high correlation and find that the global shared parameter will not be advantageous when the covariate (group) effects in the rate of change are strongly heterogeneous across outcomes. When outcomes are strongly correlated, the benefits of a global multivariate testing approach are less clear, and likely depend on the nature of the correlation between the outcomes. Our evaluation shows that a multivariate (non-shared) model may yield the highest power when covariate effects are not constant and outcome correlation is strong. The impact of covariance structure on power in a multivariate setting is known to be quite complex [14] particularly when covariate effects are not similar across highly correlated outcomes.

The application of the MLRR method to the growth study for infants exposed to HIV also illustrates the potential power gains of a multivariate approach. The width of the confidence interval for the globally estimated rate effect was noticeably smaller than the confidence intervals based on univariate estimates. Examining differences in infant growth was a natural application for this method since there are multiple measures that can be considered to quantify growth. In addition, the rate of change is a useful scale for comparison since it is invariant to scale. The non-linear nature of infant growth data make the flexible time structure of the LRR method appealing. There are other application where the multivariate rate regression approach would be useful for the comparison of groups such as longitudinal studies of aging and treatment trials with multiple end points of interest. A global shared parameter MLRR approach is also potentially applicable in areas where effect sizes are commonly small such as in studies of environmental exposures.

The utility of the MLRR method is dependent on the non-linearity of the outcomes over time. If all outcomes change linearly or approximately linearly over time, then a linear mixed model approach will be more suitable for comparing groups. Whether the MLRR approach is advantageous when some outcomes behave linearly and others are non-linear is worthy of further research. The GMPR assumption is also a limitation of the MLRR method when the difference in the rate of change is not proportional over time or is not the same across outcome. Diagnostic approaches for assessing the proportional rate assumption for a univariate LRR model are discussed by Bryan and Heagerty [8] and were implemented in this paper for the study of infant growth in a multivariate context. Relaxing the proportional rate assumption in regard to time is discussed further by Bryan and Heagerty [8]. The assumption of a global rate parameter can also be tested based on multivariate models with separate rate parameter estimates. When the global rate assumption is violated, both the univariate LRR and the MLRR approaches with separate rate parameters for each outcome could be considered.

Appendix

We describe in further detail the implementation process for the global MLRR model using Maximum Likelihood Estimation via the Newton-Raphson algorithm. For simplicity of notation, we assume a setting where a study has measured K correlated outcomes measured at J time points on N subjects with Q additional covariates measured at baseline. However, the described implementation is compatible with the situation where the number of time points and measurement times differ across outcome and across individuals. We let the observed outcomes for the ith individual, for i = 1, . . . , N, be denoted by the vector Y_i of length JK, measurement times be denoted by the vector T_i of length JK, and baseline covariates by the vector X_i of length Q. Our goal is to estimate the global effect of the covariates in X_i on the rate of change of the collection of outcomes Y_i over time. Each outcome will also have a corresponding vector W_ik of length p_k for k = 1, . . . , K for all baseline covariates to be adjusted for mean level differences in outcome k. The baseline covariates included in W_ik may vary across outcome with the exception that the X_i must be a subset.

To appropriately account for non-linearity for each outcome over time, we can define a basis of functions of time for each outcome and evaluate these bases at the observed times for each outcome across individuals. We allow the number of functions in each basis for each outcome to vary across outcome and denote the length be l_k for k = 1, . . . , K. The design matrix B_ik will denote the J × l_k matrix whose entries correspond to the basis functions for outcome k evaluated for the ith individual at each observation time.

The general framework of the log-likelihood equation for the multivariate longitudinal outcome Y_i will correspond to a multivariate normal random variable which can be expressed as

$$l({\mu }_i,{\mathbf{V}}_i)=\text{constant}-\frac{1}{2}\log \mid {\mathbf{V}}_i\mid -\frac{1}{2}{({\mathbf{Y}}_i-{\mu }_i)}^{\prime }{\mathbf{V}}_i^{-1}({\mathbf{Y}}_i-{\mu }_i)$$

where μ_i and V_i denote the vector of mean values and the covariance matrix for Y_i. Bryan and Heagerty [8] note that for situations like the current model where the likelihood equation contains parameters for which both μ_i and V_i depend on, the score and hessian equations can generally be expressed in terms of parameters η, ν, and ϕ where μ_i depends on the parameters η and ϕ, and V_i depends on the parameters ν and ϕ. The score and hessian equations are then given by the equations

$$\begin{array}{cc}\hfill {\stackrel{.}{l}}_{\eta }& ={\left(\frac{\partial {\mu }_i}{\partial \eta }\right)}^{\prime }{\mathbf{V}}_i^{-1}({\mathbf{Y}}_i-{\mu }_i)\hfill \\ \hfill {\stackrel{.}{l}}_{\nu }& =-\frac{1}{2}\text{trace}\left[{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \nu }\right)\right]+\frac{1}{2}{({\mathbf{Y}}_i-{\mu }_i)}^{\prime }{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \nu }\right){\mathbf{V}}_i^{-1}({\mathbf{Y}}_i-{\mu }_i)\hfill \\ \hfill {\stackrel{.}{l}}_{\varphi }& =-\frac{1}{2}\text{trace}\left[{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \varphi }\right)\right]+\frac{1}{2}{({\mathbf{Y}}_i-{\mu }_i)}^{\prime }{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \varphi }\right){\mathbf{V}}_i^{-1}({\mathbf{Y}}_i-{\mu }_i)+{\left(\frac{\partial {\mu }_i}{\partial \varphi }\right)}^{\prime }{\mathbf{V}}_i^{-1}({\mathbf{Y}}_i-{\mu }_i)\hfill \\ \hfill H_{\eta ,{\eta }^{\ast }}& ={\left(\frac{\partial {\mu }_i}{\partial \eta }\right)}^{\prime }{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mu }_i}{\partial {\eta }^{\ast }}\right)\hfill \\ \hfill H_{\eta ,\nu }& =0\hfill \\ \hfill H_{\eta ,\varphi }& ={\left(\frac{\partial {\mu }_i}{\partial \eta }\right)}^{\prime }{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mu }_i}{\partial \varphi }\right)\hfill \\ \hfill H_{\nu ,{\nu }^{\ast }}& =\frac{1}{2}\text{trace}\left[{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \nu }\right){\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial {\nu }^{\ast }}\right)\right]\hfill \\ \hfill H_{\nu ,\varphi }& =\frac{1}{2}\text{trace}\left[{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \nu }\right){\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \varphi }\right)\right]\hfill \\ \hfill H_{\varphi .{\varphi }^{\ast }}& =\frac{1}{2}\text{trace}\left[{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial \varphi }\right){\mathbf{V}}_i^{-1}\left(\frac{\partial {\mathbf{V}}_i}{\partial {\varphi }^{\ast }}\right)\right]-{\left(\frac{\partial {\mu }_i}{\partial \varphi }\right)}^{\prime }{\mathbf{V}}_i^{-1}\left(\frac{\partial {\mu }_i}{\partial {\varphi }^{\ast }}\right).\hfill \end{array}$$

The generally expressed score and hessian equations can be applied to the specific structure of the MLRR model evaluating these expression for the mean and variance structure equations given by

$$\begin{array}{cc}\hfill {\mu }_i(\alpha ,\theta ,\beta )& =\left(\begin{array}{c}\hfill {\mathbf{W}}_{i1}{\alpha }_1{1}_J\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{W}}_{iK}{\alpha }_K{1}_J\hfill \end{array}\right)+(1+{\mathbf{X}}_i\theta )\left(\begin{array}{c}\hfill {\mathbf{B}}_{i1}{\beta }_1\hfill \\ \hfill ⋮\hfill \\ \hfill {\mathbf{B}}_{iK}{\beta }_K\hfill \end{array}\right)\hfill \\ \hfill {\mathbf{V}}_i(\mathbf{R},\Sigma ,\beta )& ={\mathbf{Z}}_i{RZ}_i^{\prime }+\Sigma .\hfill \end{array}$$

where the coefficients for baseline differences due to covariates for outcome k are denoted by the vector α_k, the coefficients for basis functions of time for outcome k are denoted β_k, the global rate parameters associated with the rate covariates are denoted by θ, the random effects structure is given by the matrix R, the random effects design matrix for the ith individual is defined by Z_i, and Σ denotes the variance of the measurement error. For the random effects structure described in subsection 2.2, the random effect design matrix Z_i would be a JK × 2K matrix where the (2k – 1)th column takes a value of 1 for rows corresponding to outcome k and zero otherwise, and the (2k)th column takes on values of the vector B_ikβ_k for the rows corresponding to outcome k and zero otherwise. Finally, be decomposing the random effects matrix into an LDL Cholesky Decomposition [19], the derivatives of the mean function and variance function can be derived based on the above parameter specification. The component parts can then be incorporated into a standard Newton-Raphson algorithm to perform Maximum Likelihood Estimation.