Learning Linear Dynamical Systems from Multivariate Time Series: A Matrix Factorization Based Framework

Abstract

The linear dynamical system (LDS) model is arguably the most commonly used time series model for real-world engineering and financial applications due to its relative simplicity, mathematically predictable behavior, and the fact that exact inference and predictions for the model can be done efficiently. In this work, we propose a new generalized LDS framework, gLDS, for learning LDS models from a collection of multivariate time series (MTS) data based on matrix factorization, which is different from traditional EM learning and spectral learning algorithms. In gLDS, each MTS sequence is factorized as a product of a shared emission matrix and a sequence-specific (hidden) state dynamics, where an individual hidden state sequence is represented with the help of a shared transition matrix. One advantage of our generalized formulation is that various types of constraints can be easily incorporated into the learning process. Furthermore, we propose a novel temporal smoothing regularization approach for learning the LDS model, which stabilizes the model, its learning algorithm and predictions it makes. Experiments on several real-world MTS data show that (1) regular LDS models learned from gLDS are able to achieve better time series predictive performance than other LDS learning algorithms; (2) constraints can be directly integrated into the learning process to achieve special properties such as stability, low-rankness; and (3) the proposed temporal smoothing regularization encourages more stable and accurate predictions.

1 Introduction

Recent advances in data collection, data storage and information technologies have resulted in enormous collections of multivariate time series (MTS) data on various aspects of our everyday life. A variety of MTS datasets appear in economy, meteorology, Internet or vehicular traffic, healthcare and many other areas. These MTS data provide us with a unique opportunity to gain novel insights and understanding of the processes and systems generating the data. Developing and learning accurate models of MTS play important roles in forecasting, decision making and/or intelligent system support.

Various mathematical models have been proposed to study real-valued MTS data and processes [27]. Among all of them, the linear dynamical system (LDS) model stands out and is arguably the most commonly used time series model for real-world applications. Basically, an LDS is a Markovian model that assumes the dynamic behavior of the system is captured well using a small set of real-valued hidden-state variables and linear state transitions corrupted by a Gaussian noise. Due to the model’s relative simplicity, mathematically predictable behavior, and the fact that exact inference and predictions for the model can be done efficiently, LDS models have been applied widely for time series prediction [16, 18, 21, 22, 28] or object tracking [10, 17] tasks.

While in some rare LDS application scenarios, the LDS models’ parameters are known, e.g., they are derived from known physical equations, the majority of real-world applications require them to be learned from MTS data. Expectation-Maximization (EM) [6] and spectral learning [12, 25] algorithms are typically used for this task. Recently in order to meet different characteristics of MTS data, various constraints, such as sparsity, low-rankness, were integrated into the standard LDS models. Constraints are incorporated either in the hidden state inference process [1, 3, 4] or into the parameter learning process [2, 20].

In this work, we propose a new generalized LDS framework, gLDS, for learning LDS models from a collection of MTS data. Our learning framework is based on matrix factorization approach, where each MTS sequence is factorized as a product of a shared emission matrix and a sequence-specific hidden dynamics. In contrast to traditional matrix factorization, the hidden factors in gLDS may evolve in time and individual dynamics is modeled with the help of a shared transition matrix. We use alternating minimization to learn the LDS model from data. In such a case, each parameter can be optimized efficiently and the procedure is exible enough to incorporate various constraints. Furthermore, we propose a temporal smoothing regularization, which penalizes the difference of predictive results from the learned model during the learning phase, to achieve smooth forecasts from the learned LDS models.

In summary, our paper makes the following contributions:

• Compared to LDS spectral learning algorithm, our framework is able to learn the LDS model from a collection of many different MTS sequences. The spectral learning algorithm requires and learns the model from just one sequence. While it is always possible to concatenate multiple MTS sequences into one large sequence, this brute-force concatenation process may introduce a lot of non-smooth transitions leading to model imprecision.

• Compared to the LDS EM learning algorithm, parameter optimization in gLDS can be done efficiently in each iteration. The EM requires one to infer the hidden states for each training sequence. This step is avoided in gLDS.

• Constraints can be easily incorporated into our generalized framework. We show that various existing approaches, such as stable LDS [2], regularized LDS [20] are special cases of our gLDS framework.

• A novel temporal smoothing regularization and a smooth LDS model are proposed which are able to support more smooth and more accurate time series predictions.

The remainder of the paper is organized as follows: Section 2 introduces the basics of the LDS models, standard LDS learning algorithms and some recent work on constrained LDS. In Section 3, we describe our generalized learning framework and show the connections between various existing research and our framework. We proposed a temporal smoothing regularization for LDS to support more smooth and accurate predictions. In Section 4, we show that (1) models learned from gLDS support better predictions compared with standard LDS learning algorithms; and (2) various constraints can be integrated into gLDS and stability and low-rankness can be easily achieved. We summarize our work and outline potential future extensions in Section 5.

2 Background

In this section, we first introduce the notation we will use throughout this paper. Then, we review the basics of the LDS model and its two major learning algorithms: EM and spectral approaches. After that, we discuss some recent LDS extensions that incorporate various constraints into the basic LDS model in order to achieve its better performance.

2.1 Notation

Given a collection of N multivariate time series sequences {Y¹, Y², ⋯, Y^N}, we represent each multivariate sequence Y^m as an n × T_m matrix, where ${\mathbf{Y}}^m=[{\mathbf{y}}_1^m,\cdots ,{\mathbf{y}}_t^m,\cdots ,{\mathbf{y}}_{T_m}^m]$ and n is the number of time series variables and T_m is the length of sequence. ${\mathbf{y}}_t^m$ is an n × 1 vector observed at time stamp t. Correspondingly, {Z¹, Z², ⋯, Z^N} represent the collection of hidden state sequences, where ${\mathbf{Z}}^m=[{\mathbf{z}}_1^m,\cdots ,{\mathbf{z}}_t^m,\cdots ,{\mathbf{z}}_{T_m}^m]$ is a d × T_m matrix. d is the dimensionality of hidden state space and ${\mathbf{z}}_t^m$ is a d × 1 hidden state vector corresponding to ${\mathbf{y}}_t^m$. Let ${\mathbf{Z}}_{+}^m=[{\mathbf{z}}_2^m,{\mathbf{z}}_3^m,\cdots ,{\mathbf{z}}_{T_m}^m]$ and ${\mathbf{Z}}_{-}^m=[{\mathbf{z}}_1^m,{\mathbf{z}}_2^m,\cdots ,{\mathbf{z}}_{T_m-1}^m]$. We use Y, Z, Z₊, and Z₋ to denote the horizontal concatenations of {Y^m}, {Z^m}, $\{{\mathbf{Z}}_{+}^m\}$, and $\{{\mathbf{Z}}_{-}^m\}$. Here Y is an n × T matrix and Z is a d × T matrix. Z₊ and Z₋ are d × (T − N) matrices where $T={\sum }_{m=1}^N{T}_m$.

Let | · |, ‖ · ‖₂ and ‖ · ‖_F be the absolute value, the vector ℓ₂ and matrix Forbenious norms. We use Tr[·] to denote the matrix trace operator. I_d is the d × d identity matrix. Let 𝔼_z[f(·)] denote the expected value of f(·) with respect to z. For both vectors and matrices, the superscript (·)^⊤ denotes the transpose. For the sake of notational brevity, we omit the explicit sample index (m) in the rest of Section 2.

2.2 Linear Dynamical System

The LDS is an MTS model that represents observation sequences indirectly with the help of hidden states. The LDS models the dynamics of these sequences in terms of the state transition probability p(z_t|z_t−1), and state-observation probability p(y_t|z_t). These probabilities are modeled using the following equations:

$${\mathbf{z}}_t=A{\mathbf{z}}_{t-1}+{\mathit{\epsilon }}_t$$ (2.1)

$${\mathbf{y}}_t=C{\mathbf{z}}_t+{\mathit{\zeta }}_t$$ (2.2)

where the transitions among the current and previous hidden states are linear and captured in terms of a d × d transition matrix A. The stochastic component of the transition, ε_t, is modeled by a zero-mean Gaussian noise ε_t ~ 𝒩(0, Q) with a d × 1 zero mean vector and a d × d covariance matrix Q. The observational sequence is derived from the hidden states sequence. The dependencies in between the two sequences are linear and modeled using an n × d emission matrix C. A zero mean Gaussian noise ζ_t ~ 𝒩(0, R) models the stochastic relation in between the states and observations. In addition to A, C, Q, R, the LDS is defined by the initial state distribution for z₁ with mean ξ and covariance matrix Ψ, i.e., z₁ ~ 𝒩(ξ, Ψ). The complete set of the LDS parameters is Ω = {A, C, Q, R, ξ,Ψ}.

While in some LDS applications the model parameters are known a priori, in the majority of real-world applications the model parameters are unknown, and we need to learn them from MTS data. Various learning algorithms have been proposed in the past years. In the following, we briefly discuss the two major categories of these learning algorithms: Expectation-Maximization (EM) [6, 23] (See Section 2.2.1) and spectral learning algorithms [2, 5, 12, 25] (See Section 2.2.2).

2.2.1 EM Learning

The EM algorithm is an iterative procedure for finding model parameters that maximizes the likelihood of observations in the presence of hidden variables. In practice, instead of maximizing the data likelihood directly, EM algorithm usually maximizes a 𝒬 function, which is the expectation of the joint probability of both observed and hidden variables with respect to the distribution of hidden variables. The 𝒬 function is a lower bound of the true data likelihood and maximizing it will improve the data likelihood. Under the setting of learning standard LDS defined by eq.(2.1) and eq.(2.2), the 𝒬 function is defined as follows:

$$𝒬={𝔼}_{\mathbf{Z}}[\text{log }p(\mathbf{Z},\mathbf{Y})]={𝔼}_{\mathbf{Z}}[\text{log }p({\mathbf{z}}_1)]+{𝔼}_{\mathbf{Z}}[\sum _{t=1}^T\text{log }p({\mathbf{y}}_t|{\mathbf{z}}_t)]+{𝔼}_{\mathbf{Z}}[\sum _{t=2}^T\text{log }p({\mathbf{z}}_t|{\mathbf{z}}_{t-1})]$$ (2.3)

The EM algorithm alternates between maximizing the 𝒬 function with respect to the parameters Ω and with respect to the distribution of hidden states, holding the other quantities fixed. The E-step depends on 𝔼[z_t|Y], $𝔼[{\mathbf{z}}_t{\mathbf{z}}_t^{\top }|\mathbf{Y}]$ and $𝔼[{\mathbf{z}}_t{\mathbf{z}}_{t-1}^{\top }|\mathbf{Y}]$, which are sufficient statistics to compute eq.(2.3). Kalman filtering [11] and Kalman smoothing [26] algorithms are used for computing the sufficient statistics, which are provided in the supplemental material¹. The M-step re-estimate each of the parameter in Ω by taking the corresponding partial derivative of the expected log likelihood, setting to zero and solving. Update rules in M-step can be found in [6].

While the EM learning algorithm is well studied for LDS models, it is difficult to incorporate constraints on either hidden states estimation or parameter estimation during the process of learning LDS models from the collection of data. Furthermore, when the number of sequential instances increases, the EM algorithm becomes inefficient since it computes the expectation for each sequence.

2.2.2 Spectral Learning

Spectral learning methods provide a non-iterative, asymptotically unbiased LDS estimation solution in closed form. They estimate the parameters of an LDS by using singular value decomposition (SVD) to find Kalman filter estimates of the underlying state sequence [5, 12, 25]. Spectral learning methods approximate the observation matrix Y or its variants (hankel matrix) [2] into UΣV^⊤ by SVD, where U ∈ ℝ^n×d and V ∈ ℝ^T×d have orthonormal columns {u_i} and {v_i} and Σ = diag{δ₁, ⋯, δ_d} contains the singular values. The emission matrix and state sequence are estimated as Ĉ = U and Ẑ = ΣV^⊤ and the transition matrix  is obtained by solving the least square of ${\Vert A{\mathbf{Z}}_{-}-{\mathbf{Z}}_{+}\Vert }_F^2$. Based on this SVD intuition, various algorithms have been proposed, such as N4SID [24].

The advantage of spectral learning algorithms is the efficiency due to the non-iterative nature, while the major limitations are (1) it requires the sequence to be long enough in order to maintain its learning consistency; and (2) it has to conduct the SVD over each individual time series sequence and cannot be directly learned from multiple sequences.

2.3 Related Work

Recently, in order to improve the model performance and its quality, various researchers have proposed to incorporate different constraints into both the inference process (estimating hidden states Z from data given known parameters Ω) (See Section 2.3.1) and the learning process (estimating parameters Ω from data) (See Section 2.3.2).

2.3.1 C1: Constraints on LDS Inference

Most of the existing refinements focus on enforcing different types of sparsity constraints on the estimates of the hidden state (Z). For example, in [1, 3, 4] the hidden states are sparsified during the Kalman filter inference step. [4] formulates the traditional Kalman filter as a one-step update optimization procedure and incorporates sparsity constraints to achieve a sparse state estimate at each time stamp t. [1] treats all the state estimates as a state estimate matrix and enforces a row-level group lasso on the state estimate matrix.

All the methods in this category try to learn a sparse representation of the hidden-state estimation problem by assuming that all parameters of the LDS are known a priori. Hence they are not directly applicable to the problem of learning LDS models from MTS data.

2.3.2 C2: Constraints on LDS Learning

Constraints in this category are incorporated into the LDS learning process in order to achieve special model properties, such as low-rankness [20], stability [2], and others. In the following, we describe two recent constrained LDS models: regularized LDS and stable LDS.

• Regularized LDS Regularized LDS models proposed by [20] aim to learn LDS models with a low-rank transition matrix from a limited number of MTS sequences. Compared with the ordinary LDS model, the regularized LDS is able to find the intrinsic dimensionality of the hidden state and prevent the overfitting problem whenever the amount of MTS data is small.

• Stable LDS An LDS with dynamic matrix A is stable if all of A’s eigenvalues have magnitude at most 1. The stability is crucial when simulating long sequences from LDS models in order to generate representative data or infer stretches of missing values. [2] formulates the optimization of the transition matrix as a quadratic program and keeps generating linear constraints to bound the eigenvalues and hence, is able to guarantee stability.

3 The Generalized LDS Learning Framework

In this section, we propose a generalized framework, gLDS, for learning LDS models based on matrix factorization. In gLDS, (1) the LDS models can be learned from multiple MTS sequences; and (2) various constraints can be easily incorporated into the learning process. More specifically, in Section 3.1, we present the learning of gLDS and the closed form solutions for each parameter. In Section 3.2, we describe the learning process for a ridge regularized LDS model (gLDS-ridge) as one example of the gLDS framework. In Section 3.3, we show the generalization ability of gLDS by illustrating its connections to two popular models: stable LDS and the regularized LDS. In Section 3.4, we propose a novel temporal smooth regularization and show that how to incorporate it into the LDS learning procedure.

3.1 gLDS Framework

Based on the linear assumption in LDS that sequential observation vector is generated by the linear emission transformation C from hidden states at each time stamp (eq.(2.2)), we can formulate the LDS learning problem by using the matrix factorization approach [13, 15] that assumes the collection of MTS sequences are generated by a shared emission matrix and their specific hidden factors.

$$\underset{C,\mathbf{Z}}{\text{min}}{\Vert \mathbf{Y}-C\mathbf{Z}\Vert }_F^2$$ (3.4)

However, different from traditional matrix factorization models where the hidden factors are in general time independent, in LDS models, hidden factors evolve with time and are specified by eq.(2.1). Hence, similar to [2, 5], we estimate the transition matrix A by solving another least square problem as follows:

$$\underset{A,\mathbf{Z}}{\text{min}}{\Vert {\mathbf{Z}}_{+}-A{\mathbf{Z}}_{-}\Vert }_F^2$$ (3.5)

In this work, in order to learn the LDS parameters from the data, we jointly optimize both eq.(3.4) and eq.(3.5). Furthermore, in order to incorporate constraints into the learned LDS models, we add regularizations for C, A and Z into the objective function, shown as follows:

$$\underset{A,C,\mathbf{Z}}{\text{min}}{\Vert \mathbf{Y}-C\mathbf{Z}\Vert }_F^2+\lambda {\Vert {\mathbf{Z}}_{+}-A{\mathbf{Z}}_{-}\Vert }_F^2+\alpha {ℛ}_C(C)+\beta {ℛ}_{\mathbf{Z}}(\mathbf{Z})+\gamma {ℛ}_A(A)$$ (3.6)

Intuitively, this formulation of the problem aims to find an LDS model that is able to fit as accurately as possible the time series in the training data by using a simple (less complex) model.

3.1.1 Learning

As we can see from eq.(3.6), the coupling between A, C and Z makes this problem difficult to find optimal solutions for A, C and Z simultaneously, so in this work, we adopt the alternating optimization scheme to find the solution iteratively.

Optimization of A, C, and Z

We apply the alternating minimization techniques to eq.(3.6), which leads to the following three optimization problems:

$$\underset{A}{\text{min}}{\Vert {\mathbf{Z}}_{+}-A{\mathbf{Z}}_{-}\Vert }_F^2+\gamma /\lambda {ℛ}_A(A)$$ (3.7)

$$\underset{C}{\text{min}}{\Vert \mathbf{Y}-C\mathbf{Z}\Vert }_F^2+\alpha {ℛ}_C(C)$$ (3.8)

$$\underset{\mathbf{Z}}{\text{min}}{\Vert \mathbf{Y}-C\mathbf{Z}\Vert }_F^2+\lambda {\Vert {\mathbf{Z}}_{+}-A{\mathbf{Z}}_{-}\Vert }_F^2+\beta {ℛ}_{\mathbf{Z}}(\mathbf{Z})$$ (3.9)

Since optimization of a hidden state sequence Z^m is independent of other sequences, we can further decompose the optimization target Z into {Z¹, ⋯, Z^m ⋯ Z^N}. Due to the asymmetric positions of different ${\mathbf{z}}_t^m\mathrm{s}$ in Z^m, we decompose the optimization into three parts: ${\mathbf{z}}_1^m,{\mathbf{z}}_t^m$ and ${\mathbf{z}}_{T_m}^m$ (t = 2, ⋯, T_m − 1). The optimization problems for each hidden states sequence Z^m are defined as follows:

$$\underset{{\mathbf{z}}_1^m}{\text{min}}{\Vert {\mathbf{y}}_1^m-C{\mathbf{z}}_1^m\Vert }_2^2+\lambda {\Vert {\mathbf{z}}_2^m-A{\mathbf{z}}_1^m\Vert }_2^2+\beta {ℛ}_{\mathbf{Z}}({\mathbf{z}}_1^m)$$ (3.10)

$$\underset{{\mathbf{z}}_t^m}{\text{min}}{\Vert {\mathbf{y}}_t^m-C{\mathbf{z}}_t^m\Vert }_2^2+\lambda {\Vert {\mathbf{z}}_t^m-A{\mathbf{z}}_{t-1}^m\Vert }_2^2+\lambda {\Vert {\mathbf{z}}_{t+1}^m-A{\mathbf{z}}_t^m\Vert }_2^2+\beta {ℛ}_{\mathbf{Z}}({\mathbf{z}}_1^m)$$ (3.11)

$$\underset{{\mathbf{z}}_{T_m}^m}{\text{min}}{\Vert {\mathbf{y}}_{T_m}^m-C{\mathbf{z}}_{T_m}^m\Vert }_2^2+\lambda {\Vert {\mathbf{z}}_{T_m}^m-A{\mathbf{z}}_{T_m-1}^m\Vert }_2^2+\beta {ℛ}_{\mathbf{Z}}({\mathbf{z}}_{T_m}^m)$$ (3.12)

Optimization of R, Q, ξ and Ψ

Once we obtain A, C and Z, the rest of LDS’s parameters, R, Q, ξ and Ψ, can be analytically estimated as follows:

$$\hat{Q}=\frac{1}{T-N}({\mathbf{Ẑ}}_{+}-Â{\mathbf{Ẑ}}_{-}){({\mathbf{Ẑ}}_{+}-Â{\mathbf{Ẑ}}_{-})}^{\top }$$ (3.13)

$$\hat{R}=\frac{1}{T}(\mathbf{Y}-Ĉ\mathbf{Ẑ}){(\mathbf{Y}-Ĉ\mathbf{Ẑ})}^{\top }$$ (3.14)

$$\hat{\mathit{\xi }}=\frac{1}{N}\sum _{m=1}^N{\mathbf{ẑ}}_1^m$$ (3.15)

$$\hat{\mathrm{\Psi }}=\frac{1}{N}\sum _{m=1}^N{\mathbf{ẑ}}_1^m{({\mathbf{ẑ}}_1^m)}^{\top }$$ (3.16)

3.1.2 Summary

The entire LDS parameter estimation procedure in our gLDS framework is summarized by Algorithm 1.

3.2 The Ridge Model (gLDS-ridge)

Ridge regularization, a.k.a, Tikhonov regularization, ℓ₂ regularization [9], is widely used to prevent overfitting since it encourages the sum of the squares of the fitted parameters to be small. Furthermore, it alleviates the ill-posed problems in numerical methods. In our gLDS framework, we achieve the ridge model (gLDS-ridge) by setting ℛ_C(C), ℛ_A(A), and ℛ_Z(Z) to the square of Frobenius norm, i.e., ${\Vert ·\Vert }_F^2$.

Due to the differentiability of ridge regularization, we can take the partial derivatives of eqs.(3.7 – 3.12), set them to zero and solve. The results are shown as follows:

$$Â=({\mathbf{Z}}_{+}{\mathbf{Z}}_{-}^{\top }){({\mathbf{Z}}_{-}{\mathbf{Z}}_{-}^{\top }+\gamma /\lambda I_d)}^{-1}$$ (3.17)

$$Ĉ=(\mathbf{Y}{\mathbf{Z}}^{\top }){(\mathbf{Z}{\mathbf{Z}}^{\top }+\alpha I_d)}^{-1}$$ (3.18)

$${\mathbf{ẑ}}_1^m={(G+\lambda A^{\top }A)}^{-1}(C^{\top }{\mathbf{y}}_1^m+\lambda A^{\top }{\mathbf{z}}_2^m)$$ (3.19)

$${\mathbf{ẑ}}_t^m={(G+\lambda A^{\top }A+\lambda I_d)}^{-1}(F_t^m+\lambda A^{\top }{\mathbf{z}}_{t+1}^m)$$ (3.20)

$${\mathbf{ẑ}}_{T_m}^m={(G+\lambda I_d)}^{-1}{F}_{T_m}^m$$ (3.21)

where G = C^⊤C + βI_d and $F_t^m=C^{\top }{\mathbf{y}}_t^m+\lambda A{\mathbf{z}}_{t-1}^m$.

3.3 Existing Models in gLDS Framework

Constraints from both C1 (Section 2.3.1) and C2 (Section 2.3.2) can be easily incorporated into our gLDS framework due to its exibility and extensibility. Since in this work we focus on learning LDS models from MTS sequences, in the following, we describe how to formulate both the stable LDS and regularized LDS as special instances in our gLDS framework.

3.3.1 Learning Regularized LDS (gLDS-low-rank)

In order to obtain a low-rank transition matrix of the LDS model, [20] develops a Maximum a Posteriori learning framework and apply both multivariate Laplacian prior and nuclear norm prior on the A to implicitly shut down spurious and unnecessary dimensions and prevent overfitting problem simultaneously. In gLDS framework, a low-rank transition matrix A can be easily obtained by setting ${ℛ}_A(A)={\Vert A\Vert }_F^2+\frac{\lambda }{\gamma }{\gamma }_A{\Vert A\Vert }_{*}$ in eq.(3.17), which leads to the following objective function (eq.(3.22)). All the others’ updates (eqs.(3.18 – 3.16) remain the same.

$$\underset{A}{\text{min}}g(A)+{\gamma }_A{\Vert A\Vert }_{*}$$ (3.22)

where

$$g(A)={\Vert {\mathbf{Z}}_{+}-A{\mathbf{Z}}_{-}\Vert }_F^2+\gamma /\lambda {\Vert A\Vert }_F^2$$ (3.23)

Algorithm 1.

Learn the LDS model in gLDS.

INPUT:
• Initialization A(0), C(0), Z(0).
• Hyper-parameters, γ, λ, β and α.
• A collection of MTS sequences Y1, ⋯, YN.
PROCEDURE:
1:	// Optimize A, C and Z
2:	repeat
3:	Update A by solving eq.(3.7).
4:	Update C by solving eq.(3.8).
5:	for m: 1 → N do
6:	Update ${\mathbf{z}}_1^m$ by solving eq.(3.10).
7:	for t: 2 → Tm − 1 do
8:	Update ${\mathbf{z}}_t^m$ by solving eq.(3.11).
9:	end for
10:	Update ${\mathbf{z}}_{T_m}^m$ by solving eq.(3.12).
11:	end for
12:	until Convergence
13:	// Optimize Q̂, R̂, ξ̂, Ψ̂
14:	Compute Q̂, R̂, ξ̂, Ψ̂ using eqs.(3.13 – 3.16).
OUTPUT:
• Learned LDS parameters: Ω̂ = {Â, Ĉ, Q̂, R̂, ξ̂, Ψ̂}.

Since g(A) is convex and differentiable with respect to A, we can adopt the generalized gradient descent algorithm to minimize eq.(3.22). The update rule is

$$A^{(k+1)}={\text{prox}}_{{\rho }_k}(A^{(k)}-{\rho }_k\nabla g(A^{(k)}))$$ (3.24)

where ρ_k is the step size at iteration k and the proximal function prox_ρk (A) is defined as the singular value softthresholding operator,

$${\text{prox}}_{{\gamma }_A{\rho }_k}(A)=U·\text{diag}({({\sigma }_i-{\gamma }_A{\rho }_k)}_{+})·V\prime$$ (3.25)

where A = U diag(σ₁, ⋯, σ_d)V′ is the singular value decomposition (SVD) of A.

An important open question here is how to set the step size of the generalized gradient method to assure it is well behaved. Theorem 3.1 gives us a simple way to select the step size while also assuring its fast convergence rate.

Theorem 3.1

Generalized gradient descent with a fixed step size $\rho \le 1/2({\Vert {\mathbf{Z}}_{-}{\mathbf{Z}}_{-}^{\top }\Vert }_F+\gamma /\lambda )$ for minimizing eq.(3.22) has convergence rate O(1/k), where k is the number of iterations.

Proof

The proof of this theorem appears in the supplemental material.

3.3.2 Learning Stable LDS (gLDS-stable)

Stability is a desired property for dynamical modeling and it play important roles in tasks such as predictions, long term sequence simulation, etc. [2] proposes a novel method for learning stable LDS models by formulating the problem as a quadratic program. The program starts with a relaxed solution and incrementally add constraints to improve stability. In gLDS framework, by setting ℛ_A(A) = ∅, we can easily transform our optimization to the same objective function in [2]. Furthermore, we can apply the following theorem to change eq.(3.7) into the standard quadratic program formulation.

Theorem 3.2

Minimizing A from eq.(3.7) with ℛ_A(A) = ∅ is equivalent to minimizing the following problem:

$$\underset{a}{\text{min}}{a}^{\top }Ba-2q^{\top }a$$ (3.26)

where a = vec(A^⊤), $B=I_d\otimes ({\mathbf{Z}}_{-}{\mathbf{Z}}_{-}^{\top }),q=(I_d\otimes {\mathbf{Z}}_{-}{\mathbf{Z}}_{+}^{\top })\text{ vec}(I_d)$.

Proof

The proof of this theorem appears in the supplemental material.

After the quadratic program transformation, we can apply the same constraints generation techniques described in [2] to optimize the transition matrix and guarantee its stability. Details can be found in [2].

3.4 The Smooth Model (gLDS-smooth)

In this section, we propose a novel temporal smoothing regularization (Section 3.4.1), which penalizes the difference of predictive results from the learned model during the learning phase, to achieve smooth forecasts from the learned LDS models. In Section 3.4.2, we show how to incorporate the temporal smoothing regularization into gLDS and describe the corresponding learning procedure.

3.4.1 Temporal Smoothing Regularization

To incorporate predictive smoothness property in LDS models for MTS modeling and forecasting, we propose a temporal smoothing regularization term ${ℛ}_{𝒯}^m$ for each MTS sequence m:

$${ℛ}_{𝒯}^m=\frac{1}{2}\sum _{i=1}^{T_m}\sum _{j=1}^{T_m}{w}_{ij}^m{\Vert {\mathbf{ŷ}}_i^m-{\mathbf{ŷ}}_j^m\Vert }_2^2$$ (3.27)

where ${ŷ}_t^m$ is the model forecast at time stamp t and $w_{ij}^m$ is the smoothing coefficient balancing the difference between predictions ${ŷ}_i^m$ and ${ŷ}_j^m$.

Briefly, the regularization term penalizes the predictions for each time stamp that disagree with other predictions made within the same MTS sequence. The amount of penalty is controlled by a smoothing coefficient $w_{ij}^m$ that is higher for time stamps close to each other and smaller for time stamps further apart. After some algebraic manipulations, the regularization term ℛ_m can be rewritten as,

$${ℛ}_{𝒯}^m=\frac{1}{2}\sum _{i=1}^{T_m}\sum _{j=1}^{T_m}{w}_{i,j}^m{\Vert {\mathbf{ŷ}}_i^m-{\mathbf{ŷ}}_j^m\Vert }_2^2=\sum _{i=1}^{T_m}\sum _{j=1}^{T_m}\sum _{l=1}^n{w}_{i,j}^m{({ŷ}_{l,i}^m)}^2-w_{i,j}^m{ŷ}_{l,i}^m{ŷ}_{l,j}^m=\sum _{l=1}^n{\mathbf{Ŷ}}^m(l,:)(D^m-W^m){\mathbf{Ŷ}}^m{(l,:)}^{\top }=Tr[C{\mathbf{Z}}^m{L}^m{({\mathbf{Z}}^m)}^{\top }{C}^{\top }]$$ (3.28)

where Ŷ^m(l, :) represents the lth row of matrix Ŷ^m. L^m is the T_m × T_m Laplacian matrix for the mth MTS sequence, L^m = D^m − W^m. D^m is a diagonal matrix with the ith diagonal element $D_{i,i}^m={\sum }_{j=1}^{T_m}{w}_{i,j}^m$. W^m is the smoothing coefficient matrix among T_m observations and $w_{ij}^m$ represents the (i, j)th element in W^m.

In order to learn a smooth LDS model, we apply the temporal smooth regularization to each MTS sequence in the training data, which leads to the following compact form of regularization:

$${ℛ}_{𝒯}=\sum _{m=1}^N{ℛ}_{𝒯}^m=Tr[C\mathbf{Z}P{\mathbf{Z}}^{\top }{C}^{\top }]$$ (3.29)

where P is the T × T block diagonal matrix with N blocks and the mth block component is the Laplacian matrix L^m for mth MTS sequence.

3.4.2 Learning Smooth LDS

We incorporate the temporal smooth regularization (eq.(3.29)) into the objective function (eq.(3.6)). Here similar to gLDS-ridge, we set ℛ_C(C), ℛ_A(A), and ℛ_Z(Z) to the ridge regularizations (square of Frobenius norm), which leads to the following new learning objective function:

$$\underset{A,C,\mathbf{Z}}{\text{min}}{\Vert \mathbf{Y}-C\mathbf{Z}\Vert }_F^2+\lambda {\Vert {\mathbf{Z}}_{+}-A{\mathbf{Z}}_{-}\Vert }_F^2+\alpha {\Vert C\Vert }_F^2+\beta {\Vert \mathbf{Z}\Vert }_F^2+\gamma {\Vert A\Vert }_F^2+\delta Tr[C\mathbf{Z}P{\mathbf{Z}}^{\top }{C}^{\top }]$$ (3.30)

Similar to the gLDS-ridge model learning algorithm (Algorithm 1), we optimize eq.(3.30) in a coordinate descent fashion. Since the temporal smoothing regularization only involves C and Z, the update rules for A, R, Q, ξ and Ψ remain the same. The update rules for C and Z are shown as follows:

$$Ĉ=(\mathbf{Y}{\mathbf{Z}}^{\top }){(\mathbf{Z}{\mathbf{Z}}^{\top }+\delta \mathbf{Z}P{\mathbf{Z}}^{\top }+\alpha I_d)}^{-1}$$ (3.31)

$${\mathbf{ẑ}}_1^m={({\mathrm{\Gamma }}_1^m+\lambda A^{\top }A)}^{-1}({\mathrm{\Phi }}_1^m+\lambda A^{\top }{\mathbf{z}}_2^m)$$ (3.32)

$${\mathbf{ẑ}}_t^m={({\mathrm{\Gamma }}_t^m+\lambda A^{\top }A+\lambda I_d)}^{-1}({\mathrm{\Phi }}_t^m+\lambda A^{\top }{\mathbf{z}}_{t+1}^m+\lambda A{\mathbf{z}}_{t-1}^m)$$ (3.33)

$${\mathbf{ẑ}}_{T_m}^m={({\mathrm{\Gamma }}_{T_m}^m+\lambda I_d)}^{-1}({\mathrm{\Phi }}_{T_m}^m+\lambda A{\mathbf{z}}_{T_m-1}^m)$$ (3.34)

where

$${\mathrm{\Gamma }}_t^m=(1+\delta L_{t,t}-\delta W_{t,t})C^{\top }C+\beta I_d$$ (3.35)

$${\mathrm{\Phi }}_t^m=C^{\top }{\mathbf{y}}_t^m+\delta C^{\top }C\sum _{j\ne t}{W}_{t,j}{\mathbf{z}}_j^m$$ (3.36)

The entire learning procedure of our smooth LDS model is similar to Algorithm 1 by replacing eq.(3.18 – 3.21) with eqs.(3.31 – 3.34).

4 Experiments

In this experiments, we (1) qualitatively show the prediction results from our gLDS-smooth model; (2) quantitatively show that the superior predictive performance of models from our framework (gLDS-ridge and gLDS-smooth) compared with traditional LDS learning algorithms (EM and spectral algorithms); (3) stability and sparsification effects achieved by our framework. Experiments are conducted on four real-world datasets across different domains. The hyper parameters (α, β, λ and γ) used in our methods are selected (in all experiments) by the internal cross validation approach while optimizing models’ predictive performances. In the following experiments, we smooth only the pairs of two consecutive forecasts, which leads to the following smoothing coefficient matrix W^m for each sequence m: $w_{ij}^m=1$ if |i − j| = 1; otherwise, $w_{ij}^m=0$.

4.1 Datasets

• Flour price data (flourprice). It is a monthly flour price indices data from [27], which contains the flour price series in Buffalo, Minneapolis and Kansas City, from August 1972 to November 1980.

• Evap data (evap). The evaporation data contains the daily amounts of water evaporated, temperature, and barometric pressure from 10/11/1692 to 09/11/1693 [7]².

• H2O evap data (h2o_evap). It contains six MTS variables: the amount of evaporation, total global radiation, estimated net radiation, saturation deficit at max temperature, mean daily wind speed and saturation deficit at mean temperature [14]³.

• Clinical data (clinical). We test our gLDS on a MTS clinical data obtained from electronic health records of post-surgical cardiac patients in PCP database [8, 19]. We take 500 patients from the database who had their Complete Blood Count (CBC) tests⁴ done during their hospitalization. The MTS data consists of 6 individual CBC lab time series: mean corpuscular hemoglobin concentration, mean corpuscular hemoglobin, mean corpuscular volume, mean platelet volume, red blood cell and red cell distribution width.

In order to get a comprehensive evaluations of the proposed methods, in the following experiments, we vary both the training sizes and the number of hidden states. For flourprice, evap and h2o_evap datasets, we conduct the experiments on both 80% and 90% data for training and use both 5 and 10 as the hidden state size. For clinical data, we have randomly selected 100 patients out of 500 as a test set and used the remaining 400 patients for training the models and vary the hidden states from 10 to 30 with a step increase of 5.

4.2 Evaluation Metric

We use the average mean absolute percentage error (Avg-MAPE) to measure how accurate the predictions are made by the LDS models in MTS forecasting. The Avg-MAPE is defined as follows:

$$\text{Avg}-\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}=\frac{1}{nTN}\sum _{m=1}^N\sum _{l=1}^n\sum _{t=1}^{T_m}|1-{ŷ}_{l,t}^m/y_{l,t}^m|\times 100\%$$

Usually in MTS modeling, the different individual time series are in different scales and simply averaging the error values themselves is not appropriate. Averaging MAPE measures the prediction deviation proportion in terms of the true values, which is more sensible than computing the average of root mean square errors(RMSE), mean square errors(MSE) or mean absolute errors(MAE) of each time series’ forecasts.

4.3 Qualitative Prediction Analysis

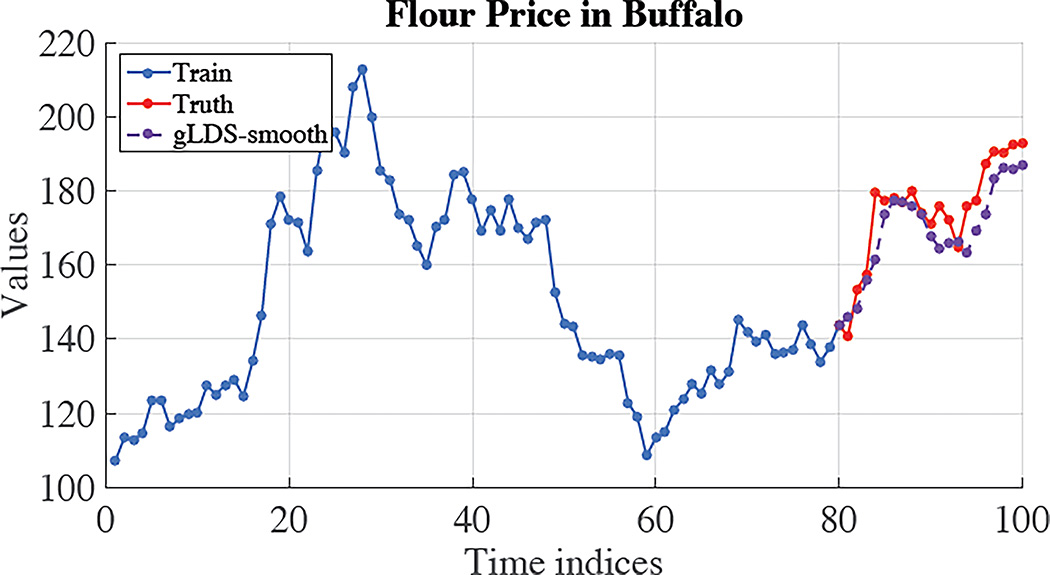
We qualitatively show the prediction effectiveness of our gLDS-smooth model. Figure 1 shows the predictions results for the flour price series in Buffalo. (Due to space limit, more results can be found in the supplemental material). 80% of the MTS is used for training and 20% is used for testing. As we can see from Figure 1, the gLDS-smooth is able to well capture the ups and downs of the time series and makes the accurate predictions.

Figure 1.

Predictions for flour price series in Buffalo.

4.4 Quantitative Prediction Analysis

In this section, we quantitatively compute and compare the prediction accuracy of the proposed methods (gLDS-ridge and gLDS-smooth) with the standard LDS learning approaches: EM (Section 2.2.1) and spectral algorithms (Section 2.2.2). The results are shown in Table 1 and Table 2. Due to the space limit, prediction results results of flourprice and h20_evap datasets are shown in the supplemental material. As we can see, methods based our framework (gLDS-ridge and gLDS-smooth) perform significantly better than all the other methods. Furthermore, due to the smooth effect of the temporal smooth regularization, gLDS-smooth supports better predictions than gLDS-ridge, which gives the best predictive performance.

Table 1.

Average-MAPE results on clinical dataset.

# of states	10	15	20	25	30
Spectral	6.29	6.24	6.32	6.04	6.00
EM	3.97	3.54	3.54	3.53	3.53
gLDS-ridge	3.22	3.21	3.21	3.21	3.21
gLDS-smooth	3.21	3.20	3.20	3.19	3.19

Table 2.

Average-MAPE results on evap dataset.

	Training: 80%		Training: 90%
# of states	5	10	5	10
Spectral	24.62	24.85	25.08	26.28
EM	17.68	14.45	16.32	17.35
gLDS-ridge	10.58	10.35	13.60	14.05
gLDS-smooth	10.35	10.27	13.39	13.68

4.5 Stability Effects of gLDS-stable

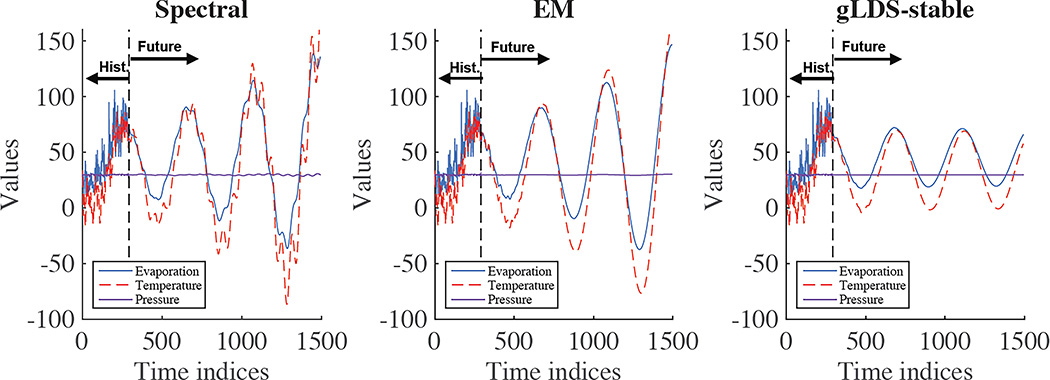
In this section, similar to [2], we show the stability effects of the gLDS-stable model learned using our framework by generating the simulated sequences in the future. The results of evap are shown in Figure 2. Due to the space limit, results of flourprice, h20_evap and clinical datasets are shown in the supplemental material. We can found that in Figure 2, the LDS models learned from EM and spectral algorithms fail to guarantee the system stability and the generated values go to infinities in the future.

Figure 2.

Training data and simulated sequences from gLDS-stable model in evap data. “Hist.” represents the historical observations and “Future” represents the sequence generated by LDS.

4.6 Sparsification Effects of gLDS-low-rank

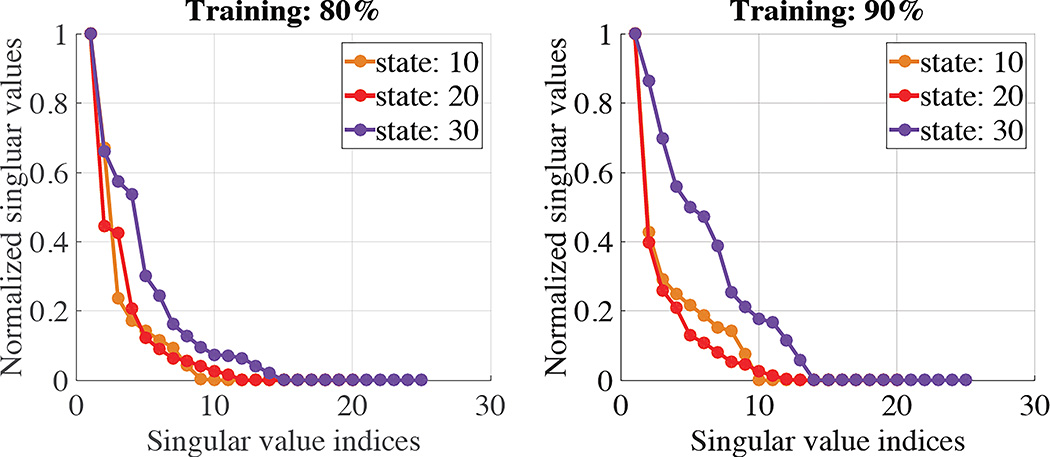
In this section, we show the sparsification effects of the gLDS-low-rank model learned using our framework. The gLDS-low-rank model is able to identify the intrinsic dimensionality of the hidden state space. The results are shown in Figure 3. As we can see, similar to the experimental results in [20], gLDS-low-rank model is able to find the intrinsic dimension of the hidden state space. Due to the space limit, results of other datasets are shown in the supplemental material.

Figure 3.

Intrinsic dimensionality recovery of the hidden state space in evap dataset.

5 Conclusion

In this paper, we presented a generalized LDS framework for learning LDS models from a collection of MTS sequences. Compared to the traditional LDS learning algorithms, the advantages of our gLDS framework are: (1) the LDS models can be learned efficiently from multiple MTS sequences; (2) constraints on both the hidden states and the parameters can be easily incorporated into the learning process; (3) it is able to support accurate MTS prediction. Furthermore, we propose a novel temporal smoothing regularization for learning the LDS models, which stabilizes the model, its learning algorithm and predictions it makes. Experimental results on several real-world datasets demonstrated that (1) gLDS are able to achieve better time series predictive performance when compared to other LDS learning algorithms; (2) the proposed temporal smoothing regularization encourages more stable and accurate predictions; and (3) constraints can be directly integrated in the learning process and special designed system properties such as stability, low-rankness can be easily achieved.